A Memetic Algorithm with a Novel Repair Heuristic for the Multiple-Choice Multidimensional Knapsack Problem

Abstract

We propose a memetic algorithm for the multiple-choice multidimensional knapsack problem (MMKP). In this study, we focus on finding good solutions for the MMKP instances, for which feasible solutions rarely exist. To find good feasible solutions, we introduce a novel repair heuristic based on the tendency function and a genetic search for the function approximation. Even when the density of feasible solutions over the entire solution space is very low, the proposed repair heuristic could successfully change infeasible solutions into feasible ones. Based on the proposed repair heuristic and effective local search, we designed a memetic algorithm that performs well on problem instances with a low density of feasible solutions. By performing experiments, we could show the superiority of our method compared with previous genetic algorithms.

1. Introduction

The 0–1 knapsack problem (KP) aims to pick up items for a knapsack to maximize the profit sum of the selected items, as long as the weight sum of the selected items does not exceed the weight capacity b of the knapsack. In formal notation, the KP aims to maximize ${\sum }_{i=1}^n{v}_i{x}_i$ subject to ${\sum }_{i=1}^n{w}_i{x}_i\le b$, where n is the number of items, $v_i$ is the profit of the i-th item, $w_i$ is the weight of the i-th item and $x_i\in \{0,1\}$. The multiple-choice multidimensional knapsack problem (MMKP) is a variant of the knapsack problem with multiple capacity constraints and multiple-choice conditions [1]. In MMKP, there are n classes of items. For class i, there are $r_i$ items, and each item j has a non-negative profit value of $v_{ij}$, a non-negative weight vector of ${\mathbf{w}}_{ij}=(w_{ij}^1,w_{ij}^2,\dots ,w_{ij}^m)$, and $b_k$ is the k-th weight capacity of the knapsack ($k=1,2,\dots ,m$), where m is the number of capacity constraints. The formal definition of the MMKP is described as follows [1]:

$$\begin{array}{cc}\hfill \mathrm{maximize}& \sum _{i=1}^n\sum _{j=1}^{r_i}{v}_{ij}{x}_{ij}\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \sum _{i=1}^n\sum _{j=1}^{r_i}{w}_{ij}^k{x}_{ij}\le b_k\mathrm{for}k\in \{1,2,\dots ,m\},\hfill \\ \hfill & \sum _{j=1}^{r_i}{x}_{ij}=1\mathrm{for}i\in \{1,2,\dots ,n\},\mathrm{and}\hfill & \hfill \\ \hfill & x_{ij}\in \{0,1\}\mathrm{for}i\in \{1,2,\dots ,n\}\mathrm{and}j\in \{1,2,\dots ,r_i\}.\hfill \end{array}$$

(1)

In the MMKP, only one item can be selected from each class. When the j-th item in the i-th class is added to the knapsack, $x_{ij}$ becomes 1, and for the other j’s, $x_{ij}$ is 0. The objective of the MMKP is to maximize the profit sum of the selected items satisfying the capacity constraints. The MMKP has various real-world applications such as the redundancy allocation problem for series-parallel systems [2], quality adaptation and admission control in multimedia services [3], quality-of-service problem for systems that must satisfy multiple requirements [4], and joint resource allocation and routing scheme in networks with cooperative relays [5,6]. A large number of other resource allocation problems can also be transformed into MMKPs. The readers can refer to [7] for more details.

The MMKP is NP-hard in the strong sense [8]. Therefore, it is not easy to develop efficient algorithms for the MMKP. Many studies have been proposed to solve the MMKP. Moser et al. [8] first proposed a heuristic algorithm for the MMKP, which is based on Lagrangian relaxation [9,10]. Toyoda [11] proposed a method based on the concept of the aggregate necessary resource for the multidimensional knapsack problem (MKP), and Khan et al. [3] proposed its improved variant for the MMKP. Chefi and Hifi proposed a column generation algorithm to solve the MMKP in [12], and they also proposed three hybrid heuristic algorithms for relatively large-scale MMKP instances in [13]. Akbar et al. [14] proposed a heuristic that constructs convex hulls to reduce the search space. Sbihi [15] proposed an exact algorithm for the MMKP, which adopted a branch-and-bound procedure and best-first search strategy. Parra-Hernandez and Dimopoulos [7] extended the idea of their heuristic approach for the MKP to the MMKP. Over the last 10 years, studies of the MMKP have focused on iterative heuristics [16,17,18,19], branch-and-bound methods [20,21], Lagrangian relaxation [22,23,24], linear programming relaxation [25], reformulation/reduction [25,26,27,28], Pareto-algebraic heuristics [20,29], approximate core [30], core-based exact algorithm [31], two-phase kernel search [32], meta-heuristics such as genetic algorithm [33], swarm intelligence [23,34,35,36,37], estimation of distribution algorithm [38], simulated annealing [39], tabu search [40], etc.

When the constraints of the MMKP are strong, it is very hard to even find feasible solutions. For these kinds of problems to which feasible solutions that satisfy the constraints are difficult to find, applying repair methods can be effective.

Repair methods generally mean strategies that change infeasible solutions into feasible ones under evolutionary computation frameworks. There have been many studies related to various repair strategies [41,42,43,44,45]. In this study, a novel repair heuristic based on the tendency function and an effective memetic algorithm (a memetic algorithm is an extension of the traditional genetic algorithm using a local search technique [46]) are proposed for the MMKP. We propose a repair heuristic that uses a genetic algorithm which differs from a memetic algorithm for solving MMKP and the tendency function. The tendency function is a function specifically designed to suit the characteristics of MMKP for the proposed repair heuristic, and it is defined as one of the main parts of our repair heuristic. It is used for transforming infeasible solutions into feasible ones, and uses tendency parameters to analyze the solution space of the given instance. A genetic algorithm is adopted to attain optimal tendency parameters. Our memetic algorithm combined with the repair heuristic searches both the feasible solution space and the infeasible one. Experimental results demonstrate that our memetic approach performs better than previous genetic algorithms.

The remainder of this paper is organized as follows. Section 2 presents related work based on genetic algorithms. We propose the tendency function and a repair heuristic derived from it in Section 3. Section 4 describes our memetic algorithm combined with the repair heuristic. Experimental results are given in Section 5. Finally, conclusions are presented in Section 6.

2. Related Work

Parra-Hernandez and Dimopoulos [7] insisted that most heuristic algorithms, Lagrangian relaxation, branch-and-bound methods, and guided local searches for the MMKP have two defects: first, when the constraints of the MMKP are relatively strong, heuristic algorithms easily return local optima and may occasionally not find feasible solutions; second, the time costs needed by these algorithms are quite large.

In this study, we focused on the first problem. A genetic algorithm (GA) [47], which is a global search method based on natural selection, can effectively escape local optima. There have been many GAs for the KP and MKP but only three studies for the MMKP. Liu [48] proposed a simple GA for the MMKP, Rasmy et al. [34] applied various mutation operators over a simple GA, and Zhou and Luo [49] proposed a GA based on multiple populations (MPGA). The above GAs attempted to find good feasible solutions that satisfied the constraints of the MMKP [7]. However, GAs can only find good feasible solutions when the constraints of the MMKP are weak. The MPGA attempted to resolve this problem through multiple populations, which consists of separate populations of feasible solutions and infeasible ones. This could find good feasible solutions even under strong MMKP constraints.

In this paper, the tendency function, repair heuristic, and memetic algorithm are introduced to solve the MMKP. Our repair heuristic searches the solution space and then finds appropriate repair rules for transforming infeasible solutions to feasible ones. Our memetic algorithm attempts to improve the quality of feasible solutions using a repair heuristic. In the next section, the tendency function and repair heuristic derived from the function are described in detail.

3. Design of a Repair Heuristic Algorithm

3.1. Tendency Function and Repair Heuristic Algorithm

We present a constructive procedure (CP) to find a feasible solution for the MMKP which considers the violating amount $\mathsf{\Delta }{w}^k$. The initial solution is generated by choosing the most valuable item from each class. The solution is selected considering no constraints, so it can be infeasible. That is, for some ks, the constraint ${\sum }_{i=1}^n{\sum }_{j=1}^{r_i}{w}_{ij}^k{x}_{ij}\le b_k$ may not be satisfied. $\mathsf{\Delta }{w}^k$ means the violating amount of the k-th constraint, ${\sum }_{i=1}^n{\sum }_{j=1}^{r_i}{w}_{ij}^k{x}_{ij}-b_k$. The procedure attempts to reduce $\mathsf{\Delta }{w}^k$ by changing an item in the most suitable dimension k [1]. If $\mathsf{\Delta }{w}^k$ is negative or equal to zero for every k, the solution is feasible. CP is described by the steps of Algorithm 1 [7]. This greedy procedure attempts to repair the most violated dimension $k_0$ which makes $\mathsf{\Delta }{w}^k$ the largest.

In general, CP finds a feasible solution when the density of the feasible solution is high (Figure 1), but it tends to suffer when the solution space is randomly created and there is no tendency, which means that the density of the feasible solutions is very low. Hence, we designed a more sophisticated repair heuristic using a new tendency utility function concept. Instead of focusing on the most violated dimension, this method tries to find the most suitable class and item to change. Suppose that there is such a function that tells us which class and item pair has the largest tendency to make an given solution feasible when the solution is changed with them. We devised a kind of function, the tendency utility function described in Algorithm 2. It has six parameters which in this study are referred to as tendency parameters. Tendency parameters can be considered as the weights of changing the status of the dimension and the tendency utility can be considered as the weighted sum of these tendency parameters. It is assumed that the appropriate values of tendency parameters are previously determined before calculating the value of the tendency utility function. We cannot just obtain the appropriate values of tendency parameters without analysis, so we also designed a genetic algorithm for finding the appropriate values of tendency parameters. This genetic algorithm is different from a memetic algorithm for solving the MMKP, which is subsequently described in Section 4.

Using tendency utility function and tendency parameters, we designed a repair heuristic based on the tendency function (RHTF). Algorithm 3 shows the steps of the RHTF. If appropriate values for tendency parameters are previously obtained and the corresponding tendency utility function is well defined, RHTF attempts to maximize the tendency utility by changing an item. This process is repeatedly applied to attain a feasible solution. A high tendency utility increases the probability of success in repairing infeasible solutions. RHTF repeatedly applies the tendency function described in Algorithm 3 to attain a feasible solution. The tendency function is also used to define a fitness function in our genetic approximation of the tendency function and works as a repair method in our memetic algorithm.

Algorithm 1 The constructive procedure (CP) for finding a feasible solution.

procedureCP(an instance of the MMKP)     for $i\leftarrow 1,2,\dots ,n$ do         $v_i\leftarrow max\{v_{ij}$ for $j=1,2,\dots ,r_i\}$;         $S_i\leftarrow j_i$;         $\varphi \left[i\right]\leftarrow j_i;x_{i\varphi \left[i\right]}\leftarrow 1$;         $w_k\leftarrow {\sum }_{i=1}^n{w}_{i\varphi \left[i\right]}^k$ for $k=1,2,\dots ,m$                                                        ▹$w_k$: the accumulated resources for constraint k     end for     $S\leftarrow (S_1,S_2,\dots ,S_n)$;     while $w_k>b_k$ for $k=1,2,\dots ,m$ do                                    ▹ destructive phase         $k_0\leftarrow \underset{1\le k\le m}{argmax}\left\{w_k\right\}$;         $i_0\leftarrow \underset{1\le i\le n}{argmax}\left\{w_{i{j}_i}^{k_0}\right\}$;         $\varphi \left[i_0\right]\leftarrow j_{i_o}$; $x_{i_0\varphi \left[i_0\right]}\leftarrow 0$;         $w_k\leftarrow w_k-w_{i_0\varphi \left[i_0\right]}^k$ for $k=1,2,\dots ,m$;         for $j\leftarrow 1,2,\dots ,r_{i_0}$ do                                                         ▹ constructive phase            if $\exists j\ne j_{i_0}$ and $w_k+w_{i_{0}j}^k<b_k$ for $k=1,2,\dots ,m$ then                $j_{i_0}\leftarrow j$; $\varphi \left[i_0\right]\leftarrow j_{i_0}$; $x_{i_{0}j}\leftarrow 1$;                $w_k\leftarrow w_k+w_{i_{0}j}^k$ for $k=1,2,\dots ,m$;                $S\leftarrow (\varphi \left[i_0\right];\varphi \left[i\right],\forall i\ne i_0,i=1,2,\dots ,n)$;                if the obtained solution S is feasible then return S;                end if            end if         end for         $j_{i_0}^{{}^{\prime }}\leftarrow \underset{1\le j\le r_{i_0}}{argmin}\left\{w_{i_{0}j}^{k_0}\right\};$         if the obtained solution S is infeasible then            $j_{i_0}\leftarrow j_{i_0}^{{}^{\prime }};\varphi \left[i_0\right]\leftarrow j_{i_0};x_{i_0\varphi \left[i_0\right]}\leftarrow 1$;         end if     end while     return S; end procedure

Algorithm 2 Tendency parameters and tendency utility function.

structure TendencyParameter { integer $mmi$, $mmd$, $ppi$, $ppd$, $mp$, $pm$; } procedureTendencyUtility(TendencyParameter $tp$, chromosome s, class c, item r)     $cur$←$s\left[c\right]$;                                                                                                                        ▹ current item     $res$← 0;     for each dimension k ($k=1,2,\dots ,m)$ do         $\mathsf{\Delta }{w}_{c,cur}\leftarrow b_k-w_{c,cur}^k$; $\mathsf{\Delta }{w}_{c,r}\leftarrow b_k-w_{c,r}^k$;         case ($\mathsf{\Delta }{w}_{c,cur}<0$, $\mathsf{\Delta }{w}_{c,r}<0$, $\mathsf{\Delta }{w}_{c,cur}\ge \mathsf{\Delta }{w}_{c,r}$)                $res\leftarrow res+tp.mmi$ × |$\mathsf{\Delta }{w}_{c,cur}-\mathsf{\Delta }{w}_{c,r}$|;         case ($\mathsf{\Delta }{w}_{c,cur}<0$, $\mathsf{\Delta }{w}_{c,r}<0$, $\mathsf{\Delta }{w}_{c,cur}<\mathsf{\Delta }{w}_{c,r}$)                $res\leftarrow res+tp.mmd$ × |$\mathsf{\Delta }{w}_{c,cur}-\mathsf{\Delta }{w}_{c,r}$|;         case ($\mathsf{\Delta }{w}_{c,cur}>0$, $\mathsf{\Delta }{w}_{c,r}>0$, $\mathsf{\Delta }{w}_{c,cur}\ge \mathsf{\Delta }{w}_{c,r}$)                $res\leftarrow res+tp.ppi$ × |$\mathsf{\Delta }{w}_{c,cur}-\mathsf{\Delta }{w}_{c,r}$|;         case ($\mathsf{\Delta }{w}_{c,cur}>0$, $\mathsf{\Delta }{w}_{c,r}>0$, $\mathsf{\Delta }{w}_{c,cur}<\mathsf{\Delta }{w}_{c,r}$)                $res\leftarrow res+tp.ppd$ × |$\mathsf{\Delta }{w}_{c,cur}-\mathsf{\Delta }{w}_{c,r}$|;         case ($\mathsf{\Delta }{w}_{c,cur}<0$, $\mathsf{\Delta }{w}_{c,r}>0$) $res\leftarrow res+tp.mp$ × |$\mathsf{\Delta }{w}_{c,cur}-\mathsf{\Delta }{w}_{c,r}$|;         case ($\mathsf{\Delta }{w}_{c,cur}>0$, $\mathsf{\Delta }{w}_{c,r}<0$) $res\leftarrow res+tp.pm$ × |$\mathsf{\Delta }{w}_{c,cur}-\mathsf{\Delta }{w}_{c,r}$|;     end for     return $res$; end procedure

Algorithm 3 The procedure for repairing an infeasible solution with the tendency function: RHTF.

procedureRHTF(TendencyParameter $tp$, chromosome s)     while stop condition is met do         Tendency($tp$,s);         if s is feasible then return s;         end if     end while end procedure procedureTendency(TendencyParameter $tp$, chromosome s)     if s is infeasible then         $(c_{max},r_{max})\leftarrow \underset{(1\le c\le n,1\le r\le r_c)}{argmax}\left\{\mathrm{TendencyUtility}(tp,s,c,r)\right\}$;                                            ▹ Change an item in s that makes the tendency utility the best.         $s\left[c_{max}\right]\leftarrow r_{max}$;     end if     return s; end procedure

3.2. Genetic Approximation of Tendency Function

A genetic approximation of the tendency function (GATF) was designed to provide the optimal tendency parameters to RHTF, which searches the repair rules to find feasible solutions. The GATF provides optimal tendency parameters to the tendency utility function described in the above subsection and our memetic algorithm, which is described later. It uses the RHTF to define a fitness function for optimizing the tendency parameters. We describe the proposed GATF in Algorithm 4.

Algorithm 4 The pseudo-code of our genetic approximation of the tendency function: GATF.

procedureGATF(given solution s)     Randomly create initial population for tendency parameters;     while stop condition is met do         Choose $paren{t}_1$ and $paren{t}_2$ from population by proportional selection;         Make offspring by recombining $paren{t}_1$ and $paren{t}_2$ using uniform crossover;         Mutate offspring by swapping randomly chosen two genes;         Get the feasibility of offspring from RHTF(offspring, given solution s) in Algorithm 3;         Replace an individual in the population with offspring;     end while end procedure

• Representation: we represent a solution using a six-integer array since the objective of GATF is to find the appropriate values of six tendency parameters. Array cells correspond to $mmi$, $mmd$, $ppi$, $ppd$, $mp$, and $pm$, which are the members of tendency parameters in Algorithm 2.
• Crossover: we used a uniform crossover method [50]. Each member of the tendency parameters is completely independent, and hence, the crossover is performed regardless of gene positions.
• Mutation: Two randomly chosen genes among the six genes are swapped.
• Fitness: we determine the fitness of a chromosome by examining the degree of changing infeasible solutions to feasible ones by applying the RHTF using the tendency parameters, which are the values of the given chromosome. For a chromosome, we set its fitness value to the repair success rate $\left(\mathrm{i}.\mathrm{e}.,\frac{\#success}{\#trials}\right)$.

4. Memetic Algorithm for the MMKP

In this section, we propose a memetic algorithm for the MMKP (MAMMKP). Algorithm 5 shows the template of our memetic algorithm.

Algorithm 5 The pseudo-code of our memetic algorithm for the MMKP: MAMMKP.

procedureMAMMKP     Randomly create initial population;     while stop condition is met do         Choose $paren{t}_1$ and $paren{t}_2$ from population by proportional selection;         Make offspring by recombining $paren{t}_1$ and $paren{t}_2$ using multi-cut circular crossover;         Mutate offspring by changing randomly chosen t genes;         Repair offspring using GATF(offspring) in Algorithm 4;         Locally optimize offspring by a variant 3-Opt;         Replace an individual in the population with offspring;     end while end procedure

4.1. Local Optimization

MAMMKP uses a variant of 3-Opt [51] for optimizing feasible solutions. In the MMKP, there are n classes and for each class i, there are $r_i$ possible choices of items. Let $\mathbf{x}$ be a feasible solution and $I_s$ be an index of selected item of $\mathbf{x}$ in class s. This means that $x_{s{I}_s}=1$ and $x_{sj}=0$ for $j\ne I_s$. The local optimization algorithm considers all three-class combinations out of n classes. For a three-class combination $(s,t,u)$, the local optimization verifies all possible combinations of items for these three classes, leaving the items of the other classes as they are in the original feasible solution $\mathbf{x}$. After all the possible combinations are verified, the best solution among them is recorded. The verification is performed for all three-class combinations, the best three-class combination $(s_0,t_0,u_0)$ is chosen, and the items of these three classes $I_{s_0}$, $I_{t_0}$, and $I_{u_0}$ are replaced by the best values. After determining the optimal values of $I_{s_0}$, $I_{t_0}$, and $I_{u_0}$, the algorithm considers three-class combinations out of the remaining classes except $(s_0,t_0,u_0)$ again. This process continues until there are no more than three classes left to consider.

Although the proposed local optimization algorithm considers three-class combinations, better solutions can be obtained by considering four-class combinations or five-class combinations. The more combinations are considered, the more areas of the solution space are searched, and consequently, the probability of finding better solutions increases. However, verifying all the possible four-class or five-class combinations takes an excessive amount of time. The complexity of the proposed 3-Opt local optimization process has an upper bound $O(\left(\genfrac{}{}{0pt}{}{n}{3}\right)\times r^3\times \frac{n}{3})$, where r is the maximum of the $r_i$’s, since there are $\left(\genfrac{}{}{0pt}{}{n}{3}\right)$ three-class combinations, each of which has at most $r^3$ alternative choices, and the number of iterations is less than $\frac{n}{3}$. Similarly, the upper bound of the complexity of the 4-Opt local optimization is $O(\left(\genfrac{}{}{0pt}{}{n}{4}\right)\times r^4\times \frac{n}{4})$, and it is too costly. Hence, we adopted 3-Opt local optimization in this study, considering the balance between time and solution quality.

4.2. Genetic Framework

• Representation: a solution is represented by a length-n integer array. The i-th gene means the index of the i-th class item.
• Crossover: a simple multi-cut circular crossover is adopted.
• Mutation: t genes are randomly changed. The value of t is limited to five or less.
• Repair: we presented a repair heuristic with a tendency function approximated by GATF in Section 3. We repair infeasible solutions using the proposed repair heuristic.
• Fitness: if a given solution is feasible, its fitness value is obtained by computing the objective value of the MMKP. However, if a feasible solution is not obtained from the repair heuristic, the fitness value is set to $-\frac{1}{m}{\sum }_{k=1}^m\frac{w_k}{b_k}$, where m is the number of constraints, and $w_k$ indicates the weight sum of the selected items on the k-th resource constraint. Unlike the previous method [49], in the case of a violation, we made the fitness value negative. As this method, strategies to give penalty to infeasible solutions have generally been used to deal with infeasible solutions in GAs [52,53,54]. The method makes the fitness value of an infeasible solution always smaller than the fitness value of a feasible one. According to the proposed fitness function, the greater the number of violated constraints is and the greater the degree of violation is, the smaller the fitness value is. This increases the probability of selecting a feasible solution with a positive fitness value and reduces the probability of selecting an infeasible solution with a negative fitness value. By doing this, we can maintain consistency that the solution with a larger fitness value is always superior to that with a smaller fitness value. This method is also useful for dealing with two different kinds of solutions (feasible solutions and infeasible ones) in a population.
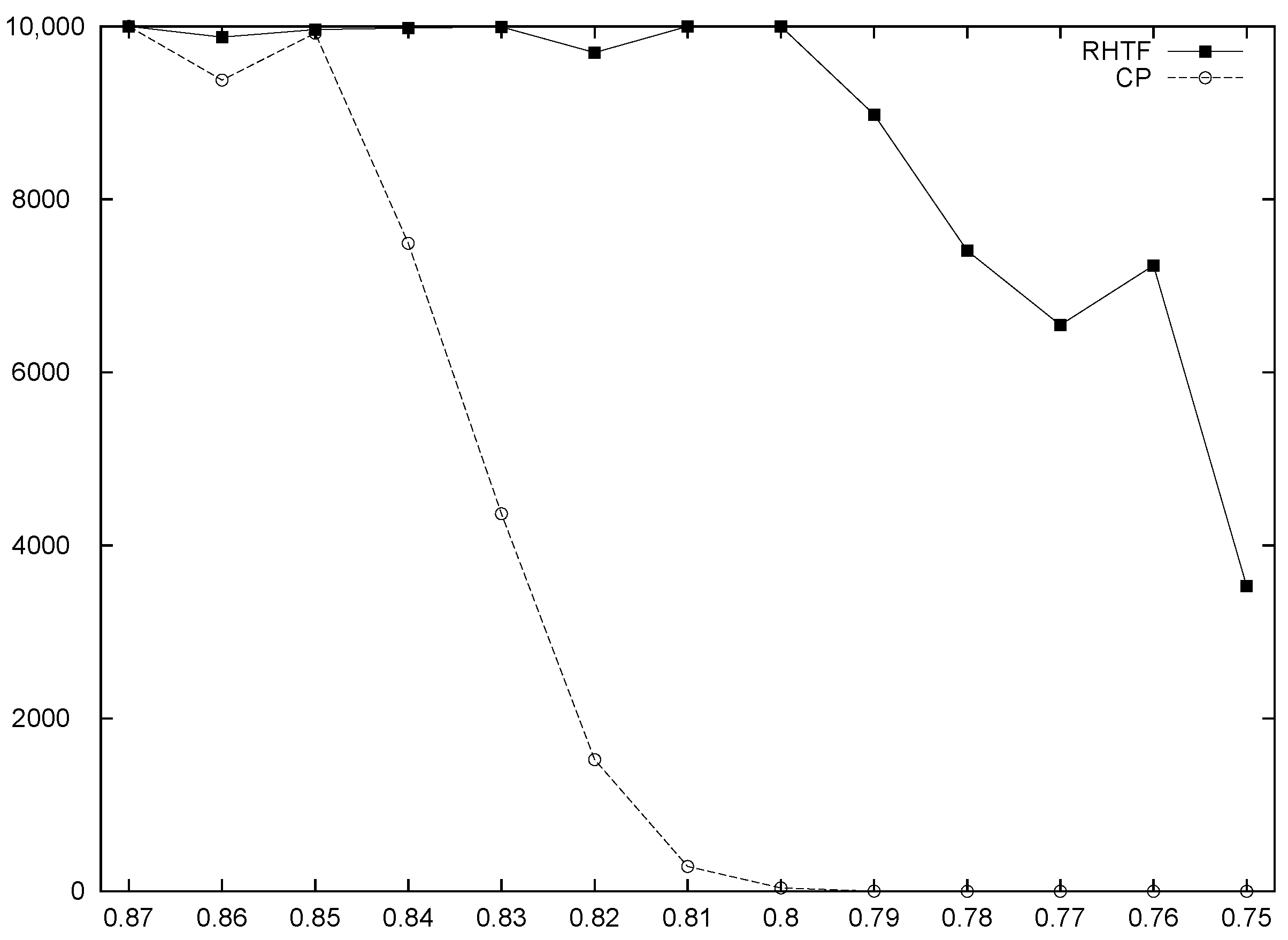
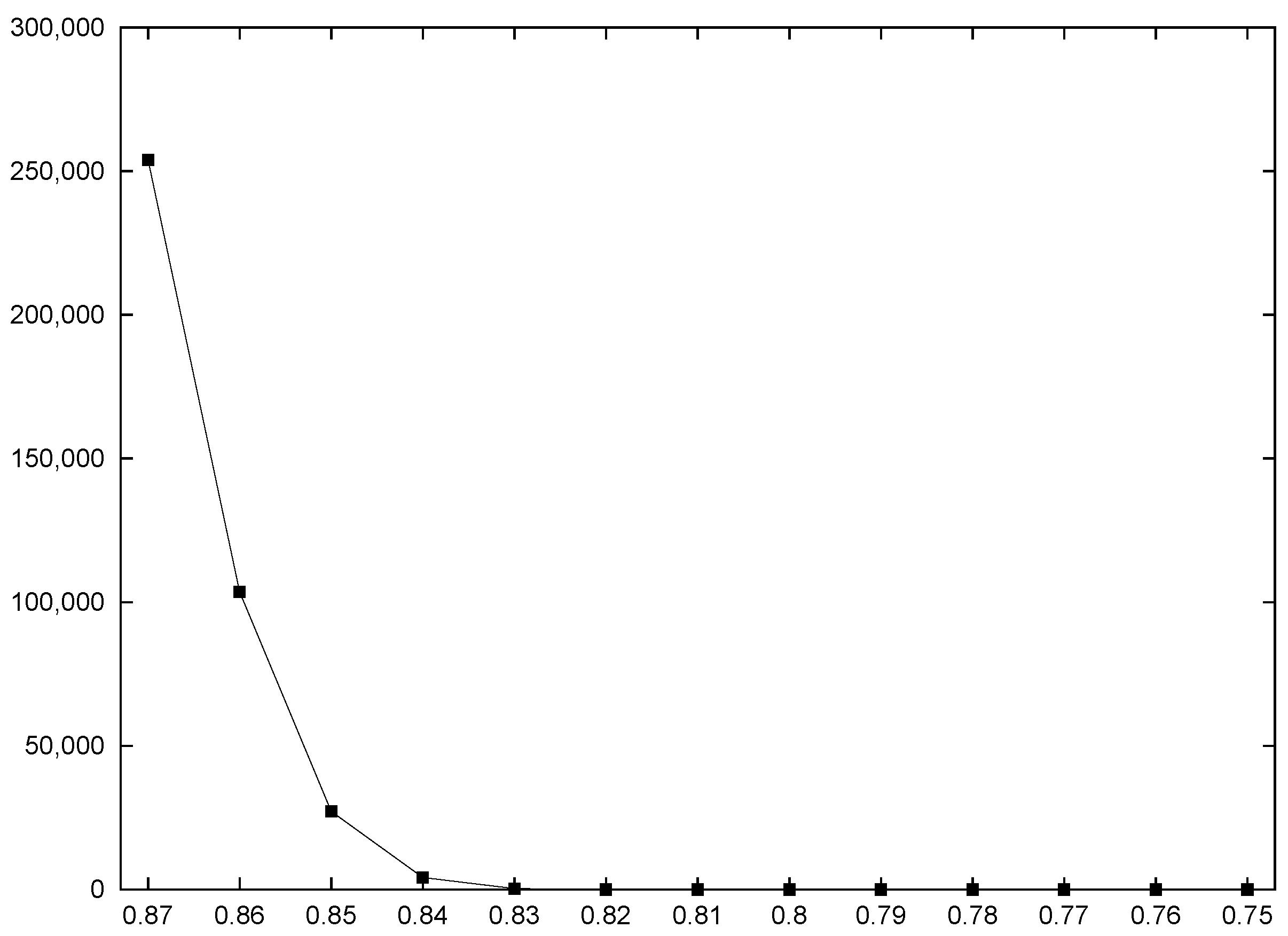
• Replacement: RHTF is most likely to find feasible solutions from infeasible ones even if the density of feasible solutions is very low. However, as shown in Figure 2, the success rate decreases as the density of feasible solutions decreases. When the RHTF fails to repair infeasible solutions, GATF attempts to transform infeasible solutions into feasible ones. Zhou [49] and Htiouech et al. [17] demonstrated that searching both feasible and infeasible solution spaces is necessary for the global optimum. In addition, we do not remove infeasible solutions from the population. Instead of a multi-population, we use the fitness value for a single population that we previously introduced. Therefore, the population is only changed by the fitness values, regardless of the feasibility of the solutions. This is possible because the fitness values of infeasible solutions are always negative. However, if the whole population is filled with feasible solutions, the memetic algorithm may lose the possibility of the performance improvement with the help of infeasible solutions, as we can see in the previous method [49]. To avoid premature convergence, we used a generational GA. The remaining 70% of individuals in the population, except for the top 30%, were replaced with new solutions. By this replacement, the memetic algorithm can avoid falling into local optima.

5. Experiments

5.1. Experimental Settings

For performance comparison, we tested all the problem instances used in [49]. These are three difficult test instances of mknapcb7, mknapcb8, and mknapcb9 provided by the OR library [55]. We conducted experiments with various constraint strength values [7] from 0.72 to 0.90. First, we investigated the density of feasible solutions by counting the number of feasible solutions among ${10}^6$ randomly generated solutions. Figure 2 shows the results for the problem instance mknapcb8. The smaller the constraint strength value is, the lower the density of feasible solutions. If the f value (constraint strength) is smaller than 0.83, the probability that a given solution is feasible becomes almost zero.

Second, we compared the performances of CP and RHTF by counting the number of cases in which infeasible solutions are changed to feasible ones among 10,000 trials. However, we note that the input of CP was originally the set of the most valuable items in the classes; however, in this MMKP instance, the values are not concerned with weights. Therefore, we input randomly created infeasible solutions. Figure 1 shows the results for the problem instance mknapcb8. In this figure, we can see that the proposed repair heuristic based on the tendency function (RHTF) performs better than the CP. In particular, when the f value is smaller than 0.8, the CP rarely finds feasible solutions, while RHTF performs well, showing relatively high success rates.

The population size and the number of generations in our GA for the approximation of the tendency function (GATF) were set to 30 and 300, respectively. In the GA, the number of feasible solutions for obtaining the fitness of a solution (tendency parameter) was set to 30. The maximum number of iterations of the tendency function in the RHTF was also set to 30.

Our code is written in C++ and ran on Linux Ubuntu 18.04.6 using the CPU of AMD Ryzen Threadripper 2990WX (32-Core) Processor 3.0 GHz and the memory of 64 GB.

5.2. Performance of the RHTF

The results comparing the CP and RHTF is given in Figure 1. This shows that the RHTF is more powerful than the CP in almost all fs. When the density of feasible solutions is below 3%, the CP fails but RHTF creates feasible solutions with a success rate of approximately 95%. Even when the density of feasible solutions is extremely low (f is $0.75$), RHTF transforms infeasible solutions into feasible ones with a success rate of nearly 40%.

5.3. Performance of the MAMMKP

We compared MAMMKP with three state-of-the-art methods, HMMKP, LGA, and MPGA, previously proposed in other studies. The experimental results of HMMKP, LGA, and MPGA are obtained from [7,48,49], respectively. In MAMMKP, the population size and number of generations were set to 200 and 500, respectively. MAMMKP terminates when 70% of the top 30% of individuals in the population are the same. For each test instance, three or four different values of f were set—where f represents the constraint strength [7].

The experimental results are given in

Table 1. Experimental results on the problem instance mknapcb7.

f	Test Set	HMMKP [7]	LGA [48]			MPGA [49]			MAMMKP
			Max	Ave	Min	Max	Ave	Min	Max	Ave	Min	CPU *
0.90	0	17,510	18,627	18,535.8	18,524	18,627	18,549.1	18,524	18,627	18,627.0	18,627	8
	1	17,948	18,081	18,077.0	17,981	18,081	18081.0	18,081	18,081	18,081.0	18,081
	2	17,049	17,688	17,688.0	17,688	17,688	17,688.0	17,688	17,688	17,688.0	17,688
	3	17,833	17,935	17,935.0	17,935	17,935	17,935.0	17,935	17,935	17,935.0	17,935
	4	17,315	18,550	18,532.8	18,483	18,550	18,548.7	18,483	18,550	18,550.0	18,550
	5	18,318	18,707	18,639.3	18,608	18,707	18,705.1	18,614	18,707	18,707.0	18,707
	6	18,045	18,141	18,135.8	18,107	18,141	18,140.6	18,119	18,141	18,141.0	18,141
	7	17,301	18,122	18,122.0	18,122	18,122	18,122.0	18,122	18,122	18,122.0	18,122
	8	17,563	18,881	18,821.9	18,799	18,881	18,869.1	18,803	18,881	18,881.0	18,881
	9	16,691	17,286	17,263.7	17,184	17,286	17,239.1	17,184	17,286	17,286.0	17,286
0.84	0	15,617	17,447	17,396.3	17,335	17,482	17,443.1	17,351	17,482	17,478.5	17,447	27
	1	15,951	17,025	17,008.8	16,855	17,120	17,026.9	17,025	17,120	17,063.0	17,025
	2	14,080	16,655	16,473.4	16,292	16,655	16,607.8	16,421	16,655	16,655.0	16,655
	3	14,876	16,986	16913.9	16,805	17,041	16,991.5	16,846	17,041	17,041.0	17,041
	4	15,595	17,531	17,531.0	17,531	17,531	17,531.0	17,531	17,531	17,531.0	17,531
	5	15,791	17,742	17,664.0	17,546	17,742	17,671.6	17,602	17,742	17,723.8	17,716
	6	15,484	17,408	17,323.0	17,250	17,425	17,394.9	17,385	17,425	17,425.0	17,425
	7	14,963	16,837	16782.5	16,692	16,985	16,855.9	16,774	16,985	16,985.0	16,985
	8	16,160	17,763	17,751.9	17,625	17,763	17,759.5	17,616	17,763	17,763.0	17,763
	9	13,098	16,325	16,235.1	16,131	16,325	16,323.6	16,289	16,325	16,316.4	16,254
0.80	0	N/A	15,597	15,333.5	14,946	15,799	15,559.6	15,404	15,799	15,680.0	15,680	61
	1		15,816	15,599.4	15,488	15,783	15,724.6	15,665	15,816	15,775.2	15,735
	2		15,469	14,954.5	14,698	15,503	15,410.3	14,951	15,503	15,496.2	15,469
	3		15,869	15,722.6	15,381	15,869	15,822.3	15,709	16,015	16,015.0	16,015
	4		16,300	16,211.9	15,694	16,300	16,300.0	16,300	16,300	16,300.0	16,300
	5		16,742	16,535.4	16,425	16,742	16,742.0	16,742	16,742	16,742.0	16,742
	6		16,045	15,889.7	15,700	16,401	16,088.8	15,966	16,401	16,151.8	16,045
	7		15,029	14,883.5	14,701	15,290	15,015.0	14,836	15,290	15,169.2	15,029
	8		16,564	16,511.0	16,401	16,564	16,559.9	16,541	16,564	16,564.0	16,564
	9		14,863	14,732.8	14,567	15,033	14,862.1	14,772	15,033	14,994.1	14,863

* Average CPU seconds on each run.

,

Table 2. Experimental results for the problem instance mknapcb8.

f	Test Set	HMMKP [7]	LGA [48]			MPGA [49]			MAMMKP
			Max	Ave	Min	Max	Ave	Min	Max	Ave	Min	CPU *
0.90	0	45,493	45,982	45,981.0	45,931	45,982	45,982.0	45,982	45,982	45,982.0	45,982	27
	1	47,130	47,291	47,278.4	47,234	47,291	47,291.0	47,291	47,291	47,291.0	47,291
	2	45,390	45,673	45,643.0	45,596	45,673	45,658.6	45,616	45,673	45,673.0	45,673
	3	45,810	45,806	45,804.2	45,804	45,810	45,808.0	45,804	45,810	45,810.0	45,810
	4	45,270	45,361	45,334.3	45,295	45,361	45,358.8	45,317	45,390	45,390.0	45,390
	5	46,611	46,611	46,611.0	46,611	46,611	46,611.0	46,611	46,611	46,611.0	46,611
	6	46,064	46,375	46,375.0	46,375	46,375	46,375.0	46,375	46,375	46,375.0	46,375
	7	45,450	46,491	45,472.2	45,459	45,491	45,486.1	45,459	45,491	45,491.0	45,491
	8	47,156	47,159	47,159.0	47,159	47,159	47,159.0	47,159	47,159	47,159.0	47,159
	9	45,859	46,149	46,148.6	46,139	46,149	46,148.8	46,139	46,149	46,149.0	46,149
0.80	0	38,523	43,230	42,980.0	42,706	43,487	43,209.9	42,872	43,530	43,460.2	43,394	356
	1	41,185	44,696	44,459.9	44,261	44,843	44,629.9	44,450	44,904	44,838.6	44,779
	2	41,259	43,237	42,938.4	42,666	43,365	43,108.3	42,806	43,388	43,365.1	43,290
	3	40,066	42,825	42,545.9	42,343	43,011	42,778.7	42,513	43,114	43,001.6	42,926
	4	38,262	43,124	42,898.3	42,688	43,308	43,040.2	42,726	43,368	43,368.0	43,368
	5	39,670	43,277	42,949.0	42,600	43,486	43,258.2	42,993	43,510	43,462.5	43,298
	6	38,547	43,675	43,415.6	43,088	43,799	43,574.6	43,330	43,823	43,798.9	43,750
	7	39,445	42,218	41,987.7	41,603	42,520	42,225.2	41,957	42,529	42,458.5	42,321
	8	40,954	44,485	44,173.5	43,955	44,713	44,446.4	44,006	44,714	44,644.0	44,603
	9	39,834	43,426	43,132.1	42,693	43,582	43,380.2	43,062	43,618	43,535.7	43,489
0.75	0	N/A	38,149	37,576.9	36,895	38,933	38,391.6	37,519	39,171	39,160.8	38,967	1251
	1		39,720	38,732.8	37,572	40,105	39,704.1	38,946	40,334	40,197.1	39,960
	2		39,000	38,208.3	37,687	39,147	38,798.0	38,392	39,271	39,207.4	39,204
	3		38,435	37,873.5	37,349	38,826	38,442.9	38,013	38,905	38,754.2	38,573
	4		38,508	37,850.3	37,059	38,508	38,728.0	38,201	39,438	39,205.6	39,019
	5		37,444	36,264.8	35,156	37,829	37,003.0	35,777	38,090	37,683.9	37,254
	6		37,536	36,587.9	35,356	38,475	37,592.2	36,747	38,706	38,339.8	38,016
	7		37,833	37,464.8	37,054	38,322	37,925.2	37,632	38,324	38,184.3	38,096
	8		38,910	38,009.4	36,874	39,647	38,911.9	38,240	39,695	39,287.4	39,014
	9		36,936	36,112.4	35,363	37,380	36,745.5	35,689	37,632	37,215.5	36,966

* Average CPU seconds on each run.

and

Table 3. Experimental results for the problem instance mknapcb9.

f	Test Set	HMMKP [7]	LGA [48]			MPGA [49]			MAMMKP
			Max	Ave	Min	Max	Ave	Min	Max	Ave	Min	CPU *
0.90	0	92,021	92,025	92,025.0	92,025	92,025	92,025.0	92,025	92,031	92,031.0	92,031	409
	1	92,371	92,371	92,371.0	92,371	92,371	92,371.0	92,371	92,371	92,371.0	92,371
	2	93,396	93,396	93,391.9	93,384	93,396	93,395.8	93,387	93,396	93,396.0	93,396
	3	91,815	91,815	91807.4	91,798	91,816	91,813.3	91,800	91,816	91,816.0	91,816
	4	93,317	93,317	93,317.0	93,317	93,317	93,317.0	93,317	93,317	93,317.0	93,317
	5	91,547	91,551	91,550.4	91,547	91,551	91,550.4	91,549	91,553	91,553.0	91,553
	6	91,480	91,480	91,480.0	91,480	91,480	91,480.0	91,480	91,480	91,480.0	91,480
	7	91,672	91,681	91,657.0	91,645	91,681	91,662.8	91,646	91,681	91,681.0	91,681
	8	93,149	93,149	93,149.0	93,149	93,149	93,149.0	93,149	93,149	93,149.0	93,149
	9	93,528	93,531	93,530.0	93,507	93,531	93,531.0	93,531	93,531	93,531.0	93,531
0.75	0	74,927	82,742	81,578.7	80,681	83,268	82,676.5	81,838	83,540	83,404.4	83,261	1004
	1	73,570	80,125	78,947.1	77,715	81,222	80,528.5	79,791	81,646	81,263.0	81,022
	2	74,739	81,493	80,523.3	79,458	82,815	81,928.0	80,756	83,149	82,961.0	82,796
	3	69,813	80,288	79,201.7	77,916	81,672	80,910.2	80,141	81,927	81,751.4	81,571
	4	74,323	82,549	81,187.4	80,028	83,572	82,779.4	81,719	84,121	83,703.6	83,423
	5	74,303	81,634	80,940.3	79,892	82,815	82,049.2	81,237	83,045	82,761.2	82,539
	6	72,018	78,658	77,265.0	75,917	79,760	78,902.2	77,990	80,037	79,658.3	79,372
	7	73,777	79,235	78,178.4	77,115	80,493	79,865.2	79,055	81,052	80,700.4	80,480
	8	74,376	80,717	79,827.0	78,840	81,970	81,262.5	80,557	82,326	82,111.3	81,899
	9	73,496	81,877	80,893.4	79,514	83,236	82,535.4	81,536	83,676	83,458.8	83,154
0.73	0	N/A	77,443	75,357.0	73,681	78,584	77,801.9	76,725	79,008	78,453.0	76,241	1078
	1		73,197	71,614.3	70,363	74,877	73,897.2	72,803	74,968	74,156.5	73,926
	2		75,731	36,528.3	0	76,904	75,552.8	73,675	77,082	76,109.5	72,681
	3		73,322	71,832.4	70,024	75,335	74,259.5	72,440	75,590	75,184.6	74,469
	4		76,382	75,142.7	74,055	78,389	77,104.6	75,914	78,567	78,235.8	77,888
	5		76,117	74,812.3	72,618	78,314	77,110.2	75,709	78,516	77,980.7	77,536
	6		71,820	67,155.3	0	73,175	71,956.2	69,992	73,523	72,753.3	69,997
	7		72,643	71,172.7	68,969	74,434	73,268.5	71,354	74,463	73,857.8	72,284
	8		75,431	73,764.9	72,038	76,600	75,811.7	73,799	76,913	76,607.3	76,337
	9		74,605	59,521.0	0	77,046	75,486.8	73,698	76,793	76,188.0	75,583
0.72	0	N/A		N/A			N/A		73,280	72,989.0	72,680	1094
	1								70,017	69,841.0	69,617
	2								71,774	71,238.0	70,434
	3								69,823	69,484.0	68,937
	4								74,896	74,682.6	74,511
	5								74,536	74,216.2	74,040
	6								68,900	68,509.4	68,143
	7								68,738	68,467.5	68,212
	8								73,458	73,208.2	73,016
	9								72,020	70,799.9	70,110

* Average CPU seconds on each run.

. Among the results of HMMKP, LGA, and MPGA marked “N/A”, this indicates that the corresponding experiment was not tested in previous studies and has no results. Among the previous three methods, HMMKP, LGA, and MPGA, MPGA had the best performance. The average results of MPGA were better than the results of HMMKP. From the results of these tables, it is also observed that MAMMKP outperformed HMMKP for all test cases. This means that MAMMKP showed a better performance than HMMKP, regardless of the number of classes, the number of dimensions, and f values. MAMMKP also showed better results than LGA and MPGA in the minimum and average values for all test cases. In particular, it showed f values of 0.75 and 0.73 on mknapcb8 and mknapcb9, respectively, which are the most difficult test cases in our experiments; thus, MAMMKP showed better results than MPGA in terms of the minimum, average, and maximum values. Furthermore, on mknapcb9 with an f value of 0.72, MPGA could not find feasible solutions, while MAMMKP always obtained feasible ones. We also conducted t-tests to compare the performances of MAMMKP and MPGA. The average results for the problem instance mknapcb7, mknapcb8, and mknapcb9 have p-values of $4.56\times {10}^{-5}$, $1.28\times {10}^{-6}$, and $4.11\times {10}^{-8}$, respectively, by the t-tests. That is, the performance of MAMMKP is significantly better than that of MPGA for the three problem instances. It is also observed that the p-value decreases as the instance number increases. This means that the more difficult the problem is, the better the performance of the MAMMKP compared to the MPGA is.

6. Concluding Remarks

When there is no concern between THE value and weight in the MMKP, it becomes a very difficult NP-hard problem. However, even on a random solution space, we could show that some repair rules for finding feasible solutions do exist. We could also demonstrate that the proposed method performed well not only in terms of finding the global optimum but also in adapting to the (feasible) solution space. We showed that our single-population GA (MAMMKP) successfully simulated the multi-population GA (MPGA) of [49] and MAMMKP performed better than MPGA.

In this study, a repair heuristic based on a tendency function was designed with human experience through experiments based on genetic algorithms. To improve the tendency function, it would be valuable to gather more information for finding repair rules from not only human experience but also analyzing the MMKP raw dataset. We left the study for designing a more sophisticated tendency function to future work. We also expect that some advanced techniques related to genetic algorithms, such as normalization based on gene similarity [56] and the basis change of binary encoding [57,58], can be adopted to solve this problem.