Multiobjective Optimization for Planning the Service Areas of Smart Parcel Locker Facilities in Logistics Last Mile Delivery
Abstract
1. Introduction
2. Literature Review
3. Mathematical Model for Multiobjective Facility Service Area Optimization
3.1. Assumptions and Notations
- The customer demand and locations are known;
- The service cannot be shut down in any smart parcel locker;
- Nonrecurring events (e.g., traffic accidents and parcels remaining unclaimed) can be ignored;
- The total demand for a location does not exceed the total capacity of lockers allocated to the location.
3.2. Multiobjective Optimization Mathematical Model
4. The Proposed TA-NSGA-II Approach
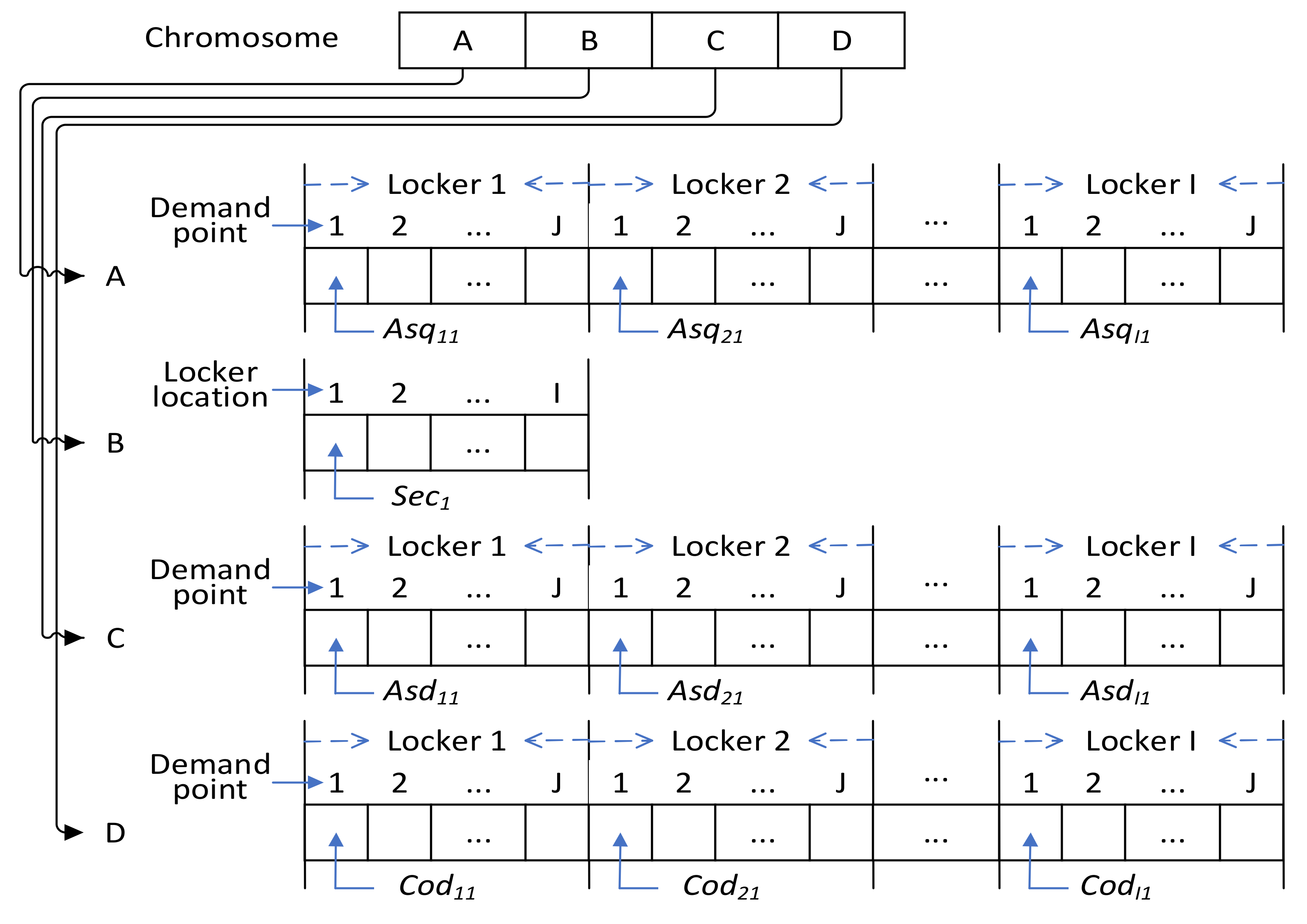
- Step 1
- Performing solution encoding and generating the initial population
- Step 2
- Calculating the fitness value of each objective
- Step 3
- Establishing the performance assessment equation
- Step 4
- Identifying factors and establishing the orthogonal array
- Step 5
- Selecting the optimal parameter combination
- Step 6
- Ranking chromosomes
- Step 7
- Calculating crowding distance
- Step 8
- Using the elitism strategy
- Step 9
- Gene cloning
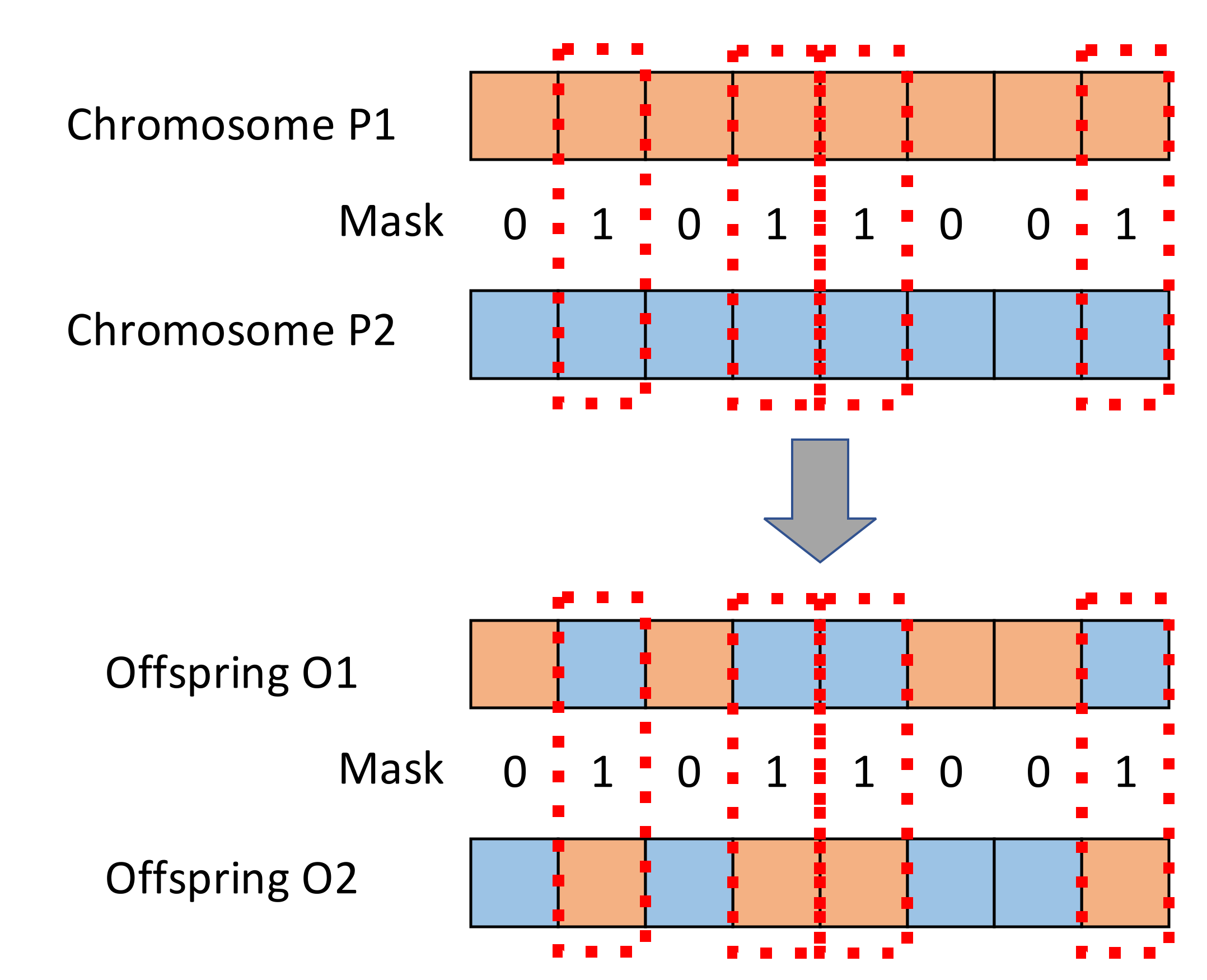
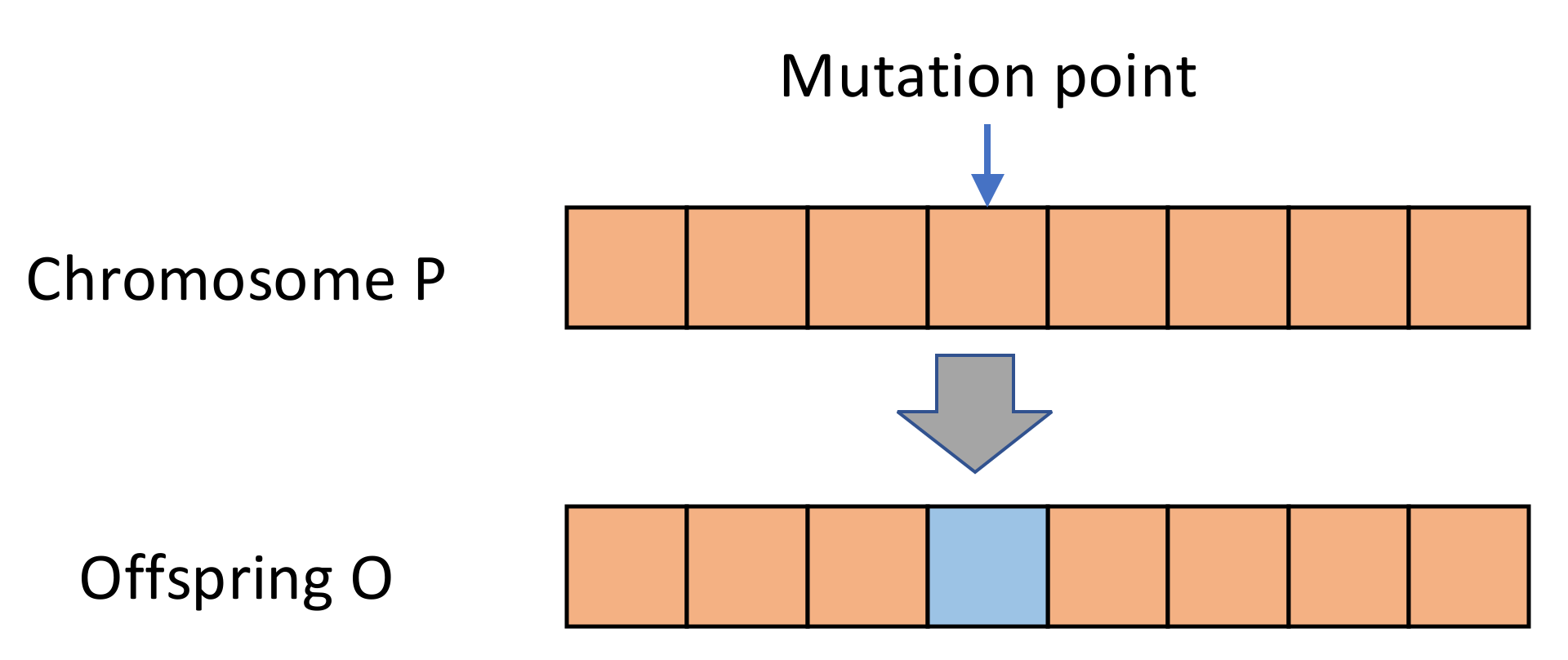
- Step 10
- Crossover and mutation
- Step 11
- Exporting the optimal solution when the termination condition is met
5. Case Study and Results
5.1. Case Description
5.2. Parameter Setting
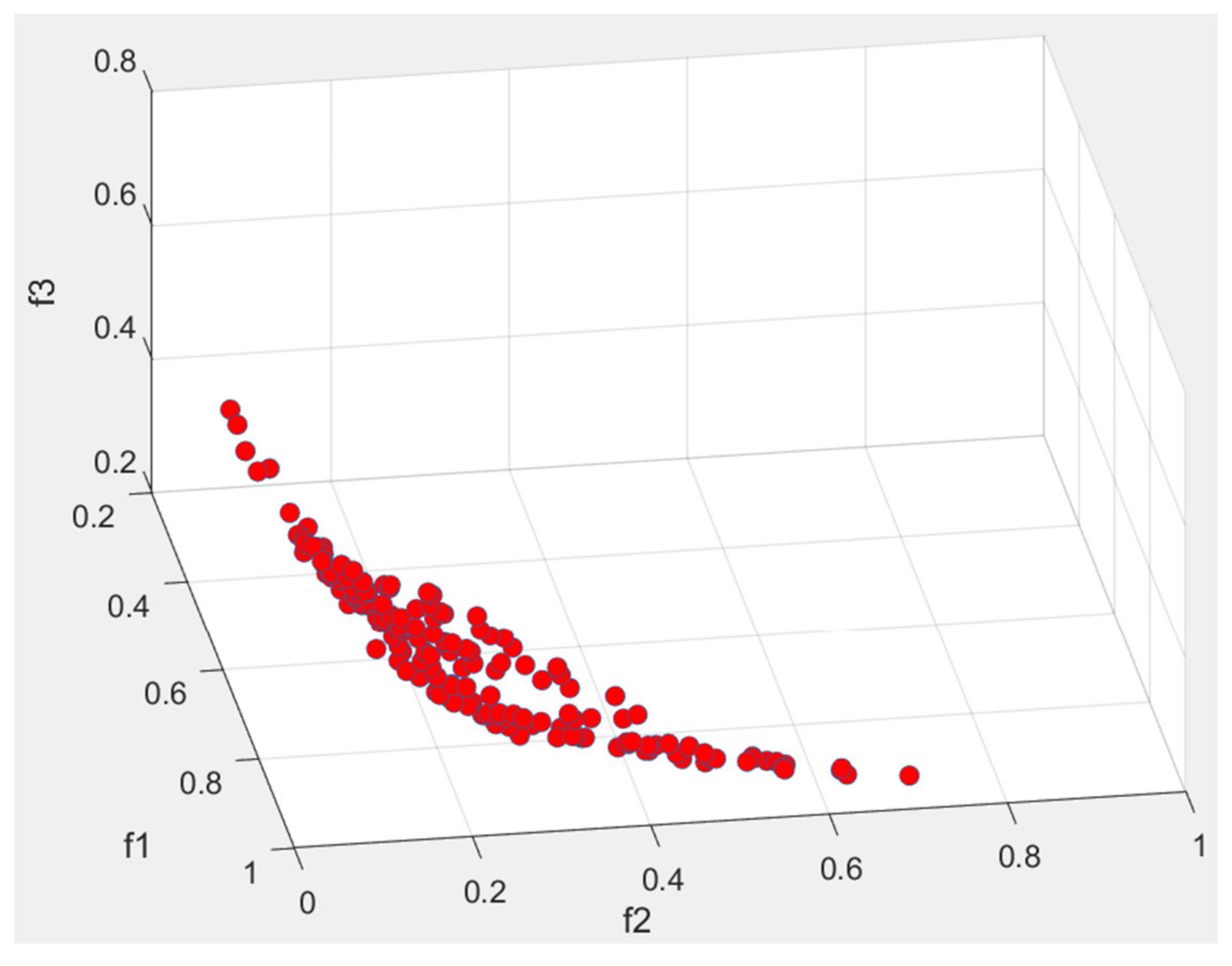
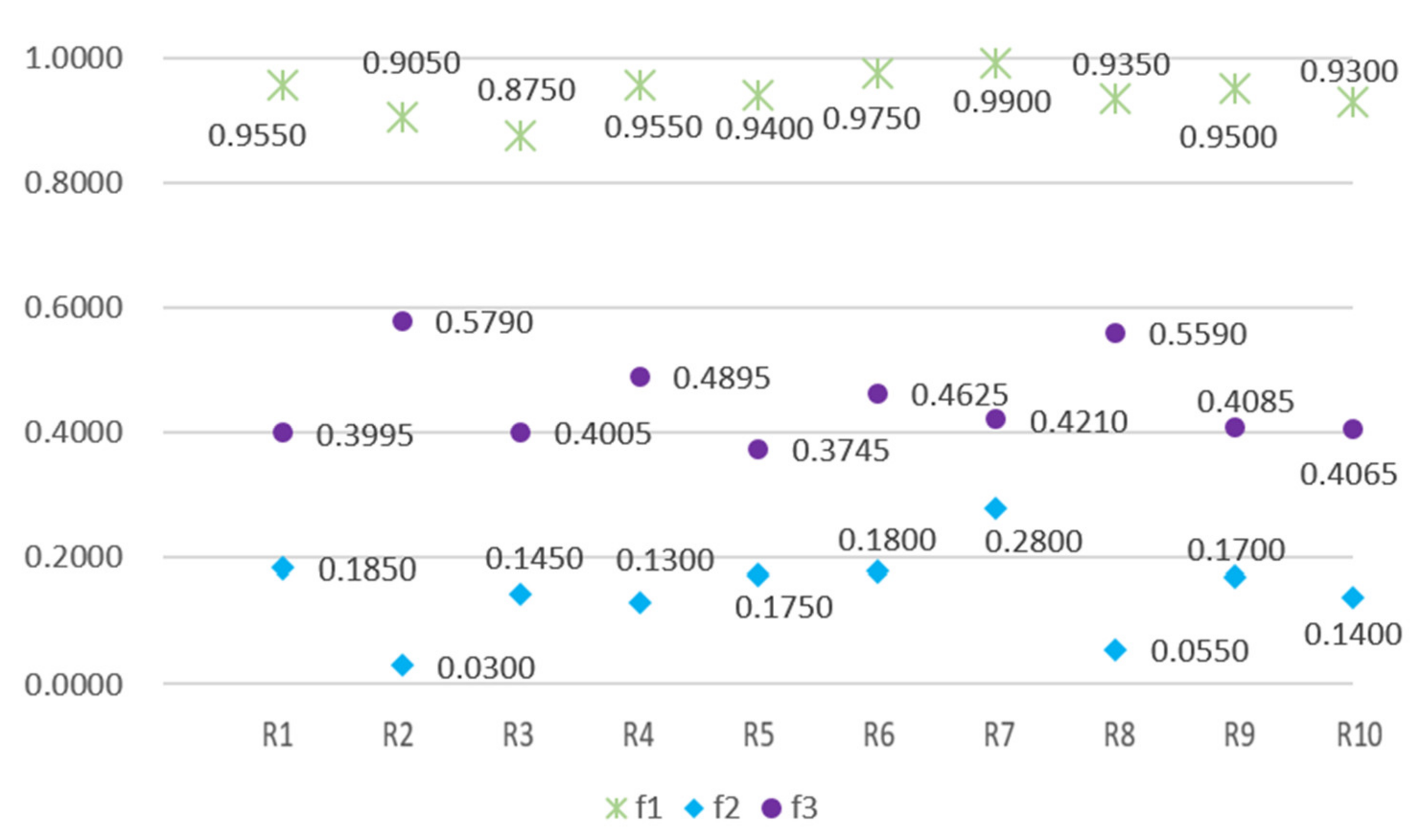
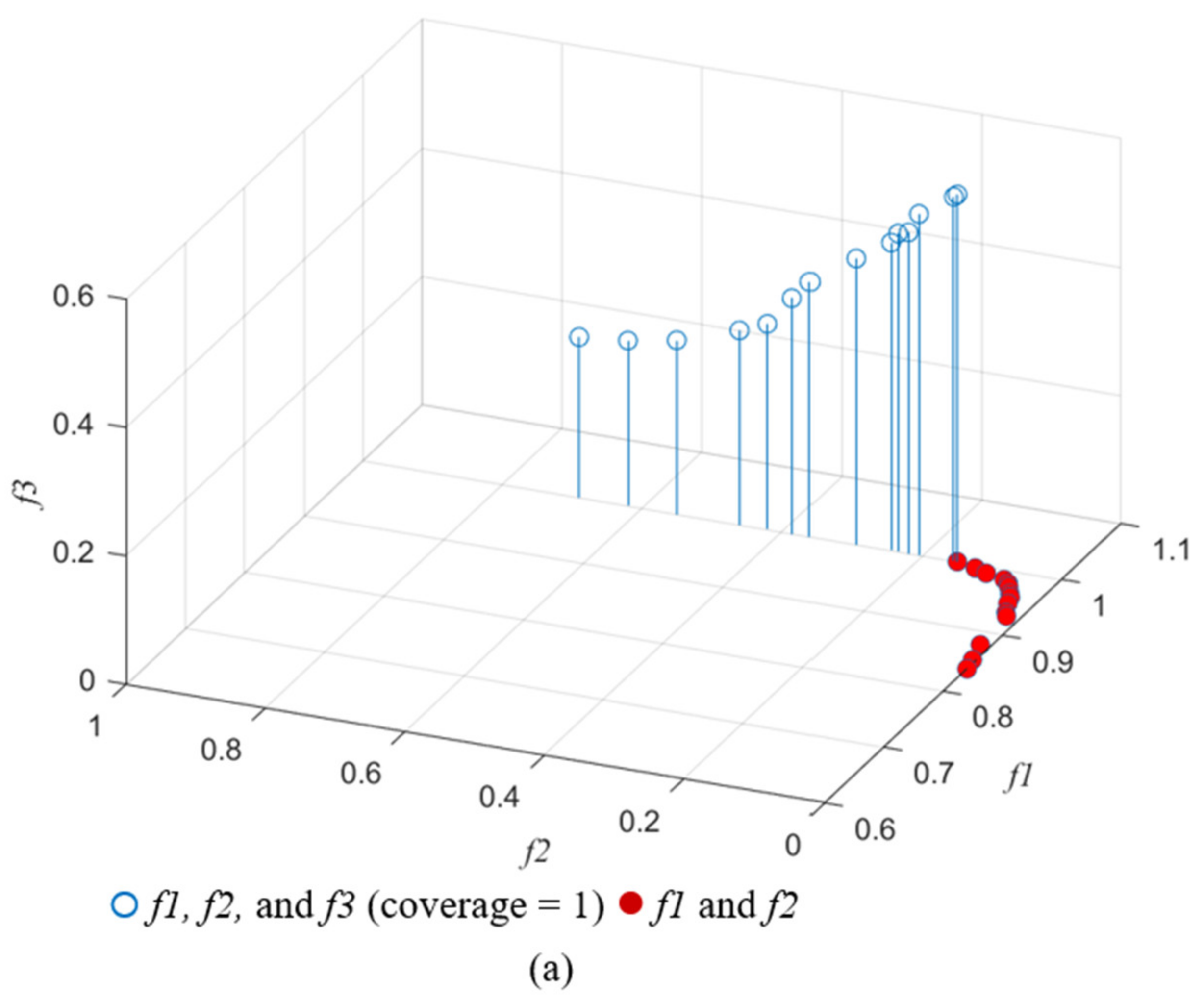
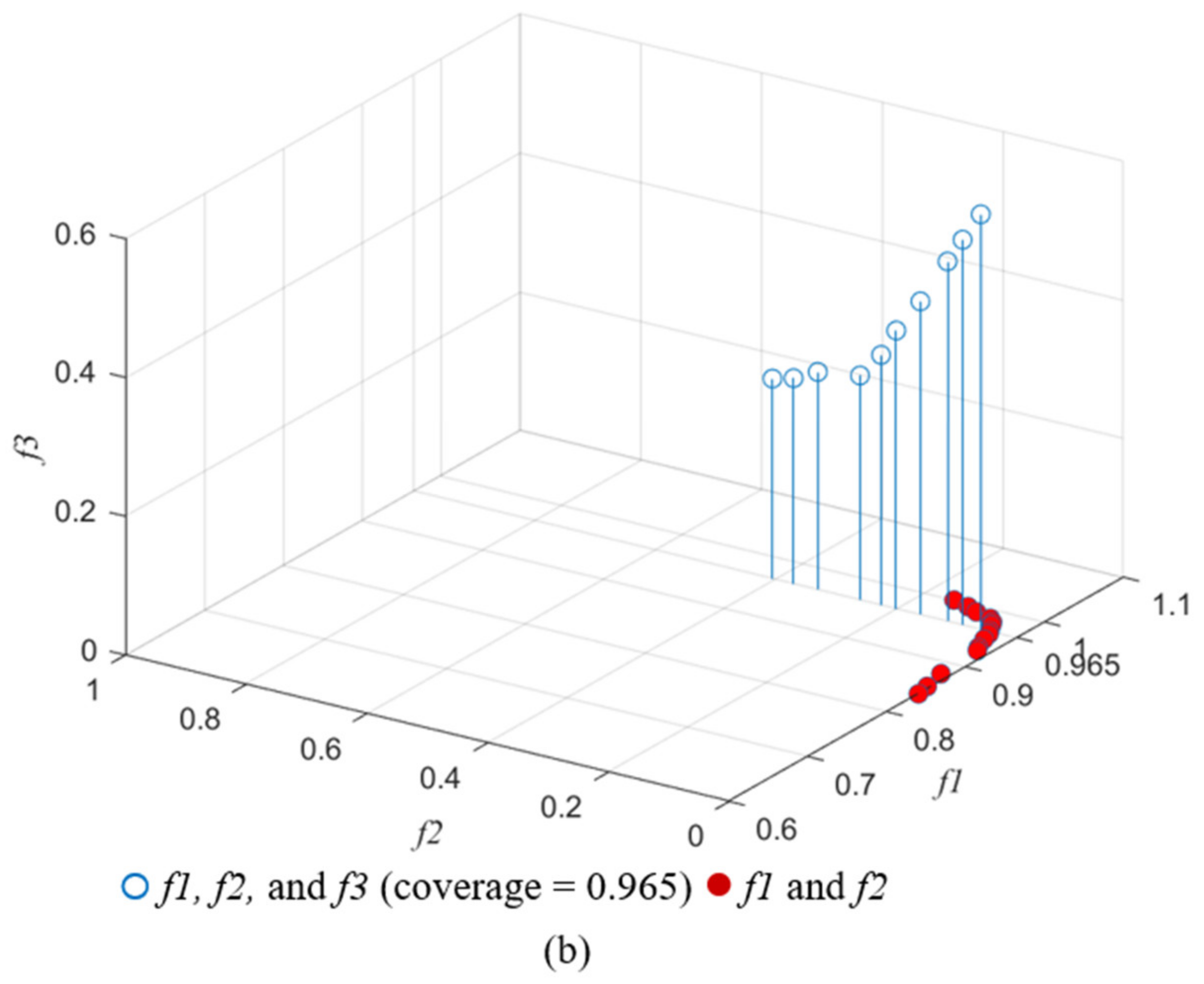
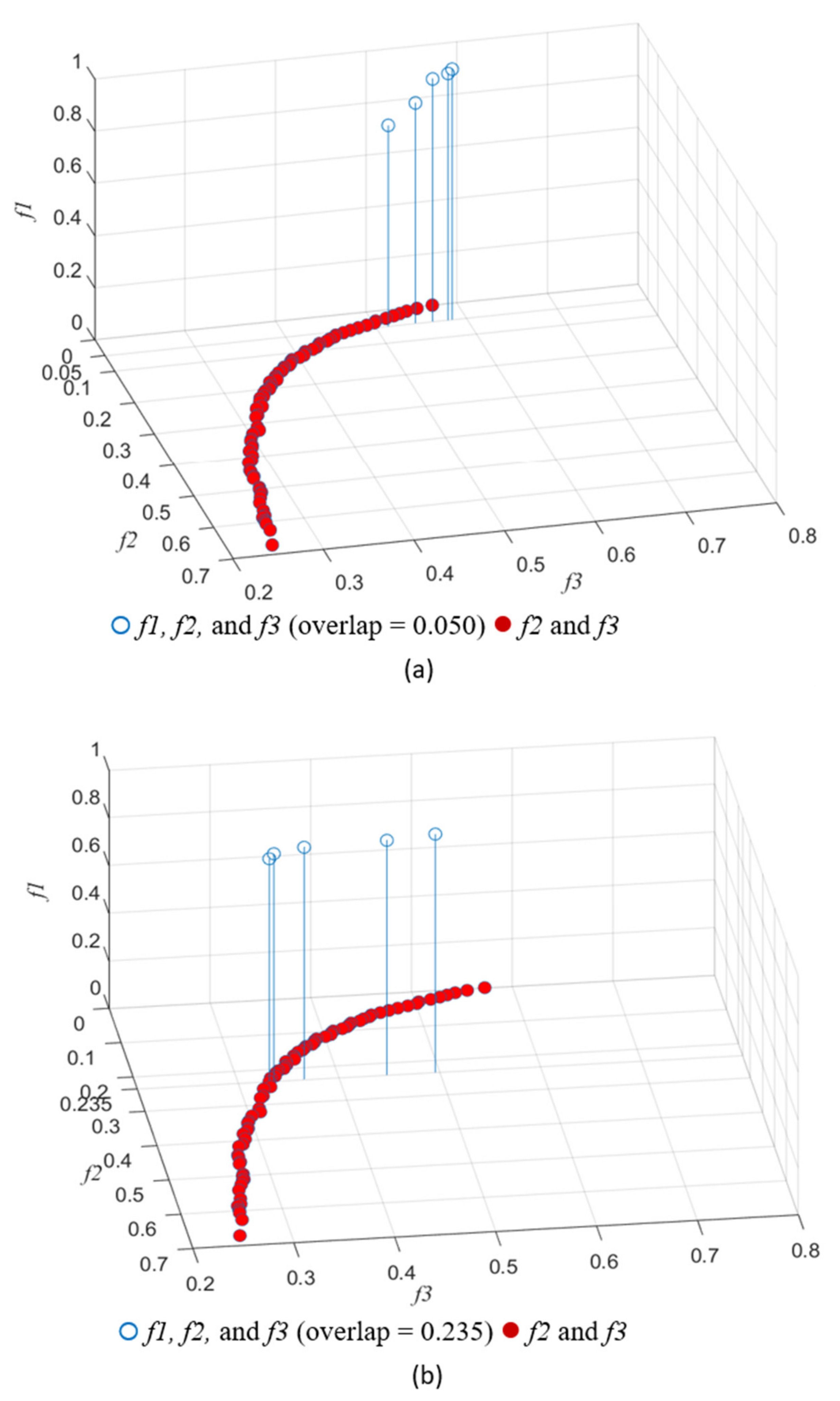
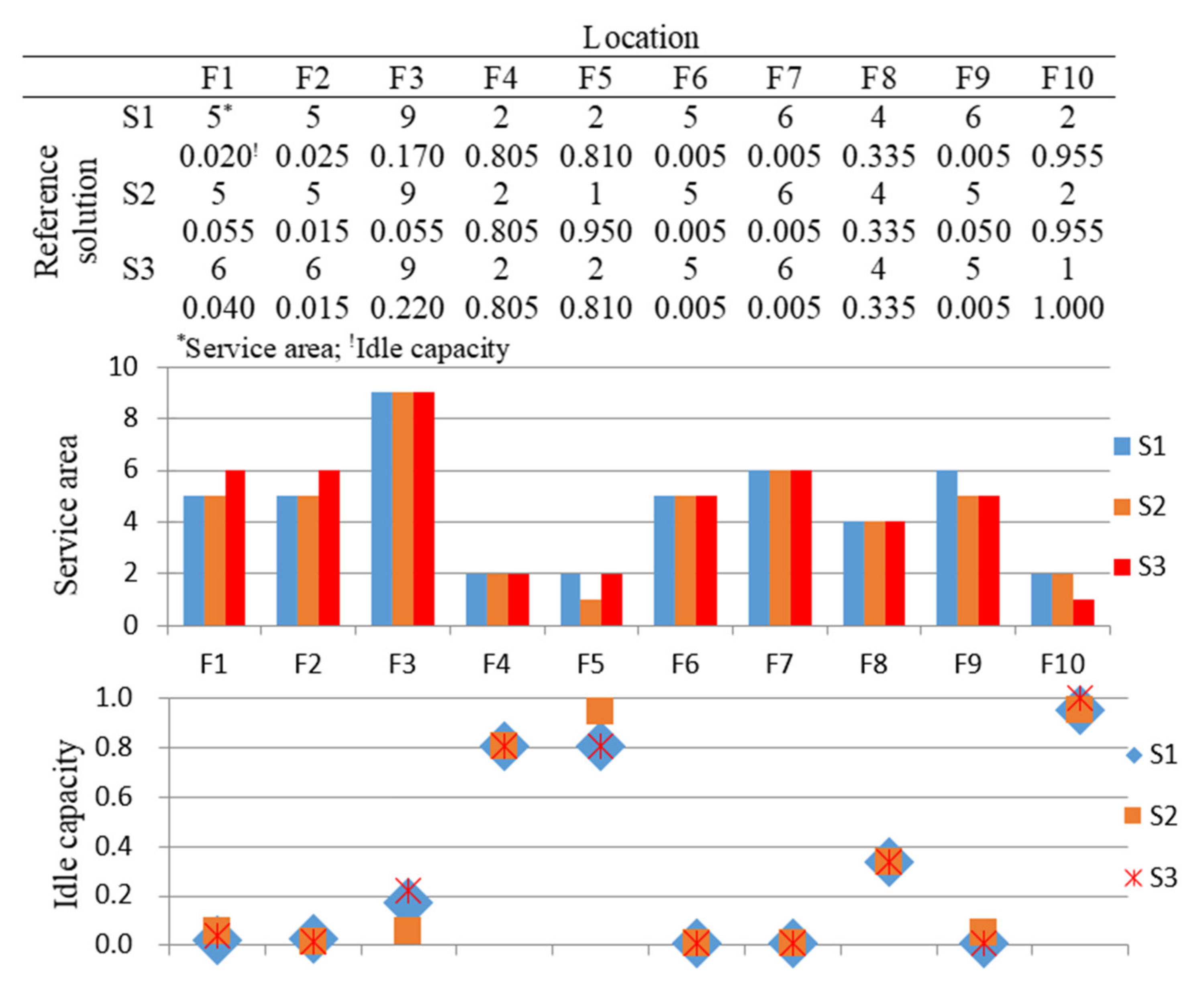
5.3. Results and Discussions
6. Conclusions and Suggestions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chevalier, S. Global Retail e-Commerce Sales 2014–2024, Statista. 2021. Available online: https://www.statista.com/statistics/379046/worldwide-retail-e-commerce-sales/ (accessed on 8 August 2021).
- Goodman, R.W. Whatever you call it, just don’t think of last-mile logistics, last. Glob. Logist. Supply Chain. Strateg. 2005, 11, 46–51. [Google Scholar]
- Gevaers, R.; Van de Voorde, E.; Vanelslander, T. Characteristics and typology of last-mile logistics from an innovation perspective in an urban context. In Proceedings of the Transportation Research Board 90th Annual Meeting, Washington, DC, USA, 23–27 January 2011; pp. 2–14. [Google Scholar]
- Caceres-Cruz, J.; Arias, P.; Guimarans, D.; Riera, D.; Juan, A.A. Rich vehicle routing problem: Survey. ACM Comput. Surv. 2015, 47, 1–28. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Prins, C. Heuristics for multi-attribute vehicle routing problems: A survey and synthesis. Eur. J. Oper. Res. 2013, 231, 1–21. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods, and Applications, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2015. [Google Scholar]
- Crainic, T.G.; Laporte, G. Fleet Management and Logistics; Springer: Boston, MA, USA, 1998. [Google Scholar]
- Anderluh, A.; Hemmelmayr, V.C.; Nolz, P.C. Synchronizing vans and cargo bikes in a city distribution network. Cent. Eur. J. Oper. Res. 2017, 25, 345–376. [Google Scholar] [CrossRef]
- Klumpp, M.; Witte, C.; Zelewski, S. Information and process requirements for electric mobility in last-mile-logistics. In Proceedings of the Sixth International Conference on Information Technologies in Environmental Engineering (ITEE2013), Lüneburg, Germany, 10–12 July 2013. [Google Scholar]
- Chong, Z.J.; Qin, B.; Bandyopadhyay, T.; Wongpiromsarn, T.; Rankin, E.S.; Ang, M.H.; Frazzoli, E.; Rus, D.; Hsu, D.; Low, K.H. Autonomous personal vehicle for the first-and last-mile transportation services. In Proceedings of the 2011 IEEE 5th International Conference on Cybernetics and Intelligent Systems (CIS), Qingdao, China, 17–19 September 2011; pp. 253–260. [Google Scholar]
- Perboli, G.; Rosano, M. Parcel delivery in urban areas: Opportunities and threats for the mix of traditional and green business models. Transp. Res. Part C Emerg. Technol. 2019, 99, 19–36. [Google Scholar] [CrossRef]
- Lee, H.L.; Chen, Y.; Gillai, B.; Rammohan, S. Technological Disruption and Innovation in Last-Mile Delivery; Stanford Graduate School of Business: Stanford, CA, USA, 2016. [Google Scholar]
- Brown, J.R.; Guiffrida, A.L. Carbon emissions comparison of last mile eelivery versus customer pickup. Int. J. Logist. Res. Appl. 2014, 17, 503–521. [Google Scholar] [CrossRef]
- Edwards, J.B.; McKinnon, A.C.; Cullinane, S.L. Comparative analysis of the carbon footprints of conventional and online retailing: A ‘last mile’ perspective. Int. J. Phys. Distrib. Logist. Manag. 2010, 40, 103–123. [Google Scholar] [CrossRef]
- Montreuil, B.; Meller, R.D.; Ballot, E. Towards a physical internet: The impact on logistics facilities and material handling systems design and innovation. In Proceedings of the 11th International Material Handling Research Colloquium, Milwaukee, WI, USA, 21–25 June 2010. [Google Scholar]
- Fazili, M.; Venkatadri, U.; Cyrus, P.; Tajbakhsh, M. Physical internet, conventional and hybrid logistic systems: A routing optimisation-based comparison using the eastern Canada road network case study. Int. J. Prod. Res. 2017, 55, 2703–2730. [Google Scholar] [CrossRef]
- Faugere, L.; Montreuil, B. Hyperconnected Pickup & Delivery Locker Networks. In Proceedings of the 4th International Physical Internet Conference, Graz, Austria, 4–6 July 2017. [Google Scholar]
- Lemke, J.; Iwan, S.; Korczak, J. Usability of the parcel lockers from the customer perspective: The research in Polish cities. Transp. Res. Procedia 2016, 16, 272–287. [Google Scholar] [CrossRef]
- Cheng, X.; Liao, S.; Hua, Z. A policy of picking up parcels for express courier service in dynamic environments. Int. J. Prod. Res. 2017, 55, 2470–2488. [Google Scholar] [CrossRef]
- Houlihan, J.B. International supply chain management. Int. J. Phys. Distrib. Logist. Manag. 1985, 15, 22–38. [Google Scholar]
- Christopher, M. Logistics and Supply Chain Management: Strategies for Reducing Costs and Improving Services, 4th ed.; Financial Times/Pitman: London, UK, 2011. [Google Scholar]
- Beamon, B.M. Supply chain design and analysis: Models and methods. Int. J. Prod. Econ. 1998, 55, 281–294. [Google Scholar] [CrossRef]
- Ellram, L. Supply-chain management: The industrial organisation perspective. Int. J. Phys. Distrib. Logist. Manag. 1991, 21, 13–22. [Google Scholar] [CrossRef]
- Lambert, D.M.; Cooper, M.C. Issues in supply chain management. Ind. Mark. Manag. 2000, 29, 65–83. [Google Scholar] [CrossRef]
- Heinemann, G.; Schwarzl, C. New Online Retailing—Innovation and Transformation; Gabler Verlag: Fairford, UK, 2010. [Google Scholar]
- Kull, T.J.; Boyer, K.; Calantone, R. Last-mile supply chain efficiency: An analysis of learning curves in online ordering. Int. J. Oper. Prod. Manag. 2007, 27, 409–434. [Google Scholar] [CrossRef]
- Maulana, S.M.; Susilo, H.; Susilo, H. Implementasi e-commerce sebagai media penjualan online (studi kasus pada toko pastbrik kota malang). J. Adm. Bisnis 2015, 29, 1–9. [Google Scholar]
- Turban, E.; King, D.; Viehland, D.; Lee, J.K. Electronic Commerce 2006: A Managerial Perspective; Bergen: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Chiu, C.M.; Wang, E.T.; Fang, Y.H.; Huang, H.Y. Understanding customers’ repeat purchase intentions in B2C e-commerce: The roles of utilitarian value, hedonic value and perceived risk. Inf. Syst. J. 2014, 24, 85–114. [Google Scholar] [CrossRef]
- Agatz, N.A.; Fleischmann, M.; Van Nunen, J.A. E-fulfillment and multi-channel distribution—A review. Eur. J. Oper. Res. 2008, 187, 339–356. [Google Scholar] [CrossRef]
- Visser, J.; Nemoto, T.; Browne, M. Home delivery and the impacts on urban freight transport: A review. Procedia Soc. Behav. Sci. 2014, 125, 15–27. [Google Scholar] [CrossRef]
- Boyer, K.K.; Prud’homme, A.M.; Chung, W. The last-mile challenge: Evaluating the effects of customer density and delivery window patterns. J. Bus. Logist. 2009, 30, 185–201. [Google Scholar] [CrossRef]
- de Souza, R.; Goh, M.; Lau, H.C.; Ng, W.S.; Tan, P.S. Collaborative urban logistics–synchronizing the last mile a Singapore research perspective. Procedia Soc. Behav. Sci. 2014, 125, 422–431. [Google Scholar] [CrossRef]
- Moroz, M.; Polkowski, Z. The last mile issue and urban logistics: Choosing parcel machines in the context of the ecological attitudes of the Y generation consumers purchasing online. Transp. Res. Procedia 2016, 16, 378–393. [Google Scholar] [CrossRef]
- Hotelling, H. Stability in Competition. Econ. J. 1929, 39, 41–57. [Google Scholar] [CrossRef]
- Owen, S.H.; Daskin, M.S. Strategic facility location: A review. Eur. J. Oper. Res. 1998, 111, 423–447. [Google Scholar] [CrossRef]
- Hakimi, S.L. Optimum locations of switching centers and the absolute centers and medians of a graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- ReVelle, C.S.; Swain, R.W. Central facilities location. Geogr. Anal. 1970, 2, 30–42. [Google Scholar] [CrossRef]
- Ghoseiri, K.; Ghannadpour, S. Solving capacitated p-median problem using genetic algorithm. In Proceedings of the 2007 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 2–4 December 2007; pp. 885–889. [Google Scholar]
- Drezner, Z.; Brimberg, J.; Mladenović, N.; Salhi, S. New heuristic algorithms for solving the planar p-median problem. Comput. Oper. Res. 2015, 62, 296–304. [Google Scholar] [CrossRef]
- Griffith, D.A.; Paelinck, J.H.P. Spatial Autocorrelation and the p-Median Problem. In Morphisms for Quantitative Spatial Analysis; Springer: Cham, Switzerland, 2018; pp. 9–24. [Google Scholar]
- Daskin, M. Network and Discrete Location; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Davidović, T.; Ramljak, D.; Šelmić, M.; Teodorović, D. Bee colony optimization for the p-center problem. Comput. Oper. Res. 2011, 38, 1367–1376. [Google Scholar] [CrossRef]
- Martínez-Merino, L.I.; Albareda-Sambola, M.; Rodríguez-Chía, A.M. The probabilistic p-center problem: Planning service for potential customers. Eur. J. Oper. Res. 2017, 262, 509–520. [Google Scholar] [CrossRef][Green Version]
- Toregas, C.; Swain, R.; ReVelle, C.; Bergman, L. The location of emergency service facilities. Oper. Res. 1971, 19, 1363–1373. [Google Scholar] [CrossRef]
- Rajagopalan, H.K.; Saydam, C.; Xiao, J. A multiperiod set covering location model for dynamic redeployment of ambulances. Comput. Oper. Res. 2008, 35, 814–826. [Google Scholar] [CrossRef]
- Ghaderi, A.; Jabalameli, M.S. Modeling the budget-constrained dynamic uncapacitated facility location–network design problem and solving it via two efficient heuristics: A case study of health care. Math. Comput. Model. 2013, 57, 382–400. [Google Scholar] [CrossRef]
- Church, R.; ReVelle, C. The maximal covering location problem. Pap. Reg. Sci. Assoc. 1974, 32, 101–118. [Google Scholar] [CrossRef]
- ReVelle, C.; Scholssberg, M.; Williams, J. Solving the maximal covering location problem with heuristic concentration. Comput. Oper. Res. 2008, 35, 427–435. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Fonseca, C.M.; Fleming, P.J. Genetic algorithms for multiobjective Optimization: Formulation, discussion and generalization. In Proceedings of the Fifth International Conference on Genetic Algorithms, Morgan Kaufmann, San Mateo, CA, USA, 1 June 1993; pp. 416–423. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mansouri, S.A. A multi-objective genetic algorithm for mixed-model sequencing on JIT assembly lines. Eur. J. Oper. Res. 2005, 167, 696–716. [Google Scholar] [CrossRef]
- Murugan, P.; Kannan, S.; Baskar, S. NSGA-II algorithm for multi-objective generation expansion planning problem. Electr. Power Syst. Res. 2009, 79, 622–628. [Google Scholar] [CrossRef]
- Berning, G.; Brandenburg, M.; Gürsoy, K.; Mehta, V.; Tölle, F.J. An integrated system solution for supply chain optimization in the chemical process industry. OR Spectr. 2002, 24, 371–401. [Google Scholar] [CrossRef]
- Li, Z.; Liao, H.; Coit, D.W. A two-stage approach for multi-objective decision making with applications to system reliability optimization. Reliab. Eng. Syst. Saf. 2009, 94, 1585–1592. [Google Scholar] [CrossRef]
- Wang, H.F.; Hsu, H.W. A closed-loop logistic model with a spanning-tree based genetic algorithm. Comput. Oper. Res. 2010, 37, 376–389. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Farahani, R.Z.; Dullaert, W. A memetic algorithm for bi-objective integrated forward/reverse logistics network design. Comput. Oper. Res. 2010, 37, 1100–1112. [Google Scholar] [CrossRef]
- Camara, M.V.O.; Ribeiro, G.M.; Tosta, M.d.C.R. A pareto optimal study for the multi-objective oil platform location problem with NSGA-II. J. Pet. Sci. Eng. 2018, 169, 258–268. [Google Scholar] [CrossRef]
- Babazadeh, H.; Alavidoost, M.H.; Zarandi, M.F.; Sayyari, S.T. An enhanced NSGA-II algorithm for fuzzy bi-objective assembly line balancing problems. Comput. Ind. Eng. 2018, 123, 189–208. [Google Scholar] [CrossRef]
- Zhang, J.; Xing, L.; Peng, G.; Yao, F.; Chen, C. A large-scale multiobjective satellite data transmission scheduling algorithm based on SVM+NSGA-II. Swarm Evol. Comput. 2019, 50, 100560. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, D.; Yuan, J.; Li, H.; Gao, Y. Application of NSGA-II algorithm for fault diagnosis in power system. Electr. Power Syst. Res. 2019, 175, 105893. [Google Scholar] [CrossRef]
- Bai, X.; Chin, K.S.; Zhou, Z. A bi-objective model for location planning of electric vehicle charging stations with GPS trajectory data. Comput. Ind. Eng. 2019, 128, 591–604. [Google Scholar] [CrossRef]
- Wang, S.; Ma, S. Efficient methods for a bi-objective nursing home location and allocation problem: A case study. Appl. Soft Comput. 2018, 65, 280–291. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength pareto evolutionary algorithm. In Proceedings of the EUROGEN 2001, Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, Athens, Greece, 19–21 September 2002; pp. 95–100. [Google Scholar]
- Rahimi-Vahed, A.R.; Mirghorbani, S.M.; Rabbani, M. A new particle swarm algorithm for a multi-objective mixed-model assembly line sequencing problem. Soft Comput. 2007, 11, 997–1012. [Google Scholar] [CrossRef]
- Farsangi, M.M.; Nezamabadi-Pour, H.; Lee, K.Y. Multi-objective VAr planning with SVC for a large power system using PSO and GA. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 5 February 2002; pp. 274–279. [Google Scholar]
- Rojas, I.; Gonzalez, J.; Pomares, H.; Merelo, J.J.; Castillo, P.A.; Romero, G. Statistical analysis of the main parameters involved in the design of a genetic algorithm. IEEE Trans. Syst. Man Cybern. Syst. 2002, 32, 31–37. [Google Scholar] [CrossRef]
- Su, P.L.; Chen, Y.S. Implementation of a genetic algorithm on MD-optimal designs for multivariate response surface models. Expert Syst. Appl. 2012, 39, 3207–3212. [Google Scholar] [CrossRef]
- Ghezavati, V.; Hosseinifar, P. Application of efficient metaheuristics to solve a new bi-objective optimization model for hub facility location problem considering value at risk criterion. Soft Comput. 2018, 22, 195–212. [Google Scholar] [CrossRef]
- Rayat, F.; Musavi, M.; Bozorgi-Amiri, A. Bi-objective reliable location-inventory-routing problem with partial backordering under disruption risks: A modified AMOSA approach. Appl. Soft Comput. 2017, 59, 622–643. [Google Scholar] [CrossRef]
| LSCP | MCLP | |
|---|---|---|
| Facility | The number of facilities is not limited | The number of facilities is limited |
| Demand point | Each point must be covered by at least one facility | Not all points must be covered |
| Objective | The number of facilities must be minimized | Service coverage must be maximized |
| Notation | Definition |
|---|---|
| Parameter | |
| i | Index of locker location |
| I | Total number of locker locations |
| j | Index of demand point |
| J | Total number of demand points |
| Total capacity of locker location i | |
| Total demand for demand point j | |
| Distance between locker location i and demand point j | |
| Decision variable | |
| Assigning quantity from demand point j to locker location i | |
| Service distance of locker location i | |
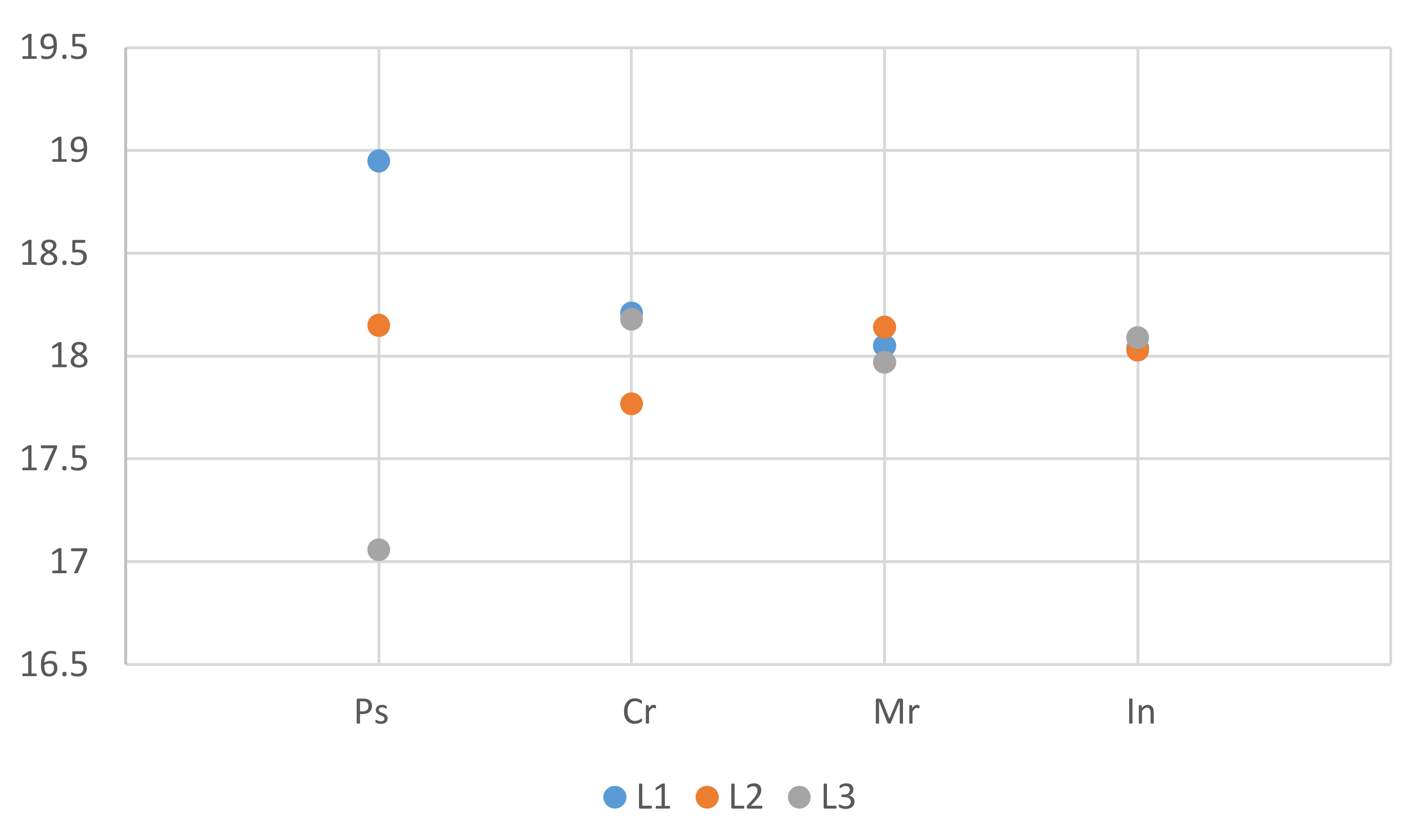
| Level | Ps | Cr | Mr | In |
|---|---|---|---|---|
| L1 | 150 | 0.9 | 0.1 | 100 |
| L2 | 100 | 0.7 | 0.06 | 500 |
| L3 | 50 | 0.8 | 0.2 | 1000 |
| Location | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Solution No. | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
| R1 | 5 * | 5 | 8 | 2 | 1 | 5 | 7 | 4 | 2 | 2 |
| 0.025 ! | 0.010 | 0.130 | 0.805 | 0.950 | 0.005 | 0.000 | 0.335 | 0.780 | 0.955 | |
| R2 | 7 | 1 | 7 | 1 | 1 | 5 | 7 | 2 | 1 | 2 |
| 0.000 | 0.970 | 0.270 | 1.000 | 0.950 | 0.000 | 0.000 | 0.750 | 0.895 | 0.955 | |
| R3 | 5 | 5 | 8 | 2 | 1 | 5 | 5 | 4 | 2 | 2 |
| 0.025 | 0.010 | 0.130 | 0.805 | 0.950 | 0.005 | 0.010 | 0.335 | 0.780 | 0.955 | |
| R4 | 7 | 1 | 8 | 1 | 1 | 6 | 7 | 4 | 2 | 3 |
| 0.005 | 0.970 | 0.025 | 1.000 | 0.950 | 0.000 | 0.000 | 0.410 | 0.780 | 0.755 | |
| R5 | 4 | 5 | 9 | 2 | 1 | 5 | 6 | 4 | 4 | 2 |
| 0.280 | 0.000 | 0.030 | 0.805 | 0.950 | 0.005 | 0.005 | 0.335 | 0.380 | 0.955 | |
| R6 | 6 | 5 | 7 | 2 | 1 | 5 | 8 | 2 | 2 | 1 |
| 0.015 | 0.000 | 0.325 | 0.805 | 0.950 | 0.000 | 0.000 | 0.750 | 0.780 | 1.000 | |
| R7 | 8 | 5 | 7 | 2 | 1 | 5 | 7 | 4 | 2 | 2 |
| 0.010 | 0.010 | 0.360 | 0.805 | 0.950 | 0.005 | 0.000 | 0.335 | 0.780 | 0.955 | |
| R8 | 7 | 1 | 7 | 1 | 1 | 6 | 7 | 2 | 1 | 3 |
| 0.000 | 0.970 | 0.270 | 1.000 | 0.950 | 0.000 | 0.000 | 0.750 | 0.895 | 0.755 | |
| R9 | 5 | 5 | 8 | 1 | 1 | 5 | 7 | 4 | 2 | 2 |
| 0.025 | 0.010 | 0.025 | 1.000 | 0.950 | 0.005 | 0.000 | 0.335 | 0.780 | 0.955 | |
| R10 | 3 | 5 | 9 | 1 | 1 | 5 | 6 | 4 | 4 | 2 |
| 0.485 | 0.010 | 0.000 | 1.000 | 0.950 | 0.005 | 0.005 | 0.335 | 0.320 | 0.955 | |
| Reference Solution | f1 | f2 | f3 |
|---|---|---|---|
| S1 | 0.9650 | 0.3300 | 0.3135 |
| S2 | 0.9650 | 0.2600 | 0.3230 |
| S3 | 0.9800 | 0.3300 | 0.3240 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, Z.-H.; Chiang, T.-A.; Luo, Y.-J. Multiobjective Optimization for Planning the Service Areas of Smart Parcel Locker Facilities in Logistics Last Mile Delivery. Mathematics 2022, 10, 422. https://doi.org/10.3390/math10030422
Che Z-H, Chiang T-A, Luo Y-J. Multiobjective Optimization for Planning the Service Areas of Smart Parcel Locker Facilities in Logistics Last Mile Delivery. Mathematics. 2022; 10(3):422. https://doi.org/10.3390/math10030422
Chicago/Turabian StyleChe, Zhen-Hua, Tzu-An Chiang, and Yun-Jhen Luo. 2022. "Multiobjective Optimization for Planning the Service Areas of Smart Parcel Locker Facilities in Logistics Last Mile Delivery" Mathematics 10, no. 3: 422. https://doi.org/10.3390/math10030422
APA StyleChe, Z.-H., Chiang, T.-A., & Luo, Y.-J. (2022). Multiobjective Optimization for Planning the Service Areas of Smart Parcel Locker Facilities in Logistics Last Mile Delivery. Mathematics, 10(3), 422. https://doi.org/10.3390/math10030422







