Multiple Periodicity in a Predator–Prey Model with Prey Refuge
Abstract
1. Introduction
2. The Existence of Multiple Positive Periodic Solutions
- (a)
- for each fixed ;
- (b)
- for each fixed , and ;then the operator equation has at least one solution in .
- Step 1
- (1)
- Since , we have
- (2)
- Since , we have
- (3)
- Since , we have
- Step 2
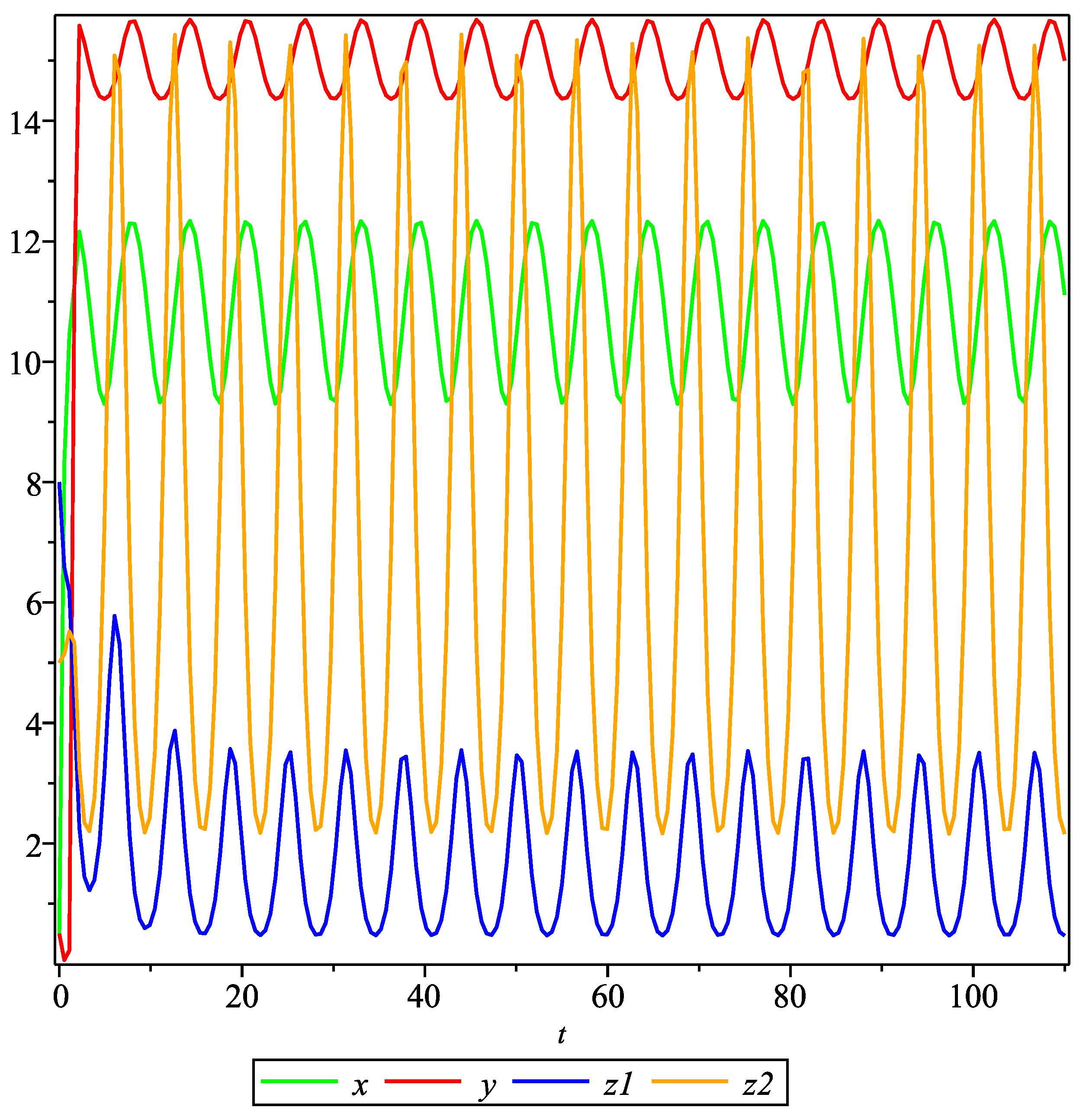
3. Example
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lotka, A. Elements of Physical Biology; Williams Wilkins Co.: Balitmore, MD, USA, 1925. [Google Scholar]
- Volterra, V. Variazioni e fluttuazioni del numero dindividui in specie animali conviventi. Mem. Acad Lincei Roma 1926, 2, 31–113. [Google Scholar]
- Chen, X.; Du, Z. Existence of positive periodic solutions for a neutral delay predator-prey model with Hassell-Varley type functional response and impulse. Qual. Theory Dyn. Syst. 2018, 17, 67–80. [Google Scholar] [CrossRef]
- Lv, Y.; Du, Z. Existence and global attractivity of a positive periodic solution to a Lotka–Volterra model with mutual interference and Holling III type functional response. Nonlinear Anal. RWA 2011, 12, 3654–3664. [Google Scholar] [CrossRef]
- Wang, D. Positive periodic solutions for a nonautonomous neutral delay prey-predator model with impulse and Hassell-Varley type functional response. Proc. Am. Math. Soc. 2014, 142, 623–638. [Google Scholar] [CrossRef]
- Wang, D. Four positive periodic solutions of a delayed plankton allelopathy system on time scales with multiple exploited (or harvesting) terms. IMA J. Appl. Math. 2013, 78, 449–473. [Google Scholar] [CrossRef]
- Yu, S.; Liu, J.; Lin, X. Multiple positive periodic solutions of a Gause-type predator-prey model with Allee effect and functional responses. AIMS Math. 2020, 5, 6135–6148. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Zhou, T. Multiple periodic solutions of a delayed predator-prey model with non-monotonic functional response and stage structure. J. Biol. Dynam. 2014, 1, 145–160. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Luo, Z. Multiple periodic solutions of a delayed predator–prey system with stage structure for the predator. Nonlinear Anal. RWA 2010, 1, 4109–4120. [Google Scholar] [CrossRef]
- Kant, S.; Kumar, V. Stability analysis of predator-prey system with migrating prey and disease infection in both species. Appl. Math. Model. 2017, 42, 509–539. [Google Scholar] [CrossRef]
- Liu, S.; Chen, L.; Liu, Z. Extinction and permanence in nonautonomous competitive system with stage structure. J. Math. Anal. Appl. 2002, 274, 667–684. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.; Xi, N.; Fu, W.; Wang, K.; Ding, X. Mathematical analysis and simulation of a Hepatitis B model with time delay: A case study for Xinjiang, China. Math. Biosci. Eng. 2020, 17, 1757–1775. [Google Scholar] [CrossRef] [PubMed]
- Lu, S. On the existence of positive periodic solutions to a Lotka-Volterra cooperative population model with multiple delays. Nonlinear Anal. 2008, 68, 1746–1753. [Google Scholar] [CrossRef]
- Song, Y.; Tang, X. Stability, steady-state bifurcations and turing patterns in a predator-prey model with herd behavior and prey-taxis. Stud. Appl. Math. 2017, 139, 371–404. [Google Scholar] [CrossRef]
- Lv, Y.; Chen, L.; Chen, F.; Li, Z. Stability and bifurcation in an SI epidemic model with additive Allee effect and time delay. Int. J. Bifurcat. Chaos 2021, 31, 2150060. [Google Scholar] [CrossRef]
- Chen, L.; Liu, T.; Chen, F. Stability and bifurcation in a two-patch model with additive Allee effect. AIMS Math. 2022, 7, 536–551. [Google Scholar] [CrossRef]
- Wei, Z.; Xia, Y.; Zhang, T. Stability and bifurcation analysis of a amensalism model with weak Allee effect. Qual. Theor. Dyn. Syst. 2020, 19, 23. [Google Scholar] [CrossRef]
- Wei, Z.; Xia, Y.; Zhang, T. Stability and bifurcation analysis of a commensal model with additive Allee effect and nonlinear growth rate. Int. J. Bifurcat. Chaos 2021, 31, 2150204. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z. Stability and Hopf bifurcation in a ratio-dependent predator prey system with stage structure. Chaos Solitons Fractals 2008, 38, 669–684. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, T.; Song, K. A stochastic model of bacterial infection associated with neutrophils. Appl. Math. Comput. 2020, 373, 125025. [Google Scholar] [CrossRef]
- Chen, L.; Chen, F. Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a constant prey refuge. Nonlinear Anal. 2010, 11, 246–252. [Google Scholar] [CrossRef]
- Gause, G.; Smaragdova, N.; Witt, A. Further studies of interaction between predators and prey. J. Anim. Ecol. 1936, 5, 1–18. [Google Scholar] [CrossRef]
- Gause, G. The Struggle for Existence; Williams Wilkins Co.: Balitmore, MD, USA, 1934. [Google Scholar]
- Magalhᾶes, S.; Rijn, P.; Montserrat, M.; Pallini, A.; Sabelis, M. Population dynamics of thrips prey and their mite predators in a refuge. Oecologia 2007, 150, 557–568. [Google Scholar]
- Ghosh, J.; Sahoo, B.; Poria, S. Prey-predator dynamics with prey refuge providing additional food to predator. Chaos Solitons Fractals 2017, 96, 110–119. [Google Scholar] [CrossRef]
- Xie, Y.; Lu, J.; Wang, Z. Stability analysis of a fractional-order diffused prey-predator model with prey refuges. Physica A 2019, 526, 120773. [Google Scholar] [CrossRef]
- Sahoo, B.; Poria, S. Effects of additional food in a delayed predator-prey model. Math. Biosci. 2015, 261, 62–73. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, B.; Poria, S. Dynamics of predator-prey system with fading memory. Appl. Math. Comput. 2019, 347, 319–333. [Google Scholar] [CrossRef]
- Jana, S.; Chakraborty, M.; Chakraborty, K.; Kar, T. Global stability and bifurcation of time delayed prey-predator system incorporating prey refuge. Math. Comput. Simulat. 2012, 85, 57–77. [Google Scholar] [CrossRef]
- Lu, W.; Xia, Y.; Bai, Y. Periodic solution of a stage-structured predator-prey model incorporating prey refuge. Math. Biosci. Eng. 2020, 4, 3160–3174. [Google Scholar] [CrossRef]
- Bush, A.; Cook, A. The effect of time delay and growth rate inhibition in the bacterial treatment of wastewater. J. Theor. Biol. 1976, 63, 385–395. [Google Scholar] [CrossRef]
- Chen, L. Mathematical Models and Methods in Ecology; Science Press: Beijing, China, 1998. (In Chinese) [Google Scholar]
- Xia, Y.; Cao, J.; Cheng, S. Multiple periodic solutions of a delayed stage-structured predator-prey model with nonmonotone functional responses. Appl. Math. Model. 2007, 9, 1947–1959. [Google Scholar] [CrossRef]
- Chen, Y. Multiple periodic solution of delayed predator-prey systems with type IV functional responses. Nonlinear Anal. 2004, 5, 45–53. [Google Scholar] [CrossRef]
- Aiello, W.; Freedman, H.; Wu, J. Analysis of a model representing stage-structured population growth with state-dependent time delay. SIAM J. Appl. Math. 1992, 52, 885–889. [Google Scholar] [CrossRef]
- Brauer, F.; Ma, Z. Stability of stage-structured population models. J. Math. Anal. Appl. 1987, 126, 301–315. [Google Scholar] [CrossRef]
- Freedman, H.; Wu, J. Persistence and global asymptotic stability of single species dispersal models with stage-structure. Q. Appl. Math. 1991, 49, 351–371. [Google Scholar] [CrossRef]
- Wang, W.; Chen, L. A predator-prey system with stage-structure for predator. Comput. Math. Appl. 1997, 33, 83–91. [Google Scholar] [CrossRef]
- Wang, W.; Mulone, G.; Salemi, F.; Salone, V. Permanence and stability of a stage-structured predator prey model. J. Math. Anal. Appl. 2001, 262, 499–528. [Google Scholar] [CrossRef]
- Fan, M.; Wang, Q.; Zou, X. Dynamics of a nonautonomous ratio-dependent predator-prey system. Proc. R. Soc. Edinb. Sect. A Math. 2003, 133, 97–118. [Google Scholar] [CrossRef]
- Fan, M.; Wong, P.; Agarwal, R. Periodicity and stability in periodic n-species Lotka-Volterra competition system with feedback controls and deviating arguments. Acta. Math. Sin. 2003, 19, 801–822. [Google Scholar] [CrossRef]
- Gaines, R.; Mawhin, J. Coincidence Degree and Nonlinear Differential Equations; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2006; Volume 568. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Xia, Y. Multiple Periodicity in a Predator–Prey Model with Prey Refuge. Mathematics 2022, 10, 421. https://doi.org/10.3390/math10030421
Lu W, Xia Y. Multiple Periodicity in a Predator–Prey Model with Prey Refuge. Mathematics. 2022; 10(3):421. https://doi.org/10.3390/math10030421
Chicago/Turabian StyleLu, Weijie, and Yonghui Xia. 2022. "Multiple Periodicity in a Predator–Prey Model with Prey Refuge" Mathematics 10, no. 3: 421. https://doi.org/10.3390/math10030421
APA StyleLu, W., & Xia, Y. (2022). Multiple Periodicity in a Predator–Prey Model with Prey Refuge. Mathematics, 10(3), 421. https://doi.org/10.3390/math10030421





