Identification of Linear Time-Invariant Systems with Dynamic Mode Decomposition
Abstract
:1. Introduction
- What is the impact of transformations of the data on the resulting DMD approximation?
- Assume that the data used to generate the DMD approximation are obtained from a linear differential equation. Can we estimate the error between the continuous dynamics and the DMD approximation?
- Are there situations in which we are even able to recover the original dynamical system from its DMD approximation?
- We show in Theorem 1 that DMD is invariant in the image of the data under linear transformations of the data.
- Theorem 2 details that DMD is able to identify discrete-time dynamics, i.e., for every initial value in the image of the data, the DMD approximation exactly recovers the discrete-time dynamics.
- In Theorem 3, we show that if the DMD approximation is constructed from data that are obtained via a RKM, then the approximation error of DMD with respect to the ordinary differential equation is in the order of the error of the RKM. If a one-stage RKM is used and the data are sufficiently rich, then the continuous-time dynamics, i.e., the matrix F in Figure 1, can be recovered cf. Lemma 1.
Notation
2. Preliminaries
2.1. Runge–Kutta Methods
2.2. Dynamic Mode Decomposition
3. System Identification and Error Analysis
3.1. Data Scaling and Invariance of the DMD Approximation
3.2. Discrete-Time Dynamics
3.3. Continuous-Time Dynamics and RK Approximation
4. Numerical Examples
- If we first transform the data with the matrixthen compute the DMD approximation, and then transform the results back, the DMD approximation for remains unchanged (see Figure 2e), confirming (14) from Theorem 1. In contrast, the prediction of the dynamics for changes (see Figure 2f), highlighting that DMD is not invariant under state-space transformations in the orthogonal complement of the data.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DMD | dynamic mode decomposition |
| IVP | initial value problem |
| ODE | ordinary differential equation |
| RKM | Runge–Kutta method |
| SVD | singular value decomposition |
References
- Benner, P.; Cohen, A.; Ohlberger, M.; Willcox, K. Model Reduction and Approximation; SIAM: Philadelphia, PA, USA, 2017. [Google Scholar] [CrossRef] [Green Version]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations: An Introduction; UNITEXT, Springer: Berlin, Germany, 2016. [Google Scholar] [CrossRef]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems; Advances in Design and Control; SIAM: Philadelphia, PA, USA, 2005; p. 489. [Google Scholar]
- Hesthaven, J.S.; Rozza, G.; Stamm, B. Certified Reduced Basis Methods for Parametrized Partial Differential Equations; Springer: Berlin, Germany, 2016. [Google Scholar]
- Antoulas, A.C.; Beattie, C.A.; Güğercin, S. Interpolatory Methods for Model Reduction; SIAM: Philadelphia, PA, USA, 2020. [Google Scholar] [CrossRef]
- Mayo, A.J.; Antoulas, A.C. A framework for the solution of the generalized realization problem. Linear Algebra Appl. 2007, 425, 634–662. [Google Scholar] [CrossRef] [Green Version]
- Beattie, C.; Gugercin, S. Realization-independent H2-approximation. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 4953–4958. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Drmač, Z.; Gugercin, S.; Beattie, C. Quadrature-Based Vector Fitting for Discretized H2 Approximation. SIAM J. Sci. Comput. 2015, 37, A625–A652. [Google Scholar] [CrossRef] [Green Version]
- Drmač, Z.; Gugercin, S.; Beattie, C. Vector Fitting for Matrix-valued Rational Approximation. SIAM J. Sci. Comput. 2015, 37, A2345–A2379. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Willcox, K. Data-driven operator inference for nonintrusive projection-based model reduction. Comput. Methods Appl. Mech. Engrg. 2016, 306, 196–215. [Google Scholar] [CrossRef] [Green Version]
- Kutz, J.; Brunton, S.; Brunton, B.; Proctor, J. Dynamic Mode Decomposition; SIAM: Philadelphia, PA, USA, 2016. [Google Scholar]
- Moler, C.; Van Loan, C. Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]
- Mezić, I. Spectral Properties of Dynamical Systems, Model Reduction and Decompositions. Nonlinear Dyn. 2005, 41, 309–325. [Google Scholar] [CrossRef]
- Hairer, E.; Nørsett, S.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems; Springer Series in Computational Mathematics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Kunkel, P.; Mehrmann, V. Differential-Algebraic Equations. Analysis and Numerical Solution; European Mathematical Society: Zürich, Switzerland, 2006. [Google Scholar]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef] [Green Version]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Higham, N. Functions of Matrices: Theory and Computation; Other Titles in Applied Mathematics; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]

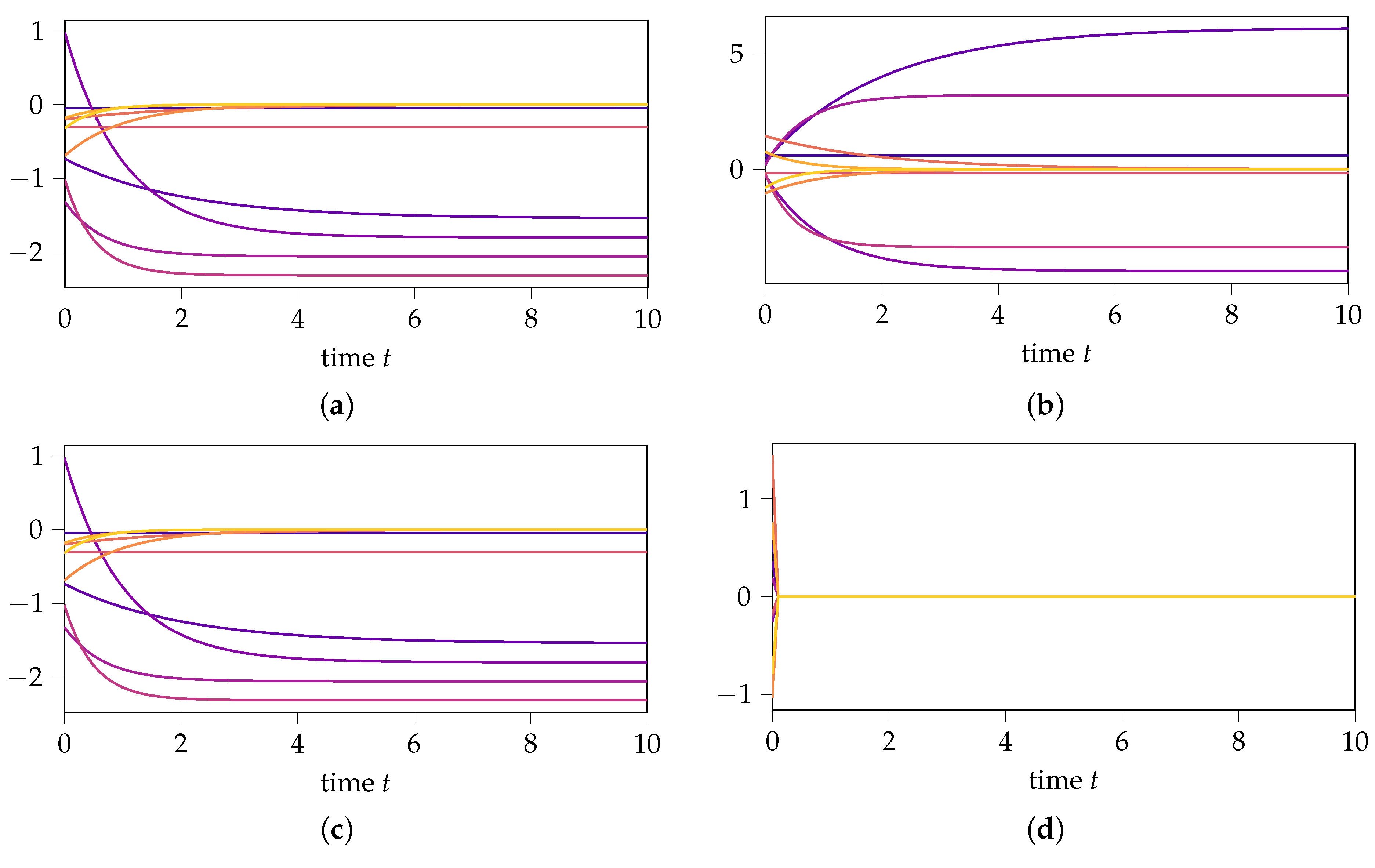
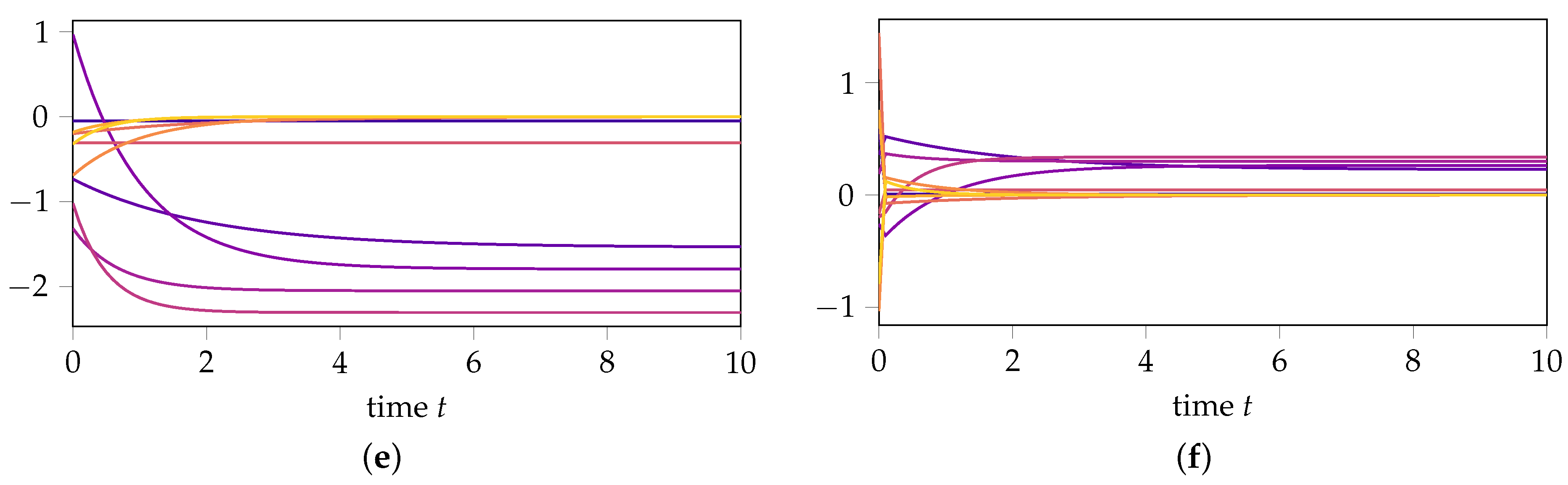
| Method | Lemma 1 | |
|---|---|---|
| explicit Euler | ||
| implicit Euler | ||
| implicit midpoint rule |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heiland, J.; Unger, B. Identification of Linear Time-Invariant Systems with Dynamic Mode Decomposition. Mathematics 2022, 10, 418. https://doi.org/10.3390/math10030418
Heiland J, Unger B. Identification of Linear Time-Invariant Systems with Dynamic Mode Decomposition. Mathematics. 2022; 10(3):418. https://doi.org/10.3390/math10030418
Chicago/Turabian StyleHeiland, Jan, and Benjamin Unger. 2022. "Identification of Linear Time-Invariant Systems with Dynamic Mode Decomposition" Mathematics 10, no. 3: 418. https://doi.org/10.3390/math10030418
APA StyleHeiland, J., & Unger, B. (2022). Identification of Linear Time-Invariant Systems with Dynamic Mode Decomposition. Mathematics, 10(3), 418. https://doi.org/10.3390/math10030418






