1. Introduction
Acrobatics evolution of flocks of birds in our skies and colorful movements of schools of fish in our oceans inspire poets and artists, as well as computer scientists and engineers. Complex behaviors exhibited by swarms of animals [
1,
2], in fact, often inspire the development of swarms of robots, passing through toy models which are progressively enriched and refined [
3].
In a swarm of robots [
3,
4,
5], every single robot is performing simple tasks and showing a simple behavior, but the interaction and information exchange amongst robots allows the accomplishment of more complex tasks, impossible to be achieved by a single unit. Typically, the collaboration in a swarm is decentralized: there is no such a thing as a “robot leader;” instead, every single robot is acting autonomously, reacting to the information received by its neighbors, and transmitting information about its own activity. Swarms of robots show the emergence of global behavior and a form of collective intelligence—a classic example is given by ants’ behavior. Thus, we can talk of
swarm intelligence [
6]. Examples of swarm intelligence are stochastic diffusion search [
7], ant colony optimization [
8], and artificial swarm intelligence [
9].
A swarm is an example of a complex system, which can be instantiated as a robot swarm. Applications of swarm robotics include field tasks, underwater tasks, and air tasks. Terrestrial, underwater, and flying autonomous simple vehicles have thus to be developed and made communicating between them. There are also miniature robots going inside the human body for healthcare purposes [
10].
From an engineering point of view, the connection between local behavior (single or subgroups of robots in a swarm) and the global behavior of a swarm is not trivial. Some existing research exploits particle analogies from physics, with a microscopic behavior described by Langevin equation, and a macroscopic behavior formalized through the Fokker–Planck Equation [
3]. A great inspiration source for mathematical modeling is also given by quantum mechanics and related quantum computing.
Recently, the widespread interest in quantum computing [
11], motivated by its computational power [
12] and formal elegance is influencing several fields of research, e.g., quantum computing has recently been applied to machine learning for artificial intelligence [
13]. In a recent study [
14], fuzzy logic is applied to a swarm of robots. Quantum logic can be considered as a particular case of fuzzy logic [
15].
Some first applications of quantum computing to swarm robotics exploit evolutionary methods inspired by particle modeling dynamics and involving Monte-Carlo simulations [
16], and the strong hypothesis of entanglement between swarm robots [
17].
Quantum applications to robots are a flourishing research field. With the exceptions of some pioneering works, quantum applications to swarm robotics appear instead as a largely unexplored domain. Another gap is the lack of simple connections of robotics, and in particular of swarm robotics, with quantum computing at and fundamental level. A closely-related research [
18], in fact, focuses on a single agent rather than on a swarm of robots.
The use of quantum computing is inspired by core ideas and discoveries in basic quantum mechanics, with energy quantization, state superposition, destructive measurement. Physics Nobel prize Richard Feynman had already hypothesized that the application of quantum principles to computer science could have enabled the construction of more powerful computers [
11]. In quantum computing, the information units
are identified with the ground and excited states of a (hydrogen) atom, respectively. Quantum computing makes use of reversible logic gates, in analogy with invertible quantum operators. The use of quantum computing is mainly motivated by computational increased efficiency. This is a flourishing research area, and thus, a connection with quantum computing can strengthen other fields of research.
In our contribution, we aim to create a general theoretical approach for interacting multi-entities with an emerging swarm behavior. As an instance of complex models with swarm behavior, we focus on robots, defining interaction terms as submatrices of the swarm matrix. As an example of an interaction term, we create a toy model with two robots, modeling robots’ behavior through a quantum circuit.
In fact, in this article we aim to address the issue of the connection between macro- and micro-behaviors in a swarm of robots, crucial for swarm modeling, by using nested matrices and the basics of quantum computing. While we choose to focus on robots, our methodology is meant to be more general: in fact, we model relationships between information exchange and behavior of interacting simple entities, showing an emergent behavior.
First, we discuss a framework to describe the progressive “embodiment” of the swarm idea, from an ideal swarm to a particular system.
Second, we propose a swarm description in terms of nested matrices describing single robots’ behaviors and their interaction. In fact, we can translate the swarm condition into a matrix structure. While in [
17] there is a matrix where all elements (robots) are entangled, here we relax this hypothesis, and we include terms describing autonomous behavior of robots, distinguishing them from the off-diagonal terms for robots’ interactions. A swarm can be described by a block matrix, where the sub-matrices along the main diagonal describe the behavior of isolated robots, and the other sub-matrices indicate the interactions between them.
Third, we work out a simple example with two robots, formalized through four quantum qubits (where the qubit is the quantum information unit), discussing the obtained results.
The experiments with the quantum circuit (corresponding to the truth table of
Table 1) are set up by typing the provided code (
Section 2) on IBM Quantum Composer and running it through a simulator (e.g., QASM simulator) or an IBM-owned quantum computer (e.g., the computer in Bogotà), to which the circuit has been remotely sent. We initialize input qubits through suitable quantum gates (Hadamard, Not, and Ry in our study). Each experiment consists of 1024 shots of the code. The population for each output state is indicated in
Table 2.
The article is organized as follows. In
Section 1.1, we summarize the key concepts of swarm robotics. In
Section 2, we provide details on the mathematical formalization of the core idea, introducing the 4-qubit case study. In
Section 3, we present our results. In
Section 4, we summarize our study and envisage possible research developments.
1.1. Swarms of Robots
Swarm robotics is an application of swarm intelligence [
6,
19] to robotics. The core idea of this discipline is the reference to social insects behavior. In fact, robots in a swarm are meant to autonomously coordinate to achieve complex goals. Organisms in a natural swarm use simple rules to govern their behavior. Every single organism in a swarm can perform a few simple actions. Communication and interaction with other organisms in the swarm enable the achievement of complex goals, e.g., heavy prey transporting, foraging, or massive and complex structures building. An intuitive definition of swarm robotics is the following:
swarm robotics is the study of how a large number of relatively simple physically embodied agents can be designed such that a desired collective behavior emerges from the local interactions among agents and between the agents and the environment [
20].
A swarm of robots is constituted by a set of interacting robots, individually performing a simple job, and collectively achieving a complex task [
3,
4]. A complex task is achieved through task partitioning. Swarms of robots show self-organizational properties. The
swarm behavior is considered as an emerging property. A swarm of robots is characterized by redundancy (the lack of a unity connection does not affect the whole behavior), flexibility (no specialization is required), and scalability (the control algorithms do not depend upon the size of the swarm). In swarm robotics, we can distinguish between a
micro level and a
macro level. The micro-level concerns the local behavior, describing single unities and pairwise interactions. The macro-level concerns global behavior, that is, the behavior of the whole swarm [
3].
1.2. Ideal Swarms
In
Section 2, we introduce the concept of an
ideal swarm of robots. The ideal swarm is ontologically different from any feasible swarm: it is an abstraction. It can be visualized as a swarm of robots that:
Can work in whatever scenario (e.g., on the ground, underwater, on-air);
Can adapt to any possible adverse condition (during a storm, after an earthquake, a tsunami, an avalanche);
Is able to communicate in any imaginable way (though laser, infrared light, visible light, radar, sonar);
Is ready for whichever task (e.g., search and rescue, object retrieval, stacking together to perform a more complex task).
It is impossible to envisage such a swarm or conceive any similar implementation.
In a nutshell, swarm conditions are relationships between individual behaviors of single robots and the overall actions of the swarm. Complex swarm behavior is supposed to emerge from simple individual actions and, as in our model, simple pairwise interactions. Differences in modeling between swimming [
21], flying [
22], and walking swarms [
23] intuitively reside on locomotion features and target scenarios to which robots should be adapted.
2. Theoretical Framework and Methods
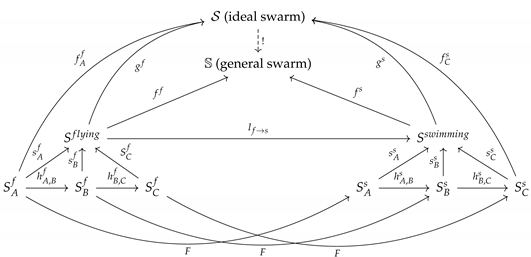
In this article, swarm conditions become conditions on matrices. Let us consider an ideal swarm (
Section 1.2); we can call it
. It can be obtained as an idealization from a general yet feasible swarm structure; let us call it
. Such a general swarm can be specialized into main typologies of swarms, such as
swimming swarms,
flying swarms, and
walking swarms. Each one of these three classes can be distinguished into more and more specific swarms, toward existing swarms, made of simple and cheap robots, which communicate between them and collaborate to perform tasks.
Moving downward in the diagram of Equation (
1) we get a progressive embodiment of the general idea, toward specific realizations of swarms of robots. Vice versa, the upward paths leads to a progressive abstraction. This diagram can be compared with the species classification in biology, which has been formalized through the concept of
colimit in Category Theory [
24]. In [
25], emergence of species similarities are shown through convergence of arrows. Here, emergence of similarities in swarm behaviors can also be thought of as arrows convergence. In fact, diagram (
1) is shaped as a colimit construction. We can have emergent behavior similarities while comparing swarms between them, but also regarding the very definition of a swarm itself: the swarm behavior is more than the sum of single robots’ movements.
In diagram (
1), horizontal comparisons are comparisons across swarms with the same degree of abstraction. The comparison between two swarms
belonging to the category
flying swarms is performed through suitable morphisms
. The comparison between characteristics of the category of
flying robots,
, with the characteristics of the category of
swimming robots,
, is represented by the arrow
. Letter
F between specific swarms of a category
flying and swarms of a category
swimming indicates a functor (a generalization of functions, mapping points of a category into points another category, and morphisms of a category into morphisms of another category). While it is not indicated here for reasons of graphical clarity,
F also maps
,
, and
.
Given an ideal swarm , here treated as a categorical colimit, there must be some characteristics to be taken into account to create a general yet feasible swarm . This is the meaning of the dotted arrow. According to the definition of a colimit in Category Theory, there is a unique morphism such that , where x is the label of a swarm category and · indicates the composition; e.g., . Specific swarms can be related to the abstract swarms through arrow compositions; e.g., and .
Each swarm in diagram (
1) can in principle be described by a matrix. In the case of existing physical swarms (
), all elements of matrices can be computed. Let us now focus on a generic swarm constituted by
n robots. The block matrix describing it is sketched in Equation (
2), where the sub-matrices along the principal diagonal describe the behavior of each single robot
, and the other sub-matrices are the pairwise interaction terms. If these interaction terms are null matrices, there are no swarm effects. Thus, off-diagonal matrices can remind us of the
coherences in quantum mechanics, i.e., the off-diagonal terms representing entanglement.
If there are only
robots, the matrix is simplified as shown in Equation (
3):
The matrix
is a block matrix which can be obtained as in Equation (
4):
where ⊗ is the Kronecker product (tensor product) between matrices. The matrices
describe the behavior of the two isolated robots. The interaction terms
and
are not equal, because they depend on:
Signals transmitted from to and reactions of (term ),
Signals transmitted from to and reactions of (term ), respectively.
How are the interaction terms built? For
, we may consider the signal robot 1 is transmitting to robot 2, and the reaction of the last one. A possible communication is “where I am, where I go.” However, even in a toy model for a swarm it is important to define a task. A task could be, for example, the achievement of a goal, as a target to reach, or as a reward to obtain. (In fact, target search is a classic task for a swarm of robots [
26]). Thus, in our simple description the signal from a robot provides information on its
position as a portion of a linear space and its
target achievement—and thus, the content of the message would be “where I am, what I found.” Hereinafter, to take into account an inner uncertainty related to the decision-making autonomy of robots, we formulate a probabilistic approach based on quantum state superposition. Thus, the possible communication scheme from
to
could be a matrix as:
where each entry is the probability amplitude to have that signal. To enrich this idea, we can add the reaction by
:
where, to a signal from
at time
, corresponds a position displacement by
at time
. The empty entries correspond to the reward from
, that will be made known by the robot only at
. The term
will thus have the same structure. To date, we did not choose a specific framework, because we are interested in creating a general approach, which can be instantiated with simple, interacting robots. In the proposed toy model, we assume to have two simple robots moving back and forth along a line.
Let us now work out a quantitative example. To this aim, we can treat the behavior of each robot as a 2-qubit quantum state, where, for the sake of simplicity, each qubit indicates the superposition of possible states of one-dimensional position (up
, down
) and of “rewards” as a reached target (yes
, no
). In total, we have a system with four qubits, that we used for a simulation with IBM simulators and real quantum computers. (
https://www.ibm.com/quantum-computing/ accessed on 10 December 2021). In Equation (
6), we indicate probability amplitudes to obtain a specific measure outcome as
.
The matrix of Equation (
5) will then be:
Let us analyze a possible realization of the scheme of communication/reaction building a reversible logic gate. The logic behind the truth tables in
Table 1 is the following. At time
, if
is in position up (
) and it gets the reward (
), then
reaches it at
, independently from its former position. However, if
does not get the reward (
), then
explores the space down (
). Same reasoning if the starting position is the inverse. Then, the roles of
and
are exchanged at
and
. (Time in quantum gates is simultaneous, while we know that a robot, received the communication from the other one, implements the decision to change the position or keep it in the following time instant). The permutation matrix associated with
Table 1 is presented in Equation (
8), with quantum states ordered as
.
The matrix in Equation (
9) shows the Toffoli gate, exploited to implement our proposed gate. The Toffoli gate is a reversible quantum gate, which takes two inputs and gives one output. It is often indicated as ccx, that is, a not (x) with two conditions.
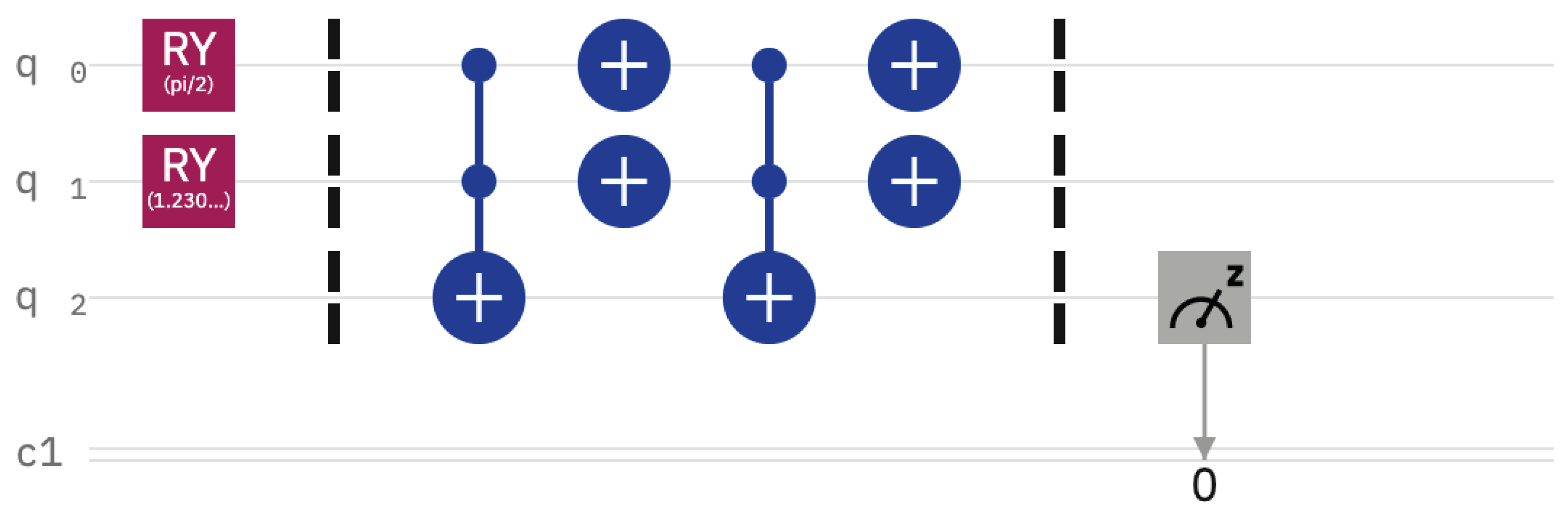
Figure 1 shows the considered quantum circuit.
In
Section 3, we show our results, obtained through the interface IBM Quantum Composer (
https://quantum-computing.ibm.com/composer/ accessed on 10 December 2021), an open computing environment, with simulators and quantum computers which can be accessed remotely. Real IBM quantum computers allow up to five qubits.
Because it was not possible to change probabilities directly in Quantum Composer, we created the Qiskit (
https://qiskit.org/ accessed on 10 December 2021) code and then exported the code lines in QASM, the coding environment required for Quantum Composer. In this way, each specific probability amplitude was obtained as a special quantum gate
; e.g., initial_state = [0.5, 0.5] (that is,
) was written as
. This particular state can also be obtained with a Hadamard gate acting on
. In the following, we present our code. The state
is obtained through a Not gate as
, because states in Quantum Composer are initialized to 0 by default. In the code, if both
and
are
(indicating position 0 and failure to reach the target, respectively), then
is flipped to
, that is,
goes to position 1. If both
and
are
(indicating position 1 and success in reaching the target, respectively), then
is flipped to
as well. This second effect is obtained by adding Not gates (x) before qubits
and
. If
and
are different between them, then
remains in the default state
.
OPENQASM 2.0;
include “qelib1.inc”
qreg q[3];
creg c[1]; //classic qubit for the measure
//states are initialized as 0 by default.
ry(pi/2) q[0]; // to obtain 0.5, 0.5 as amplitudes
//x q[1]; // to obtain input amplitude 0.0, 1.0, that is, eigenstate |1>
ry(1.2309594) q[1]; // for input amplitudes 0.7, 0.3
// 1.9106332 for input amplitudes 0.3, 0.7
barrier q[0], q[1], q[2];
ccx q[0], q[1], q[2];
x q[0];
x q[1];
ccx q[0], q[1],q[2];
x q[0];
x q[1];
barrier q[0], q[1], q[2];
measure q[2] -> c[0];
3. Results
The dataset used in the experiment is summarized in
Table 2. To replicate the experiment, it is sufficient to create an account on IBM Quantum (
https://www.ibm.com/quantum-computing/ accessed on 10 December 2021), open a Quantum Composer new file, type the given code, and customize the initial states according to the
entries in
Table 1. In IBM Quantum Composer, states are initialized by default as
. To have
, it is sufficient to use a NOT gate:
. To have the
superposition of 0 and 1, one can use the Hadamard gate H or the
gate. To obtain the other combinations, it is necessary to opportunely change the angle of the
gate. Then, one can hit the “Setup and Run” command, selecting one of the quantum computers available or one of the simulators, and waiting in a queue for the required time. The obtained values can slightly fluctuate because of quantum error, and because of the very nature of quantum world: probabilistic. No other parameters are required in this experiment. We tested the following combinations of initial states:
In
Table 2, we compare the outcomes obtained with IBM simulators and IBM quantum computers. With the quantum computer, the results are mostly as expected, but the noise is high; the simulators give a result that perfectly matches theoretical expectations.
A case of particular interest are the eigenstates, to measure the amount of possible quantum noise, and the case with random position of ( with of chances to be in 0 and to be in 1), and maximal certitude on the reward information ( with of chances to be in 1 and 0% to be in 0, or vice versa).
Results with real quantum computers can differ according to the chosen machine, and they present a higher noise. The noise is particularly evident when we tested
as eigenstates. The simulator gave us all the outcomes of
as 0 or as 1, as expected from
Table 1, while the quantum computer also presented a non-zero population of the unexpected outcome. Each run of the code gave 1024 shots of measurements. Fluctuations at each run of the code, not displayed here, are present for both typologies of computing devices.
It is not possible to carry out a comparison with other methods, because the proposed methodology is new. To the best of our knowledge, the only case of a close-related research is the application proposed by Koukam et al. [
18], where an IBM Quantum computer has been used for a reactive agent. In their study, a single robot (and not a swarm) modifies its behavior according to the external information recovered through suitable sensors.
4. Discussion and Conclusions
In this article, we started from theoretical considerations on swarms of robots, from ideal, abstract swarms down to typologies of swarms with specific existing realizations. We proposed a matrix description of a generic swarm, trying to connect the action of each single robot with the overall behavior. The proposed swarm matrix is a block matrix with sub-matrices indicating the motion of single robots, and off-diagonal blocks representing pairwise interaction terms, with signals from the i-th robot and behavioral response for the j-th robot. Aiming to shape an example of these interaction terms, we exploit the basics of quantum computing to work out a toy model with four qubits, implementing it through IBM computational resources and analyzing the obtained results.
The presented results provide information regarding output states’ likelihood. This information is related to the decision-making outcomes in a toy 2-robot swarm. The input represents incoming information from the first robot, and the output indicates the behavioral response from the second robot. The proposed quantum circuit acts as an overall gate, corresponding to an interaction term at time t in the proposed matrix representation. The interaction terms model local behaviors related to global behaviors through the proposed matrix.
Let us briefly analyze the pros and cons of the proposed strategy. The cons are mainly related to technological limitations: IBM Quantum computers are freely available only up to five qubits, while IBM Quantum simulators are available up to 32, 63, 100 and, very recently (after the submission of this article), 5000 qubits. The pros include computational power of quantum computing, proved for classic problems such as integer factorization, and generalization power of the proposed theoretical framework. In fact, we can consider robot interactions as instances of social behaviors, be they of people, animals, or neuronal entities. Thus, the proposed methodology is not limited to robots: it can instead be applied to interactions amongst multiple entities, constituting complex systems with an emergent behavior.
Future developments of the proposed research will involve the construction of more complex models, with a higher number of qubits, describing more degrees of freedom of robots. From the conceptual level, additional degrees of freedom can help us model more and more complex group behaviors, also imitating aspects of natural swarm scenarios [
1,
2]. Another point to be addressed in future research is map building as an effect of memory where robots explore their environment looking for the target. Further research can draw upon existing studies on agent-based decision-making [
27], localization and map building developed for single [
28] and multiple robots [
29,
30], to build a theoretical unification and envisage a
quantum perspective on swarms, also exploiting quantum computing computational resources.