Stochastic Analysis of Nonlinear Cancer Disease Model through Virotherapy and Computational Methods
Abstract
1. Introduction
2. Deterministic Formulation
2.1. Analysis of Model
2.2. Reproduction Number
2.3. Local Stability
3. Stochastic Cancer Virotherapy Model
3.1. Euler Maruyama Method
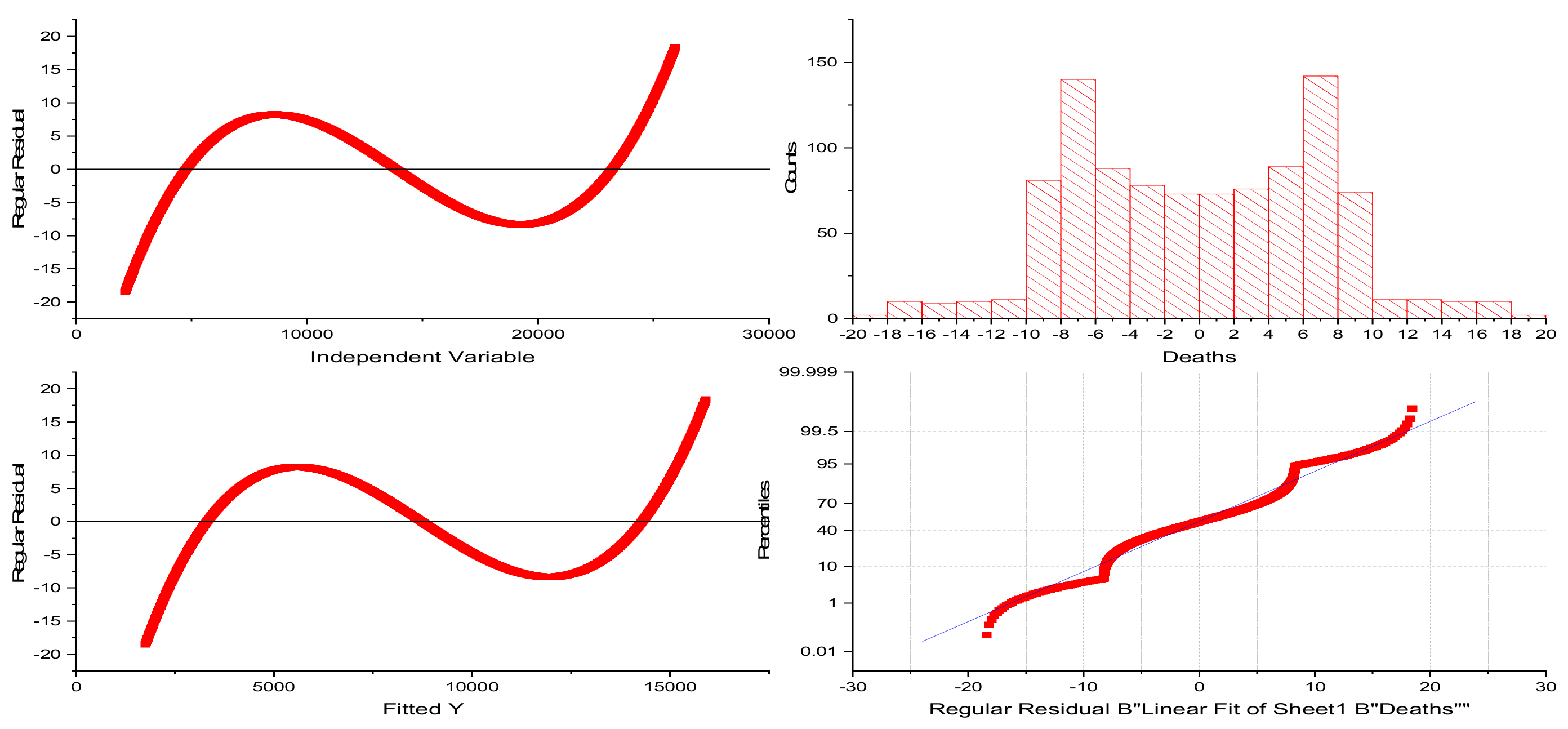
3.2. Data Curation
3.3. Non-Parametric Perturbation of Model
3.4. Positivity and Boundedness of Stochastic Model
4. Computational Methods
4.1. Stochastic Euler
4.2. Stochastic Runge Kutta
4.3. Stochastic NSFD
4.4. Stability Analysis
- (i)
- .
- (ii)
- .
- (iii)
- .
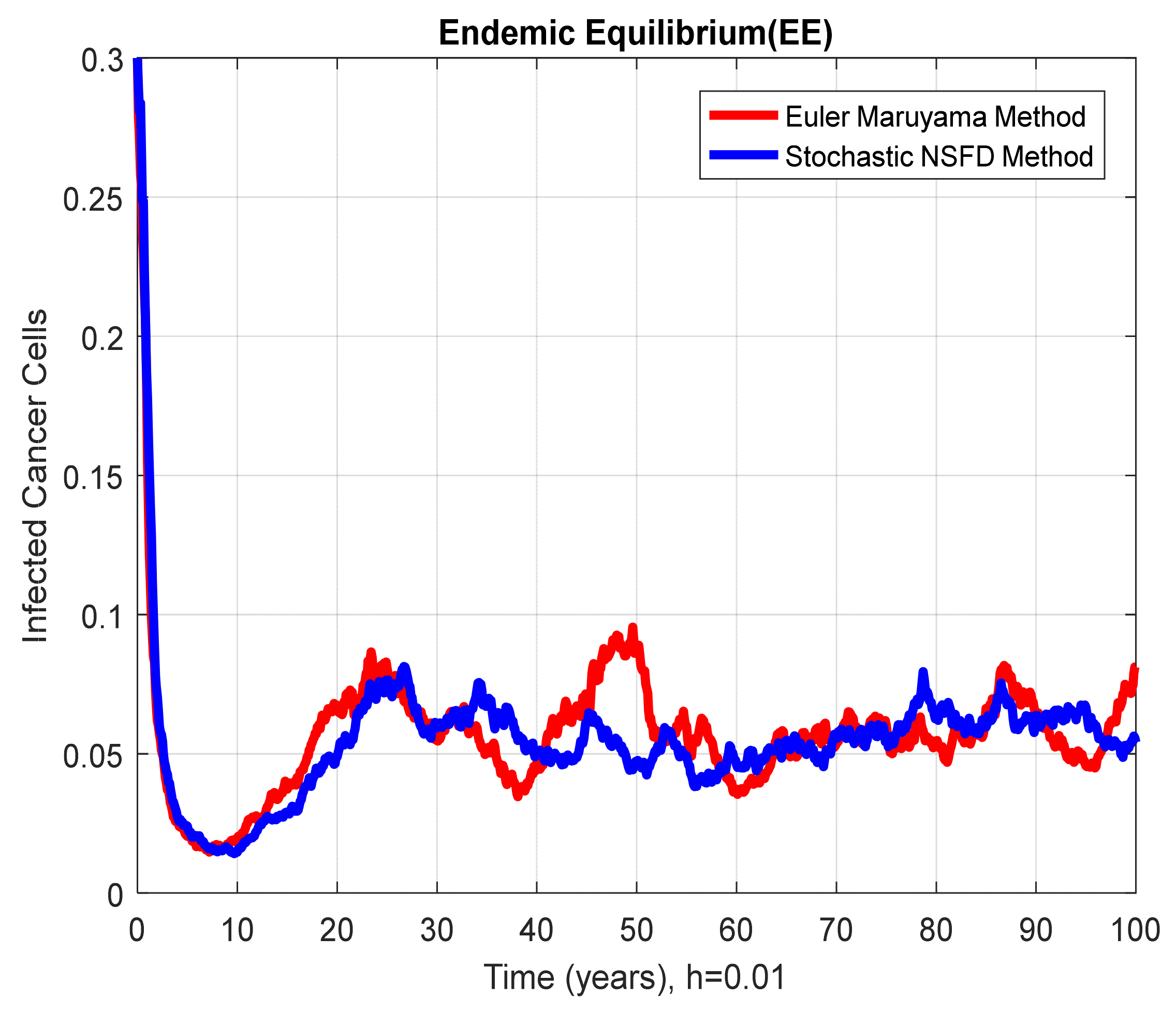
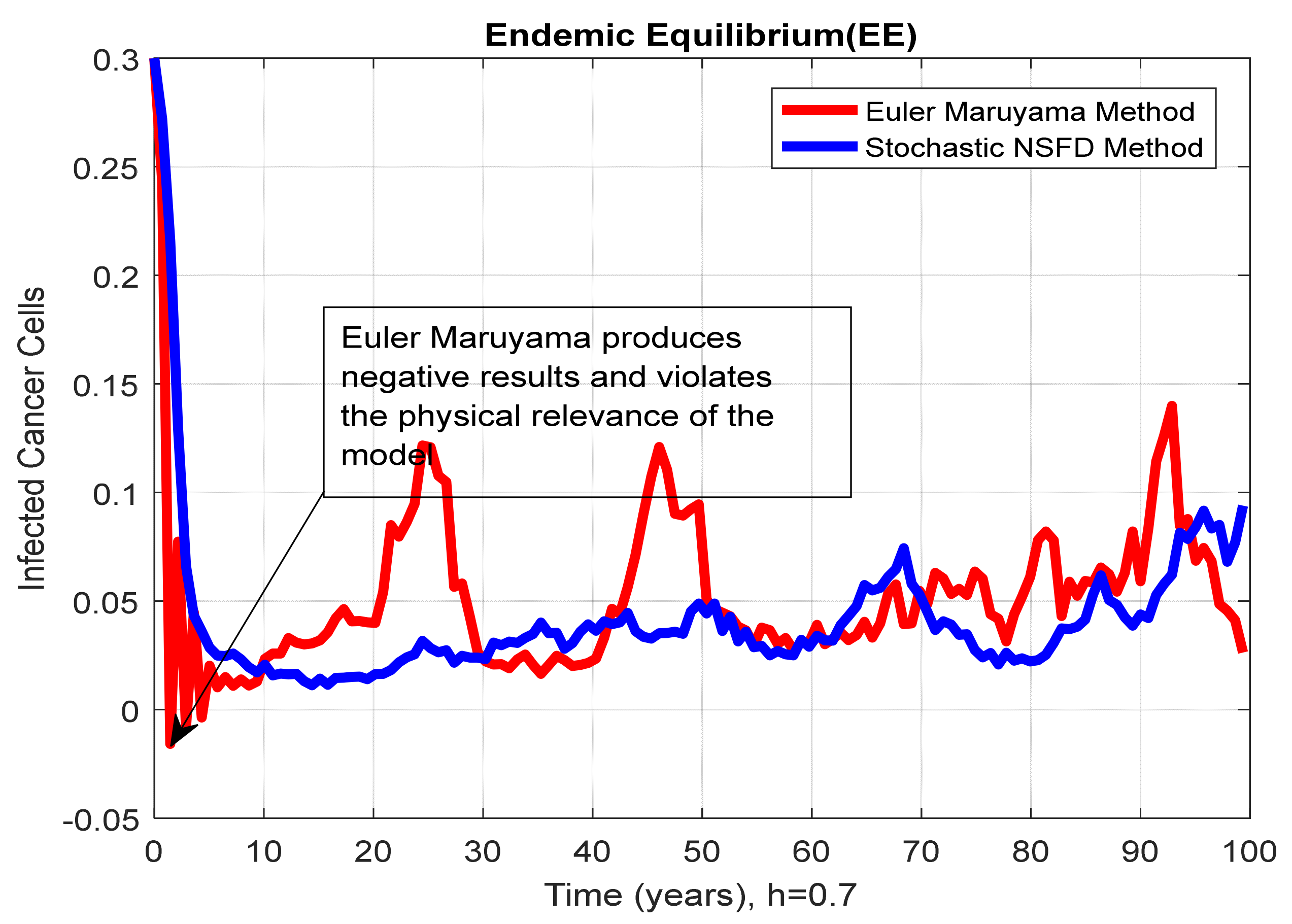
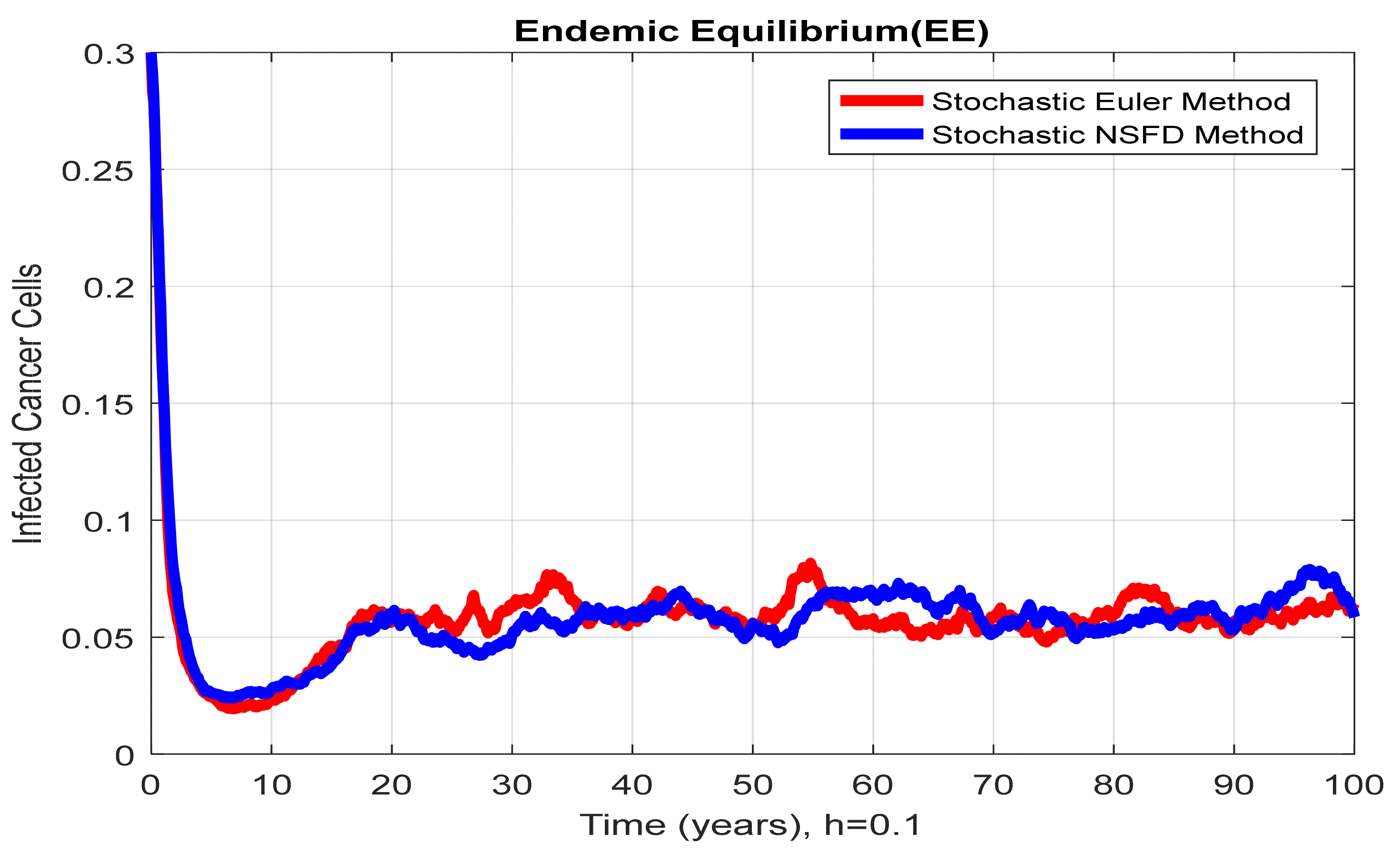
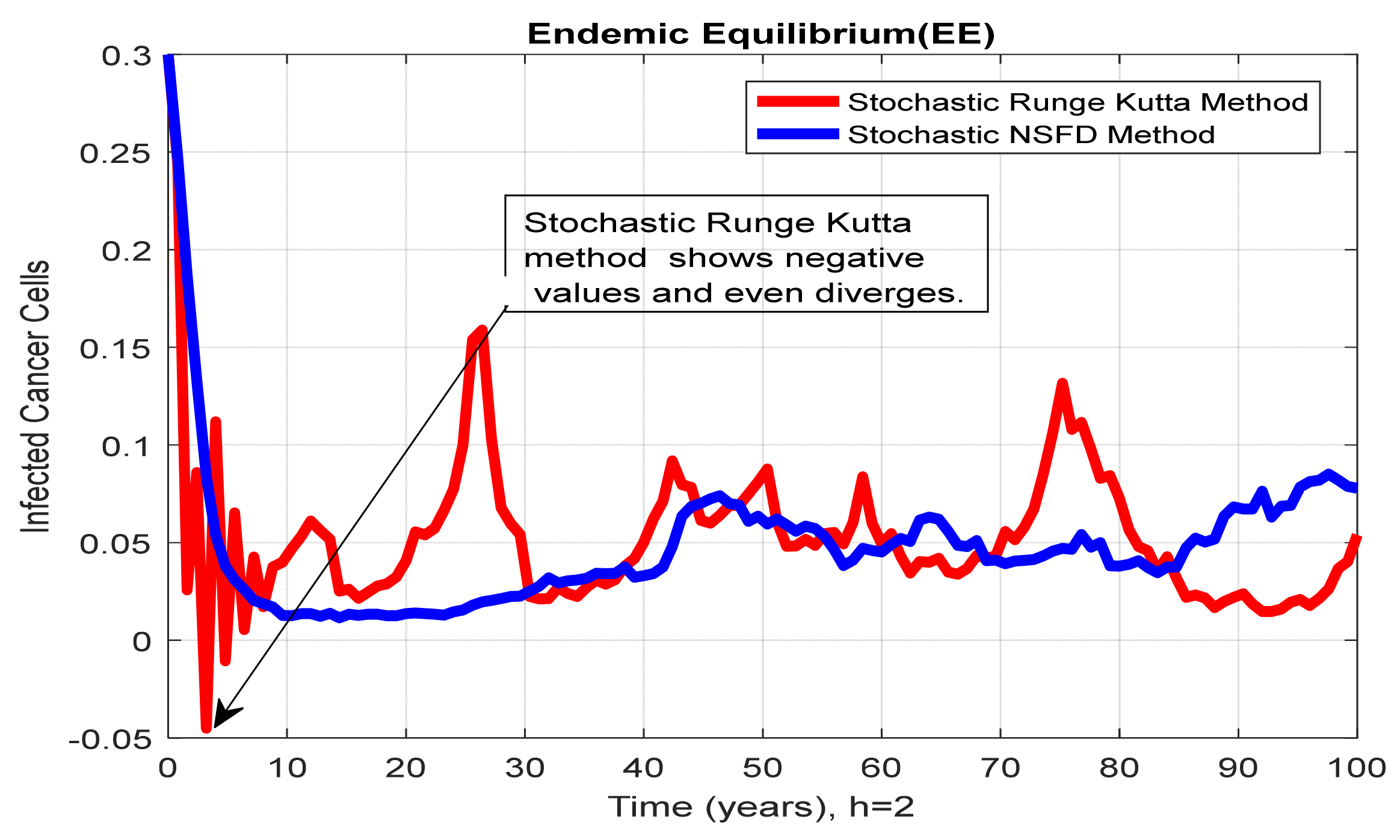
4.5. Comparison Section
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Tuwairqi, A.; Johani, O.N.A.; Simbawa, A.E. Modeling Dynamics of Cancer Virotherapy with Immune Response. Adv. Differ. Equ. 2020, 438, 1–26. [Google Scholar]
- Crivelli, J.J.; Földes, J.; Kim, P.; Wares, J.R. A mathematical model for cell cycle-specific cancer virotherapy. J. Biol. Dyn. 2012, 6, 104–120. [Google Scholar] [CrossRef] [PubMed]
- Nouni, A.; Hattaf, K.; Yousfi, N. Dynamics of a Virological Model for Cancer Therapy with Innate Immune Response. Complexity 2020, 2020, 8694821. [Google Scholar] [CrossRef]
- Storey, K.M.; Lawler, S.E.; Jackson, T.L. Modeling Oncolytic Viral Therapy, Immune Checkpoint Inhibition, and the Complex Dynamics of Innate and Adaptive Immunity in Glioblastoma Treatment. Front. Physiol. 2020, 11, 151. [Google Scholar] [CrossRef] [PubMed]
- Abernathy, Z.; Abernathy, K.; Stevens, J. A mathematical model for tumor growth and treatment using virotherapy. AIMS Math. 2020, 5, 4136–4150. [Google Scholar] [CrossRef]
- Matos, L.A.; Franco, S.L.; McFadden, G. Oncolytic Viruses and the Immune System: The Dynamic Duo. Mol. Theory 2020, 4, 349–358. [Google Scholar]
- Makaryan, S.Z.; Cess, C.G.; Finley, S.D. Modeling immune cell behavior across scales in cancer. Wiley Interdiscip. Rev. Syst. Biol. Med. 2020, 12, e1484. [Google Scholar] [CrossRef]
- Malinzi, J.; Eladdadi, A.; Sibanda, P. Modelling the spatiotemporal dynamics of chemovirotherapy cancer treatment. J. Biol. Dyn. 2017, 11, 244–274. [Google Scholar] [CrossRef]
- Bajzer, Ž.; Carr, T.; Josić, K.; Russell, S.J.; Dingli, D. Modeling of cancer virotherapy with recombinant measles viruses. J. Theor. Biol. 2008, 252, 109–122. [Google Scholar] [CrossRef]
- Timalsina, S.; Tian, J.P.; Wang, J. Mathematical and Computational Modeling for Tumor Virotherapy with Mediated Immunity. Bull. Math. Biol. 2017, 79, 1736–1758. [Google Scholar] [CrossRef]
- Rommelfanger, D.M.; Offord, C.P.; Dev, J.; Bajzer, Z.; Vile, R.G.; Dingli, D. Dynamics of Melanoma Tumor Therapy with Vesicular Stomatitis Virus: Explaining the Variability in Outcomes Using Mathematical Modeling. Gene Ther. 2012, 19, 543–549. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, Q.; Pan, J. A deterministic and stochastic model for the system dynamics of tumor–immune responses to chemotherapy. Phys. A Stat. Mech. Its Appl. 2018, 500, 162–176. [Google Scholar] [CrossRef]
- Eftimie, R.; Eftimie, G. Tumour-associated Macrophages and Oncolytic Virotherapies: A mathematical investigation into a complex-dynamics. Lett. Biomath. 2018, 5, S6–S35. [Google Scholar] [CrossRef]
- Santiago, D.N.; Heidbuechel, J.P.W.; Kandell, W.M.; Walker, R.; Djeu, J.; Engeland, C.E.; Abate-Daga, D.; Enderling, H. Fighting Cancer with Mathematics and Viruses. Viruses 2017, 9, 239. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.P.; Lee, P.P. Modeling protective anti-tumor immunity via preventative cancer vaccines using a hybrid agent-based and delay differential equation approach. PLoS Comput. Biol. 2012, 8, e1002742. [Google Scholar] [CrossRef]
- Berg, D.R.; Offord, C.P.; Kemler, I.; Ennis, M.K.; Chang, L.; Paulik, G.; Bajzer, Z.; Neuhauser, C.; Dingli, D. In vitro and in silico multidimensional modeling of oncolytic tumor virotherapy dynamics. PLoS Comput. Biol. 2019, 15, e1006773. [Google Scholar] [CrossRef]
- International Agency for Research on Cancer. Available online: https://gco.iarc.fr/today/data/factsheets/populations/586-pakistan-fact-sheets.pdf (accessed on 1 March 2021).
- Ijaz, M.F.; Attique, M.; Son, Y. Data-driven cervical cancer prediction model with outlier detection and over-sampling methods. Sensors 2020, 20, 2809. [Google Scholar] [CrossRef]
- Ijaz, M.F.; Alfian, G.; Syafrudin, M.; Rhee, J. Hybrid prediction model for type-2 diabetes and hypertension using DBSCAN-based outlier detection, synthetic minority over-sampling technique (SMOTE), and random forest. Appl. Sci. 2018, 8, 1325. [Google Scholar] [CrossRef]
- Mandal, M.; Singh, P.K.; Ijaz, M.F.; Shafi, J.; Sarkar, R. A tri-stage wrapper-filter feature selection framework for disease classification. Sensors 2021, 21, 5571. [Google Scholar] [CrossRef]
- Panigrahi, R.; Borah, S.; Bhoi, A.K.; Ijaz, M.F.; Pramanik, M.; Kumar, Y.; Jhaveri, R.H. A consolidated decision tree-based intrusion detection system for binary and multiclass imbalanced datasets. Mathematics 2021, 9, 751. [Google Scholar] [CrossRef]
- Panigrahi, R.; Borah, S.; Bhoi, A.K.; Ijaz, M.F.; Pramanik, M.; Jhaveri, R.H.; Chowdhary, C.L. Performance assessment of supervised classifiers for designing intrusion detection systems: A comprehensive review and recommendations for future research. Mathematics 2021, 9, 690. [Google Scholar] [CrossRef]
- Srinivasu, P.N.; SivaSai, J.G.; Ijaz, M.F.; Bhoi, A.K.; Kim, W.; Kang, J.J. Classification of skin disease using deep learning neural networks with mobile net V2 and LSTM. Sensors 2021, 21, 2852. [Google Scholar] [CrossRef] [PubMed]
- Arif, M.S.; Raza, A.; Rafiq, M.; Bibi, M.; Abbasi, J.N.; Nazeer, A.; Javed, U. Numerical Simulations for Stochastic Computer Virus Propagation Model. Comput. Mater. Contin. 2020, 62, 61–77. [Google Scholar] [CrossRef]
- Shatanawi, W.; Arif, M.S.; Raza, A.; Rafiq, M.; Bibi, M.; Abbasi, J.N. Structure-Preserving Dynamics of Stochastic Epidemic Model with the Saturated Incidence Rate. Comput. Mater. Contin. 2020, 64, 797–811. [Google Scholar] [CrossRef]
- Bayram, M.; Partal, T.; Buyukoz, G.O. Numerical methods for simulation of stochastic differential equations. Adv. Differ. Equ. 2018, 2018, 17. [Google Scholar] [CrossRef]
- Abukhaled, M.I.; Allen, E.J. A class of second-order Runge-Kutta methods for numerical solution of stochastic differential equations. Stoch. Anal. Appl. 1998, 16, 977–991. [Google Scholar] [CrossRef]
- Abukhaled, M.; Allen, E.J. A recursive integration method for approximate solution of stochastic differential equations. Int. J. Comput. Math. 1998, 66, 53–66. [Google Scholar] [CrossRef]
- Sghir, A.; Hadiri, S. A new numerical method for 1-D backward stochastic differential equations without using conditional expectations. Random Oper. Stoch. Equ. 2020, 28, 79–91. [Google Scholar] [CrossRef]
- Halidias, N. A novel approach to construct numerical methods for stochastic differential equations. Numer. Algorithm 2013, 66, 79–87. [Google Scholar] [CrossRef]
- Higham, D.J.; Mao, X.; Szpruch, L. Convergence, non-negativity and stability of a new Milstein scheme with applications to finance. arXiv 2012. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Convergence%2C+non-negativity+and+stability+of+a+new+Milstein+scheme+with+applications+to+finance&btnG= (accessed on 1 March 2021).
- Rebiha, Z. New numerical method for solving nonlinear stochastic integral equations. Владикавказский Математический Журнал 2020, 22. Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=New+numerical+method+for+solving+nonlinear+stochastic+integral+equations&btnG= (accessed on 1 March 2021).
- Słomiński, L. Stability of strong solutions of stochastic differential equations. Stoch. Process. Their Appl. 1989, 31, 173–202. [Google Scholar] [CrossRef][Green Version]
- Abukhaled, M.I. Mean square stability of second-order weak numerical methods for stochastic differential equations. Appl. Numer. Math. 2004, 48, 127–134. [Google Scholar] [CrossRef]

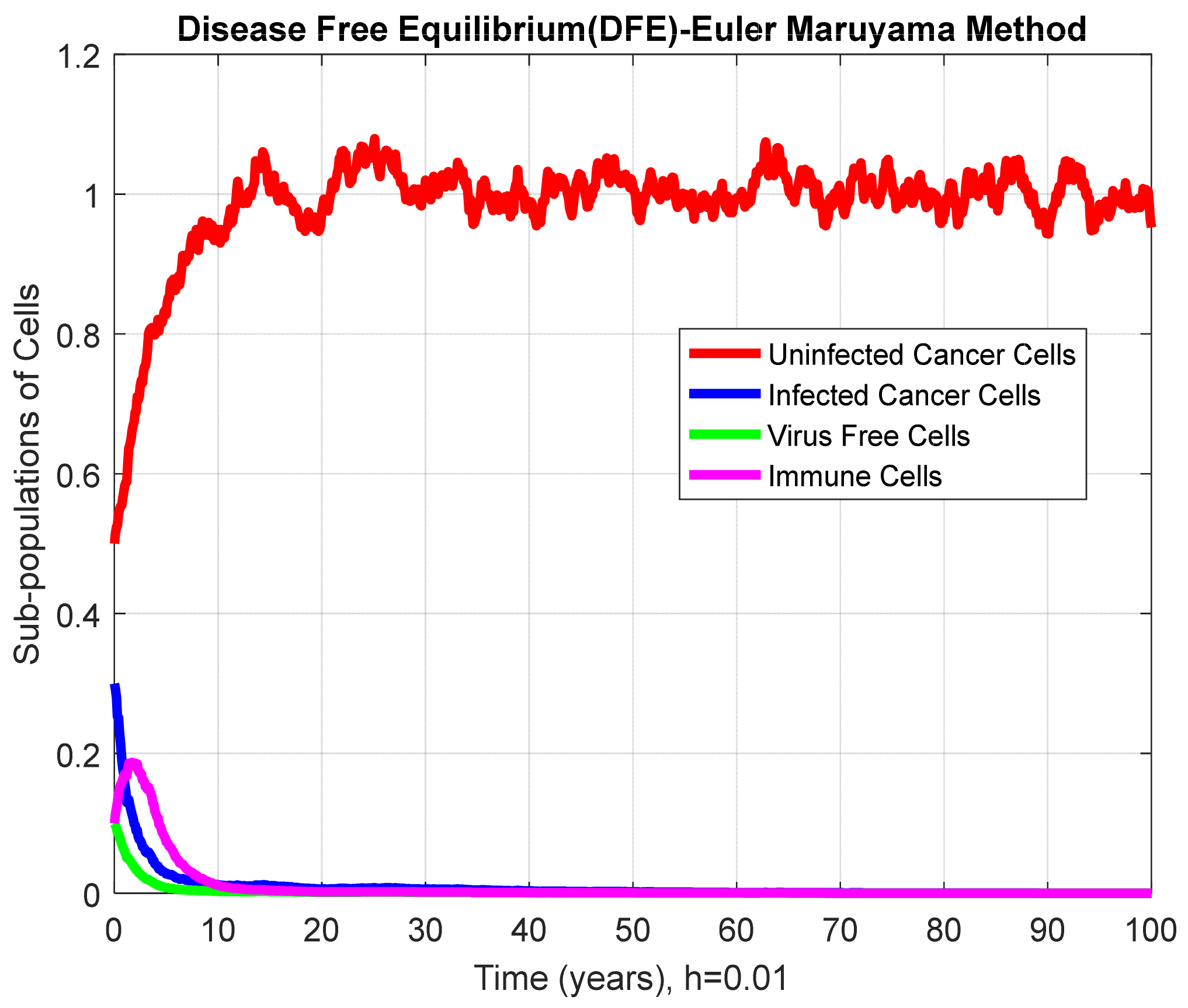
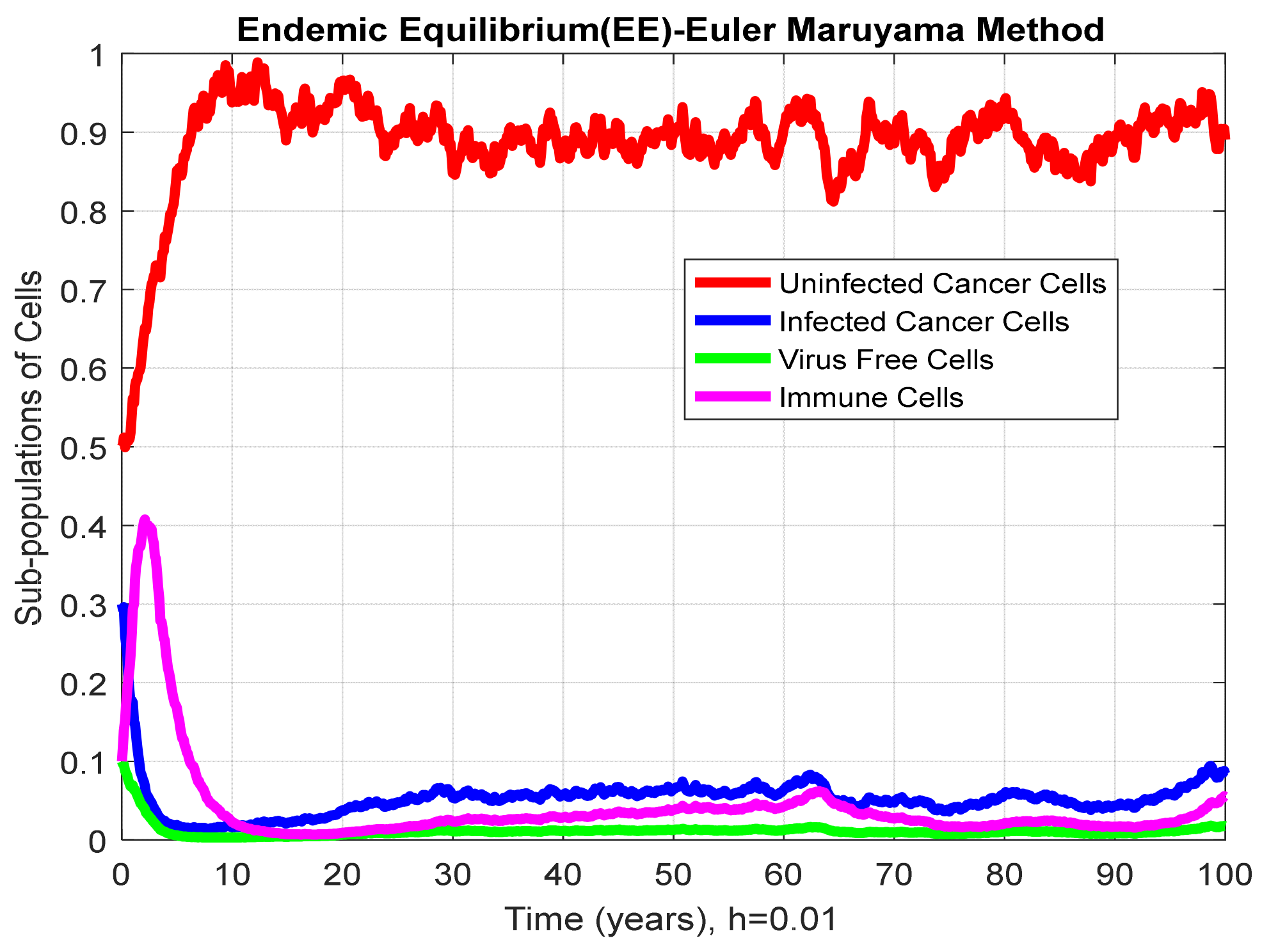




| Parameters | Values |
|---|---|
| 0.5 | |
| a | 5.1 (EE) 3.1 (DFE) |
| 0.63 | |
| 0.5 | |
| C | 5.048 (EE) 3.048(DFE) |
| b | 0.22 |
| 0.016 | |
| 0.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Awrejcewicz, J.; Rafiq, M.; Ahmed, N.; Mohsin, M. Stochastic Analysis of Nonlinear Cancer Disease Model through Virotherapy and Computational Methods. Mathematics 2022, 10, 368. https://doi.org/10.3390/math10030368
Raza A, Awrejcewicz J, Rafiq M, Ahmed N, Mohsin M. Stochastic Analysis of Nonlinear Cancer Disease Model through Virotherapy and Computational Methods. Mathematics. 2022; 10(3):368. https://doi.org/10.3390/math10030368
Chicago/Turabian StyleRaza, Ali, Jan Awrejcewicz, Muhammad Rafiq, Nauman Ahmed, and Muhammad Mohsin. 2022. "Stochastic Analysis of Nonlinear Cancer Disease Model through Virotherapy and Computational Methods" Mathematics 10, no. 3: 368. https://doi.org/10.3390/math10030368
APA StyleRaza, A., Awrejcewicz, J., Rafiq, M., Ahmed, N., & Mohsin, M. (2022). Stochastic Analysis of Nonlinear Cancer Disease Model through Virotherapy and Computational Methods. Mathematics, 10(3), 368. https://doi.org/10.3390/math10030368








