Adaptive Sliding Mode Control of Robot Manipulators with System Failures

Abstract

This paper presents a novel adaptive sliding mode controller for a class of robot manipulators with unknown disturbances and system failures, which can well achieve the asymptotic tracking, and avoid some possible singularity problems. A new virtual controller is designed such that the chosen Lyapunov function can be transformed into a non-Lipschitz function, based on which, the system states can arrive at the specified sliding surface within a finite time regardless of the existence of system failures/faults. By fusing an integral fast terminal nonsingular SMC and a robust adaptive technique, the tracking error can be steered into a preset range in a set time and some possible singularity problems are avoided elegantly. With our proposed scheme, the loss coefficient is well estimated, and the stability of the system can be guaranteed even in the presence of the total loss of actuator outputs. The experiment and simulation results are presented to illustrate the effectiveness of the proposed control scheme.

1. Introduction

Nowadays, fault-tolerant control (FTC) has drawn a great deal of attention from many researchers. This is due to the fact that in the modern industrial field, actuators and sensors are vulnerable to faults while the robot is operating, which has a high probability of leading to closed-loop instability or even causing a security incident. Generally, actuator failure can be roughly categorized into two classes: (1) partial loss of effectiveness (PLOE), and (2) total loss of effectiveness (TLOE). In robot systems, PLOE indicates that performance degradation affects actuators at one or more robot joints. Meanwhile, the TLOE means that actuators at one or more robot joints are completely out of control. Over lastest decades, a number of active approaches have been reported to compensate actuator failure. In [1,2,3], a control method based on fault diagnosis observer was developed for actuator faults of nonlinear systems. Moreover, in [4,5,6], the adaptive fault compensation control method was proposed to avoid the influence of fault diagnosis errors, which can provide excellent steady-state performance. In addition, PD and PID controllers [7,8], calculated torque controller [9], intelligent and learning controller [10], optimal controller [11], robust controller [12] were also used to compensate faults without fault diagnosis observer. However, such methods can only guarantee asymptotic convergence instead of finite-time convergence, which limits the tracking accuracy of the robot. As a result, guaranteeing the finite-time convergence of the robot becomes one of the most important procedures developing the high-accuracy controller, and recently draws considerable concerns.

To obtain the finite-time convergence of fault system, sliding mode control (SMC) has been spent and developed [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. In [16], Tarek proposed a nonsingular fast terminal SMC(NFTSMC) for obtaining fast finite-time convergence without singular problem. However, the NFTSMC did not consider a transient response. As an extension of sliding mode control, an integral SMC was investigated in [19] to enhance the transient response. But the individual approaches based on NFTSMC or ISMC have just only solved one aspect and ignored the other problems of the conventional SMC. With the recourse of ISMC and NFTSMC, Xu [20,21] further proposed integral terminal SMC (ITSMC) to obtain both finite-time convergence and fast transient response. By using acceleration information to reconstruct the control output, a more promising strategy named as high-order SMC(HSMC) was further developed in [35,36,37] to cancel the chattering phenomenon. However, in practice, the above motioned methods are only suitable for PLOE, without proper compensation, such the TOLE may cause performance degradation and even lead to instability of closed-loop systems. So, compensating for TLOE is an important issue in the adaptive control design.

To deal with this challenging problem, recently, some promising results have been reported. In [39,40], By discarding the faulty joints and remodeling the normal joints, two algorithms based on the redundant joint are suggested to minimize the speed jump of the end effector. Based on the assumption that the two redundant actuators cannot lose control at the same time, a redundant control method is developed byin [41]. Furthermore, Guanyu Lai [42] update a tuning function method for an infinite number of actuator failures. This method is novel and practical to deal with the TLOE, but this method is only suitable for general nonlinear systems, without consideration of the complex nonlinear system such as robot manipulator.

Inspired by the prior works mentioned above, we propose a novel integral nonsingular fast terminal sliding mode control (INFTSMC) for a robot with unknown disturbance and system faults, and the proposed approach can provide a finite-time convergence without singular problem, fast transient response, and high tracking precision. One of the most challenging difficulties that obstruct the development of our controller lies in the fact that tracking error is required to converge to zero within a set time in the presence of system failure, while the upper bound and type of failure are unknown. To remove this obstacle, a backstepping adaptive SMC scheme is proposed, based on which the tracking error can converge to a preset range around zero, and further converge to zero within a finite time. Technically, the main tasks in our scheme are to design a virtual control function with exponential terms to guarantee finite-time convergence of sliding surface to zero, and at the same time to design a proper sliding mode switching function to guarantee finite-time convergence of tracking error to zero. Furthermore, a redundant controller is newly proposed to ensure the stability under the case of TLOE. the main contributions of this paper are as follows:

(1)

A new virtual control scheme is constructed, based on which the continuous Lyapunov function can be transferred into the non-Lipschitz function. With this non-Lipschitz function, the system states can arrive at the specified sliding surface within a finite time even in the presence of actuator failure. Actually, such a design is not a trivial task, since it involves a major modification to the backstepping design. In particular, with the proposed scheme and INFTSMC, the tracking error cannot only be steered into a preset range, but also steered into zero within a finite time by adjusting sliding surface parameters.

(2)

In comparison with the previous works [16,19], our proposed controller additionally contains an integral fast terminal nonsingular SMC(IFTNSMC) and a robust adaptive technique. Specifically, the tracking error can be steered into a preset range in a set time and some possible singularity problems are successfully avoided. Subsequently, the robust adaptive mechanism is constructed to cancel the effects caused by actuator failures and external disturbances. Consequently, the proposed robust adaptive SMC is more feasible than those traditionally proposed.

(3)

By designing a new adaptive mechanism, the loss coefficient is well estimated and our proposed scheme can maintain the stability of the system for the TLOE case.

With the aid of these efforts, the stability of the system can be guaranteed no matter whether PLOE or TLOE.

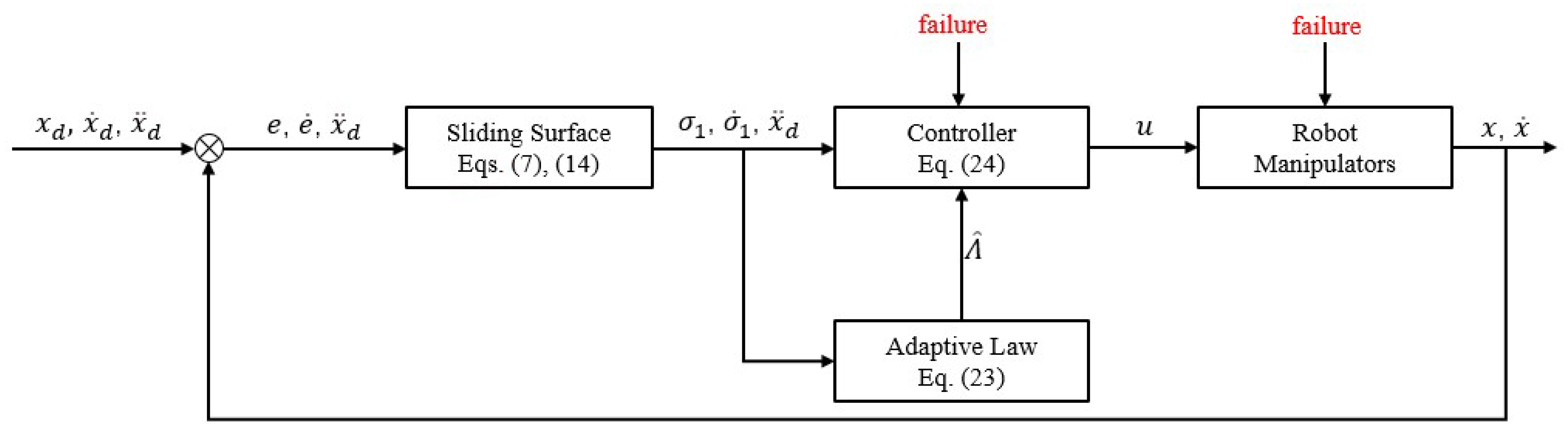
2. Problem Statement

Consider the dynamics of the robot with n-degrees can be expressed as

$$\begin{array}{cc}\hfill \ddot{q}=& M^{-1}\left(q\right)\left(\tau -H(q,\dot{q})\dot{q}-F\left(\dot{q}\right)-G\left(q\right)-{\tau }_d\right)\hfill \\ \hfill & +\gamma (t-T_f)\varphi (q,\dot{q},\tau )\hfill \end{array}$$

(1)

where $M\left(q\right)\in {\Re }^{n\times n}$ is the symmetric and uniformly positive–definite inertia matrix. $H(q,\dot{q})\in {\Re }^n$ includes the centripetal and coriolis torques. $G\left(q\right)\in {\Re }^n$ is the vector of gravitational torques. $F\left(\dot{q}\right)\in {\Re }^n$ is the vector of friction matrix. $\tau \in {\Re }^n$ is the vector of actuator inputs. ${\tau }_d$ represents a load disturbance matrix. $\varphi (q,\dot{q},\tau )\in {\Re }^n$ stands forstand for the fault components affecting on the system, $\gamma (t-T_f)\in {\Re }^n$ represents the time profile of the faults, and $T_f$ is the time of occurrence of the faults.

The term $\gamma (·)$ is a diagonal matrix having the form

$$\begin{array}{cc}\hfill \gamma (t-T_f)=& diag\{{\gamma }_1(t-T_f),{\gamma }_2(t-T_f),\dots ,{\gamma }_n(t-T_f)\}\hfill \end{array}$$

(2)

where ${\gamma }_i$ represents the effects of fault on the ith state equation.

The model of the fault function can be described as

$$\begin{array}{c}\hfill {\gamma }_i(t-T_f)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}t<T_f\hfill \\ 1\hfill & \mathrm{if}t\ge T_f\hfill \end{array}\right.\end{array}$$

(3)

Rearranging the dynamics model (1), we have

$$\begin{array}{cc}\hfill \ddot{q}=& M^{-1}\left(q\right)\tau +M^{-1}\left(q\right)(-H(q,\dot{q})\dot{q}-G\left(q\right))\hfill \\ & +M^{-1}\left(q\right)\left(-F\left(\dot{q}\right)-{\tau }_d\right)+\gamma (t-T_f)\varphi (q,\dot{q},\tau )\hfill \end{array}$$

(4)

Let $x_1=q$ and $x_2=\dot{q}$, then the closed-loop system of the robot manipulator (4) can be rewritten in the following form

$$\begin{array}{cc}\hfill & \dot{x_1}=x_2\hfill \\ \hfill & \dot{x_2}=M^{-1}\left(x_1\right)u+f(x_1,x_2)+\Delta \hfill \\ \hfill & y=x_1\hfill \end{array}$$

(5)

where $f\left(x_1,x_2\right)=M^{-1}\left(q\right)(-H(q,\dot{q})\dot{q}-G\left(q\right))$ denotes the lumped known component and $\Delta =M^{-1}\left(q\right)\left(-F\left(\dot{q}\right)-{\tau }_d\right)+\gamma (t-T_f)\varphi (q,\dot{q},\tau )$ denotes the lumped unknown component in the system dynamics.

The target of this paper is to propose a control input such that the system can provide good performance despite the existence of the disturbance, uncertainties, and system faults.

3. Adaptive Compensation Control Design

3.1. Backstepping Integral Nonsingular Fast Terminal Sliding Mode Control

In the next section, we entails the following notation

$$\begin{array}{cc}\hfill {\xi }^{\left[\alpha \right]}=& {\left({\left|{\xi }_1\right|}^{\alpha }\mathit{sign}\left({\xi }_1\right),\dots ,{\left|{\xi }_n\right|}^{\alpha }\mathit{sign}\left({\xi }_n\right)\right)}^{\mathrm{T}}\in {\Re }^n\hfill \\ \hfill & \xi \in {\Re }^n,\alpha >0\hfill \end{array}$$

(6)

Let $e=x_1-x_d$ is the trajectory tracking error, where $x_d$ stands for a desired trajectory. In order to obtain finite-time convergence, fast transient response and high tracking precision without singular problem, the SMC is chosen as:

$${\sigma }_1=\int \left({\left(\dot{e}+k_{1}e\right)}^{\left[p\right]}+k_{2}e\right)$$

(7)

where $k_1=diag(k_{11},k_{12},\dots ,k_{1n})\in {\Re }^{n\times n}$ and $k_2=diag(k_{21},k_{22},\dots ,k_{2n})\in {\Re }^{n\times n}$ representative positive definite matrices, respectively, p is a positive odd number satisfying the relation $1<p<2$.

Lemma 1.

Let $a_1$, $a_2$, …, $a_n$ and $0<b<1$ are all positive numbers; then the following inequelity holds:

$${({\displaystyle \sum _{i=1}^n}{a}_i)}^b\le {\displaystyle \sum _{i=1}^n}{a}_i^b$$

(8)

Lemma 2.

Assume $V\left(t\right)$ is a continuously differentiable scalar positive-definite function that satisfies the following differential inequality:

$$\dot{V}\left(t\right)\le -\alpha V\left(t\right)-\beta V^{\gamma }\left(t\right)\forall t\ge t_0,V\left(t_0\right)\ge 0$$

(9)

where $\alpha >0$, $\beta <0$, and $0<\gamma <1$ are constants. Thenthen, for any given $t_0$, $V\left(t\right)$ checks the following inequality:

$$\begin{array}{cc}\hfill V^{1-\gamma }\left(t\right)\le -\frac{\beta }{\alpha }+& \frac{\alpha V^{1-\gamma }\left(t_0\right)+\beta }{\alpha }exp\left(-\alpha (1-\gamma )\left(t-t_0\right)\right)\hfill \\ \hfill & t_0\le t<t_1\hfill \end{array}$$

(10)

and

$$V\left(t\right)=0\forall t\ge t_1$$

(11)

with the finite time $t_1$ satisfies

$$t_1\le t_0+\frac{1}{\alpha (1-\gamma )}ln\left(\frac{\alpha V^{1-\gamma }\left(t_0\right)+\beta }{\beta }\right)$$

(12)

Remark 1.

The proposed sliding surface (6) is proposed to combine the properties of the FTSMC [17] and NTSMC [16] such that the system can obtain fast finite-time convergence without singular problem. In addition, the integral component is employed for the sliding surface so that the system can possess the merits of the ITSMC, which enhances the transient response performance and reduces the steady state error of the system. When the sliding surface (6) converges to zero, we have ${\left(\dot{e}+k_{1}e\right)}^{\left[p\right]}+k_{2}e=0$, where e is the terminal attractor of the system. The defined finite time $t_c$ that is taken to travel from $e\left(t_r\right)\ne 0$ to $e\left(t_r+t_c\right)=0$ is given by Lemmas 1 and 2

$$\begin{array}{c}\hfill t_c\le p{k}_1(p-1)ln\left(\frac{k_1{\left({\displaystyle \sum _{i=1}^n}{e}_i^2\left(t_r\right)\right)}^{\frac{1-\frac{1}{p}}{2}}+{k_2}^{\frac{1}{p}}}{{k_2}^{\frac{1}{p}}}\right)\end{array}$$

(13)

From Equation (13), it can be concluded that the tracking error can be steered into a preset range in a set time after the sliding surface converges to zero.

The second-order equation of state based on sliding mode is established as follow

$$\begin{array}{cc}\hfill & {\dot{\sigma }}_1={\sigma }_2\hfill \\ \hfill & {\dot{\sigma }}_2=\Xi (e,\dot{e})·\left(M^{-1}\left(x_1\right)u+f\left(x_1,x_2\right)+\Delta -{\ddot{x}}_d+k_1\dot{e}\right)+k_2\dot{e}\hfill \end{array}$$

(14)

where $\Xi (e,\dot{e})=diag(p{\left|{\dot{e}}_1+k_1{e}_1\right|}^{p-1},\dots ,p{\left|{\dot{e}}_n+k_1{e}_n\right|}^{p-1})$.

In order to find an effective control input of the system (14), a backstepping design procedure is employed by introducing virtualVirtual control and virtual variables as follow:

$$\begin{array}{cc}\hfill & {\vartheta }_1\left(t\right)={\sigma }_1\left(t\right)\hfill \\ \hfill & {\vartheta }_2\left(t\right)={\sigma }_2\left(t\right)-{\alpha }_1\hfill \end{array}$$

(15)

Choose a Lyapunov candidate function as $V_1=\frac{1}{2}{{\vartheta }_1}^T{\vartheta }_1$, virtual control ${\alpha }_1\left(t\right)$ can be chosen as

$${\alpha }_1\left(t\right)=-\xi {\vartheta }_1\left(t\right)-\beta {\vartheta }_1{\left(t\right)}^{\left[\gamma \right]}$$

(16)

where $\xi ,\beta$ are positive design parameters, $\gamma$ is a positive number satisfying the relation $0.5<\gamma <1$, then

$$\begin{array}{cc}\hfill {\dot{V}}_1& ={{\vartheta }_1}^T\left({\vartheta }_2+{\alpha }_1\right)\hfill \\ \hfill & =-\xi {{\vartheta }_1}^T{\vartheta }_1-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}+{{\vartheta }_1}^T{\vartheta }_2\hfill \end{array}$$

(17)

In this step, we design a virtual control law ${\alpha }_1\left(t\right)$ to make the $V_1$ be finite time convergence if ${{\vartheta }_1}^T{\vartheta }_2=0$ is omitted.

Choose a Lyapunov candidate function as $V_2=V_1+\frac{1}{2}{{\vartheta }_2}^T{\vartheta }_2$, then

$$\begin{array}{cc}\hfill {\dot{V}}_2& ={\dot{V}}_1+{{\vartheta }_2}^T{\dot{\vartheta }}_2\hfill \\ \hfill & =-\xi {{\vartheta }_1}^T{\vartheta }_1-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}+{{\vartheta }_1}^T{\vartheta }_2+{{\vartheta }_2}^T\left({\dot{\sigma }}_2-{\dot{\alpha }}_1\right)\hfill \\ \hfill & =-\xi {{\vartheta }_1}^T{\vartheta }_1-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}+{{\vartheta }_1}^T{\vartheta }_2\hfill \\ \hfill & +{{\vartheta }_2}^T\left(\Xi \left(e,\dot{e}\right)\left(M^{-1}\left(x_1\right)u+f\left(x_1,x_2\right)+\Delta -{\ddot{x}}_d+k_1\dot{e}\right)+k_2\dot{e}-{\dot{\alpha }}_1\right)\hfill \end{array}$$

(18)

Hence, then the control law can be designed as

$$\begin{array}{cc}\hfill u\left(t\right)=& M\left(x_1\right)\left(-f\left(x_1,x_2\right)+{\ddot{x}}_d-k_1\dot{e}\right)+M\left(x_1\right)\Xi {(e,\dot{e})}^{-1}\hfill \\ \hfill & \left(-k_2\dot{e}+{\dot{\alpha }}_1-{\vartheta }_1-\xi {\vartheta }_2-sign\left({\vartheta }_2\right)(\Lambda +\varsigma )-\beta {{\vartheta }_2}^{\left[\gamma \right]}\right)\hfill \end{array}$$

(19)

where $\Lambda \ge \left|\Xi \left(\dot{e}\right)\Delta \right|$ represents the upper bound of disturbance, $\varsigma$ is a positive small constant.

Adding the proposed controller in (19) into (18), we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_2& =-\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & -\left|{\vartheta }_2\right|(\Lambda +\varsigma )+{{\vartheta }_2}^T\Xi \left(\dot{e}\right)\Delta \hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & -\left|{\vartheta }_2\right|(\Lambda +\varsigma )+\left|{\vartheta }_2\right|\left|\Xi \left(\dot{e}\right)\Delta \right|\hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \end{array}$$

(20)

Using Lemma 1 yields and replacing ${{\vartheta }_1}^T{\vartheta }_1+{{\vartheta }_2}^T{\vartheta }_2$ by $2V_2$, we can get

$${\dot{V}}_2\le -\frac{\xi }{2}{V}_2-2^{\frac{1+r}{2}}\beta {V_2}^{\frac{1+r}{2}}$$

(21)

Using Lemma 2, the finite-time convergence $V_2\left(t\right)=0$ is achieved for $t\ge t_r$ as

$$t_r\le t_0+\frac{1}{2\xi \left(1-\frac{1+\gamma }{2}\right)}\times ln\left(\frac{2\xi V_2^{1-\frac{1+\gamma }{2}}\left(t_0\right)+2^{\frac{1+\gamma }{2}}\beta }{2^{\frac{1+\gamma }{2}}\beta }\right)$$

(22)

Then, we can obtain that ${\vartheta }_1$, ${\vartheta }_2$ will converge to zero in a finite time.

It is worthy to mention that the value of $\Lambda$ can’t be obtained since it is difficult to estimate the bound value of the uncertainty, disturbance, and fault parameters in advance. To deal with this issue, a backstepping adaptive method is proposed. we consider $\widehat{\Lambda }$ is the estimate of $\Lambda$, then

$$\dot{\widehat{\Lambda }}=\frac{1}{\delta }\left|{\vartheta }_2\right|$$

(23)

Then, the control can be rewritten as

$$\begin{array}{cc}\hfill u\left(t\right)=& M\left(x_1\right)\left(-f\left(x_1,x_2\right)+{\ddot{x}}_d-k_1\dot{e}\right)+M\left(x_1\right)\Xi {(e,\dot{e})}^{-1}\hfill \\ \hfill & \left(-k_2\dot{e}+{\dot{\alpha }}_1-{\vartheta }_1-\xi {\vartheta }_2-sign\left({\vartheta }_2\right)(\widehat{\Lambda }+\varsigma )-\beta {{\vartheta }_2}^{\left[\gamma \right]}\right)\hfill \end{array}$$

(24)

Theorem 1.

Under the controller (24), the arrival time of the sliding mode surface described by (7) is finite.

Proof. 

Consider the following Lyapunov function:

$$V_3=V_2+\frac{1}{2}\delta {\tilde{\Lambda }}^2$$

(25)

where $\tilde{\Lambda }=\Lambda -\widehat{\Lambda }$ is the estimation error. □

The derivative of the $V_3$ can be obtained as

$$\begin{array}{cc}\hfill {\dot{V}}_3& ={\dot{V}}_2+\delta (\widehat{\Lambda }-\Lambda )\dot{\widehat{\Lambda }}\hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & -\left|{\vartheta }_2\right|(\widehat{\Lambda }+\varsigma )+\left|{\vartheta }_2\right|\Xi (\dot{e})\Delta +\delta (\widehat{\Lambda }-\Lambda )\dot{\widehat{\Lambda }}\hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & -\left|{\vartheta }_2\right|(\Lambda +\varsigma )+\left|{\vartheta }_2\right|\Xi \left(\dot{e}\right)\Delta \hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \end{array}$$

(26)

Then, ${\dot{V}}_3$ is negative semidefinite, which implies that ${\vartheta }_1$, ${\vartheta }_2$, $\tilde{\Lambda }$ will asymptotically converge to zerois asymptotic convergence despite the existing of uncertainties, disturbances, and faults. If $\Lambda$ is replaced by the $\widehat{\Lambda }$, the time derivative of $V_2$ can be rewritten as

$$\begin{array}{cc}\hfill {\dot{V}}_2\le & -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & -\left|{\vartheta }_2\right|(\widehat{\Lambda }+\varsigma )+\left|{\vartheta }_2\right|\left|\Xi \left(\dot{e}\right)\Delta \right|\hfill \end{array}$$

(27)

It is obvious that $\widehat{\Lambda }+\varsigma >\Lambda$ will happen in finite time since $\tilde{\Lambda }$ will asymptotically converge to zerois asymptotic convergence. Then, after finite time, the time derivative of $V_2$ can be obtained as

$$\begin{array}{cc}\hfill {\dot{V}}_2& \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & \le -\frac{\xi }{2}{V}_2-2^{\frac{1+r}{2}}\beta {V_2}^{\frac{1+r}{2}}\hfill \end{array}$$

(28)

According to (17), we can conclude that ${\vartheta }_1$, ${\vartheta }_2$ will converge to zero in a finite time when $\Lambda$ is replaced by the $\widehat{\Lambda }$ in the control law. This implies the system states can arrive at the specified sliding surface within a finite time even in the presence of actuator failure. The whole design procedure of our proposed controller is illustrated in Figure 1.

Remark 2.

The discontinuous function $sign(·)$ result in chattering phenomenon on the switching manifold. This phenomenon appears as a very high-frequency oscillation when the sliding surface $\sigma \approx 0$. To confront this problem of the chattering phenomenon, the sign function $sign(·)$ is replaced by a saturation function $sat(·)$ as follows:

$$\begin{array}{c}\hfill \mathit{sat}\left(\sigma \right)=\left\{\begin{array}{cc}sign\left(\sigma \right)\hfill & \mathrm{if} \left|\sigma \right|>\omega \\ \frac{\sigma }{\omega }\hfill & \mathrm{if} \left|\sigma \right|\le \omega \end{array}\right.\end{array}$$

(29)

where $\omega >0$ is a boundary layer.

Remark 3.

In order to eliminate the singular problem when calculating the derivative of ${\alpha }_1$, the following nonsingular function is employed:

$$\begin{array}{c}\hfill {\dot{\alpha }}_1\left(t\right)=\left\{\begin{array}{cc}-\xi {\dot{\vartheta }}_1\left(t\right)-\gamma \beta {\left|{\vartheta }_1\left(t\right)\right|}^{\gamma -1}{\dot{\vartheta }}_1\left(t\right)\hfill & \mathrm{if} {\vartheta }_1\left(t\right)\ne 0\\ -\xi {\dot{\vartheta }}_1\left(t\right)\hfill & \mathrm{if} {\vartheta }_1\left(t\right)=0\end{array}\right.\end{array}$$

(30)

where γ is a positive number satisfying the relation $0.5<\gamma <1$.

3.2. Redundant Controller Base on Adaptive Backstepping Nonsingular Fast Terminal Sliding Mode

Differing from PLOE, when TLOE type of failure occurs, these actuator outputs will totally out of control. This fault can’t be compensated by a single adaptive compensation. Hence, a redundant control method is proposed to solve this problem, which provides greater flexibility in robotic systems [41].

We denote the ith control input as $u_{ci}$. Then under failure-free case, the control input $u_{ci}$ equal to the actuator output $u_i$. But when the actuator is undergoing the failures, it can be modeled as

$$u_i=p_i{u}_{ci}$$

(31)

where $0\le p\le 1$ is the proportion of effectiveness of control signal.

The control law $u_c$ is considered as:

$$\begin{array}{cc}\hfill u\left(t\right)=& M\left(x_1\right)\left(-f\left(x_1,x_2\right)+{\ddot{x}}_d-k_1\dot{e}\right)+M\left(x_1\right)\Xi {(e,\dot{e})}^{-1}\hfill \\ \hfill & \left(-k_2\dot{e}+{\dot{\alpha }}_1-{\vartheta }_1-\xi {\vartheta }_2-sign({\vartheta }_2)(\widehat{\Lambda }+\varsigma )-\beta {{\vartheta }_2}^{\left[\gamma \right]}\right)\hfill \end{array}$$

(32)

where $\dot{\widehat{\Lambda }}$ has the same form as (15).

We consider adding the compensation input due to the lose of actuator, note that the compensation input is $u_b$, then the control input actually can be express as

$$u=p{u}_c+u_b$$

(33)

where $p=diag(p_1,p_2,\dots ,p_n){\Re }^{n\times n}$, the compensation input $u_b$ are designed as follows

$$u_b=(1-\widehat{p})u_c$$

(34)

where $\widehat{p}$ isare the estimations of the p, $\tilde{p}=p-\widehat{p}$ stands for the estimation error. Introducing an auxiliary variable k. Consider an overall Lyapunov function:

$$V_4=V_3+\frac{1}{2}{\tilde{k}}^T\tilde{k}$$

(35)

where $\tilde{k}={[{\tilde{p}}_1,{\tilde{p}}_2,\dots ,{\tilde{p}}_n]}^{\prime }$, $k={[p_1,p_2,\dots ,p_3]}^{\prime }$, $\widehat{k}={[{\widehat{p}}_1,{\widehat{p}}_2,\dots ,{\widehat{p}}_n]}^{\prime }$ The derivative of $\widehat{k}$ are set as

$$\dot{\widehat{k}}=diag({\vartheta }_2\Xi (e,\dot{e})M^{-1})u_c$$

(36)

In other words, the derivative of $\widehat{p}$ are set as

$$\dot{\widehat{p}}=diag(\dot{\widehat{k}})$$

(37)

The derivative of $V_4$ can be written as

$$\begin{array}{cc}\hfill {\dot{V}}_4& ={\dot{V}}_3-\tilde{k}\dot{\widehat{k}}\hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & +{\vartheta }_2\Xi (e,\dot{e})M^{-1}\tilde{p}{u}_c-\tilde{k}\dot{\widehat{k}}\hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \\ \hfill & +\tilde{k}·diag({\vartheta }_2\Xi (e,\dot{e})M^{-1})u_c-\tilde{k}\dot{\widehat{k}}\hfill \\ \hfill & \le -\xi {{\vartheta }_1}^T{\vartheta }_1-\xi {{\vartheta }_2}^T{\vartheta }_2-\beta {{\vartheta }_1}^T{{\vartheta }_1}^{\left[r\right]}-\beta {{\vartheta }_2}^T{{\vartheta }_2}^{\left[r\right]}\hfill \end{array}$$

(38)

Then, ${\dot{V}}_4$ is negative semidefinite, which implies that ${\vartheta }_1$, ${\vartheta }_2$ will asymptotically converge to zero. Therefore, it can be concluded that the proposed redundant controller can guarantee an asymptotically stable system even in the presence of total loss of actuator outputs. The whole design procedure of redundant controller is illustrated in Figure 2.

4. Simulation Example

In this section, to illustrate the effectiveness and applicability of the proposed control scheme (24) in compensating for actuator failures/faults, we consider a two-link planar manipulator that grasps an unknown tool as in [43]. For simplicity, the configuration parameters of the robot are assumed to be exactly known, which are represented in

Table 1. Physical parameters of double joint manipulator.

${\mathit{m}}_1$	${\mathit{l}}_1$	${\mathit{l}}_{\mathit{c}1}$	${\mathit{I}}_1$	${\mathit{m}}_{\mathit{e}}$	${\mathit{l}}_{\mathbf{ce}}$	${\mathit{I}}_{\mathit{e}}$	${\mathit{\delta }}_{\mathit{e}}$	${\mathit{e}}_1$	${\mathit{e}}_2$
1 kg	1 m	$\frac{1}{2}$ m	$\frac{1}{12}$ kg	3 kg	1 m	$\frac{2}{5}$ kg	0	$-\frac{7}{12}$	9.81

.

The desired trajectory of the system is selected as follows

$$\begin{array}{c}\hfill x_d=\left[\begin{array}{c}0.33+0.1\ast \sin (0.54+3t)\hfill \\ 0.41+0.1\ast \cos (0.54+3t)\hfill \end{array}\right]\end{array}$$

(39)

In this step, we mainly research the specific implementation of our proposed controller in the MATLAB platform. the parameters $k_1$, $k_2$, p, $\xi$, $\beta$, $\gamma$, $\eta$ and $\delta$ are chosen as $k_1$ = 1, $k_2$ = 0.8, $p=9$, $\xi =180$, $\beta =60$, $\gamma =0.6$, $\eta =0.15$ and $\delta =0.5$.

To further demonstrate the superior performance of the proposed method, we utilize two advanced controllers to compare the simulation results. These are NTSMC and NFTSMC.

Firstly, the situation without uncertainties is considered. The tracking performance of the system in cartesian space under the three controllers are shown in Figure 3 and Figure 4. It is observed that our proposed controller and NFTSMC can track the trajectory more quickly than NTSMC. in addition, due to the merit of the integral component, our proposed controller provides lower steady-state error than NFTSMC. This phenomenon is more obvious in joint 2.

Subsequently, two uncertainties, which, respectively, are the disturbance and system fault are considered. the designed parameters are chosen to be the same as the first situation. The friction and disturbance term is modeled as

$$F\left(q\right)+{\tau }_d=\left[\begin{array}{c}0.5{\dot{q}}_1+sin\left(3q_1\right)+0.3sin\left({\dot{q}}_1\right)\hfill \\ 1.3{\dot{q}}_2+1.1sin\left(2q_2\right)+0.8sin\left({\dot{q}}_2\right)\hfill \end{array}\right]$$

(40)

the system fault function are considered as following

$$\begin{array}{c}\hfill \varphi (q,\dot{q},\tau )=\left[\begin{array}{c}\begin{array}{c}\left(\begin{array}{c}15\sin \left(q_1{q}_2\right)+3\cos \left({\dot{q}}_1{q}_2\right)\hfill \\ +0.3\cos \left({\dot{q}}_2\right)\hfill \end{array}\right)T_{f1}\ge 1\hfill \end{array}\hfill \\ \begin{array}{c}-0.2u_2{T}_{f1}\ge 1\hfill \end{array}\hfill \end{array}\right]\end{array}$$

(41)

It is assumed that an abrupt fault ${\varphi }_1=15sin\left(q_1{q}_2\right)+3cos\left({\dot{q}}_1{q}_2\right)+0.3cos\left({\dot{q}}_2\right)$ occurs in the first actuator from the time $t\ge 1$ s, while the second actuator losses $20\%$ its effectiveness from the time $t\ge 1$ s.

The evolutions of tracking error and velocity error under the three controllers is shown in Figure 4, Figure 5 and Figure 6, respectively. Comparing NTSMC and NFTSMC and our scheme, NFTSMC and our scheme have faster transient response property compared to NTSMC. It is easy to find that NTSMC and NFTSMC have larger steady-state errors than our scheme as the disturbance and fault are introduced. The reason behind the better performance of our proposed controller is two folds. Firstly, integral SMC can provide high tracking precision and less chattering, while NFTSMC can provide a fast transient response. Since the proposed scheme used the INFTSMC, it can preserve the merits of the ITSMC and NFTSMC simultaneously. Secondly, the proposed design topology follows the design procedure of the backstepping control technique, and thus the finite-time convergence of the system can be guaranteed based on the Lyapunov criterion.

The variation of the adaptive parameter for normal and fault operations are shown in Figure 7. From this figure, it is shown that with our method the robust adaptive $\widehat{\Lambda }$ will converge to some stable values when the system is stable. In addition, supposing that the parameters $k_1$, $k_2$, $\xi$ and $\beta$ are set to be larger, but the parameters $\delta$ is chosen smaller, then the convergence speed of the adaptive parameter could be made faster. Moreover, in comparison with Figure 7a,b, it is indicated that the value of adaptive law increased when the faults occur. It is proved that the bound value of the fault is estimated by the adaptive law.

Under the TLOE, we conduct the simulation when the controller given in (32) is adopted. In the simulation, we assume that the actuator output loses 100%, the designed parameters are selected as $k_1$ = 1, $k_2$ = 0.8, $p=9$, $\xi =180$, $\beta =60$, $\gamma =0.6$, $\eta =0.15$ and $\delta =0.5$.

It is observed from Figure 8 and Figure 9 that our previously proposed controller can’t ensure stability for TLOE, while even if the actuator has been completely damaged, the satisfactory tracking performance can also be achieved by the novel redundant controller. This is because the loss coefficient of the actuator has been estimated online by adaptive law in the redundant controller design.

5. Conclusions

This paper presents a new sliding mode adaptive controller to compensate for actuator failures of robot manipulators within a finite time. By using the newly developed non-smooth Lyapunov function analysis, we establish the relationship among the stability of the closed-loop system, the upper bound of failures, and controller design parameters. Subsequently, a novel SMC is derived to improve both transient and steady-state tracking performances. Moreover, a singular problem is successfully avoided even in the presence of system failures, and a redundant control mechanism is additionally designed to compensate for actuator input loss in the TLOE case. Finally, simulations have been conducted to verify the effectiveness of the proposed controller.