Zeroing Neural Networks Combined with Gradient for Solving Time-Varying Linear Matrix Equations in Finite Time with Noise Resistance

Abstract

Due to the time delay and some unavoidable noise factors, obtaining a real-time solution of dynamic time-varying linear matrix equation (LME) problems is of great importance in the scientific and engineering fields. In this paper, based on the philosophy of zeroing neural networks (ZNN), we propose an integration-enhanced combined accelerating zeroing neural network (IEAZNN) model to solve LME problem accurately and efficiently. Different from most of the existing ZNNs research, there are two error functions combined in the IEAZNN model, among which the gradient of the energy function is the first design for the purpose of decreasing the norm-based error to zero and the second one is adding an integral term to resist additive noise. On the strength of novel combination in two error functions, the IEAZNN model is capable of converging in finite time and resisting noise at the same time. Moreover, theoretical proof and numerical verification results show that the IEAZNN model can achieve high accuracy and fast convergence speed in solving time-varying LME problems compared with the conventional ZNN (CZNN) and integration-enhanced ZNN (IEZNN) models, even in various kinds of noise environments.

1. Introduction

The advances in computer science have extended its use in various fields of application, such as the robotics domain [1,2,3], adaptive neural tracking control [4] and image-processing [5]. Among all the applications mentioned above, the linear matrix equation (LME) is one of the most commonly seen problems. Therefore, how to solve the LME is a crucial challenge. Numerous efforts have been made to solve LME difficulties more effectively. A common way of dealing with LMEs is to use Newton’s iteration method [6,7,8]. However, there may be some problems related to the running time and the algorithm’s complexity [9] in the case of high-dimensional or large-scale matrix operations, and the complexity of the numerical iterative algorithm is proportional to the cube of the matrix dimension [10]. In general, such numerical methods may not be able to meet the requirements of real-time applications due to their inherent iterative nature when used to solve time-varying LME problems.

Recently, due to the intensive study of neural networks, many dynamic simulation solvers based on recurrent neural networks (RNN) have been studied and developed to process LMEs in parallel [11,12,13,14]. Different from numerical algorithms, the RNN is famous for its parallel computing advantages, which helps greatly to promote computational efficiency. As a result, neural dynamic methods are now considered a powerful alternative to online computation of matrix problems due to their parallel distribution properties and the convenience of hardware implementation [15,16]. As a typical RNN, the gradient-based neural network (GNN) is designed to solve the minimization problems [8,17,18,19]. However, when coping with time-dependent cases, GNN produces relatively large lag errors [20]. As a result, a new kind of continuous-time RNN called zeroing neural network (ZNN) has emerged for solving various time-dependent problems, such as matrix inversion [21], the Lyapunov equation [15,22] and the Sylvester equation [23]. From the perspective of solution results, the state solution of ZNN can start from any initial state and converge globally to the theoretical solution with exponential speed. In order to accelerate the convergence speed, the finite-time zeroing neural network model (FTZNN) [24] was developed to solve the time-varying matrix inversion problem, in which the upper bound of finite convergence time was calculated theoretically.

Although ZNN can achieve finite-time convergence, its denoising ability is limited and cannot qualify for solving accurately in the case of noisy systems [25]. Since external noise is unavoidable and some noise will inevitably appear in the hardware implementation of the neural network model [26], some anti-noise ZNN models have been developed [22,25,26,27]. The paper [26] presents a discrete-time zeroing neural algorithm for solving linear equations using control techniques, focusing on solving discrete time-varying linear equations with various noises. In the literature [22], a noise-tolerant zeroing neural network (NTZNN) model is proposed to solve the nonstationary Lyapunov equation under various types of noise interference. An integration-enhanced noise-tolerant zeroing neural network (IENTZNN) model is defined and considered to calculate the outer inverse of time-varying matrix in the presence of various noises [27]. By using a novel activation function (NAF), the authors proposed a new interference-tolerant fast convergence zeroing neural network (ITFCZNN) for solving dynamic matrix inversion (DMI) [25]. Additionally, the most classic anti-noise model is IEZNN [28], which can be used to solve time-varying LME in various noisy environments. Compared with the conventional ZNN, the main improvement of the IEZNN model lies in introducing an integral term of error on the right side of ZNN to resist additional injected noise. However, due to the intrinsic properties of linearity, the IEZNN model can only achieve exponential convergence in theory [28]. In general, the CZNN with nonlinear activation function can achieve finite-time convergence but cannot resist noise, while the improved noise-resistant neural network models such as IEZNN cannot achieve finite-time convergence. As a result, more and more research is focusing on developing models that can effectively resist noise while solving the problem in a finite amount of time.

Different from other previous research methods, in this paper, we propose a new interference-tolerant and fast convergence zeroing neural network for solving dynamic matrix inversion using the gradient of the energy function as the first error function to obtain the superior convergence; then, a new second error function is constructed for noise resistance. To overcome the exponential convergence speed, the novel integration-enhanced combined accelerating zeroing neural network (IEAZNN) model is developed to solve the time-varying LME problem. From the comparison and experimental results, the proposed IEAZNN model can exactly and efficiently solve the time-varying LME without lagging error in a finite time, even in noisy environments.

The rest of the article is organized as follows. Section 2 lists the time-varying LME to be solved, and presents the traditional CZNN model and noise-resistant IEZNN model with an integral term to solve the equation for comparison. In Section 3, the improved ZNN model with accelerated solution is formed by a new error definition based on the energy function gradient of time-varying LME, and a new IEAZNN model with both noise resistance and finite-time convergence is obtained. Then, the convergence, finite time and stability of the IEAZNN model are proved. The MATLAB simulation results are presented in Section 4, in which the CZNN model, IEZNN model and the proposed IEAZNN model are digitally verified with no noise, constant noise and dynamic linear noise, respectively. The conclusions are summarized in the final section. Before ending this section, the main contributions of this article are listed as follows:

(1)

Specially for the design of IEAZNN model, the gradient of the energy function is used as the first error function for superior convergence. To resist noise influences, a new, second error function is designed based on the IEZNN model. Then, the IEAZNN is developed for the anti-noise and finite-time convergence.

(2)

Different from other ZNN models, which are either for achieving anti-noise or finite time convergence, the presented IEAZNN model is noise-tolerant and has the advantage of finite-time convergence at the same time.

(3)

The theoretical analyses and experimental comparisons show that the proposed IEAZNN model in this paper performs well in both convergence speed and solution accuracy under various noise disturbances.

2. Problem Formulation and Related Models

Consider the same time-varying LME in [29]:

$$A\left(t\right)X\left(t\right)B\left(t\right)=C\left(t\right)$$

(1)

where $A\left(t\right)\in R^{m\times m}$, $B\left(t\right)\in R^{n\times n}$ and $C\left(t\right)\in R^{m\times n}$ are smooth and differentiable time-varying coefficient matrices. $X\left(t\right)\in R^{m\times n}$ is the time-varying unknown matrix that we need to solve in real time to satisfy the time-varying problem (1). The problem (1) solving is widely applied to many practical problems in control theory and has been mentioned in many papers [5,29,30].

2.1. Conventional ZNN Model

The conventional ZNN (CZNN) [2,11,21,22,28,29,31] is designed to systematically resolve time-varying matrix inversion in real time while eliminating the lagging errors. For solving the above time-varying LME (1), the CZNN design formula can be written as

$$\dot{S}\left(t\right)=-{\gamma }_{1}S\left(t\right)$$

(2)

where ${\gamma }_1\in R$ is used to scale the convergence rate of the solution and ${\gamma }_1>$ 0. In order to achieve the time-varying unknown matrix $X\left(t\right)$ of the time-varying LME problem (1), error function $S\left(t\right)$ should be defined as $S\left(t\right)=A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right)$. Then, take the derivative of $S\left(t\right)$ as $\dot{S}\left(t\right)$ and substitute it into the above CZNN design Formula (2). Thus, by expanding the Formula (2), the following CZNN solver can be obtained to solve the time-varying LME problem (1):

$$A\left(t\right)\dot{X}\left(t\right)B\left(t\right)=-{\gamma }_1(A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right))-\dot{A}\left(t\right)X\left(t\right)B\left(t\right)-A\left(t\right)X\left(t\right)\dot{B}\left(t\right)+\dot{C}\left(t\right)$$

(3)

However, the shortcoming of the above CZNN is that when there exists noise, the solution of the model is difficult to converge or fails to converge to the theoretical ones. Intuitively speaking, after adding noise to the right side of the design Formula (2), one can have $\dot{S}\left(t\right)=-{\gamma }_{1}S\left(t\right)+\mathrm{noise}$. Evidently, when the CZNN model (3) is exploited to solve (1), error $S\left(t\right)=A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right)$ does not really decrease to 0; so, $X\left(t\right)$ will not converge to the theoretical solution $X^{*}\left(t\right)$.

2.2. Integration-Enhanced ZNN Model

In order to solve the above accuracy problem during the solving procedure in the presence of noise, an integration-enhanced ZNN (IEZNN) model was proposed [28]. The main improvement of IEZNN compared with CZNN is to add an integral term to the right side of (2). The IEZNN design formula can be summarized as follows:

$$\dot{S}\left(t\right)=-{\gamma }_{1}S\left(t\right)-\omega {\int }_0^{t}S\left(\sigma \right)d\sigma$$

(4)

where ${\gamma }_1$ is the same as defined in CZNN (2) and $\omega >$ 0 are the design parameters to scale the convergence of IEZNN. By following the design formula of IEZNN (4) and considering $S\left(t\right)=A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right)$, an IEZNN model can be obtained for solving time-varying LME (1) as follows:

$$\begin{array}{cc}\hfill A\left(t\right)\dot{X}\left(t\right)B\left(t\right)=& -{\gamma }_1(A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right))-\omega {\int }_0^t(A\left(\sigma \right)X\left(\sigma \right)B\left(\sigma \right)-C\left(\sigma \right))d\sigma \hfill \\ & -\dot{A}\left(t\right)X\left(t\right)B\left(t\right)-A\left(t\right)X\left(t\right)\dot{B}\left(t\right)+\dot{C}\left(t\right)\hfill \end{array}$$

(5)

By the research investigations in [28], (5) is the complete form of the noise-resistant IEZNN model, which has a high noise tolerance and is able to converge to a theoretical solution of the time-varying matrix inversion problem. However, the IEZNN model cannot achieve finite-time convergence because no nonlinear activation function [15] is used.

3. Noise-Enduring IEAZNN Model

When there exists external noise interference, the aforementioned CZNN model (3) cannot solve with zero-free the time-varying LME (1) [22], while the IEZNN model (5) can resist noise interference by means of adding an integral term but cannot achieve finite-time convergence. Since noise interference is unavoidable in both nature and practice, in this section, we design and implement an anti-noise interference model that can converge in a finite amount of time, shown in Equation (9).

3.1. Model Design

In order to solve problem (1), as for CZNN (2) and IEZNN (4), the design formula is constructed based on an error function $S\left(t\right)\in R^{m\times n}$ for solving time-varying LME (1). Different from the design of CZNN and IEZNN, the error function $S\left(t\right)$ will be replaced by the gradient of an energy function depicted as the following steps:

(1)

By the classical gradient-based algorithm [12,15,18,29] and the general construction process [15], first, a non-negative scalar-valued norm basis energy function $\epsilon \left(X\right)$ can be defined as $\epsilon \left(X\right)={\parallel AXB-C\parallel }_F^2/2=\mathrm{trace}({(AXB-C)}^{\top }(AXB-C))/2$ with t omitted for written convenience.

(2)

By the property of the trace, we can obtain the above derivative of $\epsilon \left(X\right)$, $\frac{\partial \epsilon \left(X\right)}{\partial X}=A^{\top }AXB{B}^{\top }-A^{\top }C{B}^{\top }$, with respect to X.

(3)

Define $G\left(t\right):=\frac{\partial \epsilon \left(X\right)}{\partial X}$ to replace the error function $S\left(t\right)$ in (2).

In the absence of noise interference, when the error function $S\left(t\right)$ converges to 0, it means that the solution $X\left(t\right)$ of the time-varying LME problem (1) can converge to the theoretical solution $X^{*}\left(t\right)$ by the following ZNN model:

$$\dot{S}\left(t\right)=-{\gamma }_{1}S\left(t\right)-{\gamma }_2{S}^{\frac{q}{p}}\left(t\right)$$

(6)

However, $X\left(t\right)$ is no longer the exact solution of the original LME problem (1) under the interference of various external noises. In order to overcome this problem, in this section, a new error function $E\left(t\right)\in R^{m\times n}$, which is completely different from the error $S\left(t\right)=A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right)$, is designed as follows:

$$E\left(t\right)=G\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma$$

(7)

where p and q denote the positive odd integers satisfying $p>q$. The integral term is composed of two parts, which can speed up the convergence of the model against noise to a certain extent, and is equivalent to the role of the activation function [32]. Similarly, in order to solve the time-varying problem (1) accurately and effectively, based on the new error function $E\left(t\right)$, an improved design idea is introduced as follows:

$$\dot{E}\left(t\right)=-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)$$

(8)

where the design parameter ${\gamma }_2>0$, which is the same as ${\gamma }_1$. As for Equation (8), the first item $\left({\gamma }_{1}E\left(t\right)\right)$ mainly affect the convergence speed, which controls dominantly the convergence rate of the neural network for a related big residual error at the beginning of the solution. However, when $E\left(t\right)$ gradually closes to nearby the zero point, the convergence speed of the neural network is mainly decided by the second term of (8) $({\gamma }_2{E}^{\frac{q}{p}}\left(t\right))$. Therefore, the ZNN model based on (8) can have superior convergence properties. By the new error function (7) and combining (8), the integration-enhanced combined accelerated zeroing neural network (IEAZNN) model can be expressed as follows:

$$\begin{array}{cc}\hfill \dot{G\left(t\right)}+\omega (G\left(t\right)+G^{\frac{q}{p}}\left(t\right))=& -{\gamma }_1(G\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma )\hfill \\ & -{\gamma }_2{(G\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma )}^{\frac{q}{p}}\hfill \end{array}$$

(9)

For model (9), according to $G\left(t\right)=A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right)$, we can obtain the following IEAZNN model for the time-varying problem (1), solving

$$\begin{array}{cc}\hfill & A^{\top }\left(t\right)A\left(t\right)\dot{X\left(t\right)}B\left(t\right)B^{\top }\left(t\right)=\hfill \\ & -{\gamma }_1(A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma )\hfill \\ & -{\gamma }_2{(A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma )}^{\frac{q}{p}}\hfill \\ & -\dot{A^{\top }\left(t\right)}A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)\dot{A\left(t\right)}X\left(t\right)B\left(t\right)B^{\top }\left(t\right)\hfill \\ & -A^{\top }\left(t\right)A\left(t\right)X\left(t\right)\dot{B\left(t\right)}{B}^{\top }\left(t\right)-A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)\dot{B^{\top }\left(t\right)}+\dot{A^{\top }\left(t\right)}C\left(t\right)B^{\top }\left(t\right)\hfill \\ & +A^{\top }\left(t\right)\dot{C\left(t\right)}{B}^{\top }\left(t\right)-\omega (A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right)\hfill \\ & +{(A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right))}^{\frac{q}{p}})+A^{\top }\left(t\right)C\left(t\right)\dot{B^{\top }\left(t\right)}\hfill \end{array}$$

(10)

As discussed in the presentation nearby Equation (7), the IEAZNN model (10) is a noise-resistant model evolved by the improved design idea (8). Consider that there unavoidably exists noise in the practical engineering applications; thus, the IEAZNN (10) could be further written as the following form associated with noise.

$$\begin{array}{cc}\hfill & A^{\top }\left(t\right)A\left(t\right)\dot{X\left(t\right)}B\left(t\right)B^{\top }\left(t\right)=\hfill \\ & -{\gamma }_1(A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma )\hfill \\ & -{\gamma }_2{(A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma )}^{\frac{q}{p}}\hfill \\ & -\dot{A^{\top }\left(t\right)}A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)\dot{A\left(t\right)}X\left(t\right)B\left(t\right)B^{\top }\left(t\right)\hfill \\ & -A^{\top }\left(t\right)A\left(t\right)X\left(t\right)\dot{B\left(t\right)}{B}^{\top }\left(t\right)-A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)\dot{B^{\top }\left(t\right)}+\dot{A^{\top }\left(t\right)}C\left(t\right)B^{\top }\left(t\right)\hfill \\ & +A^{\top }\left(t\right)\dot{C\left(t\right)}{B}^{\top }\left(t\right)-\omega (A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right)\hfill \\ & +{(A^{\top }\left(t\right)A\left(t\right)X\left(t\right)B\left(t\right)B^{\top }\left(t\right)-A^{\top }\left(t\right)C\left(t\right)B^{\top }\left(t\right))}^{\frac{q}{p}})+A^{\top }\left(t\right)C\left(t\right)\dot{B^{\top }\left(t\right)}+\mathrm{noise}\hfill \end{array}$$

(11)

In this paper, we carry out the theoretical analysis and experiment simulation in three cases (i.e., noise-free, constant noise and dynamic linear noise) for the noised model (11).

3.2. Theoretical Analyses

This section theoretically analyzes the convergence, stability and finite time for the noise-resistant model (10), together with the detailed proof on the noised-model (11) for achieving convergence to the theoretical solution even in a noisy environment.

Theorem 1. 

The IEAZNN model (10) can globally converge to the theoretical time-varying solution $X^{*}\left(t\right)$ beginning from any initial state $X_0=X\left(0\right)\in R^{m\times n}$ by taking into account the coefficient matrices $A\left(t\right)$, $B\left(t\right)$ and $C\left(t\right)$ in the time-varying LME problem (1) under the assumption that there is a single unique solution.

Proof. 

According to (7), we can define a candidate Lyapunov function [15,33] as follows:

$$V_E\left(t\right)=\frac{1}{2}{E}^2\left(t\right),$$

(12)

and the time derivative of (12) with respect to time t can be written as

$${\dot{V}}_E\left(t\right)=E\left(t\right)\dot{E}\left(t\right)=-{\gamma }_1{E}^2\left(t\right)-{\gamma }_2{E}^{\frac{p+q}{p}}\left(t\right)$$

(13)

Evidently, from (12) and (13), $V_E\left(t\right)\ge 0$ and ${\dot{V}}_E\left(t\right)\le 0$. According to the Lyapunov stability principle [15,16], we can know that $E\left(t\right)=G\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma$ will eventually converge to 0. At that time, $G\left(t\right)=-\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma$, and $\dot{G}\left(t\right)=-\omega (G\left(t\right)+G^{\frac{q}{p}}\left(t\right))$ can be further obtained. Similar to (12), we proceed to define a new candidate Lyapunov function as follows:

$$V_G\left(t\right)=\frac{1}{2}{G}^2\left(t\right)$$

(14)

Obviously, $V_G\left(t\right)\ge 0$, and the derivative of $V_G\left(t\right)$ is formed as follows:

$$\dot{V_G}\left(t\right)=G\left(t\right)\dot{G}\left(t\right)=-\omega (G^2\left(t\right)+G^{\frac{p+q}{p}}\left(t\right))$$

(15)

From the above analysis, we can obtain ${\dot{V}}_G\left(t\right)\le 0$. According to the Lyapunov stability principle [15], $G\left(t\right)$ also will eventually converge to 0, which implies that the solution $X\left(t\right)$ can converge to theoretical solution $X^{*}\left(t\right)$. This proof is thus completed.    □

Theorem 2. 

Starting from any initial value, the IEAZNN model (10) can globally converge to the theoretical solution $X^{*}\left(t\right)$ in a limited time; the upper bound of the convergence time is $T\le \frac{p}{{\gamma }_1(p-q)}\ln \frac{{\gamma }_1{E}^{\frac{p-q}{p}}\left(0\right)+{\gamma }_2}{{\gamma }_2}+\frac{p}{\omega (p-q)}\ln (G^{\frac{p-q}{p}}\left(0\right)+1)$, where $E\left(0\right)$ and $G\left(0\right)$ are the error initial values.

Proof. 

During the convergence period, the total finite convergence time T can be divided into two parts, namely, the time $T_E$ when $E\left(t\right)$ decreases to 0 in (7) and the time $T_G$ when $G\left(t\right)$ decreases to 0 in (7)—that is, the total convergence time $T=T_E+T_G$. To compute $T_E$, combine (7) and (8); then, we have

$$\begin{array}{cc}\hfill \dot{E}\left(t\right)=\frac{dE\left(t\right)}{dt}=& -{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)\hfill \\ \hfill dt=& \frac{1}{-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)}dE\left(t\right)\hfill \\ \hfill {\int }_0^{T_E}dt=& {\int }_{E\left(0\right)}^0\frac{1}{-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)}dE\left(t\right)\hfill \\ \hfill T_E=& \frac{p}{p-q}{\int }_0^{E^{\frac{p-q}{p}}\left(0\right)}\frac{1}{{\gamma }_1{E}^{\frac{p-q}{p}}\left(t\right)+{\gamma }_2}d{E}^{\frac{p-q}{p}}\left(t\right)\hfill \\ \hfill =& \frac{p}{{\gamma }_1(p-q)}\ln \frac{{\gamma }_1{E}^{\frac{p-q}{p}}\left(0\right)+{\gamma }_2}{{\gamma }_2}\hfill \end{array}$$

(16)

Thus, we can know that $E\left(t\right)=G\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma$ converges to 0 within $T_E$ = $\frac{p}{{\gamma }_1(p-q)}\ln \frac{{\gamma }_1{E}^{\frac{p-q}{p}}\left(0\right)+{\gamma }_2}{{\gamma }_2}$ seconds. When $E\left(t\right)$ converges to 0, we can know $E\left(t\right)=-\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma$; thus, $\dot{G}\left(t\right)$ can be written as follows:

$$\dot{G}\left(t\right)=-\omega (G\left(t\right)+G^{\frac{q}{p}}\left(t\right))$$

(17)

Our ultimate goal is to obtain the $X\left(t\right)$ to be solved by reducing $G\left(t\right)$ to 0. Therefore, we need to prove the convergence time $T_G$ from (17) at the time when $E\left(t\right)$ is reduced to 0. Thus, we have

$$\begin{array}{cc}\hfill \dot{G}\left(t\right)=\frac{dG\left(t\right)}{dt}=& -\omega (G\left(t\right)+G^{\frac{q}{p}}\left(t\right))\hfill \\ \hfill dt=& \frac{1}{-\omega (G\left(t\right)+G^{\frac{q}{p}}\left(t\right))}dG\left(t\right)\hfill \\ \hfill {\int }_0^{T_G}dt=& {\int }_{G\left(0\right)}^0\frac{1}{-\omega (G\left(t\right)+G^{\frac{q}{p}}\left(t\right))}dG\left(t\right)\hfill \\ \hfill T_G=& \frac{p}{\omega (p-q)}{\int }_0^{G^{\frac{p-q}{p}}\left(0\right)}\frac{1}{G^{\frac{p-q}{p}}\left(t\right)+1}d{G}^{\frac{p-q}{p}}\left(t\right)\hfill \\ \hfill =& \frac{p}{\omega (p-q)}\ln (G^{\frac{p-q}{p}}\left(0\right)+1)\hfill \end{array}$$

(18)

As above derivations, we can obtain the time $T_G$ for the error $G\left(t\right)$ converging to 0. As a whole, the error $E\left(t\right)$ is reduced to 0 within $T_E=\frac{p}{{\gamma }_1(p-q)}\ln \frac{{\gamma }_1{E}^{\frac{p-q}{p}}\left(0\right)+{\gamma }_2}{{\gamma }_2}$ seconds, and starting from the time when $E\left(t\right)=0$, the time $T_G=\frac{p}{\omega (p-q)}\ln (G^{\frac{p-q}{p}}\left(0\right)+1)$ when $G\left(t\right)$ is reduced to 0. Therefore, the upper bound of the total convergence time of (10) is

$$T=T_E+T_G=\frac{p}{{\gamma }_1(p-q)}\ln \frac{{\gamma }_1{E}^{\frac{p-q}{p}}\left(0\right)+{\gamma }_2}{{\gamma }_2}+\frac{p}{\omega (p-q)}\ln (G^{\frac{p-q}{p}}\left(0\right)+1).$$

(19)

   □

Theorem 3. 

Assuming that the time-varying LME problem (1) has an optimal solution, the noise-perturbed IEAZNN model (11) can stably converge to the theoretical solution from any initial value under the presence of different noise disturbances.

Proof. 

According to Equations (8) and (11), we can obtain the simple expression of the perturbed model

$$\dot{E}\left(t\right)=-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)+\mathrm{noise}$$

(20)

with $E\left(t\right)=G\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma$. Similarly, we define the candidate Lyapunov function for (20) as follows:

$$L\left(t\right)=\frac{{(-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)+\mathrm{noise})}^2}{2}$$

(21)

Then, the derivative $\dot{L\left(t\right)}$ of $L\left(t\right)$ can be written as follows:

$$\begin{array}{cc}\hfill \dot{L\left(t\right)}& ={(-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)+\mathrm{noise})}^2(-{\gamma }_1-{\gamma }_2\frac{q}{p}{E}^{\frac{p-q}{p}}\left(t\right))\hfill \end{array}$$

(22)

By observing Equation (22), there is no question that ${(-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)+\mathrm{noise})}^2\ge 0$. ${\gamma }_1,{\gamma }_2$, q and p are greater than 0; moreover, $p>q$ are both odd, which promises that $-{\gamma }_1-{\gamma }_2\frac{q}{p}{E}^{\frac{p-q}{p}}\left(t\right)$ is negative—that is, $\dot{L}\left(t\right)\le 0$, since $L\left(t\right)$ is defined by Equation (21) and $L\left(t\right)\ge 0$. According to the Lyapunov stability principle [15], we can know that $L\left(t\right)$ will eventually converge to 0. At that time, $(-{\gamma }_{1}E\left(t\right)-{\gamma }_2{E}^{\frac{q}{p}}\left(t\right)+\mathrm{noise})=\dot{E}\left(t\right)=0$.

As $E\left(t\right)=G\left(t\right)+\omega {\int }_0^t(G\left(\sigma \right)+G^{\frac{q}{p}}\left(\sigma \right))d\sigma$, expressed in Equation (7), when $\dot{E}\left(t\right)$ is equal to 0, we can further obtain $\dot{G}\left(t\right)=-\omega (G\left(t\right)+G^{\frac{q}{p}}\left(t\right))$ written in Equation (18), of which the convergence has been proven. That is to say, we have successfully proved the stability and convergence of the perturbed IEAZNN model (11), which can still accurately solve the time-varying LME (1) in a noisy environment.    □

4. Comparative Verifications

This section would give out two illustrative examples to show the convergence performance of the presented neural models. In the first example, we compared the convergence effects of the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10) under no noise, constant noise and dynamic linear noise. Subsequently, the performance of IEAZNN under random noise is analyzed. Additionally, under the condition that there is no noise, the ZNN model (6) is applied to solve the image deblurring problem.

Example 1. 

In the previous sections, we presented the CZNN model (3), IEAZNN (10) and perturbed IEAZNN (11), together with the theory analysis of convergence, finiteness of time and model robustness. In order to further verify the superiorities of the proposed IEAZNN model (10) as compared with the existing CZNN model (3) and the IEZNN model (5), an illustrative example is given in this section with the following coefficient matrices in time-varying LME problem (1), the same in [29]:

$$A\left(t\right)=\left[\begin{array}{cc}\sin t& \cos t\\ -\cos t& \sin t\end{array}\right],B\left(t\right)=\left[\begin{array}{ccc}2& \sin t+\cos t& \sin t\\ -\cos t& 2& \cos t\\ \sin t-2& 2-\sin t& 2-\sin t\end{array}\right],$$

$$\begin{array}{c}\hfill C\left(t\right)=\left[\begin{array}{ccc}2+\sin t\cos t-2\cos t& 3\cos t+\sin t-\sin t\cos t& \sin t+2\cos t-\sin t\cos t\\ -\cos t+{\sin }^{2}t-2\sin t& 2+2\sin t-{\sin }^{2}t& \cos t+2\sin t-{\sin }^{2}t\end{array}\right].\end{array}$$

The following theoretical solution $X^{*}$ can be obtained using the MATLAB tool [34]:

$$X^{*}\left(t\right)=\left[\begin{array}{ccc}\sin t& -\cos t& 0\\ \cos t& \sin t& 1\end{array}\right],$$

which is used to verify the accuracy of the abovementioned three solvers under the following different noise cases. Meanwhile, according to the above theoretical proof and model characteristics, p and q will be set as 5 and 3, respectively, in the experiment. In order to better introduce the Matlab application, a brief presentation of the algorithm is presented in Algorithm 1:

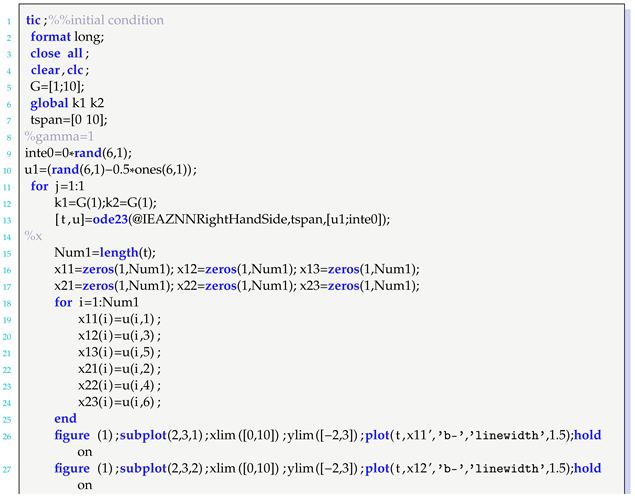
Algorithm 1: Matlab program core ideas.

${\gamma }_1,{\gamma }_2$← 1, $\omega =10$ repeat IEAZNN model (10) until t=10 for i← 1 to 6 do figure(1); plot(t,$X_i$) error ←$A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right)$, theo ←$A^{†}\left(t\right)C\left(t\right)B^{†}\left(t\right)$ for j← 1 to 6 do figure(1); plot(t,$the{o}_j$) figure(2); plot(t,norm(error))

Case 1. 

No Noise: First of all, the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10) start from the same random initial value with the same other conditions. Figure 1 shows the convergence of the three models with different design parameters ${\gamma }_1={\gamma }_2=1$ and ${\gamma }_1={\gamma }_2=10$ under the absence of noise, where Figure 1a depicts the fitting relationship between the $X\left(t\right)$ solved by the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10), and the theoretical solution $X^{*}$ (red line) when ${\gamma }_1={\gamma }_2=1$ and $\omega =10$. It can be seen that the three models can eventually converge to the theoretical solution when there is no noise interference. Figure 1b shows the convergence performance of residual error ${\parallel S\left(t\right)=A\left(t\right)X\left(t\right)B\left(t\right)-C\left(t\right)\parallel }_F$, which corresponds to $X\left(t\right)$ shown in Figure 1a, in which all three models have good convergence accuracy. Compared with Figure 1a, the design parameters ${\gamma }_1$ and ${\gamma }_2$ are increased to 10 in Figure 1c. Obviously, $X\left(t\right)$ by the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10) can still converge to the theoretical solution, and the convergence time is shorter in comparison with Figure 1b with ${\gamma }_1={\gamma }_2=1$. Similarly, Figure 1d shows the residual error, which corresponds to Figure 1c. It shows that although CZNN model (3) converges faster, the IEAZNN model (10) has higher convergence accuracy reaching the ${10}^{-6}$ level, and is better than those of the CZNN model (3) and the IEZNN model (5), both of which can only reach the ${10}^{-4}$ level. It is worth mentioning that, when the design parameters increase, the IEAZNN model (10) converges faster than the IEZNN model (5) with zero noise. The code about this figure can be found in Appendix A.

Case 2. 

Constant Noise:Figure 2 shows the convergence performance of the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10) under constant noise $c=2$, the same as in [32]. Figure 2a depicts the fitting relationship between $X\left(t\right)$ solved by the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10), and the theoretical solution $X^{*}$ (red line) with ${\gamma }_1={\gamma }_2=1$ and $\omega =10$. It can be seen that under the condition of constant noise $c=2$, only the IEZNN model (5) and IEAZNN model (10) involved with an integral term can converge to the theoretical solution, while the CZNN model (3) without the integral term cannot resist noise. Figure 2b shows the residual error, which corresponds to $X\left(t\right)$, shown in Figure 2a. It shows that both the IEZNN and IEAZNN have good convergence effects when ${\gamma }_1={\gamma }_2=1$, and the convergence accuracy of the IEZNN model (5) reaches the ${10}^{-4}$ level, which is better than the IEAZNN’s ${10}^{-3}$ level. Notably, when design parameters are not so large, such as ${\gamma }_1={\gamma }_2=1$, the IEAZNN model (10) deals with noise by adding the integral term into the error, and the design idea (8) has two parts controlled by design parameters, which makes the IEAZNN model (10) have no advantages compared with the IEZNN model when solving LME (1) dynamically. However, along with the increase of design parameters, ${\gamma }_1={\gamma }_2$ to 10. Obviously, the IEZNN model (5) and IEAZNN model (10) can still converge to the theoretical solution, and the convergence time is shorter than that of the case when ${\gamma }_1={\gamma }_2=1$. Although, when ${\gamma }_1$ is increased to 10, the CZNN model (3) is still unable to resist noise, and the convergence effect is better than that of the case when ${\gamma }_1=1$ with a low error level. Additionally, as shown in Figure 2d, compared with the IEZNN model (5), the IEAZNN model (10) can not only greatly shorten the convergence time but also have better convergence accuracy with the ${10}^{-5}$ level, which is better than the ${10}^{-3}$ level of IEZNN model (5).

Case 3. 

Dynamic Linear Noise:Figure 3 shows the convergence performance of the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10) under dynamic linear noise $\mathrm{noise}=0.6t$ [32]. Likewise, the comparison experiments start from the same random initial value, ensuring that all other conditions are the same. As shown in Figure 3a, it is obvious that when the CZNN model (3) is used, $X\left(t\right)$ cannot converge to the theoretical solution $X^{*}$ when ${\gamma }_1={\gamma }_2=1$ and $\omega =10$, only $X\left(t\right)$ of the IEZNN model (5) and IEAZNN model (10) can converge to the theoretical solution. Figure 3b shows that the residual error of the traditional CZNN model (3) decreases at the beginning, and then starts to increase after several seconds with a divergent trend. On the other hand, the residual error of the IEZNN model (5) and the IEAZNN model (10) can achieve convergence but the residual convergence speed and convergence accuracy of the IEZNN model (5) are not as good as those of the IEAZNN model (10). For example, when ${\gamma }_1={\gamma }_2=1$, the residual error convergence accuracy of the IEAZNN model (10) can reach the ${10}^{-2}$ level, which is better than the ${10}^{-1}$ of the IEZNN model (5). As shown in Figure 3c,d, although the residual error of the traditional CZNN model (3) still cannot be reduced to 0, the increase is smaller than that of the case when ${\gamma }_1=1$. In addition, the convergence speed and convergence accuracy of the residuals of the IEAZNN model (10) have been further improved, in which the residual can converge to zero within 1 s and the convergence accuracy reaches the order of magnitude of ${10}^{-3}$. In contrast, under the interference of dynamic linear noise, neither the convergence accuracy nor the convergence time of the residual error of the IEZNN model (5) are obviously improved with the increase in ${\gamma }_1$, and the convergence accuracy can only reach the ${10}^{-1}$ level.

In order to simulate the irregular noise in nature as much as possible, the IEAZNN model (10) is used to solve the LME (1) dynamically under the interference of random noise. From Figure 4, it can be clearly seen that the IEAZNN model (10) performs very well under the interference of random noise, not only with high convergence accuracy but also with short convergence time. It can be seen from Figure 4b that when ${\gamma }_1={\gamma }_2=1$, the residual error convergence accuracy of the IEAZNN model (10) can reach the ${10}^{-3}$ level.

It can be seen from the above comparative experiments that when ${\gamma }_1={\gamma }_2=1$, the convergence time of the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10) are basically the same. However, when ${\gamma }_1$ and ${\gamma }_2$ increase to 10, the IEAZNN model (10) can converge in about 1 s, and its comprehensive convergence effect is the best. For comparing the experiment results more intuitively, the convergence precision of the CZNN model (3), the IEZNN model (5) and the IEAZNN model (10) are summarized in

Table 1. Comparison of solving accuracies of the CZNN model (3), IEZNN model (5) and IEAZNN model (10) under different noise and design parameters.

		No Noise	Constant Noise	Dynamic Bounded Noise
	CZNN	${10}^{-4}$	Cannot reach convergence	Cannot reach convergence
${\gamma }_1={\gamma }_2=1$	IEZNN	${10}^{-5}$	${10}^{-4}$	${10}^{-1}$
	IEAZNN	${10}^{-3}$	${10}^{-3}$	${10}^{-2}$
	CZNN	${10}^{-4}$	Cannot reach convergence	Cannot reach convergence
${\gamma }_1={\gamma }_2=10$	IEZNN	${10}^{-4}$	${10}^{-3}$	${10}^{-1}$
	IEAZNN	${10}^{-6}$	${10}^{-5}$	${10}^{-3}$

under different noise and design parameters. From Table 1, we have the following facts:

(1)

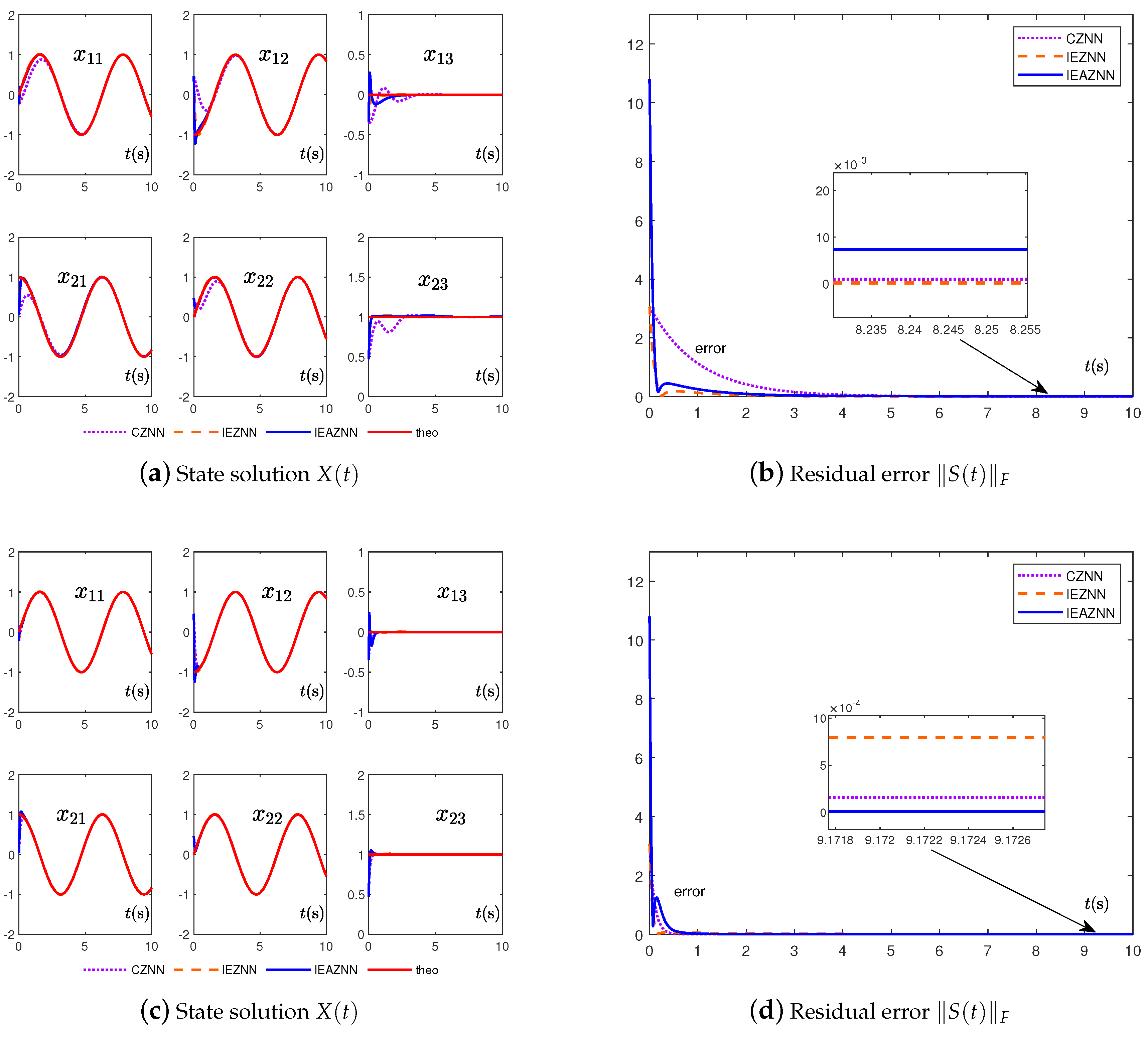
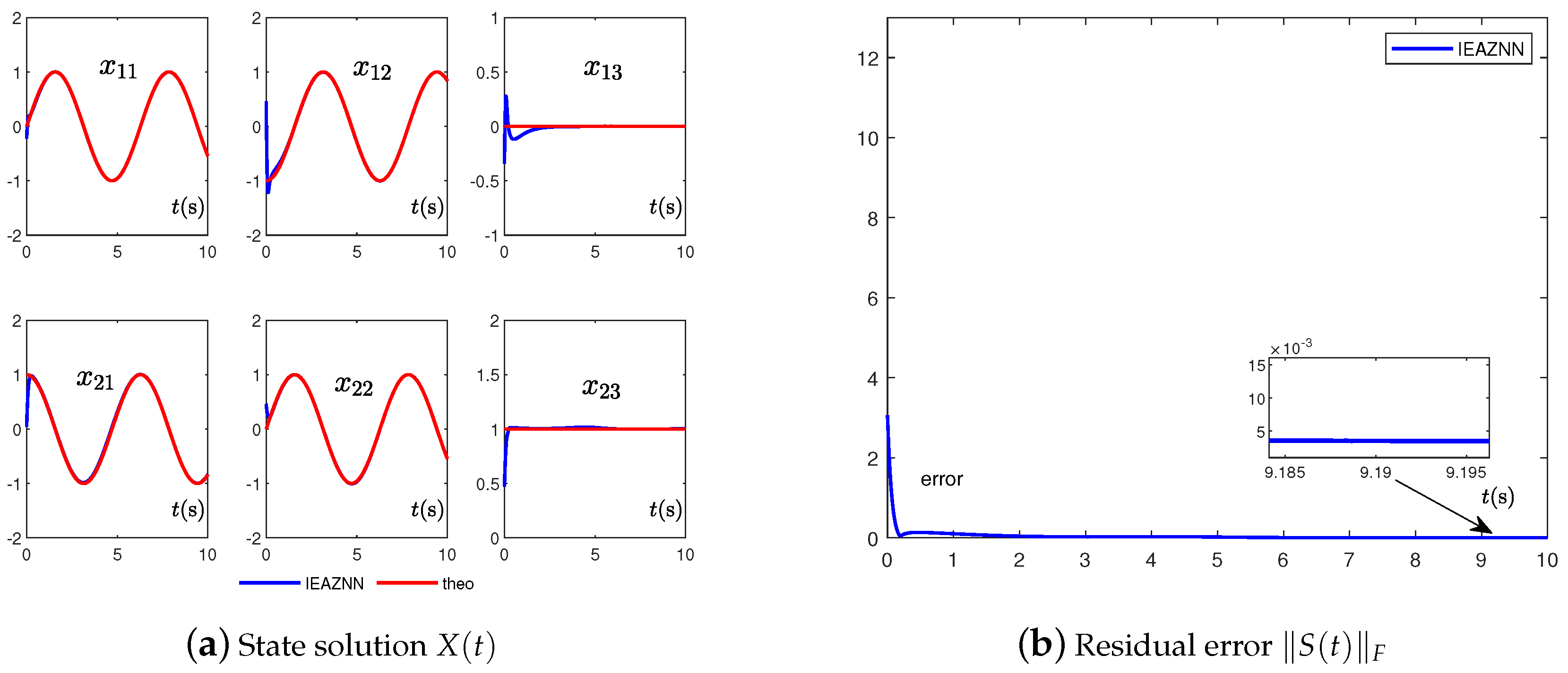
In the case of zero-noise interference, the convergence effect of the CZNN model (3) is stable and the accuracy is high whether ${\gamma }_1=1$ or ${\gamma }_1=10$. Once there is noise interference, the CZNN model (3) cannot accurately solve the time-varying LME (1). However, whether there exists noise or not, the IEZNN model (5) and IEAZNN model (10) can always accurately solve the LME problem (1).

(2)

Because of the different design formulas, the presented IEAZNN model (10) in this paper has higher convergence accuracy and better convergence performance when dealing with dynamic linear noise, whether ${\gamma }_1={\gamma }_2=1$ or ${\gamma }_1={\gamma }_2=10$, in comparison with the other two ZNN models.

(3)

With the increase in ${\gamma }_1$ and ${\gamma }_2$, among these three ZNN models, the convergence accuracy of the IEAZNN model (10) proposed in this paper is the highest whether there exists noise or not. It shows that the IEAZNN model (10) has advantages in solving the time-varying LME problems.

Example 2. 

In the application of image blurring, we consider the time-invariant special case of LME (1). A and B represent a 100 × 100-dimensional Toeplitz matrix [5], which is constructed by formula (23) and $A=B$. X represents the original image, and C represents the blurred image. We consider $r=8$. The ZNN model (6) is used for image deblurring, and the results are shown in Figure 5.

$$a_{ij}=\left\{\begin{array}{ccc}\hfill \frac{1}{2r-1},& \hfill & \hfill |i-j|\le r\\ \hfill 0,& \hfill & \hfill otherwise.\end{array}\right.$$

(23)

${\gamma }_1={\gamma }_2=1$ is set for this experiment, and other conditions are the same as Example 1. Compared with the original Figure 5a, although the deblurred Figure 5c has some minor defects, it can restore the blurred image Figure 5b to a visible state, which is almost the same as Figure 5a.

5. Conclusions

In order to achieve finite-time convergence, high convergence accuracy and anti-noise robustness in LME solving in the presence of noise, an integration-enhanced combined accelerating zeroing neural network (IEAZNN) is designed, verified and applied in this paper. Different from the general existing ZNN models, IEAZNN first takes the gradient of the energy function as the initial error, and then obtains the reconstructed error by the help of the design idea of IEZNN. Next, this paper provides the proofs of global stability and finite convergence time under zero noise and different noise situations for the designed IEAZNN model. Finally, numerical simulations are conducted to verify the convergence characteristic of the IEAZNN model, and comparisons among the CZNN model and IEZNN model are performed to illustrate the superior performance of the proposed method. Future studies might concentrate on how to apply the IEAZNN model to practical engineering applications.