Multi-AGV Dynamic Scheduling in an Automated Container Terminal: A Deep Reinforcement Learning Approach
Abstract
1. Introduction
- (1)
- The dynamic scheduling problem of AGVs at automated terminals is formulated as a Markov decision process, in which the dynamic information of the terminal system, such as the number of tasks, task waiting time, task transportation distance, the working/idle status of the AGVs and the position of the AGVs, are modeled as input states.
- (2)
- A novel dynamic AGV scheduling approach based on DQN is proposed, where the optimal mixed rule and AGV assignments can be selected efficiently to minimize the total completion time of AGVs and the total waiting time of QCs.
- (3)
- A simulation model is built on Tecnomatix Plant Simulation software according to an automated terminal in Shanghai, China. Simulation-based experiments are conducted to evaluate the performance of the proposed approach. The experimental results show that the proposed approach outperforms the conventional heuristic approach based on GA and rule-based scheduling.
2. Literature Review
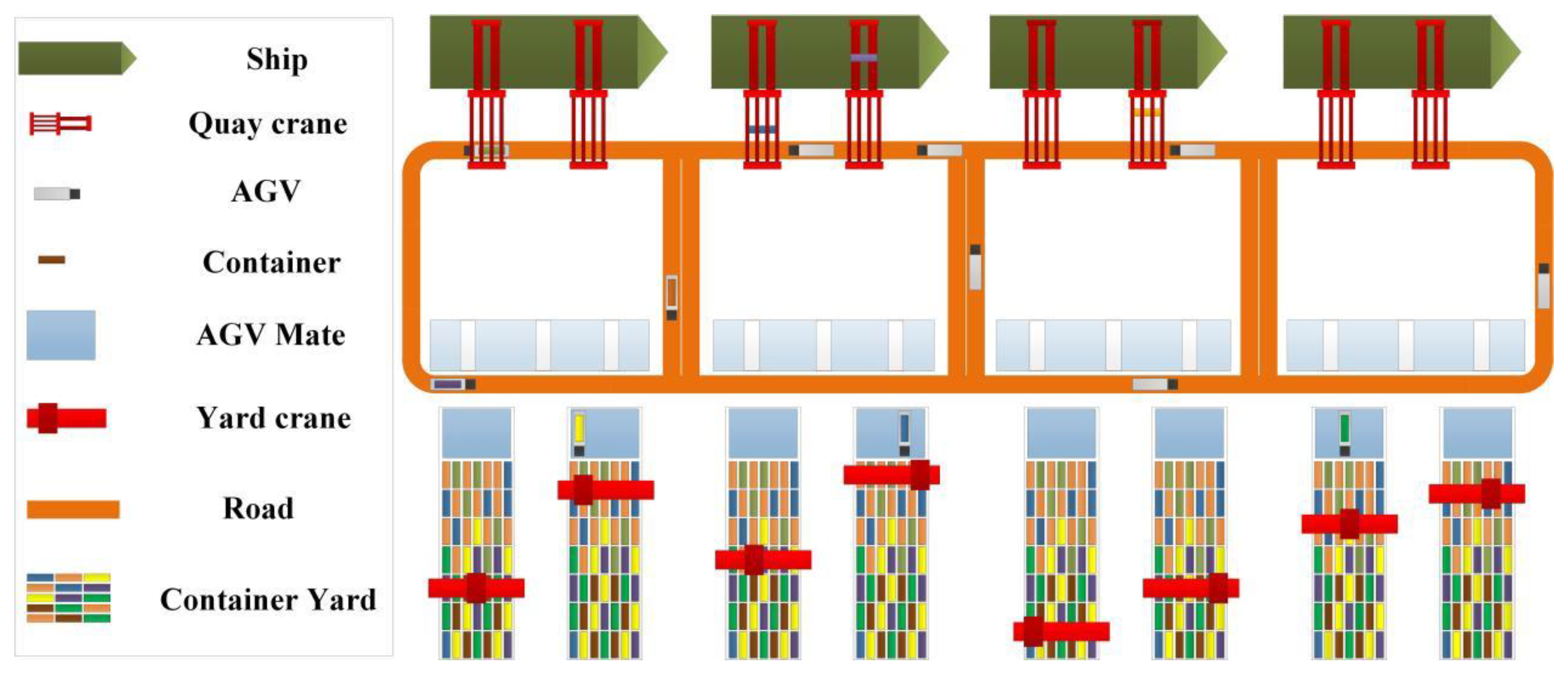
3. Problem Formulation
3.1. MDP Model the Dynamic Scheduling of Multi-AGVs
3.2. State Definition
- (1)
- is the number of container tasks current on QCs which waiting for AGV transport, indicating the current workload in the terminal.
- (2)
- represents the average waiting time of the container task, which is waiting for AGV transport currently on QCs. It indicates the average urgency of the current task. The is defined as follows:where is the waiting time of the k-th container task that awaits transportation by the AGVs.
- (3)
- represents the average transportation distance of the container tasks on the QCs. This metric reflects the average workload per task and is defined as follows:where is the travel distance of the k-th task from the related QC to its destination location at the yard.
- (4)
- represents the working status of all the alternative AGVs, which can be represented by a binary vector in the form of:where represents the working status of AGV i as “Working” and represents the working status of AGV as “Idle”.
- (5)
- represents the dynamic position of AGV in the port, determined by a given pair of coordinates .
3.3. Action Definition
3.4. Reward Function
3.5. Optimal Mixed Rule Policy Based on Reinforcement Learning
- (1)
- Prediction: given a policy and evaluation function, the value function corresponding to a state and action, denoted as , is:where is the expected value of reward when the state starts from , takes action and follows policy [26,27,28]. For any pair of , we can calculate its value function based on Equation (10).
- (2)
- Control: to find the optimal policy based on the value function. As the goal of reinforcement learning is to obtain the optimal policy, i.e., the optimal selection of actions in different states, with multiple scheduling rules used as actions, the mixed rule policy in our proposed model can be defined as the expected discounted future reward when the agent takes action in state as follows:where is the discount factor and is the current reward at time . Based on Equation (12), the multi-AGV dynamic scheduling problem is to find an optimal mixed rule policy in each state such that the reward obtained in the following form is maximized:
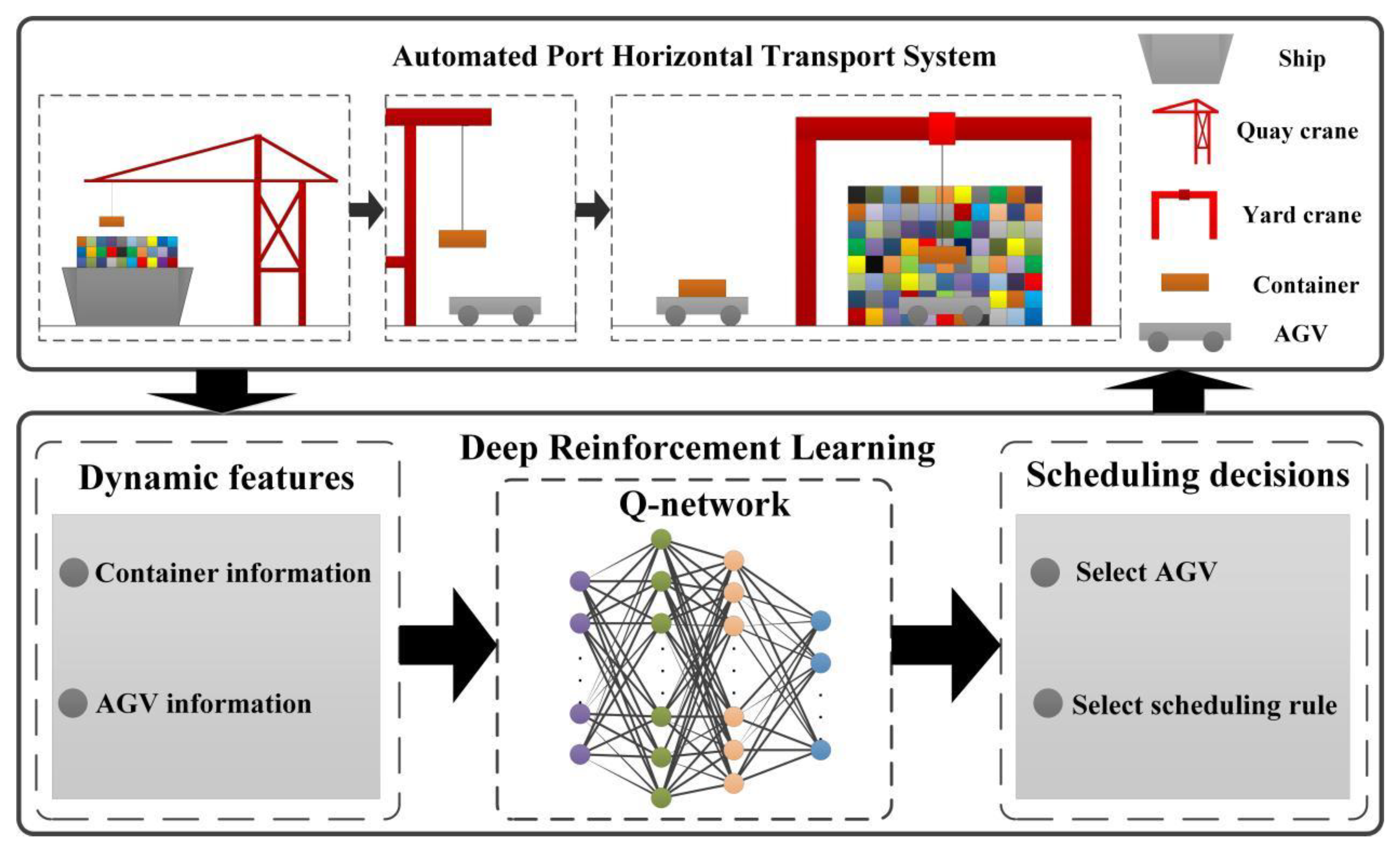
4. DQN-Based Scheduling Approach
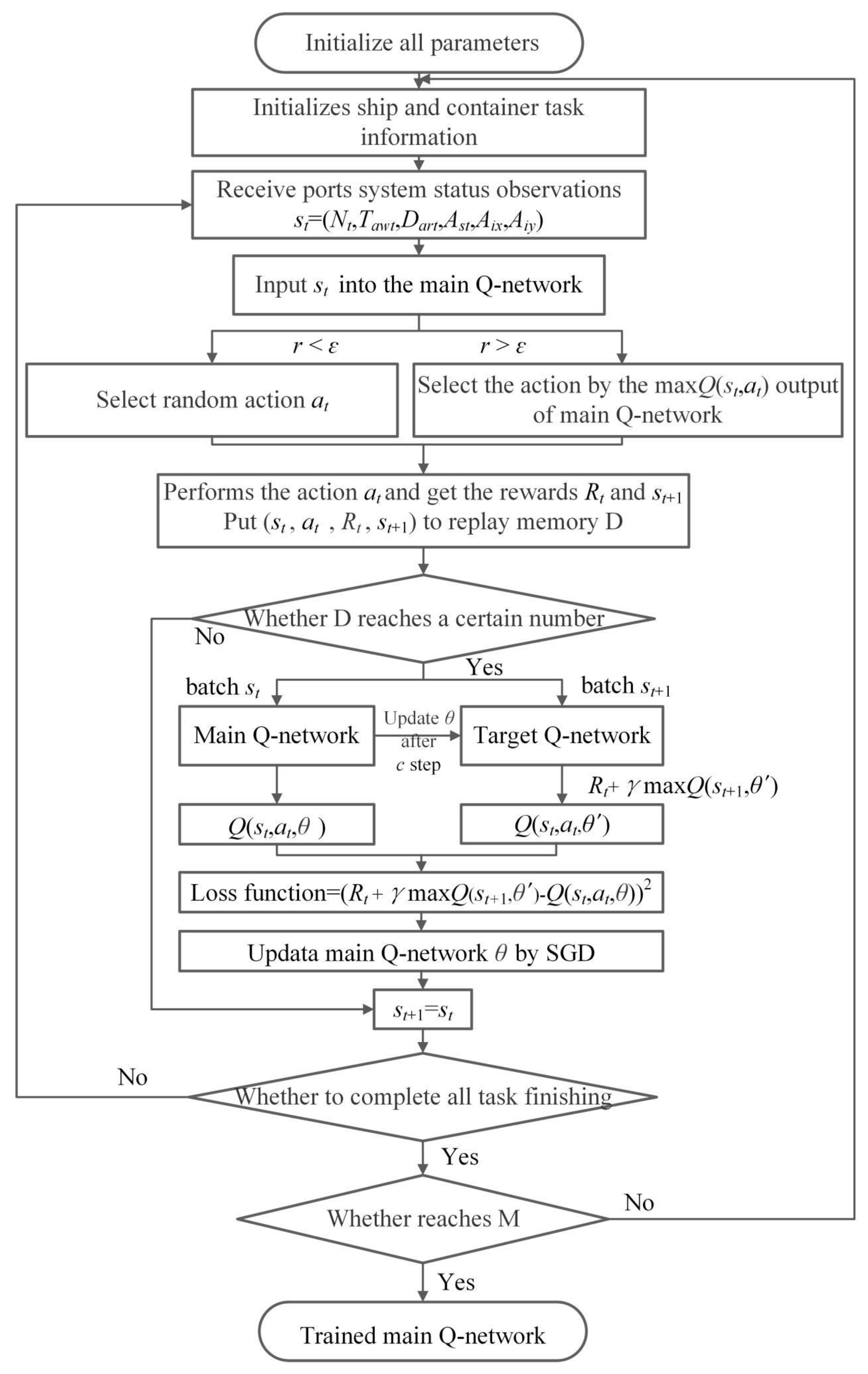
4.1. DQN Training Process
| Algorithm 1: deep Q-learning with experience reply |
End For End For |
4.2. Scheduling Procedure with Mixed Rules
5. Simulation-Based Experiments
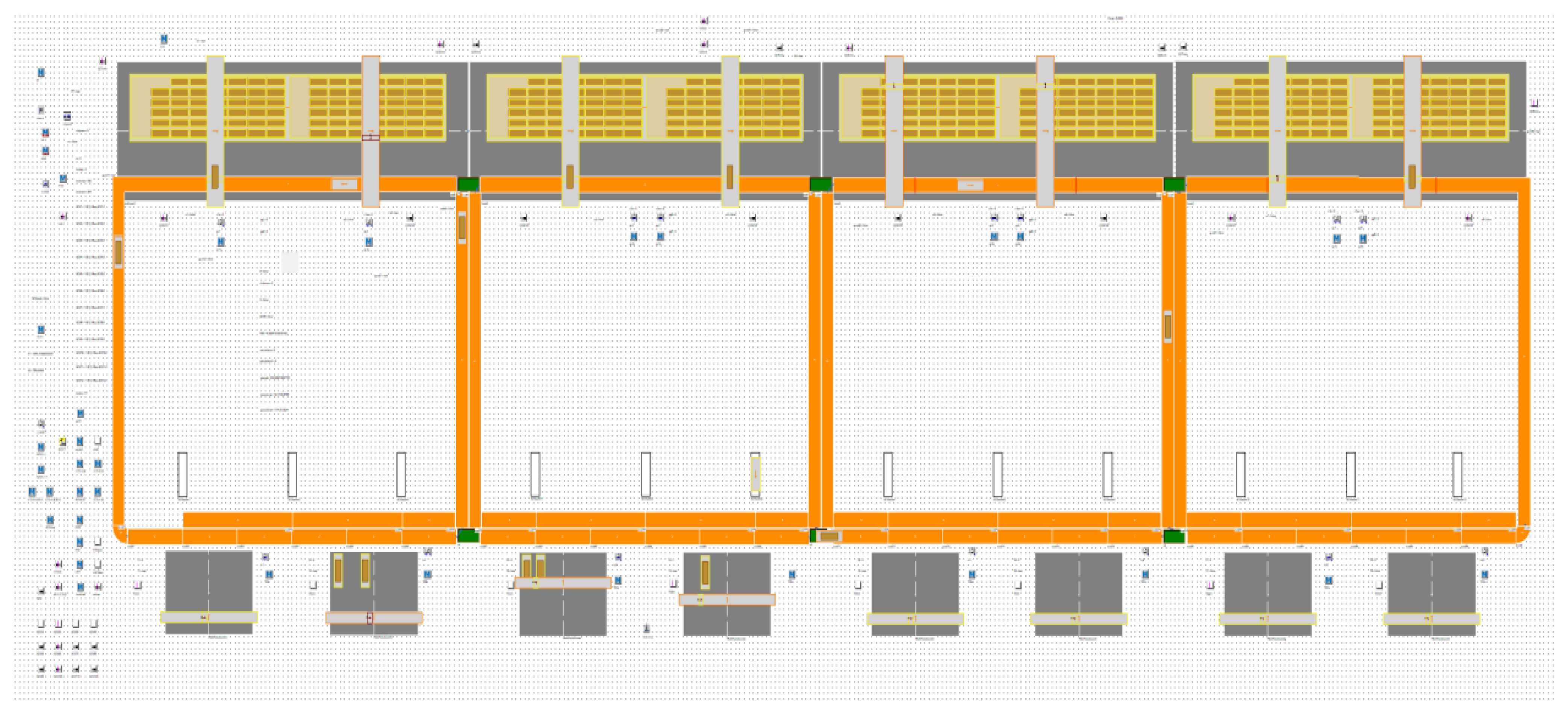
5.1. Simulation Set Up
- (1)
- All pending containers are standardized 20 ft TEUs;
- (2)
- The problem of turning over the box is not considered;
- (3)
- The information of the container task is randomly generated;
- (4)
- The order of unloading of the QCs is predetermined;
- (5)
- All containers are import containers;
- (6)
- All AGV roads in the simulation scene are one-way streets;
- (7)
- Each AGV can only transport one container at a time;
- (8)
- When the AGV transports the container to the designated yard, it needs to wait for the YC to unload the container it carries for the task to be considered “completed”;
- (9)
- When the AGV completes its current task, and there are currently no incoming tasks, it will return to the AGV waiting area;
- (10)
- All AGVs’ navigation methods are the shortest path policy. Each container has its own key attributes, including container ID, the container from QC, container destination, container yard, the current waiting time for the AGV and the estimated distance to be transported.
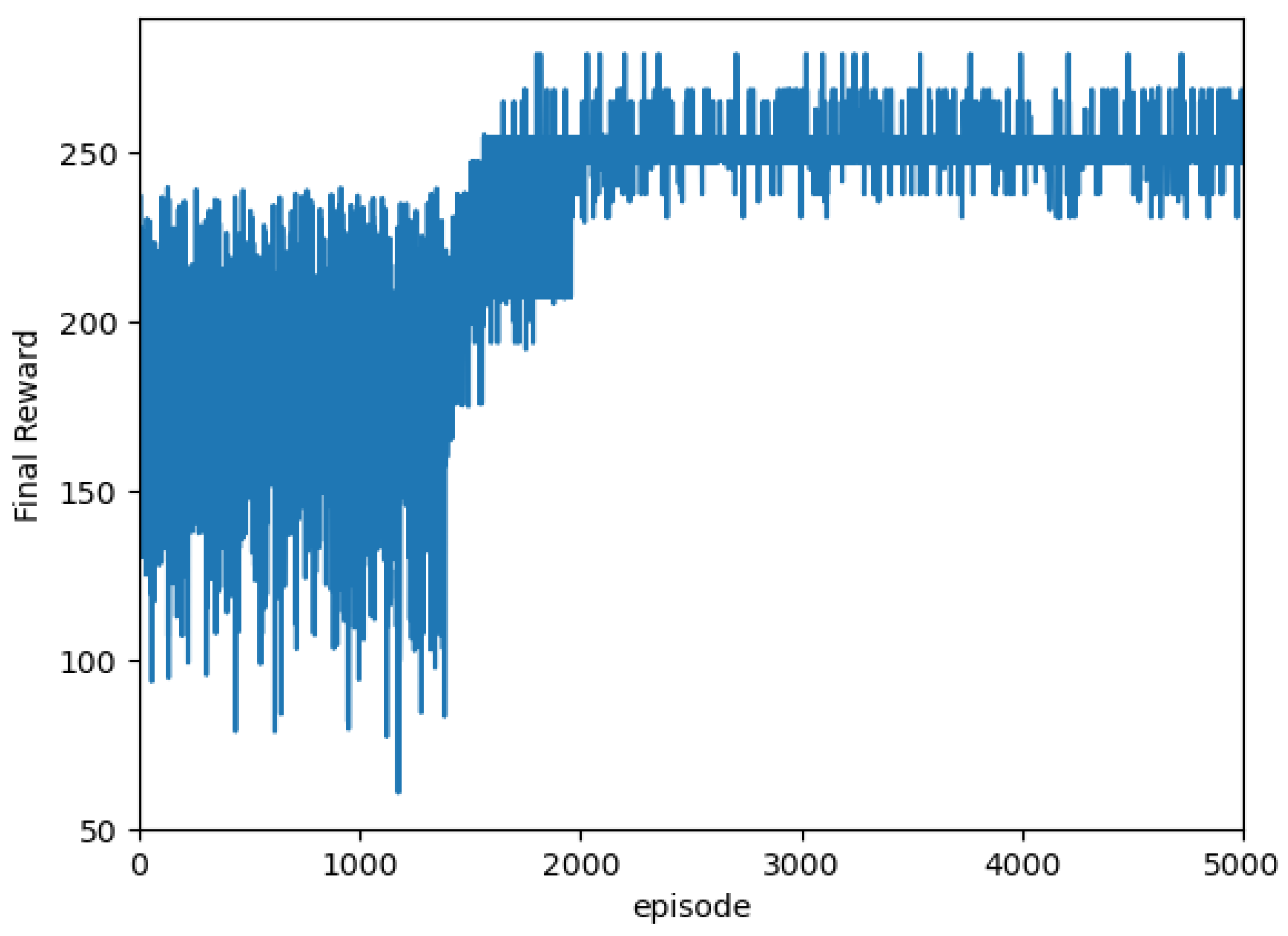
5.2. Implementation of DQN-Based Multi-AGV Dynamic Scheduling
6. Results and Discussions
6.1. Testing Case Description
6.2. Results Analysis
6.2.1. Comparison of Results Based on DQN and Genetic Algorithm (GA)
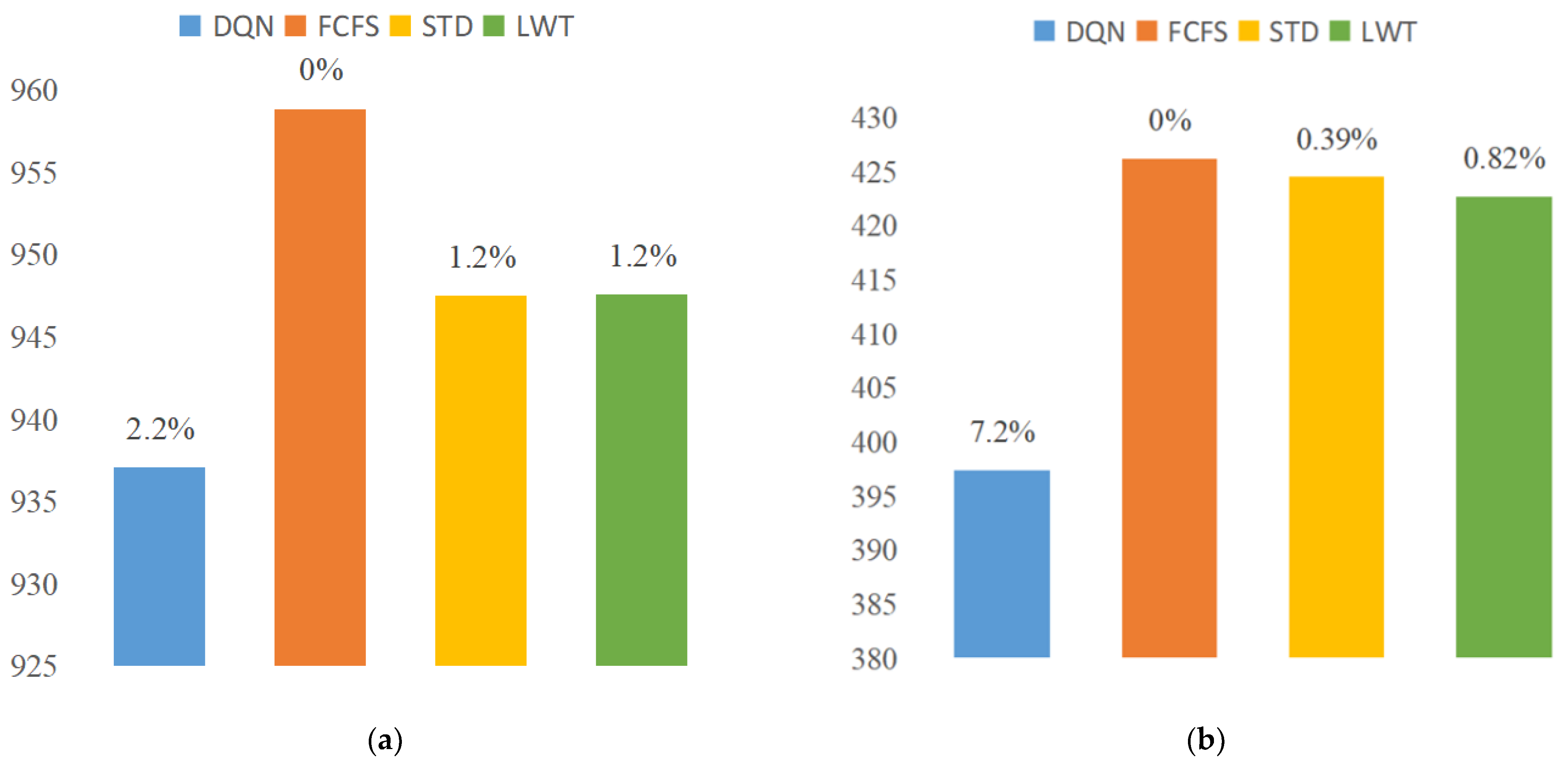
6.2.2. Dynamic Scheduling Comparison
7. Conclusions and Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Li, W.; Petering, M.E.H.; Goh, M.; Souza, R.D. Scheduling Multiple Yard Cranes with Crane Interference and Safety Distance Requirement. Transp. Sci. 2015, 49, 990–1005. [Google Scholar] [CrossRef]
- Chen, X.; He, S.; Zhang, Y.; Tong, L.; Shang, P.; Zhou, X. Yard crane and AGV scheduling in automated container terminal: A multi-robot task allocation framework. Transp. Res. Part C Emerg. Technol. 2020, 114, 241–271. [Google Scholar] [CrossRef]
- Yang, Y.; Zhong, M.; Dessouky, Y.; Postolache, O. An integrated scheduling method for AGV routing in automated container terminals. Comput. Ind. Eng. 2018, 126, 482–493. [Google Scholar] [CrossRef]
- Xu, Y.; Qi, L.; Luan, W.; Guo, X.; Ma, H. Load-In-Load-Out AGV Route Planning in Automatic Container Terminal. IEEE Access 2020, 8, 157081–157088. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, Y.; Dessouky, Y.; Postolache, O. Multi-AGV scheduling for conflict-free path planning in automated container terminals. Comput. Ind. Eng. 2020, 142, 106371. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Hu, W.X.; Duan, J.G.; Qin, J.Y. Cooperative Scheduling of AGV and ASC in Automation Container Terminal Relay Operation Mode. Math. Probl. Eng. 2021, 2021, 5764012. [Google Scholar] [CrossRef]
- Klein, C.M.; Kim, J. AGV dispatching. Int. J. Prod. Res. 1996, 34, 95–110. [Google Scholar] [CrossRef]
- Sabuncuoglu, I. A study of scheduling rules of flexible manufacturing systems: A simulation approach. Int. J. Prod. Res. 1998, 36, 527–546. [Google Scholar] [CrossRef]
- Shiue, Y.-R.; Lee, K.-C.; Su, C.-T. Real-time scheduling for a smart factory using a reinforcement learning approach. Comput. Ind. Eng. 2018, 125, 604–614. [Google Scholar] [CrossRef]
- Angeloudis, P.; Bell, M.G.H. An uncertainty-aware AGV assignment algorithm for automated container terminals. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 354–366. [Google Scholar] [CrossRef]
- Gawrilow, E.; Klimm, M.; Möhring, R.H.; Stenzel, B. Conflict-free vehicle routing. EURO J. Transp. Logist. 2012, 1, 87–111. [Google Scholar] [CrossRef]
- Cai, B.; Huang, S.; Liu, D.; Dissanayake, G. Rescheduling policies for large-scale task allocation of autonomous straddle carriers under uncertainty at automated container terminals. Robot. Auton. Syst. 2014, 62, 506–514. [Google Scholar] [CrossRef]
- Clausen, C.; Wechsler, H. Quad-Q-learning. IEEE Trans. Neural Netw. 2000, 11, 279–294. [Google Scholar] [CrossRef] [PubMed]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-Learning Algorithms: A Comprehensive Classification and Applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Tang, H.; Wang, A.; Xue, F.; Yang, J.; Cao, Y. A Novel Hierarchical Soft Actor-Critic Algorithm for Multi-Logistics Robots Task Allocation. IEEE Access 2021, 9, 42568–42582. [Google Scholar] [CrossRef]
- Watanabe, M.; Furukawa, M.; Kakazu, Y. Intelligent AGV driving toward an autonomous decentralized manufacturing system [Article; Proceedings Paper]. Robot. Comput.-Integr. Manuf. 2001, 17, 57–64. [Google Scholar] [CrossRef]
- Xia, Y.; Wu, L.; Wang, Z.; Zheng, X.; Jin, J. Cluster-Enabled Cooperative Scheduling Based on Reinforcement Learning for High-Mobility Vehicular Networks. IEEE Trans. Veh. Technol. 2020, 69, 12664–12678. [Google Scholar] [CrossRef]
- Kim, D.; Lee, T.; Kim, S.; Lee, B.; Youn, H.Y. Adaptive packet scheduling in IoT environment based on Q-learning. J. Ambient Intell. Hum. Comput. 2020, 11, 2225–2235. [Google Scholar] [CrossRef]
- Fotuhi, F.; Huynh, N.; Vidal, J.M.; Xie, Y. Modeling yard crane operators as reinforcement learning agents. Res. Transp. Econ. 2013, 42, 3–12. [Google Scholar] [CrossRef]
- de León, A.D.; Lalla-Ruiz, E.; Melián-Batista, B.; Marcos Moreno-Vega, J. A Machine Learning-based system for berth scheduling at bulk terminals. Expert Syst. Appl. 2017, 87, 170–182. [Google Scholar] [CrossRef]
- Jeon, S.M.; Kim, K.H.; Kopfer, H. Routing automated guided vehicles in container terminals through the Q-learning technique. Logist. Res. 2010, 3, 19–27. [Google Scholar] [CrossRef]
- Choe, R.; Kim, J.; Ryu, K.R. Online preference learning for adaptive dispatching of AGVs in an automated container terminal. Appl. Soft Comput. 2016, 38, 647–660. [Google Scholar] [CrossRef]
- Wan, Z.; Li, H.; He, H.; Prokhorov, D. Model-Free Real-Time EV Charging Scheduling Based on Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 10, 5246–5257. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Han, X.; He, H.; Wu, J.; Peng, J.; Li, Y. Energy management based on reinforcement learning with double deep Q-learning for a hybrid electric tracked vehicle. Appl. Energy 2019, 254, 113708. [Google Scholar] [CrossRef]
- Buşoniu, L.; de Bruin, T.; Tolić, D.; Kober, J.; Palunko, I. Reinforcement learning for control: Performance, stability, and deep approximators. Annu. Rev. Control 2018, 46, 8–28. [Google Scholar] [CrossRef]
- Kubalik, J.; Derner, E.; Zegklitz, J.; Babuska, R. Symbolic Regression Methods for Reinforcement Learning. IEEE Access 2021, 9, 139697–139711. [Google Scholar] [CrossRef]
- Montague, P.R. Reinforcement learning: An introduction. Trends Cogn. Sci. 1999, 3, 360. [Google Scholar] [CrossRef]
- Pan, J.; Wang, X.; Cheng, Y.; Yu, Q.; Jie, P.; Xuesong, W.; Wang, X. Multisource Transfer Double DQN Based on Actor Learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2227–2238. [Google Scholar] [CrossRef]
- Stelzer, A.; Hirschmüller, H.; Görner, M. Stereo-vision-based navigation of a six-legged walking robot in unknown rough terrain. Int. J. Robot. Res. 2012, 31, 381–402. [Google Scholar] [CrossRef]
- Zheng, J.F.; Mao, S.R.; Wu, Z.Y.; Kong, P.C.; Qiang, H. Improved Path Planning for Indoor Patrol Robot Based on Deep Reinforcement Learning. Symmetry 2022, 14, 132. [Google Scholar] [CrossRef]
- Liu, B.; Liang, Y. Optimal function approximation with ReLU neural networks. Neurocomputing 2021, 435, 216–227. [Google Scholar] [CrossRef]
- Wang, B.; Osher, S.J. Graph interpolating activation improves both natural and robust accuracies in data-efficient deep learning. Eur. J. Appl. Math. 2021, 32, 540–569. [Google Scholar] [CrossRef]
- da Motta Salles Barreto, A.; Anderson, C.W. Restricted gradient-descent algorithm for value-function approximation in reinforcement learning. Artif. Intell. 2008, 172, 454–482. [Google Scholar] [CrossRef]




| Rule | Description | Advantage | Shortcoming |
|---|---|---|---|
| FCFS | Tasks are selected based on the order of arrival | FCFS can ensure the overall efficiency and smoothness of scheduling | FCF is not effective at meeting other metrics than efficiency, such as task priorities and travel costs |
| STD | Task with the shortest trip will be selected first | STD can improve overall efficiency to a certain extent | STD can cause longer wait times for tasks and longer trips |
| LWT | Task with the longest waiting time will be selected first | LWT can effectively reduce the waiting time for tasks and ensure production efficiency | LWT cannot effectively meet other metrics than waiting time, such as efficiency and travel costs |
| Layer | Number of Nodes | Activation Function | Description |
|---|---|---|---|
| Input layer | 28 | None | Used to accept system state |
| hidden layer 1 | 350 | ReLU | None |
| hidden layer 2 | 140 | ReLU | None |
| Output layer | 36 | Softmax | for output action |
| ID | From | Destination | Waiting Time | Transport Distance |
|---|---|---|---|---|
| 001 | QC1 | container yard6 | 55 s | 284.54 |
| 002 | QC4 | container yard2 | 186 s | 247.0 |
| 003 | QC3 | container yard7 | 255 s | 278.9 |
| 004 | QC5 | container yard4 | 78 s | 203.6 |
| 005 | QC8 | container yard3 | 396 s | 279.4 |
| N × A | Total Waiting Time of QCs (min) | Total Completion Time of AGVs (min) | Makespan (min) | |||
|---|---|---|---|---|---|---|
| DQN | GA | DQN | GA | DQN | GA | |
| 48 × 4 | 142.89 | 144.84 | 103.74 | 96.93 | 28.14 | 27.29 |
| 96 × 6 | 181.54 | 217.58 | 210.43 | 198.57 | 38.64 | 41.56 |
| 192 × 8 | 294.54 | 425.63 | 439.78 | 405.20 | 60.21 | 73.45 |
| 384 × 12 | 397.40 | 801.61 | 937.09 | 829.30 | 93.08 | 143.93 |
| N × A | DQN | GA |
|---|---|---|
| 48 × 4 | 3.24 s | 20 min |
| 96 × 6 | 7.95 s | 42 min |
| 192 × 8 | 10.95 s | 69 min |
| 384 × 12 | 21.02 s | 135 min |
| N × A | DQN | FCFS | STD | LWT |
|---|---|---|---|---|
| 48 × 4 | 142.891 | 162.609 | 138.670 | 128.690 |
| 96 × 6 | 181.545 | 204.300 | 189.323 | 207.723 |
| 192 × 8 | 294.548 | 350.697 | 325.924 | 318.611 |
| 384 × 12 | 397.404 | 426.185 | 424.501 | 422.681 |
| N × A | DQN | FCFS | STD | LWT |
|---|---|---|---|---|
| 48 × 4 | 103.748 | 107.570 | 111.710 | 110.347 |
| 96 × 6 | 210.433 | 219.130 | 217.960 | 211.420 |
| 192 × 8 | 439.785 | 441.478 | 442.928 | 442.493 |
| 384 × 12 | 937.090 | 958.891 | 947.500 | 947.610 |
| N × A | DQN | FCFS | STD | LWT |
|---|---|---|---|---|
| 48 × 4 | 3.24 s | 1.11 s | 1.15 s | 1.10 s |
| 96 × 6 | 7.95 s | 2.08 s | 2.29 s | 2.05 s |
| 192 × 8 | 10.95 s | 4.05 s | 4.16 s | 4.03 s |
| 384 × 12 | 21.02 s | 8.06 s | 8.28 s | 7.91 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Liang, C.; Wang, Y.; Shi, J.; Lim, G. Multi-AGV Dynamic Scheduling in an Automated Container Terminal: A Deep Reinforcement Learning Approach. Mathematics 2022, 10, 4575. https://doi.org/10.3390/math10234575
Zheng X, Liang C, Wang Y, Shi J, Lim G. Multi-AGV Dynamic Scheduling in an Automated Container Terminal: A Deep Reinforcement Learning Approach. Mathematics. 2022; 10(23):4575. https://doi.org/10.3390/math10234575
Chicago/Turabian StyleZheng, Xiyan, Chengji Liang, Yu Wang, Jian Shi, and Gino Lim. 2022. "Multi-AGV Dynamic Scheduling in an Automated Container Terminal: A Deep Reinforcement Learning Approach" Mathematics 10, no. 23: 4575. https://doi.org/10.3390/math10234575
APA StyleZheng, X., Liang, C., Wang, Y., Shi, J., & Lim, G. (2022). Multi-AGV Dynamic Scheduling in an Automated Container Terminal: A Deep Reinforcement Learning Approach. Mathematics, 10(23), 4575. https://doi.org/10.3390/math10234575






