Radiative MHD Nanofluid Flow Due to a Linearly Stretching Sheet with Convective Heating and Viscous Dissipation
Abstract
1. Introduction
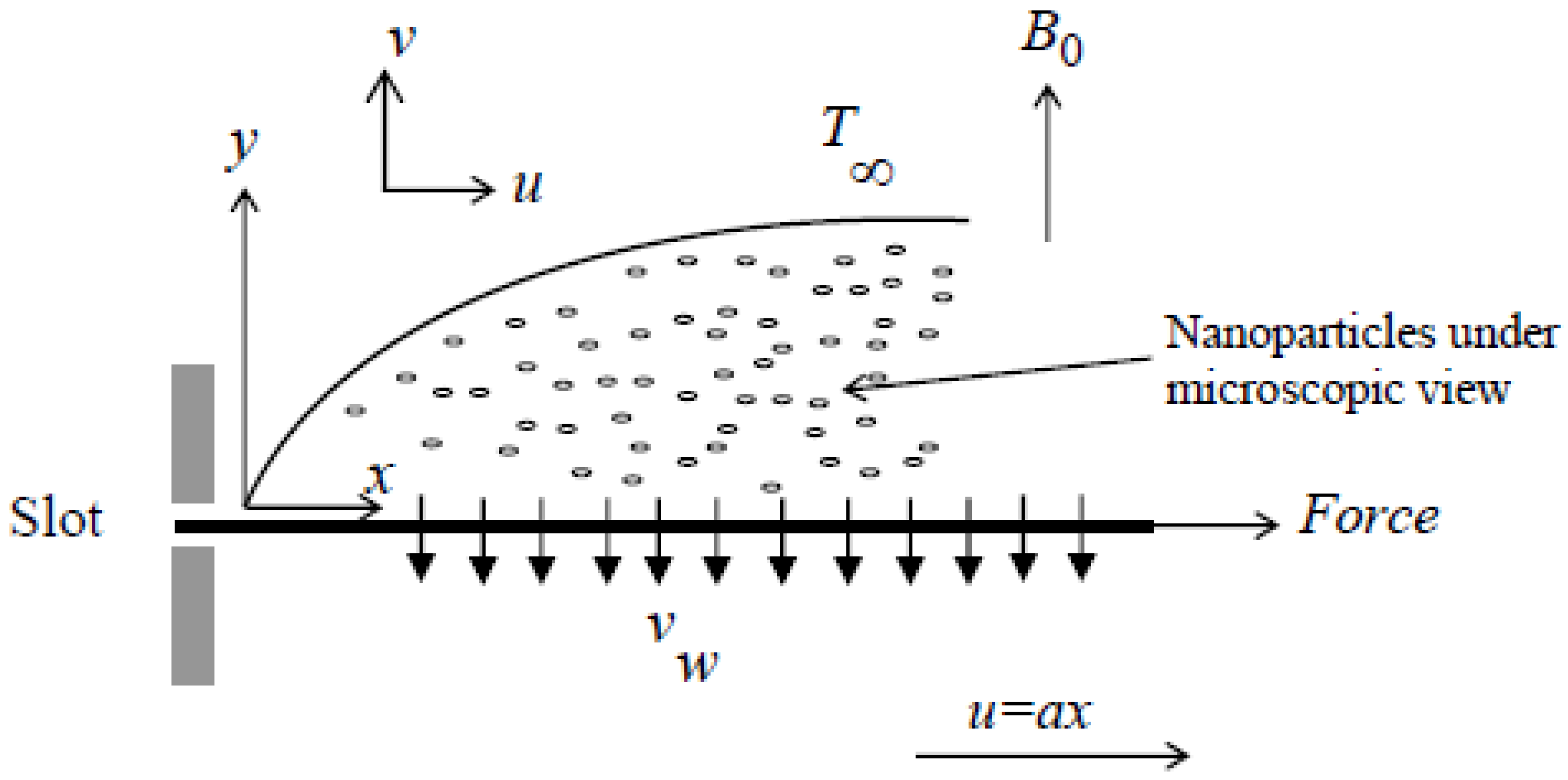
2. Problem Formulation
3. Physical and Graphical Interpretation of Results
4. Conclusions
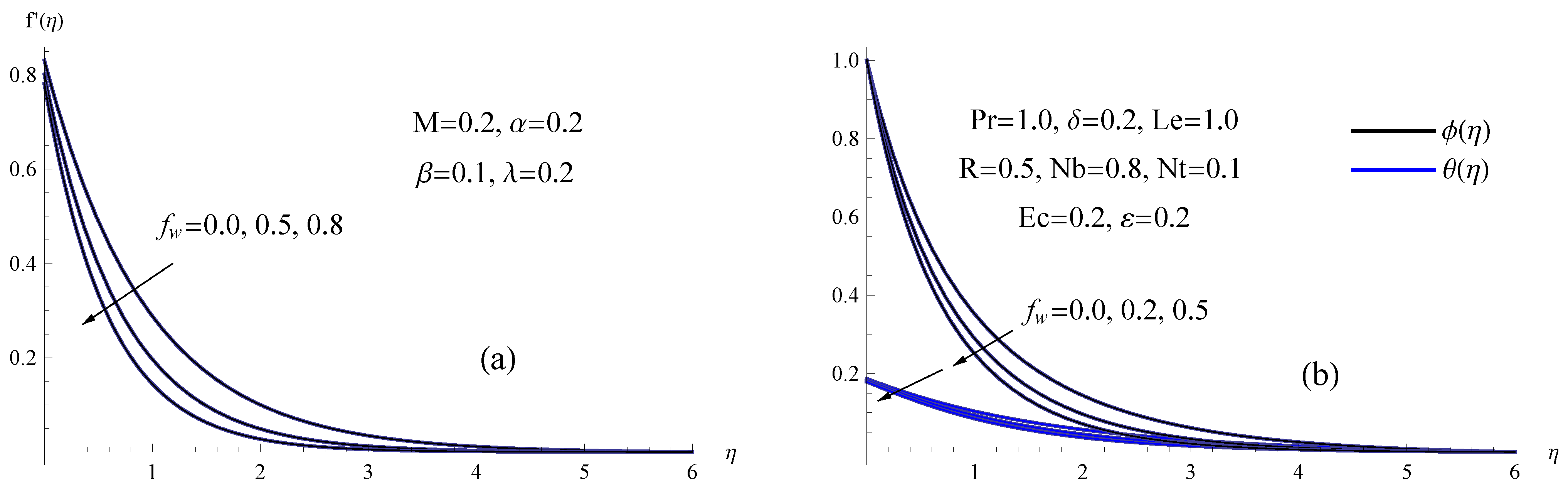
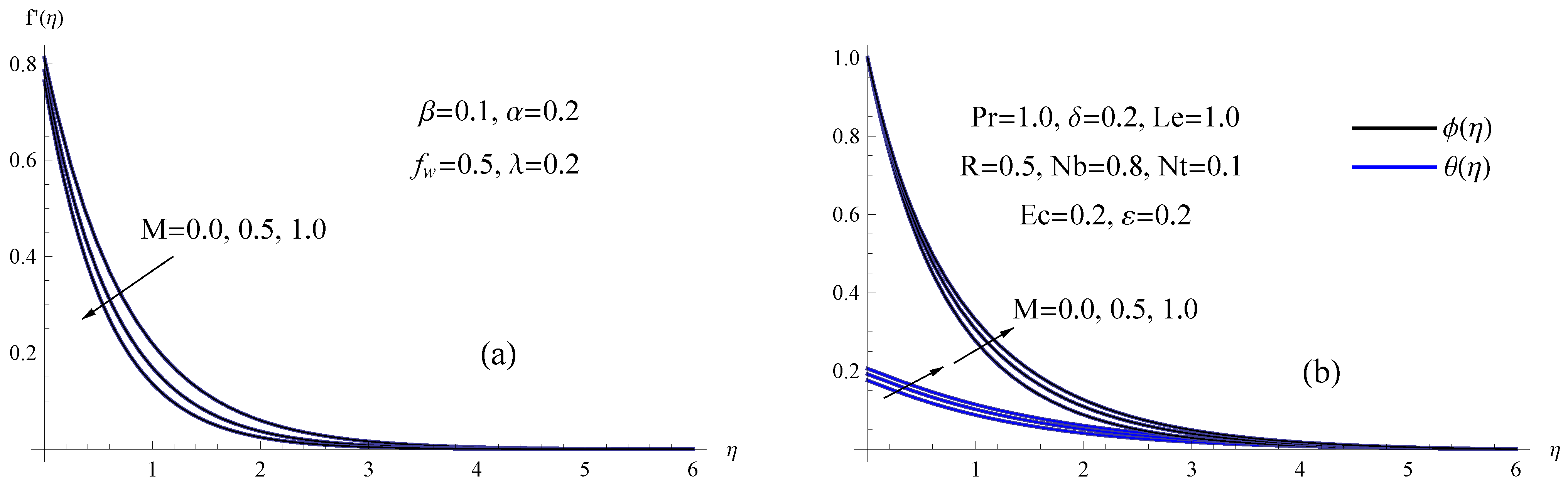
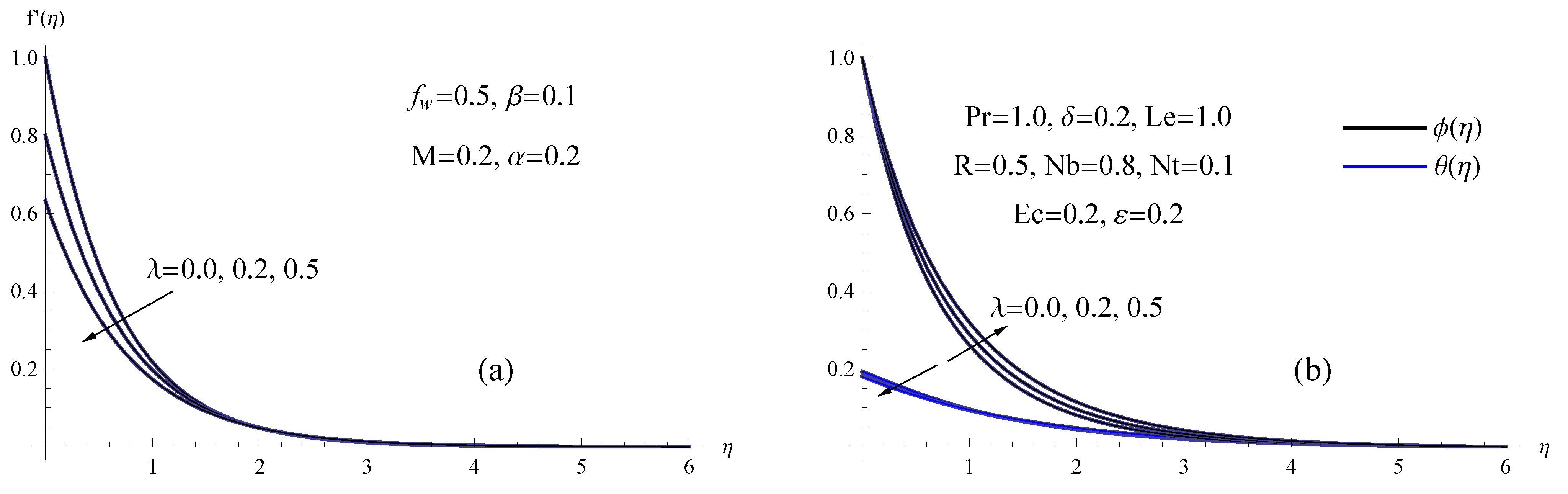
- The increased Maxwell parameter, slip velocity parameter, viscosity parameter, magnetic number and suction parameter diminishes the nanofluid velocity.
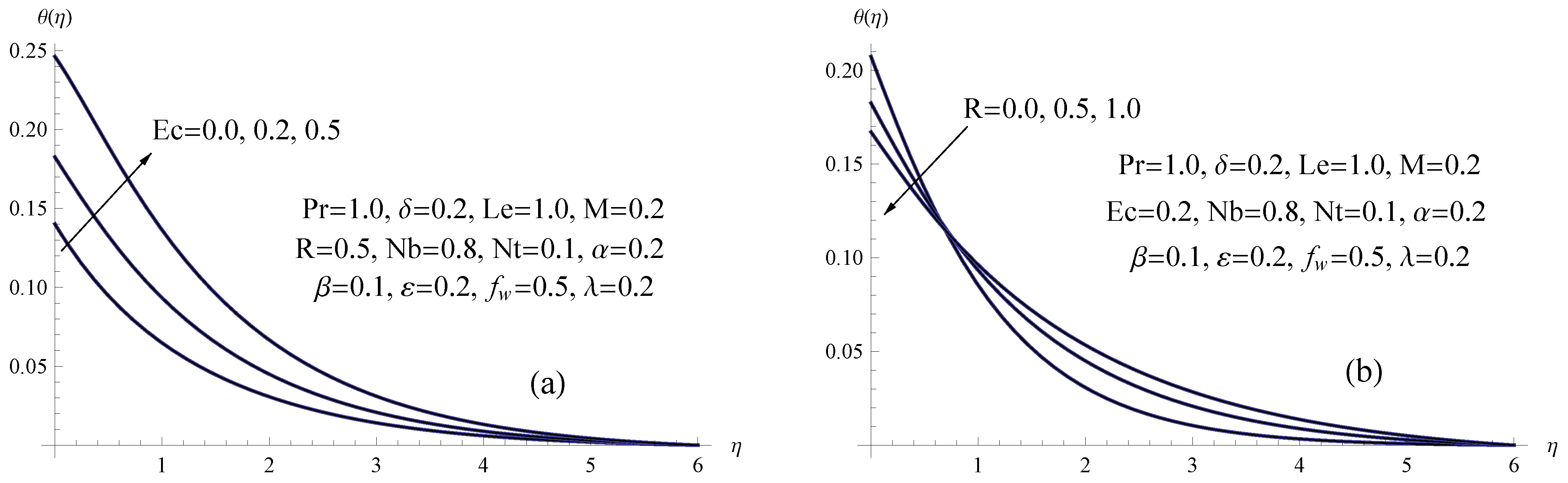
- Eckert number and surface-convection parameter values that are larger result in magnifying values for the temperature field.
- The suction parameter, thermal conductivity parameter and magnetic parameter all raise the skin-friction coefficient.
- The results showed that the existence of thermophoresis and Brownian motion makes the heat transmission phenomena more effective.
- Higher radiation and suction parameter values result in a larger Sherwood number, while Maxwell and slip velocity parameter values result in a smaller Sherwood number.
- A larger magnetic number, Brownian motion parameter, viscosity parameter and Maxwell parameter will result in a temperature rise whereas a higher suction parameter and slip velocity parameter will reduce the temperature.
- The concentration of the nanofluid is severely degraded as the viscosity, magnetic number, Maxwell and slip velocity parameters drop.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Greek Symbols
| nanofluid density (kg m) | |
| the ambient nanofluid density (kg m) | |
| the dimensionless Maxwell parameter | |
| the Maxwell coefficient (S) | |
| coefficient of viscosity (kg m) | |
| the ambient nanofluid viscosity (kg m) | |
| kinematic viscosity (m s) | |
| the ambient kinematic viscosity (m s) | |
| dimensionless temperature | |
| dimensionless concentration | |
| slip velocity factor (m) | |
| slip velocity parameter | |
| electrical conductivity (S m) | |
| Stefan–Boltzmann constant (W m K) | |
| the surface convection parameter | |
| similarity variable | |
| thermal conductivity (W m K) | |
| the ambient nanofluid thermal conductivity (W m K) | |
| thermal conductivity parameter |
Superscripts
| ′ | differentiation with respect to |
| ∞ | free stream condition |
| w | wall condition |
Nomenclature
| a | velocity coefficient (s) |
| A | is a constant (K m) |
| strength of a uniform magnetic field (T) | |
| c | is a constant (mol L m) |
| specific heat at constant pressure (J kg K) | |
| C | nanoparticles concentration (mol L) |
| skin friction coefficient | |
| surface nanoparticles concentration (mol L) | |
| ambient nanoparticles concentration (mol L) | |
| Brownian diffusion coefficient (m s) | |
| thermophoresis diffusion coefficient (m s) | |
| Eckret number | |
| f | dimensionless stream function |
| suction parameter | |
| the heat transfer coefficient (W m K) | |
| mean absorption coefficient (m) | |
| Lewis parameter | |
| M | magnetic parameter |
| Brownian motion parameter | |
| thermophoresis parameter | |
| local Nusselt number | |
| Prandtl number | |
| R | radiation parameter |
| local Reynolds number | |
| local Sherwood number | |
| T | nanofluid temperature (K) |
| convection temperature (K) | |
| ambient temperature (K) | |
| u | velocity component in the x-direction (m s) |
| v | velocity component in the y-direction (m s) |
| suction velocity (m s) | |
| Cartesian coordinates (m) |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME FED 1995, 231, 99–103. [Google Scholar]
- Yu, W.; France, D.M.; Routbort, J.L.; Choi, S.U.S. Review and comparison of nanofluid thermal conductivity and heat transfer enhancements. Heat Transf. Eng. 2008, 29, 432–460. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Mass Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Awais, M.; Hayat, T.; Irum, S.; Alsaedi, A. Heat generation/absorption effects in a boundary layer stretched flow of Maxwell nanofluid; Analytic and Numeric solutions. PLoS ONE 2015, 10, e0129814. [Google Scholar] [CrossRef]
- Shafique, Z.; Mustafa, M.; Mushtaq, A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy. Res. Phys. 2016, 6, 627–633. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A.; Khan, M.I. Radiative flow of micropolar nanofluid accounting thermophoresis and Brownian moment. Int. J. Hydrogen Energy 2017, 42, 16821–16833. [Google Scholar] [CrossRef]
- Sharma, K.; Gupta, S. Viscous dissipation and thermal radiation effects in MHD flow of Jeffrey nanofluid through impermeable surface with heat generation/absorption. Nonlinear Eng. 2017, 6, 153–166. [Google Scholar] [CrossRef]
- Patel, H.R.; Mittal, A.S.; Darji, R.R. MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation. Int. Commun. Heat Mass Transf. 2019, 108, 104322. [Google Scholar] [CrossRef]
- Noor, N.A.M.; Shafie, S.; Admon, M.A. Slip effects on MHD squeezing flow of Jeffrey nanofluid in horizontal channel with chemical reaction. Mathematics 2021, 9, 1215. [Google Scholar] [CrossRef]
- Mangathai, P.; Reddy, B.R.; Sidhartha, C. Unsteady MHD Williamson and Casson nanofluid flow in the presence of radiation and viscous dissipation. Turk. J. Comput. Math. Educ. 2021, 12, 1036–1051. [Google Scholar]
- Alotaibi, H.; Althubiti, S.; Eid, M.R.; Mahny, K.L. Numerical treatment of MHD flow of Casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Comput. Mater. Contin. 2021, 66, 229–245. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Abelman, S.; Ganji, D.D. Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. Int. J. Heat Mass Transf. 2014, 79, 212–222. [Google Scholar] [CrossRef]
- Hussain, S. Finite element solution for MHD flow of nanofluids with heat and mass transfer through a porous media with thermal radiation, viscous dissipation and chemical reaction effects. Adv. Appl. Math. Mech. 2017, 9, 904–923. [Google Scholar] [CrossRef]
- Ibrahim, W.; Negera, M. Viscous dissipation effect on Williamson nanofluid over stretching/shrinking wedge with thermal radiation and chemical reaction. J. Phys. Commun. 2020, 4, 045015. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Sherif, E.M.; Seikh, A.H. Magnetohydrodynamic (MHD) flow of micropolar fluid with effects of viscous dissipation and joule heating over an exponential shrinking sheet: Triple solutions and stability analysis. Symmetry 2020, 12, 142. [Google Scholar] [CrossRef]
- Saadi, F.A.; Worthy, A.; Alrihieli, H.; Nelson, M. Localised spatial structures in the Thomas model. Math. Comput. Simul. 2022, 194, 141–158. [Google Scholar] [CrossRef]
- Li, X.; Alrihieli, H.; Algehyne, E.A.; Khan, M.A.; Alshahrani, M.Y.; Alraey, Y.; BilalRiaze, M. Application of piecewise fractional differential equation to COVID-19 infection dynamics. Results Phys. 2022, 39, 105685. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Farooq, U. Mixed convective flow of Maxwell nanofluid past a porous vertical stretched surface—An optimal solution. Results Phys. 2016, 6, 1072–1079. [Google Scholar] [CrossRef]
- Bardos, C.; Golse, F.; Perthame, B. The Rosseland approximation for the radiative transfer equations. Commun. Pure Appl. Math. 1987, 40, 691–721. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Alrihieli, H.; Saeed, A.; Alduais, F.S.; Hayat, A.U.; Kumam, P. Numerical simulation of 3D Darcy & Forchheimer fluid flow with the energy and mass transfer over an irregular permeable surface. Sci. Rep. 2022, 12, 14629. [Google Scholar]
- Megahed, A.M. Improvement of heat transfer mechanism through a Maxwell fluid flow over a stretching sheet embedded in a porous medium and convectively heated. Math. Comput. Simul. 2021, 187, 97–109. [Google Scholar] [CrossRef]
- Megahed, A.M.; Reddy, M.G.; Abbas, W. Modeling of MHD fluid flow over an unsteady stretching sheet with thermal radiation, variable fluid properties and heat flux. Math. Comput. Simul. 2021, 185, 583–593. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Heat transfer over an unsteady stretching permeable surface with prescribed wall temperature. Nonlinear Anal. Real World Appl. 2009, 10, 2909–2913. [Google Scholar] [CrossRef]


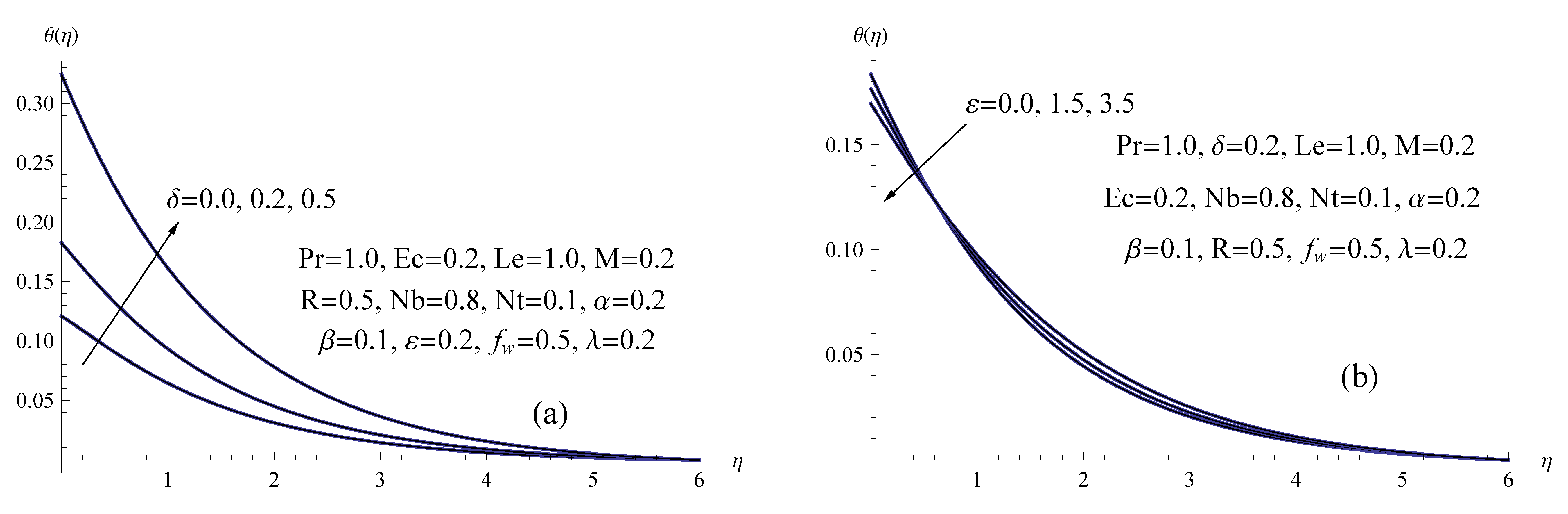
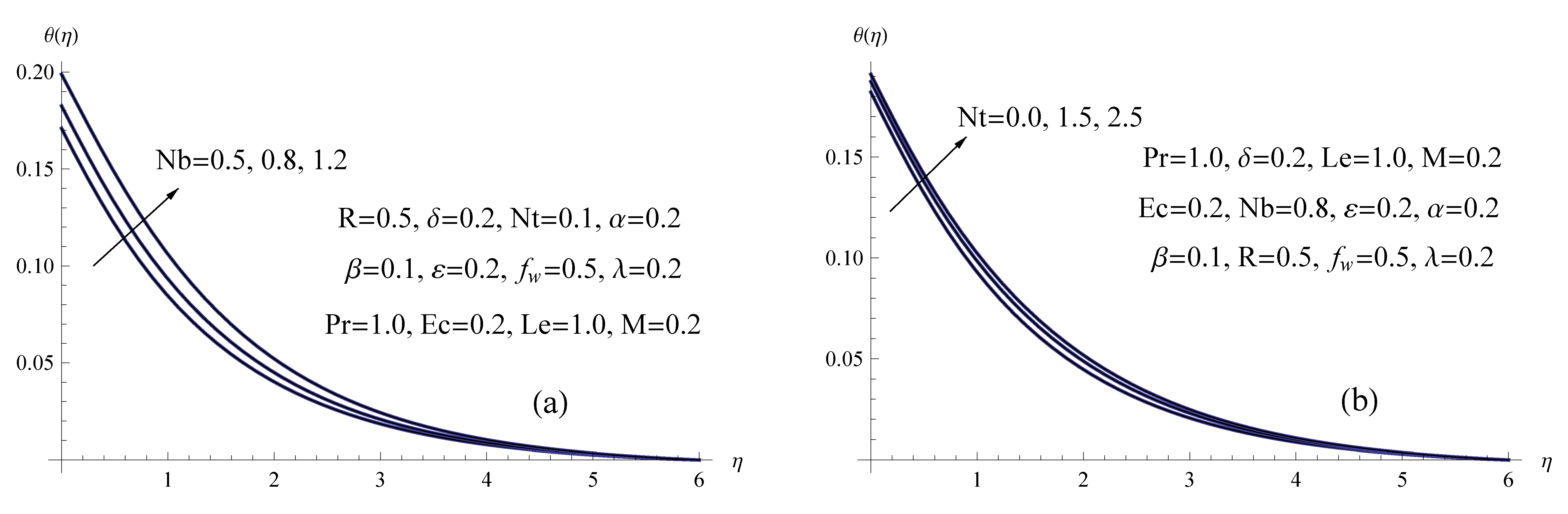
| Pr | , | Ishak et al. [23] | Present Work |
|---|---|---|---|
| 0.72 | −1.5 | 0.4570 | 0.457001520 |
| 1.0 | −1.5 | 0.5000 | 0.500000000 |
| 10 | −1.5 | 0.6542 | 0.654211910 |
| 0.72 | 0.0 | 0.8086 | 0.808589088 |
| 1.0 | 0.0 | 1.0000 | 1.000000000 |
| 3.0 | 0.0 | 1.9237 | 1.923689985 |
| 10.0 | 0.0 | 3.7207 | 3.720699510 |
| 0.72 | 1.5 | 1.4944 | 1.494389791 |
| 1.0 | 1.5 | 2.0000 | 2.000002010 |
| 10 | 1.5 | 16.0842 | 16.08419892 |
| M | R | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 1.010101 | 0.106808 | 1.404140 |
| 0.2 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.980241 | 0.105987 | 1.361981 |
| 0.5 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.937128 | 0.104581 | 1.291542 |
| 0.1 | 0.0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.845444 | 0.105775 | 1.168950 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.995036 | 0.106410 | 1.383612 |
| 0.1 | 0.8 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 1.095980 | 0.106979 | 1.536251 |
| 0.1 | 0.5 | 0.0 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.937012 | 0.107398 | 1.414660 |
| 0.1 | 0.5 | 0.5 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 1.071621 | 0.105056 | 1.342411 |
| 0.1 | 0.5 | 1.0 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 1.179310 | 0.103068 | 1.284550 |
| 0.1 | 0.5 | 0.2 | 0.0 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 1.003950 | 0.106514 | 1.388790 |
| 0.1 | 0.5 | 0.2 | 1.0 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.958801 | 0.105961 | 1.360981 |
| 0.1 | 0.5 | 0.2 | 2.5 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.888192 | 0.104945 | 1.308652 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.0 | 0.2 | 0.5 | 0.2 | 0.2 | 1.329681 | 0.104874 | 1.515341 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.995036 | 0.106410 | 1.383612 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.5 | 0.2 | 0.5 | 0.2 | 0.2 | 0.734743 | 0.106767 | 1.258561 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.0 | 0.5 | 0.2 | 0.2 | 0.997361 | 0.112547 | 1.383421 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.995036 | 0.106410 | 1.383612 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.5 | 0.5 | 0.2 | 0.2 | 0.991547 | 0.097316 | 1.383845 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.0 | 0.2 | 0.2 | 0.994306 | 0.152219 | 1.379111 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.995036 | 0.106410 | 1.383612 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 1.0 | 0.2 | 0.2 | 0.995541 | 0.081922 | 1.386090 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.0 | 0.2 | 0.997938 | 0.057677 | 1.389350 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.2 | 0.995036 | 0.106410 | 1.383612 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.5 | 0.2 | 0.988322 | 0.215834 | 1.370541 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 0.0 | 0.995008 | 0.108859 | 1.383361 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 1.5 | 0.995196 | 0.093315 | 1.384910 |
| 0.1 | 0.5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.2 | 3.5 | 0.995396 | 0.079346 | 1.386282 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrihieli, H.; Alrehili, M.; Megahed, A.M. Radiative MHD Nanofluid Flow Due to a Linearly Stretching Sheet with Convective Heating and Viscous Dissipation. Mathematics 2022, 10, 4743. https://doi.org/10.3390/math10244743
Alrihieli H, Alrehili M, Megahed AM. Radiative MHD Nanofluid Flow Due to a Linearly Stretching Sheet with Convective Heating and Viscous Dissipation. Mathematics. 2022; 10(24):4743. https://doi.org/10.3390/math10244743
Chicago/Turabian StyleAlrihieli, Haifaa, Mohammed Alrehili, and Ahmed M. Megahed. 2022. "Radiative MHD Nanofluid Flow Due to a Linearly Stretching Sheet with Convective Heating and Viscous Dissipation" Mathematics 10, no. 24: 4743. https://doi.org/10.3390/math10244743
APA StyleAlrihieli, H., Alrehili, M., & Megahed, A. M. (2022). Radiative MHD Nanofluid Flow Due to a Linearly Stretching Sheet with Convective Heating and Viscous Dissipation. Mathematics, 10(24), 4743. https://doi.org/10.3390/math10244743






