Alfven [
1] was the pioneer of the field of magnetohydrodynamics (MHD) and since the study of MHD is still a subject that researchers are quite interested in Due to its extensive applications in daily life, for example blood flow control during surgery, magnetic endoscopy, cell separation, magnetic devices, tumor treatment, and drug targeting to mention just a few. Collectively, MHD plays a key role in industrial and biomedical sciences [
2]. Owing to such importance, various recent studies performed by researchers such as Mustafa [
3] have studied magnetized viscous flow by way of nonlinear surfaces. It has been demonstrated that temperature and flow fields have a straightforward analytical expression. He offered precise formulations for wall shear stress. He concludes that strong magnetic fields thin both the momentum and temperature layers. Additionally, as opposed to lower branches, upper branch solutions were more thoroughly chilled, resulting in increased heat transfer rates. The magnetized fluid by way of a porous channel with a radiation assumption was investigated by Akinbowale [
4]. Heat and mass transfer are examined in relation to important rheological parameters such as the magnetic and pressure gradient, the radiation parameter, and Prandtl and Reynolds numbers. It was found that increasing the pressure results in an increase in velocity, with the greatest effect occurring toward the center of the flow channel, whereas increasing the radiation parameter causes the temperature distribution to decrease, with the greatest effect occurring toward the electrically conducting wall. Hanumesh et al. [
5] studied MHD peristaltic flow through an asymmetric tapered tube. Through a porous material, fluid with varied transport characteristics is transported. A low Reynolds number and a long wavelength were the fundamental assumptions used to formulate the problem. The momentum and energy equations’ solutions were obtained using the perturbation method. The graphed answers show that a key factor in controlling the fluid velocity in the channel’s center is the varying viscosity. The MHD fluid caused by an unstable stretched sheet with an expanded heat flux was into consideration by Ahmed et al. [
6]. It was presumed that thermal conductivity and viscosity would change with the temperature. The flow equations were solved by an efficient shooting method and the Runge–Kutta algorithm. Graphical representations and in-depth analysis were carried out to examine the flow field. Liaqat et al. [
7] studied heat transfer using self-propelled bioconvective microorganisms submerged in a water-based MHD nanofluid that included Cattaneo–Christov characteristics. Through Matlab programming, a finite element method was used to establish the numerical outcomes of the collection of non-linear equations. An important finding was that the density of the liquid was enhanced toward the melting factor. MHD micropolar tangent hyperbolic fluid flow toward the stretched surface was investigated by Pardeep et al. [
8]. The collection of partial differential equations was transformed using similarity transformations to obtain the theoretically specified ordinary differential system. The issue was mathematically resolved using the bvp4c method. The major goal of this extensive investigation was to enhance heat transformation under the influence of numerous parameters. A number of physical factors were used to depict the heat transfer, skin friction, temperature, and velocity. It was discovered that changes in velocity and temperature profiles drove changes in the parameters that affected the size of the nanoparticles and the rate of heat transfer.
The Casson fluid model [
9] has received a lot of attention from researchers due to its unique characteristics. Compared to conventional viscoplastic models, the Casson fluid model more closely matches rheological data for a variety of materials. Casson fluid, a shear-thinning fluid, is predicted to have a yield stress below which there is no flow, an infinite viscosity at a zero shear rate, and zero viscosity at an infinite shear rate. Casson fluids include intense fruit liquids, tomato sauce, soup, honey, and jellies. Furthermore, it is an approximate rheological model for chocolate and blood. Additionally, Casson fluid exhibits yield stress and is crucial in the biomechanics and polymer processing sectors. Owing to such importance, various researchers have considered the examination of the Casson flow field in various configurations such as Reddy et al. [
10] who investigated the importance of the Soret and Hall effects on Casson fluid toward a vertical surface. The dimensional equations that control flow were converted into dimensionless equations by dimensionless variables, leading to the discovery of the analytical solution via the homotopy analysis method (HAM), which was then contrasted with the Adomain decomposition method (ADM) solution. With a particular focus on the physical factors involved in the current investigation, the heat and mass transfer rates against the Casson fluid parameter were visually illustrated. When the upper disk is assumed to be impermeable and the bottom one is assumed to be porous, Mohyud-Din and Khan [
11] explored the time-dependent Casson fluid flow. The controlling equations were transformed by using transformations. The formulas for the temperature and velocity were obtained using HAM. The effects of several physical parameters were explored towards Eckert, squeeze numbers, and dimensionless length. The system’s overall inaccuracy was calculated for both the suction and injection situations using Mathematica Package BVPh2.0. For emerging parameters, surface quantities were reported. For both the presence and absence of a magnetic field, Casson fluid was studied by Abro and Khan [
12]. The Fabrizio–Caputo fractional derivative was used to obtain the flow formulation. Analytical solutions were identified. The Fox-H and Mittag–Leffler functions were used to express the generic solutions for the flow field. Finally, a graphical representation was provided using the relevant parameters, and it was seen that the behavior of the Caputo–Fabrizio and ordinary fractional fluid models for the fluid flow was reciprocal. The analysis of time independent naturally convective flow was identified by Kataria and Patel [
13]. A vertical plate was passed over by a Casson fluid flow. The flow equations were resolved numerically in Matlab and resolved analytically using the Laplace transform method. Sherwood, Nusselt numbers, and skin friction expressions were discovered. By creating graphs, the properties of the flow field were examined, and the physical elements were thoroughly explained. The examination of the Casson liquid over a disk as a semi-infinite zone was presented by Rehman et al. [
14]. The Casson nano-liquid flow was achieved by rotating a rigid disk at a fixed angular frequency. By creating a homogenous magnetic field normal to the axial direction, magnetic interaction was taken into consideration. The chemical reaction, heat generation, heat absorption, and Navier’s slip condition were manifested during disk rotation. In order to create an ordinary differential system, the obtained flow narrating differential equations was reduced. The Von Karman method of the scheme was used to achieve this. Instead of continuing with the standard built-in system, a computational approach was developed to produce correct trends. By using graphical and tabular structures, the effects of the flow parameters were studied. It was found that the Casson fluid parameter caused both the tangential and radial velocities to decrease. Neeraja et al. [
15] explored convective and viscous dissipation effects on magnetized Casson fluid. Using the gunshot method, the flow equations were resolved. The governing parameters affected the temperature, solid displacement, liquid velocity, and concentration. For the Casson parameter, the liquid velocity and consequently the solid displacement were reduced. When compared to the previous results, the current results showed a logical agreement. In the context of emerging mass and heat transfer technologies, Rasool et al. [
16] examined the properties of Casson nanofluid flow via porous media across a non-linear stretching surface. The Darcy–Forchheimer relation allows for an incompressible viscous nanofluid of the Casson type to pass through the specified porous material. For the nanoparticles’ velocity, temperature, and concentration, slip boundary conditions were applied. Attendance was made to Brownian diffusion and thermophoresis. To numerically solve the problem, a Runge–Kutta (RK) scheme of fourth order was used. Graphs were created for a range of progressive non-dimensionalized parameter values, and numerical data were used to examine changes in wall drag factor, heat transfer rates, and mass transfer rates. The results show that the porous media offer resistance to fluid flow and the strength of the inertial impact decreases the momentum boundary layer. The thermophoresis and Brownian motion were discovered to have a progressive relationship with temperature. For increasing values of the slip parameters, there is a decrease in the magnitude of the rate of heat and mass transfers. Over a horizontal plate the Casson nanofluid flow through use of the non-Darcy porous medium, Farooq et al. [
17] reported their findings. By utilizing the proper non-similar transformations, the equations were converted into a dimensionless model. Through the use of bvp4c, local non-similarity was used to solve the dimensionless partial differential system. In-depth research was carried out on the effects of the newly discovered non-dimensional characteristics on the flow field. Additionally, the influences of variables on the skin friction and the rate of heat transfer were investigated. Finally, using publicly available data, comparisons between locally similar solutions and non-similar solutions were completed. Ramesh et al. [
18] investigated the time-dependent and incompressible Casson squeezing flow in between disks. In the flow phenomena, the nanofluid theory (Buongiorno model) was realized. For the lower disks, concentration, temperature, and velocity slip were also included. The similarity functions were completed first to ultimate flow equations and they were solved by the RK-5 scheme. The results were presented in relation to the various physical quantities. A higher Reynolds number caused a decline in radial velocity. The vortex viscosity parameter first increases and subsequently decreases the microrotational field.
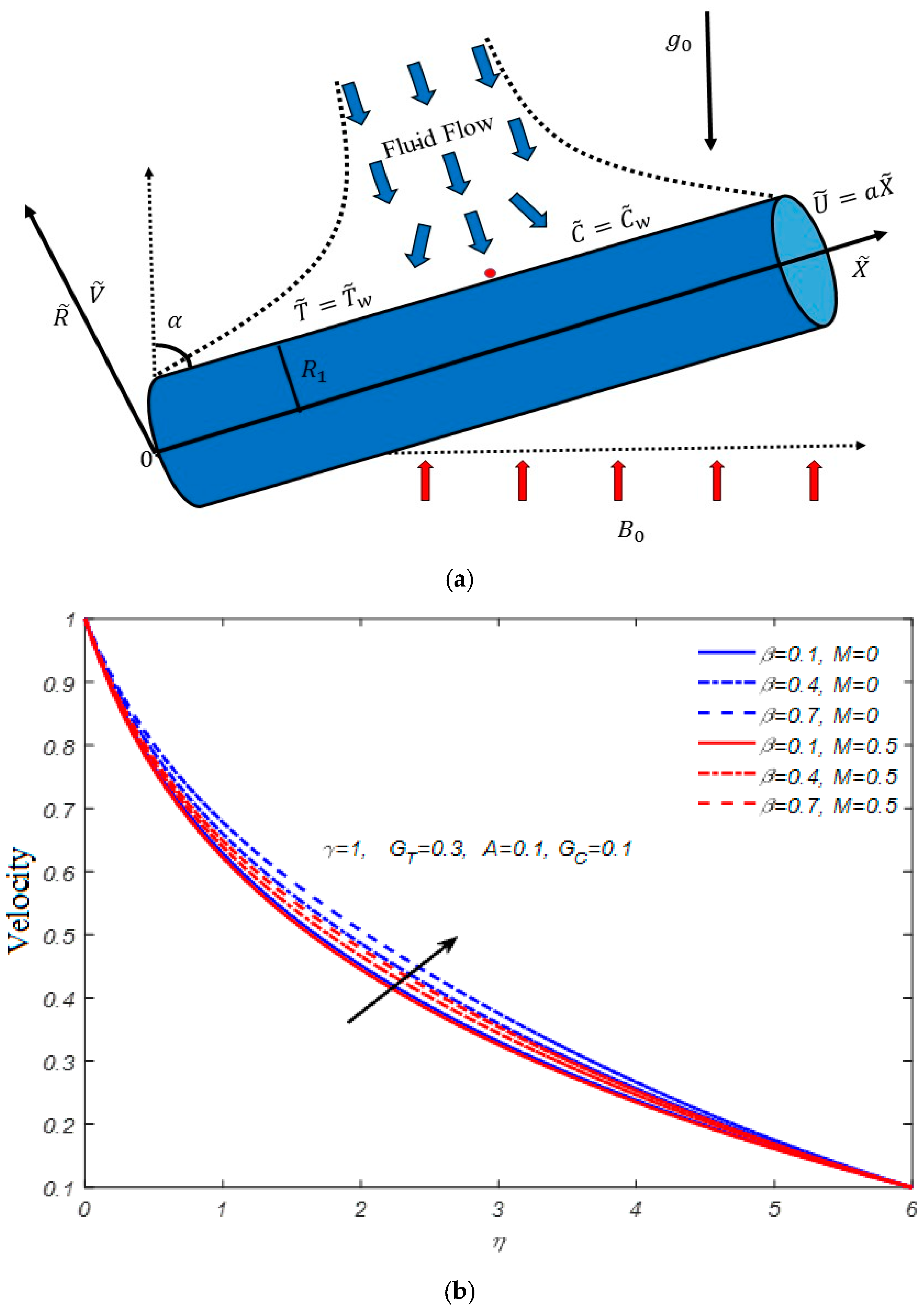
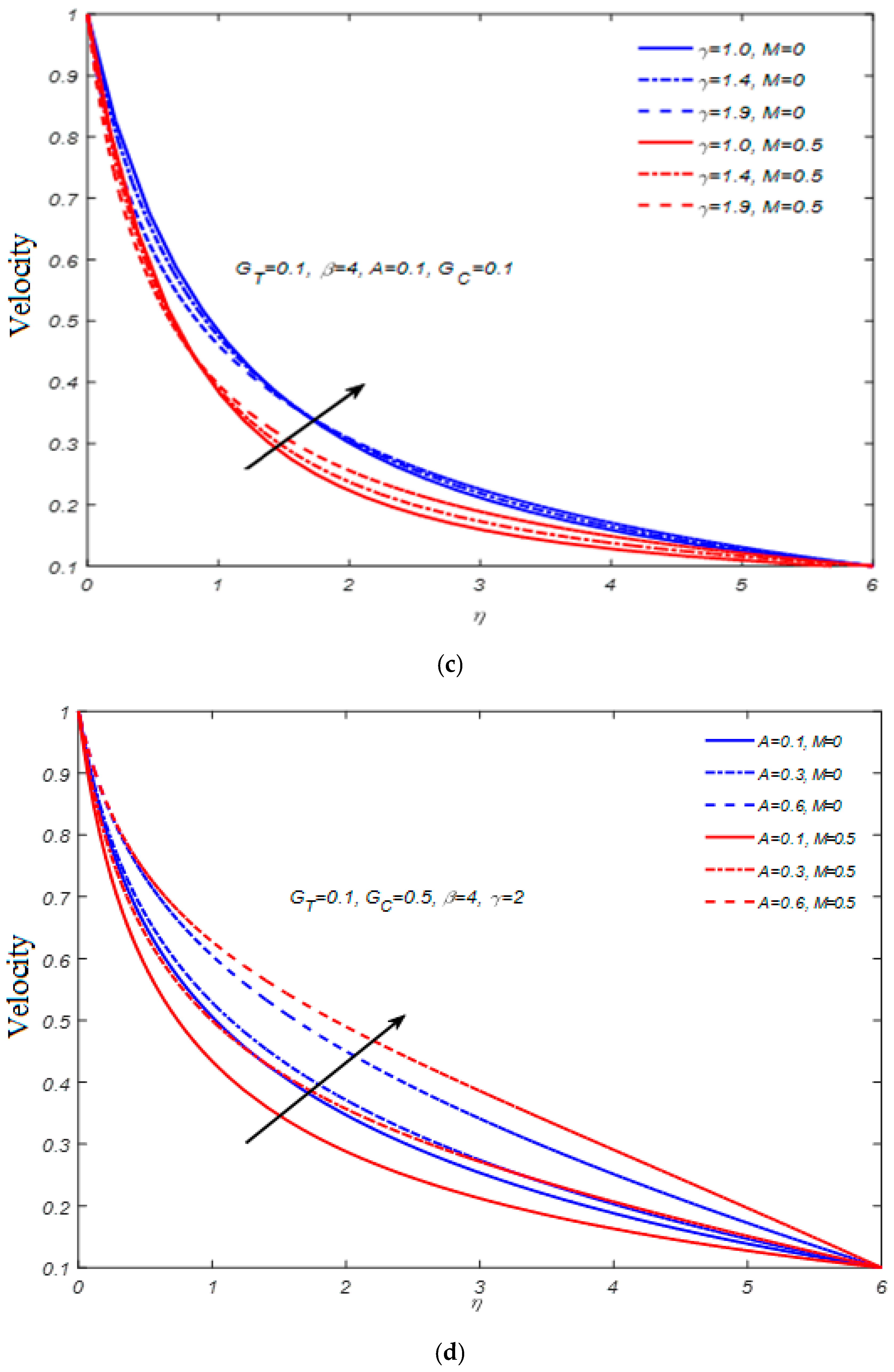
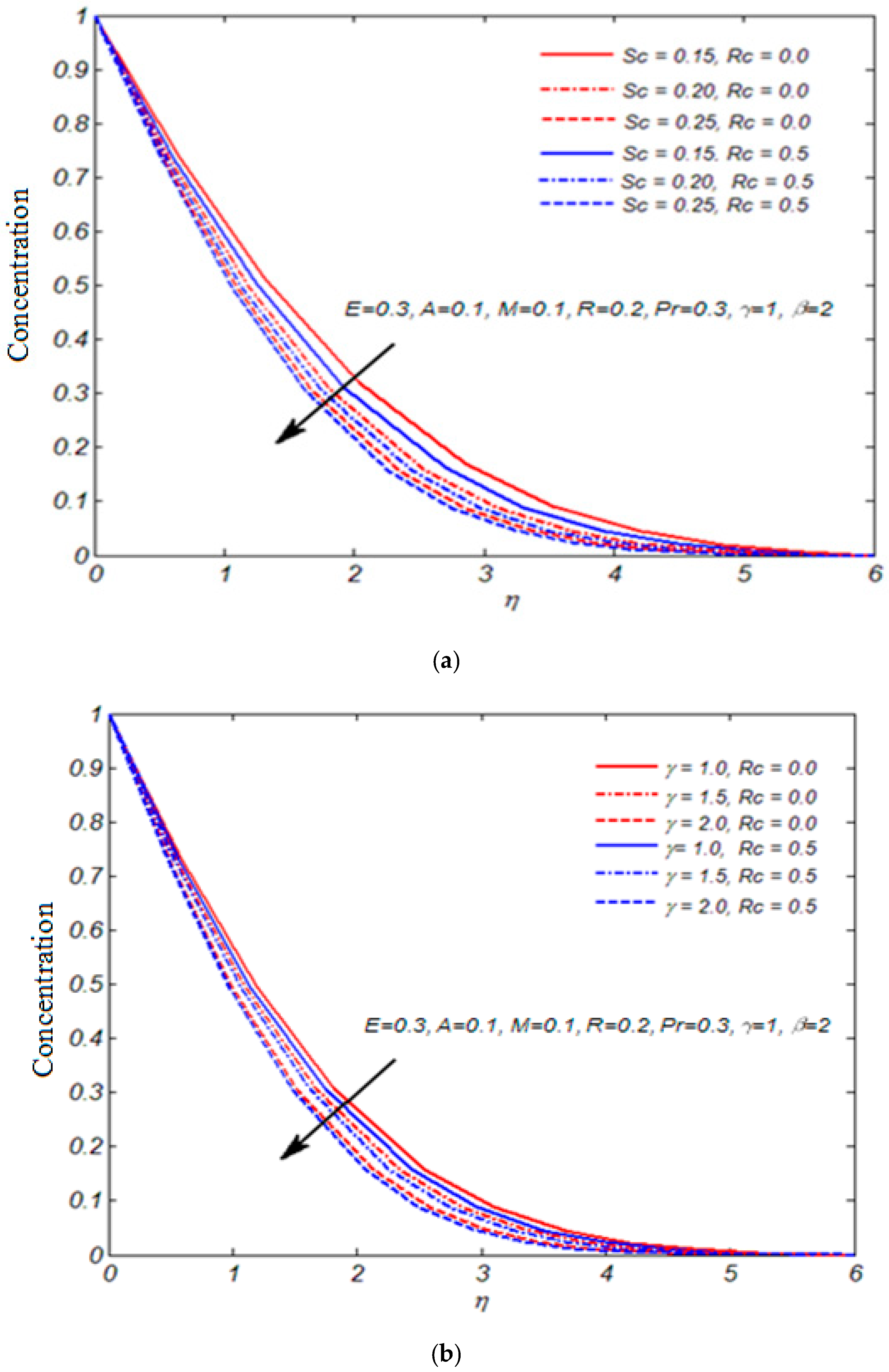
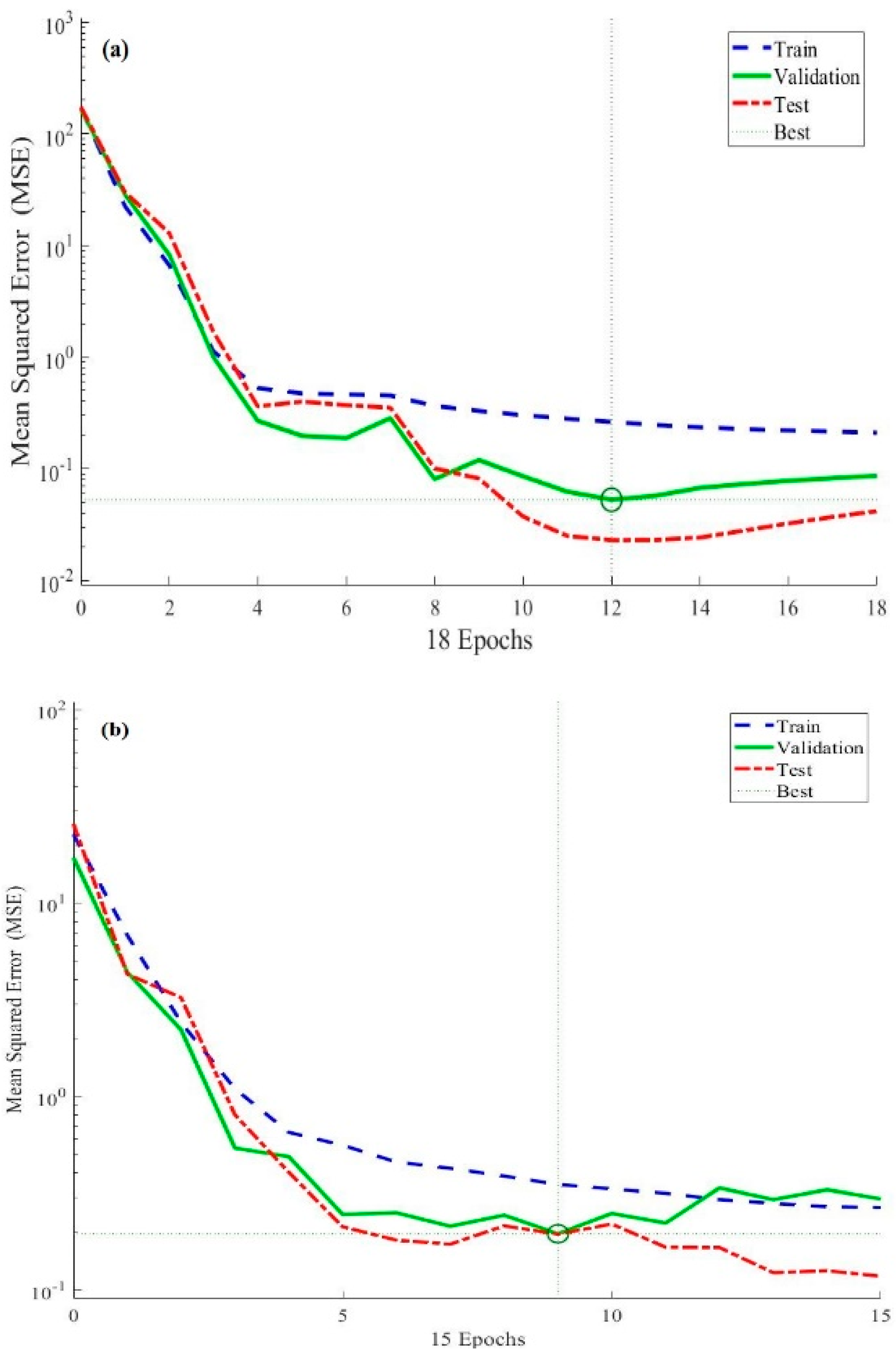
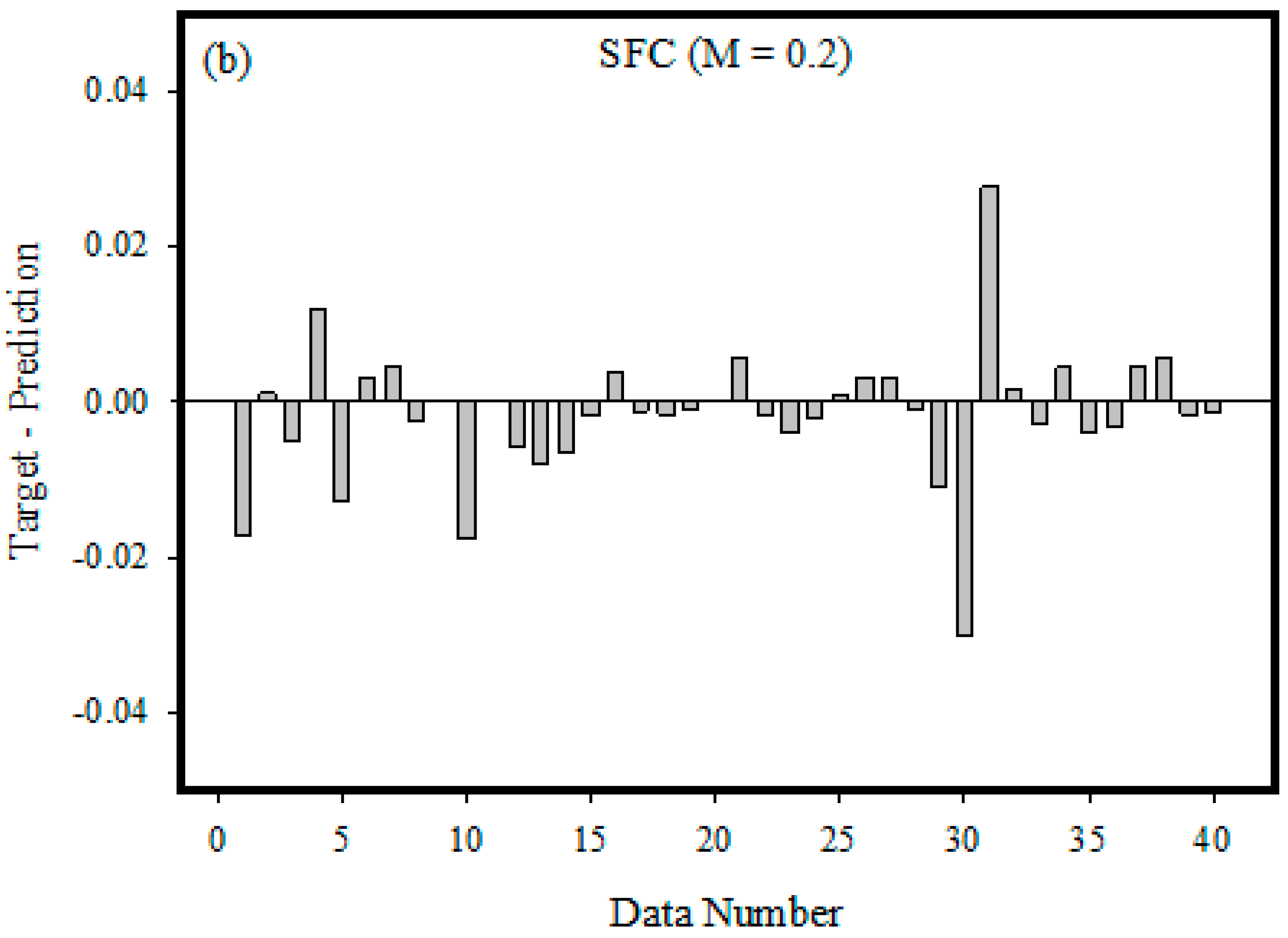
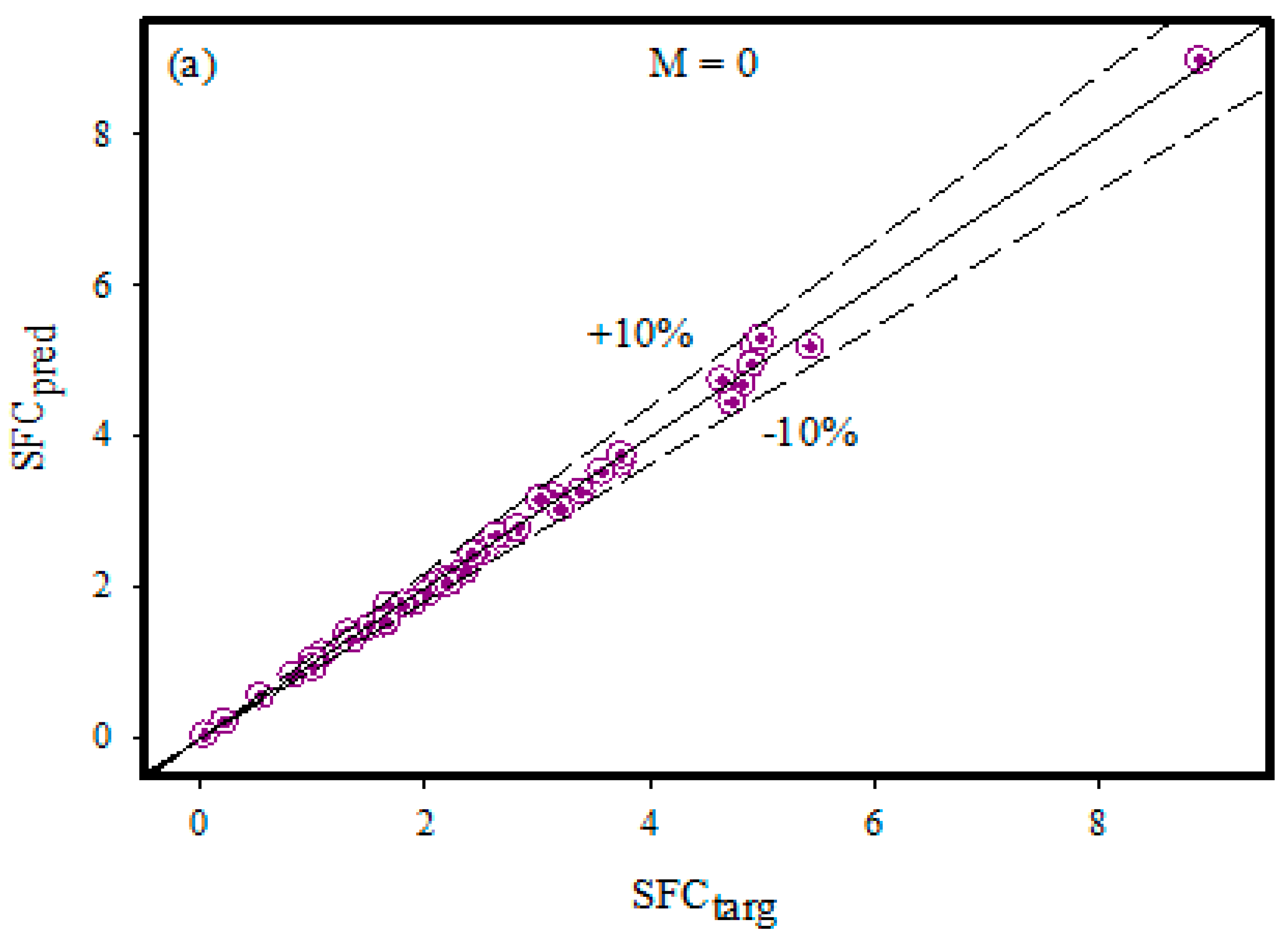
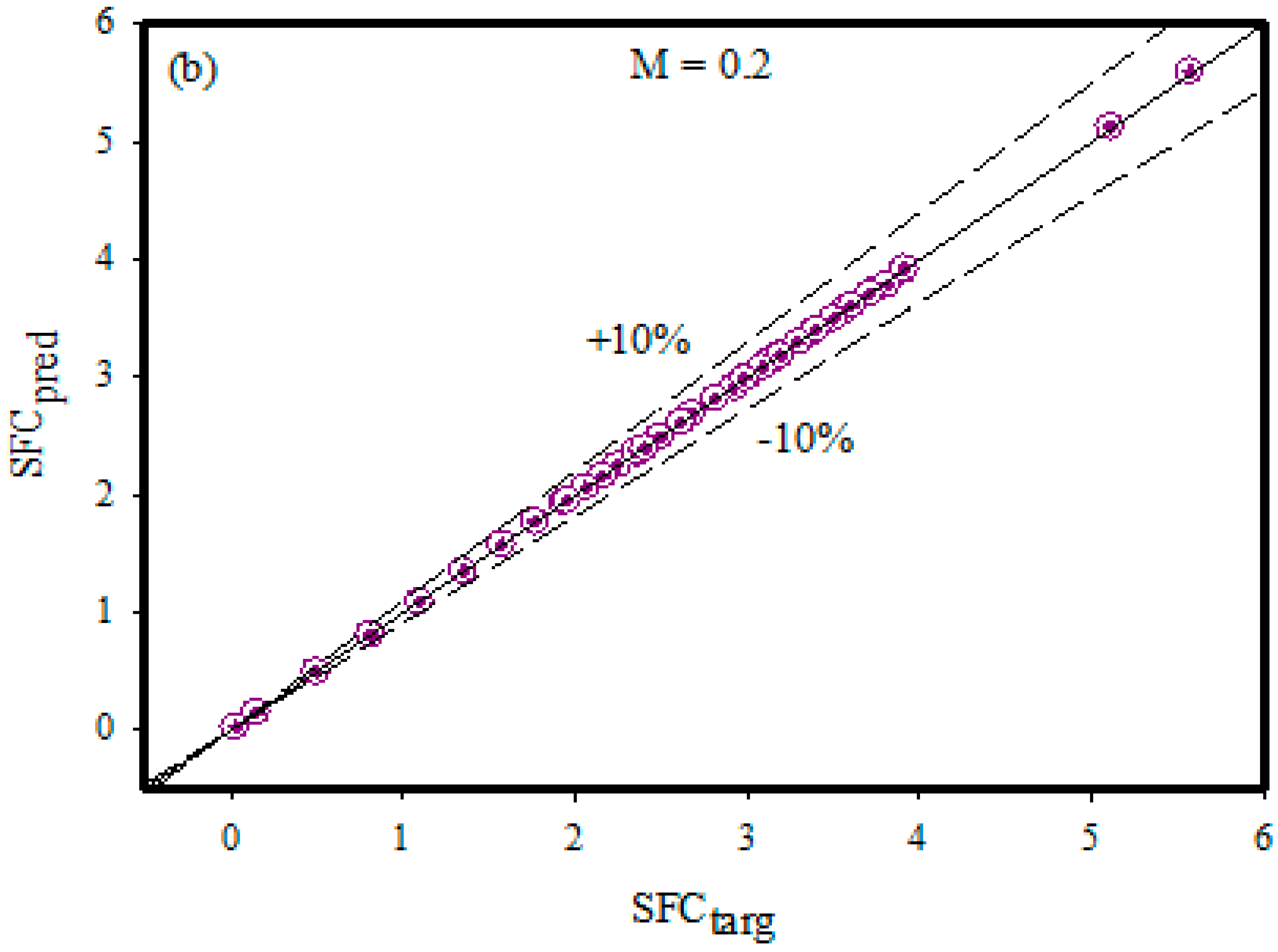
Owing to the importance of the Casson fluid model, artificial neural networking models are constructed for two different boundary layer flow regimes, namely non-magnetized and magnetized flow fields. The Casson fluid flow towards the stretching cylinder is mathematically formulated in the presence of a heat generation effect, viscous dissipation, mixed convection, temperature-dependent variable thermal conductivity, thermal radiations, and first-order chemical reaction effects. The ultimate flow equations are solved by the use of the shooting method. The skin friction coefficient (SFC) is estimated at the cylindrical surface. We constructed artificial neural networking models for better estimation of the skin friction coefficient. We believe that by following the present outcomes of the Casson fluid flow regime, one can extend the idea to investigate the time-independent shear rate and shear stress characteristics of molten chocolate, yogurt, blood, and many other culinary and biological materials. The present research contributes to answering the following concerns: