Abstract
In this study, two closed-form solutions for determining the first two natural frequencies of the flapwise bending vibration of a cracked Euler–Bernoulli beam at low rotational speed have been developed. To solve the governing differential equations of motion, the Frobenius method of solution in power series has been used. The crack has been modeled using two undamaged parts of the beam connected by a rotational spring. From the previous results, two novel polynomial expressions have been developed to obtain the first two natural frequencies as a function of angular velocity, slenderness ratio, cube radius and crack characteristics (depth and location). These expressions have been formulated using multiple regression techniques. To the knowledge of the authors, there is no similar expressions in the literature, which calculate, in a simple way, the first two natural frequencies based on beam features and crack parameters, without the need to know or solve the differential equations of motion governing the beam. In summary, the derived natural frequency expressions provide an extremely simple, practical, and accurate instrument for studying the dynamic behavior of rotating cracked Euler–Bernoulli beams at low angular speed, especially useful, in the future, to establish small-scale wind turbines’ maintenance planes.
Keywords:
cracked Euler–Bernoulli rotating beam; natural frequencies; closed-form solution; slenderness; low angular velocity; Frobenius; series solution MSC:
74-10
1. Introduction
The blades of different devices such as wind turbines, small-scale wind turbines, helicopters, open rotors and drones are examples of mechanical components that may present cracks that, due to operating conditions, grow to catastrophic failure. These rotating blades work under bending and tensile stresses producing stress variations over time. The combination of stresses with defects, extreme temperatures and aggressive environmental conditions can lead to crack growth. These mechanical components are common in many strategic industrial sectors of great economic and social interest, such as renewable energies and aeronautics. Therefore, from a safety point of view, it is essential to achieve acceptable levels of reliability during operation.
Due to its geometrical characteristics, a rotating blade is usually modeled as a beam based on the theories of the Euler–Bernouilli, Rayleigh, or Timoshenko beams. The difference between them lies mainly in the geometrical conditions and in the mechanical effects they are able to reproduce. In addition, it is necessary to take into account the range of speeds at which these blades operate, which is variable depending on the use of the machinery to which they belong. For instance, turbine blades may revolve at several thousand revolutions per minute, although helicopter blades typically rotate at few hundred revolutions per minute and wind turbines typically function at less than 20 revolutions per minute. For the case of slender blades subjected to low rotational speeds, the Euler Bernoulli beam is the most suitable model [1].
Determining the modal characteristics of rotating beams is crucial for their design and for the evaluation of their performance, so that numerous researchers, i.e., [1,2], have studied this topic in the past. The mechanical behavior of the a rotating beam, both in the plane of rotation (chordwise direction) and out of it (flapwise direction), depends on the centrifugal force that emerges due to rotation and varies with distance from the center of rotation.
Rotating blades are mechanical elements whose guidelines that can be straight or warped. On the other hand, the geometry of their cross-sections can be modeled as uniform [3,4] or variable (tapered) [5,6]. In relation to the boundary conditions, one end of the rotating blade is always free and the other can be modeled, depending on the applications, as a cantilevered end, as in the case of wind turbine blades, or with the end simply supported, as in the case of helicopter blades. Finally, regarding the materials, composite materials are mostly used for wind turbine blades [7], while metal alloys are used for turbine blades [8]. However, recent studies on simple beam models found in the literature, applicable to both cases, use either metals, aluminum alloys [9,10], or composite materials [11,12].
Focusing on healthy rotating beams, in the literature, numerous studies of their dynamic behavior can be found [4,13]. Regardless of the beam model used, Euler–Bernoulli, Rayleigh or Timoshenko beams, the equation that arises is a complex resolution fourth order differential equation with variable coefficients. Different methods used to address the problem can be found in the literature such as the Rayleigh–Ritz method [14,15,16], the finite element method [17,18], the differential transform method [19], the Frobenius method [9,20,21] or the Galerkin method [22]. Of these, those that give rise to closed-form solutions are particularly interesting when the inverse problem is to be addressed a posteriori.
From a safety point of view, it is particularly important to know the dynamic behavior of damaged mechanical elements.The study of these kinds of elements has been carried out for several decades, collected in various articles such as the exhaustive review of Dimarogonas [23]. The presence of a defect, such as a crack, produces a local stiffness loss that affects the transverse displacements, which increase, and the vibration frequencies, which decrease. As a general rule, studies have focused on one-dimensional mechanical elements such as beams and shafts [24,25,26] since these are a very good simplification of common components in industry. On crack modeling, most authors model the cracked beam as two beams connected by one or more springs, located in the section that contains the crack, and whose stiffness represents the increase in local flexibility as a result of its presence. In most of the works, the stiffness of the spring is obtained from the application of Fracture Mechanics concepts such as the Stress Intensity Factor (SIF) or the integral J, such as in [27,28]. When addressing the problem of studying the behavior of the blade with a defect, the appearance of a crack implies the modification of the movement equations, requiring the introduction of terms that take into account the effect of damage. According to Fracture Mechanics, as already indicated, a crack can be considered as an additional local flexibility due to the increase in strain energy that occurs in the vicinity of the crack front (stress energy release rate method, SERR) [29,30]. The procedures used to solve the equations of motion of the cracked beam do not differ from those previously mentioned for intact beams.
Unlike what happens with intact rotating beams and with non-rotating cracked beams, for which the number of papers is very large, to the authors’ knowledge, the number of papers on the behavior of cracked rotating beams is small. The first studies that can be found date from the late 1980s. In these early works, for example, Lien et al. [22] and Chen et al. [31] used a finite element model to analyze the effect of the crack on the vibratory behavior and stability of the rotating beam, taking into account the effects of shear stress and rotational inertia; Datta et al. [32] quantitatively studied the influence of the size and position of the defect on the natural frequency of a short blade with a crack that is always open; Wauer [33] formulated the equation of motion of an Euler Bernoulli beam by substituting the effect of the crack for a torsion spring with flexibility equal to that of the cracked section; and Krawczuk [34] studied the changes of the natural frequencies assuming an Euler–Bernoulli beam with an always open crack using the finite element method. More recently, Cheng et al. [35] have studied the influence of various parameters on the vibratory characteristics of tapered cracked rotating beams using the finite element method; Liu et al. [36,37] have formulated a 3D finite element model that allows for studying different aspects of the behavior of cracked blades; Yashar et al. [38,39] have compared the behavior of an intact and a cracked beam using two methods, Rayleigh–Ritz and finite element, in different planes of motion, Lee et al. [9] have used the transfer matrix and Frobenius methods to solve the equation of motion in rotating beams with multiple cracks and Karimi et al. [40] have studied the stability of a non-uniform rotating beam using the finite element method. Although, in cracked beams, the presence of cracks affects both flapwise and chordwise vibrations, and the first case studies are in the majority of the works, such as [9,41] because they are not coupled with others as is the case with axial and chordwise directions [3].
In order to establish adequate maintenance plans, it is necessary to have a good knowledge of the relationship between certain variables that characterize the dynamic behavior of the beam (such as natural frequencies) and the properties of the crack (usually depth and location). In cracked rotating beams, it is complex to achieve this because, on the one hand, it is not easy to solve the governing differential equations of motion and, on the other hand, there are two opposite effects. The first one is an increase of flexibility due to the presence of the crack, and the other one is a decrease of flexibility due to the rotating speed. The compensation of both effects can make damage detection more difficult [9]. In addition, the effect of angular velocity on stiffness is not linear, and it is much greater for high speeds than for lower ones. Therefore, it is advisable that studies of both speed ranges be performed separately.
In this work, the determination of the first two natural frequencies in the flapwise bending direction of cracked slender beams, rotating at low speeds, has been proposed. It should be said that the first two natural frequencies have been chosen because they are the ones that are usually available for real beams. For this purpose, the equations of motion have been solved by modeling the presence of the crack by means of a torsion spring, and the resolution has been carried out using the Frobenius method. The results have been compared with others in the literature and a great similarity has been found. The developed expressions allow the calculation of the frequencies as a function of the main variables such as the rotation speed, the slenderness coefficient, the hub radius and the crack characteristics (depth and location). To the authors’ knowledge, there is no similar expressions in the literature, which calculate, in a simple way, the first two natural frequencies based on beam features and crack parameters, without the need to know or solve differential equations. These closed-form solutions, obtained for low rotation speeds, will be especially useful in the future to establish maintenance planes for small-scale wind turbines.
The paper is organized as follows: Section 2 is devoted to the formulation and solution of the well-known differential equations of motion governing the beam, as well as to the verification of the goodness of the results obtained. Section 3, Section 4 and Section 5 are completely novel. In Section 3, the closed-form solutions of the first two natural frequencies are developed, while in Section 4 they are validated. Finally, the results of the application of the calculated closed-form solutions are presented in Section 5.
2. Mathematical Model and Formulation of the Problem
2.1. Model of the Cracked Euler–Bernoulli Rotating Beam
In this work, a cracked Euler–Bernoulli rotating beam with the characteristics described below is considered. Let us consider a uniform beam of length L, whose rectangular cross-section, with double symmetry, is a rectangle having a height H and a thickness b. The beam rotates with constant angular velocity around axis . The crack, whose depth is a, is located at a distance from the junction between the hub and the beam, point O, which is the origin of the reference frame. Figure 1 shows the scheme of the cracked beam, where R is the radius of the hub attached to the beam. On the other hand, only the transverse deflection along the coordinate z (flapwise) is considered, i.e., the displacement shown in Figure 1.
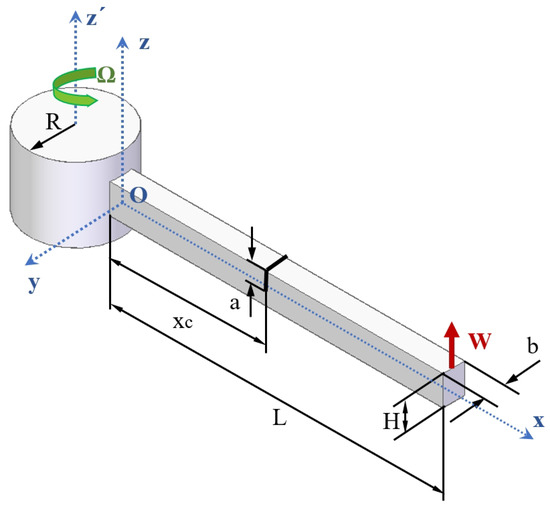
Figure 1.
Scheme of the cracked rotating beam.
The differential equation governing the motion of an intact rotating beam, Equation (1), is a fourth order equation that can be obtained using Newton’s Second Law [9,21]:
where t is the time, is the density of the material, E is the Young’s modulus, A represents the area of the cross section, and I is the moment of inertia of the rectangular section. Finally, is the centrifugal force appearing in the axial direction as a consequence of the rotation, which can be calculated by expression (2):
Equation (1) can be solved by using the classical separation of variables method as:
where represents the natural frequency of vibration, and is the dimensionless displacement.
In the case of a cracked beam, the model is made with two intact beams connected by a massless spring, see Figure 2, where K represents the stiffness (inverse of the flexibility) introduced by the crack that is equal to the spring stiffness, according to [29], given by expression (6). In addition, the dimensionless position of the crack is assumed to be , as expressed in (7).
with being the Poisson ratio of the beam material:
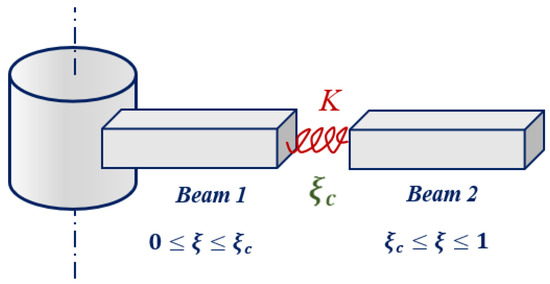
Figure 2.
Scheme of the cracked beam model by joining two intact beams.
The equation of motion for an intact beam (1) becomes (8) for a cracked beam.
where and represent the Beam 1 and Beam 2 dimensionless displacements, respectively, see Figure 2, along the z direction.
To solve the above differential equations, the four following boundary conditions are needed, two for each end of the beam:
In addition, the four compatibility conditions corresponding to the cracked section, must be satisfied as well:
being:
2.2. Solving the Equation of Motion
The solution of the equation of motion previously presented is approached using the Frobenius method [9,21,42]. Following this method, the solution of the differential equation is expressed in the form of power series (12):
where are the series coefficients, and j is an indeterminate exponent.
The function represents both and , since both expressions are identical before applying the boundary conditions.
Substituting (12) in (8), the indicial Equation (13) and the recurrence relationship (14) can be obtained [43]:
being:
The four roots of the indicial Equation (13) are . Now, the four linearly independent solutions can be obtained from these roots (16):
2.3. Verification of the Analytical Model
To demonstrate the accuracy of the present model, some results obtained from the application of the model have been compared with others reported in literature. First, a comparison with data from [9] has been carried out. Secondly, in order to study the hub radius influence, a comparison with some results from Banerjee et al. [43] has been made. The authors of this work have not found any studies dealing with beams rotating at low speeds, so the comparisons explained above have been performed with the lowest possible speeds found in the literature. Table 1 shows the comparison with the results obtained by Lee et al. [9] for a beam with the following characteristics: m, m, m, , GPa, and . In addition, two rotation speeds ( and rad/s), a healthy beam and a cracked beam with different crack positions () with have been considered. Moreover, to check non-zero r values, in Table 2, the comparison with [43] is presented, in dimensionless terms, for and . Furthermore, both Table 1 and Table 2 show the convergence of the power series in all cases; this allows for determining the optimal number of terms of the power series.

Table 1.
Comparison between the present model results and results from Lee et al. [9]. Reprinted/adapted with permission from [9]. 2016, Springer Nature.

Table 2.
Comparison between the present model results and results from Banerjee [43]. Reprinted/adapted with permission from [43]. 2000, Elsevier.
Although the Frobenius method allows the calculation of infinite natural frequencies as long as the number of terms of the series is adequate, in this work, only the first two natural frequencies have been calculated because they are the most common and usually available in real beams.
According to the comparisons shown in Table 1 and Table 2, the model offers accurate results and the convergence of the power series method is very good. In all cases, the value of the calculated natural frequencies with 30 terms in the power series (marked in yellow) coincide the reference ones (marked in blue).
3. Determination of the Closed-Form Solutions
In this section, two novel polynomial expressions for the first two natural frequencies of a cracked Euler–Bernoulli rotating beam at low angular speed have been determined in terms of the angular velocity, slenderness ratio, hub radius, crack location and crack depth. To the best of the authors’ knowledge, no such expressions have been found in the literature for the time being.
For this purpose, firstly, let us consider a beam of length mm, thickness mm, Young’s modulus GPa, Poisson ratio and density . The fist two dimensionless natural frequencies, and , have been calculated for different cases of the beam under consideration.The analyzed cases have been selected in accordance with the following:
- Slenderness ratio: and 220, according to (18)
- Dimensionless hub radius: and ;
- Dimensionless crack location: and ;
- Dimensionless crack depth: and , where corresponds to a healthy beam.
In a previous step, the suitability of an independent low speed model, different than a high speed one, will be verified. Figure 3 and Figure 4 show the dimensionless natural frequencies, and , respectively, vs. the rotational speed , from 0 to 300 rad/s. The results correspond to a random case (, , and ). The behavior of other cases coincides with that presented here.
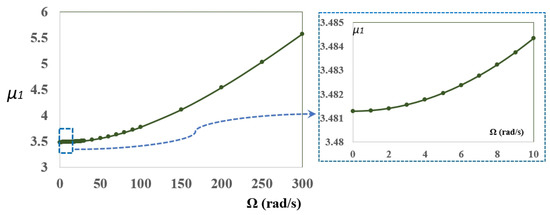
Figure 3.
Dimensionless natural frequency, , vs. rotational speed for: , , and .
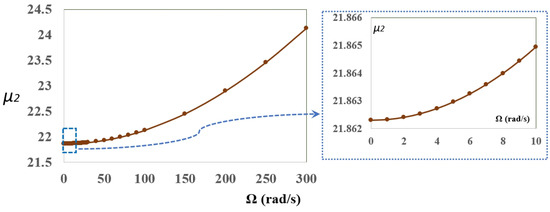
Figure 4.
Dimensionless natural frequency, , vs. rotational speed for: , , and .
As can be seen in Figure 3 and Figure 4, the effect of the rotational speed on natural frequencies is not linear, it is much greater for high speeds than for lower ones. This can be seen even better in Figure 5a,b, where the slope values of the previous curves are shown, for and , respectively.
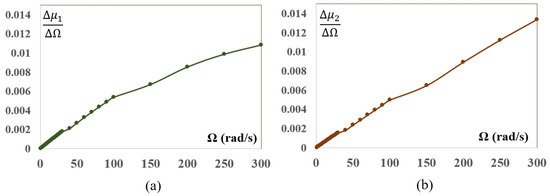
Figure 5.
Slope of the curve dimensionless natural frequencies vs. rotational speed for: , , and . (a) and (b) .
According to the above mentioned considerations, the expressions are determined only for low rotation speeds. Specifically, the considered values of angular velocity are and 10 rad/s. To determine both closed-form solutions, the corresponding non-dimensional rotational speed values, M, have been used.
Therefore, the combination of all these parameters has produced 4416 cases, 96 for healthy beams and 4320 for cracked ones that have been used to determine the two closed-form solutions.
As an example, Figure 6a,b show the general shape of the dimensionless frequencies, and , respectively, as a function of different values of and . As before, these are results for this random case: , and rad/s. For the rest of the slenderness, hub radius and rotational speed values, the figures have similar shape.
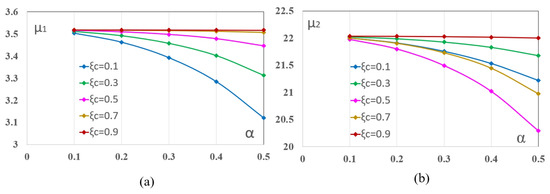
Figure 6.
Dimensionless frequency for different values of and (, and rad/s). (a) and (b) .
Figure 6a,b show curves of the same shape. In the case of , (a), it is observed that the frequency is lower as the crack is deeper and closer to the rotation axis.
Regarding , (b), it decreases with crack depth, but, regarding the location, a minimum is reached when the crack is in the middle section.
Although the mode shapes associated with the natural frequencies are not necessary to calculate the closed-form solutions, as an example, Figure 7 and Figure 8 show the first and second modes, respectively, when , , , rad/s and for three different crack depths ( and ). In both cases, figures within the detail rectangles show that, in the vicinity of the crack, , there are differences in the modes related with the size of the defect.
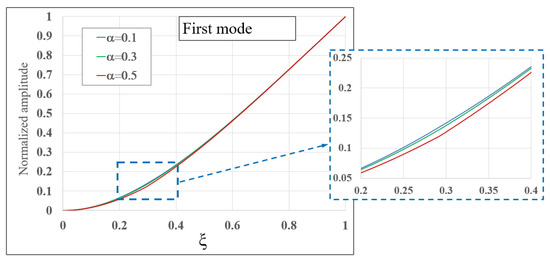
Figure 7.
First mode shape for the case , , , rad/s and for three different crack depths ( and ).
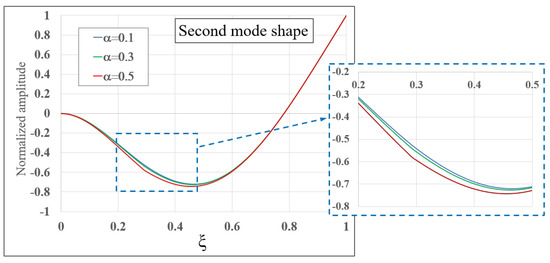
Figure 8.
Second mode shape for the case , , , rad/s and for three different crack depths ( and ).
According to the shape of the curves shown in Figure 6a,b, for a given set of values of M, , r and , the plots representing the dimensionless crack depth vs. or , have similar shape, regardless of the considered values of the other parameters. Taking advance on this idea, Figure 9a,b show the schematics of the vs. and vs. , respectively. As can be seen, both schemes are similar, differing only in the value of .
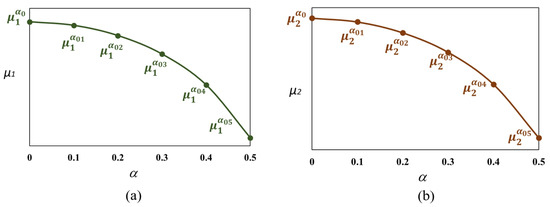
Figure 9.
Schemes of the graphs vs. (a) and vs. (b).
The first step in determining the two closed-form solutions is to obtain polynomials using multiple regression techniques. The objective is the calculation of , , , , and , as a function of M (dimensionless rotation speed), r (dimensionless hub radius), (slenderness ratio) and (dimensionless crack location), taking into account all the calculated results from the present model, where q can be 1 or 2, representing the first or second natural frequency, respectively. For a better understanding, to are superscripts indicating which value of the dimensionless crack depth is being considered in each case, while the superscript represents a general case. In the second step, the general equations of the curves shown in Figure 9a,b are derived from previous results. In addition, finally, in the third step, the non-dimensional frequencies are calculated as a function of the five mentioned parameters. To explain this procedure graphically, a schematic flowchart is shown in Figure 10. The procedure is the same for both dimensionless natural frequencies.
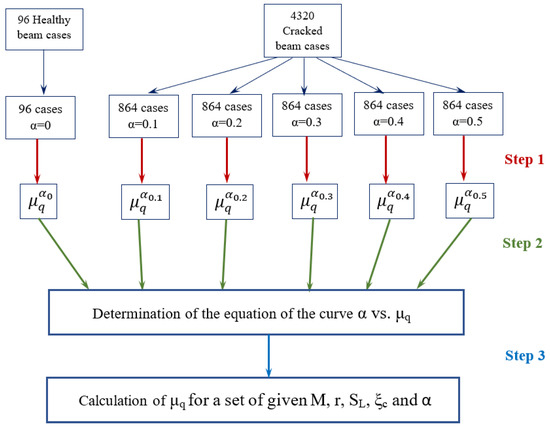
Figure 10.
Scheme of the whole procedure to calculate the two closed-form solutions of non-dimensional natural frequencies.
The expressions calculated in Step 1 (see Figure 10) all have a similar format, according to (19):
where i, j, k and l are the degrees of the polynomials in M, r, and , respectively. are the coefficients of the fits, which can be found in the public repository [44], and, finally, , , and are the values obtained for the best fit. The values for each case together with the coefficients and the mean square errors (MSE) are shown in Table 3.

Table 3.
Grades of the best fits, coefficients and MSE.
The general expressions of curves vs. are in the form of the Equation (20):
where to are twelve unknown coefficients, six for and six for that are calculated according to (21) expressions:
Finally, from previous equations, for any data set (M,r, , ,), both and can be estimated.
4. Reliability of the Closed-Form Solutions
To assess the reliability of the proposed model, the results have been compared with those obtained from the original data. Figure 11a,b show, for all cases, the percentage error calculated as (22) for and , respectively, with respect to the original values.
with and being the real and estimated values, respectively.
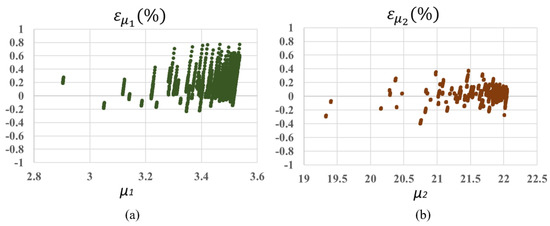
Figure 11.
Percent error for (a) and (b).
As can be seen in Figure 11, the estimation of the frequencies using the closed-form solutions is considered to be very good, since the error always remains under 1.0% for and 0.5% for . In addition, the mean percentage error () for each combination of crack depth () and its location (), including all rotation velocity (M), hub radius (r) and slenderness ratio (), is shown in Figure 12a,b, for and , respectively. In addition, finally, for both dimensionless natural frequencies, the mean percentage error for each rotation velocity, including all the values of the rest parameters, is shown in Figure 13.
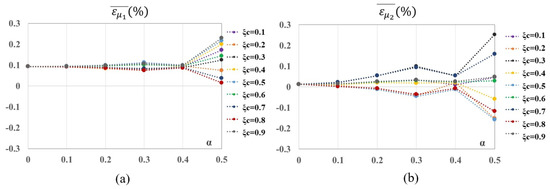
Figure 12.
Mean percentage error considering each combination of and for (a) and (b).
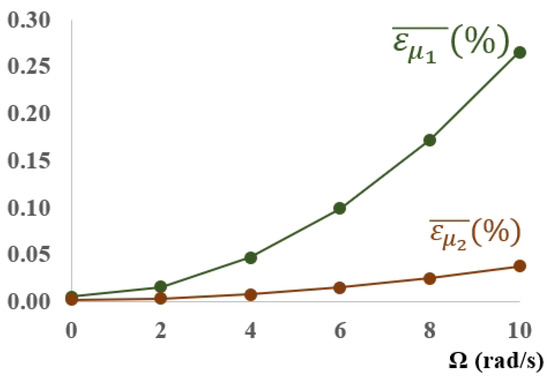
Figure 13.
Mean percentage error for each rotation velocity for and .
As can be observed in Figure 12, the mean error is less than for all depths, except for that, in the case of , is as high as . For large crack depths (), the mean errors increase, but they never exceed . On the other hand, according to Figure 13, the mean errors increase with rotational speed, with this trend being stronger for . In any case, the comparison between the results obtained from the original data and those from the closed-form solutions can be considered acceptable, as the errors obtained are very small.
5. Application of the Model, Discussion and Results
In this section, the developed two closed-form solutions have been applied to another set of values that have been randomly chosen, different from those used to derive the expressions. The new considered random cases are:
Set 1
- rad/s
- and
- and
Set 2
- rad/s
- and
- and
In Figure 14a–d, the percentage errors calculated according to (22) are plotted for both and , and for Set 1 and Set 2 values. As expected, the calculated errors are larger than those obtained for the data used to develop the closed-form solutions. In general, the calculated errors are larger for than for . On the other hand, for both and , the percentage errors are maximum for the deepest cracks and at a location closest to the hub, being about in the worst case. However, the absolute mean percentage errors are less than , namely, , , and for Set1-, Set1-, Set2- and Set2-, respectively. Regarding the slenderness ratio and the hub radius, they do not influence the value of errors. In summary, although the errors have logically increased with respect to those shown in Figure 11, Figure 12 and Figure 13, they can be considered acceptable values for a practical application of the two developed closed-form solutions, especially in the case of incipient cracks, around , and situated at a dimensionless location () greater than 1/3.
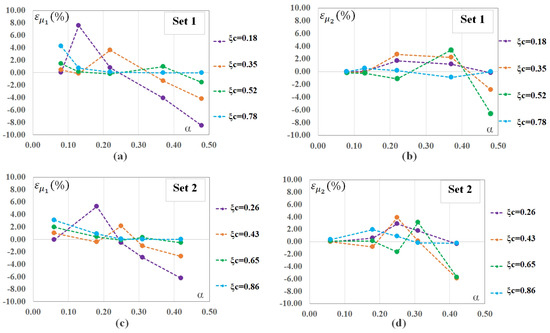
Figure 14.
Closed-form solutions application to random data, different from those used to develop them. Percentage errors between real values and estimated ones. (a) Set 1. vs. ; (b) Set 1. vs. ; (c) Set 2. vs. ; (d) Set 2. vs. .
6. Conclusions
This work presents the calculation of the first two natural frequencies in bending in the flapwise direction of cracked slender beams rotating at low rotational speeds as a function of angular velocity, beam slenderness ratio, hub radius and crack depth and location. To this end, the crack has been modeled by a rotational spring connecting the two undamaged parts, and then the governing differential equations of motion of the cracked beam have been solved using the Frobenius method of solution in power series. The results have been validated by comparison with results from the literature. From the solutions of the equations of motion, two expressions for the first two natural frequencies have been formulated using multiple regression techniques. Subsequently, on the one hand, the results obtained from the expressions have been compared with the original data used for their formulation. The agreement is very satisfactory since the errors are extremely small. In addition, on the other hand, the two closed-form solutions developed have been applied to another set of values, chosen at random and different from those used to develop the expressions. Although the obtained errors are larger than before, they are acceptable for a practical application of the calculated expressions, especially for incipient cracks around , and situated at a dimensionless location () greater than 1/3. To the authors’ knowledge, there is no similar expression in the literature that calculates, in a simple way, the first two natural frequencies from the beam characteristics and crack parameters, without the need to know or solve the differential equations of motion governing the beam. In summary, the expressions for the derived natural frequencies provide an extremely simple, practical and accurate tool to study the dynamic behavior of cracked Euler–Bernoulli beams rotating at low angular velocity, especially useful, in the future, to establish maintenance plans for small-scale wind turbines.
Author Contributions
The authors contributions can be briefly summarized as follows. Conceptualization, B.M.-A. and L.R.; Formal analysis, B.M.-A.; Funding acquisition, B.M.-A. and L.R.; Investigation, B.M.-A., L.R. and P.R.; Methodology, B.M.-A. and L.R.; Project administration, B.M.-A. and L.R.; Supervision, L.R.; Validation, B.M.-A. and P.R.; Writing—original draft, B.M.-A., L.R. and P.R.; Writing—review and editing, B.M.-A., L.R. and P.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the “Agencia Estatal de Investigacion” (AEI) of the Government of Spain through the project PID2019-104799GB-I00/AEI/10.13039/501100011033 and by the “Comunidad de Madrid” (Spain) through the project EPUC3M20.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in GitHub at https://doi.org/10.5281/zenodo.7404726 accessed on 8 December 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jackson, D.R. Dynamic stiffness matrix method for the free vibration analysis of rotating uniform shear beams. Proc. ASME Des. Eng. Tech. Conf. 2009, 1, 1315–1324. [Google Scholar]
- Bazoune, A. Survey on Modal Frequencies of Centrifugally Stiffened Beams. Shock Vib. Dig. 2005, 37, 449–469. [Google Scholar] [CrossRef]
- Kim, H.; Yoo, H.H.; Chung, J. Dynamic model for free vibration and response analysis of rotating beams. J. Sound Vib. 2013, 332, 5917–5928. [Google Scholar] [CrossRef]
- Banerjee, J.R. Dynamic stiffness formulation and free vibration analysis of centrifugally stiffened Timoshenko beams. Comput. Struct. 2001, 247, 97–115. [Google Scholar] [CrossRef]
- Bazoune, A.; Khulief, Y.A.; Stephen, N.G. Further results for modal characteristics of rotating tapered Timoshenko beams. J. Sound Vib. 1999, 219, 157–174. [Google Scholar] [CrossRef]
- Ozgumus, O.O.; Kaya, M.O. Vibration analysis of a rotating tapered Timoshenko beam using DTM. Meccanica 2010, 45, 33–42. [Google Scholar] [CrossRef]
- Mishnaevsky, L.; Branner, K.; Nørgaard Petersen, H.; Beauson, J.; McGugan, M.; Sørensen, F. Materials for Wind Turbine Blades: An Overview. Materials 2017, 10, 1285. [Google Scholar] [CrossRef]
- Zhu, M. Design and analysis of steam turbine blades. IOP Conf. Ser. J. Phys. Conf. Ser. 2019, 1300, 012056. [Google Scholar] [CrossRef]
- Lee, J.W.; Lee, J.Y. In-plane bending vibration analysis of a rotating beamwith multiple edge cracks by using the transfer matrix method. Meccanica 2017, 52, 1143–1157. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Shiao, S.Y.; Liao, W.I. Damage detection of rotating wind turbine blades using local flexibility method and long-gauge fiber Bragg grating sensors. Meas. Sci. Technol. 2018, 29, 015108. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, D.; Dong, Y. Effect of cracks on nonlinear flexural vibration of rotating Timoshenko functionally graded material beam having large amplitude motion. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 232, 930–940. [Google Scholar]
- Fang, J.; Zhou, D.; Dong, Y. Three-dimensional vibration of rotating functionally graded beams. J. Vib. Control 2018, 24, 3292–3306. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, D. In-Plane Vibration Analysis of Rotating Tapered Timoshenko Beams. Int. J. Appl. Mech. 2016, 8, 1650064. [Google Scholar] [CrossRef]
- Bhat, R.B. Transverse vibrations of a rotating uniform cantilever beam with tip mass as predicted by using beam characteristic orthogonal polynomials in the Rayleigh–Ritz Method. J. Sound Vib. 1896, 105, 199–210. [Google Scholar] [CrossRef]
- Yoo, H.H.; Cho, J.E.; Chung, J. Modal analysis at shape optimization of rotating cantilever beams. J. Sound Vib. 2006, 290, 223–241. [Google Scholar] [CrossRef]
- Mazanoglu, K.; Guler, S. Flap-wise and chord-wise vibrations of axially functionally grades tapered beams rotating around a hub. Mech. Syst. Signal Process 2017, 89, 97–107. [Google Scholar] [CrossRef]
- Rao, S.S.; Gupta, R.S. Finite Element vibration analysis of rotating Timoshenko beams. J. Sound Vib. 2001, 242, 103–124. [Google Scholar] [CrossRef]
- Cai, G.P.; Hong, J.Z.; Yang, S.X. Model study and active control of a rotating flexible cantilever beam. J. Sound Vib. 2004, 46, 871–889. [Google Scholar] [CrossRef]
- Özdemir, Ö.; Kaya, M.O. Flapwise bending vibration analysis of a rotating tapered cantilever Bernoulli-Euler beam by differential transform method. J. Sound Vib. 2006, 289, 413–420. [Google Scholar] [CrossRef]
- Wright, A.D.; Smith, C.E.; Thresher, R.W.; Wang, J.L.C. Vibration modes of centrifugally stiffened beams. J. Appl. Mech. 1982, 49, 197–202. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Su, H.; Jackson, D.R. Free vibration of rotating tapered beams using the dynamic stiffness method. J. Sound Vib. 2006, 298, 1034–1054. [Google Scholar] [CrossRef]
- Chen, L.-W.; Chen, C.-L. Vibration and stability of crack thick rotating blades. Comput. Struct. 1988, 28, 67–74. [Google Scholar]
- Dimarogonas, A.D. Vibration of cracked structures: A state of the art review. Eng. Fract. Mech. 1996, 55, 831–857. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Technical Report; Los Alamos National Lab.: Los Alamos, NM, USA, 1996. [Google Scholar]
- Carden, E.P.; Fanning, P. Vibration based condition monitoring: A review, Structural Health Monitoring. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Loya, J.A.; Rubio, L.; Fernández-Sáez, J. Natural frequencies for bending vibrations of Timoshenko cracked beams. J. Sound Vib. 2006, 290, 640–653. [Google Scholar] [CrossRef]
- Muñoz-Abella, B.; Rubio, L.; Rubio, P.; Montero, L. Elliptical crack identification in a non-rotating shaft. Shock Vib. 2018, 2018, 4623035. [Google Scholar]
- Chondros, T.G.; Dimaragonas, A.D.; Yao, Y. A continuous cracked beam vibration theory. J. Sound Vib. 1998, 215, 17–34. [Google Scholar] [CrossRef]
- Fernández-Sáez, J.; Rubio, L.; Navarro, C. Approximate calculation of the fundamental frequency for bending vibrations of cracked beams. J. Sound Vib. 1999, 225, 345–352. [Google Scholar] [CrossRef]
- Chen, L.W.; Shen, G.S. Vibration analysis of a rotating orthotropic blade with an open crack by the finite element method. In Proceedings of the third International Conference on Rotor Dynamics, Lyon, France, 10–12 September 1990. [Google Scholar]
- Datta, P.K.; Ganguli, R. Vibration characteristics of a rotating blade with localized damage including the effects of shear deformation and rotary inertia. Comput. Struct. 1990, 36, 1129–1133. [Google Scholar] [CrossRef]
- Wauer, J. Dynamics of cracked rotating blades. Appl. Mech. Rev. 1991, 44, 273–278. [Google Scholar] [CrossRef]
- Krawczuk, M. Natural vibration of cracked rotating beams. Acta Mech. 1993, 99, 35–48. [Google Scholar] [CrossRef]
- Cheng, Y.; Yu, Z.; Wu, X.; Yuan, Y. Vibration analysis of a cracked rotating tapered beam using the p-version finite element method. Finite Elem. Anal. Des. 2011, 47, 825–834. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, D. Crack modeling of rotating blades with cracked hexahedral finite element method. Mech. Syst. Signal Process 2014, 46, 406–423. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, D.; Chu, F. Influence of alternating loads on nonlinear vibration characteristics of cracked blade in rotor system. J. Sound Vib. 2015, 353, 205–219. [Google Scholar] [CrossRef]
- Yashar, A.; Ghandchi-Tehrani, M.; Ferguson, N. Dynamic behaviour of a rotating cracked beam. J. Phys. Conf. Ser. 2016, 744, 012057. [Google Scholar] [CrossRef]
- Yashar, A.; Ferguson, N.; Ghandchi-Tehrani, M. Simplified modelling and analysis of a rotating Euler–Bernoulli beam with a single cracked edge. J. Sound Vib. 2018, 420, 346–356. [Google Scholar] [CrossRef]
- Karimi-Nobandegani, A.; Fazelzadeh, S.A.; Ghavanloo, E. Flutter Instability of Cracked Rotating Non-Uniform Beams Subjected to Distributed Follower Force. Int. J. Struct. Stab. Dyn. 2018, 18, 1850001–1850021. [Google Scholar] [CrossRef]
- Masoud, A.A.; Al-Said, S. A new algorithm for crack localization in a rotating Timoshenko beam. J. Vib. Control 2009, 15, 1541–1561. [Google Scholar] [CrossRef]
- Lee, J.W.; Lee, J.Y. Free vibration analysis of a rotating double-tapered beam using the transfer matrix method. J. Mech. Sci. Technol. 2020, 34, 2731–2744. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free vibration of centrifugally stiffness uniform and tapered beams using the dynamic stiffness method. J. Sound Vib. 2000, 233, 857–875. [Google Scholar] [CrossRef]
- Muñoz-Abella, B.; Rubio, L.; Rubio, P. GitHub Repository. Coefficients. Coefficients Low-Speed EB Cracked Rotating Beam. 2022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).