A New Mixture Differential Cryptanalysis on Round-Reduced AES
Abstract
:1. Introduction
1.1. Related Work
1.2. Our Contribution
- We verify the 5-round mixture differential distinguisher deduced from the MILP method experimentally on small-scale AES practically. With lookup-table-based implementation, the verification efficiency is improved about 20 times. Compared with the textbook implementation, the verification time with 5-round encryption is decreased from more than 20 min to about 1 min when running on 32 parallel threads with an AMD Ryzen Threadripper 3970X Processor. We also refined the MILP-based automatic tool for searching for mixture differential distinguishers to illustrate all trails to form the distinguisher.
- In the key recovery aspect, we give a 6-round key recovery attack on AES-128 by directly exploiting the automatically deduced 5-round secret key distinguisher with data/time complexity reduced to . The previous best attack in the same fashion was by Grassi [16], with data/time/memory complexity being . Our methods present a dramatic decrease in data and time complexity with the same memory complexity.
- Further, a novel 7-round key recovery attack on AES-192 that directly exploits a 6-round secret-key distinguisher is also presented. Though this attack has higher complexity than some previous ones, this is the first direct utilization of a 6-round secret-key distinguisher to do key recovery attacks on 7-round AES with complexity lower than a brute-force attack.
2. Preliminary
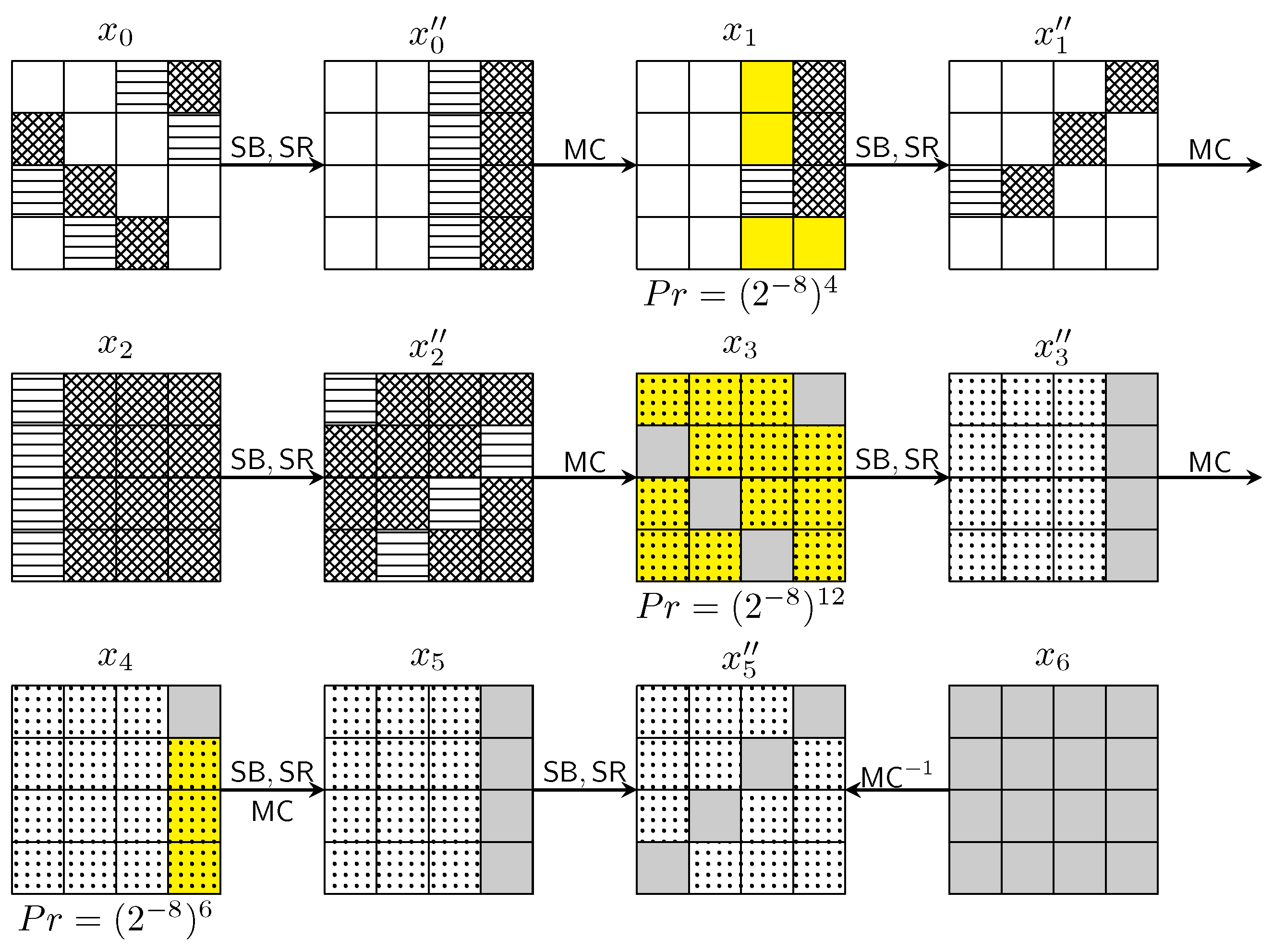
2.1. A Brief Description of AES
- SubBytes (): each byte of is substituted by another byte according to an invertible 8-bit to get state . The substitution is determined by a table called Sbox, which is a permutation of 8-bit elements. The Sbox and inverse Sbox are given in Appendix A. An inverse Sbox is used in decryption, and this step is denoted by InvSubBytes.
- ShiftRows (): the j-th () row of state is cyclicly shifted by j bytes to the left to get state . Cyclic shifting to the right with the same offsets is applied in decryption, and this step is denoted by InvShiftRows.
- MixColumn (): multiply each column of by a MDS (maximum distance separable) matrix over . The MDS matrix and its inverse arewhere each element in the matrix is an element in defined by the irreducible polynomial , and multiplication and addition are also performed in this field. Multiplication of on each column is performed in decryption, and this step is denoted by InvMixColumn. The MDS property ensures that the number of non-zero bytes among the input column and output column is no less than 5, except for the all-zero case, i.e., the branch number being 5.
- AddRoundKey (): XORing a 128-bit subkey to the state to get .
2.2. Metrics of Evaluation of Cryptanalysis Methods
2.3. Mixture Differentials
- copy pattern , which means the second pair is a copy of the first pair. This pattern is denoted by “c” and shown graphically as
.
- exchange pattern , which means the second pair is acquired by exchange of the two values in the first pair. This pattern is denoted by “e” and shown graphically as
.
- shift pattern , which means the second pair is acquired by shifting an inactive pair, denoted by “s” and shown graphically as
.
- inactive pattern , which consists of four equal bytes. This pattern is denoted by “-” and shown graphically as
.
 . Throughout this paper, mixture patterns or mixture differential patterns include these five quadruple patterns. Probability for a random quadruple to have a “c”, “e” or “s” pattern is , and probability to have an inactive pattern is , where w is width of the word.
. Throughout this paper, mixture patterns or mixture differential patterns include these five quadruple patterns. Probability for a random quadruple to have a “c”, “e” or “s” pattern is , and probability to have an inactive pattern is , where w is width of the word.3. Mixture Differential Distinguishers
3.1. Search for Mixture Differential Distinguishers with MILP Model
- , mixture pattern encoding variables for the s-th byte in the input state to the r-th round, i.e., . We have iff .
- , column-wise mixture pattern encoding variables for the t-th input column for operation in the r-th round. Note that an input column to layer is a diagonal of the input state, i.e., . We have iff .
- , probability encoding variables. By considering the first-order differential property, the probability to have some mixture pattern on is . For example, for a random input quadruple, the probability of an output byte conforming a “”, “” or “” pattern is , and it is for a “-” pattern.
- together with . The former indicates whether the second-order differential is 0 for , i.e., iff . The latter describes that the assignment of holds with probability . If the s-th is active for both the first pair and the second pair in the quadruple, with probability () we have , or we have with probability 1 (). If the s-th is inactive for both pairs, with probability 1 (). If the s-th is inactive for only one pair, we have with probability 1 ().
- , indicates whether second-order differential is 0 on . We have .
- , a dummy variable used as a label. We have .
- , number of activity variables reduced considering second-order differential properties. The probability of the mixture pattern trail covering R rounds is estimated as .
| Algorithm 1 MILP model to get the probability of given mixture patterns |
|
3.2. Verification of 5-Round Distinguishers
3.3. Illustration of 6-Round Distinguishers
4. Key Recovery Attacks
4.1. Key Recovery on 6-Round AES-128
- For each quadruple, do the MITM procedure on four groups:
- (a)
- For the first group, guess , compute the value on both the first pair and the second pair, and store the current guess in a hash table T indexed by this 16-bit value. After this step, each item of T contains on average one element.
- (b)
- Guess and compute the value on both the first pair and the second pair. Look up the table T by this 16-bit value and get the candidate for the combination . Increase the counter for the first group. After this step, on average, candidates are suggested.
- (c)
- Repeat Step 1(a)–(b) for the other three groups.
- To have h-bit advantage of key exhaustive search on each group, combine the top candidates suggested by each counter to get candidates of the full 128-bit key . Check with plaintext–ciphertext pairs.
4.2. Key Recovery on 7-Round AES-192
- For each quadruple, do the MITM procedure on four groups:
- (a)
- For the first group, guess , compute the value on both the first pair and the second pair, and store the current guess in a hash table T indexed by this 16-bit value. After this step, each item of T contains, on average, one element.
- (b)
- Guess and compute the value on both the first pair and the second pair. Look up the table T by this 16-bit value and get the candidate for the combination . Test if the last two equations in Equation (6) are satisfied under this candidate on both the first pair and the second pair. This test is a filter with probability . If so, increase the counter; otherwise, discard the key candidate.
- (c)
- Repeat Step 1(a–b) for the other three groups.
- To have h-bit advantage of key exhaustive search on each group, combine the top candidates indicated by each counter to form full 128-bit key and combine with the other 64-bit keys that are independent of . Check the candidate keys with plaintext–ciphertext pairs.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MILP | Mixed Integer Linear Programming |
| MITM | Meet-in-the-Middle |
| SubBytes | |
| ShiftRows | |
| MixColumn |
Appendix A. AES Encryption Parameters
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0a | 0b | 0c | 0d | 0e | 0f | |
| 00 | 63 | 7c | 77 | 7b | f2 | 6b | 6f | c5 | 30 | 01 | 67 | 2b | fe | d7 | ab | 76 |
| 10 | ca | 82 | c9 | 7d | fa | 59 | 47 | f0 | ad | d4 | a2 | af | 9c | a4 | 72 | c0 |
| 20 | b7 | fd | 93 | 26 | 36 | 3f | f7 | cc | 34 | a5 | e5 | f1 | 71 | d8 | 31 | 15 |
| 30 | 04 | c7 | 23 | c3 | 18 | 96 | 05 | 9a | 07 | 12 | 80 | e2 | eb | 27 | b2 | 75 |
| 40 | 09 | 83 | 2c | 1a | 1b | 6e | 5a | a0 | 52 | 3b | d6 | b3 | 29 | e3 | 2f | 84 |
| 50 | 53 | d1 | 00 | ed | 20 | fc | b1 | 5b | 6a | cb | be | 39 | 4a | 4c | 58 | cf |
| 60 | d0 | ef | aa | fb | 43 | 4d | 33 | 85 | 45 | f9 | 02 | 7f | 50 | 3c | 9f | a8 |
| 70 | 51 | a3 | 40 | 8f | 92 | 9d | 38 | f5 | bc | b6 | da | 21 | 10 | ff | f3 | d2 |
| 80 | cd | 0c | 13 | ec | 5f | 97 | 44 | 17 | c4 | a7 | 7e | 3d | 64 | 5d | 19 | 73 |
| 90 | 60 | 81 | 4f | dc | 22 | 2a | 90 | 88 | 46 | ee | b8 | 14 | de | 5e | 0b | db |
| a0 | e0 | 32 | 3a | 0a | 49 | 06 | 24 | 5c | c2 | d3 | ac | 62 | 91 | 95 | e4 | 79 |
| b0 | e7 | c8 | 37 | 6d | 8d | d5 | 4e | a9 | 6c | 56 | f4 | ea | 65 | 7a | ae | 08 |
| c0 | ba | 78 | 25 | 2e | 1c | a6 | b4 | c6 | e8 | dd | 74 | 1f | 4b | bd | 8b | 8a |
| d0 | 70 | 3e | b5 | 66 | 48 | 03 | f6 | 0e | 61 | 35 | 57 | b9 | 86 | c1 | 1d | 9e |
| e0 | e1 | f8 | 98 | 11 | 69 | d9 | 8e | 94 | 9b | 1e | 87 | e9 | ce | 55 | 28 | df |
| f0 | 8c | a1 | 89 | 0d | bf | e6 | 42 | 68 | 41 | 99 | 2d | 0f | b0 | 54 | bb | 16 |
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0a | 0b | 0c | 0d | 0e | 0f | |
| 00 | 52 | 09 | 6a | d5 | 30 | 36 | a5 | 38 | bf | 40 | a3 | 9e | 81 | f3 | d7 | fb |
| 10 | 7c | e3 | 39 | 82 | 9b | 2f | ff | 87 | 34 | 8e | 43 | 44 | c4 | de | e9 | cb |
| 20 | 54 | 7b | 94 | 32 | a6 | c2 | 23 | 3d | ee | 4c | 95 | 0b | 42 | fa | c3 | 4e |
| 30 | 08 | 2e | a1 | 66 | 28 | d9 | 24 | b2 | 76 | 5b | a2 | 49 | 6d | 8b | d1 | 25 |
| 40 | 72 | f8 | f6 | 64 | 86 | 68 | 98 | 16 | d4 | a4 | 5c | cc | 5d | 65 | b6 | 92 |
| 50 | 6c | 70 | 48 | 50 | fd | ed | b9 | da | 5e | 15 | 46 | 57 | a7 | 8d | 9d | 84 |
| 60 | 90 | d8 | ab | 00 | 8c | bc | d3 | 0a | f7 | e4 | 58 | 05 | b8 | b3 | 45 | 06 |
| 70 | d0 | 2c | 1e | 8f | ca | 3f | 0f | 02 | c1 | af | bd | 03 | 01 | 13 | 8a | 6b |
| 80 | 3a | 91 | 11 | 41 | 4f | 67 | dc | ea | 97 | f2 | cf | ce | f0 | b4 | e6 | 73 |
| 90 | 96 | ac | 74 | 22 | e7 | ad | 35 | 85 | e2 | f9 | 37 | e8 | 1c | 75 | df | 6e |
| a0 | 47 | f1 | 1a | 71 | 1d | 29 | c5 | 89 | 6f | b7 | 62 | 0e | aa | 18 | be | 1b |
| b0 | fc | 56 | 3e | 4b | c6 | d2 | 79 | 20 | 9a | db | c0 | fe | 78 | cd | 5a | f4 |
| c0 | 1f | dd | a8 | 33 | 88 | 07 | c7 | 31 | b1 | 12 | 10 | 59 | 27 | 80 | ec | 5f |
| d0 | 60 | 51 | 7f | a9 | 19 | b5 | 4a | 0d | 2d | e5 | 7a | 9f | 93 | c9 | 9c | ef |
| e0 | a0 | e0 | 3b | 4d | ae | 2a | f5 | b0 | c8 | eb | bb | 3c | 83 | 53 | 99 | 61 |
| f0 | 17 | 2b | 04 | 7e | ba | 77 | d6 | 26 | e1 | 69 | 14 | 63 | 55 | 21 | 0c | 7d |
Appendix B. Inequality Templates Used in MILP Model
| No. | Inequalities |
|---|---|
| Template 1 | (0, 0, 0, 1, −1, 1, 0), (1, 1, 0, −1, 0, 0, 0), (0, 0, 0, 1, 1, −1, 0), (−1, −1, 1, −1, 1, 1, 1), (1, −1, 0, 1, 0, 0, 0), (−1, 1, 0, 1, 0, 0, 0), (1, 1, 1, −1, −1, −1, 1), (1, 0, −1, 0, 1, 0, 0), (0, 1, −1, 0, 0, 1, 0), (0, −1, 1, 0, 0, 1, 0), (−1, 0, 1, 0, 1, 0, 0) |
| Template 2 | (1, 1, 1, 1, 1, −4, 1, 1, 0), (1, 1, 1, 1, −4, 1, 1, 1, 0), (1, −4, 1, 1, 1, 1, 1, 1, 0), (1, 1, 1, 1, 1, 1, 1, −4, 0), (1, 1, 1, −4, 1, 1, 1, 1, 0), (−4, 1, 1, 1, 1, 1, 1, 1, 0), (1, 1, −4, 1, 1, 1, 1, 1, 0), (1, 1, 1, 1, 1, 1, −4, 1, 0) |
| Template 3 | (1, 2, 3, 3, 1, 2, −2, −1, −3, −1, −2, −1, −5, −3, 0), (8, −14, −14, 4, 4, −10, −6, 6, 6, −1, −1, 7, 16, 6, 14), (−4, 0, 4, −2, 2, −2, 4, −1, −3, 2, −2, 3, 6, 4, 0), (−10, −14, 4, −14, 4, 8, 7, 6, −1, 6, −1, −6, 16, 6, 14), (−14, 8, −14, 4, −10, 4, 6, −6, 6, −1, 7, −1, 16, 6, 14), (4, −6, 4, 8, 4, −8, −2, 4, −6, −5, −1, 5, 0, 4, 2), (−2, −4, 2, 0, −2, 4, 2, 4, −2, −1, 3, −3, 6, 4, 0), (2, 4, −2, −2, 4, 6, −1, −1, 0, 0, −1, −3, −6, −4, 0), (4, 2, −2, −4, 0, −2, −3, −2, 3, 4, −1, 2, 6, 4, 0), (4, 4, 4, 4, 4, 4, −1, −1, −2, −3, −4, −4, −14, −10, 0), (−2, 4, 4, 2, 4, −2, −2, −3, 1, −2, 0, 1, −6, −2, 0), (4, −2, 4, 4, −2, 2, 1, −2, −3, 0, 1, −2, −6, −2, 0), (0, 0, 0, −2, −2, −2, 1, 1, −2, 1, 2, 2, 4, 2, 2), (−4, −3, −2, −4, −3, −2, −1, 3, 3, 2, 3, −1, 6, 2, 10), (−2, −2, −2, −2, −2, −2, 2, 0, 2, 1, −1, 1, 3, 2, 7) |
| Template 4 | (1, −1, 1, 1, −1, 1, −1, −2, 0), (−1, 1, 1, 1, 1, −1, −1, −2, 0), (1, 1, −1, −1, 1, 1, −1, −2, 0), (1, 1, 1, −1, −1, −1, 1, 0, 0), (1, −1, −1, 1, 1, −1, 1, 0, 0), (−1, 1, −1, 1, −1, 1, 1, 0, 0), (−1, −1, 1, −1, 1, 1, 1, 0, 0), (0, 0, −1, 0, −1, −1, 1, 1, 2) |
| Template 5 | (1, 1, −1, −1, 1, −1, 1, 1, 0), (0, 0, 1, 1, 0, −1, 0, 0, 0), (0, 0, 0, 0, 0, 1, 1, −1, 0), (0, 0, 0, 0, 0, 1, −1, 1, 0), (0, 0, 0, 1, −1, 0, 0, 1, 0), (0, 0, 1, 0, 1, 0, −1, 0, 0), (1, 1, 1, −1, −1, 1, 1, −1, 0), (0, 0, −1, 1, 0, 1, 0, 0, 0), (0, 0, 0, 1, 1, 0, 0, −1, 0), (0, 0, −1, −1, 1, −1, 1, 1, 1), (0, 0, 1, −1, 0, 1, 0, 0, 0), (0, 0, 1, 0, −1, 0, 1, 0, 0), (1, 1, 1, 1, 1, −1, −1, −1, 0) |
| Template 6 | (0, −1, 0, 0, −1, 1), (0, 0, 1, 0, −1, 0), (1, 1, −1, 0, 1, 0), (−1, 0, 0, 0, −1, 1) |
Appendix C. Mixture Differential Trails of 6-Round AES
| No. | ||||
|---|---|---|---|---|
| 0 | ---- ---- --c- xxx- | cccc xxxx xxxx xxxx | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 1 | ---- ---- c-c- x-x- | cccc xxxx cccc xxxx | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 2 | ---- ---- -c-c -x-x | xxxx cccc xxxx cccc | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 3 | ---- ---- ---c -xxx | xxxx xxxx xxxx cccc | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 4 | ---- ---- c--- x-xx | xxxx xxxx cccc xxxx | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 5 | ---- ---- --cc -xx- | cccc xxxx xxxx cccc | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 6 | ---- ---- -c-c -x-x | xxxx cccc xxxx cccc | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 7 | ---- ---- -c-- xx-x | xxxx cccc xxxx xxxx | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 8 | ---- ---- cc-c ---x | xxxx cccc cccc cccc | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 9 | ---- ---- cc-- x--x | xxxx cccc cccc xxxx | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 10 | ---- ---- c-cc --x- | cccc xxxx cccc cccc | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 11 | ---- ---- -ccc -x-- | cccc cccc xxxx cccc | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 12 | ---- ---- -cc- xx-- | cccc cccc xxxx xxxx | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 13 | ---- ---- ccc- x--- | cccc cccc cccc xxxx | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 14 | ---- ---- c-cc --x- | cccc xxxx cccc cccc | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 15 | ---- ---- ---c -xxx | xxxx xxxx xxxx cccc | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 16 | ---- ---- cc-c ---x | xxxx cccc cccc cccc | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 17 | ---- ---- --cc -xx- | cccc xxxx xxxx cccc | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 18 | ---- ---- -c-c -x-x | xxxx cccc xxxx cccc | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 19 | ---- ---- -ccc -x-- | cccc cccc xxxx cccc | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 20 | ---- ---- c--c --xx | xxxx xxxx cccc cccc | s*ss ss*s sss* *sss | ssss ssss ssss *sss |
| 21 | ---- ---- c--c --xx | xxxx xxxx cccc cccc | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 22 | ---- ---- c--- x-xx | xxxx xxxx cccc xxxx | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 23 | ---- ---- cc-c ---x | xxxx cccc cccc cccc | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 24 | ---- ---- ccc- x--- | cccc cccc cccc xxxx | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 25 | ---- ---- ---c -xxx | xxxx xxxx xxxx cccc | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 26 | ---- ---- c-cc --x- | cccc xxxx cccc cccc | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 27 | ---- ---- -ccc -x-- | cccc cccc xxxx cccc | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 28 | ---- ---- c--c --xx | xxxx xxxx cccc cccc | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 29 | ---- ---- c--c --xx | xxxx xxxx cccc cccc | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 30 | ---- ---- c-c- x-x- | cccc xxxx cccc xxxx | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 31 | ---- ---- --cc -xx- | cccc xxxx xxxx cccc | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 32 | ---- ---- -c-- xx-x | xxxx cccc xxxx xxxx | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 33 | ---- ---- c--- x-xx | xxxx xxxx cccc xxxx | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 34 | ---- ---- c-c- x-x- | cccc xxxx cccc xxxx | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 35 | ---- ---- cc-- x--x | xxxx cccc cccc xxxx | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 36 | ---- ---- --c- xxx- | cccc xxxx xxxx xxxx | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 37 | ---- ---- cc-- x--x | xxxx cccc cccc xxxx | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 38 | ---- ---- -cc- xx-- | cccc cccc xxxx xxxx | sss* *sss s*ss ss*s | ssss ss*s ssss ssss |
| 39 | ---- ---- --c- xxx- | cccc xxxx xxxx xxxx | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 40 | ---- ---- -c-- xx-x | xxxx cccc xxxx xxxx | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 41 | ---- ---- ccc- x--- | cccc cccc cccc xxxx | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 42 | ---- ---- -cc- xx-- | cccc cccc xxxx xxxx | *sss s*ss ss*s sss* | s*ss ssss ssss ssss |
| 43 | ---- ---- cc-c ---x | xxxx cccc cccc cccc | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 44 | ---- ---- cc-- x--x | xxxx cccc cccc xxxx | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 45 | ---- ---- c-cc --x- | cccc xxxx cccc cccc | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 46 | ---- ---- c-c- x-x- | cccc xxxx cccc xxxx | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 47 | ---- ---- ccc- x--- | cccc cccc cccc xxxx | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 48 | ---- ---- ---c -xxx | xxxx xxxx xxxx cccc | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 49 | ---- ---- --cc -xx- | cccc xxxx xxxx cccc | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 50 | ---- ---- c--- x-xx | xxxx xxxx cccc xxxx | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 51 | ---- ---- -ccc -x-- | cccc cccc xxxx cccc | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 52 | ---- ---- -cc- xx-- | cccc cccc xxxx xxxx | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 53 | ---- ---- -c-c -x-x | xxxx cccc xxxx cccc | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 54 | ---- ---- -c-- xx-x | xxxx cccc xxxx xxxx | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
| 55 | ---- ---- --c- xxx- | cccc xxxx xxxx xxxx | ss*s sss* *sss s*ss | ssss ssss sss* ssss |
References
- National Institute of Standards and Technology. FIPS PUB 197: Advanced Encryption Standard (AES). pub-NIST; 2001. Available online: http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf (accessed on 10 October 2022).
- Kocher, P.; Jaffe, J.; Jun, B. Differential Power Analysis. In Advances in Cryptology — CRYPTO’ 99. CRYPTO 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 388–397. [Google Scholar]
- Biham, E.; Shamir, A. Differential Fault Analysis of Secret Key Cryptosystems. In Advances in Cryptology — CRYPTO ’97. CRYPTO 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 513–525. [Google Scholar]
- Qiao, K.; Sun, S.; Zhang, Z.; Wang, A.; Zhu, L. Quadruple Differential Distinguishers and an Automatic Searching Tool. TechRxiv Preprint. 2022. Available online: https://www.techrxiv.org/articles/preprint/Quadruple_Differential_Distinguishers_and_an_Automatic_Searching_Tool/21186376 (accessed on 10 October 2022).
- Gilbert, H.; Minier, M. A Collision Attack on 7 Rounds of Rijndael. In Proceedings of the AES Candidate Conference, New York, NY, USA, 13–14 April 2000; Volume 2000, pp. 230–241. [Google Scholar]
- Biham, E.; Shamir, A. Differential Cryptanalysis of DES-like Cryptosystems. J. Cryptol. 1991, 4, 3–72. [Google Scholar] [CrossRef]
- Biham, E.; Biryukov, A.; Shamir, A. Cryptanalysis of Skipjack Reduced to 31 Rounds Using Impossible Differentials. In Advances in Cryptology–EUROCRYPT 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 12–23. [Google Scholar]
- Cheon, J.H.; Kim, M.; Kim, K.; Jung-Yeun, L.; Kang, S. Improved Impossible Differential Cryptanalysis of Rijndael and Crypton. In Information Security and Cryptology — ICISC 2001. ICISC 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 39–49. [Google Scholar]
- Derbez, P.; Fouque, P.A. Exhausting Demirci-Selçuk Meet-in-the-Middle Attacks against Reduced-round AES. In Fast Software Encryption. FSE 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 541–560. [Google Scholar]
- Derbez, P.; Fouque, P.A.; Jean, J. Improved Key Recovery Attacks on Reduced-round AES in the Single-key Setting. In Advances in Cryptology – EUROCRYPT 2013. EUROCRYPT 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 371–387. [Google Scholar]
- Daemen, J.; Rijmen, V. The Design of Rijndael: AES-the Advanced Encryption Standard; Springer: New York, NY, USA, 2002. [Google Scholar]
- Ferguson, N.; Kelsey, J.; Lucks, S.; Schneier, B.; Stay, M.; Wagner, D.; Whiting, D. Improved Cryptanalysis of Rijndael. In Fast Software Encryption. FSE 2000; Goos, G., Hartmanis, J., van Leeuwen, J., Schneier, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–230. [Google Scholar]
- Tunstall, M. Improved “Partial Sums”-based Square Attack on AES. In Proceedings of the International Conference on Security and Cryptography-SECRYPT 2012, Rome, Italy, 24–27 July 2012; SciTePress: Setúbal, Portugal, 2012; pp. 25–34. [Google Scholar]
- Grassi, L.; Rechberger, C.; Rønjom, S. A New Structural-Differential Property of 5-Round AES. In Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017; Coron, J.S., Nielsen, J.B., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 289–317. [Google Scholar]
- Grassi, L. Mixture Differential Cryptanalysis: A New Approach to Distinguishers and Attacks on round-reduced AES. IACR Trans. Symmetric Cryptol. 2018, 2018, 133–160. [Google Scholar] [CrossRef]
- Grassi, L. Probabilistic Mixture Differential Cryptanalysis on Round-reduced AES. In Selected Areas in Cryptography – SAC 2019. SAC 2019; Springer: Cham, Switzerland, 2019; pp. 53–84. [Google Scholar]
- Bar-On, A.; Dunkelman, O.; Keller, N.; Ronen, E.; Shamir, A. Improved Key Recovery Attacks on Reduced-Round AES with Practical Data and Memory Complexities. In Advances in Cryptology–CRYPTO 2018; Shacham, H., Boldyreva, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 185–212. [Google Scholar] [CrossRef]
- Bar-On, A.; Dunkelman, O.; Keller, N.; Ronen, E.; Shamir, A. Improved Key Recovery Attacks on Reduced-round AES with Practical Data and Memory Complexities. J. Cryptol. 2020, 33, 1003–1043. [Google Scholar] [CrossRef]
- Dunkelman, O.; Keller, N.; Ronen, E.; Shamir, A. The Retracing Boomerang Attack. In Advances in Cryptology—EUROCRYPT 2020; Canteaut, A., Ishai, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 280–309. [Google Scholar]
- Boura, C.; Canteaut, A.; Coggia, D. A General Proof Framework for Recent AES Distinguishers. IACR Trans. Symmetric Cryptol. 2019, 2019, 170–191. [Google Scholar] [CrossRef]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2022. Available online: https://www.gurobi.com (accessed on 10 October 2022).
- Sun, S.; Hu, L.; Wang, P.; Qiao, K.; Ma, X.; Song, L. Automatic Security Evaluation and (Related-key) Differential Characteristic Search: Application to SIMON, PRESENT, LBlock, DES (L) and Other Bit-oriented Block Ciphers. In Advances in Cryptology–ASIACRYPT 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 158–178. [Google Scholar]
- Sun, S.; Gerault, D.; Lafourcade, P.; Yang, Q.; Todo, Y.; Qiao, K.; Hu, L. Analysis of AES, SKINNY, and Others with Constraint Programming. IACR Trans. Symmetric Cryptol. 2017, 2017, 281–306. [Google Scholar] [CrossRef]
- Xiang, Z.; Zhang, W.; Bao, Z.; Lin, D. Applying MILP Method to Searching Integral Distinguishers Based on Division Property for 6 Lightweight Block Ciphers. In Advances in Cryptology—ASIACRYPT 2016; Cheon, J.H., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 648–678. [Google Scholar]
- Shi, D.; Sun, S.; Derbez, P.; Todo, Y.; Sun, B.; Hu, L. Programming the Demirci-Selçuk Meet-in-the-Middle Attack with Constraints. In Advances in Cryptology—ASIACRYPT 2018; Springer: Cham, Switzerland, 2018; pp. 3–34. [Google Scholar]
- Dong, X.; Zhang, Z.; Sun, S.; Wei, C.; Wang, X.; Hu, L. Automatic Classical and Quantum Rebound Attacks on AES-Like Hashing by Exploiting Related-Key Differentials. In Advances in Cryptology—ASIACRYPT 2021; Springer: Cham, Switzerland, 2021; pp. 241–271. [Google Scholar]
- Bao, Z.; Dong, X.; Guo, J.; Li, Z.; Shi, D.; Sun, S.; Wang, X. Automatic Search of Meet-in-the-Middle Preimage Attacks on AES-like Hashing. In Advances in Cryptology – EUROCRYPT 2021; Springer: Cham, Switzerland, 2021; pp. 771–804. [Google Scholar]
- Sakiyama, K.; Sasaki, Y.; Li, Y. Security of Block Ciphers: From Algorithm Design to Hardware Implementation; John Wiley & Sons: Singapore Pte. Ltd, 2016. [Google Scholar]
- Cid, C.; Murphy, S.; Robshaw, M.J.B. Small Scale Variants of the AES. In Fast Software Encryption. FSE 2005; Gilbert, H., Handschuh, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 145–162. [Google Scholar]
- The OpenSSL Project. OpenSSL: The Open Source toolkit for SSL/TLS. Available online: https://www.openssl.org/ (accessed on 10 October 2022).
- Selçuk, A.A. On Probability of Success in Linear and Differential Cryptanalysis. J. Cryptol. 2008, 21, 131–147. [Google Scholar] [CrossRef]


| No. | Rd. | Mix. Pattern for | Mix. Pattern for | Single Prob. | #Trails Prob. | AES Prob. | Rand. |
|---|---|---|---|---|---|---|---|
| 1 | 5 | 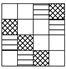 |  | 15 | |||
| 2 | 6 | 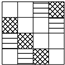 |  | 56 |
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 6 | B | 5 | 4 | 2 | E | 7 | A | 9 | D | F | C | 3 | 1 | 0 | 8 |
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| c66a | 5bbe | a55f | 844c | 4226 | fee1 | e779 | 7aad | |
| ac66 | e5bb | fa55 | c844 | 6422 | 1fee | 9e77 | d7aa | |
| 6ac6 | be5b | 5fa5 | 4c84 | 2642 | e1fe | 79e7 | ad7a | |
| 66ac | bbe5 | 55fa | 44c8 | 2264 | ee1f | 779e | aad7 | |
| x | 8 | 9 | a | b | c | d | e | f |
| 1998 | 9dd4 | dff2 | bcc7 | 6335 | 2113 | 0 | 388b | |
| 8199 | 49dd | 2dff | 7bcc | 5633 | 3211 | 0 | b388 | |
| 9819 | d49d | f2df | c7bc | 3563 | 1321 | 0 | 8b38 | |
| 9981 | dd49 | ff2d | cc7b | 3356 | 1132 | 0 | 88b3 |
| Version | R | Method | Data (CP) | Time (ENC.) | Memory | (16-byte) | Ref. |
|---|---|---|---|---|---|---|---|
| AES-128 | 6 | Partial Sum | 4 | [13] | |||
| Integral | 4 | [11] | |||||
| Mixture Diff. | 4 | [17] | |||||
| Mixture Diff. | 5 | Ours | |||||
| Mixture Diff. | 5 | [16] | |||||
| MITM | — | [9] | |||||
| Imp. Differential | 4 | [8] | |||||
| AES-192 | 7 | MITM | — | [10] | |||
| MITM | — | [9] | |||||
| Collision | 4 | [5] | |||||
| Square | 4 | [12] | |||||
| Mixture Diff. | 4 | [17] | |||||
| Mixture Diff. | 6 | Ours |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, K.; Cheng, J.; Ou, C. A New Mixture Differential Cryptanalysis on Round-Reduced AES. Mathematics 2022, 10, 4736. https://doi.org/10.3390/math10244736
Qiao K, Cheng J, Ou C. A New Mixture Differential Cryptanalysis on Round-Reduced AES. Mathematics. 2022; 10(24):4736. https://doi.org/10.3390/math10244736
Chicago/Turabian StyleQiao, Kexin, Junjie Cheng, and Changhai Ou. 2022. "A New Mixture Differential Cryptanalysis on Round-Reduced AES" Mathematics 10, no. 24: 4736. https://doi.org/10.3390/math10244736
APA StyleQiao, K., Cheng, J., & Ou, C. (2022). A New Mixture Differential Cryptanalysis on Round-Reduced AES. Mathematics, 10(24), 4736. https://doi.org/10.3390/math10244736











