Effect of Hydrostatic Initial Stress on a Rotating Half-Space in the Context of a Two-Relaxation Power-Law Model
Abstract
1. Introduction
2. Basic Governing Equations
2.1. Heat Conduction Equation
2.2. The Stress-Displacement-Temperature Relations
2.3. Equations of Motion
3. Formulation of the Problem
4. Solution of the Problem
5. Boundary Conditions
5.1. Mechanical Conditions
5.2. Thermal Condition
6. Different Thermoelasticity Theories
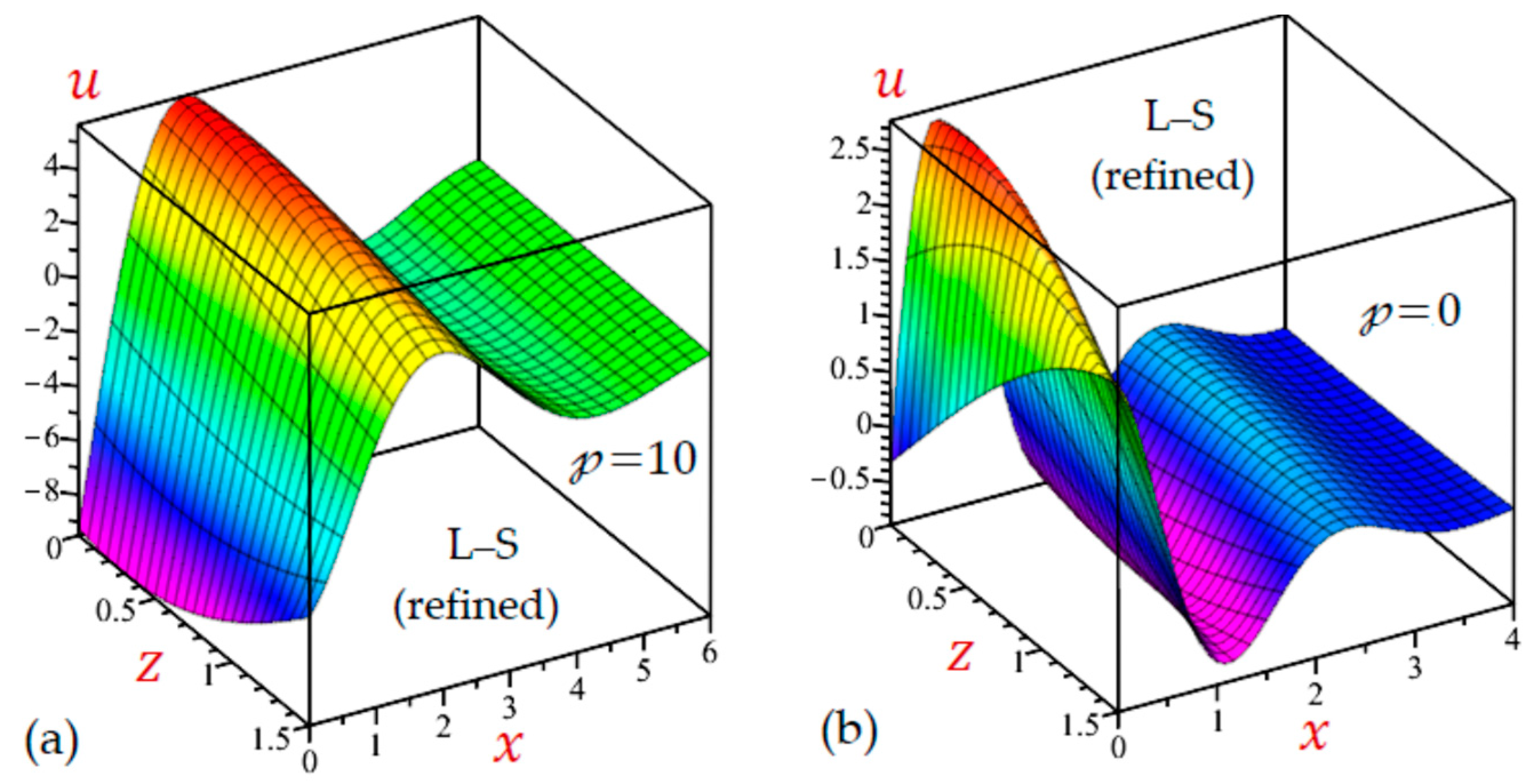
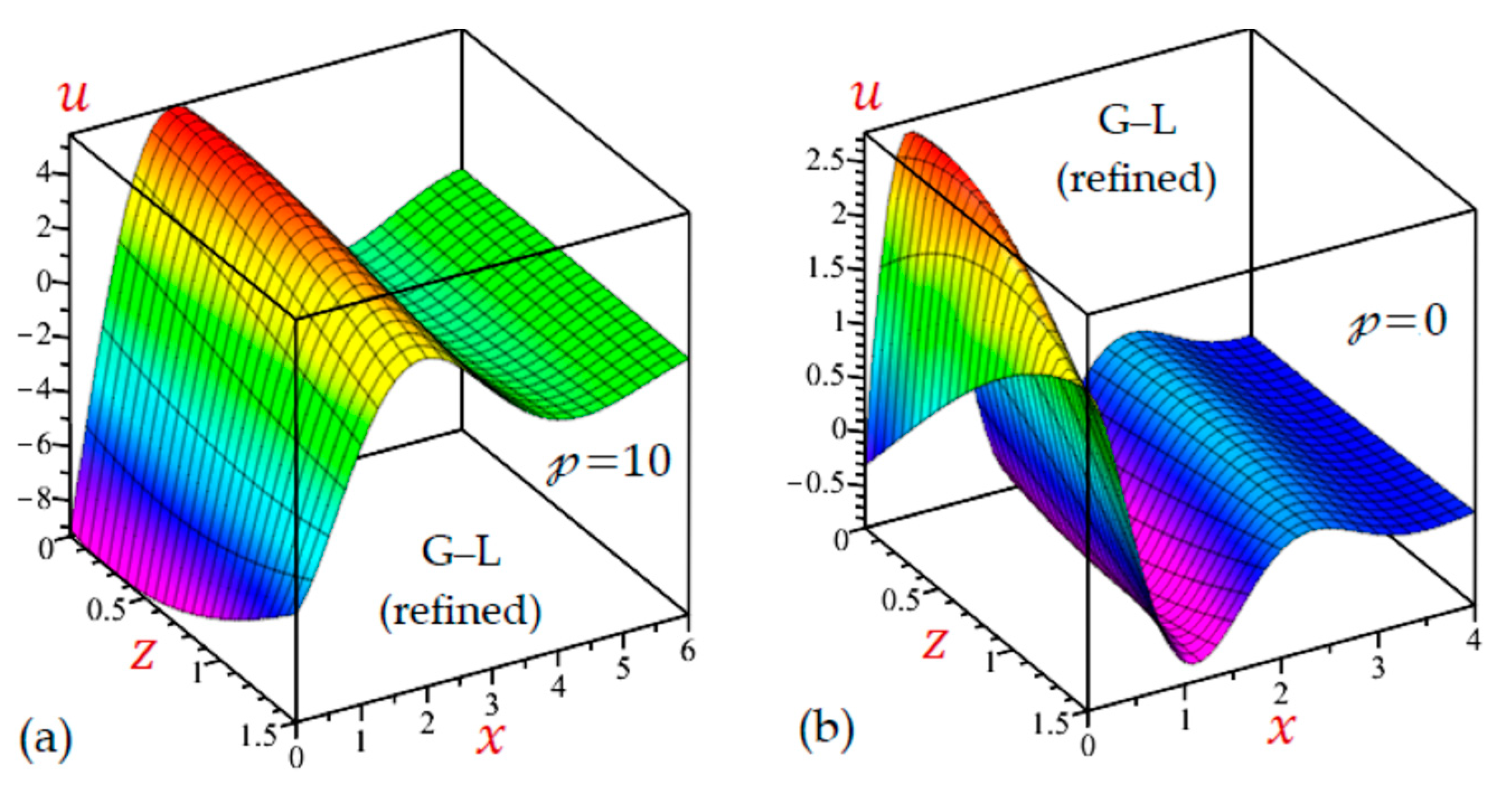
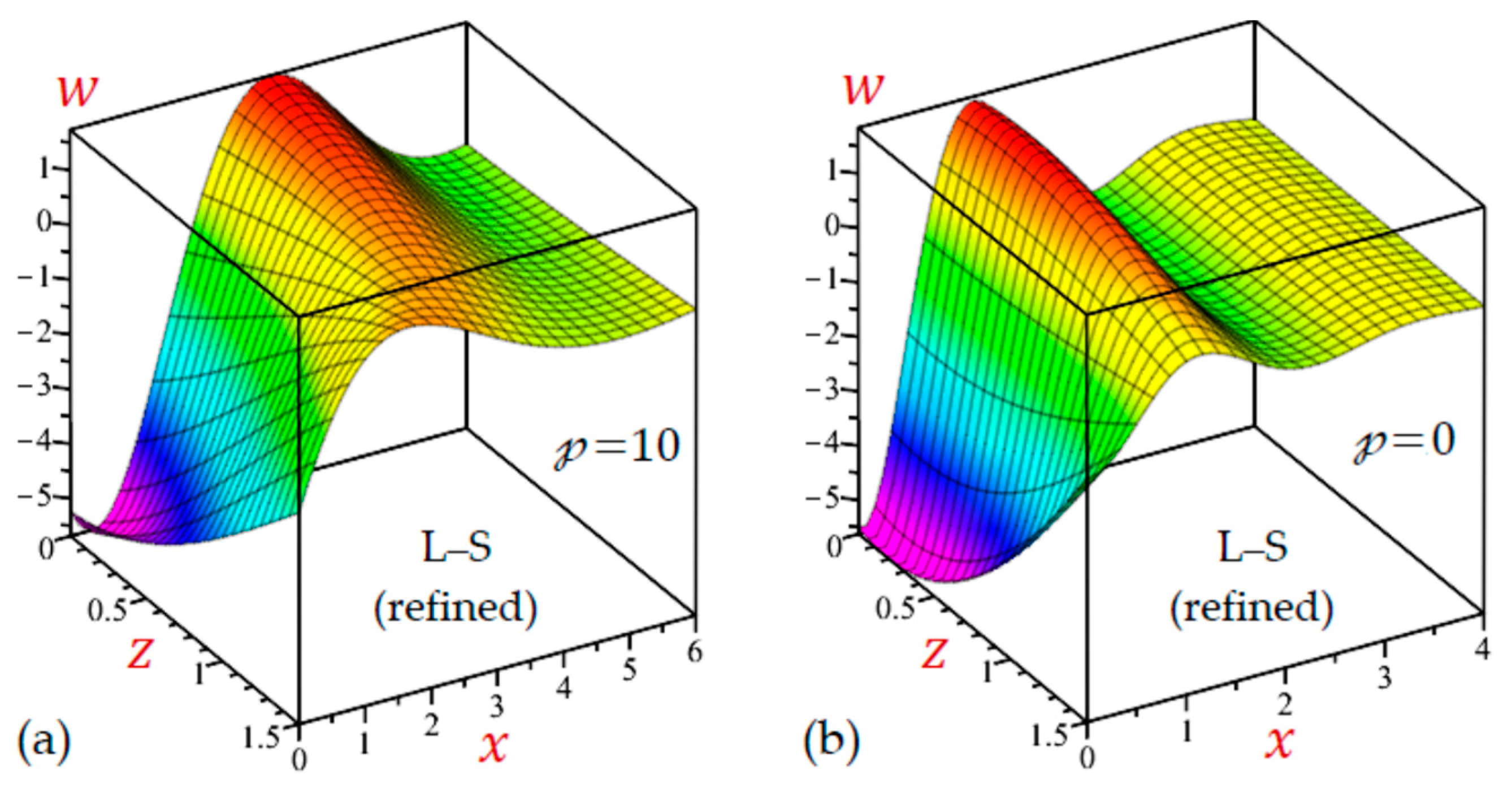
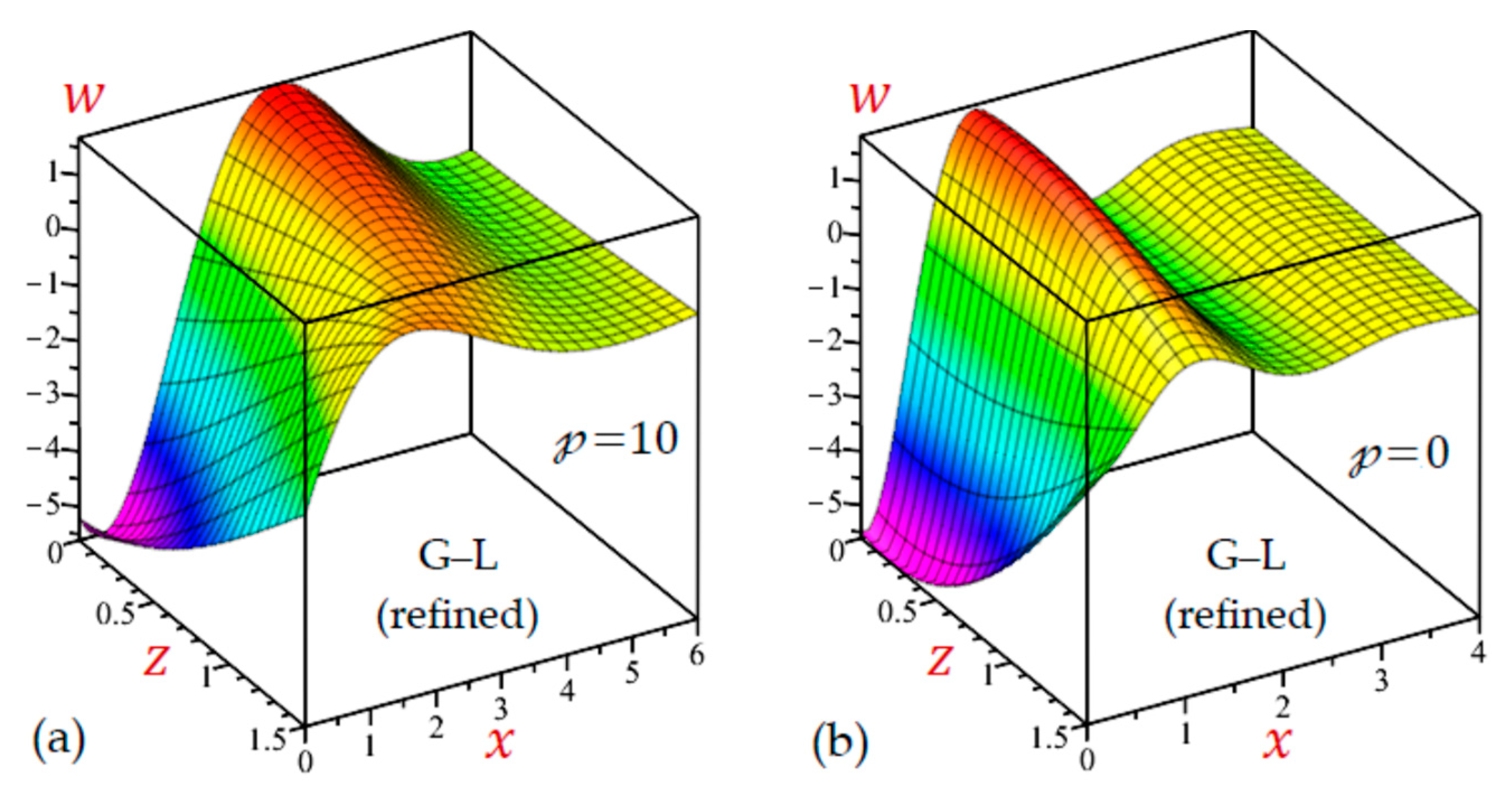
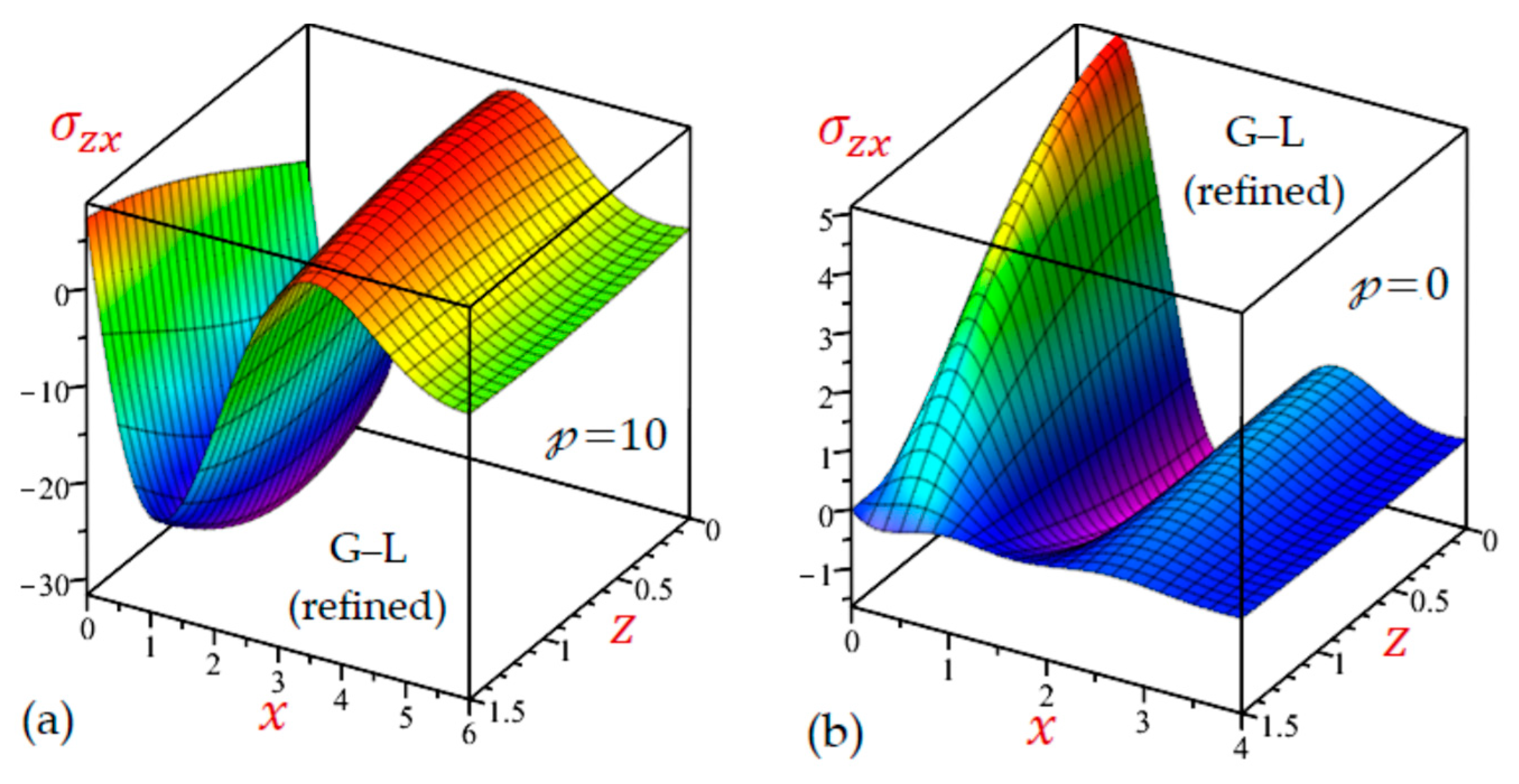
7. Numerical Results and Discussions
7.1. Validation
- The refined L–S and G–L theories are developed with equals from 2 to 5. Nevertheless, the simple L–S and G–L theories are essentially provided when .
- The incredibly accurate results are generated when .
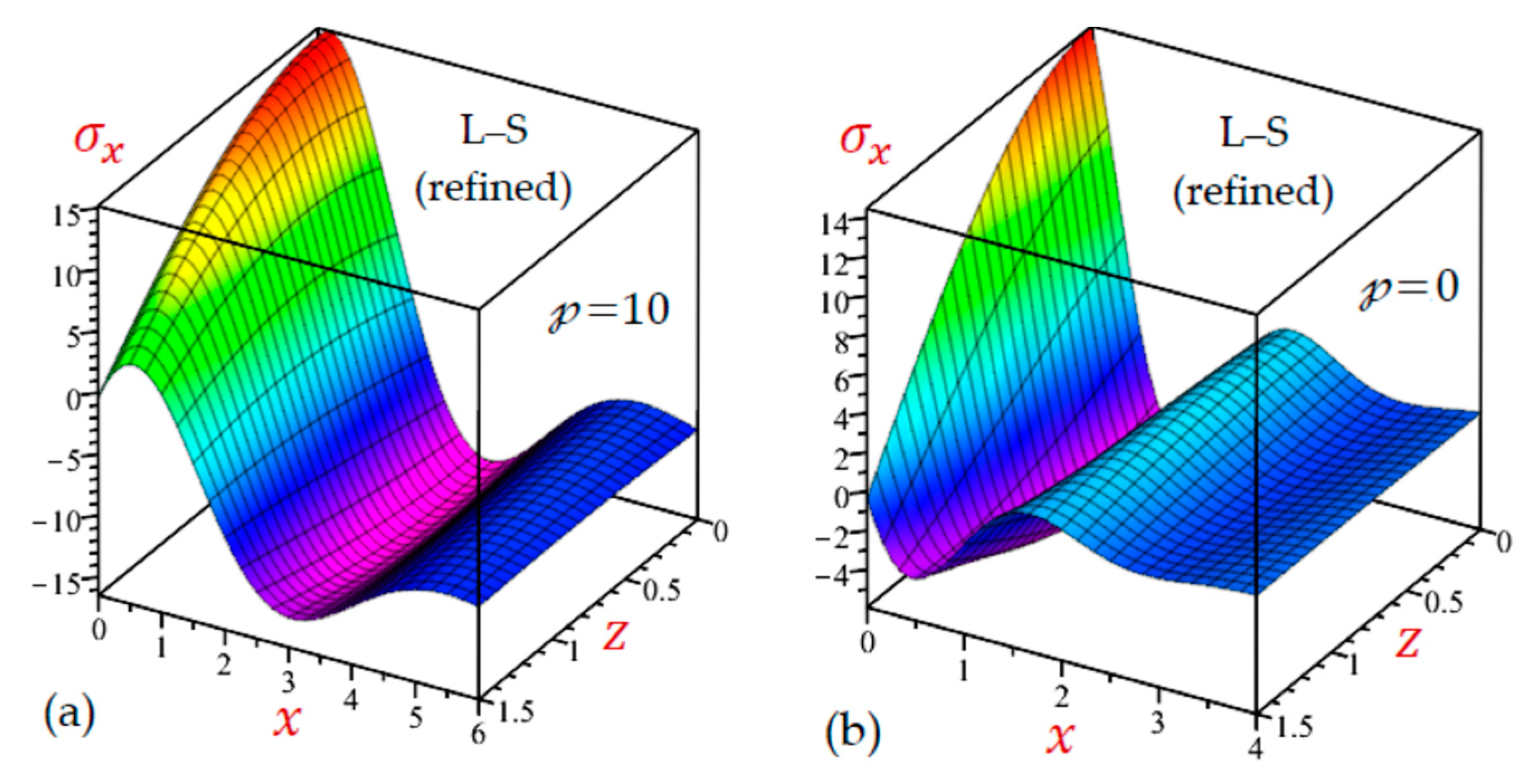
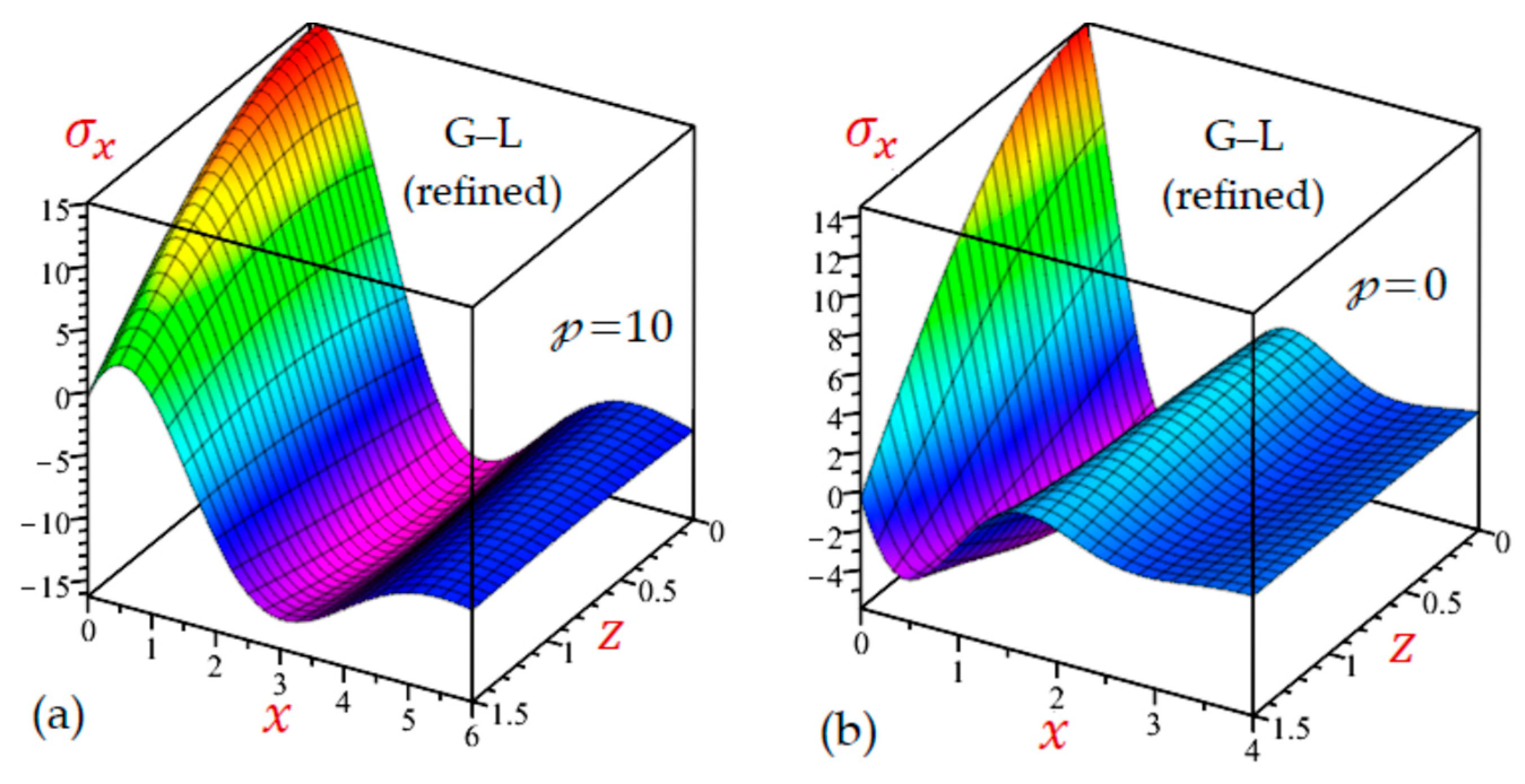
- The outcomes of the refined L–S and G–L theories are decreased as increases and may be unchanged when .
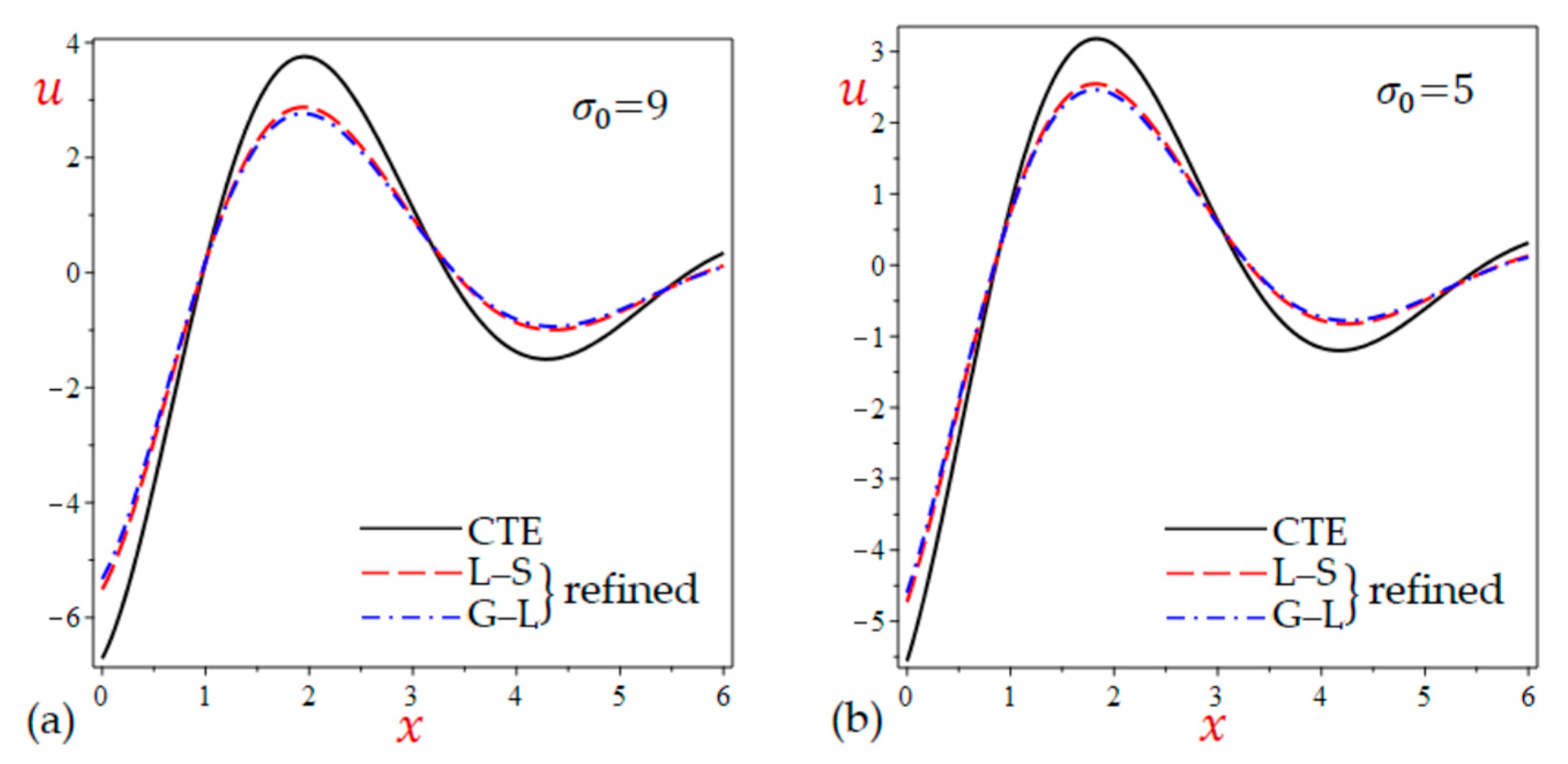
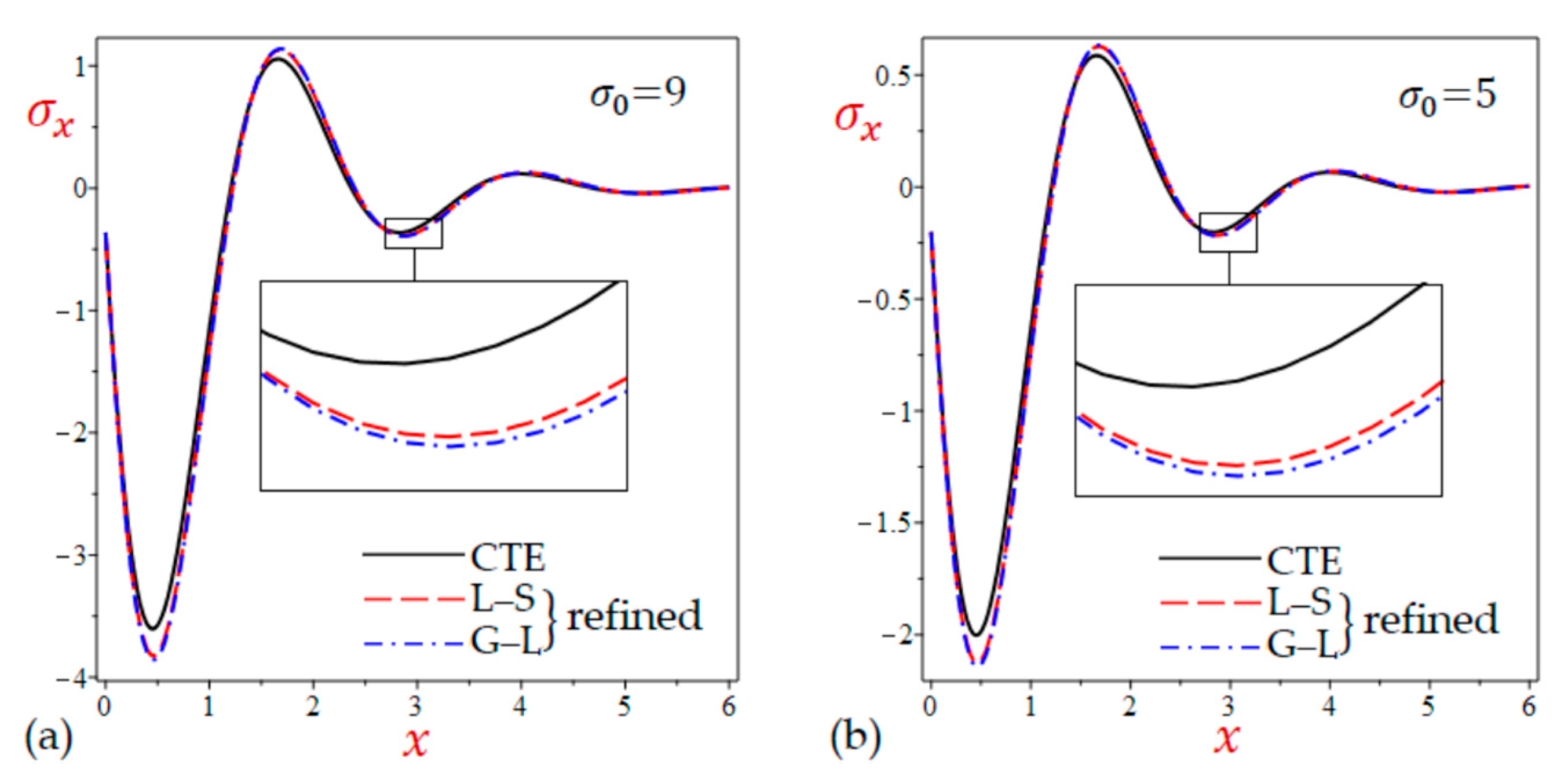
- For both values of the initial stress , the temperature and displacements of the simple and refined L–S theories are greater than the corresponding ones of the simple and refined G–L theories and less than the results of the CTE theory. This is already shown in Table 1 for the half-plane with initial pressure ().
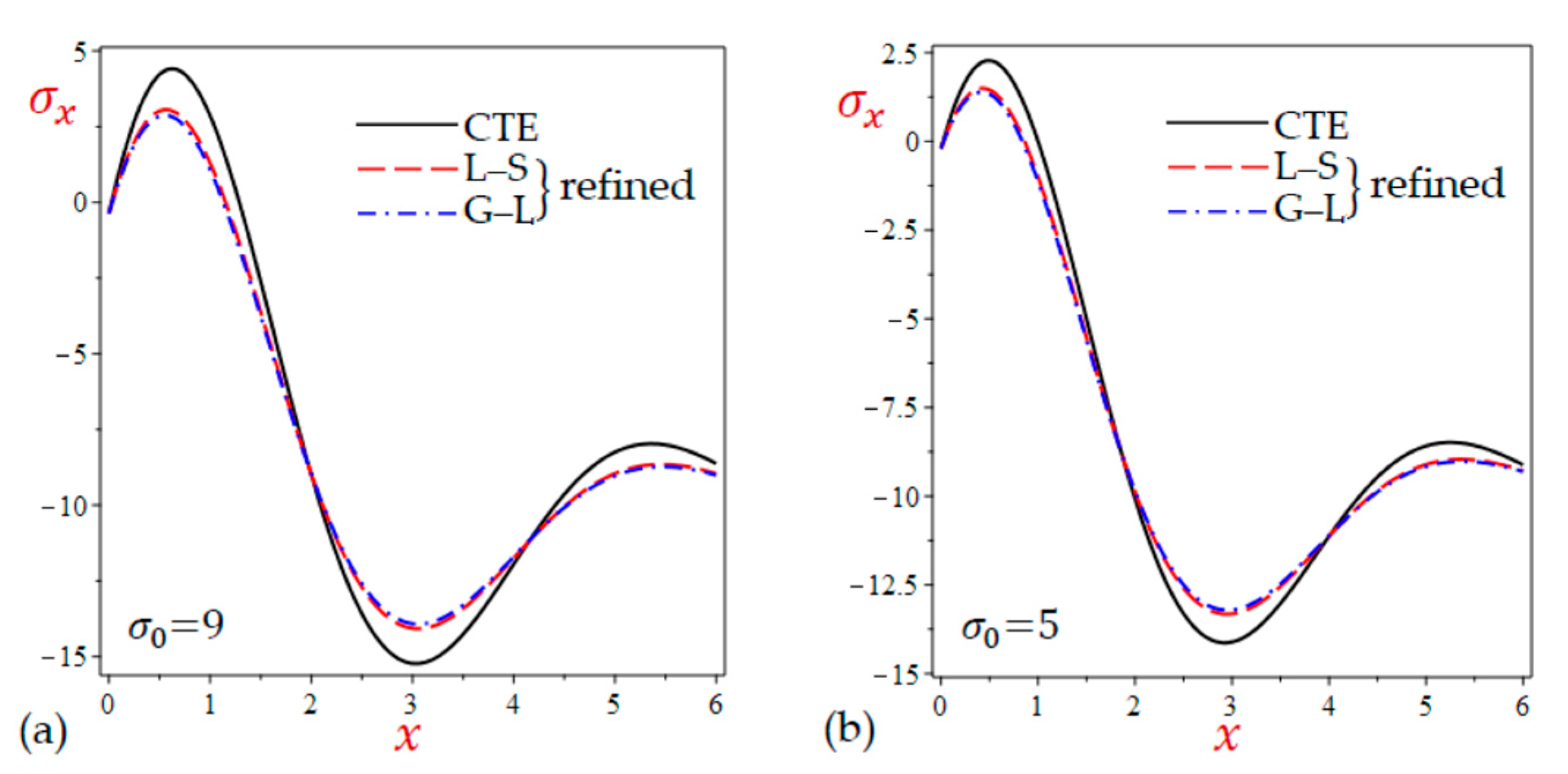
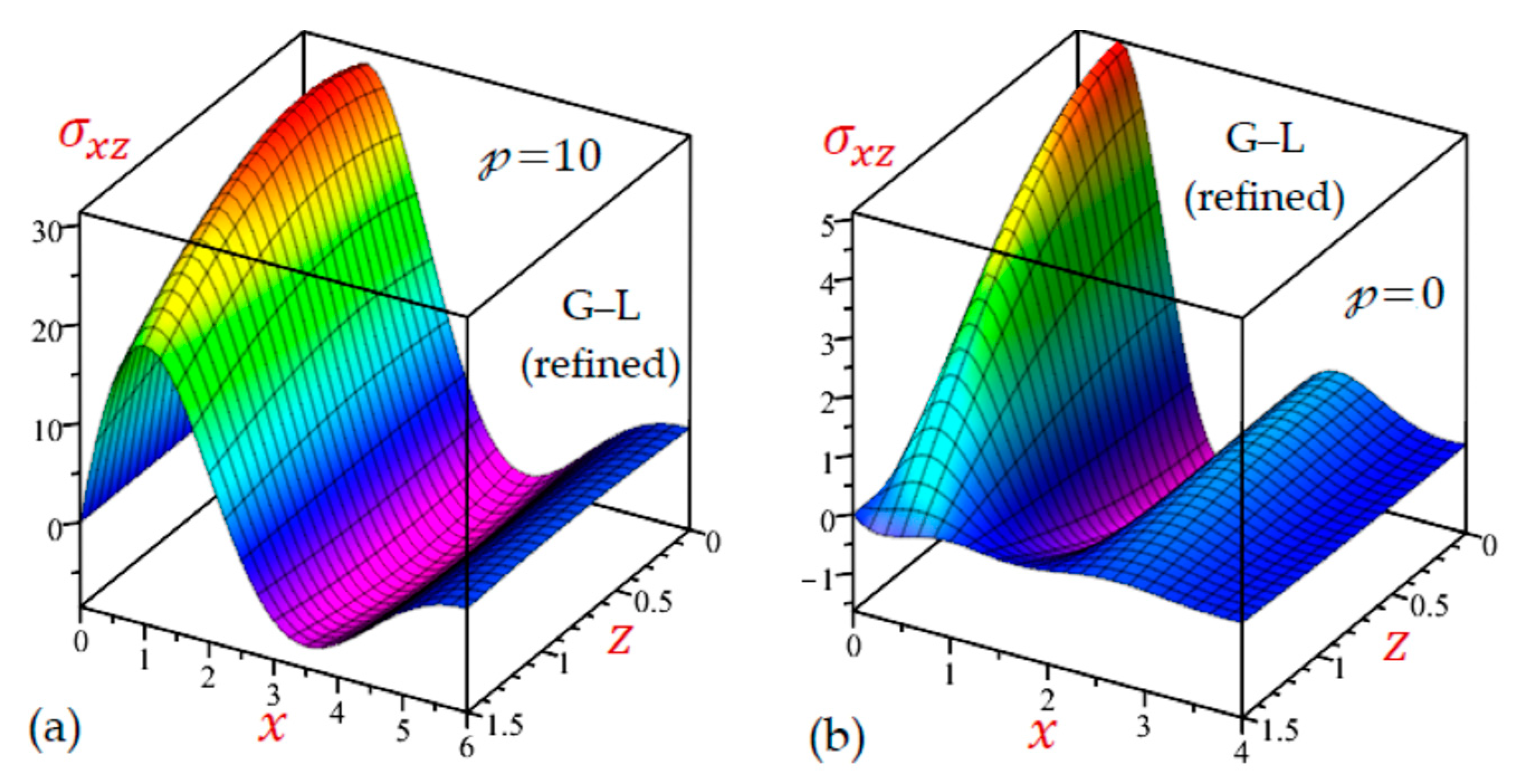
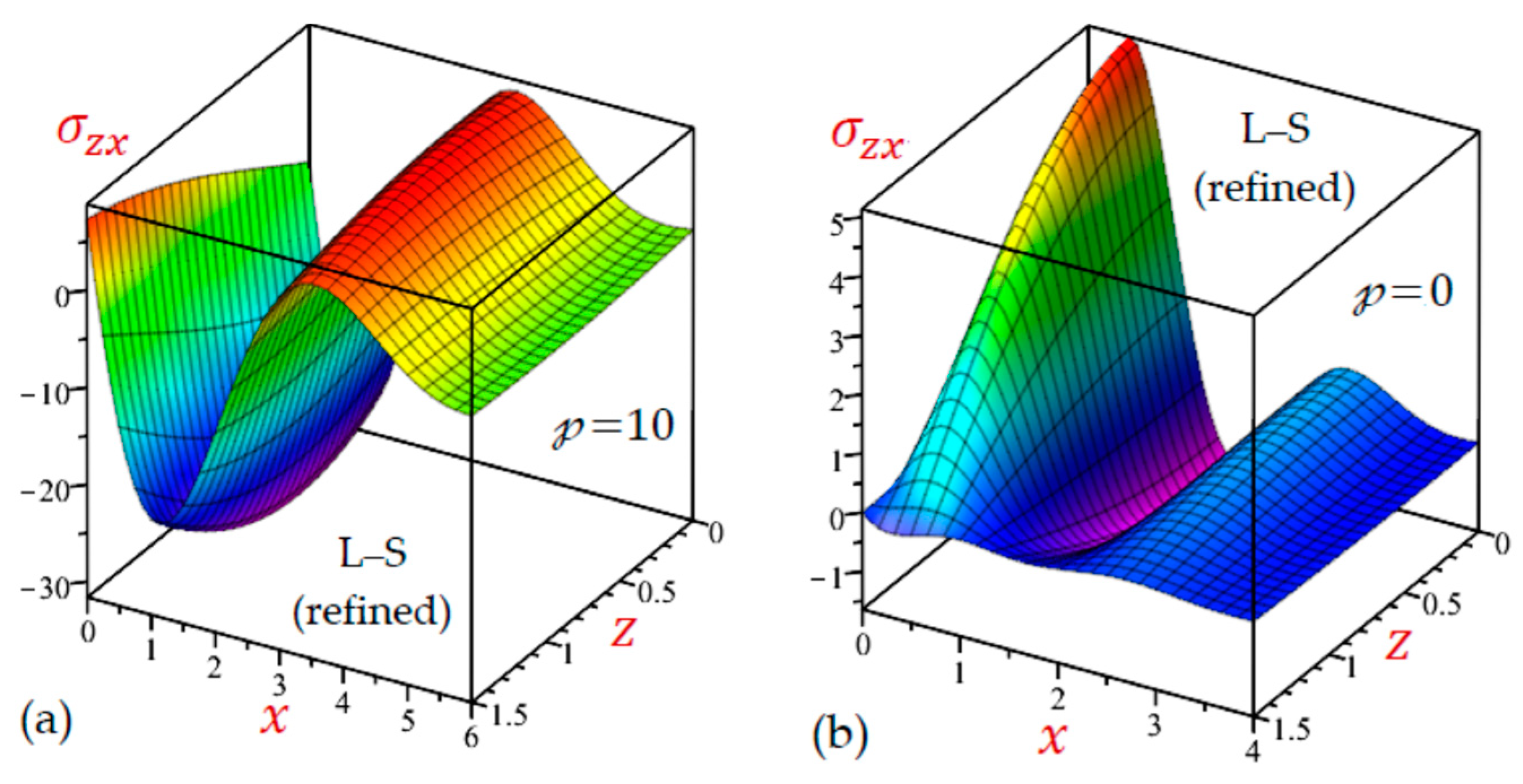
- Table 2 shows that the results of during all theories are very close to each other, especially when . The results of the CTE theory are the largest ones for other stresses and .
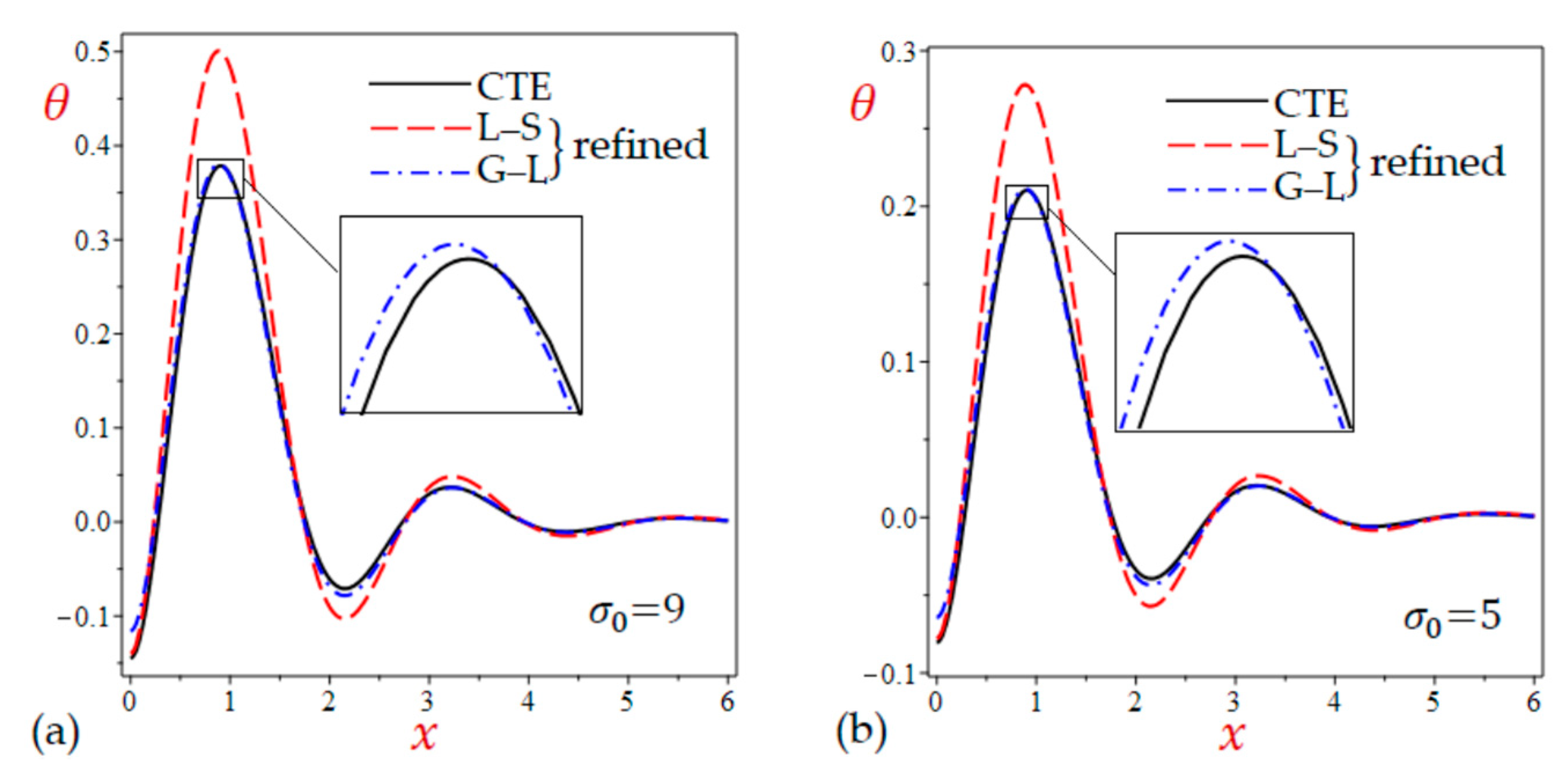
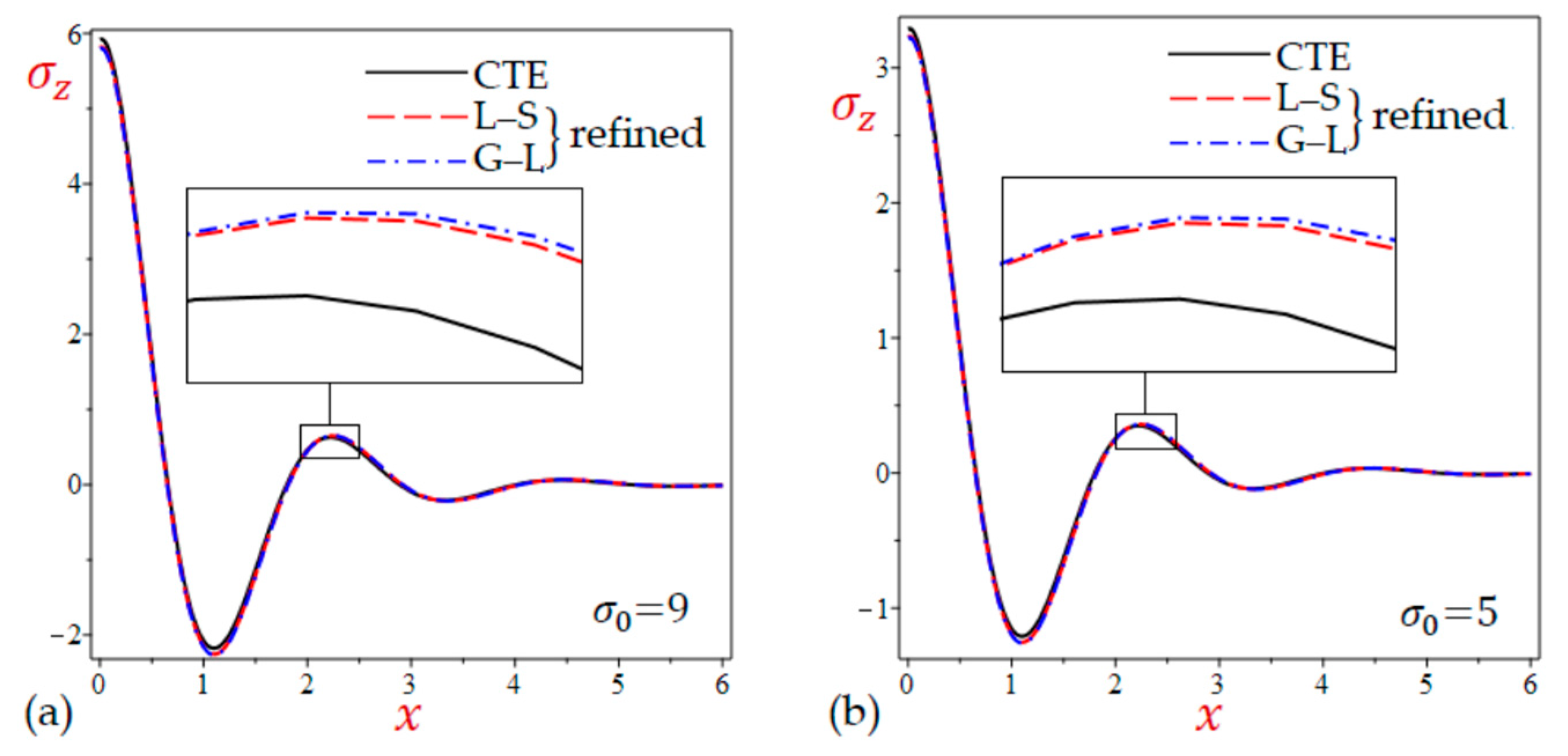
- As shown in Table 3 for the rotating half-space without initial pressure (), the temperatures due to the simple and refined L–S theories are the greatest ones. However, the temperatures due to the simple and refined G–L theories are very close to those due to the CTE theory.
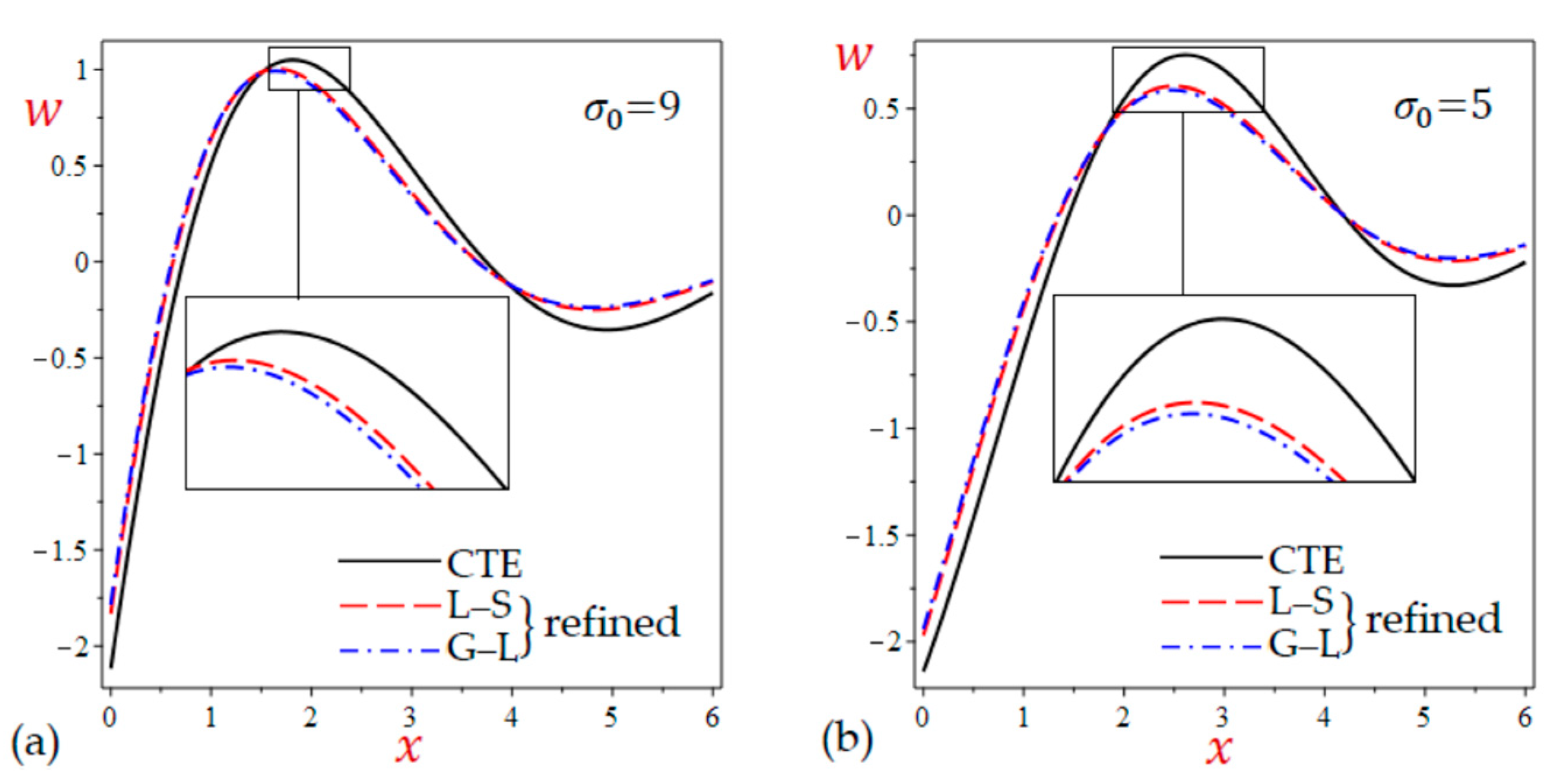
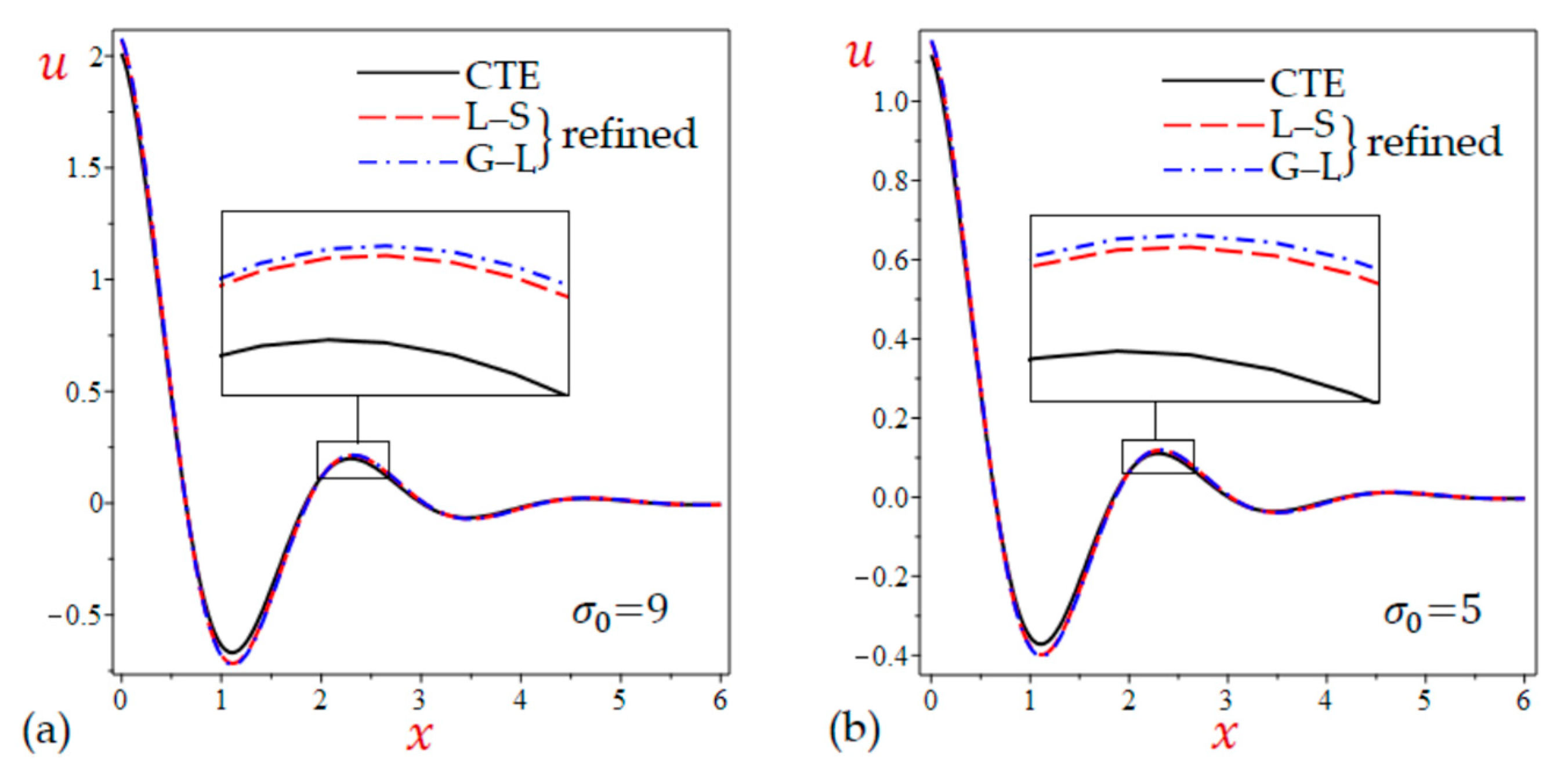
- The results of horizontal displacement due to the simple and refined L–S and G–L theories are very close and both of them are greater than those of the CTE theory.
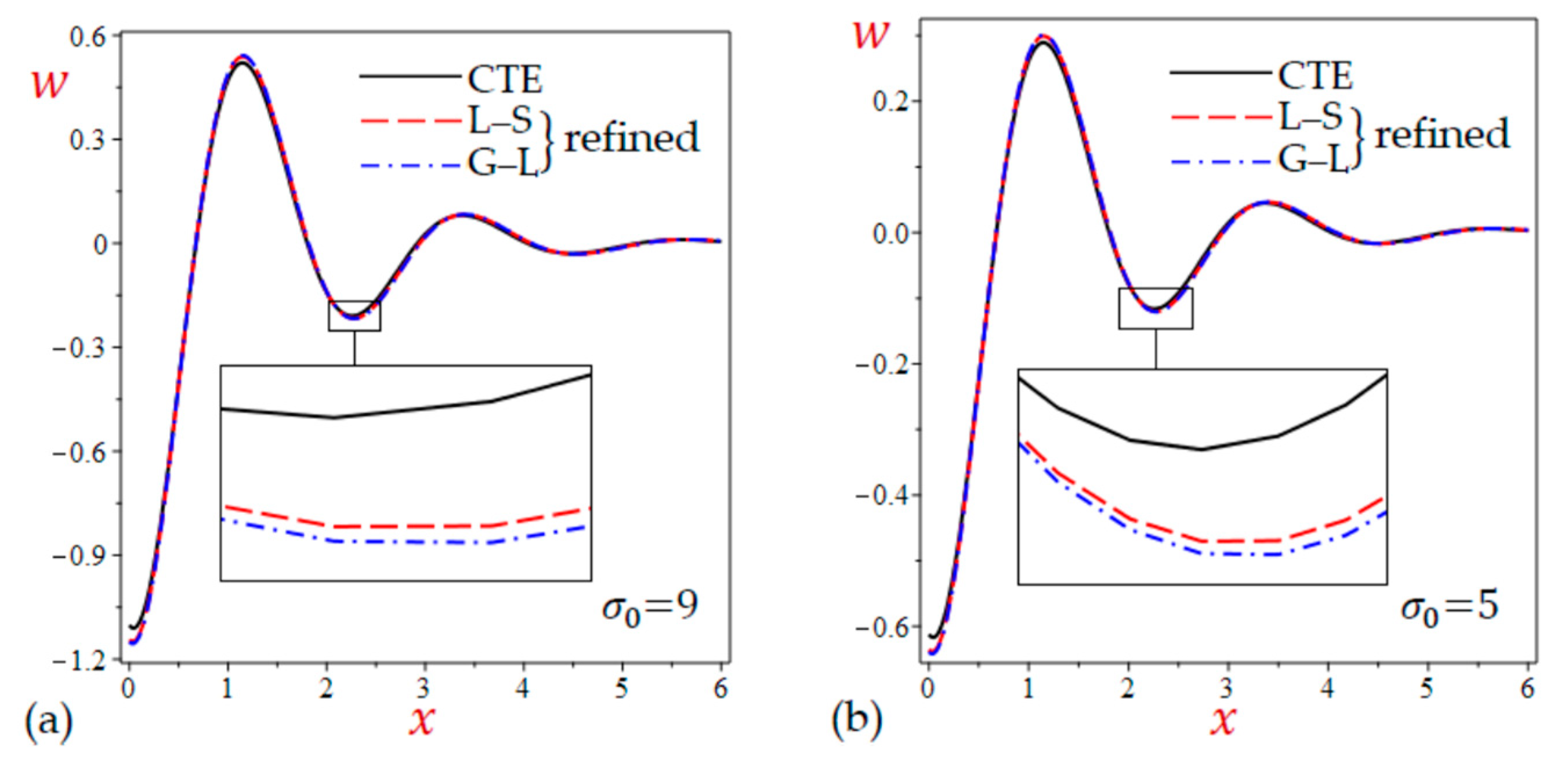
- The results of vertical displacement due to the simple and refined L–S and G–L theories are very close and both of them are smaller than those of the CTE theory.
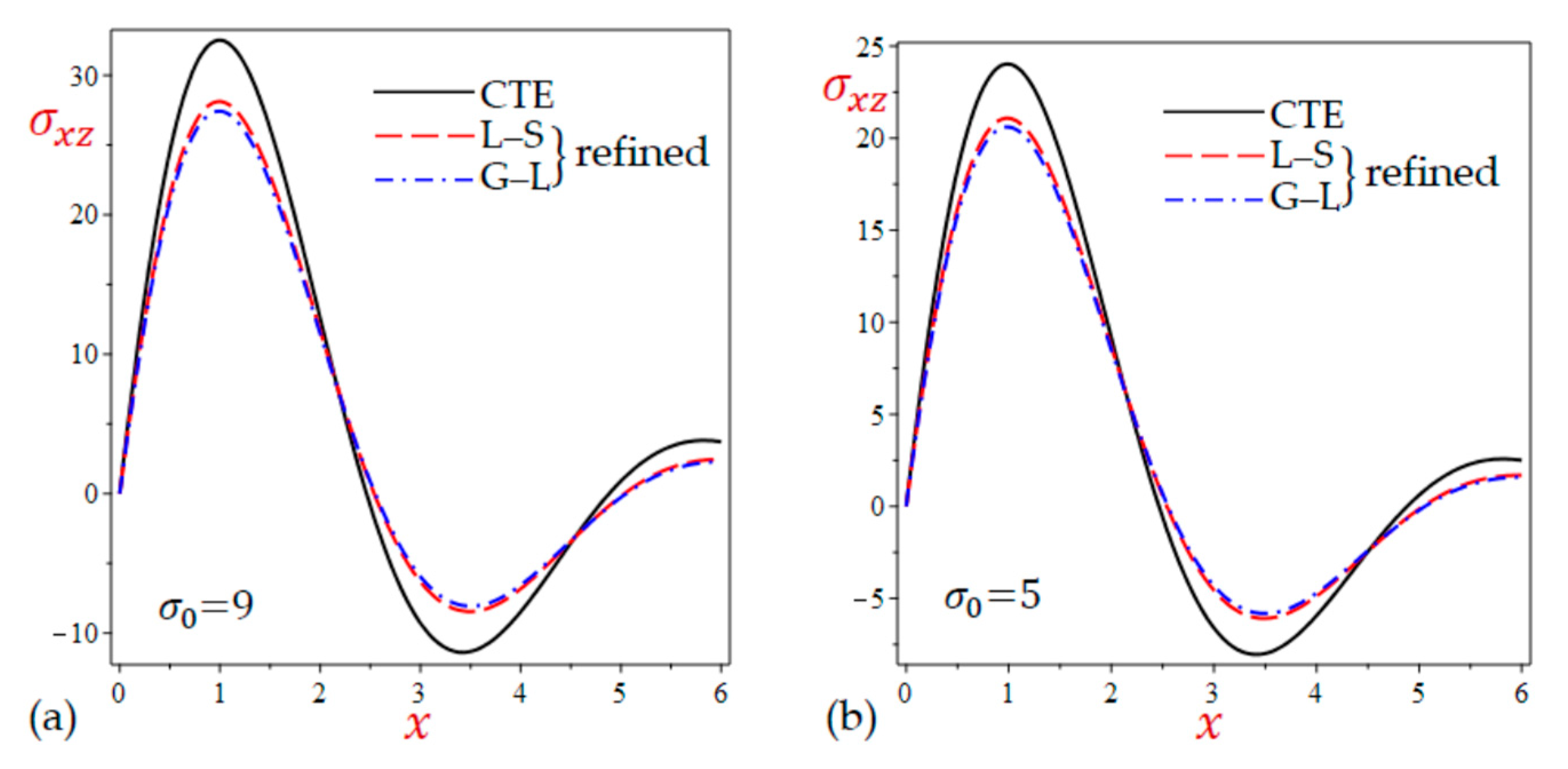
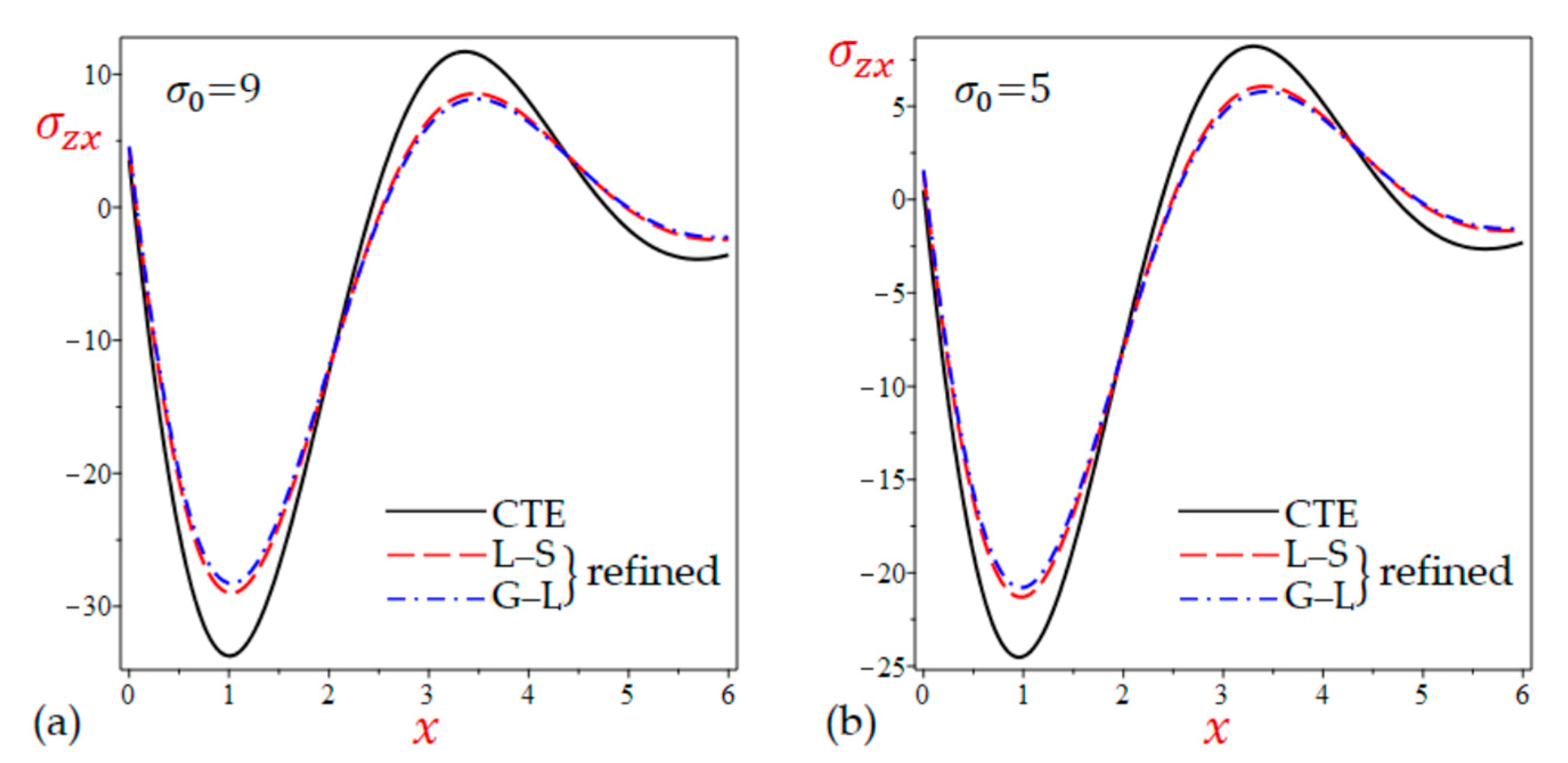
- Table 4 shows that the results of the normal and shear stresses during all theories are very close to each other. The results of the CTE theory are the smallest ones for the transverse normal stress and the largest ones for the transverse shear stress . However, the results of the longitudinal stress are due to the simple and refined G–L theories being the largest ones.
7.2. The 2D Applications
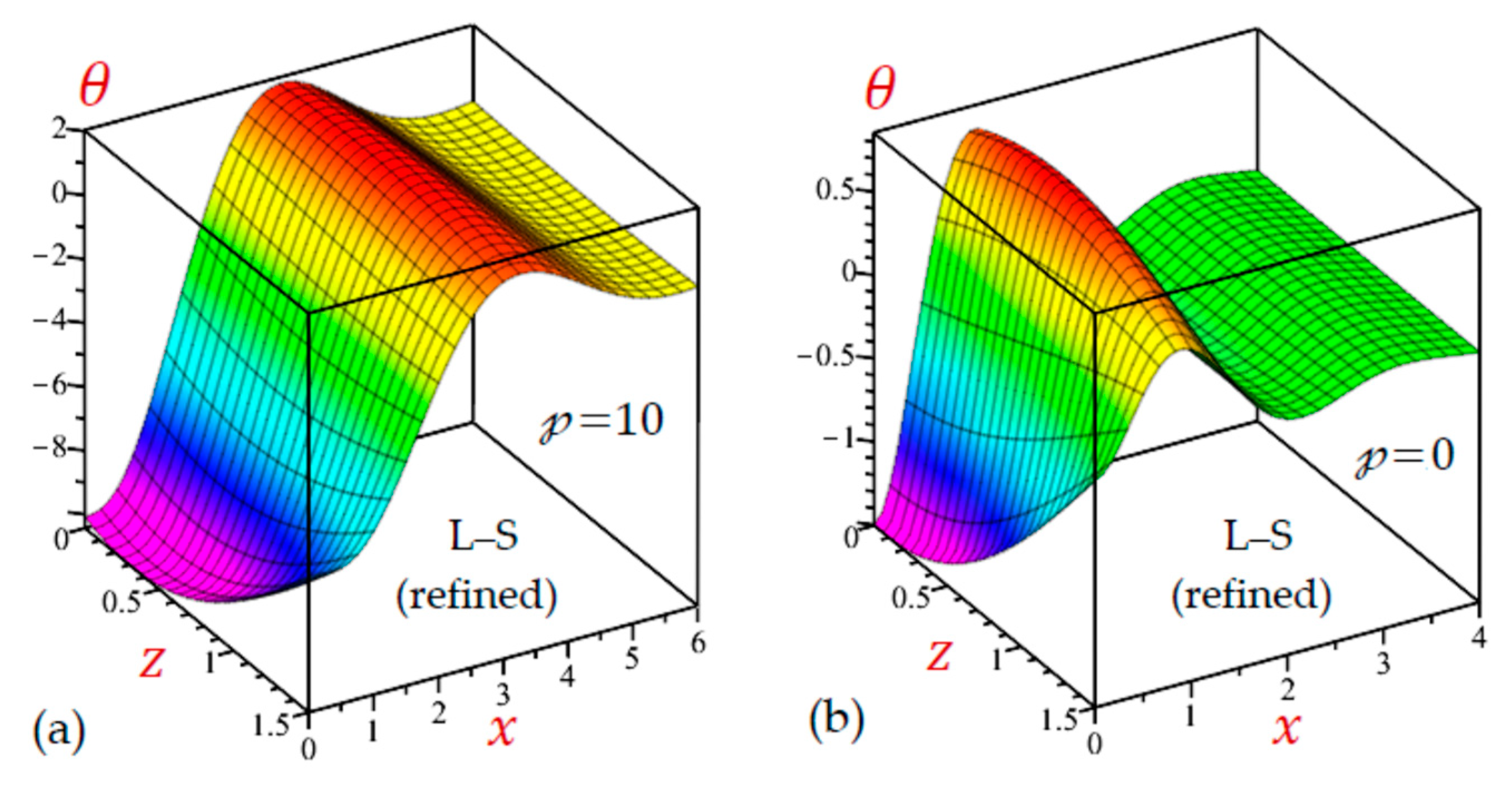
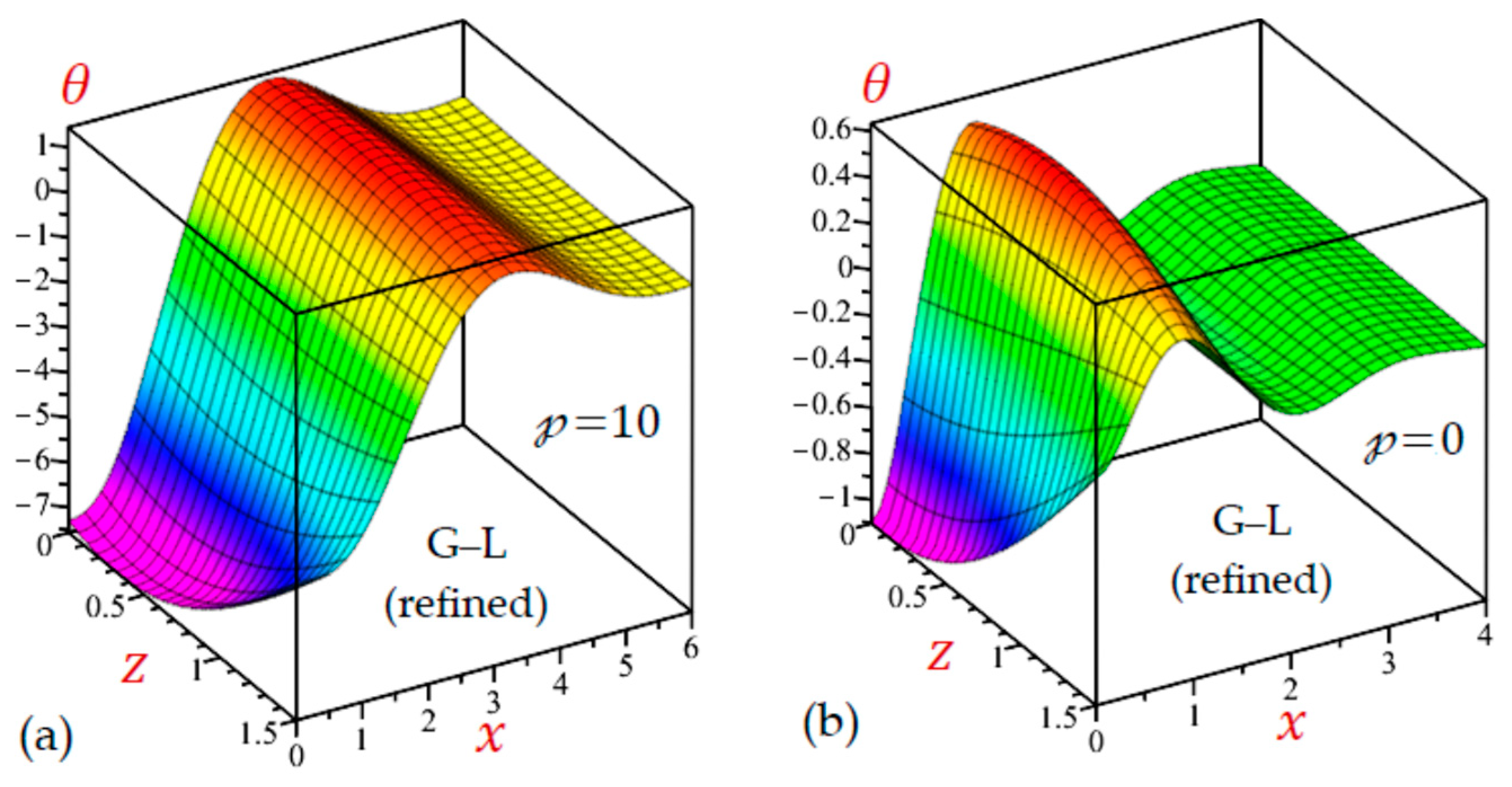
7.3. The 3D Applications
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ailawalia, P.; Narah, N.S. Effect of rotation in a generalized thermoelastic medium with hydrostatic initial stress subjected to ramp-type heating and loading. Int. J. Thermophys. 2009, 30, 2078–2097. [Google Scholar] [CrossRef]
- Ailawalia, P.; Budhiraja, S.; Singh, B. Effect of hydrostatic initial stress and rotation in Green-Naghdi (type III) thermoelastic half-space. Multidiscip. Model. Mater. Struct. 2011, 7, 131–145. [Google Scholar] [CrossRef]
- Abd-Alla, A.M.; Abo-Dahab, S.M. Effect of rotation and initial stress on an infinite generalized magneto-thermoelastic diffusion body with a spherical cavity. J. Therm. Stress. 2012, 35, 892–912. [Google Scholar] [CrossRef]
- Saeed, A.M.; Lotfy, K.; El-Bary, A.; Ahmed, M. Thermoelastic with photogenerated model of rotating microstretch semiconductor medium under the influence of initial stress. Results Phys. 2021, 31, 104967. [Google Scholar] [CrossRef]
- Fahmy, M.A.; El-Shahat, T.M. The effect of initial stress and inhomogeneity on the thermoelastic stresses in a rotating anisotropic solid. Arch. Appl. Mech. 2008, 78, 431–442. [Google Scholar] [CrossRef]
- Ailawalia, P.; Kumar, S.; Pathania, D. Effect of rotation in a generalized thermoelastic medium with two temperature under hydrostatic initial stress and gravity. Multidiscip. Model. Mater. Struct. 2010, 6, 185–205. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, R. Wave propagation in transversely isotropic generalized thermoelastic half-space with voids under initial stress. Multidiscip. Model. Mater. Struct. 2011, 7, 440–468. [Google Scholar] [CrossRef]
- Li, C.; Yu, Y.; Tian, X. Effect of rotation on plane waves of generalized electromagnetothermoelastics with diffusion for a half-space. J. Therm. Stress. 2016, 39, 27–43. [Google Scholar] [CrossRef]
- Deswal, S.; Sheoran, D.; Kalkal, K.K. A two-dimensional half-space problem in an initially stressed rotating medium with micro temperature. Multidiscip. Model. Mater. Struct. 2020, 16, 1313–1335. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y. A Two-Dimensional Generalized Electromagnetothermoelastic Diffusion Problem for a Rotating Half-Space. Math. Probl. Eng. 2014, 2014, 964218. [Google Scholar] [CrossRef]
- Deswal, S.; Hooda, N. A Two-Dimensional Problem for a Rotating Magneto-Thermoelastic Half-Space with Voids and Gravity in a Two-Temperature Generalized Thermoelasticity Theory. J. Mech. 2015, 31, 639–651. [Google Scholar] [CrossRef]
- Bijarnia, R.; Singh, B. Propagation of plane waves in a rotating transversely isotropic two temperature generalized thermoelastic solid half-space with voids. Int. J. Appl. Mech. Eng. 2016, 21, 285–301. [Google Scholar] [CrossRef]
- Das, B.; Chakraborty, S.; Lahiri, A. Generalized magnetothermoelastic interaction for a rotating half space. Int. J. Appl. Comput. Math. 2018, 4, 92. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Abbas, I.A. Effect of rotation on plane waves at the free surface of a fibre-reinforced thermoelastic half-space using the finite element method. Meccanica 2011, 46, 413–421. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–306. [Google Scholar] [CrossRef]
- Abbas, I.A.; Othman, M.I. Generalized thermoelastic interaction in a fiber-reinforced anisotropic half-space under hydrostatic initial stress. J. Vib. Control 2011, 18, 175–182. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M. A two-temperature generalized magneto-thermoelastic formulation for a rotating medium with thermal shock under hydrostatic initial stress. Contin. Mech. Thermodyn. 2020, 32, 883–900. [Google Scholar] [CrossRef]
- Kaur, I.; Lata, P.; Singh, K. Thermomechanical deformation in a transversely isotropic magneto-thermoelastic rotating solids under initial stress. Partial. Differ. Equ. Appl. Math. 2021, 3, 100028. [Google Scholar] [CrossRef]
- Kutbi, M.A.; Zenkour, A.M. Thermomechanical waves in an axisymmetric rotating disk using refined Green–Naghdi models. Int. J. Appl. Mech. 2021, 13, 2150035. [Google Scholar] [CrossRef]
- Lotfy, K.; El-Bary, A.A. Wave propagation of generalized magneto-thermoelastic interactions in an elastic medium under influence of initial stress. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 919–931. [Google Scholar] [CrossRef]
- Deswal, S.; Sheoran, S.S.; Kalkal, K.K. The Effect of Magnetic Field and Initial Stress on Fractional Order Generalized Thermoelastic Half-Space. J. Math. 2013, 2013, 489863. [Google Scholar] [CrossRef]
- Santra, S.; Das, N.C.; Kumar, R.; Lahiri, A. Three-dimensional fractional order generalized thermoelastic problem under the effect of rotation in a half space. J. Therm. Stress. 2015, 38, 309–324. [Google Scholar] [CrossRef]
- Sarkar, N.; Lotfy, K. A 2D problem of time-fractional heat order for two-temperature thermoelasticity under hydrostatic initial stress. Mech. Adv. Mater. Struct. 2018, 25, 279–285. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Zenkour, A.M. On the generalized thermoelasticity problem for an infinite fibre-reinforced thick plate under initial stress. Adv. Appl. Math. Mech. 2014, 6, 783–796. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Zenkour, A.M. Dynamic characteristics of initially stressed viscoelastic microbeams induced by ultra-intense lasers. Indian J. Phys. 2020, 94, 779–788. [Google Scholar] [CrossRef]
- Abouelregal, A.; Zenkour, A.M. Fractional viscoelastic Voigt’s model for initially stressed microbeams induced by ultrashort laser heat source. Waves Random Complex Media 2020, 30, 687–703. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1991, 432, 171–194. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. On undamped heat waves in an elastic solid. J. Therm. Stress. 1992, 15, 253–264. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Chattopadhyay, N.C.; Biswas, M. Study of thermal stress generated in an elastic half-space in the context of generalized thermoelasticity theory. J. Therm. Stress. 2007, 30, 107–124. [Google Scholar] [CrossRef]
- Othman, M.I.; Song, Y. Reflection of plane waves from an elastic solid half-space under hydrostatic initial stress without energy dissipation. Int. J. Solids Struct. 2007, 44, 5651–5664. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Atwa, S.Y. Thermoelastic plane waves for an elastic solid half-space under hydrostatic initial stress of type III. Meccanica 2011, 47, 1337–1347. [Google Scholar] [CrossRef]
- Abbas, I.A.; Zenkour, A.M. The effect of rotation and initial stress on thermal shock problem for a fiber-reinforced anisotropic half-space using green-naghdi theory. J. Comput. Theor. Nanosci. 2014, 11, 331–338. [Google Scholar] [CrossRef]
- Said, S.M. Deformation of a rotating two-temperature generalized-magneto thermoelastic medium with internal heat source due to hydrostatic initial stress. Meccanica 2015, 50, 2077–2091. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Zidan, M.E.M.; Hilal, M.I.M. The effect of initial stress on thermoelastic rotating medium with voids due to laser pulse heating with energy dissipation. J. Therm. Stress. 2015, 38, 835–853. [Google Scholar] [CrossRef]
- Xiong, Q.-L.; Tian, X. Effect of initial stress on a fiber-reinforced thermoelastic porous media without energy dissipation. Transp. Porous Media 2016, 111, 81–95. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abd-Alla, A.M.; Alotaibi, H.A. On an influence of thermal stresses and magnetic field in thermoelastic half-space without energy dissipation. J. Therm. Stress. 2017, 40, 267–280. [Google Scholar] [CrossRef]
- Singh, B. Effect of hydrostatic initial stresses on waves in a thermoelastic solid half-space. Appl. Math. Comput. 2007, 198, 494–505. [Google Scholar] [CrossRef]
- Abo-Dahab, S.; Mohamed, R. Influence of magnetic field and hydrostatic initial stress on wave reflection from a generalized thermoelastic solid half-space. J. Vib. Control 2010, 16, 685–699. [Google Scholar] [CrossRef]
- Sarkar, N.; Atwa, S.Y.; Othman, M.I.A. The effect of hydrostatic initial stress on the plane waves in a fiber-reinforced magneto-thermoelastic medium with fractional derivative heat transfer. Int. Appl. Mech. 2016, 52, 203–216. [Google Scholar] [CrossRef]
- Singh, M.C.; Chakraborty, N. Reflection of a plane magneto-thermoelastic wave at the boundary of a solid half-space in presence of initial stress. Appl. Math. Model. 2014, 39, 1409–1421. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Abo-Dahab, S.M.; Alsebaey, O.N.S. Reflection of plane waves from a rotating magneto-thermoelastic medium with two-temperature and initial stress under three theories. Mech. Mech. Eng. 2017, 21, 217–232. [Google Scholar]
- Othman, M.I.A.; Eraki, E.E.M. Generalized magneto-thermoelastic half-space with diffusion under initial stress using three-phase-lag model. Mech. Based Des. Struct. Mach. 2017, 45, 145–159. [Google Scholar] [CrossRef]
- Yuan, X.; Jiang, Q. Reflection of plane waves from rotating pyroelectric half-space under initial stresses. ZAMM J. Appl. Math. Mech. Z. Für Angew. Math. Mech. 2017, 97, 365–374. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Rida, S.Z.; Mohamed, R.A.; Kilany, A.A. Rotation, initial stress, gravity and electromagnetic field effect on p wave reflection from stress-free surface elastic half-space with voids under three thermoelastic models. Mech. Mech. Eng. 2018, 22, 313–328. [Google Scholar] [CrossRef]
- Zenkour, A.M. Thermoelastic diffusion problem for a half-space due to a refined dual-phase-lag Green-Naghdi model. J. Ocean Eng. Sci. 2020, 5, 214–222. [Google Scholar] [CrossRef]
- Zenkour, A.M. Wave propagation of a gravitated piezo-thermoelastic half-space via a refined multi-phase-lags theory. Mech. Adv. Mater. Struct. 2020, 27, 1923–1934. [Google Scholar] [CrossRef]
- Kutbi, M.A.; Zenkour, A.M. Refined dual-phase-lag Green–Naghdi models for thermoelastic diffusion in an infinite medium. Waves Random Complex Media 2022, 32, 947–967. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Refined Lord–Shulman theory for 1d response of skin tissue under ramp-type heat. Materials 2022, 15, 6292. [Google Scholar] [CrossRef]
- Zenkour, A.M. Thermal diffusion of an unbounded solid with a spherical cavity via refined three-phase-lag Green–Naghdi models. Indian J. Phys. 2022, 96, 1087–1104. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoclasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]






| Theory | |||||||
|---|---|---|---|---|---|---|---|
| CTE | 1.890364 | 2.996973 | 1.847246 | 1.365965 | 2.409226 | 1.434999 | |
| L–S | simple | 1.832256 | 2.604654 | 1.462894 | 1.346071 | 2.090542 | 1.138687 |
| 1.822702 | 2.563813 | 1.423560 | 1.341577 | 2.056822 | 1.107933 | ||
| 1.821655 | 2.560139 | 1.419911 | 1.341048 | 2.053746 | 1.105058 | ||
| 1.821568 | 2.559885 | 1.419648 | 1.341003 | 2.053531 | 1.104849 | ||
| 1.821562 | 2.559872 | 1.419633 | 1.340999 | 2.053519 | 1.104837 | ||
| G–L | simple | 1.361227 | 2.563666 | 1.418260 | 0.999593 | 2.056354 | 1.104261 |
| 1.296335 | 2.514292 | 1.369209 | 0.953542 | 2.015296 | 1.065907 | ||
| 1.289281 | 2.509351 | 1.364012 | 0.948486 | 2.011112 | 1.061815 | ||
| 1.288682 | 2.508974 | 1.363583 | 0.948053 | 2.010785 | 1.061475 | ||
| 1.288642 | 2.508951 | 1.363554 | 0.948024 | 2.010765 | 1.061453 | ||
| Theory | |||||||
|---|---|---|---|---|---|---|---|
| CTE | 4.223049 | 5.080442 | 9.613937 | 2.280856 | 0.804530 | 7.509281 | |
| L–S | simple | 3.158542 | 5.097106 | 8.721411 | 1.553304 | 0.934364 | 7.011773 |
| 3.032111 | 5.089880 | 8.615998 | 1.463906 | 0.942645 | 6.950218 | ||
| 3.019749 | 5.088609 | 8.605439 | 1.455013 | 0.943041 | 6.943900 | ||
| 3.018817 | 5.088472 | 8.604620 | 1.454332 | 0.943040 | 6.943399 | ||
| 3.018761 | 5.088461 | 8.604569 | 1.454291 | 0.943038 | 6.943367 | ||
| G–L | simple | 3.027316 | 5.096085 | 8.568865 | 1.462244 | 0.948727 | 6.913201 |
| 2.867656 | 5.085937 | 8.424122 | 1.348946 | 0.958633 | 6.824960 | ||
| 2.849907 | 5.083973 | 8.407134 | 1.336130 | 0.959136 | 6.814227 | ||
| 2.848387 | 5.083733 | 8.405606 | 1.335016 | 0.959128 | 6.813234 | ||
| 2.848284 | 5.083712 | 8.405498 | 1.334939 | 0.959124 | 6.813161 | ||
| Theory | |||||||
|---|---|---|---|---|---|---|---|
| CTE | 0.630417 | 0.279556 | 1.603015 | 0.350231 | 0.155309 | 0.890564 | |
| L–S | simple | 0.819987 | 0.282788 | 1.574989 | 0.455548 | 0.157104 | 0.874994 |
| 0.848295 | 0.282858 | 1.571541 | 0.471275 | 0.157143 | 0.873078 | ||
| 0.851151 | 0.282830 | 1.571224 | 0.472862 | 0.157128 | 0.872902 | ||
| 0.851368 | 0.282825 | 1.571202 | 0.472982 | 0.157125 | 0.872890 | ||
| 0.851381 | 0.282824 | 1.571200 | 0.472989 | 0.157125 | 0.872889 | ||
| G–L | simple | 0.629805 | 0.283580 | 1.571955 | 0.349892 | 0.157544 | 0.873308 |
| 0.629652 | 0.283818 | 1.567726 | 0.349807 | 0.157677 | 0.870959 | ||
| 0.629666 | 0.283804 | 1.567293 | 0.349814 | 0.157669 | 0.870718 | ||
| 0.629670 | 0.283800 | 1.567260 | 0.349817 | 0.157666 | 0.870699 | ||
| 0.629671 | 0.283799 | 1.567258 | 0.349817 | 0.157666 | 0.870699 | ||
| Theory | |||||||
|---|---|---|---|---|---|---|---|
| CTE | 0.677300 | 0.445521 | 2.406474 | 0.376278 | 0.247511 | 1.336930 | |
| L–S | simple | 0.761076 | 0.449179 | 2.380849 | 0.422820 | 0.249544 | 1.322694 |
| 0.774165 | 0.450059 | 2.378418 | 0.430092 | 0.250033 | 1.321343 | ||
| 0.775488 | 0.450134 | 2.378250 | 0.430827 | 0.250075 | 1.321250 | ||
| 0.775587 | 0.450138 | 2.378243 | 0.430882 | 0.250077 | 1.321246 | ||
| 0.775593 | 0.450138 | 2.378243 | 0.430885 | 0.250077 | 1.321246 | ||
| G–L | simple | 0.769812 | 0.448273 | 2.378538 | 0.427673 | 0.249040 | 1.321410 |
| 0.785880 | 0.448914 | 2.375733 | 0.436600 | 0.249397 | 1.319852 | ||
| 0.787678 | 0.448944 | 2.375531 | 0.437599 | 0.249413 | 1.319739 | ||
| 0.787827 | 0.448942 | 2.375522 | 0.437682 | 0.249412 | 1.319735 | ||
| 0.787837 | 0.448941 | 2.375522 | 0.437687 | 0.249412 | 1.319735 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljadani, M.H.; Zenkour, A.M. Effect of Hydrostatic Initial Stress on a Rotating Half-Space in the Context of a Two-Relaxation Power-Law Model. Mathematics 2022, 10, 4727. https://doi.org/10.3390/math10244727
Aljadani MH, Zenkour AM. Effect of Hydrostatic Initial Stress on a Rotating Half-Space in the Context of a Two-Relaxation Power-Law Model. Mathematics. 2022; 10(24):4727. https://doi.org/10.3390/math10244727
Chicago/Turabian StyleAljadani, Maryam H., and Ashraf M. Zenkour. 2022. "Effect of Hydrostatic Initial Stress on a Rotating Half-Space in the Context of a Two-Relaxation Power-Law Model" Mathematics 10, no. 24: 4727. https://doi.org/10.3390/math10244727
APA StyleAljadani, M. H., & Zenkour, A. M. (2022). Effect of Hydrostatic Initial Stress on a Rotating Half-Space in the Context of a Two-Relaxation Power-Law Model. Mathematics, 10(24), 4727. https://doi.org/10.3390/math10244727







