Abstract
Many surveys are performed using non-probability methods such as web surveys, social networks surveys, or opt-in panels. The estimates made from these data sources are usually biased and must be adjusted to make them representative of the target population. Techniques to mitigate this selection bias in non-probability samples often involve calibration, propensity score adjustment, or statistical matching. In this article, we consider the problem of estimating the finite population distribution function in the context of non-probability surveys and show how some methodologies formulated for linear parameters can be adapted to this functional parameter, both theoretically and empirically, thus enhancing the accuracy and efficiency of the estimates made.
MSC:
62D05
1. Introduction
Distribution function estimation is an important topic in survey research. This approach offers valuable benefits in the context of probability surveys and has been the focus of much research attention in recent years. It is especially useful when the underlying goal is to determine the proportion of values of a study variable that are less than or equal to a certain value. For example, knowledge of the distribution function makes it possible to obtain the reliability function, which is commonly used in life data analysis and reliability engineering []. Furthermore, the distribution function allows us to examine whether two samples originate from the same population [].
Additionally, the finite population distribution function can be used to calculate certain parameters, such as population quantiles. In several areas of study [,,], quantiles are of special interest. For example, rates of extreme pediatric obesity are defined as the body mass index at or above the 99th percentile []. In another area, that of ozone concentrations, the 5th percentile is a measure of the baseline condition, while the 95th reflects peak concentration levels []. In economics, some variables, such as income, have skewed distributions and in this case quantiles provide a more suitable measure of location than the mean [,]. Also in this field, quantiles allow us to obtain measures such as the poverty line and the poverty gap [,], as well as inequality parameters indicators such as the headcount index, which measures the proportion of individuals classified as poor within a given population []. Other analyses of inequality, such as those focusing on wages or income distribution, also require measures based on percentile ratios []. In these cases, estimating the distribution function is also more useful than calculating totals and means []. In view of these considerations, some studies have focused on the auxiliary population information available at the estimation stage to gain more accurate values for the distribution function and quantiles [,,,]. One means of incorporating auxiliary information to develop new estimators of the distribution function is to employ the calibration method, which was originally designed to estimate the total population []. An extensive body of research has been conducted in this area, and various implementations of the calibration approach have been applied in the probability survey context to obtain estimators of the distribution function and the quantiles [,,,,,,,,]. The use of calibration techniques has also been considered for estimating the distribution function when a probability survey is subject to non-response [].
As part of the global commitment to fight poverty and social exclusion, many government agencies wish to know the proportion of the population living below the poverty line, in order to monitor the effectiveness of their policies []. One way to obtain this information is to conduct probabilistic surveys, based on representative samples of the target population. The aim of survey sampling theory is to maximize the reliability of the estimates thus obtained.
For a sample to be considered probabilistic and therefore valid for drawing inferences regarding the population, it must be selected under the assumption that all the individuals in the target population have a known and non-null probability of inclusion.
In recent years, alternative data sources to probabilistic samples have been considered, such as big data and web surveys. These approaches offer certain advantages over traditional probability sampling: estimates in near real time may be obtained, data access is easier, and data collection costs are lower. In these non-traditional methods, the data generating process is different and the subsequent analysis is based on non-probability samples. Despite the above advantages, this method also presents serious issues, especially the fact that the selection procedure for the units included in the sample is unknown and so the estimates obtained may be biased, since the sample itself does not necessarily provide a valid picture of the entire population. In other words, the sample is potentially exposed to self-selection bias [,].
Many studies of survey sampling have been undertaken to reduce selection bias in the methods used to estimate population totals and means, and this research has been reviewed in [,,,,,], among others. The methods considered include inverse probability weighting [,], inverse sampling [], mass imputation [], doubly robust methods [], kernel smoothing methods [], statistical matching combined with propensity score adjustment [], and calibration combined with propensity score adjustment [,]. However, despite the extensive literature available on using calibration techniques to estimate the distribution function and the population mean under conditions of self-selection bias, little attention has been paid to the development of efficient methods for estimating the population distribution function under these conditions.
To address this research gap, we propose a general framework for drawing statistical inferences for the distribution function with non-probability survey samples when auxiliary information is available. We discuss different methods of adjusting for self-selection bias, depending on the type of information available, applying calibration, propensity score, and statistical matching techniques.
The rest of the paper is organized as follows: in Section 2, we review the estimation of the distribution function from probability and non-probability samples, in order to establish the basic framework and the notation employed. In Section 3, we then propose several estimators for the distribution function, based on calibration, propensity score adjustment (PSA) and statistical matching (SM), taking into consideration that the non-smooth nature of the finite population distribution function produces certain complexities, which are resolved in different ways. The properties of the proposed estimators are described in Section 4, after which we present the results obtained from the simulation studies performed with these estimators. In the final section, we summarize the main conclusions drawn and suggest possible lines of further research in this area.
2. Basic Setup for Estimating the Distribution Function
Let U denote a finite population of size N, . Let be a self-selected sample of size , self-selected from U. Let y be the variable of interest in the survey estimation. We assume that is known for all sample units. Our goal is to estimate the distribution function for the study variable y, which can be defined as follows:
where denotes the Heaviside function, given by:
In the absence of auxiliary information, the distribution function can be estimated by the naive estimator, defined by
If the convenience sample suffers from selection bias, the above estimator will provide biased results.
Let R be an indicator variable of an element being in , such that
If we know , the error of will be:
with and being .
By applying the expectation of the mean difference, we obtain the selection bias of the estimator, as follows:
where denotes the expectation with respect to the random mechanism for .
The mean squared error is obtained by:
because
Therefore, a non-probability sampling design with means that the analysis results are subject to selection bias. This is the main problem addressed in our study.
3. Proposed Estimators
The key to successful weighting to eliminate bias in self-selection surveys lies in the use of appropriate auxiliary information. To address this question, let us consider J auxiliary variables and let be the vector of auxiliary variables at unit k.
We distinguish three different cases, called InfoTP, InfoES, and InfoES, depending on the information at hand ([])
- InfoTP: Only the population vector totals of the auxiliary variables, , are known.
- InfoES: Information is available at the level of a probability sample conducted on the same target population as the non-probability survey, with good coverage and high response rates. The vector of auxiliary variables is known for every unit in this reference sample.
- InfoEP: Information is available at the level of the population U: the vector of auxiliary variables is known for every .
Below, we consider various adjustment methods, depending on the type of information available.
3.1. InfoTP
The calibration method, originally developed by Deville and Särndall [] for the estimation of totals, can be adapted to estimate the distribution function. This approach enables us to incorporate the auxiliary information available through the auxiliary vector in several ways [,,,,,].
In the case of InfoTP, the calibration can be performed on the totals: given a pseudo-distance , and denoting , we seek new calibrated weights that are the solution to the following minimization problem
subject to
The resulting calibrated estimator of the distribution function is given by:
Ref. [] proposes a family of pseudo-distance with which to develop calibration estimators. One of the distances proposed is the chi-square distance given by
where is positive weights that are usually assumed as uniform although unequal weights are sometimes preferred.
The resulting calibrated weights with the minimization of (7) subject to the conditions (5) are given by:
where
In the estimation of totals and means, previous research has shown that the exclusive use of calibration fails to eliminate self-selection bias if this approach is not combined with other methods, such as propensity score adjustment (PSA) [,]. Thus, in terms of bias reduction, the results of the calibration and PSA combination clearly surpass those obtained with only calibration weighting [].
In order to incorporate methods such as PSA and to develop new estimators that overcome the problems met with the estimator, we consider other scenarios as follows.
3.2. InfoES
Let be a probability sample of size selected from U under a probability sampling design in which is the first-order inclusion probability for individual k. The covariates are common to both samples, but we only have measurements of the variable of interest y for the individuals in the convenience sample. The original design weight of the individual k in the reference (probability) sample is denoted by .
First, we consider a calibration method for reweighting based on the proposal given in [], calibrating from the pseudo-variable:
The new weights are obtained by minimizing the chi-square distance (7) subject to the following conditions:
where for are points chosen arbitrarily and where we assume that and are positive constants.
The resulting calibrated estimator of the distribution function is given by:
in which the calibrated weights are given by:
with
and
The calibrated weights (13) and the weights for the samples and , respectively, give the same estimates for the distribution function of the pseudo-variable g, when evaluated over the set of points .
In the case of InfoES information, the most popular adjustment method in non-probability settings is propensity score adjustment [,,,,,]. This method, developed by [], can be used to estimate the distribution function, as described below.
Under PSA, it is assumed that each element of U has a probability (propensity) of being selected for , which can be formulated as
We assume that the response selection mechanism is ignorable and follows a parametric model:
for a known function with second continuous derivatives with respect to an unknown parameter .
We estimate the propensity scores by using data from both the self-selection and the probability samples. The maximum likelihood estimator (MLE) of is , where corresponds to the value of that maximizes the pseudo-log-likelihood function:
The resulting propensities can then be used to calculate new weights, . Thus, we define the inverse propensity weighting estimator of the distribution function as:
Another PSA-based estimator can be obtained using the weights []. In this respect, Refs. [,] proposed other PSA weights whereby the combined sample () is grouped into g equally-sized strata of similar propensity scores from which an average propensity is calculated for each group.
The estimator (17) can be obtained as a special case of the general framework on inference for the general parameter proposed in []. The latter authors present an estimator that uses the propensity score for each individual in the survey weighted by the estimating equation under logistic regression, thus obtaining the asymptotic variance of the estimator.
A third approach to dealing with InfoES information is that of statistical matching, by which imputed values are created for all elements in the probability sample. This method was introduced by [] and is based on modeling the relationship between and , using the self-selected sample to predict for the probability sample. The question then is how to predict the values .
To do so, let us assume a working population model where is the unknown parameter. We further assume that the population model holds for the sample . Using the data from this sample, we can obtain an estimator which is consistent for under the model assumed. From , we then propose the matching estimator for the distribution function as:
where is the predicted value of under the above model. The estimator (18) is consistent if the model for the study variable is correctly specified.
A more complex estimator for the distribution function can be constructed using the idea of double robust estimation [], which is based on the following considerations. Firstly, the propensity score adjusted estimator (17) requires that the propensity score model be correctly specified. Moreover, the imputation-based estimator (18) requires that the working population model be correctly specified. An estimator is called doubly robust if the estimator is consistent whenever one of these two models is correctly specified []. Hence, the double robust estimator of the distribution function is defined as:
The estimator (19) is double robust because it is consistent if either the model for the participation probabilities or the model for the study variable is correctly specified.
3.3. InfoEP
In the case of InfoEP, an initial possibility is to consider a similar calibrated estimator, based on the proposal given in []. The new weights are obtained by minimizing the chi-square distance 7 subject to the following conditions:
where is the finite distribution function of g at the points .
The resulting calibrated estimator of the distribution function is:
where the calibrated weights are given by:
with
gives perfect estimates for the distribution function of the pseudo-variable g, when evaluated over the set of points .
We define a model-based estimator based on the non-probability sample as
and a model-assisted estimator by
4. Properties of Proposed Estimators
When estimating the distribution function, the estimator considered should satisfy the following distribution function properties:
- (i)
- should be continuous on the right;
- (ii)
- should be monotonically nondecreasing;
- (iii)
- ;
- (iv)
- {.
If an estimator of the distribution function is a genuine distribution function, i.e., meets the above conditions, it can be used directly for estimating the quantiles []. Specifically, the quantile can be estimated as:
Since the Heaviside function is continuous on the right, it is clear that all the proposed estimators satisfy conditions (i) and (iii).
In general, however, estimator does not satisfy conditions (ii) or (iv). In order to meet condition (ii), let us consider the specific pseudo-distances that guarantee positive calibrated weights . In this respect, Ref. [] proposed some pseudo-distances which always produce positive weights whilst avoiding extremely large ones. Some of these pseudo-distances may be considered in estimator in order to satisfy condition (ii). In addition, to meet condition (iv), we can add the constraint:
to condition (5).
Similarly, conditions (ii) and (iv are not generally met by the estimators or ). Regarding condition (ii), and following [], the weights and are always positive if for all units in the population. Thus, under the usual uniform choice , both estimators satisfy condition (ii). To meet condition (iv), in the case of estimator , we can add the constraint (25) to the conditions (11), while, for estimator , we can take a value that is large enough so .
The estimator based on the weights verifies condition (ii) if weights , whereas if is based on , then it meets condition (ii) when . Consequently, if , the estimator based on both and satisfies condition (ii). Thus, through the model selected to estimate propensities , condition (ii) can be met. For example, an extended option in the estimation of propensities is that of the logistic regression model
that verifies the condition . Hence, if we choose this model, condition (ii) is met by regardless of whether we use the weight or the weight .
To ensure that condition (iv) is met with the estimator , it can be divided by the sum of weights, that is, or .
Estimator satisfies condition (ii) but not condition (iv). To ensure the latter, again we can divide by the sum of its weights, that is, .
Finally, whereas the estimator satisfies all the conditions, and do not meet conditions (ii) or (iv). Condition (iv) can be met by both and when they are divided by the sum of their respective weights, but these estimators, in general, are not monotonic non-decreasing functions and therefore are not genuine distribution functions. In both cases, we might consider the general procedure described in [] to obtain a monotonous non-decreasing version of the estimators and . However, this procedure always increases the computational cost when estimating quantiles.
5. Simulation Study
In this section, we conduct a Monte Carlo study to compare the efficiency of the estimators presented in Section 3.2. The simulation study was programmed in R and Python. New code was developed to calculate the estimator considered. Python was only used for training and applying the machine learning models in order to take advantage of the package Optuna [] for hyperparameter optimization. However, R was chosen as the main programming language since the functions wtd.quantile, from the package reldist [], and qgeneric, from the package flexsurv [], facilitate the implementation of custom quantiles. To show that the superiority of some estimators depends on the data, we define various setups based on different sampling strategies for the probability and nonprobability samples. In this analysis, only InfoES information is used.
5.1. Data
The dataset used in the simulation was collected between 2011 and 2012, in the Spanish Life Conditions Survey []. Using criteria harmonized for all European Union countries, the Living Conditions Survey generates a reference source of statistics on income distribution and social exclusion within Europe. The dataset was filtered to rule out individuals and variables with large quantities of missing data. Following this procedure, the resulting pseudopopulation had a size of .
The following variables were used in the simulation:
- Demographics
- : 1 if the individual has a computer at home, and 0 otherwise;
- : 1 if the individual is male, and 0 otherwise;
- : the individual’s age in years;
- : 1 if the individual lives in a medium-density population area, and 0 otherwise;
- : 1 if the individual lives in a low-density population area, and 0 otherwise.
- Analysis variable
- : Household expenses in EUR.
Let us consider two setups. In the first, the sampling procedure is the same as that used to select the sample in the Spanish Life Conditions Survey: the probability sample is obtained by stratified cluster sampling, whereby the strata are defined by the NUTS2 regions and the clusters are composed of the households within these regions, extracted with probabilities proportional to the household size. The number of households to be selected, m, is estimated by dividing (the sample size of ) by the mean household size. For , . According to this procedure, the final sample size of is .
In the second setup, the reference probability sample is drawn by Midzuno sampling with probabilities proportional to the minimum household income necessary for basic subsistence.
To generate the nonprobability sample, , the following scenarios were considered:
- SC1: Simple random sampling from the population with
- SC2: Unequal probability sampling from the full pseudopopulation, where the probability of selection for the i-th individual, , is given as follows:
- SC3: Unequal probability sampling from the full pseudopopulation, where the probability of selection for the i-th individual, , is given as follows:
These participation mechanisms create weights with different models and levels of variability. Figure 1, Figure 2 and Figure 3 show the resulting histogram of propensities.
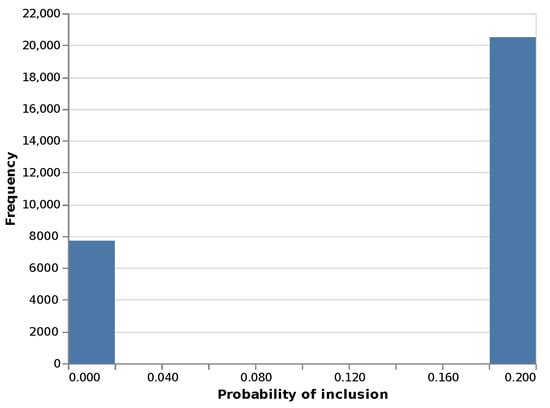
Figure 1.
Histogram of population propensities in SC1.
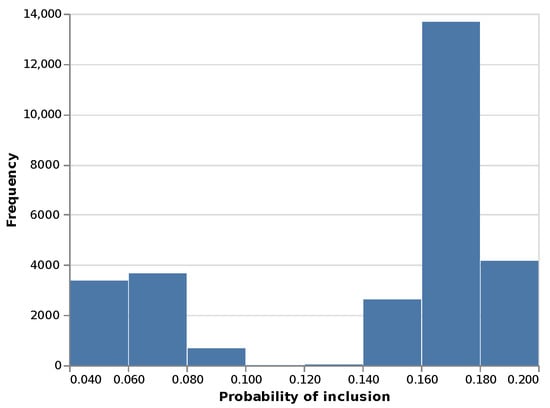
Figure 2.
Histogram of population propensities in SC2.
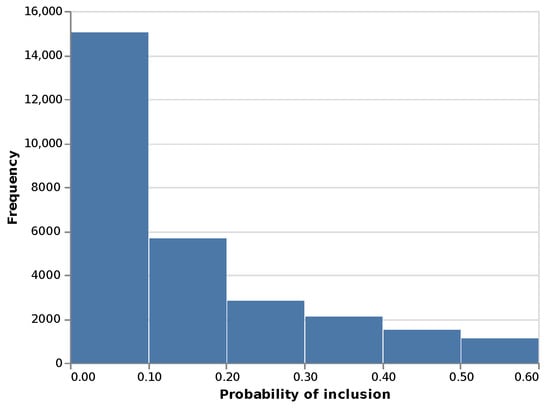
Figure 3.
Histogram of population propensities in SC3.
By this procedure, we obtained nonprobability samples with sizes and 6000.
5.2. Simulation
In each simulation, the following parameters were estimated:
- The quantiles , and
- The distribution function at points , and .
The following methods for estimating these parameters were compared:
- Naive estimator, using the sample distribution function of the sample to draw inferences.
- The proposed calibrated estimator where for corresponds to , , and .
- The proposed PSA estimator .
- The proposed SM estimator .
- The proposed DR estimator .
All five demographic variables were considered potential predictors of propensities, and predicted values for both logistic and linear regression models. In addition, a state-of-the-art machine learning method, XGBoost [], was used as an alternative to these two models in order to evaluate the effect of the method used to estimate propensities and predict values. Refs. [,] show that this technique can improve the representativity of self-selection surveys with respect to other prediction methods.
The quantile is estimated as follows:
where is one of the five above estimators of .
One thousand simulations were run for each context. The resulting mean bias, standard deviation, and root mean square error were measured in relative numbers to make them comparable across different scenarios. The formulas used for their calculation were:
where is the estimation of a parameter in the i-th simulation and is the mean of the 1000 estimations.
5.3. Results
The relative bias of estimators is shown in Table 1, for all scenarios and sample sizes.

Table 1.
Bias (%) for each reference probability sample, parameter, non-probability sampling and size, method and machine learning model (linear/logistic regression or XGBoost).
These results show that the performance of the methods is very similar for each of the probability sample selections considered. The following comments refer to the first columns. i.e., those corresponding to the situation in which the probability sample is chosen through a stratified cluster scheme.
The naive estimator for all parameters in Scenario 1, where there is also coverage bias, reflects a very large degree of bias, which is not eliminated by increasing the sample size. The calibration estimator achieves a considerable reduction in the bias when XGBoost is used to predict the values but does not achieve a significant reduction in the bias with linear regression. For some parameters, this bias is even greater than that of the naive estimator.
As expected, in Scenario 1, the PSA-based estimators do not eliminate the self-selection bias, since there is no relationship between the variables of interest and the probability of participation, and the machine learning method used to predict the propensities has little influence. These results are comparable to those reported by [], who observed that it is important to add covariates related to the study goal in order to make PSA useful.
On the contrary, with the SM method, the ML technique is of determinant importance: the estimators based on linear regression perform very badly, in general, since there is no linear relationship between the values to be predicted and the covariates. However, the XGBoost method works well in the case of nonlinearity and allows us to select the useful covariates in the prediction. A noteworthy finding is the large amount of bias shown by the regression-based estimator for quantiles and , while the version based on XGBoost achieves a very significant error reduction. A very similar pattern of behavior was observed in all cases between the SM and the DR estimators.
With Scenario 2, the estimators present a different behavior pattern. The probability of participation depends on all the covariates, and the PSA method reduces the self-selection bias considerably, in all cases. The ML method has less impact, and the degree of bias reduction achieved is similar in the two methods. Comparable results were obtained with SM and DR, the methods based on calibration. In these cases, the bias reduction in relation to the values obtained with the naive estimator is very large and does not depend on the ML method used. No clear pattern emerged as to which of the methods was the best: for some parameters ( and ), the calibration method worked better, while for others (), the PSA achieved the greatest reduction in bias, and in yet others () the best estimates were produced by SM and DR.
In Scenario 3, where the probability of participating depends only on the age covariate, the calibration estimators, DR and SM, also performed well, obtaining a good level of bias reduction. The estimator based on PSA with logistic regression was the best of all in this respect, for all parameters. However, when XGBoost was used, this decrease in bias was not observed in some parameters. This may be due to the fact that this ML method is very sensitive to the choice of hyperparameters and in these simulations the default parameters were chosen and no hyperparameter optimization was performed. Table 2 shows the relative RMSE of these estimators, for each scenario.

Table 2.
RMSE (%) for each reference probability sample, parameter, non-probability sampling and size, method, and machine learning model (linear/logistic regression or XGBoost).
In Scenario 1, the estimators that use linear or logistic regression are the least efficient, due to the bias that is present. Calibrated SM and DR estimators based on XGBoost improve efficiency by reducing bias. Moreover, the RMSE reduction is very strong in some parameters ( and ). However, the PSA-based estimates do not produce a significant reduction in RMSE because the propensities cannot be modeled from the covariates.
In Scenarios 2 and 3, all the proposed methods effectively reduce the error in the estimates, with the exception of PSA with XGBoost in some cases, as discussed above.
To determine whether this problem encountered with the XGBoost method in some situations can be resolved with an appropriate choice of hyperparameters, we repeated the simulation using a hyperparameter optimization process based on the Tree-structured Parzen Estimator (TPE) algorithm []. In this procedure, the error is estimated by cross-validation on the logistic loss obtained by each possible model over the training data. Accordingly, this process could be replicated in a real-world scenario.
Table 3 and Table 4 show the bias and RMSE values for the estimators with this new simulation for Scenario 2 and Setup 2 (the worst scenario for PSA with the default XGBoost method). Similar results were obtained for all other situations, but for reasons of space they are not shown in this paper.

Table 3.
Bias (%) including hyperparameter optimization when overfitting.

Table 4.
RMSE (%) including hyperparameter optimization when overfitting.
These results clearly show that, by optimizing the hyperparameters, we have considerably reduced the bias and error of the estimators.
6. Discussion
In recent years, the use of survey-based online research has expanded considerably. Web surveys are an attractive option in many fields of sociological investigation due to their low fieldwork costs and rapid data collection. However, this survey mode is also subject to many limitations in terms of accurately representing the target population, and the estimates thus obtained are highly likely to present coverage and/or self-selection bias. Various correction techniques, such as calibration, propensity score adjustment, and statistical matching, have been proposed as a means of reducing or eliminating these forms of bias.
Our paper focuses on the question of estimating the distribution function. This issue is important: the distribution function is a basic statistic underlying many others; for purposes such as assessing and comparing finite populations, it can be more revealing than the use of simple means and totals. Indeed, many previous studies have been undertaken to consider how calibration techniques may be applied to the estimation of the distribution function in the context of a probability survey [,,,,,,,,] and even to overcome the problem of non-response []. However, to our knowledge, very few, if any, studies have addressed this issue from the standpoint of a non-probability survey. Accordingly, we analyze the efficiency obtained by certain bias-correction techniques such as calibration, propensity score adjustment, and statistical matching in various situations within a non-probability survey context. In this analysis, we consider the performance of several estimators in terms of reducing self-selection bias, using a representative survey sample as a proxy for the target population. Among the results obtained by the estimators proposed for the distribution function, needs specific pseudo-distances in order to satisfy condition (ii). The estimator is always a genuine distribution function and under favorable conditions, the estimators and also obtain a genuine distribution function. Moreover, with minor modifications, the estimators (under a logistic regression model) and also satisfy the distribution function conditions. On the other hand, the estimators and are not generally monotonically nondecreasing functions, and therefore when estimating quantiles, an additional process, which increases the computational cost, must be applied. All the estimators included in our proposal can be used under linear and nonlinear models. Self-evidently, , , , , and are applicable to linear or nonlinear models. While the calibrated estimators and assume a linear model, due to the pseudo-variable , the combination with XGBoost enables them to be used with other models too. Furthermore, and can cover the nonlinear case through the procedure described in []. The behavior of all these estimators is demonstrated through simulation studies.
Although further investigation is needed, our results show that self-selection bias can be greatly reduced by any of the four methods considered, particularly when appropriate covariates and a valid machine learning technique are used, both in estimating propensities and in predicting values. However, our investigation did not enable us to determine which method is best in all situations. Specifically, for each parameter and bias-reduction method, different behavior patterns were obtained. Nevertheless, in general, the calibration method based on XGBoost is fairly efficient in any situation.
Although the methods proposed are shown to be effective in reducing the MSE of quantile and distribution function estimates in various situations, certain limitations exist and must be acknowledged. For the PS-based method, for example, the amount of bias reduction achieved depends on how well the propensity model predictors predict the outcome. If the propensity model is poorly fitted, the PS estimates may even be more biased than naive estimates. This is also the case with estimators based on SM, which need a good model in order to accurately predict the y-values. In addition, for the distribution function, the issue is even more complex; although there is a good linear relationship between y and the covariates x, this relationship is not necessarily transferred to the jump functions . In practice, it is often difficult to decide whether the auxiliary variables contain all the components needed to characterize the selection mechanism and the superpopulation model. Therefore, when selecting the covariates and the function of the model, it is essential to use flexible ML techniques.
Finally, the present study does not address the question of the estimation of variance. Plug-in estimators can be used to construct variance estimators from the expression of the asymptotic variance, but the issue is not simple, as the variance depends on the probability of the sample being selected and on the selection mechanism described by the propensity model. In estimating the variance for nonlinear parameters, jackknife and bootstrap techniques [] might be useful and should be considered in future research in this area.
Author Contributions
M.d.M.R., S.M.-P. and L.C.-M. contributed equally to the conceptualization of this study, its methodology, software, and original draft preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministerio de Ciencia, Innovación y Universidades (Grant No. PID2019-106861RB-I00), IMAG-Maria de Maeztu CEX2020-001105-M/AEI/10.13039/501100011033 and FEDER/Junta de Andalucía-Consejería de Transformación Económica, Industria, Conocimiento y Universidades (FQM170-UGR20).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Acal, C.; Ruiz-Castro, J.E.; Aguilera, A.M.; Jiménez-Molinos, F.; Roldán, J.B. Phase-type distributions for studying variability in resistive memories. J. Comput. Appl. Math. 2019, 345, 23–32. [Google Scholar] [CrossRef]
- Alba-Fernández, M.V.; Batsidis, A.; Jiménez-Gamero, M.D.; Jodrá, P. A class of tests for the two-sample problem for count data. J. Comput. Appl. Math. 2017, 318, 220–229. [Google Scholar] [CrossRef]
- Decker, R.A.; Haltiwanger, J.; Jarmin, R.S.; Miranda, J. Declining business dynamism: What we know and the way forward. Am. Econ. Rev. 2016, 106, 203–207. [Google Scholar] [CrossRef]
- Gallagher, C.M.; Meliker, J.R. Blood and urine cadmium, blood pressure, and hypertension: A systematic review and metaanalysis. Environ. Health Perspect. 2010, 118, 1676–1684. [Google Scholar] [CrossRef] [PubMed]
- Medialdea, L.; Bogin, B.; Thiam, M.; Vargas, A.; Marrodán, M.D.; Dossou, N.I. Severe acute malnutrition morphological patterns in children under five. Sci. Rep. 2021, 11, 4237. [Google Scholar] [CrossRef] [PubMed]
- Vander Wal, J.S.; Mitchell, E.R. Psychological complications of pediatric obesity. Pediatr. Clin. 2011, 58, 1393–1401. [Google Scholar] [CrossRef]
- Wilson, R.C.; Fleming, Z.L.; Monks, P.S.; Clain, G.; Henne, S.; Konovalov, I.B.; Menut, L. Have primary emission reduction measures reduced ozone across Europe? An analysis of European rural background ozone trends 1996, Äì2005. Atmos. Chem. Phys. 2012, 12, 437–454. [Google Scholar] [CrossRef]
- Decker, R.; Haltiwanger, J.; Jarmin, R.; Miranda, J. The role of entrepreneurship in US job creation and economic dynamism. J. Econ. Perspect. 2014, 28, 3–24. [Google Scholar] [CrossRef]
- Dickens, R.; Manning, A. Has the national minimum wage reduced UK wage inequality? J. R. Stat. Soc. Ser. A Stat. Soc. 2004, 167, 613–626. [Google Scholar] [CrossRef]
- De Haan, J.; Pleninger, R.; Sturm, J.E. Does financial development reduce the poverty gap? Soc. Indic. Res. 2022, 161, 1–27. [Google Scholar] [CrossRef]
- Jolliffe, D.; Prydz, E.B. Estimating international poverty lines from comparable national thresholds. J. Econ. Inequal. 2016, 14, 185–198. [Google Scholar] [CrossRef]
- Martínez, S.; Illescas, M.; Martínez, H.; Arcos, A. Calibration estimator for Head Count Index. Int. J. Comput. Math. 2020, 97, 51–62. [Google Scholar] [CrossRef]
- Sedransk, N.; Sedransk, J. Distinguishing among distributions using data from complex sample designs. J. Am. Stat. Assoc. 1979, 74, 754–760. [Google Scholar] [CrossRef]
- Chambers, R.L.; Dunstan, R. Estimating distribution functions from survey data. Biometrika 1986, 73, 597–604. [Google Scholar] [CrossRef]
- Chen, J.; Wu, C. Estimation of distribution function and quantiles using the model-calibrated pseudo empirical likelihood method. Stat. Sin. 2002, 12, 1223–1239. [Google Scholar]
- Rao, J.N.K.; Kovar, J.G.; Mantel, H.J. On estimating distribution functions and quantiles from survey data using auxiliary information. Biometrika 1990, 77, 365–375. [Google Scholar] [CrossRef]
- Silva, P.L.D.; Skinner, C.J. Estimating distribution functions with auxiliary information using poststratification. J. Off. Stat. 1995, 11, 277–294. [Google Scholar]
- Deville, J.C.; Särndal, C.E. Calibration estimators in survey sampling. J. Am. Stat. Assoc. 1992, 87, 376–382. [Google Scholar] [CrossRef]
- Arcos, A.; Martínez, S.; Rueda, M.; Martínez, H. Distribution function estimates from dual frame context. J. Comput. Appl. Math. 2017, 318, 242–252. [Google Scholar] [CrossRef]
- Harms, T.; Duchesne, P. On calibration estimation for quantiles. Surv. Methodol. 2006, 32, 37–52. [Google Scholar]
- Martínez, S.; Rueda, M.; Arcos, A.; Martínez, H. Optimum calibration points estimating distribution functions. J. Comput. Appl. Math. 2010, 233, 2265–2277. [Google Scholar] [CrossRef]
- Martínez, S.; Rueda, M.; Martínez, H.; Arcos, A. Optimal dimension and optimal auxiliary vector to construct calibration estimators of the distribution function. J. Comput. Appl. Math. 2017, 318, 444–459. [Google Scholar] [CrossRef]
- Martínez, S.; Rueda, M.; Illescas, M. The optimization problem of quantile and poverty measures estimation based on calibration. J. Comput. Appl. Math. 2022, 45, 113054. [Google Scholar] [CrossRef]
- Mayor-Gallego, J.A.; Moreno-Rebollo, J.L.; Jiménez-Gamero, M.D. Estimation of the finite population distribution function using a global penalized calibration method. AStA Adv. Stat. Anal. 2019, 103, 1–35. [Google Scholar] [CrossRef]
- Rueda, M.; Martínez, S.; Martínez, H.; Arcos, A. Estimation of the distribution function with calibration methods. J. Stat. Plan. Inference 2007, 137, 435–448. [Google Scholar] [CrossRef]
- Singh, H.P.; Singh, S.; Kozak, M. A family of estimators of finite-population distribution function using auxiliary information. Acta Appl. Math. 2008, 104, 115–130. [Google Scholar] [CrossRef]
- Wu, C. Optimal calibration estimators in survey sampling. Biometrika 2003, 90, 937–951. [Google Scholar] [CrossRef]
- Rueda, M.; Martínez, S.; Illescas, M. Treating nonresponse in the estimation of the distribution function. Math. Comput. Simul. 2021, 186, 136–144. [Google Scholar] [CrossRef]
- Bradshaw, J.; Mayhew, E. Understanding extreme poverty in the European Union. Eur. J. Homelessness 2010, 4, 171–186. [Google Scholar]
- Bethlehem, J. Selection Bias in Web Surveys. Int. Stat. Rev. 2010, 78, 161–188. [Google Scholar] [CrossRef]
- Chen, Y.; Li, P.; Wu, C. Doubly Robust Inference with Nonprobability Survey Samples. J. Am. Stat. Assoc. 2019, 115, 2011–2021. [Google Scholar] [CrossRef]
- Beaumont, J.F. Are probability surveys bound to disappear for the production of official statistics? Surv. Methodol. 2020, 46, 1–29. [Google Scholar]
- Buelens, B.; Burger, J.; van den Brakel, J.A. Comparing Inference Methods for Non-probability Samples. Int. Stat. Rev. 2018, 86, 322–343. [Google Scholar] [CrossRef]
- Kim, J.K.; Wang, Z. Sampling techniques for big data analysis. Int. Stat. Rev. 2019, 87, S177–S191. [Google Scholar] [CrossRef]
- Rao, J.N.K. On Making Valid Inferences by Integrating Data from Surveys and Other Sources. Sankhya B 2020, 83, 242–272. [Google Scholar] [CrossRef]
- Valliant, R. Comparing alternatives for estimation from nonprobability samples. J. Surv. Stat. Methodol. 2020, 8, 231–263. [Google Scholar] [CrossRef]
- Yang, S.; Kim, J.K. Statistical data integration in survey sampling: A review. Jpn. J. Stat. Data Sci. 2020, 3, 625–650. [Google Scholar] [CrossRef]
- Lee, S. Propensity Score Adjustment as a Weighting Scheme for Volunteer Panel Web Surveys. J. Off. Stat. 2006, 22, 329–349. [Google Scholar]
- Lee, S.; Valliant, R. Estimation for Volunteer Panel Web Surveys Using Propensity Score Adjustment and Calibration Adjustment. Sociol. Method Res. 2009, 37, 319–343. [Google Scholar] [CrossRef]
- Rivers, D. Sampling for Web Surveys. In Proceedings of the Joint Statistical Meetings, Salt Lake City, UT, USA, 29 July–2 August 2007. [Google Scholar]
- Wang, L.; Graubard, B.I.; Katki, H.A.; Li, Y. Improving external validity of epidemiologic cohort analyses: A kernel weighting approach. J. R. Stat. Soc. Ser. A Stat. Soc. 2020, 183, 1293–1311. [Google Scholar] [CrossRef]
- Castro-Martín, L.; Rueda, M.D.M.; Ferri-García, R. Combining statistical matching and propensity score adjustment for inference from non-probability surveys. J. Comput. Appl. Math. 2021, 404, 113414. [Google Scholar] [CrossRef]
- Ferri-García, R.; Rueda, M.M. Efficiency of Propensity Score Adjustment and calibration on the estimation from non-probabilistic online surveys. SORT Stat. Oper. Res. Trans. 2018, 42, 1–10. [Google Scholar]
- Rueda, M.; Ferri-García, R.; Castro, L. The R package NonProbEst for estimation in non-probability survey. R J. 2020, 12, 406–418. [Google Scholar] [CrossRef]
- Elliott, M.R.; Valliant, R. Inference for Nonprobability Samples. Stat. Sci. 2017, 32, 249–264. [Google Scholar] [CrossRef]
- Ferri-García, R.; Rueda, M.D.M. Propensity score adjustment using machine learning classification algorithms to control selection bias in online surveys. PLoS ONE 2020, 15, e0231500. [Google Scholar] [CrossRef]
- Valliant, R.; Dever, J.A. Estimating Propensity Adjustments for Volunteer Web Surveys. Sociol. Method Res. 2011, 40, 105–137. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Schonlau, M.; Couper, M. Options for Conducting Web Surveys. Stat. Sci. 2017, 32, 279–292. [Google Scholar] [CrossRef]
- Castro-Martín, L.; Rueda, M.D.M.; Ferri-García, R. Estimating General Parameters from Non-Probability Surveys Using Propensity Score Adjustment. Mathematics 2020, 8, 2096. [Google Scholar] [CrossRef]
- Wu, C.; Thompson, M.E. Sampling Theory and Practice; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Handcoc, M.S. Relative Distribution Methods; Version 1.7-1. 2022. Available online: https://CRAN.R-project.org/package=reldist (accessed on 20 October 2022).
- Jackson, C.H. flexsurv: A platform for parametric survival modeling in R. J. Stat. Softw. 2016, 70, i08. [Google Scholar] [CrossRef]
- National Institute of Statistics. Life Conditions Survey—Microdata; National Institute of Statistics: Washington, DC, USA, 2012. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Castro-Martín, L.; Rueda, M.D.M.; Ferri-García, R. Inference from Non-Probability Surveys with Statistical Matching and Propensity Score Adjustment Using Modern Prediction Techniques. Mathematics 2020, 8, 879. [Google Scholar] [CrossRef]
- Castro-Martín, L.; Rueda, M.D.M.; Ferri-García, R.; Hernando-Tamayo, C. On the Use of Gradient Boosting Methods to Improve the Estimation with Data Obtained with Self-Selection Procedures. Mathematics 2021, 9, 2991. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Volume 24. [Google Scholar]
- Rueda, M.; Sánchez-Borrego, I.; Arcos, A.; Martínez, S. Model-calibration estimation of the distribution function using nonparametric regression. Metrika 2010, 71, 33–44. [Google Scholar] [CrossRef]
- Wolter, K.M. Introduction to Variance Estimation, 2nd ed.; Springer Inc.: New York, NY, USA, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).