An Uncertain Sandwich Impulsive Control System with Impulsive Time Windows
Abstract
1. Introduction
2. Preliminaries
3. Exponential Stability Analysis
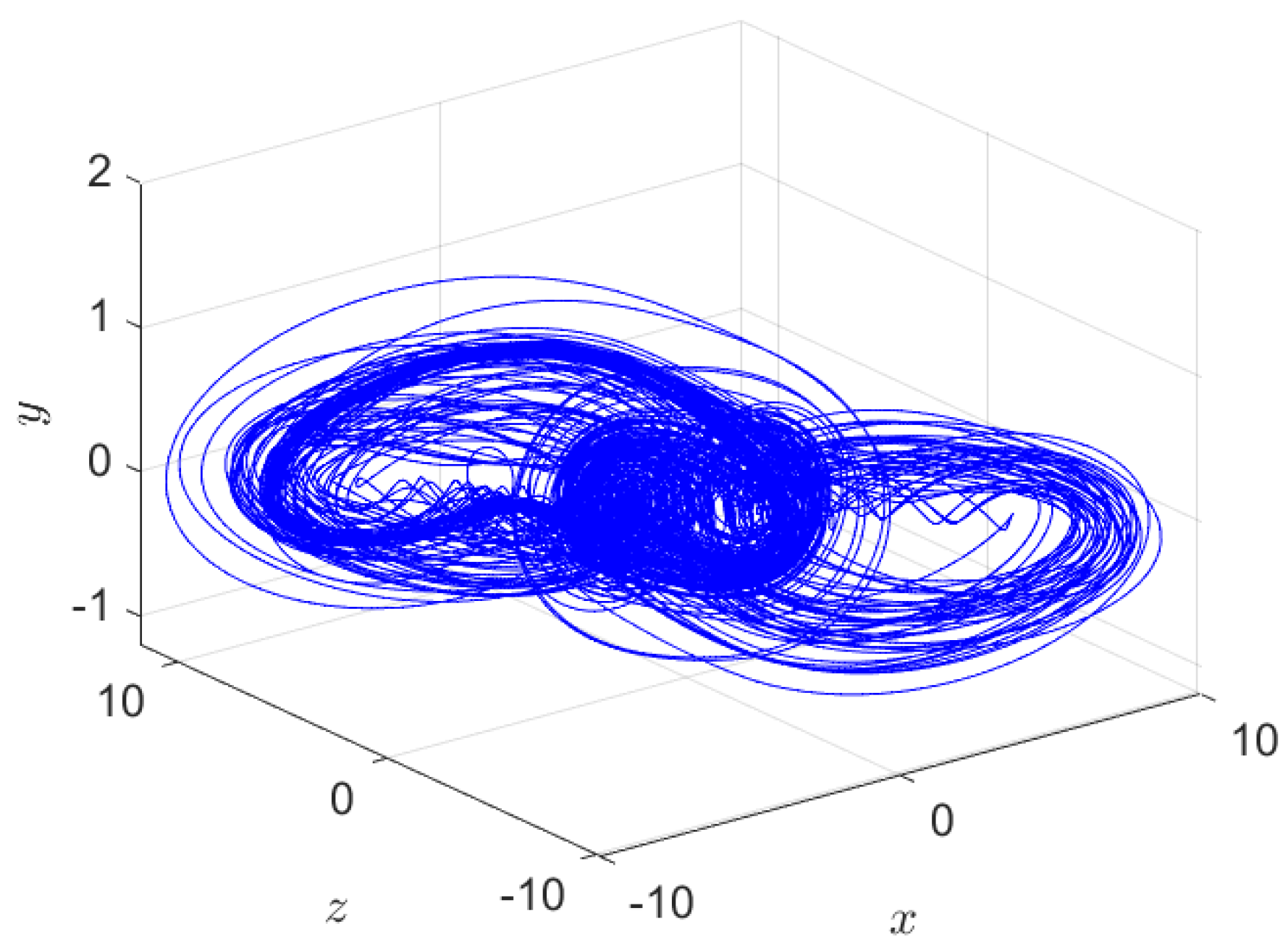
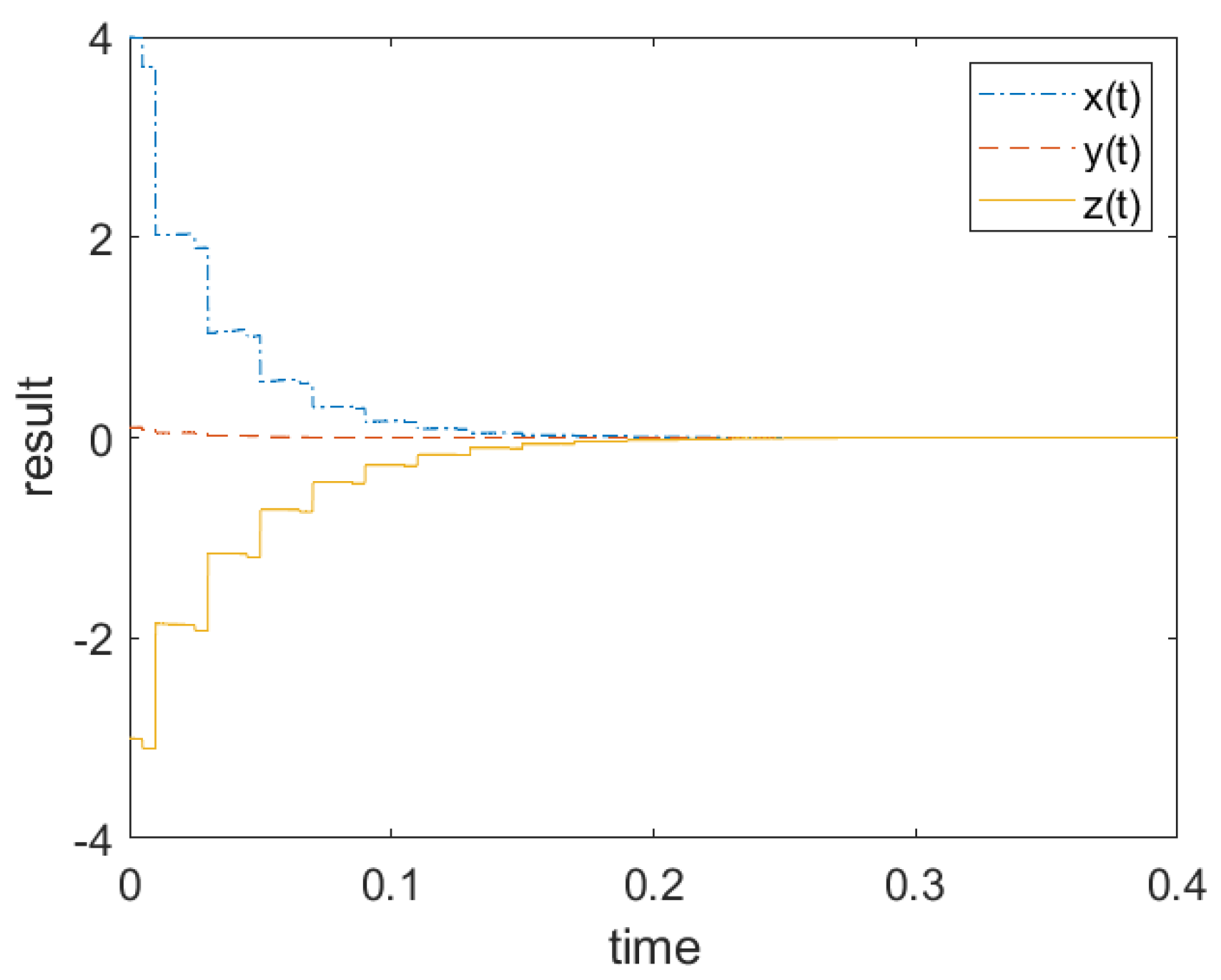
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Milman, V.; Myshkis, A. On the Stability of Motion in the Presence of Impulses. Sib. Math. J. 1960, 1, 233–237. [Google Scholar]
- Lakshmikantham, V.; Simeonov, P.S. Theory of Impulsive Differential Equations; World Scientific: Singapore, 1989. [Google Scholar]
- Yang, T. Impulsive Control Theory; Springer: Berlin, Germany, 2001. [Google Scholar]
- Samoilenko, A.M.; Perestyuk, N.A. Impulsive Differential Equations; World Scientific: Singapore, 1995. [Google Scholar]
- Li, X.; Yang, X.; Huang, T. Persistence of delayed cooperative models: Impulsive control method. App. Math. Comput. 2019, 342, 130–146. [Google Scholar] [CrossRef]
- Zhan, T.; Ma, S.; Liu, X. Synchronization of singular switched complex networks via impulsive control with all nonsynchronized subnetworks. Int. J. Robust Nonlinear Control 2019, 29, 4872–4887. [Google Scholar] [CrossRef]
- Hespanha, J.P.; Liberzon, D.; Teel, A.R. Lyapunov conditions for input-to-state stability of impulsive systems. Automatica 2008, 44, 2735–2744. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, X.; Shi, P.; Qian, F. Input-to-state stability for nonlinear systems with stochastic impulses. Automatica 2020, 113, 108766. [Google Scholar] [CrossRef]
- Chin, W.; Ott, E.; Nusse, H.E.; Grebogi, E. Grazing bifurcations in impact oscillators. Phys. Rev. E 1994, 20, 4427–4444. [Google Scholar] [CrossRef]
- Dankowicz, H.; Nordmark, A.B. On the origin and bifurcations of stick-slip oscillators. Physica D 2000, 136, 280–302. [Google Scholar] [CrossRef]
- Haddad, W.; Chellaboina, V.; Nersesov, S. Impulsive and Hybrid Dynamcial Systems: Stability, Dissipativity and Control; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Goebel, R.; Sanfelice, R.G.; Teel, A.R. Hybrid Dynamical Systems: Modeling, Stability, and Robustness; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Gilbert, E.; Harasty, G. A class of fixed-time fuel-optimal impulsive control problems and an efficient algorithm for their solution. IEEE Trans. Automat. Control 1971, 16, 1–11. [Google Scholar] [CrossRef]
- Chazov, V.V.; Ivandikov, F.I.; Kuchumov, A.A.; Kurakhtenkov, L.V.; Magsumov, V.R. An algorithm for maintaining a given structure of an earth satellite constellation. In Proceedings of the Systems of Signal Synchronization, Generating and Processing in Telecommunications, Yaroslavl, Russia, 1–3 July 2019; pp. 1–4. [Google Scholar]
- Liang, X.; Pei, Y.; Zhu, M.; Lv, Y. Multiple kinds of optimal impulse control strategies on plant pest predator model with eco epidemiology. Appl. Math. Comput. 2016, 287, 1–11. [Google Scholar] [CrossRef]
- Wu, E.; Yang, X. Adaptive synchronization of coupled nonidentical chaotic systems with complex variables and stochastic perturbations. Nonlinear Dynam. 2015, 84, 261–269. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, X.; Yang, S.; Ahmed, A. Finite-time and fixed-time bipartite synchronization of complex networks with signed graphs. Math. Comput. Simulat. 2021, 188, 319–329. [Google Scholar] [CrossRef]
- Stojanovski, T.; Kocarev, L.; Parlitz, U. Driving and synchronizing by chaotic impulses. Phy. Rev. E 1996, 54, 2128–2131. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Gao, X.; Zhong, W.; Qian, F. Secure impulsive synchronization control of multi-agent systems under deception attacks. Inform. Sci. 2018, 459, 354–368. [Google Scholar] [CrossRef]
- Lu, J.; Ho, D.W.C.; Cao, J. A unified synchronization criterion for impulsive dynamical networks. Automatica 2010, 46, 1215–1221. [Google Scholar] [CrossRef]
- Cui, Q.; Li, L.; Cao, J.; Alsaadi, F.E. Synchronization of Kuramoto-oscillator networks under event-triggered delayed impulsive control. Physica A 2022, 608, 128250. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K. Stabilization of nonlinear time-delay systems: Distributed-delay dependent impulsive control. Syst. Control Lett. 2018, 120, 17–22. [Google Scholar] [CrossRef]
- Wu, J.; Li, X. Stability of nonlinear differential systems with state-dependent delayed impulses. Automatica 2016, 64, 63–69. [Google Scholar]
- Li, X.; Peng, D.; Cao, J. Lyapunov stability for Impulsive systems via event-triggered impulsive control. IEEE Trans. Automat. Control 2020, 65, 4908–4913. [Google Scholar] [CrossRef]
- Cheng, P.; Deng, F.; Yao, F. Almost sure exponential stability and stochastic stabilization of stochastic differential systems with impulsive effects. Nonlinear Anal. 2018, 30, 106–117. [Google Scholar] [CrossRef]
- Dashkovskiy, S.; Mironchenko, A. Input-to-state stability of nonlinear impulsive systems. SIAM J. Control Optim. 2013, 51, 1962–1987. [Google Scholar] [CrossRef]
- Feketa, P.; Bajcinca, N. On robustness of impulsive stabilization. Automatica 2019, 104, 48–56. [Google Scholar] [CrossRef]
- Slyn’ko, V.; Tunc, C. Stability of abstract linear switched impulsive differential equations. Automatica 2019, 107, 433–441. [Google Scholar] [CrossRef]
- Myshkis, A.D.; Samoilenko, A.M. Systems with shocks at prescribed instants of time. Mat. Sb. 1967, 74, 202–208. [Google Scholar]
- Feng, Y.; Li, C.; Huang, T. Periodically multiple state-jumps impulsive control systems with impulse time windows. Neurocomputing 2016, 193, 7–13. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, T.; He, X.; Li, C. Global exponential stability of inertial memristor-based neural networks with time-varying delays and impulses. Neural Netw. 2017, 95, 102–109. [Google Scholar]
- Rajchaki, G.; Chantho, P.; Niezabito, M.; Raja, R.; Baleanu, D.; Pratap, A. Impulsive effects on stability and passivity analysis of memristor-based fractional-order competitive neural networks. Neurocomputing 2020, 417, 290–301. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, X.; Wang, Z.; Wang, W. A nonlinear impulsive control system with impulse time windows and un-fixed coefficient of impulsive intensity. In Proceedings of the 2019 International Conference on Information, Cybernetics, and Computational Social Systems, Chongqing, China, 27–30 September 2019; pp. 67–71. [Google Scholar]
- Naghshtabrizi, P.; Hespanha, J.; Teel, A. Exponential stability of impulsive systems with application to uncertain sampled-data systems. Syst. Control Lett. 2018, 57, 378–385. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, J.; Li, C.; Huang, T.; Che, H. Linear impulsive control system with impulse time windows. J. Vib. Control 2017, 23, 111–118. [Google Scholar] [CrossRef]
- Yang, D.; Qiu, G.; Li, C. Global exponential stability of memristive neural networks with impulse time window and time-varying delays. Neurocomputing 2015, 17, 1021–1026. [Google Scholar] [CrossRef]
- Wang, X.; Li, C.; Huang, T.; Pan, X. Impulsive control and synchronization of nonlinear system with impulse time window. Nonlinear Dyn. 2014, 78, 2837–2845. [Google Scholar] [CrossRef]
- Feng, Y.; Li, C.; Huang, T. Sandwich control systems with impulse time windows. Int. J. Mach. Learn Cyb. 2017, 8, 2009–2015. [Google Scholar] [CrossRef]
- Liao, C.; Tu, D.; Feng, Y.; Zhang, W.; Wang, Z.; Onasanya, B.O. A Sandwich Control System with Dual Stochastic Impulses. IEEE CAA J. Autom. Sin. 2022, 9, 741–744. [Google Scholar] [CrossRef]
- Xiao, L.; Ling, B.; Xing, R.; Bing, H.; Isaac, E. Combined active learning Kriging with optimal saturation nonlinear vibration control for uncertain systems with both aleatory and epistemic uncertainties. J. Non-Linear Mech. 2022, 148, 104267. [Google Scholar]
- Feketa, P.; Klinshov, V.; Lücken, L. A survey on the modeling of hybrid behaviors: How to account for impulsive jumps properly. Commum. Nonlinear Sci. Simul. 2021, 103, 105955. [Google Scholar] [CrossRef]
- Xie, L.; Fu, M.; Souza, C. Control and quadratic stabilization of systems with parameter uncertainty via output feedback. IEEE Trans. Autom. Control 1992, 37, 1253–1256. [Google Scholar] [CrossRef]
- Ren, Z.; Wen, S.; Li, Q.; Feng, Y.; Tang, N. Stability analysis for nonlinear impulsive control system with uncertainty factors. Comput. Intel. Neurosc. 2022, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wen, G.; Zhai, X.; Peng, Z.; Rahmani, A. Fault-Tolerant secure consensus tracking of delayed nonlinear multi-agent systems with deception attacks and uncertain parameters via impulsive control. Commun. Nonlinear Sci. Numer. Simulat. 2020, 19, 105043–105077. [Google Scholar] [CrossRef]
- Lin, J.; Cai, J.; Ma, M. Impulsive practical synchronization of hyperchaotic systems with uncertain parameters. In Proceedings of the 27th China Control and Decision Making Conference, Qingdao, China, 23–25 May 2015; pp. 2391–2395. [Google Scholar]
- Singh, V. Robust stability of cellular neural networks with delay: Linear matrix inequality approach, Control Theory and Applications. IEE Proc. Control Theory Appl. 2004, 151, 125–129. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, L.; Souza, C. Robust control of a class of uncertain nonlinear systems. Syst. Control Lett. 1992, 19, 139–149. [Google Scholar] [CrossRef]
- Hale, J.K.; Verduyn-Lunel, S.M. Introduction to Functional Differential Eqnations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Boyd, S.; Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadephia, PA, USA, 1994. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Chen, J.; Qu, D.; Li, K.; Luo, F. An Uncertain Sandwich Impulsive Control System with Impulsive Time Windows. Mathematics 2022, 10, 4708. https://doi.org/10.3390/math10244708
Chen H, Chen J, Qu D, Li K, Luo F. An Uncertain Sandwich Impulsive Control System with Impulsive Time Windows. Mathematics. 2022; 10(24):4708. https://doi.org/10.3390/math10244708
Chicago/Turabian StyleChen, Huafei, Jia Chen, Dan Qu, Kelin Li, and Fei Luo. 2022. "An Uncertain Sandwich Impulsive Control System with Impulsive Time Windows" Mathematics 10, no. 24: 4708. https://doi.org/10.3390/math10244708
APA StyleChen, H., Chen, J., Qu, D., Li, K., & Luo, F. (2022). An Uncertain Sandwich Impulsive Control System with Impulsive Time Windows. Mathematics, 10(24), 4708. https://doi.org/10.3390/math10244708





