Economic Dispatch for Smart Buildings with Load Demand of High Volatility Based on Quasi-Quadratic Online Adaptive Dynamic Programming
Abstract
1. Introduction
1.1. Literature Review
1.2. Motivation and Contributions
- A kind of online ADP is proposed to iteratively obtain optimal economic dispatch for smart buildings with high volatility of load demand. The online algorithm allows parameters of controller to achieve optimal control with the changing of load demand.
- A quasi-quadratic form parametric structure is designed for the implementation of QOADP with a bias term to counteract the effects of uncertainties. To simplify the function approximation structure in the proposed algorithm, the feedforward information of the uncontrollable state is taken into account in the iterative value function and the iterative controller.
2. EMS of Smart Buildings
3. Building Energy Management Strategy
3.1. Iterative QOADP Algorithm
3.2. Parametric Structure Design for Value Function
4. Implementation of the Proposed Algorithm
| Algorithm 1: Data-driven QOADP algorithm |
Initialization: 1: Collect data of an EMS 2: Choose an initial array of , which ensures initial to be positive semi-definite. 3: Choose the maximum time step . Iteration (Online): 4: Let , and let . 6: Let . 8: If , go to next step. Otherwise, go to Step 6. 9: return. |
5. Hardware-in-Loop Experimental Verification
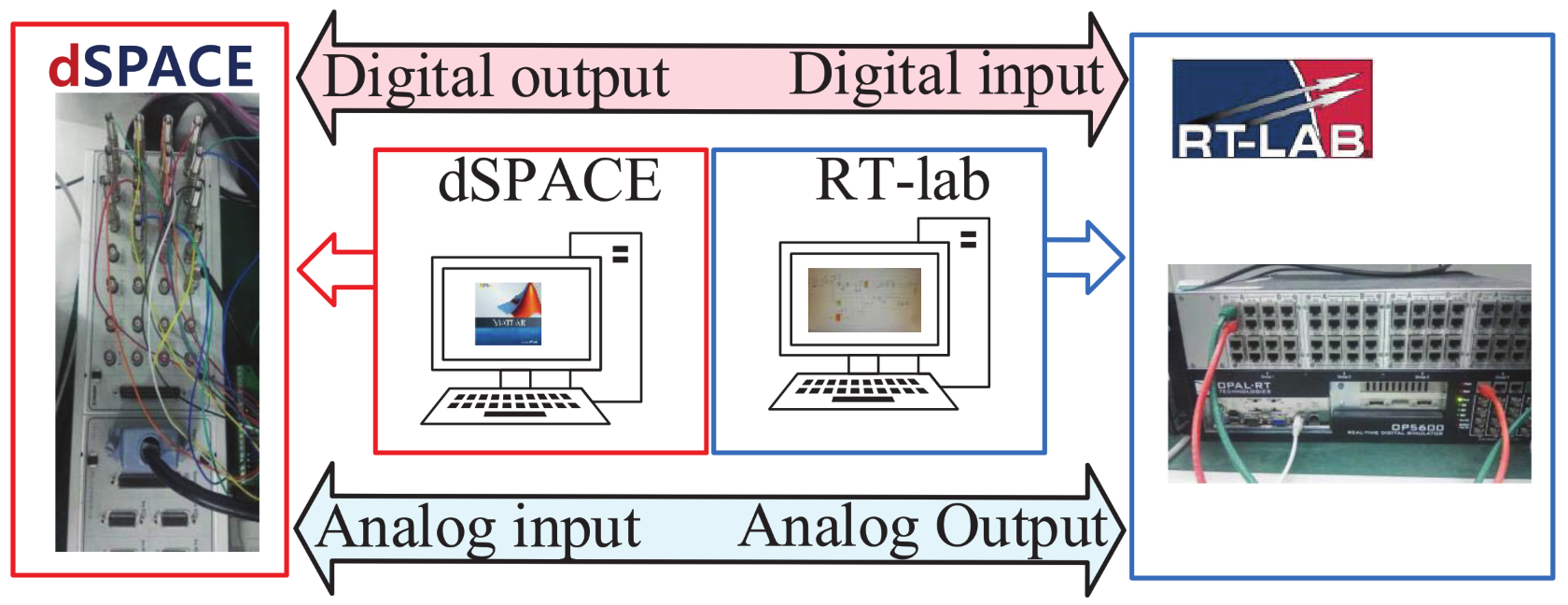
5.1. HIL Platform
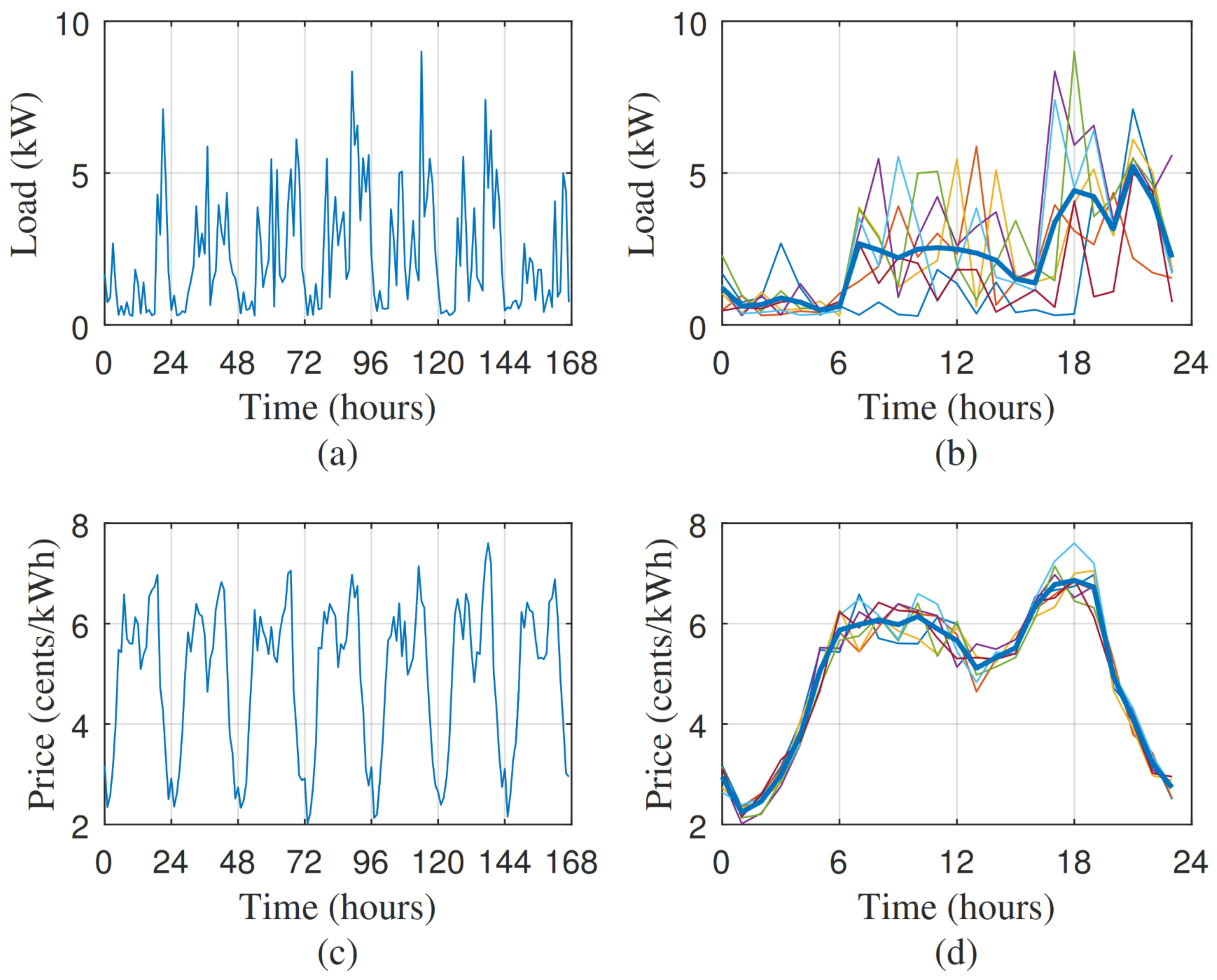
5.2. Dataset
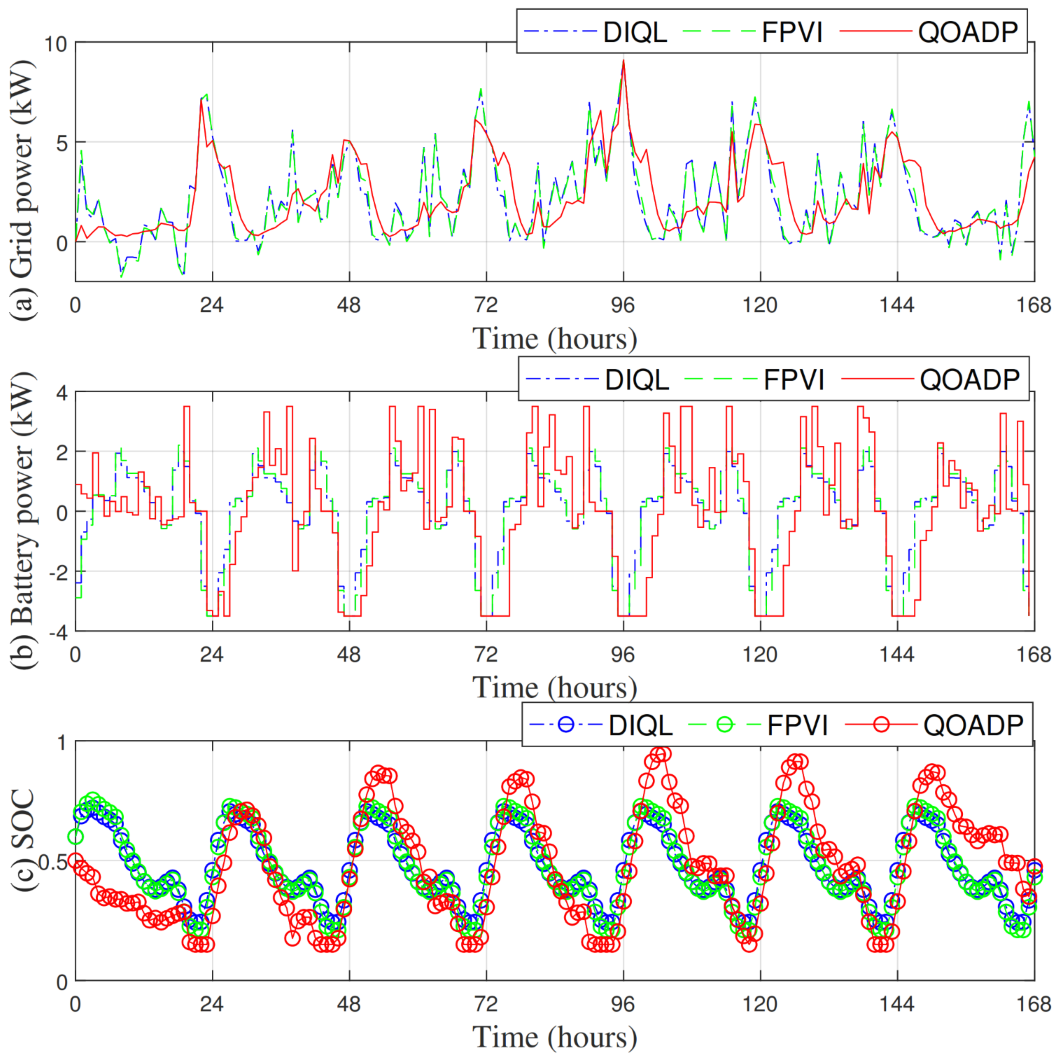
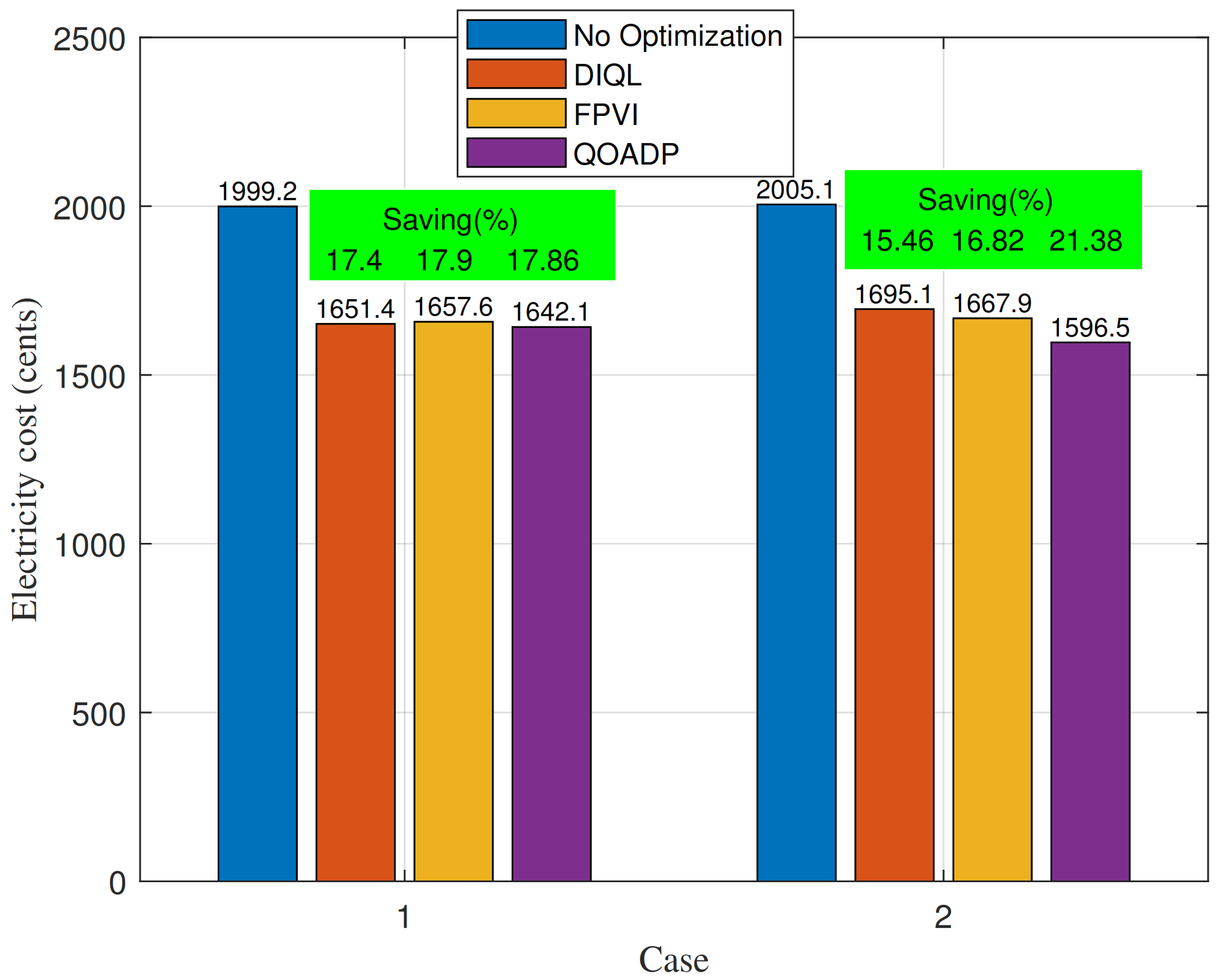
5.3. Case 1: Periodic Load Demand
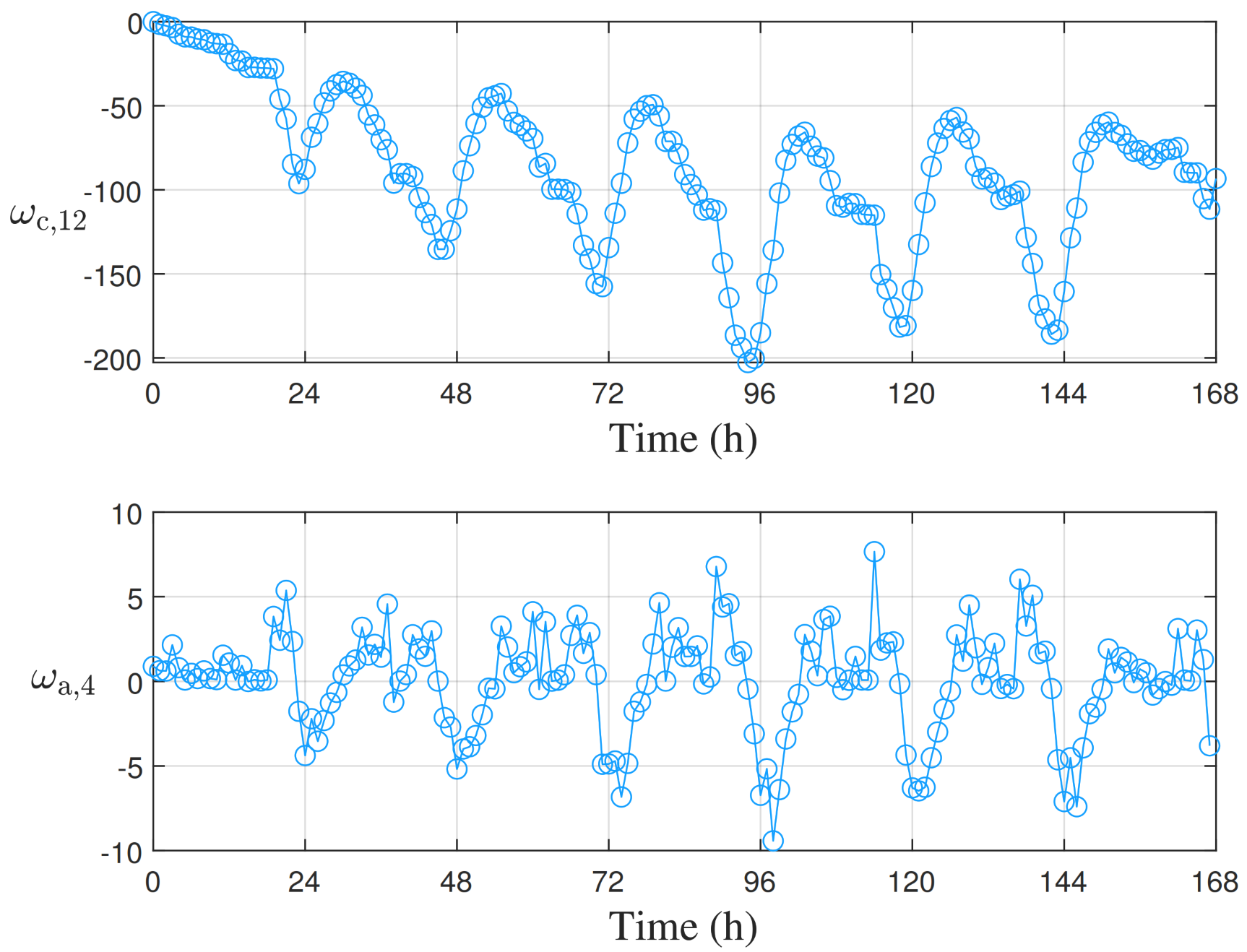
5.4. Case 2: Load Demand of High Volatility
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| i | iteration steps. |
| time steps (hours). | |
| Power from the utility grid at time t (kW). | |
| Battery discharging/charging power at time t (kW). | |
| Building load at time t (kW). | |
| Charging/discharging efficiency of Power electronic converter in the storage system. | |
| State of charge of the battery at time t. | |
| Rated energy of battery (kWh). | |
| Minimum value of . | |
| Maximum value of . | |
| Battery rated discharging/charging power at time t (kW). | |
| Transition function of building load (continuous time). | |
| Transition function of building load (discrete time). | |
| Sampling time. | |
| Controllable system state vector. | |
| Unontrollable system state vector. | |
| System state vector, , . | |
| System control vector, . | |
| control sequence from time k to ∞. | |
| System transition function. | |
| Drift dynamics, input dynamics, disturbance dynamics. | |
| Utility function. | |
| Real-time electricity price at time k (cents/kWh) | |
| Performance index function. | |
| Discount factor, . |
References
- Zhou, B.; Zou, J.; Chung, C.Y.; Wang, H.; Liu, N.; Voropai, N.; Xu, D. Multi-microgrid Energy Management Systems: Architecture, Communication, and Scheduling Strategies. J. Mod. Power Syst. Clean Energy 2021, 9, 463–476. [Google Scholar] [CrossRef]
- Yu, L.; Qin, S.; Zhang, M.; Shen, C.; Jiang, T.; Guan, X. A Review of Deep Reinforcement Learning for Smart Building Energy Management. IEEE Internet Things J. 2021, 8, 12046–12063. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Yang, C.; Xie, S.; Zhang, Y. Online Control and Near-Optimal Algorithm for Distributed Energy Storage Sharing in Smart Grid. IEEE Trans. Smart Grid 2020, 11, 2552–2562. [Google Scholar] [CrossRef]
- Giraldo, J.S.; Castrillon, J.A.; López, J.C.; Rider, M.J.; Castro, C.A. Microgrids Energy Management Using Robust Convex Programming. IEEE Trans. Smart Grid 2019, 10, 4520–4530. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Xie, S.; Xie, L. Chance Constrained Scheduling and Pricing for Multi-Service Battery Energy Storage. IEEE Trans. Smart Grid 2021, 12, 5030–5042. [Google Scholar] [CrossRef]
- Zhang, G.; Yuan, J.; Li, Z.; Yu, S.S.; Chen, S.Z.; Trinh, H.; Zhang, Y. Forming a Reliable Hybrid Microgrid Using Electric Spring Coupled With Non-Sensitive Loads and ESS. IEEE Trans. Smart Grid 2020, 11, 2867–2879. [Google Scholar] [CrossRef]
- Fan, L.; Wang, Y.; Wei, H.; Zhang, Y.; Zheng, P.; Huang, T.; Li, W. A GA-based online real-time optimized energy management strategy for plug-in hybrid electric vehicles. Energy 2022, 241, 122811. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y. Optimal Energy Management of Wind-Battery Hybrid Power System With Two-Scale Dynamic Programming. IEEE Trans. Sustain. Energy 2013, 4, 765–773. [Google Scholar] [CrossRef]
- Meng, X.; Li, Q.; Zhang, G.; Chen, W. Efficient Multidimensional Dynamic Programming-Based Energy Management Strategy for Global Composite Operating Cost Minimization for Fuel Cell Trams. IEEE Trans. Transp. Electrif. 2022, 8, 1807–1818. [Google Scholar] [CrossRef]
- Liu, D.; Xue, S.; Zhao, B.; Luo, B.; Wei, Q. Adaptive Dynamic Programming for Control: A Survey and Recent Advances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 142–160. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D. Reinforcement learning and adaptive dynamic programming for feedback control. IEEE Circuits Syst. Mag. 2009, 9, 32–50. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.; Vamvoudakis, K.G. Reinforcement Learning and Feedback Control: Using Natural Decision Methods to Design Optimal Adaptive Controllers. IEEE Control. Syst. Mag. 2012, 32, 76–105. [Google Scholar] [CrossRef]
- Fuselli, D.; De Angelis, F.; Boaro, M.; Squartini, S.; Wei, Q.; Liu, D.; Piazza, F. Action dependent heuristic dynamic programming for home energy resource scheduling. Int. J. Electr. Power Energy Syst. 2013, 48, 148–160. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Wei, Q.; Liu, X. Residential energy scheduling for variable weather solar energy based on adaptive dynamic programming. IEEE/CAA J. Autom. Sin. 2018, 5, 36–46. [Google Scholar] [CrossRef]
- Zhao, Z.; Keerthisinghe, C. A Fast and Optimal Smart Home Energy Management System: State-Space Approximate Dynamic Programming. IEEE Access 2020, 8, 184151–184159. [Google Scholar] [CrossRef]
- Yuan, J.; Yu, S.S.; Zhang, G.; Lim, C.P.; Trinh, H.; Zhang, Y. Design and HIL Realization of an Online Adaptive Dynamic Programming Approach for Real-Time Economic Operations of Household Energy Systems. IEEE Trans. Smart Grid 2022, 13, 330–341. [Google Scholar] [CrossRef]
- Shuai, H.; Fang, J.; Ai, X.; Tang, Y.; Wen, J.; He, H. Stochastic Optimization of Economic Dispatch for Microgrid Based on Approximate Dynamic Programming. IEEE Trans. Smart Grid 2019, 10, 2440–2452. [Google Scholar] [CrossRef]
- Li, H.; Wan, Z.; He, H. Real-Time Residential Demand Response. IEEE Trans. Smart Grid 2020, 11, 4144–4154. [Google Scholar] [CrossRef]
- Shang, Y.; Wu, W.; Guo, J.; Ma, Z.; Sheng, W.; Lv, Z.; Fu, C. Stochastic dispatch of energy storage in microgrids: An augmented reinforcement learning approach. Appl. Energy 2020, 261, 114423. [Google Scholar] [CrossRef]
- Shuai, H.; He, H. Online Scheduling of a Residential Microgrid via Monte-Carlo Tree Search and a Learned Model. IEEE Trans. Smart Grid 2021, 12, 1073–1087. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D.; Shi, G. A novel dual iterative Q-learning method for optimal battery management in smart residential environments. IEEE Trans. Ind. Electron. 2015, 62, 2509–2518. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D.; Liu, Y.; Song, R. Optimal constrained self-learning battery sequential management in microgrid via adaptive dynamic programming. IEEE/CAA J. Autom. Sin. 2017, 4, 168–176. [Google Scholar] [CrossRef]
- Wei, Q.; Shi, G.; Song, R.; Liu, Y. Adaptive Dynamic Programming-Based Optimal Control Scheme for Energy Storage Systems With Solar Renewable Energy. IEEE Trans. Ind. Electron. 2017, 64, 5468–5478. [Google Scholar] [CrossRef]
- Wei, Q.; Liao, Z.; Song, R.; Zhang, P.; Wang, Z.; Xiao, J. Self-Learning Optimal Control for Ice-Storage Air Conditioning Systems via Data-Based Adaptive Dynamic Programming. IEEE Trans. Ind. Electron. 2021, 68, 3599–3608. [Google Scholar] [CrossRef]
- Wei, Q.; Liao, Z.; Shi, G. Generalized Actor-Critic Learning Optimal Control in Smart Home Energy Management. IEEE Trans. Ind. Inform. 2021, 17, 6614–6623. [Google Scholar] [CrossRef]
- Shi, G.; Liu, D.; Wei, Q. Echo state network-based Q-learning method for optimal battery control of offices combined with renewable energy. IET Control. Theory Appl. 2017, 11, 915–922. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, D.; Li, X.; Wang, D. Control-Limited Adaptive Dynamic Programming for Multi-Battery Energy Storage Systems. IEEE Trans. Smart Grid 2019, 10, 4235–4244. [Google Scholar] [CrossRef]
- Al-Tamimi, A.; Lewis, F.L.; Abu-Khalaf, M. Discrete-Time Nonlinear HJB Solution Using Approximate Dynamic Programming: Convergence Proof. IEEE Trans. Syst. Man Cybern. Part (Cybernetics) 2008, 38, 943–949. [Google Scholar] [CrossRef]
- Wang, D.; Liu, D.; Wei, Q.; Zhao, D.; Jin, N. Optimal control of unknown nonaffine nonlinear discrete-time systems based on adaptive dynamic programming. Automatica 2012, 48, 1825–1832. [Google Scholar] [CrossRef]
- Liu, D.; Wei, Q. Policy Iteration Adaptive Dynamic Programming Algorithm for Discrete-Time Nonlinear Systems. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 621–634. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; He, H.; Ren, S.; Weng, G. Real-Time Demand Side Management for a Microgrid Considering Uncertainties. IEEE Trans. Smart Grid 2019, 10, 3401–3414. [Google Scholar] [CrossRef]
- Wei, Q.; Lewis, F.L.; Liu, D.; Song, R.; Lin, H. Discrete-Time Local Value Iteration Adaptive Dynamic Programming: Convergence Analysis. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 875–891. [Google Scholar] [CrossRef]
- Xue, S.; Luo, B.; Liu, D. Event-Triggered Adaptive Dynamic Programming for Zero-Sum Game of Partially Unknown Continuous-Time Nonlinear Systems. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 50, 3189–3199. [Google Scholar] [CrossRef]
- Liu, D.; Wei, Q.; Wang, D.; Yang, X.; Li, H. Adaptive Dynamic Programming with Applications in Optimal Control; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]




| Parameters | Value |
|---|---|
| Capacity of battery in kWh | 25 |
| Upper bound of SOC | 0.9 |
| Lower bound of SOC | 0.15 |
| Rated power output of the battery in kW | 3.5 |
| Initial energy of battery in kWh | 12.5 |
| Discount factor | 0.996 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Zhu, Z.; Wang, J. Economic Dispatch for Smart Buildings with Load Demand of High Volatility Based on Quasi-Quadratic Online Adaptive Dynamic Programming. Mathematics 2022, 10, 4701. https://doi.org/10.3390/math10244701
Chen K, Zhu Z, Wang J. Economic Dispatch for Smart Buildings with Load Demand of High Volatility Based on Quasi-Quadratic Online Adaptive Dynamic Programming. Mathematics. 2022; 10(24):4701. https://doi.org/10.3390/math10244701
Chicago/Turabian StyleChen, Kairui, Zhangmou Zhu, and Jianhui Wang. 2022. "Economic Dispatch for Smart Buildings with Load Demand of High Volatility Based on Quasi-Quadratic Online Adaptive Dynamic Programming" Mathematics 10, no. 24: 4701. https://doi.org/10.3390/math10244701
APA StyleChen, K., Zhu, Z., & Wang, J. (2022). Economic Dispatch for Smart Buildings with Load Demand of High Volatility Based on Quasi-Quadratic Online Adaptive Dynamic Programming. Mathematics, 10(24), 4701. https://doi.org/10.3390/math10244701







