Bootstrapping Not Independent and Not Identically Distributed Data

Abstract

Classical normal asymptotics could bring serious pitfalls in statistical inference, because some parameters appearing in the limit distributions are unknown and, moreover, complicated to estimated (from a theoretical as well as computational point of view). Due to this, plenty of stochastic approaches for constructing confidence intervals and testing hypotheses cannot be directly applied. Bootstrap seems to be a plausible alternative. A methodological framework for bootstrapping not independent and not identically distributed data is presented together with theoretical justification of the proposed procedures. Among others, bootstrap laws of large numbers and central limit theorems are provided. The developed methods are utilized in insurance and psychometry.

1. Introduction and Motivation

Stochastic inference frequently relies on the limiting normal distribution, which allows the characterization of large sample (asymptotic) behavior of the considered statistics. However, some entities of the asymptotic distribution such as the variance–covariance matrix quite often depend on the parameters or other quantities, which cannot be estimated directly from the data. In addition, this estimation can be performed neither theoretically nor computationally. Bootstrap methods—a class of resampling techniques—serve as suitable alternatives. Additional problems arise, when the underlying data do not form a random sample, simply because they cannot be considered as independent or identically distributed. Thus, the bootstrap techniques developed for independent and identically distributed (IID) observations need to be adjusted and suited up for the not independent and not identically distributed (NINID) data. The main goal of this paper is to postulate a theoretical setup and a methodological framework, which enable us to show how the bootstrap procedures should be accommodated for the NINID observations and, simultaneously, to formally justify the validity of such approaches. It is prerequisite to realize that there are two sources of randomness when bootstrapping: the first randomness comes from the data themselves, the second randomness is brought by the chance from random resampling. Therefore, we need to access, quantify, and control both sources.

However, it is not sufficient to give just the algorithmic procedures for bootstrapping the parameters of interest. It is also desired to possess fundamental mathematical guaranties that the particular bootstrap technique provides reasonable results. A possible way how to postulate such validity is to formulate proper stochastic convergences, assuring that the bootstrapped parameter is distributionally close to the estimator of the unknown parameter of interest.

1.1. State of the Art

The bootstrap was introduced by Efron in [1]. This theoretical concept was consequently investigated by [2] in the case of independent and identically distributed data. Monographs [3] or [4] provide a bootstrap “first” course overview. A comprehensive theoretical summary for the bootstrap methods can be found in [5]. Various types of the dependent bootstrap procedures were proposed and [6] provided a extensive summary. Subsampling within the bootstrap framework was given by [7]. The block bootstrap approach was independently suggested by [8,9] for the case of sample mean. [10,11] extended these results, but still considered only strictly stationary processes. Reference [12] generalized previous approaches for non-stationary processes. Bootstrapping panel data with non-stationary, heteroscedastic, and outlying observations was elaborated by [13]. Permutation bootstrap for the exchangeable observations was summarized by [14]. An application of the dependent block bootstrap approach for the regression setup was performed in [15,16]. In contrast to this theoretical asymptotic result, the practical finite sample properties for the dependent bootstrap were studied by [17,18,19].

1.2. Structure of the Paper

The organization of the paper is as follows. The bootstrap procedures for IID and NINID data are summarized in Section 2. Consequently, Section 3 postulates asymptotic relations and closeness in the bootstrap world. Various bootstrap laws of large numbers are derived in Section 4. The validity of the considered bootstrap methods are guaranteed by the bootstrap central limit theorems provided in Section 5. Practical applications to the problems from insurance and psychometry are shown in Section 6. Conclusions are relegated to Section 7, while all the proofs are collected in the Appendix A.

2. Bootstrap Methods for NINID Data

A brief summary for bootstrapping the IID data is going to be provided. After that, an extension for the NINID observations is given.

2.1. Independent Bootstrap

An independent bootstrap requires no distributional assumptions and, moreover, independence of the input multivariate observations ${\left\{{\mathbf{\xi }}_i\right\}}_{i=1}^n$ is assumed while resampling is being performed. It is also often called the nonparametric bootstrap and it refers to the simplest scheme of independent resampling from the original observations $[{\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n]$. The main idea behind the independent bootstrap lies in the resampling of the independent column data ${\mathbf{\xi }}_i$’s with replacement in order to obtain the bootstrapped data ${\mathbf{\xi }}_i^{*}$. Now, an entity of interest is calculated from the new “starred” data ${\mathbf{\xi }}_i^{*}$’s, e.g., a test statistic or an estimator of an unknown parameter. It is desired that the new distribution of the bootstrapped entity mimics the original distribution of the concerned statistics. From now on, we concentrate on the bootstrap for the mean parameter. However, the presented approaches can be generalized for other parameters of interest as well, but this goes beyond the scope of this paper.

Assuming identical distribution and finite variance of ${\mathbf{\xi }}_i$’s, the central limit theorem holds for the sample mean

$${\overline{\mathbf{\xi }}}_n:=\frac{1}{n}\sum _{i=1}^n{\mathbf{\xi }}_i.$$

Thus, $\sqrt{n}({\overline{\mathbf{\xi }}}_n-\mathbb{E}{\mathbf{\xi }}_1)$ has asymptotic multivariate normal distribution. The bootstrapped version of ${\overline{\mathbf{\xi }}}_n$ becomes

$${\overline{\mathbf{\xi }}}_n^{*}:=\frac{1}{n}\sum _{i=1}^n{\mathbf{\xi }}_i^{*}.$$

Afterwards, it is necessary to asymptotically compare the distributions of

$$\sqrt{n}({\overline{\mathbf{\xi }}}_n-\mathbb{E}{\mathbf{\xi }}_1)\mathrm{and}\sqrt{n}({\overline{\mathbf{\xi }}}_n^{*}-{\overline{\mathbf{\xi }}}_n)$$

In a proper mathematical way to be sure that the empirical distribution of the bootstrap estimate ${\overline{\mathbf{\xi }}}_n^{*}$ of the mean can be used instead of the distribution of ${\overline{\mathbf{\xi }}}_n$. The asymptotic closeness of $\sqrt{n}({\overline{\mathbf{\xi }}}_n-\mathbb{E}{\mathbf{\xi }}_1)$ and $\sqrt{n}({\overline{\mathbf{\xi }}}_n^{*}-{\overline{\mathbf{\xi }}}_n)$ will be clarified and proved later on in Section 5. An algorithm for the independent bootstrap is shown in Procedure 1 and its validity will be proved in Theorem 6.

Procedure 1 Independent bootstrap for the sample mean.

Input: Data consisting of n IID vectors of observations ${\mathbf{\xi }}_i$.

Output: Empirical bootstrap distribution of ${\overline{\mathbf{\xi }}}_n$, i.e., the empirical distribution, where the probability mass $1/B$ concentrates at each of ${}_{\left(1\right)}{\overline{\mathbf{\xi }}}_n^{*},\dots ,{}_{\left(B\right)}{\overline{\mathbf{\xi }}}_n^{*}$.

1: calculate the sample mean ${\overline{\mathbf{\xi }}}_n$ 2: for$b=1$ to B do $//$ repeat in order to obtain empirical distribution of ${\overline{\mathbf{\xi }}}_n$ 3:  $[{}_{\left(b\right)}{\mathbf{\xi }}_1^{*},\dots ,{}_{\left(b\right)}{\mathbf{\xi }}_n^{*}]$ resampled with replacement from the columns of $[{\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n]$ 4:  re-calculate ${}_{\left(b\right)}{\overline{\mathbf{\xi }}}_n^{*}\leftarrow n^{-1}{\sum }_{i=1}^n{}_{\left(b\right)}{\mathbf{\xi }}_i^{*}$ 5: end for

It is silently supposed that the bootstrapped sample is of the same size as the original one, i.e., ${\left\{{\mathbf{\xi }}_i\right\}}_{i=1}^n$ and ${\left\{{\mathbf{\xi }}_i^{*}\right\}}_{i=1}^n$. Generally, one may consider resampled bootstrapped data ${\left\{{\mathbf{\xi }}_i^{*}\right\}}_{i=1}^m$ consisting of m resamples from the data ${\left\{{\mathbf{\xi }}_i\right\}}_{i=1}^n$ having sample size n. Thereby, an additional condition needs to be postulated on the rate of the sample sizes:

$$m=\mathcal{O}\left(n\right),n\to \infty \&n=\mathcal{O}\left(m\right),m\to \infty .$$

There is, however, no need to distinguish between the same sample size and two different sample sizes (the original one and the bootstrap one), which are asymptotically equivalent, at least from the theoretical asymptotic point of view. However, there could be some computational improvements when considering various samples size of the resampled data, which is not the target of this research.

2.2. Moving Block Bootstrap

Intuitively, a problem will arise when considering dependent and/or not identically distributed observations. A generalization of the independent bootstrap (case sampling with replacement)—block bootstrap—can be used. Instead of sampling individual cases, the blocks of adjacent observations are resampled with replacement. Stacking individual adjacent cases together into one solid block partly preserves the dependence between consecutive observations. Since the “weak” dependence can be seen as an asymptotic independence, the blocks can be resampled independently. It is a way how to achieve that the dependence between faraway observations is vanishing.

A plethora of types of block bootstrap techniques were suggested. A comprehensive summary is provided by [6]. In general, the way of drawing the blocks of observations defines the difference among the block bootstrap versions. Bootstrapping blocks, which do not overlap, is performed in the non-overlapping block bootstrap. Since some observations are not allowed to be joined into the same block, this approach is less efficient for estimation [20]. Therefore, the moving block bootstrap (MBB) is considered here. The key idea of the MBB is forming the consecutive block of observations from the previous one through shifting the “stacking window” by one observation ahead. The MBB technique for the sample mean of multivariate observations is described in Procedure 2 in detail.

Procedure 2 Moving block bootstrap for the sample mean.

Input: Data consisting of n NINID vectors of observations ${\mathbf{\xi }}_i$ and $n=mb$.

Output: Empirical bootstrap distribution of sample mean ${\overline{\mathbf{\xi }}}_n$, i.e., the empirical distribution, where the probability mass $1/D$ concentrates at each of ${}_{\left(1\right)}{\overline{\mathbf{\xi }}}_n^{*},\dots ,{}_{\left(D\right)}{\overline{\mathbf{\xi }}}_n^{*}$.

1: define ${\mathbf{B}}_j$ as the block of b consecutive ${\mathbf{\xi }}_i$’s starting from ${\mathbf{\xi }}_j$, that is ${\mathbf{B}}_j=[{\mathbf{\xi }}_j,\dots ,{\mathbf{\xi }}_{j+b-1}]$ for $j=1,\dots ,q$, where $q:=n-b+1$ 2: for$d=1$ to D do $//$ repeat in order to obtain empirical distribution of ${\overline{\mathbf{\xi }}}_n$ 3:  resample with replacement ${}_{\left(d\right)}{\mathbf{C}}_1,\dots ,{}_{\left(d\right)}{\mathbf{C}}_m$ independently from $\{{\mathbf{B}}_1,\dots ,{\mathbf{B}}_q\}$ with equal probability $1/q$, where each ${}_{\left(d\right)}{\mathbf{C}}_i,i=1,\dots ,m$, is a block of size b with ${}_{\left(d\right)}{\mathbf{C}}_i=[{}_{\left(d\right)}{\mathbf{c}}_{i1},\dots ,{}_{\left(d\right)}{\mathbf{c}}_{ib}]$ 4:  the MBB resample of size n, denoted by ${}_{\left(d\right)}{\mathbf{\xi }}_1^{*},\dots ,{}_{\left(d\right)}{\mathbf{\xi }}_n^{*}$, is formed by joining the ${}_{\left(d\right)}{\mathbf{C}}_1,\dots ,{}_{\left(d\right)}{\mathbf{C}}_m$ to one big block, i.e., ${}_{\left(d\right)}{\mathbf{\xi }}_i^{*}={}_{\left(d\right)}{\mathbf{c}}_{\tau \nu }$ for $\tau =\left[\right(i-1)/b]+1$, $\nu =i-b\tau$, and $i=1,\dots ,n//$${}_{\left(d\right)}{\mathsf{\Xi }}^{*}\equiv [{}_{\left(d\right)}{\mathbf{\xi }}_1^{*},\dots ,{}_{\left(d\right)}{\mathbf{\xi }}_n^{*}]$ is called the MBB version of $\mathsf{\Xi }\equiv {[{\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n]}^{\top }$. 5:  let the resample average be ${}_{\left(d\right)}{\overline{\mathbf{\xi }}}_n^{*}\leftarrow n^{-1}{\sum }_{i=1}^n{}_{\left(d\right)}{\mathbf{\xi }}_i^{*}$ 6: end for

Let ${\mathbb{P}}^{*}$ be the (bootstrap) distribution of ${}_{\left(d\right)}{\mathbf{C}}_i$ conditional on the sample $\{{\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n\}$. So, given ${\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n$, the m random blocks, ${}_{\left(d\right)}{\mathbf{C}}_1,\dots ,{}_{\left(d\right)}{\mathbf{C}}_m$, are IID distributed according to ${\mathbb{P}}^{*}$. The length of the blocks—blocksize—is denoted by $b\in \mathbb{N}$. Without loss of generality to the asymptotic properties, let us suppose that $b\mid n$, i.e., there exist $m\in \mathbb{N}$ such that $n=mb$. In other words, we just neglect an integer division problem. For practical and computational purposes, if $b\nmid n$, then we can truncate the quotient $n/b$ to an integer value, see [21].

An extension of the MBB is a circular block bootstrap, where the observations are not ordered on a single line, but they are put into a circle. The order of the observations is preserved with the only exception that the last observation on the circle is followed by the first one. Hence, the stacking window can join the first and the last observations into one block. The application of the circular block bootstrap as an extension of the MBB is postponed for some further work and is not considered in this paper.

2.3. Blocksize

A length of the blocks–the blocksize b–in the MBB procedure is a crucial decision. It indeed affects the bootstrapped statistics and the consequent statistical inference. The blocksize can be therefore considered as a nuisance, but also a tuning parameter. It will be derived in the forthcoming theory that $b=o\left(n^{1/2}\right)$ as $n\to \infty$. However, for the practical and computational purposes, this asymptotic choice of b is rather cumbersome. With respect to the simulation studies from [12], it may be concluded that the blocksize choice $b=\mathcal{O}\left(n^{1/3}\right)$ as $n\to \infty$ could be asymptotically optimal according to the minimal mean square error of the moving block bootstrap variance estimator.

3. Types of Bootstrap Convergences

We would like to show that $\sqrt{n}({\overline{\mathbf{\xi }}}_n-\mathbb{E}{\mathbf{\xi }}_1)$ and $\sqrt{n}({\overline{\mathbf{\xi }}}_n^{*}-{\overline{\mathbf{\xi }}}_n)$asymptotically coincide. This means that using the bootstrap distribution is no worse than using the asymptotic normal approximation. However, it does not mean that the bootstrap distribution better approximates the finite sample distribution of $\sqrt{n}({\overline{\mathbf{\xi }}}_n-\mathbb{E}{\mathbf{\xi }}_1)$. To state this mathematically, we firstly need some formalization. For the rest of this paper, we link $\parallel ·\parallel$ together with any unitarily invariant matrix norm, e.g., the Frobenius matrix norm (and, in case of vectors, with the Euclidean norm).

Suppose that ${\{{\mathbf{\xi }}_n,{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n,{\mathbf{\zeta }}_n^{*},{\mathbf{\chi }}_n\}}_{n=1}^{\infty }$ are sequences of random vectors/matrices, which elements exist on a probability space $(\mathsf{\Omega },\mathcal{F},\mathbb{P})$. The components of these sequences do not necessarily have to have the same dimension, e.g., ${\mathbf{\zeta }}_n$ and ${\mathbf{\zeta }}_{n+1}$ can have different dimensions for some $n\in \mathbb{N}$. Let us define a conditional probability given ${\mathbf{\zeta }}_n$

$${\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}[·]:={\mathbb{E}}_{\mathbb{P}}[\mathcal{I}(·)|{\mathbf{\zeta }}_n].$$

Definition 1. 

Conditional weak convergence almost surely and in probability to each other. Let ${\{{\mathbf{\xi }}_n,{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n\}}_{n=1}^{\infty }$ be sequences of random vectors/matrices. If for every real-valued bounded continuous function f holds

$$\mathbb{E}\left[f\left({\mathbf{\xi }}_n^{*}\right)\right]-\mathbb{E}\left[f\left({\mathbf{\xi }}_n\right)\right]\underset{n\to \infty }{\to }0,$$

then ${\mathbf{\xi }}_n^{*}$ and ${\mathbf{\xi }}_n$ are said to be approaching each other in distribution. In short, we write

$${\mathbf{\xi }}_n^{*}\underset{n\to \infty }{\overset{\mathcal{D}}{⟷}}{\mathbf{\xi }}_n.$$

if for every real-valued bounded continuous function f holds

$$\mathbb{E}\left[f\left({\mathbf{\xi }}_n^{*}\right)|{\mathbf{\zeta }}_n\right]-\mathbb{E}\left[f\left({\mathbf{\xi }}_n\right)\right]\underset{n\to \infty }{\overset{\left[\mathbb{P}\right]-a.s.}{\to }}0,$$

then ${\mathbf{\xi }}_n^{*}$ conditioned on ${\mathbf{\zeta }}_n$ and ${\mathbf{\xi }}_n$ are said to be approaching each other in distribution $\left[\mathbb{P}\right]$-almost surely along ${\mathbf{\zeta }}_n$. In short, we write

$${\mathbf{\xi }}_n^{*}|{\mathbf{\zeta }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\right[\mathbb{P}]-a.s.)}{⟷}}{\mathbf{\xi }}_n.$$

if for every real-valued bounded continuous function f holds

$$\mathbb{E}\left[f\left({\mathbf{\xi }}_n^{*}\right)|{\mathbf{\zeta }}_n\right]-\mathbb{E}\left[f\left({\mathbf{\xi }}_n\right)\right]\underset{n\to \infty }{\overset{\mathbb{P}}{\to }}0,$$

then ${\mathbf{\xi }}_n^{*}$ conditioned on ${\mathbf{\zeta }}_n$ and ${\mathbf{\xi }}_n$ are said to be approaching each other in distribution in probability $\mathbb{P}$ along ${\mathbf{\zeta }}_n$. In short, we write

$${\mathbf{\xi }}_n^{*}|{\mathbf{\zeta }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{⟷}}{\mathbf{\xi }}_n.$$

In the same manner as above, we may define the distributional convergence on the “conditional” (resampled) level to a random variable ${\mathbf{\xi }}_0$ (“constant” law).

Definition 2. 

Conditional weak convergence almost surely and in probability to a constant law. Let ${\{{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n\}}_{n=1}^{\infty }$ be sequences of random vectors/matrices and ${\mathbf{\xi }}_0$ be a random vector/matrix. If for every real-valued bounded continuous function f holds

$$\mathbb{E}\left[f\left({\mathbf{\xi }}_n^{*}\right)|{\mathbf{\zeta }}_n\right]\underset{n\to \infty }{\overset{\left[\mathbb{P}\right]-a.s.}{\to }}\mathbb{E}\left[f\left({\mathbf{\xi }}_0\right)\right],$$

then ${\mathbf{\xi }}_n^{*}$ conditioned on ${\mathbf{\zeta }}_n$ is said to converge to ${\mathbf{\xi }}_0$ in distribution $\left[\mathbb{P}\right]$-almost surely along ${\mathbf{\zeta }}_n$. In short, we write

$${\mathbf{\xi }}_n^{*}|{\mathbf{\zeta }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\right[\mathbb{P}]-a.s.)}{\to }}{\mathbf{\xi }}_0.$$

if for every real-valued bounded continuous function f holds

$$\mathbb{E}\left[f\left({\mathbf{\xi }}_n^{*}\right)|{\mathbf{\zeta }}_n\right]\underset{n\to \infty }{\overset{\mathbb{P}}{\to }}\mathbb{E}\left[f\left({\mathbf{\xi }}_0\right)\right],$$

then ${\mathbf{\xi }}_n^{*}$ conditioned on ${\mathbf{\zeta }}_n$ is said to converge to ${\mathbf{\xi }}_0$ in distribution in probability $\mathbb{P}$ along ${\mathbf{\zeta }}_n$. In short, we write

$${\mathbf{\xi }}_n^{*}|{\mathbf{\zeta }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\xi }}_0.$$

Approaching in distribution to each other is often called weakly approaching to each other (almost surely or in probability along some sequence). The portmanteau lemma [22] ensures that Definition 1 is indeed appropriate. Hence, it gives equivalent characterizations for the weak convergence in distribution. To define convergence in probability ${\mathbb{P}}^{*}$, it means, convergences on the conditional level, two types of convergence in probability ${\mathbb{P}}^{*}$ are defined: convergence in probability $\mathbb{P}$ and convergence in $\left[\mathbb{P}\right]$-almost surely.

Definition 3. 

Convergence in conditional probability. Let ${\{{\mathbf{\xi }}_n,{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n\}}_{n=1}^{\infty }$ be sequences of random vectors/matrices. To say that ${\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n$ converges in probability ${\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}$ to zero $\left[\mathbb{P}\right]$-almost surely as n tends to infinity, i.e.,

$${\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n\underset{n\to \infty }{\overset{{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}(\left[\mathbb{P}\right]-a.s.)}{\to }}\mathbf{0},$$

means

$$\forall ϵ>0:\mathbb{P}\left[\underset{n\to \infty }{lim}{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}[\parallel {\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n\parallel \ge ϵ]=0\right]=1.$$

(1)

to say that ${\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n$ converges in probability ${\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}$ to zero in probability $\mathbb{P}$ as n tends to infinity, i.e.,

$${\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n\underset{n\to \infty }{\overset{{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}\left(\mathbb{P}\right)}{\to }}\mathbf{0},$$

means

$$\forall ϵ>0,\forall \tau >0:\underset{n\to \infty }{lim}\mathbb{P}\left[{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}[\parallel {\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n\parallel \ge ϵ]\ge \tau \right]=0.$$

(2)

Alternatively, (1) and (2) from Definition 3 can be read as

$$\forall ϵ>0:\left\{{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}[\parallel {\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n\parallel \ge ϵ]\underset{n\to \infty }{\overset{\left[\mathbb{P}\right]-a.s.}{\to }}0\right\}$$

and

$$\forall ϵ>0:\left\{{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}[\parallel {\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_n\parallel \ge ϵ]\underset{n\to \infty }{\overset{\mathbb{P}}{\to }}0\right\},$$

respectively.

In the same manner as above, we may define the convergence in probability ${\mathbb{P}}^{*}$ on the resampled level to a random variable ${\mathbf{\xi }}_0$ (does not depend on n).

Definition 4. 

Convergence in conditional probability to a variable. Let ${\{{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n\}}_{n=1}^{\infty }$ be sequences of random vectors/matrices and ${\mathbf{\xi }}_0$ is a random vector/matrix. To say that ${\mathbf{\xi }}_n^{*}$ converges to ${\mathbf{\xi }}_0$ in probability ${\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}$$\left[\mathbb{P}\right]$-almost surely as n tends to infinity, i.e.,

$${\mathbf{\xi }}_n^{*}\underset{n\to \infty }{\overset{{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\xi }}_0,$$

means that ${\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_0$ converges in probability ${\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}$ to zero $\left[\mathbb{P}\right]$-almost surely as n tends to infinity. To say that ${\mathbf{\xi }}_n^{*}$ converges to ${\mathbf{\xi }}_0$ in probability ${\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}$ in probability $\mathbb{P}$ as n tends to infinity, i.e.,

$${\mathbf{\xi }}_n^{*}\underset{n\to \infty }{\overset{{\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}\left(\mathbb{P}\right)}{\to }}{\mathbf{\xi }}_0,$$

means that ${\mathbf{\xi }}_n^{*}-{\mathbf{\xi }}_0$ converges in probability ${\mathbb{P}}_{{\mathbf{\zeta }}_n}^{*}$ to zero in probability $\mathbb{P}$ as n tends to infinity.

3.1. Properties of the Bootstrap Convergences

Important results concerning previously defined types of convergences summarized in the forthcoming will play a crucial role later on. Prokhorov’s theorem can be extended into our setup.

Lemma 1. 

Assume that ${\left\{{\mathbf{\xi }}_n\right\}}_{n=1}^{\infty }$ is tight. Then the following statements are equivalent:

(i) 

$${\mathbf{\xi }}_n^{*}|{\mathbf{\zeta }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{⟷}}{\mathbf{\xi }}_n.$$

(ii) 

For each subsequence ${\left\{n_i\right\}}_{i=1}^{\infty }$ such that

$${\mathbf{\xi }}_{n_i}\underset{i\to \infty }{\overset{\mathcal{D}}{\to }}{\mathbf{\xi }}_0$$

for some random vector/matrix ${\mathbf{\xi }}_0$,

$${\mathbf{\xi }}_{n_i}^{*}|{\mathbf{\zeta }}_{n_i}\underset{i\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\xi }}_0$$

too.

(iii) 

For each subsequence ${\left\{n_i\right\}}_{i=1}^{\infty }$ there exists a subsequence ${\left\{n_{i_k}\right\}}_{k=1}^{\infty }$ such that ${\mathbf{\xi }}_{n_{i_k}}^{*}$ conditional on ${\mathbf{\zeta }}_{n_{i_k}}$ converges in distribution in probability $\mathbb{P}$ to the distributional limit of ${\mathbf{\xi }}_{n_{i_k}}$ as $k\to \infty$.

We need to extend Slutsky’s theorem for our “bootstrap world”, i.e., to have a stability property for conditional distributions.

Theorem 1. 

Slutsky’s extended theorem. Suppose that ${\{{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n^{*},{\mathbf{\chi }}_n\}}_{n=1}^{\infty }$ are sequences of random vectors/matrices. Then,

$${\mathbf{\xi }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\xi }}_0$$

(3)

and

$${\mathbf{\zeta }}_n^{*}\underset{n\to \infty }{\overset{{\mathbb{P}}_{{\mathbf{\chi }}_n}^{*}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\zeta }}_0,$$

(4)

where ${\mathbf{\xi }}_0$ is a random matrix/vector and ${\mathbf{\zeta }}_0$ is a non-random element, implies (for suitable vector/matrix dimensions):

(i) 

$[{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n^{*}]|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}[{\mathbf{\xi }}_0,{\mathbf{\zeta }}_0];$

(ii) 

$[{\mathbf{\zeta }}_n^{*},{\mathbf{\xi }}_n^{*}]|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}[{\mathbf{\zeta }}_0,{\mathbf{\xi }}_0];$

(iii) 

${\mathbf{\xi }}_n^{*}+{\mathbf{\zeta }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\xi }}_0+{\mathbf{\zeta }}_0$;

(iv) 

${\mathbf{\xi }}_n^{*}{\mathbf{\zeta }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\xi }}_0{\mathbf{\zeta }}_0$;

(v) 

${\mathbf{\zeta }}_n^{*}{\mathbf{\xi }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\zeta }}_0{\mathbf{\xi }}_0$;

(vi) 

${\left({\mathbf{\zeta }}_n^{*}\right)}^{-1}{\mathbf{\xi }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\zeta }}_0^{-1}{\mathbf{\xi }}_0$, provided that ${\mathbf{\zeta }}_n^{*}$ and ${\mathbf{\zeta }}_0$ are invertible;

(vii) 

${\mathbf{\xi }}_n^{*}{\left({\mathbf{\zeta }}_n^{*}\right)}^{-1}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}(\left[\mathbb{P}\right]-a.s.)}{\to }}{\mathbf{\xi }}_0{\mathbf{\zeta }}_0^{-1}$, provided that ${\mathbf{\zeta }}_n^{*}$ and ${\mathbf{\zeta }}_0$ are invertible.

Moreover,

$${\mathbf{\xi }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\xi }}_0$$

(5)

and

$${\mathbf{\zeta }}_n^{*}\underset{n\to \infty }{\overset{{\mathbb{P}}_{{\mathbf{\chi }}_n}^{*}\left(\mathbb{P}\right)}{\to }}{\mathbf{\zeta }}_0,$$

(6)

where ${\mathbf{\xi }}_0$ is a random matrix/vector and ${\mathbf{\zeta }}_0$ is a non-random element, implies (for suitable vector/matrix dimensions):

(viii) 

$[{\mathbf{\xi }}_n^{*},{\mathbf{\zeta }}_n^{*}]|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}[{\mathbf{\xi }}_0,{\mathbf{\zeta }}_0];$

(ix) 

$[{\mathbf{\zeta }}_n^{*},{\mathbf{\xi }}_n^{*}]|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}[{\mathbf{\zeta }}_0,{\mathbf{\xi }}_0];$

(x) 

${\mathbf{\xi }}_n^{*}+{\mathbf{\zeta }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\xi }}_0+{\mathbf{\zeta }}_0$;

(xi) 

${\mathbf{\xi }}_n^{*}{\mathbf{\zeta }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\xi }}_0{\mathbf{\zeta }}_0$;

(xii) 

${\mathbf{\zeta }}_n^{*}{\mathbf{\xi }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\zeta }}_0{\mathbf{\xi }}_0$;

(xiii) 

${\left({\mathbf{\zeta }}_n^{*}\right)}^{-1}{\mathbf{\xi }}_n^{*}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\zeta }}_0^{-1}{\mathbf{\xi }}_0$, provided that ${\mathbf{\zeta }}_n^{*}$ and ${\mathbf{\zeta }}_0$ are invertible;

(xiv) 

${\mathbf{\xi }}_n^{*}{\left({\mathbf{\zeta }}_n^{*}\right)}^{-1}|{\mathbf{\chi }}_n\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{\to }}{\mathbf{\xi }}_0{\mathbf{\zeta }}_0^{-1}$, provided that ${\mathbf{\zeta }}_n^{*}$ and ${\mathbf{\zeta }}_0$ are invertible.

3.2. Weak Dependence

In order to overcome the assumption of independent observations, the dependence between data needs to be specified. It is assumed that ${\left\{{\mathbf{\xi }}_n\right\}}_{n=1}^{\infty }$ is a sequence of random elements on a probability space $(\mathsf{\Omega },\mathcal{F},\mathbb{P})$. For sub-$\sigma$-fields $\mathcal{A},\mathcal{B}\subseteq \mathcal{F}$, we define

$$\begin{array}{cc}\hfill \alpha (\mathcal{A},\mathcal{B})& :=\underset{A\in \mathcal{A},B\in \mathcal{B}}{sup}\left|\mathbb{P}(A\cap B)-\mathbb{P}\left(A\right)\mathbb{P}\left(B\right)\right|,\hfill \\ \hfill \phi (\mathcal{A},\mathcal{B})& :=\underset{A\in \mathcal{A},B\in \mathcal{B},\mathbb{P}\left(A\right)>0}{sup}\left|\mathbb{P}(B|A)-\mathbb{P}(B)\right|.\hfill \end{array}$$

Intuitively, $\alpha$ and $\phi$ measure the dependence of the events in $\mathcal{B}$ on those in $\mathcal{A}$. Henceforth, let us define a filtration ${\mathcal{F}}_m^n:=\sigma ({\mathbf{\xi }}_i\in \mathcal{F},m\le i\le n)$.

There are many ways how to describe weak dependence or, in other words, asymptotic independence of random variables [23]. Here, we concentrate on two approaches, however other ways of defining dependence can be involved, [24]. A sequence ${\left\{{\mathbf{\xi }}_n\right\}}_{n=1}^{\infty }$ of random elements (e.g., variables) is said to be strong mixing ($\alpha$-mixing) if

$$\alpha \left(n\right):=\underset{k\in \mathbb{N}}{sup}\alpha ({\mathcal{F}}_1^k,{\mathcal{F}}_{k+n}^{\infty })\to 0,n\to \infty ;$$

(7)

Moreover, it is said to be uniformly strong mixing ($\phi$-mixing) if

$$\phi \left(n\right):=\underset{k\in \mathbb{N}}{sup}\phi ({\mathcal{F}}_1^k,{\mathcal{F}}_{k+n}^{\infty })\to 0,n\to \infty .$$

(8)

Uniformly strong mixing–introduced by [25]–implies strong mixing [26], which was presented by [27]. Coefficients of dependence $\alpha \left(n\right)$ and $\phi \left(n\right)$ measure how much dependence exists between events separated by at least n observations or time periods [28].

In [29], a class of m-dependent processes was comprehensively and intensively analyzed. These types of time series are $\phi$-mixing, since are finite order ARMA processes with innovations satisfying Doeblin’s condition, ([30], p. 168) or ([31], p. 192). Hence, the ARMA processes with continuously distributed stationary innovations and bounded variance are $\alpha$-mixing and, thus, $\phi$-mixing. Finite order processes, which do not satisfy Doeblin’s condition, can be shown to be $\alpha$-mixing ([32], pp. 312–313). Reference [33] provides general conditions under which stationary Markov processes are $\alpha$-mixing. Since functions of mixing processes are themselves mixing [23], time-varying functions of any of the processes just mentioned are mixing as well.

It has to be emphasized that any form of errors’ stationarity is not assumed. Omitting this, sometimes restrictive, assumption strengthen our results. It is obvious that $\alpha (\mathcal{A},\mathcal{B})=\alpha (\mathcal{B},\mathcal{A})$ for arbitrary sub-$\sigma$-fields $\mathcal{A},\mathcal{B}\subseteq \mathcal{F}$. This type of symmetry does not hold for $\phi$-dependence. Indeed, ([33], pp. 213–214) constructed some strictly stationary Markov chains that are $\phi$-mixing but not “time-reversed” $\phi$-mixing. Therefore, it is not possible to “interchange” the past with the future regarding the definition of the $\phi$-mixing coefficient.

A strong law of large numbers (SLLN) for $\alpha$-dependent non-identically distributed variables needs to be recalled.

Lemma 2. 

Strong law of large numbers for α-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of α-mixing random variables satisfying

$$\underset{n\in \mathbb{N}}{sup}\mathbb{E}{|{\xi }_n|}^q<\infty$$

(9)

for some $q>1$. Suppose that there exists $\delta >0$ such that as $n\to \infty$,

$$\alpha \left(n\right)=\left\{\begin{array}{cc}\mathcal{O}\left(n^{-\frac{q}{2q-2}-\delta }\right)\hfill & if1<q<2,\hfill \\ \mathcal{O}\left(n^{-\frac{2}{q}-\delta }\right)\hfill & ifq\ge 2.\hfill \end{array}\right.$$

(10)

then

$$\underset{n\to \infty }{lim}\frac{{\sum }_{i=1}^n({\xi }_i-\mathbb{E}{\xi }_i)}{n}=0a.s.$$

Furthermore, a SLLN for $\phi$-dependent non-identically distributed variables is desired as well.

Lemma 3. 

Strong law of large numbers for φ-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean φ-mixing random variables satisfying

$$\sum _{n=1}^{\infty }\sqrt{\phi \left(n\right)}<\infty$$

(11)

and let ${\left\{b_n\right\}}_{n=1}^{\infty }$ be a non-decreasing unbounded sequence of positive numbers. Assume that

$$\sum _{n=1}^{\infty }\frac{\mathbb{E}{\xi }_n^2}{b_n^2}<\infty ,$$

(12)

then

$$\underset{n\to \infty }{lim}\frac{{\sum }_{i=1}^n{\xi }_i}{b_n}=0a.s.$$

For a given random sequence ${\xi }_{\circ }\equiv {\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ of random elements, the dependence coefficients $\alpha \left(n\right)$ will be denoted $\alpha ({\xi }_{\circ },n)$. Analogous notation is used for $\phi$-mixing sequences. Moreover, an auxiliary lemma for latter application of the SLLN for non-identically distributed random variables is stated.

The following lemma describes an asymptotic behavior of $\alpha$- and $\phi$-mixing coefficients of the corresponding random sequences after a transformation. More precisely, the Borel transformation preserves the property of $\alpha$- and $\phi$-mixing and, moreover, sustains the rate of the mixing coefficients.

Lemma 4. 

Suppose that for each $m=1,2,\dots$, ${\xi }_{\circ }^{\left(m\right)}:={\{{\xi }_k^{\left(m\right)}\}}_{k\in \mathbb{Z}}$ is a sequence of random variables. Suppose the sequences ${\xi }_{\circ }^{\left(m\right)}$, $m=1,2,\dots$ are independent of each other. Suppose that for each $k\in \mathbb{Z}$, $h_k:\mathbb{R}\times \mathbb{R}\times \dots \to \mathbb{R}$ is a Borel function. Define the sequence ${\xi }_{\circ }:={\left\{{\xi }_k\right\}}_{k\in \mathbb{Z}}$ of random variables by

$${\xi }_k:=h_k\left({\xi }_k^{\left(1\right)},{\xi }_k^{\left(2\right)},\dots \right),k\in \mathbb{Z}.$$

then for each $n\ge 1$, the following statements hold:

(i) 

$\alpha ({\xi }_{\circ },n)\le {\sum }_{m=1}^{\infty }\alpha ({\xi }_{\circ }^{\left(m\right)},n)$,

(ii) 

$\phi ({\xi }_{\circ },n)\le {\sum }_{m=1}^{\infty }\phi ({\xi }_{\circ }^{\left(m\right)},n)$.

Let $S_n:={\sum }_{i=1}^n{\xi }_i$ and ${\varsigma }_n^2:=\mathbb{V}ar{S}_n$. For a random element from the Skorokhod space $D[0,1]$,

$${\mathcal{W}}_n\left(t\right):=\frac{S_{\left[nt\right]}}{{\varsigma }_n},0\le t\le 1,$$

(13)

where $[·]$ denotes the nearest integer function, a functional central limit theorem—also called a weak invariance principle—can be applied. This principle, now for $\alpha$-mixing variables, will be postulated.

Lemma 5. 

WIP for α-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean α-mixing random variables with

$$\underset{n\in \mathbb{N}}{sup}\mathbb{E}{|{\xi }_n|}^{2+\omega }<\infty$$

(14)

and

$$\sum _{n=1}^{\infty }\alpha {\left(n\right)}^{\omega /(2+\omega )}<\infty$$

(15)

for some $\omega >0$. Suppose that

$$\frac{\mathbb{E}{S}_n^2}{n}\to {\varsigma }^2>0,n\to \infty$$

(16)

is satisfied. Then

$${\mathcal{W}}_n\stackrel{D[0,1]}{\to }\mathcal{W},n\to \infty .$$

(17)

where $\mathcal{W}$ stands for the standard Wiener process.

Since the central limit theorem is just a special case of the weak invariance principle, then a corollary of previous Lemma 5 can be stated.

Corollary 1. 

Central limit theorem for α-mixing. Suppose that all the assumptions of Lemma 5 on a sequence of zero mean α-mixing random variables ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ are satisfied. Then

$$\frac{S_n}{{\varsigma }_n}\stackrel{\mathcal{D}}{\to }\mathcal{N}(0,1),n\to \infty .$$

(18)

Lemma 6. 

Lindeberg central limit theorem for φ-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean φ-mixing random variables having finite variance. Suppose that the Lindeberg condition

$$\forall \delta >0:\underset{n\to \infty }{lim}\frac{1}{{\varsigma }_n^2}\sum _{i=1}^n\mathbb{E}{\xi }_i^2\mathcal{I}\{|{\xi }_i|>\delta {\varsigma }_n\}=0$$

(19)

is satisfied. Then

$$\frac{S_n}{{\varsigma }_n}\stackrel{\mathcal{D}}{\to }\mathcal{N}(0,1),n\to \infty .$$

The Lindeberg condition (19) can be replaced by a stronger type of the Lyapunov condition. This fact leads into the following corollary, which is more comfortable for us from the point of applicability.

Corollary 2. 

Central limit theorem for φ-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean φ-mixing random variables such that

$$\underset{n\in \mathbb{N}}{sup}\mathbb{E}{|{\xi }_n|}^{2+\omega }<\infty$$

(20)

for some $\omega >0$ and

$$\frac{\mathbb{E}{S}_n^2}{n}\to {\varsigma }^2>0,n\to \infty .$$

(21)

then

$$\frac{S_n}{{\varsigma }_n}\stackrel{\mathcal{D}}{\to }\mathcal{N}(0,1),n\to \infty .$$

(22)

Assumption (21) may even be replaced by a weaker one:

$$\underset{n\to \infty }{lim\; inf}\frac{\mathbb{E}{S}_n^2}{n}={\varsigma }^2>0,$$

where the limit inferior is used instead of the original limit. Assuming that a sequence of random variables is $\phi$-mixing implies that this sequence is $\alpha$-mixing. On the other hand, the central limit theorem for $\phi$-mixing (Corollary 2) has weaker assumptions than the central limit theorem for $\alpha$-mixing (Corollary 1). Indeed, Corollary 2 does not require any assumption on mixing rate$\phi \left(n\right)$ such as Assumption (15) on $\alpha$-mixing rates.

The previous theoretical results contain the variance ${\varsigma }_n^2$ for the underlying process of random variables. One may additionally assume that

$$\underset{n\to \infty }{lim}\frac{{\varsigma }_n^2}{n}={\varsigma }^2,$$

where ${\varsigma }^2$ is the so-called long run variance, which sometimes needs to be estimated. If ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ are zero mean and stationary, then this long run variance can be decomposed in the following way

$${\varsigma }^2=\mathbb{E}{\xi }_1^2+2\sum _{i=1}^{\infty }\mathbb{E}{\xi }_1{\xi }_{i+1}.$$

Often, the Bartlett estimator is used to estimate the long run variance, i.e.,

$${\widehat{\varsigma }}_n^2\left(m\right)=\widehat{R}\left(0\right)+2\sum _{1\le k\le m}\left(1-\frac{k}{m}\right)\widehat{R}\left(k\right),m<n,$$

where

$$\widehat{R}\left(k\right)=\frac{1}{n}\sum _{1\le i\le n-k}({\xi }_i-{\overline{\xi }}_n)({\xi }_{i+k}-{\overline{\xi }}_n),0\le k<n.$$

The consistency properties of the above described Bartlett estimator and of its modification are studied in [34]. Other similar types of estimators can be used instead, for instance Parzen kernels [35].

4. Bootstrap Laws of Large Numbers

A theoretical mid-step for showing validity of the bootstrap methods are the bootstrap laws of large numbers. From now on, we mean by a bootstrap version of $\mathbf{\xi }\equiv {[{\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n]}^{\top }$ its (randomly) resampled sequence with replacement—denoted by ${\mathbf{\xi }}^{*}\equiv {[{\mathbf{\xi }}_1^{*},\dots ,{\mathbf{\xi }}_n^{*}]}^{\top }$—with the same length, where for each $i\in \{1,\dots ,n\}$ holds ${\mathbb{P}}_{\mathbf{\xi }}^{*}[{\mathbf{\xi }}_i^{*}={\mathbf{\xi }}_j]=1/n,j=1,\dots ,n$. So, ${\mathbf{\xi }}_i^{*}$ has a discrete uniform distribution on $\{{\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n\}$ for every $i=1,\dots ,n$.

4.1. Bootstrap Weak LLN for Independent Data

First of all, a base stone for the consistency of the independent bootstrap lies in the bootstrap weak law of large numbers (BWLLN).

Theorem 2. 

Bootstrap weak law of large numbers. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of independent random variables. If

$$\underset{n\in \mathbb{N}}{sup}{\mathbb{E}}_{\mathbb{P}}{\xi }_n^2<\infty ,$$

(23)

then

$$n^{-1}\sum _{i=1}^n{\xi }_i^{*}-n^{-1}\sum _{i=1}^n{\xi }_i\underset{n\to \infty }{\overset{{\mathbb{P}}_{\mathbf{\xi }}^{*}\left(\mathbb{P}\right)}{\to }}0,$$

(24)

where ${\mathbf{\xi }}^{*}\equiv {[{\xi }_1^{*},\dots ,{\xi }_n^{*}]}^{\top }$ is the bootstrapped version of $\mathbf{\xi }\equiv {[{\xi }_1,\dots ,{\xi }_n]}^{\top }$.

4.2. Bootstrap Weak LLNs for NINID

Now, the BWLLN for the non-stationary $\alpha$-mixing is given.

Theorem 3. 

Bootstrap weak law of large numbers for α-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean α-mixing random variables satisfying

$$\underset{n\in \mathbb{N}}{sup}\mathbb{E}{\xi }_n^2<\infty .$$

(25)

assume that there exists $\delta >0$ such that

$$\alpha \left(n\right)=\mathcal{O}\left(n^{-1-\delta }\right),n\to \infty .$$

(26)

if $b\to \infty$ and $b=o\left(n^{1/2}\right),n\to \infty$, then, under the MBB Procedure 2,

$$n^{-1}\sum _{i=1}^n{\xi }_i^{*}-n^{-1}\sum _{i=1}^n{\xi }_i\underset{n\to \infty }{\overset{{\mathbb{P}}_{\mathbf{\xi }}^{*}\left(\mathbb{P}\right)}{\to }}0,$$

where ${\mathbf{\xi }}^{*}\equiv {[{\xi }_1^{*},\dots ,{\xi }_n^{*}]}^{\top }$ is the MBB version of $\mathbf{\xi }\equiv {[{\xi }_1,\dots ,{\xi }_n]}^{\top }$.

Similarly, the BWLLN is stated for the $\phi$-mixing sequences.

Theorem 4. 

Bootstrap weak law of large numbers for φ-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean φ-mixing random variables satisfying

$$\sum _{n=1}^{\infty }\frac{\mathbb{E}{\xi }_n^2}{n^2}<\infty$$

and

$$\sum _{n=1}^{\infty }\sqrt{\phi \left(n\right)}<\infty .$$

(27)

if $b\to \infty$ and $b=o\left(n^{1/2}\right),n\to \infty$, then, under the MBB Procedure 2,

$$n^{-1}\sum _{i=1}^n{\xi }_i^{*}-n^{-1}\sum _{i=1}^n{\xi }_i\underset{n\to \infty }{\overset{{\mathbb{P}}_{\mathbf{\xi }}^{*}\left(\mathbb{P}\right)}{\to }}0,$$

where ${\mathbf{\xi }}^{*}\equiv {[{\xi }_1^{*},\dots ,{\xi }_n^{*}]}^{\top }$ is the MBB version of $\mathbf{\xi }\equiv {[{\xi }_1,\dots ,{\xi }_n]}^{\top }$.

5. Bootstrap Central Limit Theorems

If a statistic converges to a normal distribution, then the interest is to asymptotically compare this original limiting distribution to the bootstrap one. The main theoretical results for the asymptotic validity of the bootstrap methods lie in showing that the bootstrap distribution properly mimics the asymptotic one.

5.1. Bootstrap CLT for Independent Data

A pylon for the proof of central limit theorem for the bootstrapped sample is created by an extension of the well-known Berry–Esseen theorem.

Theorem 5. 

Berry–Esseen-Katz theorem. Let g be a non-negative, even, non-decreasing function on $[0,\infty )$ satisfying:

(i) 

${lim}_{x\to \infty }g\left(x\right)=\infty$,

(ii) 

$x/g\left(x\right)$ is defined for all $x\in \mathbb{R}$ and non-decreasing on $[0,\infty )$.

Assume that ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ are IID random variables such that $\mathbb{E}{\xi }_1=0$ and $\mathbb{V}ar{\xi }_1={\varsigma }^2>0$. If

$$\mathbb{E}{\xi }_1^{2}g\left({\xi }_1\right)<\infty ,$$

then there exists a constant $C>0$, such that for all $n\in \mathbb{N}$ holds

$$\underset{x\in \mathbb{R}}{sup}\left|\mathbb{P}\left[\frac{1}{\sqrt{n{\varsigma }^2}}\sum _{i=1}^n{\xi }_i\le x\right]-{\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }}exp\left\{-\frac{t^2}{2}\right\}dt\right|\le \frac{C\mathbb{E}{\xi }_1^{2}g\left({\xi }_1/\varsigma \right)}{{\varsigma }^{2}g\left(\sqrt{n}\right)}.$$

A bootstrap central limit theorem provides the desired approximate distributional closeness and, thus, appropriateness of the bootstrap.

Theorem 6. 

Bootstrap central limit theorem for independent variables. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean independent random variables satisfying

$$\underset{n\in \mathbb{N}}{sup}{\mathbb{E}}_{\mathbb{P}}{\xi }_n^4<\infty .$$

(28)

suppose that ${\mathbf{\xi }}^{*}\equiv {[{\xi }_1^{*},\dots ,{\xi }_n^{*}]}^{\top }$ is the bootstrapped version of $\mathbf{\xi }\equiv {[{\xi }_1,\dots ,{\xi }_n]}^{\top }$ and denote

$${\overline{\xi }}_n:=n^{-1}\sum _{i=1}^n{\xi }_i,{\overline{\xi }}_n^{*}:=n^{-1}\sum _{i=1}^n{\xi }_i^{*},and{\varsigma }_n^2:=\sum _{i=1}^n\mathbb{V}ar{}_{\mathbb{P}}{\xi }_i.$$

if

$$\underset{n\to \infty }{lim\; inf}\frac{{\varsigma }_n^2}{n}={\varsigma }^2>0,$$

(29)

then

$$\underset{x\in \mathbb{R}}{sup}\left|{\mathbb{P}}_{\mathbf{\xi }}^{*}\left[\frac{n}{\sqrt{{\varsigma }_n^2}}\left({\overline{\xi }}_n^{*}-{\overline{\xi }}_n\right)\le x\right]-\mathbb{P}\left[\frac{n}{\sqrt{{\varsigma }_n^2}}{\overline{\xi }}_n\le x\right]\right|\underset{n\to \infty }{\overset{\mathbb{P}}{\to }}0.$$

(30)

Assumption (28) may seem a little bit restrictive. It may be weakened to

$$\sum _{n=1}^{\infty }\frac{{\mathbb{E}}_{\mathbb{P}}{\xi }_n^4}{n^2}<\infty \mathrm{and}\underset{n\in \mathbb{N}}{sup}{\mathbb{E}}_{\mathbb{P}}{|{\xi }_n|}^{2+\omega }<\infty ,\mathrm{for} \mathrm{some}\omega >0;$$

As found out while going through the proof of Theorem 6. On the other hand, the previous weaker premises are rather complicated to verify for transformed errors in the proof of bootstrap consistency, which will be noticed later on. Reference [36] strengthened Assumption (28) and replaced by

$$\underset{n\in \mathbb{N}}{sup}{\mathbb{E}}_{\mathbb{P}}{|\sqrt{n}{\xi }_n|}^{4+\omega }<\infty ,$$

(31)

For some $\omega >0$. Afterwards, bootstrap CLT 6 provides a stronger result:

$$\underset{x\in \mathbb{R}}{sup}\left|{\mathbb{P}}_{\mathbf{\xi }}^{*}\left[\frac{n}{\sqrt{{\varsigma }_n^2}}\left({\overline{\xi }}_n^{*}-{\overline{\xi }}_n\right)\le x\right]-\mathbb{P}\left[\frac{n}{\sqrt{{\varsigma }_n^2}}{\overline{\xi }}_n\le x\right]\right|\underset{n\to \infty }{\overset{\left[\mathbb{P}\right]-a.s.}{\to }}0,$$

(32)

whereas the convergence in distribution in probability is replaced by the convergence in distribution almost surely. In spite of this, Assumption (31) can be considered as too much restrictive.

Our situation would become much easier, when IID variables are assumed. Let us have a look at the proof of Theorem 6. If ${\mathbb{E}}_{\mathbb{P}}{|{\xi }_1|}^{2+\omega }<\infty$ for some $\omega >0$ is additionally assumed, then the right-hand side of (A7) converges to zero $\left[\mathbb{P}\right]$-almost surely. In addition, finite $(2+\omega )$-th moment would be enough to prove (ii) and, thus, Relation (32) holds under such conditions.

The equiboundedness of the fourth moments (28) in the bootstrap CLT is needed, because the second conditional moment is necessary for the existence of $\mathbb{V}ar{}_{{\mathbb{P}}_{\mathbf{\xi }}^{*}}{\xi }_1^{*}$ and, consequently, the equiboundedness of the second moment of the second conditional moment is used for the convergence $\left[\mathbb{P}\right]$-almost surely of $\mathbb{V}ar{}_{{\mathbb{P}}_{\mathbf{\xi }}^{*}}{\xi }_1^{*}$. The equiboundedness of the fourth moments in the BCLT can be weakened when bearing in mind identically distributed variables.

Let us concentrate on the conditional variance of sum of the resampled data. The conditional variance $\mathbb{V}ar{}_{{\mathbb{P}}_{\mathbf{\xi }}^{*}}{\xi }_1^{*}$ used for the normalization in (30) may be simply replaced by $n^{-1}{\varsigma }_n^2$, see the proof of the BCLT (6). Therefore, is makes the assertion of the BCLT even stronger and, hence, more applicable.

A utilization of the Cramér–Wold device helps us to derive a bootstrap version of the CLT for random vectors.

Theorem 7. 

Bootstrap multivariate central limit theorem for independent vectors. Let ${\left\{{\mathbf{\xi }}_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean independent q-dimensional random vectors satisfying

$$\underset{n\in \mathbb{N}}{sup}{\mathbb{E}}_{\mathbb{P}}{|{\xi }_{j,n}|}^4<\infty ,j\in \{1,\dots ,q\},$$

(33)

where ${\mathbf{\xi }}_n\equiv {[{\xi }_{1,n},\dots ,{\xi }_{q,n}]}^{\top }\in {\mathbb{R}}^q,n\in \mathbb{N}$. Assume that ${\mathsf{\Xi }}^{*}\equiv {[{\mathbf{\xi }}_1^{*},\dots ,{\mathbf{\xi }}_n^{*}]}^{\top }$ is the bootstrapped version of $\mathsf{\Xi }\equiv {[{\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_n]}^{\top }$. Denote

$${\overline{\mathbf{\xi }}}_n:=n^{-1}\sum _{i=1}^n{\mathbf{\xi }}_i,{\overline{\mathbf{\xi }}}_n^{*}:=n^{-1}\sum _{i=1}^n{\mathbf{\xi }}_i^{*},and{\mathsf{\Gamma }}_n:=\sum _{i=1}^n\mathbb{V}ar{}_{\mathbb{P}}{\mathbf{\xi }}_i.$$

if

$$\underset{n\to \infty }{lim}\frac{1}{n}{\mathsf{\Gamma }}_n=\mathsf{\Gamma }>\mathbf{0},$$

(34)

then

$$n{\mathsf{\Gamma }}_n^{-1/2}\left({\overline{\mathbf{\xi }}}_n^{*}-{\overline{\mathbf{\xi }}}_n\right)|\mathsf{\Xi }\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{⟷}}n{\mathsf{\Gamma }}_n^{-1/2}{\overline{\mathbf{\xi }}}_n$$

(35)

and, moreover,

$$\sqrt{n}\left({\overline{\mathbf{\xi }}}_n^{*}-{\mathbb{E}}_{{\mathbb{P}}^{*}}{\mathbf{\xi }}_1^{*}\right)|\mathsf{\Xi }\underset{n\to \infty }{\overset{\mathcal{D}\left(\mathbb{P}\right)}{⟷}}\sqrt{n}{\overline{\mathbf{\xi }}}_n.$$

(36)

5.2. Bootstrap CLTs for NINID

Lastly, the central limit theorems for the bootstrapped sample mean from non-stationary strong mixing or uniformly strong mixing sequences are stated.

Theorem 8. 

Bootstrap central limit theorem for α-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean α-mixing random variables with

$$\underset{n\in \mathbb{N}}{sup}\mathbb{E}{|{\xi }_n|}^{4+\omega }<\infty$$

(37)

and

$$\alpha \left(n\right)=\mathcal{O}\left(n^{-1-\delta }\right),n\to \infty$$

(38)

for some $\omega >0$ and $\delta >0$ such that

$$\frac{4}{\omega }<\delta .$$

(39)

denote

$${\overline{\xi }}_n:=n^{-1}\sum _{i=1}^n{\xi }_{i}and{\overline{\xi }}_n^{*}:=n^{-1}\sum _{i=1}^n{\xi }_i^{*}.$$

suppose that

$$\underset{n\to \infty }{lim\; inf}\frac{\mathbb{E}{S}_n^2}{n}={\varsigma }^2>0$$

(40)

is satisfied. If $b\to \infty$ and $b=o\left(n^{1/2}\right),n\to \infty$, then, under the MBB Procedure 2,

$$\underset{x\in \mathbb{R}}{sup}\left|{\mathbb{P}}_{\mathbf{\xi }}^{*}\left(\frac{n}{\sqrt{\mathbb{E}{S}_n^2}}\left({\overline{\xi }}_n^{*}-{\overline{\xi }}_n\right)\le x\right)-\mathbb{P}\left(\frac{n}{\sqrt{\mathbb{E}{S}_n^2}}{\overline{\xi }}_n\le x\right)\right|\stackrel{\mathbb{P}}{\to }0,n\to \infty ,$$

(41)

where ${\mathbf{\xi }}^{*}\equiv {[{\xi }_1^{*},\dots ,{\xi }_n^{*}]}^{\top }$ is the MBB version of $\mathbf{\xi }\equiv {[{\xi }_1,\dots ,{\xi }_n]}^{\top }$.

Similar theorem for IID random variables was proved by [37]. Furthermore, a version of this BCLT in case of stationary $\alpha$-mixing is given by [11].

Theorem 9. 

Bootstrap central limit theorem for φ-mixing. Let ${\left\{{\xi }_n\right\}}_{n=1}^{\infty }$ be a sequence of zero mean φ-mixing random variables with

$$\underset{n\in \mathbb{N}}{sup}\mathbb{E}{|{\xi }_n|}^4<\infty$$

(42)

and

$$\phi \left(n\right)=\mathcal{O}\left(n^{-2-\delta }\right),n\to \infty$$

(43)

for some $\delta >0$. Denote

$${\overline{\xi }}_n:=n^{-1}\sum _{i=1}^n{\xi }_{i}and{\overline{\xi }}_n^{*}:=n^{-1}\sum _{i=1}^n{\xi }_i^{*}.$$

suppose that

$$\underset{n\to \infty }{lim\; inf}\frac{\mathbb{E}{S}_n^2}{n}={\varsigma }^2>0$$

(44)

is satisfied. If $b\to \infty$ and $b=o\left(n^{1/2}\right),n\to \infty$, then, under the MBB Procedure 2,

$$\underset{x\in \mathbb{R}}{sup}\left|{\mathbb{P}}_{\mathbf{\xi }}^{*}\left(\frac{n}{\sqrt{\mathbb{E}{S}_n^2}}\left({\overline{\xi }}_n^{*}-{\overline{\xi }}_n\right)\le x\right)-\mathbb{P}\left(\frac{n}{\sqrt{\mathbb{E}{S}_n^2}}{\overline{\xi }}_n\le x\right)\right|\stackrel{\mathbb{P}}{\to }0,n\to \infty ,$$

(45)

where ${\mathbf{\xi }}^{*}\equiv {[{\xi }_1^{*},\dots ,{\xi }_n^{*}]}^{\top }$ is the MBB version of $\mathbf{\xi }\equiv {[{\xi }_1,\dots ,{\xi }_n]}^{\top }$.

With respect to Theorem 7, one may also postulate the multivariate version of the central limit theorem for the $\alpha$- and $\phi$-mixing accordingly, based on the bootstrap univariate CLT (8) and (9) using the Cramér–Wold device.

6. Real Data Analyses

If the data are indeed not independent and/or not identically distributed, using a proper resampling method can lead to, for instance, improvement in precision. We are going to deal with two real problems, where the first one comes from psychometric evaluation and the second one has grounds in non-life insurance. Handling the data as NINID will provide narrower confidence intervals for the mean parameter in both cases compared to the incorrect approach, when the data are falsely considered as IID.

6.1. Psychometry

Psychometric evaluation through a test with many binary (i.e., 0–1) answers from one subject naturally brings a question, what is the probability of the “correct” answer. This parameter of interest for the underlying Bernoulli distribution is nothing else than its mean. Thus, the sample mean is the consistent and asymptotically normal estimator of the parameter of probability of the correct answer. If the data are dependent, one cannot rely on normal asymptotics when constructing the confidence interval for the mean of the Bernoulli distribution, because the corresponding limiting variance is unknown [38,39,40]. Therefore, bootstrapping can provide a suitable solution. However, a proper bootstrap technique needs to be chosen and applied.

The above described issue is going to be illustrated on the dataset from “Programme for International Student Assessment (PISA) 2012 U.S. Math Assessment”, which can be downloaded from (https://tmsalab.github.io/edmdata/, accessed on 12 November 2022). This dataset was discussed in [41]. We concentrated on one subject, who was randomly selected (ID = 15) and s/he responded on $n=34$ items. The dependence between the subject’s answers comes from the fact that all the items are answered by the same subject, having the same abilities, knowledge, and state of mind during the examination.

We utilize the independent bootstrap (ignoring the dependence among the responses) and the moving block bootstrap with the blocksize $b=\lfloor n^{1/3}\rfloor =3$. The results for resampling the sample mean are shown in

Table 1. Empirical distributional quantities of the sample mean based on the independent bootstrap (incorrect approach) against moving block bootstrap (proper approach) for the correct/incorrect answers by a subject from the Programme for International Student Assessment (PISA) 2012–U.S. Math Assessment; number of observations n = 34.

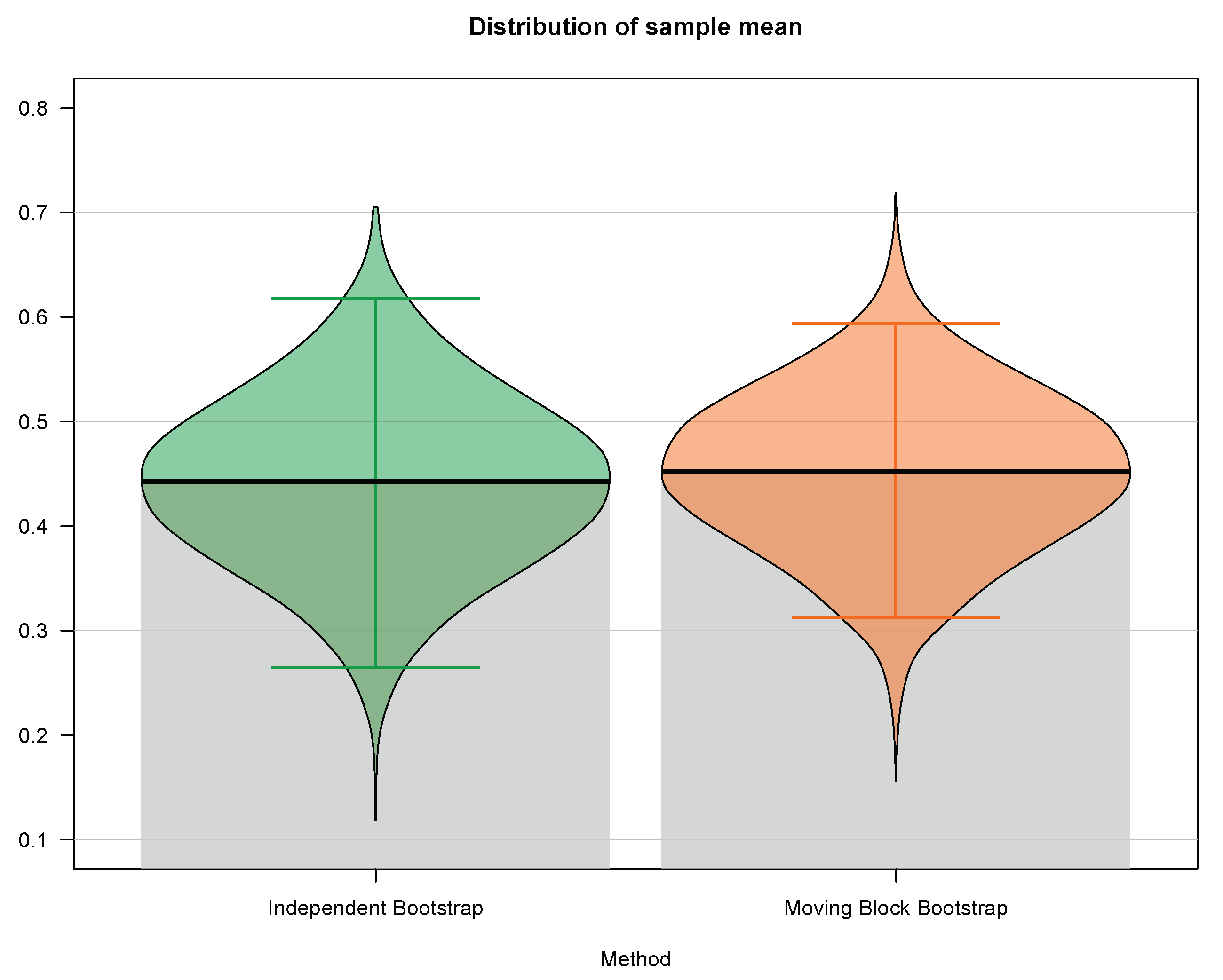
Empirical Quantity	Independent Bootstrap	Moving Block Bootstrap
$2.5$th percentile	0.2647	0.3125
First quartile	0.3824	0.4062
Median	0.4412	0.4375
Third quartile	0.5000	0.4999
97.5th percentile	0.6176	0.5938

and in Figure 1.

One may notice, from Table 1 as well as from Figure 1, that the difference between the 97.5th percentile and the 2.5th percentile, which serves as a 95% confidence interval, is narrower in case of the moving block bootstrap approach. Indeed, the 95% confidence interval based on independent bootstrap is [0.2647, 0.6176], whereas the 95% confidence interval based on moving block bootstrap is [0.3125, 0.5938]. Hence, the lengths of the confidence intervals are 0.3529 and 0.2813 for the independent and the moving block bootstrap, respectively, which yields approximately 20% reduction in the confidence interval’s length and, thus, an increase in estimation precision. In the end, the standard deviation for the independent bootstrap is 0.0851, whereas the standard deviation for the mooving block bootstrap drops down to 0.0764, which also provides an increase in precision by taking into account the underlying dependence among the data.

6.2. Insurance

In non-life insurance, the claims are traditionally split into the attritional and large claims, see, for example, [42]. One of the most fundamental tasks in non-life insurance, conducted on regular basis, is risk reserving assessment analysis, which amounts to predict the overall loss reserves to cover possible future claims. In order to do that, one firstly needs to estimate stochastically the distributional characteristics of the historical claims [43]. Here, we concentrate on estimation of the unknown mean for a reinsurance caped layer of large claims. Since the considered reinsurance layer will be bounded, there is no issue of assuming that the expectation of the underlying claims belonging to this layer exists.

We use the large fire insurance claims in Denmark from Thursday 3rd January 1980 until Monday 31st December 1990. The data called “Danish Fire Insurance Claims” were supplied by Mette Rytgaard of Copenhagen Re. They were described in [44] and can be freely downloaded from (https://tmsalab.github.io/edmdata/, accessed on 12 November 2022). Note that these data form an irregular time series, which does not contradict the notion of weak dependence. On contrary, the concept of mixing is very suitable for the unequally spaced time series [45]. We think of the reinsurance caped layer covering the large claims starting from 20M DKK (Danish crowns) up to 100M DKK, which consists n = 33 fire claims. The parameter of interest for the underlying unknown distribution is the mean. Again, it exists due to the fact that the layer is bounded from below as well as from above. Hence, the sample mean is the consistent and asymptotically normal estimator of the mean parameter. If the data are dependent and non-stationary (and, thus, not identically distributed), one cannot rely on normal asymptotics when constructing the confidence interval for the mean, because the corresponding limiting variance becomes unknown [46,47,48]. Therefore, the proper bootstrap method can provide a suitable solution.

The independent bootstrap (ignoring the dependence and non-stationarity among the fire claims) and the moving block bootstrap with the blocksize $b=\lfloor n^{1/3}\rfloor =3$ are applied. The results for resampling the sample mean are numerically displayed in

Table 2. Empirical distributional quantities of the sample mean based on the independent bootstrap (blue—incorrect approach) against moving block bootstrap (red—proper approach) for the Danish Fire Insurance Claims belonging to the reinsurance layer starting from 20M DKK (Danish crowns) up to 100M DKK; number of observations n = 33.

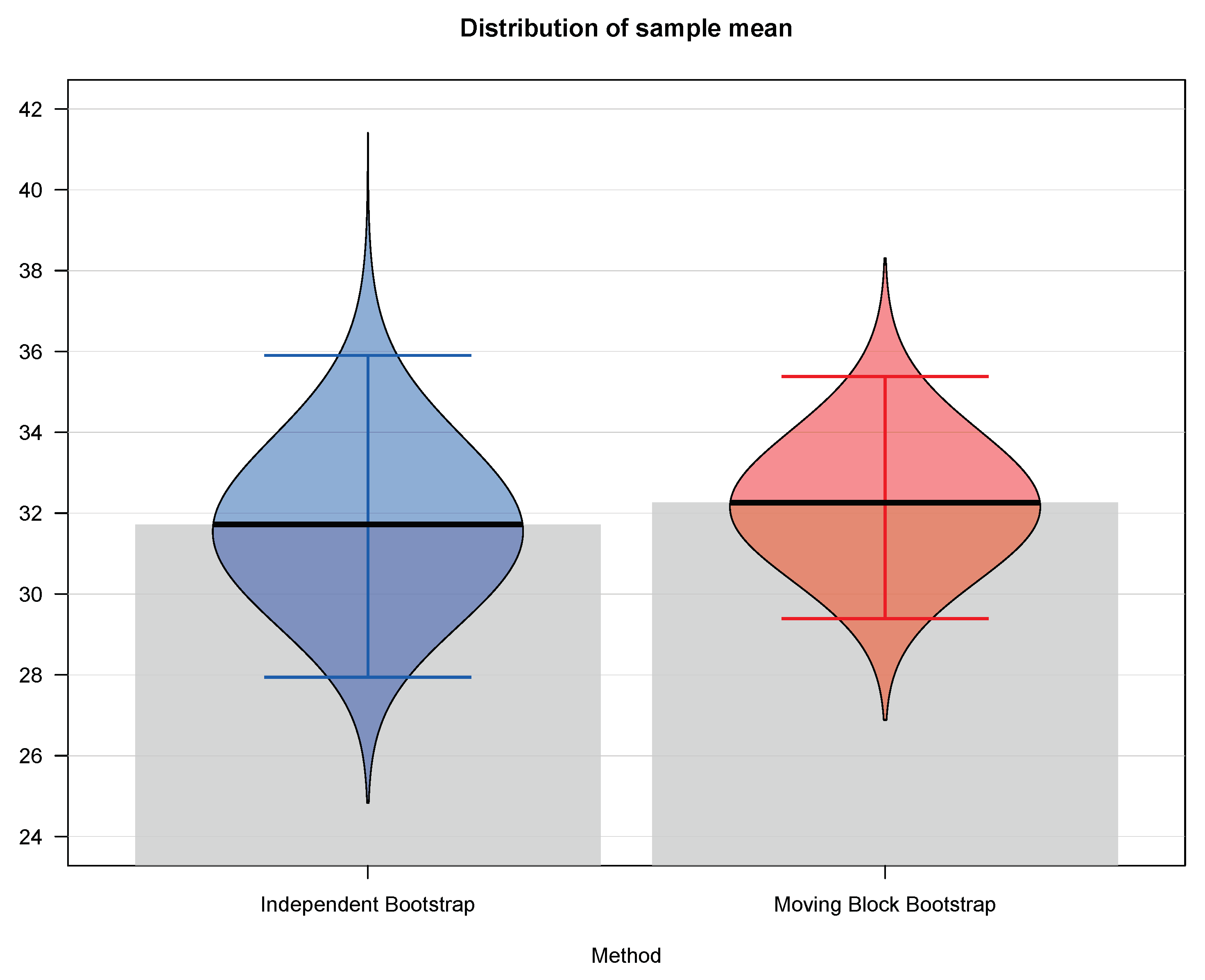
Empirical Quantity	Independent Bootstrap	Moving Block Bootstrap
2.5th percentile	27.94	29.39
First quartile	30.28	31.20
Median	31.64	32.20
Third quartile	33.08	33.29
97.5th percentile	35.90	35.38

. Additional to that, the empirical distributions of the sample mean based on the both resampling techniques together with the empirical distributional quantities from Table 2 are graphically visualized in Figure 2.

Table 2 as well as Figure 2 clearly reveal that the 95% confidence interval, which is the difference between the 97.5th percentile and the 2.5th percentile, is narrower in case of the moving block bootstrap procedure. Truly, the 95% confidence interval based on independent bootstrap is [27.94, 35.90], whereas the 95% confidence interval based on moving block bootstrap is [29.39, 35.38]. Hence, the lengths of the confidence intervals are 7.96 and 5.99 for the independent and the moving block bootstrap, respectively, which gives approximately 25% reduction in the confidence interval’s length. This provides an increase in estimation precision, which can be incorporated and employed in the reserving techniques for not independent and not identically distributed data, see [49,50,51,52]. On top of that, the standard deviation for the independent bootstrap is 2.054, whereas the standard deviation for the mooving block bootstrap drops down to 1.521, which again confirms an increase in accuracy by assuming the underlying dependence in the data.

7. Conclusions and Discussion

Asymptotic normality of the estimators or test statistics might be computationally unattainable and, hence, it can fail in practical applications. The discussed disadvantageous asymptotic properties lead to usage of the distributional-free resampling methods even for the IID observations. On top of that, the bootstrap procedures for a class of not independent and not identically distributed data are given together with their theoretical validity. There are three main methodological contributions to the bootstrap inference developed in this paper: (i) asymptotic closeness of the unknown stochastic quantities and their bootstrap counterparts is properly mathematically formalized; (ii) laws of large numbers for the bootstrapped $\alpha$-mixing and $\phi$-mixing random variables and vectors are postulated and proved; (iii) central limit theorems for the bootstrapped NINID observations are provided, which serve as justifications of the popular computer intensive techniques. Lastly, the theoretically valid approaches are practically performed on the problems from psychometry and insurance.

The concept of weak dependence provides a very flexible framework and it allows to handle any autocorrelation structure for the observations, if the mixing conditions are satisfied. Furthermore, if the parameter of interest is not the mean, our developed methodology can still be useful. Suppose that the corresponding estimator of the unknown parameter can be somehow linearized and, thus, rewritten as a continuous functional of a mean of the random variables plus some remainder, which is negligible in probability. This can be achieved, for instance, through the stochastic Taylor expansion. Then, one may apply the derived bootstrap machinery on the mean from the continuous functional and, additionally, use the continuous mapping theorem to obtain validity for bootstrapping the parameter of interest.