A Look at the Primary Order Preserving Properties of Stochastic Orders: Theorems, Counterexamples and Applications in Cognitive Psychology

Abstract

In this paper, we prove that for a set of ten univariate stochastic orders including the usual order, a univariate stochastic order preserves either both, one or none of additivity and multiplication properties over the vector space of real-valued random variables. Then, classifying participant’s quickness in a mental chronometry trial to “weakly faster” and “strongly faster”, we use the above results for the usual stochastic order to establish necessary and sufficient conditions for a participant to be strongly faster than the other in terms of the fitted Wald, Exponentially modified Wald(ExW), and Exponentially modified Gaussian(ExG) distributional parameters. This research field remains uncultivated for other univariate stochastic orders and in several directions.

1. Introduction

1.1. Univariate Stochastic Orders

In their 1934 book on inequalities, Hardy, Littlewood and Polya introduced the concept of majorization as one of the fundamental building blocks of stochastic orders. Later in 1955, Lehmann introduced the concept of stochastic orders on real valued random variables, [1]. Since then, inspired by their application in many fields there has been a growing literature on these orders specially from 1994. They have been playing a key role in comparison of different probability models in wide range of research areas such as survival analysis, reliability, queuing theory, biology and actuarial science. They serve as an informative comparison criteria between different distributions much more effective than low informative distributional point comparisons of means, medians, variance and interquartile range (IQR). In almost all cases, they have the same fundamental properties of usual order ≤ in real numbers including reflexivity, anti-symmetry, transitivity.

1.2. Motivation

This paper deals with exploring another aspect of stochastic orders including order preserving additive and multiplicative properties. Our investigation originates from natural existence of earlier fundamental properties in both the set of real numbers equipped with usual order and the set of real-valued random variables equipped with one of stochastic orders. Given existence of the mentioned order preserving properties on the set of real numbers equipped with the usual order, there was a missing investigation on their parallel existential conditions for the case of the set of real-valued random variables equipped with a stochastic order.

Our second motivation has roots in theory of reaction times distributions in cognitive psychology. Here, the reaction times have been modelled with a variety of distributions including the single two parametric ones such as Gamma and Lognormal; and; convolutionary three parametric ones such as Ex-Gaussian and Ex-Wald. Despite documentation of stochastic order comparison of the first category of distributions, the stochastic order comparison of the second category is still missing in the literature.

Our third motivation has roots in the comparison of participants’ quickness in mental chronometry trials. While the current used mean or median statistic present some weak evidence on performance comparison between participants, using the entire distribution of experimental data yields to more informative comparison. This work aims to classify participants’ trial performance quickness by presenting two new definitions aiming to put light on some uncultivated areas in the literature.

1.3. Study Outline

This paper is divided into four sections. In the first section, we provide the required definitions and established results for the follow up sections. Then, in the second section, we discuss order preserving additive and multiplicative properties for ten univariate stochastic orders including the usual, the moment, the Laplace transform, the increasing convex, the starshaped, the moment generating function, the convolution, the hazard rate, the likelihood ratio and the mean residual life order. Then, in the third section we present two definitions of the performance quickness in a mental chronometry trial. Then, we present some applications for the Ex-Gaussian, Wald and Ex-Wald distributions in cognitive psychology. We conclude the work with a discussion section on the current results and future directions.

2. Preliminaries

The reader who has studied the concepts of order and stochastic order is well acquainted with the following definitions and results. For an essential account of the mentioned concepts, see [2,3,4]. We begin with some definitions:

Definition 1.

Let P and Q be ordered sets. A map $\varphi :P\to Q$ is said to be order preserving whenever $x\le y$ in P implies $\varphi \left(x\right)\le \varphi \left(y\right),$ in $Q.$

When $P=Q$ are real valued vector spaces, and for fixed $z\in P$ the maps ${\varphi }_z^{add}\left(x\right)=x+z$ and ${\varphi }_z^{mul}\left(x\right)=xz(0<z)$ are order preserving, it is said that the order ≤ has additivity and multiplication properties.

It is trivial that for the case $P=\mathbb{R}$ equipped with its usual order ≤, the order has additivity and multiplication properties. From now onward, throughout this paper it is assumed that P is the set of all real valued random variables. For the orders related to this P we begin with some of the most well-known ones [1,3,4]:

Definition 2.

Let X and Y be two real-valued random variables with associated CDFs $F_X,F_Y$, Laplace transforms $L_X,L_Y,$ moment generating function $M_X,M_Y,$ and mean residual life functions $m_X,m_Y,$ respectively. Then, X is said to be less or equal than Y in the:

(i) 

usual stochastic order denoted by $X{\le }_{st}Y$, if $F_X\left(t\right)\ge F_Y\left(t\right)$ for all $t\in \mathbb{R}.$

(ii) 

moment order, denoted by $X{\le }_{m}Y$, if for $0\le X,Y$ we have: $E\left(X^m\right)\le E\left(Y^m\right)$ for all $m\in \mathbb{N}.$

(iii) 

Laplace transformation order, denoted by $X{\le }_{Lt}Y$, if with assumption $0\le X,Y$ we have: $L_X\left(s\right)\ge L_Y\left(s\right)$ for all $s\in {\mathbb{R}}^{+}.$

(iv) 

increasing convex order denoted by $X{\le }_{icx}Y,$ if: $E\left(g\right(X\left)\right)\le E\left(g\right(Y\left)\right)$ for all increasing convex functions g.

(v) 

starshaped order denoted by $X{\le }_{ss}Y,$ if: $E\left(g\right(X\left)\right)\le E\left(g\right(Y\left)\right)$: for all starshaped functions $g:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}.$

(vi) 

moment generating function denoted by $X{\le }_{\mathrm{mgf}}Y$, if with assumption $0\le X,Y$ we have: $M_X\left(s\right)\le M_Y\left(s\right)$ for all $s\in {\mathbb{R}}^{+}.$

(vii) 

convolution order, denoted by $X{\le }_{conv}Y$, if for some non-negative independent random variable U of $X,$$Y{=}_{st}X+U.$

(viii) 

hazard rate order, denoted by $X{\le }_{hr}Y,$ if for the hazard function $r\left(t\right)=\frac{\frac{dF\left(t\right)}{dt}}{1-F\left(t\right)}$ we have: $r_X\left(t\right)\ge r_Y\left(t\right)$ for all $t\in \mathbb{R}.$

(ix) 

likelihood ratio order, denoted by $X{\le }_{lr}Y,$ if the likelihood ratio function $f_{ratio}\left(t\right)=\frac{\frac{d{F}_X\left(t\right)}{dt}}{\frac{d{F}_Y\left(t\right)}{dt}}$ is decreasing for all $t\in \mathbb{R}.$

(x) 

mean residual life order, denoted by $X{\le }_{mrl}Y,$ if for the mean residual function $m\left(t\right)=\frac{{\int }_t^{+\infty }(1-F\left(u\right))du}{1-F\left(t\right)}$ we have: $m_X\left(t\right)\le m_Y\left(t\right)$ for all $t\in \mathbb{R}.$

The following corollary presents a useful criteria to compare two distributions in the usual stochastic order:

Corollary 1.

Let X and Y be two real-valued random variables with associated Cumulative Distribution Function (CDF)s $F_X$, and $F_Y$, respectively. Let $X{\le }_{st}Y,$ and consider the likelihood ratio function $f_{ratio}\left(t\right)=\frac{\frac{d{F}_X\left(t\right)}{dt}}{\frac{d{F}_Y\left(t\right)}{dt}}.$ Then:

(i) 

$\underset{t\to +\infty }{lim}{f}_{ratio}\left(t\right)\le 1$,

(ii) 

$\underset{t\to -\infty }{lim}{f}_{ratio}\left(t\right)\ge 1.$

The following example for the case of normal distribution $N(\mu ,{\sigma }^2)$ with mean $\mu$, and the exponential distribution $Exp\left(\tau \right)$ with mean $\tau$ is easily verified using Definition 2 and Corollary 1. It also has key applications in the subsequent sections. The other parts relates to key two parametric reaction times distributions widely used in cognitive psychology [3]:

Example 1.

(i) 

$N({\mu }_X,{\sigma }_X^2){\le }_{st}N({\mu }_Y,{\sigma }_Y^2)$ if and only if ${\mu }_X\le {\mu }_Y$ and ${\sigma }_X={\sigma }_Y.$

(ii) 

$Exp\left({\tau }_X\right){\le }_{st}Exp\left({\tau }_Y\right)$ if and only if ${\tau }_X\le {\tau }_Y$.

(iii) 

$lognormal({\mu }_X,{\sigma }_X^2){\le }_{st}lognormal({\mu }_Y,{\sigma }_Y^2)$ if and only if ${\mu }_X\le {\mu }_Y$ and ${\sigma }_X={\sigma }_Y.$

(iv) 

$Gamma({\alpha }_X,{\beta }_X){\le }_{st}Gamma({\alpha }_Y,{\beta }_Y)$ if and only if ${\alpha }_X\le {\alpha }_Y$ and ${\beta }_X\le {\beta }_Y.$

(iv) 

$Weibull({\alpha }_X,{\beta }_X){\le }_{st}Weibull({\alpha }_Y,{\beta }_Y)$ if and only if ${\alpha }_X\le {\alpha }_Y$ and ${\beta }_X={\beta }_Y.$

It has been mentioned in the literature that usual stochastic order is reflexive, anti-symmetric and transitive [3]. Regarding order preserving maps on P we have [4]:

Theorem 1.

If $X{\le }_{ord}Y$ and $\varphi :\mathbb{R}\to \mathbb{R}$ is any increasing function, then $\varphi \left(X\right){\le }_{ord}\varphi \left(Y\right)$ where ${\le }_{ord}$ refers to ${\le }_{st}$, ${\le }_{hr}$ or ${\le }_{lr}.$

In particular, for constant random variable $Z_0$, ${\varphi }_{Z_0}^{add}$ and ${\varphi }_{Z_0}^{mul}$ are order preserving and hence the usual stochastic order is additive and multiplicative in this special case. However, the case in general is still unknown.

An straightforward verification shows that considering the subset $P_0$ of all constant real-valued random variables of P equipped with one of above four stochastic orders, the order has both of mentioned order preserving properties. This is a parallel result to the case of real numbers $\mathbb{R}$ equipped with the usual order ≤. The following lemma will be useful in the proof of the upcoming theorems in the next section, [3,4].

Lemma 1.

Let $X,Y$ be two real valued random variables with associated CDFs $F_X,F_Y$, and Laplace transforms $L_X,L_Y,$ respectively. Then:

(i) 

$X{\le }_{icx}Y$ if and only if: ${\int }_x^{+\infty }(1-F_X\left(t\right))dt\le {\int }_x^{+\infty }(1-F_Y\left(t\right))dt,$ for all $x\in \mathbb{R}.$

(ii) 

$X{\le }_{ss}Y$ if and only if: ${\int }_x^{+\infty }td{F}_X\left(t\right)\le {\int }_x^{+\infty }td{F}_Y\left(t\right)$ for all $x\in {\mathbb{R}}_0^{+}.$

(iii) 

$X{\le }_{conv}Y$ if and only if for ${\varphi }_{X,Y}=\frac{L_Y}{L_X}$ we have: ${(-1)}^n.{\varphi }_{X,Y}^{\left(n\right)}\left(s\right)\ge 0\mathrm{for}\mathrm{all}s\in {\mathbb{R}}^{+},n\in \mathbb{N}.$

(iv) 

$X{\le }_{mgf}Y$ if and only if: $-Y{\le }_{Lt}-X.$

(v) 

$X{\le }_{mrl}Y$ with given finite means if and only if $g_{ratio}\left(t\right)=\frac{{\int }_t^{+\infty }(1-F_X\left(u\right))du}{{\int }_t^{+\infty }(1-F_Y\left(u\right))du}$ is decreasing.

We conclude this section with a remark on the independency of involved random variables:

Remark 1.

Considering any pair of real numbers $x_0,y_0$ as constant random variables $X=x_0$ and $Y=y_0$, it is trivial that any constant random variable $Z=z_0$ is independent from each of them. Hence, it is natural to maintain this independency assumption for inferential results for the case of non-constant random variables.

3. Order Preserving Properties of Univariate Stochastic Orders

This section deals with general properties of univariate stochastic order. Throughout this section, we assume the given random variable Z is independent from X and Y. First of all, for the case of reflexivity, anti-symmetry and transitivity, it is easy to show that all of these orders are preserving these properties. Second, we discuss the additivity and multiplication properties. Then, we present an evidence of the necessity of the independence of $X,Z(Y,Z)$ and the positivity of the random variable Z in the preservation of the multiplication conditions.

Theorem 2.

A univariate stochastic order ${\le }_{ord}$ may preserve either both additivity and multiplication, or one of them, or none of them.

Proof. 

Indeed, we prove the results based on the following Table 1 and Table 2:

Table 1. A Summary of order preserving properties of ten univariate stochastic orders.

		Order Preserving Property
#	Order Type	Addition	Multiplication
i	Usual ${\le }_{st}$	✓	✓
ii	Moment ${\le }_m$	✓	✓
iii	Laplace transformation ${\le }_{Lt}$	✓	✓
iv	Increasing Convex ${\le }_{icx}$	✓	✓
v	Starshaped ${\le }_{ss}$	✓	✓
vi	Moment generating function ${\le }_{mgf}$	✓	✓
vii	Convolution ${\le }_{conv}$	✓	X
viii	Hazard Rate ${\le }_{hr}$	X	X
ix	Likelihood ratio ${\le }_{lr}$	X	X
x	Mean residual life ${\le }_{mrl}$	X	X

Table 2. A Summary of counterexamples of additivity and multiplication order preserving in the univariate stochastic orders.

#	Order Type	Addition $\mathbf{X}+\mathbf{Z}{\nleqq }_{\mathbf{ord}}\mathbf{Y}+\mathbf{Z}$	Multiplication $\mathbf{XZ}{\nleqq }_{\mathbf{ord}}\mathbf{YZ}$
vii	Convolution ${\le }_{conv}$	NA	Take $X\stackrel{d}{=}Exp\left(1\right),$$Y\stackrel{d}{=}Exp\left(0.5\right),$ and $Z\stackrel{d}{=}B\left(0.5\right).$ Consider ${\varphi }_{XZ,YZ}^{{}^{\prime }}$ sign change and use Lemma 1.
viii	Hazard Rate ${\le }_{hr}$	Take $X\stackrel{d}{=}Exp\left(2.5\right),Y\stackrel{d}{=}$ $Exp\left(1.5\right),$ and $Z\stackrel{d}{=}log$ $logistic(shape=3,scale=1).$ Here: $r_{X+Z}\left(5\right)=0.6887492<0.8289970=r_{Y+Z}\left(5\right).$	Take $X\stackrel{d}{=}exp\left(Exp\left(2.5\right)\right),$ $Y\stackrel{d}{=}exp\left(Exp\left(1.5\right)\right),$ and $Z\stackrel{d}{=}exp(loglogistic$ $(shape=3,scale=1)).$ Apply Theorem 1 for $\varphi =log$.
ix	Likelihood ratio ${\le }_{lr}$	Take $X\stackrel{d}{=}N(0,1),$ $Y\stackrel{d}{=}N(1,1),$ and $Z\stackrel{d}{=}Cauchy(location=0,$ $scale=1)$. Then, consider ${\left(t_i\right)}_{i=1}^3=(1,3,7),$ and ${\left(f_{ratio}\left(t_i\right)\right)}_{i=1}^3=(0.799634,$ $0.4814513,0.7214805).$	Take $X\stackrel{d}{=}exp\left(N(0,1)\right),$ $Y\stackrel{d}{=}exp\left(N(1,1)\right),$ and $Z\stackrel{d}{=}exp(Cauchy$ $(location=0,scale=1))$. Apply Theorem 1 for $\varphi =log$.
x	Mean residual life ${\le }_{mrl}$	Take $X\stackrel{d}{=}N(0,1),$ $Y\stackrel{d}{=}N(1,2),$ and $Z\stackrel{d}{=}lognormal(meanlog=$ 0.25, $sdlog=1)$. Then, consider ${\left(t_i\right)}_{i=1}^3$ $=(1,3,5),$ and ${\left(g_{ratio}\left(t_i\right)\right)}_{i=1}^3=(0.5973625,$ $0.5301898,0.5913812).$	Take $X\stackrel{d}{=}N(0,1),$ $Y\stackrel{d}{=}N(1,2),$ and $Z\stackrel{d}{=}exp\left(lognormal\right(meanlog=$ 0.25, $sdlog=1\left)\right)$. Then, consider ${\left(t_i\right)}_{i=1}^3$ $=(-10,2,30),$ and ${\left(g_{ratio}\left(t_i\right)\right)}_{i=1}^3=(0.5632457,$ $0.5092787,0.5181358).$

The summary of proofs in the Table 1 are as follows: First, to prove the case for the usual stochastic order ${\le }_{st},$ it is sufficient to use the convolutionary integral representation of the involved CDFs ($F_{Y+Z},F_{X+Z},F_{YZ},F_{XZ}$)in terms of component CDFs($F_X,F_Y,F_Z$). Second, the proof for the case of moment order ${\le }_m,$ is straightforward using the Definition 2 (ii). Third, the proof for the case of Laplace transformation order ${\le }_{Lt},$ is straightforward using the Definition 2 (iii). Fourth, the proof for the case of increasing convex order ${\le }_{icx},$ is done using repetitive applications of the Lemma 1 and the Fubini’s theorem. Fifth, the proof for the case of starshaped order ${\le }_{ss}$ is similar to that of increasing convex order ${\le }_{icx}.$ Sixth, the result for the case of moment generating function order ${\le }_{mgf}$ is a direct consequence from the additivity for Laplace transformation order and Lemma 1. Seventh, the additivity result for the case of convolution order ${\le }_{conv}$ follows from two applications of Lemma 1 and given condition.

The summary of counterexamples supporting results for rows (vii–x) in the Table 1 are as follows in Table 2. Note that some of their special cases are established. Some examples include additivity for the hazard rate order ${\le }_{hr}$ (when Z has the increasing failure rate (IFR) [4] (Lemma 1.B.3)); additivity for the likelihood ratio order ${\le }_{lr}$ (when $X,Y,Z$ all have logconcave densities, [4] (Theorem.1.C.9)); and, additivity for the mean residual life order ${\le }_{mrl}$ (when Z has IFR, [3] (Theorem.2.4.22)).

The computations for the above counterexamples are presented in the supplementary materials. This completes the proof. □

Remark 2.

In Theorem 2 the case of additivity and multipliciation for the usual stochastic order and the increasing convex order can be proved using [4] Theorem 1.A.3(b) and Theorem 4.A.15, respectively with $m=2,X_1=X,X_2=Z,Y_1=Y,Y_2=Z,$ and consideration of two bi-variate increasing functions ${\psi }_1(u,v)=u+v$ (for additivity) and ${\psi }_2(u,v)=uv$ (for multiplication).

Remark 3.

In the Theorem 2, the assumption of the independence is necessary for preserving the additivity, the multiplication. Also, the assumption of positivity of the random variable Z is necessary for preserving the multiplication. To see this, first, for the additivity case take $X\stackrel{d}{=}N(0,\frac{1}{2}),Y\stackrel{d}{=}N(1,\frac{1}{2})$ and $Z=-X$ with given usual stochastic order yielding $X+Z{\nleqq }_{st}Y+Z.$ Next, for the multiplicity case, take $X\stackrel{d}{=}logN(0,\frac{1}{2}),Y\stackrel{d}{=}logN(1,\frac{1}{2})$ and $Z=X^{-1}$ with given usual stochastic order yielding $XZ{\nleqq }_{st}YZ.$ Finally, for the positivity of random variable $Z,$ take $X\stackrel{d}{=}N(0,1),Y\stackrel{d}{=}N(1,1)$ and $Z\stackrel{d}{=}0.5({\delta }_{\{-1\}}+{\delta }_{\{+1\}})$ with given usual stochastic order implying $XZ{\nleqq }_{st}YZ.$ The verifications are all straightforward.

We finish this section with a brief note on the applications of Theorem 2. One of its key applications is when one aims to compare two given single component convolutionary distributions or two given two-component mixture distributions. In both after-mentioned scenarios, Theorem 2 presents sufficient conditions for the comparisons. In case of parametric distributions, these sufficient conditions are explained in terms of involved parameters as we will see in the next section.

4. Applications in Cognitive Psychology

This section presents some applications of the Theorem 2 in the area of cognitive psychology. In mental chronometry trials, a participant is considered faster than the other when the point estimation (e.g., mean, median) of their trial reaction times is statistically less than the other. Given that most reaction times distributions are skewed, the mean statistics presents poor measure of central tendency for these distributions and the median statistics presents somewhat biased estimations [5], it is natural to shift the focus on the participant’s entire distribution of the trial reaction times. To distinguish these perspectives, we present two definitions:

Definition 3.

A participant is “weakly faster” than the other in a mental chronometry trial when the former’s reaction times point statistics (e.g., mean, median) is significantly smaller than the later one.

Definition 4.

A participant is “strongly faster” than the other in a mental chronometry trial when in a given stochastic order ${\le }_{ord}$ the former’s reaction times distribution is smaller than the later one.

Remark 4.

It is trivial that for the case of usual stochastic order, the Definition 4 yields the Definition 3. However, its converse statement is false. As a counterexample, let $X\stackrel{d}{=}lognormal(0,2)$ and $Y\stackrel{d}{=}lognormal(1,4).$ Then, $E\left(X\right)=e<e^3=E\left(Y\right),$ but, by Example 1, $X{\nleqq }_{st}Y.$ This yields the Venn diagram shown in Figure 1:

Figure 1. The Venn diagram for the concepts of “strongly faster“ and the “weakly faster”.

This work focuses on the concept of “strongly faster” presented in the Definition 4. Referring to the results in the Table 1 in the proof of the Theorem 2, from now on we assume the underlying stochastic order for comparisons is the usual stochastic order ${\le }_{st}.$ Furthermore, only single component distributions as in [6] are considered requiring the preservation of only additivity (The mixture distributions as in [7] require preservation of both additivity and multiplication). In particular, when the distributions of interest are parametric, describing their stochastic order in terms of their associated parameters is plausible. In this section we consider two of the most prominent single component convolutionary reactions times distributions: The Ex-Gaussian distribution and the the Ex-Wald distribution.

4.1. The Exponentially Modified Gaussian (ExG) Distribution

Response inhibition in human brain has two main components: reactive inhibition and proactive inhibition. Various distributional models including convolutionary distributions and mixture distributions have been proposed to describe these components [6,7,8]. The first convolutionary distribution playing such key role is the well-known exponentially modified Gaussian(ExG) distribution [9]. This distribution is defined by $ExG(\mu ,\sigma ,\tau )\stackrel{d}{=}N(\mu ,{\sigma }^2)+Exp\left(\tau \right)$ and its mean and variance are given by $\mu +\tau$ and ${\sigma }^2+{\tau }^2,$ respectively. Its density function and cumulative function are respectively given by:

$$\begin{array}{ccc}\hfill f_{ExG}(t;\mu ,\sigma ,\tau )& =& \frac{1}{\tau }exp(-\frac{t-\mu }{\tau }+\frac{{\sigma }^2}{2{\tau }^2})\times \mathsf{\Phi }(\frac{t-\mu }{\sigma }-\frac{\sigma }{\tau }):t\in \mathbb{R},\sigma ,\tau >0\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill F_{ExG}(t;\mu ,\sigma ,\tau )& =& \mathsf{\Phi }\left(\frac{t-\mu }{\sigma }\right)-exp(-\frac{t-\mu }{\tau }+\frac{{\sigma }^2}{2{\tau }^2})\times \mathsf{\Phi }(\frac{t-\mu }{\sigma }-\frac{\sigma }{\tau }),\hfill \end{array}$$

(2)

where $\mathsf{\Phi }$ denotes the CDF of the standard normal distribution.

In its single distribution format [6] and the two components mixture format [7] it is applied to describe the brain reactive inhibition. Furthermore, its differences of two components known as the asymmetric Laplace Gaussian(ALG) distribution [8,10,11] is applied to describe the brain proactive inhibition. Given ExG extensive usage to describe human brain reaction times, we are interested to compare these distributions in terms of their parameters. This characterizes which experimental participant has faster inhibition than the other in terms of the fitted distributional parameters adding more insights to the underlying processes [12,13]:

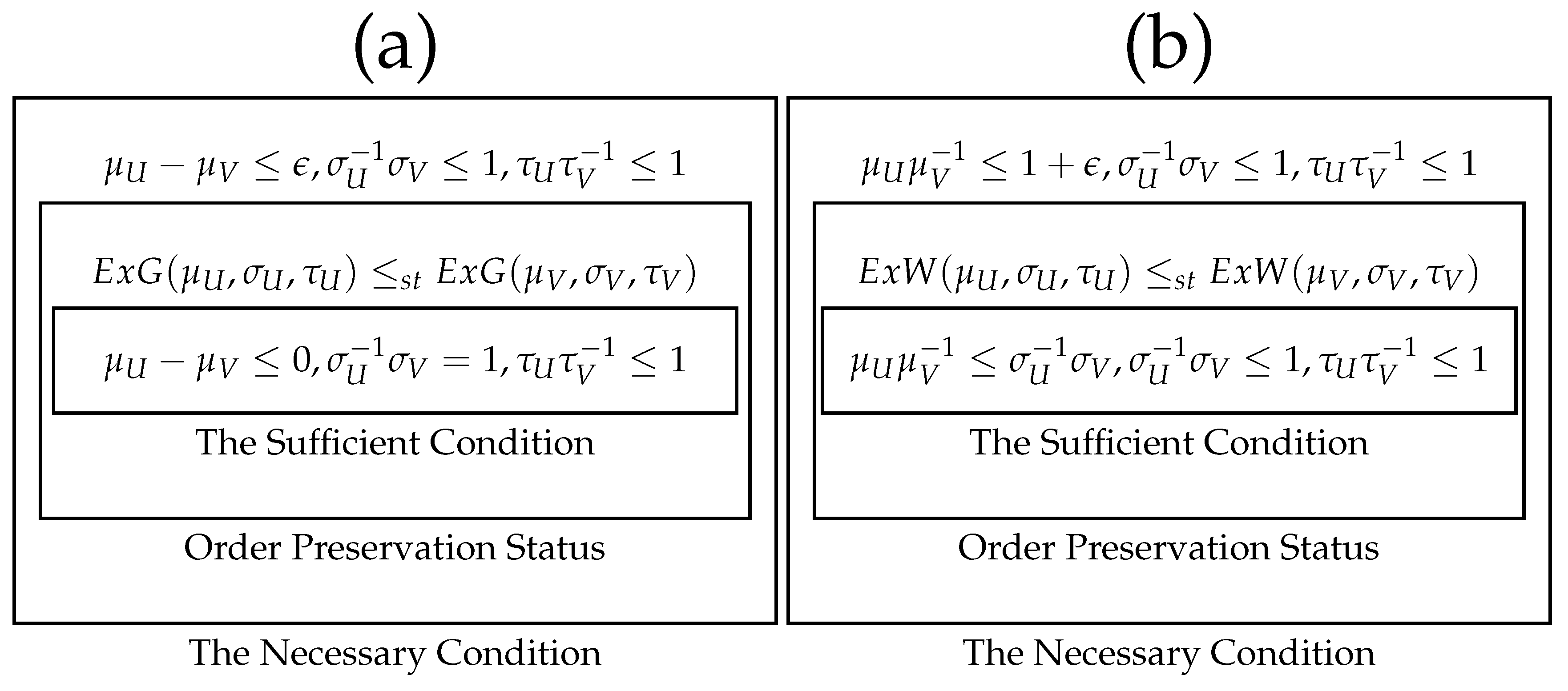
Theorem 3.

Given two parametric distributions $U\stackrel{d}{=}ExG({\mu }_U,{\sigma }_U,{\tau }_U)$ and $V\stackrel{d}{=}ExG({\mu }_V,{\sigma }_V,{\tau }_V),$ in which ${\mu }_U,{\mu }_V\in \mathbb{R}$ and ${\sigma }_U,{\sigma }_V,{\tau }_U,{\tau }_V\in {\mathbb{R}}^{+}.$ Then:

(i) 

$U{\le }_{st}V$ whenever ${\mu }_U\le {\mu }_V,{\sigma }_U={\sigma }_V,$ and ${\tau }_U\le {\tau }_V,$

(ii) 

$U{\le }_{st}V$ only if ${\mu }_U\le {\mu }_V+ϵ(ϵ={\tau }_V-{\tau }_U),{\sigma }_U^{-1}\le {\sigma }_V^{-1},$ and ${\tau }_U\le {\tau }_V.$

Proof. 

To prove part (i), by an application of Example 1, two applications of Theorem 2, and considering the transitivity of the usual stochastic order it follows that:

$$\begin{array}{ccc}\hfill U& \stackrel{d}{=}& ExG({\mu }_U,{\sigma }_U,{\tau }_U)=N({\mu }_U,{\sigma }_U^2)+Exp\left({\tau }_U\right){\le }_{st}N({\mu }_V,{\sigma }_V^2)+Exp\left({\tau }_U\right)\hfill \\ & {\le }_{st}& N({\mu }_V,{\sigma }_V^2)+Exp\left({\tau }_V\right)\stackrel{d}{=}ExG({\mu }_V,{\sigma }_V,{\tau }_V)\stackrel{d}{=}V.\hfill \end{array}$$

(3)

To prove part (ii) first of all, consider the likelihood ratio function:

$$\begin{array}{ccc}\hfill f_{ratio}\left(t\right)& =& \frac{f_{ExG}(t;{\mu }_U,{\sigma }_U,{\tau }_U)}{f_{ExG}(t;{\mu }_V,{\sigma }_V,{\tau }_V)}\hfill \\ & =& \frac{\frac{1}{{\tau }_U}exp(-\frac{t-{\mu }_U}{{\tau }_U}+\frac{{\sigma }_U^2}{2{\tau }_U^2})}{\frac{1}{{\tau }_V}exp(-\frac{t-{\mu }_V}{{\tau }_V}+\frac{{\sigma }_V^2}{2{\tau }_V^2})}\times \frac{\mathsf{\Phi }(\frac{t-{\mu }_U}{{\sigma }_U}-\frac{{\sigma }_U}{{\tau }_U})}{\mathsf{\Phi }(\frac{t-{\mu }_V}{{\sigma }_V}-\frac{{\sigma }_V}{{\tau }_V})},\hfill \\ & =& e.\frac{\mathsf{\Phi }(a_{1}t+b_1)}{exp(ct+d)\mathsf{\Phi }(a_{2}t+b_2)}\mathrm{for}\mathrm{all}t\in \mathbb{R},\hfill \end{array}$$

(4)

where in which $e={\tau }_V{\tau }_U^{-1},a_1={\sigma }_U^{-1}>0,a_2={\sigma }_V^{-1}>0,b_1=-({\mu }_U{\sigma }_U^{-1}+{\sigma }_U{\tau }_U^{-1}),b_2=-({\mu }_V{\sigma }_V^{-1}+{\sigma }_V{\tau }_V^{-1}),$ $c=-({\tau }_V^{-1}-{\tau }_U^{-1})$ and $d=-((\frac{{\mu }_U}{{\tau }_U}-\frac{{\mu }_V}{{\tau }_V})+(\frac{{\sigma }_U^2}{2{\tau }_U^2}-\frac{{\sigma }_V^2}{2{\tau }_V^2})).$ Now, by Corollary 1 (i) in which $\underset{t\to +\infty }{lim}{f}_{ratio}\left(t\right)\le 1,$ we have $c\ge 0$ or equivalently ${\tau }_U\le {\tau }_V.$

Second, applying L’Hopital’s rule(LHR), it follows:

$$\begin{array}{ccc}\hfill \underset{t\to -\infty }{lim}{f}_{ratio}\left(t\right)& =& \underset{t\to -\infty }{lim}(e.\frac{\mathsf{\Phi }(a_{1}t+b_1)}{exp(ct+d)\mathsf{\Phi }(a_{2}t+b_2)})\hfill \\ & \stackrel{LHR}{=}& \underset{t\to -\infty }{lim}\left(a_{1}e\frac{exp(-{(a_{1}t+b_1)}^2/2-(ct+d))}{\sqrt{2\pi }c\mathsf{\Phi }(a_{2}t+b_2)+a_{2}exp(-{(a_{2}t+b_2)}^2/2)}\right)\hfill \\ & \stackrel{LHR}{=}& \underset{t\to -\infty }{lim}\left(\frac{a_1}{a_2}e\left(\frac{a_1(a_{1}t+b_1)+c}{a_2(a_{2}t+b_2)-c}\right)\left(\frac{exp(-{(a_{1}t+b_1)}^2/2-(ct+d))}{exp(-{(a_{2}t+b_2)}^2/2)}\right)\right)\hfill \\ & =& {\left(\frac{a_1}{a_2}\right)}^{3}e\underset{t\to -\infty }{lim}exp(\left(\frac{a_2^2-a_1^2}{2}\right)t^2+(a_2{b}_2-a_1{b}_1-c)t+\frac{b_2^2-b_1^2-2d}{2}).\hfill \end{array}$$

(5)

Again, similar to the previous case, by Corollary 1 (ii) in which $\underset{t\to -\infty }{lim}{f}_{ratio}\left(t\right)\ge 1,$ we have $\frac{a_2^2-a_1^2}{2}\ge 0$ or equivalently ${\sigma }_V^{-1}\ge {\sigma }_U^{-1}.$ Third, by definition, ${\mu }_U+{\tau }_U=E\left(U\right)\le E\left(V\right)={\mu }_V+{\tau }_V,$ yielding the plausible statement. □

Remark 5.

Theorem 3 (ii) provides a necessary but insufficient condition. To see this, we present two counterexamples:

Counterexample 1.

$ϵ=1>0:$ Let $U\stackrel{d}{=}ExG(0,1,1)$ and $V\stackrel{d}{=}ExG(-0.5,1,2).$ Then, given $F_{ExG}(1;0,1,1)=0.0566962<0.0776955=F_{ExG}(1;-0.5,1,2)$ (See supplementary materials) we have $U{\nleqq }_{st}V.$

Counterexample 2.

$ϵ=0:$ Let $U\stackrel{d}{=}ExG(0,4,1)$ and $V\stackrel{d}{=}ExG(1,1,1).$ Then, given $F_{ExG}(4;0,4,1)=0.7676428<0.9184325=F_{ExG}(4;1,1,1)$ (See supplementary materials) we have $U{\nleqq }_{st}V.$

4.2. The Exponentially Modified Wald (ExW) Distribution

A key characteristics of the ExG distribution is its increasing hazard function. However, in many applications, the hazard function of the reaction times are peaked. This problem encouraged researchers to consider other candidate distributions with peaked hazard functions including the Wald and the exponentially modified Wald (ExW) distributions. These distribution have applications in mental health [14,15] and have been introduced in various parametric forms [14,15,16,17,18,19]. The ExW distribution is defined by $ExW(\mu ,\sigma ,\tau )\stackrel{d}{=}Wald(\mu ,{\sigma }^2)+Exp\left(\tau \right)$ and its mean and variance are given by $\mu +\tau$ and ${\mu }^3{\sigma }^2+{\tau }^2,$ respectively. Here, the Wald or Inverse Gaussian(IG) component has the mean $\mu$ and the dispersion parameter ${\sigma }^2$ (or shape parameter ${\sigma }^{-2}$). The density function and CDF of the Wald and ExW distributions are given by:

$$\begin{array}{ccc}\hfill f_W(t;\mu ,\sigma )& =& \frac{1}{\sqrt{2\pi }\sigma t^{\frac{3}{2}}}exp(-\frac{{(t-\mu )}^2}{2{\sigma }^2{\mu }^{2}t}):t\in {\mathbb{R}}_0^{+},\mu ,\sigma >0,\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill F_W(t;\mu ,\sigma )& =& \mathsf{\Phi }\left(\frac{t-\mu }{\sigma \mu \sqrt{t}}\right)+exp\left(\frac{2}{\mu {\sigma }^2}\right)\mathsf{\Phi }\left(\frac{-t-\mu }{\sigma \mu \sqrt{t}}\right),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill f_{ExW}(t;\mu ,\sigma ,\tau )& =& \frac{1}{\tau }exp(\frac{-t}{\tau }+\frac{1-\mu k}{\mu {\sigma }^2})\times F_W(t;k,\sigma ):k=\sqrt{\frac{\tau -2{\mu }^2{\sigma }^2}{{\mu }^2\tau }}>0,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill F_{ExW}(t;\mu ,\sigma ,\tau )& =& F_W(t;\mu ,\sigma )-exp(\frac{-t}{\tau }+\frac{1-\mu k}{\mu {\sigma }^2})\times F_W(t;k,\sigma ),\hfill \end{array}$$

(9)

where as before $\mathsf{\Phi }$ denotes the CDF of the standard normal distribution. To discuss the usual stochastic order relationship between ExW distributions, we need the plausible relationships for its components as in the case of ExG distribution. We first establish the relationship between the usual stochastic order between two Wald random variables and their associated parameters similar to the two parametric reaction time distributions presented in Example 1 (iii–iv):

Lemma 2.

$Wald({\mu }_X,{\sigma }_X^2){\le }_{st}Wald({\mu }_Y,{\sigma }_Y^2)$ if and only if ${\mu }_X{\mu }_Y^{-1}\le {\sigma }_X^{-1}{\sigma }_Y\le 1.$

Proof. 

To prove the necessity, consider the likelihood ratio function:

$$\begin{array}{ccc}& & f_{ratio}\left(t\right)=\frac{f_W(t;{\mu }_X,{\sigma }_X)}{f_W(t;{\mu }_Y,{\sigma }_Y)}=\frac{\frac{1}{\sqrt{2\pi }{\sigma }_X{t}^{\frac{3}{2}}}exp(-\frac{{(t-{\mu }_X)}^2}{2{\sigma }_X^2{\mu }_X^{2}t})}{\frac{1}{\sqrt{2\pi }{\sigma }_Y{t}^{\frac{3}{2}}}exp(-\frac{{(t-{\mu }_Y)}^2}{2{\sigma }_Y^2{\mu }_Y^{2}t})}=d.exp(at+b+c{t}^{-1}),\hfill \end{array}$$

(10)

where in which $d=\frac{{\sigma }_Y}{{\sigma }_X},a=\frac{\frac{1}{2}}{{\sigma }_Y^2{\mu }_Y^2}-\frac{\frac{1}{2}}{{\sigma }_X^2{\mu }_X^2},b=-(\frac{1}{{\sigma }_Y^2{\mu }_Y}-\frac{1}{{\sigma }_X^2{\mu }_X})$ and $c=\frac{\frac{1}{2}}{{\sigma }_Y^2}-\frac{\frac{1}{2}}{{\sigma }_X^2}.$ Now, again by Corollary 1 in which $\underset{t\to +\infty }{lim}{f}_{ratio}\left(t\right)\le 1,$ it follows $a\le 0$ or equivalently:

$$\begin{array}{ccc}\hfill {\mu }_X{\mu }_Y^{-1}& \le & {\sigma }_X^{-1}{\sigma }_Y.\hfill \end{array}$$

(11)

Next, another application of Corollary 1 in which $\underset{t\to 0^{+}}{lim}{f}_{ratio}\left(t\right)\ge 1,$ yields $c\ge 0$ or equivalently:

$$\begin{array}{ccc}\hfill {\sigma }_X^{-1}{\sigma }_Y& \le & 1.\hfill \end{array}$$

(12)

Consequently, by combining the inequalities (11) and (12) the assertion follows.

To prove the sufficiency, we note that given the condition we have:

$$\begin{array}{ccc}\hfill & & \frac{d}{dt}log\left(f_{ratio}\left(t\right)\right)=a-c{t}^{-2}\le 0,\mathrm{for}\mathrm{all}t\in {\mathbb{R}}_0^{+}.\hfill \end{array}$$

(13)

Hence, $f_{ratio}$ is decreasing function on ${\mathbb{R}}_0^{+}$ and consequently, by Definition 2 (viii) $X{\le }_{lr}Y.$ But, the likelihood ratio stochastic order yields the usual stochastic order [4] (Theorem 1.C.1, page 43). This completes the proof. □

Remark 6.

A simple modification in the proof of Lemma 2 and the usage of Definition 4 (ix) shows that the similar statement for the case of likelihood ratio stochastic order ${\le }_{lr}$ holds as well.

Equipped with Theorem 2 and Lemma 2, we are now able to present the twin of Theorem 3 for the case of ExW distribution:

Theorem 4.

Given two parametric distributions $U\stackrel{d}{=}ExW({\mu }_U,{\sigma }_U,{\tau }_U)$ and $V\stackrel{d}{=}ExW({\mu }_V,{\sigma }_V,{\tau }_V),$ in which ${\mu }_U,{\mu }_V,{\sigma }_U,{\sigma }_V,{\tau }_U,{\tau }_V,k_U,k_V\in {\mathbb{R}}^{+}.$ Then:

(i) 

$U{\le }_{st}V$ whenever ${\mu }_U{\mu }_V^{-1}\le {\sigma }_U^{-1}{\sigma }_V\le 1$ and ${\tau }_U\le {\tau }_V,$

(ii) 

$U{\le }_{st}V$ only if ${\mu }_U\le {\mu }_V+ϵ(ϵ={\tau }_V-{\tau }_U),{\sigma }_U^{-1}{\sigma }_V\le 1,$ and ${\tau }_U\le {\tau }_V.$

Proof. 

We repeat the process presented in the proof of Theorem 3 (for the case of ExG distribution) with some modifications. To prove part (i), by an application of Lemma 2, two applications of Theorem 2, and considering the transitivity of the usual stochastic order it follows that:

$$\begin{array}{ccc}\hfill U& \stackrel{d}{=}& ExW({\mu }_U,{\sigma }_U,{\tau }_U)=Wald({\mu }_U,{\sigma }_U^2)+Exp\left({\tau }_U\right){\le }_{st}Wald({\mu }_V,{\sigma }_V^2)+Exp\left({\tau }_U\right)\hfill \\ & {\le }_{st}& Wald({\mu }_V,{\sigma }_V^2)+Exp\left({\tau }_V\right)\stackrel{d}{=}ExW({\mu }_V,{\sigma }_V,{\tau }_V)\stackrel{d}{=}V.\hfill \end{array}$$

(14)

To prove part (ii), first of all, consider the likelihood ratio function:

$$\begin{array}{ccc}\hfill f_{ratio}\left(t\right)& =& \frac{f_{ExW}(t;{\mu }_U,{\sigma }_U,{\tau }_U)}{f_{ExW}(t;{\mu }_V,{\sigma }_V,{\tau }_V)}=\frac{\frac{1}{{\tau }_U}exp(\frac{-t}{{\tau }_U}+\frac{1-{\mu }_U{k}_U}{{\mu }_U{\sigma }_U^2})\times F_W(t;k_U,{\sigma }_U)}{\frac{1}{{\tau }_V}exp(\frac{-t}{{\tau }_V}+\frac{1-{\mu }_V{k}_V}{{\mu }_V{\sigma }_V^2})\times F_W(t;k_V,{\sigma }_V)}\hfill \\ & =& g.\frac{F_W(t;k_U,{\sigma }_U)}{exp(et+f)F_W(t;k_V,{\sigma }_V)}\mathrm{for}\mathrm{all}t\in \mathbb{R},\hfill \end{array}$$

(15)

where in which $g={\tau }_V{\tau }_U^{-1}>0,e=-({\tau }_V^{-1}-{\tau }_U^{-1}),$ and $f=\frac{1-{\mu }_V{k}_V}{{\mu }_V{\sigma }_V^2}-\frac{1-{\mu }_U{k}_U}{{\mu }_U{\sigma }_U^2}.$ Now, by Corollary 1 (i) in which $\underset{t\to +\infty }{lim}{f}_{ratio}\left(t\right)\le 1,$ we have $e\ge 0$ or equivalently ${\tau }_U\le {\tau }_V.$

Second, applying L’Hopital’s rule(LHR), it follows:

$$\begin{array}{ccc}\hfill \underset{t\to 0^{+}}{lim}{f}_{ratio}\left(t\right)& =& \underset{t\to 0^{+}}{lim}g.\frac{F_W(t;k_U,{\sigma }_U)}{exp(et+f)F_W(t;k_V,{\sigma }_V)}=\frac{g}{exp\left(f\right)}\underset{t\to 0^{+}}{lim}\frac{F_W(t;k_U,{\sigma }_U)}{F_W(t;k_V,{\sigma }_V)}\hfill \\ & \stackrel{LHR}{=}& \frac{g}{exp\left(f\right)}\underset{t\to 0^{+}}{lim}\frac{f_W(t;k_U,{\sigma }_U)}{f_W(t;k_V,{\sigma }_V)}=\frac{g}{exp\left(f\right)}\underset{t\to 0^{+}}{lim}dexp(at+b+c{t}^{-1}),\hfill \end{array}$$

(16)

where in which $d=\frac{{\sigma }_V}{{\sigma }_U}>0,a=\frac{\frac{1}{2}}{{\sigma }_V^2{k}_V^2}-\frac{\frac{1}{2}}{{\sigma }_U^2{k}_U^2},b=-(\frac{1}{{\sigma }_V^2{k}_V}-\frac{1}{{\sigma }_U^2{k}_U})$ and $c=\frac{\frac{1}{2}}{{\sigma }_V^2}-\frac{\frac{1}{2}}{{\sigma }_U^2}.$ A final application of Corollary 1 in which $\underset{t\to 0^{+}}{lim}{f}_{ratio}\left(t\right)\ge 1,$ yields $c\ge 0$ or equivalently:

$$\begin{array}{ccc}\hfill {\sigma }_U^{-1}{\sigma }_V& \le & 1.\hfill \end{array}$$

(17)

The proof of the third part is as in Theorem 3. □

Remark 7.

Theorem 4 (ii) provides a necessary but insufficient condition. To see this, we present two counterexamples:

Counterexample 3.

$ϵ=0.05>0:$ Let $U\stackrel{d}{=}ExW(0.10,0.10,0.00025)$ and $V\stackrel{d}{=}ExW(0.05,$$0.10,0.05025).$ Then, given$F_{ExW}(0.10;0.10,0.10,0.00025)=0.5<1.0=F_{ExW}(0.10;0.05,0.10,0.00025)$(See Supplementary Materials) we have $U{\nleqq }_{st}V.$

Counterexample 4.

$ϵ=0:$ Let $U\stackrel{d}{=}ExW(0.10,0.10,0.00025)$ and $V\stackrel{d}{=}ExW(0.10,$0.05, 0.00025). Then, given $F_{ExW}(0.1025;0.10,0.10,0.00025)=0.782560<0.940825=F_{ExW}$(0.1025; 0.10,0.05, 0.00025)(See Supplementary Materials) we have $U{\nleqq }_{st}V.$

5. Discussion

5.1. Summary & Contributions

This work presented a report on fundamental order preserving properties of addition and multiplication for the case of real-valued univariate random variables. It generalized the case from the usual order on the real numbers to the usual stochastic order maintaining the assumptions of independence of involved random variables $(X,Z)$ and $(Y,Z)$ and the positivity of the random variable $Z.$ However, investigation over other types of univariate stochastic orders showed that preservation of these fundamental properties varied by the type of considered order. Hence, to compare the convolutionary reaction times distributions such as ExG and ExW in terms of their involved parameters, the researchers need to ensure the preservation of their addition and multiplication under the assumed stochastic order ${\le }_{ord}.$ We established these conditions for the most promising candidate -the usual stochastic order ${\le }_{st}$—and investigated the comparison of convolutionary reaction time distributions ExG and ExW.

We discuss the similarity and differences in preservation of orders in terms of parameters of fitted ExG and ExW distributions presented in Section 4. First of all, in both cases, the sufficient condition is strictly stronger than the necessary condition. Furthermore, given the Counterexamples 1–4 the set of ordered distributions is proper subset of the distributions with the associated necessary conditions. On the other hand, the sufficient condition for the case of ExW distribution has one extra component (4 vs. 3) compared to the ExG distribution. Also, for ExW case the condition for the $\mu$ parameter is manifested through the division rather than the difference in the ExG case. Figure 2 presents the relative position of the necessary conditions, preserved usual stochastic orders and the sufficient conditions in both Theorems 3 and 4.

Figure 2. The Venn diagram for the association between usual stochastic relationship and the parameters: (a) ExG distribution; (b) ExW distribution.

We finish this section with a key application of the presented results in Theorems 3 and 4 for clinicians. While participant’s performance have been compared in terms of the Definition 3 across a wide spectrum of clinical conditions such as Attention Deficit Hyperactivity Disorder(ADHD), Autism Spectrum Disorder (ASD), Healthy Controls(HL), and Obsessive Compulsive Disorder(OCD) [20,21,22], there is still missing research to compare them in terms of the Definition 4. Given the stronger nature of performance presented in later definition, such research may present more information on the participant’s performance. Table 3 presents a variety of two-parametric and three-parametric distributional options for the researchers:

Table 3. A summary of quickness status in terms of parameters of key two parametric and three parametric reaction time distributions.

#	Distributions $\mathit{X},\mathit{Y}$	Weakly Faster $\mathit{E}\left(\mathit{X}\right)\le \mathit{E}\left(\mathit{Y}\right)$	Strongly Faster $\mathit{X}{\le }_{\mathrm{st}}\mathit{Y}$ The Sufficient Condition	The Necessary Condition
i	$\mathit{l}\mathit{o}\mathit{g}\mathit{n}\mathit{o}\mathit{r}\mathit{m}\mathit{a}\mathit{l}(\mathit{\mu },{\mathit{\sigma }}^2)$	$exp({\mathit{\mu }}_{\mathit{X}}+\frac{{\mathit{\sigma }}_{\mathit{X}}^2}{2})\le exp({\mathit{\mu }}_{\mathit{Y}}+\frac{{\mathit{\sigma }}_{\mathit{Y}}^2}{2})$	${\mathit{\mu }}_{\mathit{X}}\le {\mathit{\mu }}_{\mathit{Y}}$ and ${\mathit{\sigma }}_{\mathit{X}}={\mathit{\sigma }}_{\mathit{Y}}.$	${\mathit{\mu }}_{\mathit{X}}\le {\mathit{\mu }}_{\mathit{Y}}$ and ${\mathit{\sigma }}_{\mathit{X}}={\mathit{\sigma }}_{\mathit{Y}}.$
ii	$\mathit{G}\mathit{a}\mathit{m}\mathit{m}\mathit{a}(\mathit{\alpha },\mathit{\beta })$	${\mathit{\alpha }}_{\mathit{X}}{\mathit{\beta }}_{\mathit{X}}\le {\mathit{\alpha }}_{\mathit{Y}}{\mathit{\beta }}_{\mathit{Y}}$	${\mathit{\alpha }}_{\mathit{X}}\le {\mathit{\alpha }}_{\mathit{Y}}$ and ${\mathit{\beta }}_{\mathit{X}}\le {\mathit{\beta }}_{\mathit{Y}}.$	${\mathit{\alpha }}_{\mathit{X}}\le {\mathit{\alpha }}_{\mathit{Y}}$ and ${\mathit{\beta }}_{\mathit{X}}\le {\mathit{\beta }}_{\mathit{Y}}.$
iii	$\mathit{W}\mathit{e}\mathit{i}\mathit{b}\mathit{u}\mathit{l}\mathit{l}(\mathit{\alpha },\mathit{\beta })$	${\mathit{\alpha }}_{\mathit{X}}\mathsf{\Gamma }(1+{\mathit{\beta }}_{\mathit{X}}^{-1})\le {\mathit{\alpha }}_{\mathit{Y}}\mathsf{\Gamma }(1+{\mathit{\beta }}_{\mathit{Y}}^{-1})$	${\mathit{\alpha }}_{\mathit{X}}\le {\mathit{\alpha }}_{\mathit{Y}}$ and ${\mathit{\beta }}_{\mathit{X}}={\mathit{\beta }}_{\mathit{Y}}.$	${\mathit{\alpha }}_{\mathit{X}}\le {\mathit{\alpha }}_{\mathit{Y}}$ and ${\mathit{\beta }}_{\mathit{X}}={\mathit{\beta }}_{\mathit{Y}}.$
iv	$\mathit{W}\mathit{a}\mathit{l}\mathit{d}(\mathit{\mu },{\mathit{\sigma }}^2)$	${\mathit{\mu }}_{\mathit{X}}\le {\mathit{\mu }}_{\mathit{Y}}$	${\mathit{\mu }}_{\mathit{X}}{\mathit{\mu }}_{\mathit{Y}}^{-1}\le {\mathit{\sigma }}_{\mathit{X}}^{-1}{\mathit{\sigma }}_{\mathit{Y}}\le 1.$	${\mathit{\mu }}_{\mathit{X}}{\mathit{\mu }}_{\mathit{Y}}^{-1}\le {\mathit{\sigma }}_{\mathit{X}}^{-1}{\mathit{\sigma }}_{\mathit{Y}}\le 1.$
v	$\mathit{E}\mathit{x}\mathit{G}(\mathit{\mu },\mathit{\sigma },\mathit{\tau })$	${\mathit{\mu }}_{\mathit{X}}+{\mathit{\tau }}_{\mathit{X}}\le {\mathit{\mu }}_{\mathit{Y}}+{\mathit{\tau }}_{\mathit{Y}}$	${\mathit{\mu }}_{\mathit{X}}-{\mathit{\mu }}_{\mathit{Y}}\le 0,{\mathit{\sigma }}_{\mathit{X}}^{-1}{\mathit{\sigma }}_{\mathit{Y}}=1,$ and ${\mathit{\tau }}_{\mathit{X}}{\mathit{\tau }}_{\mathit{Y}}^{-1}\le 1.$	${\mathit{\mu }}_{\mathit{X}}-{\mathit{\mu }}_{\mathit{Y}}\le \mathit{ϵ},{\mathit{\sigma }}_{\mathit{X}}^{-1}{\mathit{\sigma }}_{\mathit{Y}}\le 1,$ and ${\mathit{\tau }}_{\mathit{X}}{\mathit{\tau }}_{\mathit{Y}}^{-1}\le 1.$
vi	$\mathit{E}\mathit{x}\mathit{W}(\mathit{\mu },\mathit{\sigma },\mathit{\tau })$	${\mathit{\mu }}_{\mathit{X}}+{\mathit{\tau }}_{\mathit{X}}\le {\mathit{\mu }}_{\mathit{Y}}+{\mathit{\tau }}_{\mathit{Y}}$	${\mathit{\mu }}_{\mathit{X}}{\mathit{\mu }}_{\mathit{Y}}^{-1}\le {\mathit{\sigma }}_{\mathit{X}}^{-1}{\mathit{\sigma }}_{\mathit{Y}},{\mathit{\sigma }}_{\mathit{X}}^{-1}{\mathit{\sigma }}_{\mathit{Y}}\le 1,$ and ${\mathit{\tau }}_{\mathit{X}}{\mathit{\tau }}_{\mathit{Y}}^{-1}\le 1.$	${\mathit{\mu }}_{\mathit{X}}{\mathit{\mu }}_{\mathit{Y}}^{-1}\le 1+\mathit{ϵ},{\mathit{\sigma }}_{\mathit{X}}^{-1}{\mathit{\sigma }}_{\mathit{Y}}\le 1,$ and ${\mathit{\tau }}_{\mathit{X}}{\mathit{\tau }}_{\mathit{Y}}^{-1}\le 1.$

5.2. Limitations & Future Work

The limitations of this work are clear and each one on its own creates ground for future work. Eight of them are as follows: First, there are other types of univariate stochastic orders that this study did not cover their preservation properties. Some of them included the harmonic mean residual life order, Lorenz order, dilation order, dispersive order, excessive wealth order, peakedness order, pth order, star order, superadditive order, factorial moment order, and total time on test order, [3,4]. Second, the case of order preservation under additivity and multiplication for the multivatiate random variables is still unknown. Third, the application in psychology was limited to the case convolutionary ExG with increasing hazard function and the case for convolutionary ExW distribution [12,16,17,18] with peaked hazard function. However, the case for the ALG distribution is still unknown. Fourth, we discuss the application in cognitive psychology for only the usual stochastic order while the results of Theorems 3 and 4 remain unclear for other stochastic orders such as the moment order, the Laplace transformation order, the Increasing convex order, the Starshaped order, the moment generating function order, and the convolution order. Fifth, while we interpreted the case for usual stochastic order in terms of being strongly faster, the interpretations for other stochastic orders remains unknown. Sixth, there is need of clarification of relationship between these parameters for two participants and the underlying brain processes. Seventh, to establish the necessary conditions presented in Theorems 3 and 4 we used Corollary 1 while we could consider the case in Theorem 1.A.12 [1]. This direction on its own is a single stand alone research. Finally, we presented only one application of the preservation of the orders (as in the case of usual stochastic order) and it is plausible to investigate possibility of application in other fields.

5.3. Conclusions

This work has discussed the order preservation under summation and multiplication for variety of univariate stochastic orders. For the case of usual stochastic order, it used its preserving status to discuss the necessary and sufficient parametric conditions for the convolutionary ExG and ExW distributions. This finding presents criteria for the cognitive psychologists to compare participants’ performance in terms of their fitted distributional parameters.