Mathematical Exchange Rates Modeling: Equilibrium and Nonequilibrium Dynamics

Abstract

The development of the author’s concept of the International Flows Equilibrium Exchange Rate (IFEER) is the basis for the mathematical exchange rate modeling of two interconnected equal economies. IFEER-concept allows modeling the exchange rate dynamics of relatively medium-term equilibrium and short- and long-term disequilibrium. Discrete and integral versions of the concept are the basis for further modeling. New structural models of medium-, short- and long-term dynamics and new final structural dependencies of the exchange rate on the system of fundamental factors are the main results. The models include mathematically formalized export-import and capital flows and international competitive advantages indicators. The modeling allowed the revealing of the structural pricing mechanism of the exchange rate dynamics from new positions. We verify the US dollar to the Russian ruble exchange rate modeling during periods of financial and economic crises in recent Russian history, based on a systematic analysis of the exchange rate policy. Because of the analysis, the fall in export prices of oil and other energy carriers in international markets, the rise in consumer prices within the country, and the fall in aggregate output are the main reasons for the fall of the Russian ruble. The conducted modeling allows for the evaluation of the short-term contribution to the crisis depreciation dynamics. The mathematical tools allow for the development of the decision-making process on the exchange rate regulation.

1. Introduction

The exchange rate is one of the most important and complex macroeconomic indicators. It embodies both all the troubles and the positive trends of the economy. At the microeconomic level, the exchange rate signals market participants about the quality of currency and monetary policy measures. Thus, in the absence of other changes in the financial and economic environment, the public perceives any form of devaluation of the national currency as a weak monetary policy compared to the policy in other countries.

In the context of this work, the research of R. Moreno [1] identified three main directions of the monetary and monetary policy of central banks in developing countries:

• inflation control,
• maintaining the stability of foreign trade and capital flows,
• maintaining overall financial stability within the country.

It is significant that all three main directions of monetary policy have special attention to the exchange rate (in real or nominal terms) and its dynamics. This only underlines the importance of the exchange rate policy of central banks in the system of available macroeconomic management tools.

Mathematical methods are widely used directly in modeling modern international world economic relations, currency and economic unions, capital movements and exchange rates, macroeconomic management.

The economic scientific literature has maintained a steady interest in structural fundamental factor models of exchange rates over the past decades. The results of the study conducted by C.M. Engel, N.C. Mark, and K.D. West are indicative, which are reflected in the title of the article: “Exchange Rate Models Are Not as Bad as You Think” [2].

One of the first and most meaningful is the monetary approach to the exchange rate. The model of P. Hooper and J. Morton [3] with tight prices and real financial well-being largely predetermined the development of this direction. Following them, M. Mussa [4,5,6] and J. Frenkel [7,8]) carried out structural modeling of the exchange rate and the balance of payments. The continuation is the model of J. Frenkel and H. Johnson [9].

A modification of the classic monetarist exchange rate models is the portfolio balance model. In it, supply and demand in the financial assets market determine the equilibrium exchange rate [10].

The development of the theory has now led to the emergence of a new broad class of models that consider the behavior of nominal and real exchange rates. Dynamic stochastic general equilibrium models (DSGE models) include a number of assumptions regarding nominal rigidity and market failures. One of the significant representatives of this class is the monopolistic competition model of two equal open economies developed by M. Obstfeld and K. Rogoff [11].

C.M. Engel, N.C. Mark and K.D. West [2], R. MacDonald and M.P. Taylor [12], J. Chen and Mark N. C. [13], V.-W. Cheung, M. Chinn, A.G. Pascual [14], V. Dropsy [15], and others show the high applicability of fundamental determinants models in practice. The research was conducted on currency pairs based on both “real” (US dollar, British pound, Canadian dollar) and “past” (German mark, French franc) currencies. Econometric studies of fundamental determinants models based on Euro developed by I. Chowdhury [16], R. H. Clarida, L. Sarno, M.P. Taylor, G. Valente [17], B. Kempa [18] show the same.

On the other hand, the econometric works of K. Iwatsubo, I. W. Marsh [19], R. Rebitzky [20], S. Heiden, C. Klein, B. Zwergel [21] emphasize the influence of expectations or the appearance of fundamental data on the dynamics of exchange rates.

At the same time, little attention is paid to the mathematical modeling of short-term disequilibrium. First, R. Dornbush’s models [22,23] show short-term exchange rate overshooting. The development of this topic is the work of the author [24].

The author does not aim in this work to comprehensively describe the literature on this topic due to its volume. It is necessary to mention, in addition, the classical mathematical fundamental factor models of exchange rates R.A. Mundell [25], L. Killian [26], A.C. Stockman [27], P.B. Clark and R. MacDonald [28], which are the basis of modern economic theory. Each model includes its own system of fundamental factors. However, macroeconomic factors related to real output and financial indicators are the basis.

In the context of these studies, we note works that pay close attention to the short- and long-term exchange rate dynamics. The paper [29] used the Long Short-Term Memory Networks (LSTM) framework to predict the exchange rate of Ghanaian Cedis to US Dollar, Euro, and British Pound, using historical macroeconomic data. In the context of this work, the composition of these factors is indicative: fundamental macroeconomic variables, past exchange rates, and commodity prices (gold, cocoa, and crude oil). M. Li, F. Qin, and Z. Zhang [30] employed a portfolio approach to assessing the effect of exchange rate expectation on Chinese Rénmínbì (RMB) internationalization with significant attention to short-term capital flows. The paper [31] investigated the long-term relationship between exchange rate level, volatility, and international trade performance. The results of the work emphasize the importance of the relationship between these indicators.

The productive applied tools for the study of nonlinear financial dynamics have an interdisciplinary basis. Discrete neurons have received extensive attention as an effective model for studying neural dynamics, including the discrete-time Courbage-Nekorkin-Vdovin model [32] and low-dimensional deterministic Rulkov map model [33]. They are reliable, simple, numerically stable, and show high computational efficiency. Rulkov neuron has shown very rich nonlinear dynamic behavior and remarkable characteristics. This is also widely used in financial computing. G. Orlando, M. Bufalo, and R. Stoop [34] find that a deterministic model performs at least as well as one of the best stochastic models (ARIMA-GARCH) in terms of simulations. However, it may offer additional insight into the essential mechanisms that drive financial markets.

As can be seen, different methods and approaches are the focus when modeling the exchange rate. At the same time, from the standpoint of structural and analytical modeling, the vast majority of known models of economic theory cannot provide adequate results for assessing the dynamic mechanism of the equilibrium real or nominal exchange rate. So, some of them are based on the principles of deviation from a steady state. The exchange rate is often expressed in terms of individual preferences based on the theory of purchasing power parity (PPP). However, V.-W. Cheung, M. Chinn, A. Pascual [14] came to a negative conclusion when studying the ability of the PPP approach to predict future changes in the nominal exchange rate.

Structurally, the modeling and analysis of the exchange rate in most well-known models of economic theory are limited to the framework of the current balance. They also do not explicitly operate with capital flows.

Changes in the current account balance and the competitive advantage indicator are expressed in terms of changes in the exchange rate. However, the role of the exchange rate in the regulation of the balance of payments and the role of the competitive advantages indicator in specific foreign trade flows (and, partly, in capital flows) requires modeling development and disclosure of the exchange rate formation mechanism.

However, the fundamental macroeconomic factors continue to be basic drivers of the dynamics of exchange rates. In this paper, we develop a systematic approach to model the dynamics of exchange rates of two equal, interconnected economies based on international flows of the balance of payments. This distinguishes the development of this article from the author’s models of the ruble exchange rate, made according to the methodology “Small Economy—the Rest of the World” [35,36]. This aims to further development of the author’s concept of IFEER (International Flows Equilibrium Exchange Rate modeling). The new exchange rate models will explicitly include mathematically formalized export-import and capital flows and international competitive advantages indicators. The approach will allow us to study the exchange rate dynamics relative to medium-term equilibrium and long-term and short-term disequilibrium.

The identification of the structural dynamic dependence of the exchange rate on its main factors makes it possible to simplify the development of sound management decisions on exchange rate regulation.

2. IFEER Conceptual Approach: Discrete and Integral Variants

Let us consider all N real market transactions at nominal exchange rates $e_i,i\in (1,N)$(direct quote) on the foreign exchange market that occurred over a certain period.

Denote $e_i,D_i,R_i$ in the i-th operation: the nominal exchange rate, the amount in a certain foreign currency, and the amount in the national currency, respectively.

These variables are connected by ratios: $e_i{D}_i=R_i$. Therefore, $e_i=R_i/D_i$.

The contribution of each transaction is different. It depends on the volume of the transaction.

The applied economic and mathematical modeling methods in studying the exchange rate dynamics are directly determined by the exchange rate management regime.

First, we are interested in the free-floating regime of the world’s major currencies.

Under these conditions, we define the synthetic value of the exchange rate as the sum of exchange rates weighted by the volume of their market transactions in the corresponding foreign currencies:

$$\begin{array}{cc}& \end{array}e\equiv {\displaystyle \sum _{i=1}^N\frac{D_i}{{\displaystyle \sum _{j=1}^N{D}_j}}\times e_i}={\displaystyle \sum _{i=1}^{N}w(i)\times e_i}$$

(1)

The weight function w(i) defines the contribution of the particular i-th transaction, depending on the volume in the foreign currency:

$$w(i)=\frac{D_i}{{\displaystyle \sum _{j=1}^T{D}_j}}.$$

The weight limit is: ${\displaystyle \sum _{i=1}^{N}w(i)=1}$.

Then you can get a summation by i:

$$\begin{array}{cc}& \end{array}e={\displaystyle \sum _{i=1}^N\frac{D_i}{{\displaystyle \sum _{j=1}^N{D}_j}}\times \frac{R_i}{D_i}}=\raisebox{1ex}{${\displaystyle \sum _{i=1}^N{R}_i}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{j=1}^N{D}_j}$}\right.$$

As a result, the weighted average exchange rate for a certain period is equal to the sum of the ratio of funds in domestic and foreign currencies on the foreign exchange market during this period. In terms of the above, with the separation of operations on current accounts and capital flows, it is possible to disaggregate the flow functions of the country’s balance of payments after reordering transactions:

$$\begin{array}{cc}& e=\raisebox{1ex}{$({\displaystyle \sum _{i=1}^L{R}_i{}^{CA}}+{\displaystyle \sum _{i=L+1}^N{R}_i{}^K})$}\!\left/ \!\raisebox{-1ex}{$({\displaystyle \sum _{i=1}^L{D}_i{}^{CA}}+{\displaystyle \sum _{i=L+1}^N{D}_i{}^K})$}\right.=(I\end{array}+K^{-})\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$(E+K^{+})$}\right.$$

Here funds with the upper index CA belong to the current balance; funds with the upper index K belong to the capital flows balance. For convenience, the units are designated:

$$\begin{array}{cc}\hfill \begin{array}{cc}I={\displaystyle \sum _{i=1}^L{R}_i{}^{CA}},& K^{-}={\displaystyle \sum _{i=L+1}^N{R}_i{}^K},\\ E={\displaystyle \sum _{i=1}^L{D}_i{}^{CA}},& K^{+}={\displaystyle \sum _{i=L+1}^N{D}_i{}^K}.\end{array}\hfill & \end{array}$$

In dynamic terms, in the period T we get:

$$\begin{array}{cc}& e_T=(I_T\end{array}+K_T{}^{-})\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$(E_T+K_T{}^{+})$}\right.,$$

(2)

where $E_T$ is the inflow of export foreign exchange earnings, $I_T$ is the demand for imports in the national currency. The capital movement is the outflow of the national currency ${K_T}^{-}$ and the inflow of foreign currency $K_T{}^{+}$.

The equality of the parties guarantees the symmetry of the dynamics of their exchange rates in (2)—in particular, the outflow of capital is the inflow of capital for the opposite side:

$$\begin{array}{c}\begin{array}{cc}& e_T=(I_T\end{array}+{K_T}^{-})\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$(E_T+{K_T}^{+})$}\right.=\\ =(E_T^{\ast }+K_T{}^{\ast +})\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$(E_T+K_T{}^{+})$}\right.=\hspace{1em}\hspace{1em}\\ =(E_T^{\ast }+K_T{}^{\ast +})\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$(I_T^{\ast }+K_T{}^{\ast -})$}\right.=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$e_T^{\ast }$}\right..\end{array}$$

(3)

The asterisk (*) hereafter refers to the economic indicators of the opposite side.

Next, consider the integral version of this approach. It can be useful to justify short-term modeling.

Let D(t) and R(t) be related cash flows in foreign and national currencies on the market. The analogue (1) in differential form at moment t is:

$$e(t)\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.=\raisebox{1ex}{$\partial R(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.$$

(4)

Thus:

$$\frac{\raisebox{1ex}{$\partial R(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}{\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}=e(t)$$

(5)

We introduce the weight function w(t) for the exchange rate by analogy with the previously used discrete version. In this integral version, the weight function w(t) is also based on the total volume of the foreign currency funds in a period T:

$$w(t)=\left[\frac{\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}\right].$$

(6)

As a result, we will define the exchange rate as an integral:

$$e\left(T\right)={{\displaystyle \int }}_{T}w\left(t\right)e\left(t\right)dt.$$

(7)

Let us substitute the weight Function (6) in Formula (7):

$$\begin{gathered} e(T)={\displaystyle \underset{T}{\int }w(t)}e(t)dt={\displaystyle \underset{T}{\int }\left[\frac{\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}\right]}e(t)dt= \\ ={\displaystyle \underset{T}{\int }\left[\frac{\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.e(t)}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}\right]}dt. \end{gathered}$$

After that, we can take the denominator beyond the integral:

$$\begin{array}{l}e(T)={\displaystyle \underset{T}{\int }\left[\frac{\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.e(t)}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}\right]}dt={\displaystyle \underset{T}{\int }\left[\frac{\raisebox{1ex}{$\partial R(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}\right]}dt=\\ =\frac{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial R(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}\end{array}$$

As a result, we will disaggregate the streaming functions according to the balance of payments:

$$e(T)=\frac{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial R(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}=\frac{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial R^{CA}(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt+{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial R^K(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}{{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D^{CA}(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt+{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D^K(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt}$$

(8)

Let us define the components of this Formula (8):

$$\begin{array}{l}{\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial R^{CA}(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt=I_T,\\ {\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial R^K(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt=K_T{}^{-},\\ {\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D^{CA}(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt=E_T,\\ {\displaystyle \underset{T}{\int }\raisebox{1ex}{$\partial D^K(t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.}dt=K_T{}^{+}\end{array}$$

At this conceptual level, the exchange rate dependence has a dynamic form in the period T:

$$\begin{array}{cc}& e(T)=e_T=(I_T\end{array}+K_T{}^{-})\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$(E_T+K_T{}^{+})$}\right..$$

(9)

The results of Formulas (3) and (9) coincide. This allows us to apply a conceptual IFEER approach to modeling the exchange rate on various time horizons, including a short-term plan.

3. Mathematical Exchange Rate Modeling: Medium-Term Dynamics

The two-period model is the basis of mathematical constructions.

Next, we will use the lower symbol t instead of T for the selected period as an indicator of the dynamism of the process in accordance with the accepted designations in science. Here and further, we will also use lowercase letters to denote parameters and indicators of time dynamics and capital letters to denote the qualitative attribute of the variables.

The decisions of exporting manufacturers determine the volume of export foreign exchange earnings delivered to the domestic market in the period t (next, we will explain the economic meaning of this dependence):

$$E(t)=E_t=k_E{P}_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z$$

(10)

where: $Q_t$− the real national product,

$P_t{}^{\ast }$—the cumulative foreign price level.

Let us explain the dependence (10). Depending on (10), export foreign exchange earnings in the financial market are part $k_E$ of total production $Q_t$ in foreign prices $P_t{}^{\ast }$. At the same time $x\ne -1$, $k_E—$ constant.

Here the aggregate output is averaged in dynamics. The indicators of the degree with it have the following weights:

$$\frac{1}{x+1}+\frac{x}{x+1}=1$$

The key fundamental factor of decision-making in (10) in the period t − 1 is the real exchange rate, which represents an indicator of international competitive advantages:

$$e^R{}_{t-1}=e_{t-1}\raisebox{1ex}{$P_{t-1}^{*}$}\!\left/ \!\raisebox{-1ex}{$P_{t-1}$}\right..$$

(11)

The configurable parameters in the exponents δ and z take into account the magnitude of the responses of the export streaming function to changes in the aggregate product and the real exchange rate.

The export foreign exchange earnings of opposite sides according to the construction of the model:

$$\begin{array}{l}I(t)=I_t=E_t^{\ast }=k_I{P}_t({Q_t}^{\ast \frac{1}{x+1}}{Q_{t-1}}^{\ast \frac{x}{x+1}}{)}^{\lambda }({e*}_{t-1}^R{)}^{-y}=\\ =k_I{P}_t({Q_t}^{\ast \frac{1}{x+1}}{Q_{t-1}}^{\ast \frac{x}{x+1}}{)}^{\lambda }(e_{t-1}^R{)}^y.\end{array}$$

(12)

The degree indicators y and λ are also parameters of the responses of the streaming function. Dependencies (10) and (12) are related as follows: z − y = x, k_I is also a constant.

Here we used the properties of streaming functions:

$$\begin{array}{c}I*\hspace{0.17em}=\hspace{0.17em}E\hspace{0.17em},\hspace{0.17em}E*\hspace{0.17em}=\hspace{0.17em}I\end{array}$$

Next, the proposed IFEER concept makes it possible to include in the mathematical modeling of the exchange rate such a determinant of the world economy factor as the movement of capital.

Accordingly, we will put hypotheses about the form of basic dependencies: the capital inflow functions are part $k_{k^{+}}$ of total production $Q_t$ in foreign prices $P_t{}^{\ast }$, which foreign investors want to buy at their prices for investment and savings purposes. Thus, the capital inflow function is an increasing function by aggregate prices and by the real aggregate product. This function is also increasing by the terms of trade since their increase leads to an improvement in investment conditions and an increase in the capital inflow.

Let us use the properties of the streaming functions:

$$\begin{array}{l}{K}^{\ast -}=K^{+},\\ K^{\ast +}=K^{-}.\end{array}$$

(13)

Thus, in accordance with the above, we put the functional dependence of the capital inflow:

$$K^{+}(t)=K_t{}^{+}=k_{K^{+}}{P}_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z$$

(14)

Degree indicators also contain configurable parameters.

Quite symmetrically, the function of capital outflow is:

$$K_t{}^{\ast +}=k_{K^{-}}{P}_t^{}{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(e{*}_{\begin{array}{l}t-1\\ \end{array}}^R)}^{-y}$$

(15)

But in accordance with properties (13), we can rewrite the dependence of capital flows:

$$K^{-}(t)=K_t{}^{-}=K_t{}^{\ast +}=k_{K^{-}}{P}_t^{}{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^y$$

(16)

Then, substituting functional dependencies (10)–(15) into (3) and considering that $e^{\ast R}{}_{t-1}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$e^R{}_{t-1}$}\right.$:

$$\begin{gathered} \begin{array}{cc}& e_t\end{array}=\frac{k_I{P}_t{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\lambda }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^y+k_{K^{-}}{P}_t{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^y}{k_E{P}_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z+k_{K^{+}}{P}_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z}= \\ =\frac{P_t{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^y(k_I{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\lambda -\rho }+k_{K^{-}})}{P_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z(k_E{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta -\theta }+k_{K^{+}})}. \end{gathered}$$

(17)

We use the properties of indicators $\lambda \approx \rho ,\delta \approx \theta$ and the greater dynamic stability of the averaged terms ${(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta -\theta }$ and ${(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\lambda -\rho }$ comparatively with the volatility of internal and external prices. Then in the medium term, let’s put a constant:

$$\frac{(k_I{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\lambda -\rho }+k_{K^{-}})}{(k_E{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta -\theta }+k_{K^{+}})}={(k)}^{x+1}=const$$

(18)

Rewrite (17) in the form:

$$e_t=\frac{P_t{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(k)}^{x+1}}{P_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{(e_{\begin{array}{l}t-1\\ \end{array}}^{}\frac{P_{t-1}^{\ast }}{P_{t-1}^{}})}^x}$$

Let’s move to the left part ${(e_{t-1})}^x$:

$$\begin{array}{cc}& e_t\end{array}{(e_{\begin{array}{l}t-1\\ \end{array}}^{})}^x=\left(k\frac{P_t}{P_t^{\ast }}{Q}_t{{}^{\ast }}^{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}{Q}_t{}^{-\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}\right){\left(k\frac{P_{t-1}}{P_{t-1}^{\ast }}{Q}_{t-1}{{}^{\ast }}^{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}{Q}_{t-1}{}^{-\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}\right)}^x$$

We get after a temporary separation of the variables involved in the modeling:

$$\begin{array}{cc}& e_t=\end{array}k\frac{P_t}{P_t^{\ast }}{Q}_t{{}^{\ast }}^{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}{Q}_t{}^{{}^{-\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}}.$$

For convenience, we will redefine ${\rho }^{\prime }=\frac{\rho }{x+1}$ and ${\theta }^{\prime }=\frac{\theta }{x+1}$ and project the model to a multi-period case:

$$\begin{array}{cc}& e(t,Q(t),Q^{\ast }(t),P(t),P^{\ast }(t))=e_t=\end{array}k\frac{P(t)}{P^{\ast }(t)}{Q}^{\ast }{(t)}^{\ast }{}^{\rho \prime }Q{(t)}^{-\theta \prime }.$$

(19)

As a result, we get a dynamic dependence of the exchange rate on the main fundamental external and internal macroeconomic factors. This is medium-term dependence.

4. Dynamics of the Russian Ruble Exchange Rate: Empiricism and Practice

The periods of financial and economic crises in recent Russian history in 1998, 2008, and 2014 are the most fruitful for conducting empirical research.

Note that the USD/RUR exchange rate is a core. The exchange rates of other currencies to the ruble are calculated through the system of cross-rates.

In this regard, the pricing mechanism of export products of Russian companies, based on the prices of the main world commodity exchanges in US dollars, is important. Therefore, we used P* indices, related to the actual export prices of Russian goods, as a determinant. During the periods under review, different data were available, which is determined by the peculiarities of the Russian state statistics (according to the Federal State Statistics Service [37,38,39]).

The index of average actual export prices was calculated using the formula:

$$P^{\ast }(t)=P_t*={\displaystyle \sum _{i=1}^K(P_t^{*}(i)\times w(i))}$$

where $P_t*(i)$ is the price index of the export goods group, $w(i)$ is the weight of this group in the total Russian exports. In the entire commodity nomenclature of Russian exports during these periods, three (K = 3) groups dominated: mineral raw materials, ferrous and non-ferrous metals, machinery, and equipment. The proportionality coefficients adjusted the weights so that their sum was 1.

The P* index was constructed by the author due to its absence in official statistics. Its construction was quite laborious.

The consumer price index is the determinant P. Q is the index of aggregate real output. Since the interpretation of the Q*-factor is economically difficult, and it is the least volatile, then Q* = 1 is accepted in calculations:

$$\begin{array}{cc}& e(t,Q(t),P(t),P^{\ast }(t))=\end{array}{e}_t=k\frac{P(t)}{P^{\ast }(t)}Q{(t)}^{-\theta \prime }.$$

In the process of verification and analysis of simulation results, we will adjust the internal parameter of the main research Formula (19). We equate the coefficient k to the ruble exchange rate to the US dollar at the starting point of the research period.

Provided at the starting point P(start) = 1, P*(start) = 1, Q(start) = 1 the optimization model is:

$$\frac{1}{N}{{\displaystyle \sum _{t=1}^N\left(ND{(e)}_t\right)}}^2\underset{\theta \prime }{\to }\min$$

where $ND{(e)}_t=\frac{e_t(\theta \prime )-e_t}{e_t}$ is the normalized deviations,

$e_t(\theta \prime )$ is the calculated ruble exchange rate according to Formula (19),

$e_t$ is the nominal exchange rate to the US dollar.

This special procedure for adjusting the internal coefficients of the model was chosen to conduct an empirical analysis. This is because a multifactorial nonlinear relationship is being investigated due to the nature of the exchange rate since it changed several times during the studied periods. Therefore, standard statistical indicators, including those applied in accordance with the Gauss-Markov theorem, are not applicable here. The author here means such widely known and used regression quality indicators as R²-Adjusted, Student and Fisher test statistics, and so forth. Thus, we used the average of normalized deviations (AND) and the average of absolute normalized deviations (AAND) as the model quality indicators:

$$\begin{array}{cc}AND=\frac{1}{N}{\displaystyle \sum _{t=1}^N\left(ND{(e)}_t\right),}& AAND=\frac{1}{N}{\displaystyle \sum _{t=1}^N\left|ND{(e)}_t\right|}\end{array}.$$

They are directly related to the parameter estimation procedure.

In particular, similar indicators are the basic quality indicators when building the hybrid model of complete ensemble empirical mode decomposition (CEEMDAN) based multilayer long short-term memory (MLSTM) networks that adopts the multilayer stacked architecture to forecast the trend of exchange rate [40].

In the period August 1997–March 1999, the official exchange rate of the Central Bank of Russia, based on trading on the MICEX (Moscow Interbank Currency Exchange), is the nominal rate. It is closely connected with the interbank market. As a result of numerical simulation using the MS EXEL tabular processor (version 2013) at a given coefficient k = 5.83 (the official ruble exchange rate in August 1997), the value of the parameter was established ${\theta }^{\prime }=0.27$.

Figure 1 (author’s calculations, monthly data) shows the dynamics of the official exchange rate of the Central Bank of the Russian Federation e(nominal) and the calculated ruble exchange rate $e_t\left({\theta }^{\prime }\right)$ when using the real GDP index as a determinant Q and the average actual export price index as a determinant P*.

AND = 14.3% and AAND = −4.3%. Possible deviations can also be explained by the inaccuracy of calculations (primarily the index of actual export prices), intra-monthly fluctuations in the nominal exchange rate, as well as a random component.

When analyzing the dynamics in Figure 1, two periods of the discrepancy between the nominal settlement and official ruble exchange rates are clearly distinguishable:

• The first period lasted until August 1998. An excess of the calculated over the official exchange rate characterizes it. During this period, the ruble exchange rate was restrained due to the sale by the Central Bank of Russia of a significant part of the gold and foreign exchange reserves, which decreased from $24.5 billion in August 1997 to $12.5 billion in August 1998, and foreign loans received at that time from international monetary organizations. This was a consequence of the policy pursued by the Bank of Russia during this period. It is important here that the Bank of Russia pursued a policy of controlled floating of the ruble exchange rate. There were certain restrictions on export-import operations and capital transactions. According to the author and a number of other Russian economists, this currency regime was “too much controlled floating”. In fact, it was a quasi-fixed regime.
• In the second period (from August 1998 to March 1999), the opposite picture is observed. The excess of the nominal ruble exchange rate over the calculated rates is explained by the actions of the Minister’s Cabinet on 17 August 1998, as a result of which there was a sharp excess of the capital leakage values over the calculated medium-term values. At the same time, there is a stabilization of the Central Bank’s reserves, which indicates that the balance of payments is in an equilibrium position in the medium term.

Thus, as a result of the analysis, it is possible to identify the main reasons for the fall in the ruble exchange rate in August 1997–March 1999: rising consumer prices, falling export prices, falling GDP, and significant capital outflow.

In this context, «unclean» controlled floating is one of the important factors for the deviation of the calculated results from market data.

In this regard, during 2007–2009, the Bank of Russia conducted a regime of “relatively rigid” controlled floating of the national currency with a revised range of fluctuations. Compared to the previous period of 1997–1998, restrictions on export-import operations and capital transactions have been significantly reduced.

In the period from December 2007 to June 2009, the average nominal exchange rate of the US dollar to the ruble for the period (month) calculated by the Central Bank of Russia is considered the nominal exchange rate. As a result of numerical simulation, with a given coefficient k = 24.57 (the average nominal rate for December 2007), the parameter value was established θ’ = −0.63.

In Figure 2 presents the average nominal exchange rate of the US dollar to the ruble e(nominal) and the dynamics of the calculated ruble exchange rate depending on the real GDP index.

As a result, AND = 13.5% and AAND = −5.1% for the calculated ruble exchange rate.

First, negative values of this parameter signal that there were revaluation tendencies of the ruble exchange rate.

When analyzing the dynamics of the nominal exchange rate of the national currency in Figure 2, two periods of divergence of both the calculated rates and the nominal ruble exchange rate are distinguished. However, in contrast to the period of 1997–1999 discussed above, this has similar factors, but it happens in a different scenario:

1.

The first period lasted until July-August 2008. The excess of the nominal rate over the calculated rates already characterizes it. During this period, the revaluation trends of the ruble exchange rate were restrained by the replenishment of foreign reserves by the Central Bank of Russia. It sterilized a significant amount of foreign currency coming into the country through the export of primary mineral raw materials. This was, among other things, a consequence of capital inflows due to a significant increase in the loan debt of the banks and private sector in the short and medium term.

Currency interventions have led to unprecedented growth in the Russian history of international reserves to 596.5 billion US dollars on 1 August 2008, with a permanent increase in the index of the ruble real exchange rate to the US dollar and to the European currency. This is a consequence of the exchange rate policy in this period.

2.

The second period covers the time of the crisis processes beginning that are generally external in nature. However, this has significantly affected the development of the Russian economy. From September 2008 to June 2009, the public watched the reverse process: the excess of the calculated rate over the nominal ruble exchange rate. This happened with a capital drain compensated by the Central Bank of Russia. Only in the period of September–December 2008 the banking and other private sector liabilities decreased by 35.1, with an increase in assets by 120.1 billion US dollars due to significant sales of international reserves.

In the period after February 2009, there was the stabilization of Russia’s international reserves. This generally speaks about the stabilization of the balance of payments in the medium term.

As a result of the analysis, we can identify as the main reason for the fall in the ruble exchange rate in the period September 2008–February 2009. It was a significant drop in actual export prices (including oil and other energy prices). This happened because of the global market deterioration with incomparably low (by the standards of the period 1997–1998) growth in consumer prices and a short-term drop in GDP.

Since the end of 2014, the Bank of Russia has been following a floating exchange rate regime. A floating exchange rate is a necessary condition for the effective implementation of monetary policy within the framework of the inflation-targeting strategy. The exchange rate of foreign currency to the ruble is determined by the balance of supply and demand of a foreign currency in the foreign exchange market (The Main Directions of the Unified State Monetary Policy, [41]).

During the currency crisis in 2014, the nominal exchange rate of the US dollar to the Russian ruble at the end of the period (month) calculated by the Bank of Russia is considered the nominal exchange rate [42]. The price index of the Brent oil mixture on ICE (Intercontinental Exchange, data from the Bloomberg information terminal) was the determinant P*. This is due to the predominance of oil in the exports and the close correlation of other Russian export products with the oil prices. The construction of a complete index of actual export prices has become extremely difficult due to the lack of government statistics. The real GDP index was the determinant Q [43].

As a result of numerical modeling, the parameter value was determined θ’ = 0.45 (Figure 3, author’s calculations).

AND = 0.28% and AAND = 2.98%. This indicates the high quality of the model (19).

As a result of the analysis conducted during this period, it is possible to single out as the main reason for the fall of the US dollar against the ruble a twofold drop in export prices of oil and other energy carriers on international markets. This is due to the overwhelming predominance of mineral raw materials in the index of average actual export prices. During this period, the growth of consumer prices within the country also had a significant unidirectional impact on the result.

The media also cited the fall in oil prices on international markets as one of the causes of the 2014–2015 currency crisis. However, this is an attribute of other periods under consideration.

It is important to note here that in the last period in 2013–2015 when the Bank of Russia completely switched to the floating exchange rate policy, the simulation results correlated much better with market data compared to previous periods.

5. Modeling of Short-Term Effects of Exchange Rate Dynamics

We assume that the medium-term dependencies (10) and (12) will retain their structure in the short-term mathematical modeling due to certain economic inertia of current balance operations.

In this context, it is necessary to modify the functional dependencies of capital outflow and inflow to model the short-term dynamics of the exchange rate. In this case, the coefficients k cease to be constants. We need to introduce a function

${(k_{K^{-}})}_t=k_{K^{-}}(t)$, for example, which increases over time for the capital outflow dependence during the economic and financial crises.

Consequently, the functional dependence of capital outflow has the form:

$$K_t{{}^{-}}_{}=k_{K^{-}}(t)P_t^{}{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^y$$

(20)

In the short term, during the economic and financial crisis in the foreign exchange market, there will be a significant increase in the rate of capital outflow. This guarantees a strict increment in (20) of the function $k_{k^{-}}\left(t\right)$ by t.

The functional dependence of capital inflow is determined symmetrically:

$$K_t{}^{+}=k_{K^{+}}(t)P_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z$$

(21)

In the short term, with a sharp reduction in capital inflows in Formula (21), the function $k_{k^{+}}\left(t\right)$ by t is dynamically strictly decreasing.

The modeling methodology guarantees the interconnectedness of functional dependencies:

$$K_t{{}^{-}}_{}=K_t{}^{\ast +}=k_{K^{-}}(t)P_t^{}{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^y.$$

(22)

Substitute Functions (20) and (21) in (3). Term (18) will change in the short term and will receive additional dynamic features:

$$\frac{(k_I{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\lambda -\rho }+k_{K^{-}}(t))}{(k_E{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta -\theta }+k_{K^{+}}(t))}={(k(t))}^{x+1}$$

(23)

Omitting the intermediate calculations by analogy, we rewrite (17) in the form:

$$e_t=\frac{P_t{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{(k(t))}^{x+1}}{P_t^{\ast }{k}_E{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{(e_{\begin{array}{l}t-1\\ \end{array}}^{}\frac{P_{t-1}^{\ast }}{P_{t-1}^{}})}^x}$$

(24)

After a temporary separation of the variables, we get:

$$\begin{array}{cc}& e_t=\end{array}k(t)\frac{P_t}{P_t^{\ast }}{Q}_t{{}^{\ast }}^{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}{Q}_t{}^{-\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}.$$

After re-designation:

$$\begin{array}{cc}& e(t,Q(t),Q^{\ast }(t),P(t),P^{\ast }(t))=e_t=\end{array}k(t)\frac{P(t)}{P^{\ast }(t)}{Q}^{\ast }{(t)}^{\ast }{}^{{\rho }^{\prime }}Q{(t)}^{-{\theta }^{\prime }}.$$

(25)

The function k(t) in (20) and (21) in the short term is responsible for explosive changes in the exchange rate in this multifactorial nonlinear dependence.

The term $(Q_{t-1}{}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}{Q}_t{}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.})$, in comparison with the other components in the formulas, is quite stable. At the same time, the strict increase in the function $k_{k^{-}}\left(t\right)$ in Formula (20) and the strict decrease in the function $k_{k^{+}}\left(t\right)$ in Formula (21) dynamically in a short-term crisis period guarantee a strict increase of the function k(t) in (25).

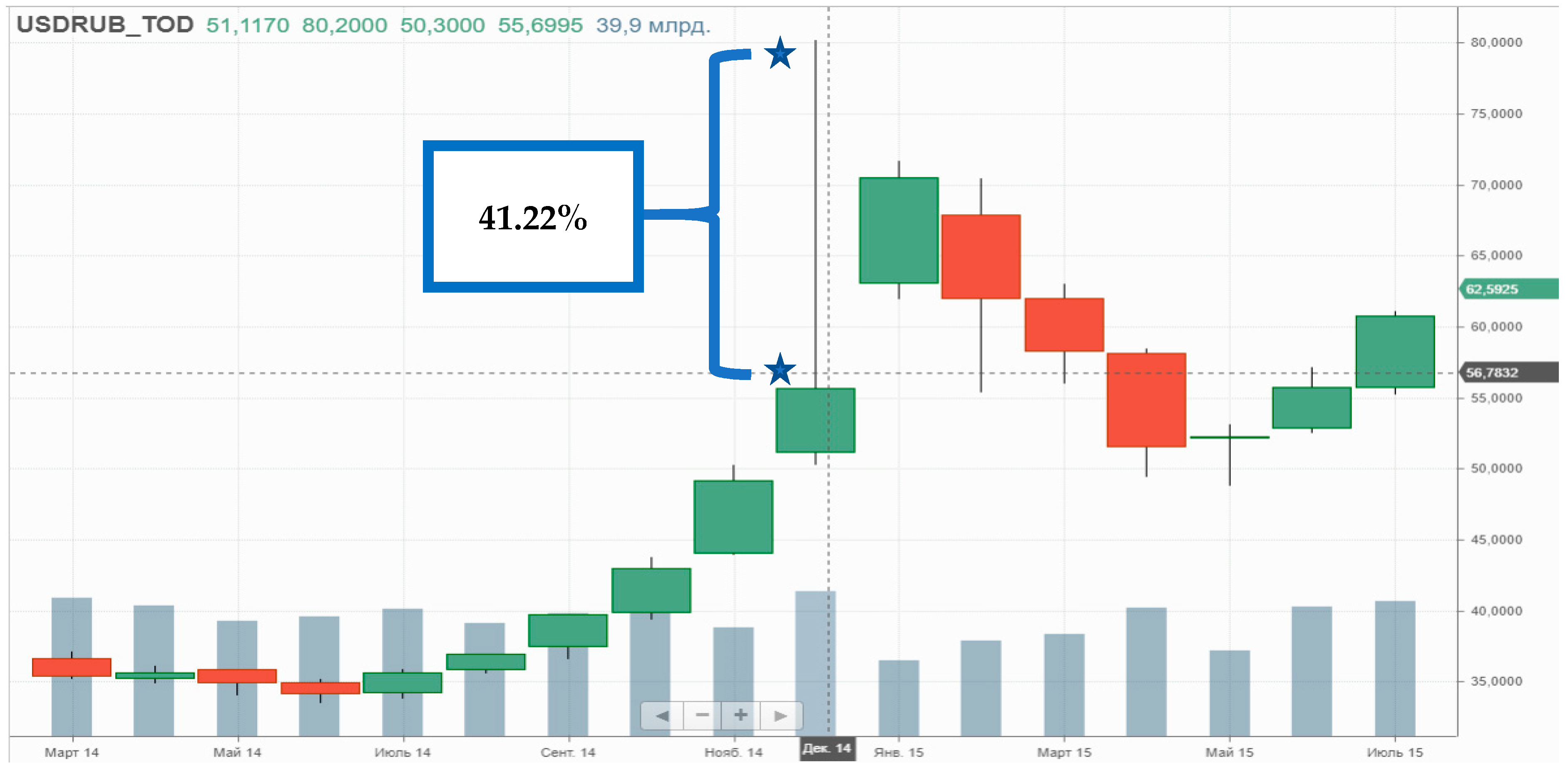
The conducted modeling allows us to evaluate the contribution of the function k(t). In certain periods, it can be quite significant. Consider the crisis period of 2014–2015. In accordance with the calculations based on (19) and Figure 3 of the previous paragraph, the average equilibrium exchange rate for November–December 2014 was 56.79 USD/RUR. This directly corresponds to the officially published rate of the Bank of Russia, 56.26 USD/RUR in December, which is also calculated as the average rate for the period. Figure 4 shows the actual TODAY quotes (USDRUB_TOD, according to the FINAM News Agency [44]). The market maximum was 80.2 USD/RUR in December 2014, which allows us to estimate the short-term contribution of the function k(t) to the crisis depreciation dynamics (the stars in Figure 4 indicate the levels of exchange rates):

$$\begin{array}{l}\frac{e_{\mathrm{December} }(\mathrm{market} \mathrm{maximum} )-e_{\mathrm{December} }(\mathrm{calculated} \mathrm{equilibrium} )}{e_{\mathrm{December} }(\mathrm{calculated} \mathrm{equilibrium} )}=\\ =\frac{80.2 -56.79 }{56.79 }=41.22\%.\end{array}$$

This negative effect was obtained, among other things, due to the loss of the management levers of the foreign exchange market by the Bank of Russia. The possibility of such situations should lead to closer attention to the Russian ruble dynamics from the monetary authorities.

The impact of the function k(t) on other considered periods could not be estimated due to the lack of data.

6. Mathematical Exchange Rate Modeling: Long-Term Dynamics

For the purposes of this study, it is necessary to make the following assumption: in the functional dependence (10), the coefficient $k_E$ ceases to be a constant in the long term. It becomes a dynamic function $k_{E,l}(t)$. This is important in the long term for modeling:

$$E_t=k_{E,l}(t)P_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z$$

(26)

Let us discuss the dynamic properties of the function $k_{E,l}(t)$. The increasing or decreasing type of function is very important. For example, for export-oriented commodity-producing countries, restructuring towards intermediate products may become a key. Including the Russian version, world practice shows that the dynamics of prices for intermediate products outstrip the prices of primary raw materials.

In the context of mathematical modeling, this leads to an increase in currency flows in the long term compared to the short term. The increased share of services in the export structure may also affect this direction. In this case, the function $k_{E,l}(t)$ strictly increases by t.

In this optimistic scenario, an improvement in the country’s investment climate can be expected in the long term. This will lead to a significant increase in capital inflows due to an increase in the portfolio and direct investments. In this case, the function $k_{K^{+},l}^{}(t)$ in Formula (27) also increases strictly by t:

$$K_t{}^{+}=k_{K^{+},l}^{}(t)P_t^{\ast }{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{(e_{\begin{array}{l}t-1\\ \end{array}}^R)}^z$$

(27)

Similarly earlier, we substitute dependencies (26) and (27) in (3):

$$e_t=\frac{k_I{P}_t{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\lambda }{\left(e_{t-1}^R\right)}^y+k_{}{P}_t{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\rho }{\left(e_{t-1}^R\right)}^y}{k_{E,l}(t)P_t^{ *}{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta }{\left(e_{t-1}^R\right)}^z+k_{K^{+},l}(t)P_t^{ *}{(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\theta }{\left(e_{t-1}^R\right)}^z}$$

(28)

Define the function K(t):

$$\frac{(k_I{(Q_t{{}^{\ast }}^{\frac{1}{x+1}}{Q}_{t-1}{{}^{\ast }}^{\frac{x}{x+1}})}^{\lambda -\rho }+k_{K^{-}})}{(k_{E,l}(t){(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}})}^{\delta -\theta }+k_{K^{+},l}(t))}=K{(t)}^{x+1}$$

(29)

Regroup in this case (11):

$$\begin{array}{cc}& e_t\end{array}{(e_{\begin{array}{l}t-1\\ \end{array}}^{})}^x=\left(K(t)\frac{P_t}{P_t^{\ast }}{Q}_t{{}^{\ast }}^{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}{Q}_t{}^{-\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}\right){\left(K(t)\frac{P_{t-1}}{P_{t-1}^{\ast }}{Q}_{t-1}{{}^{\ast }}^{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}{Q}_{t-1}{}^{-\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}\right)}^x$$

Similarly earlier, we carry out a temporary separation of the variables and project the model to a multi-period case:

$$\begin{array}{c}\begin{array}{cc}& e(t,Q(t),Q^{\ast }(t),P(t),P^{\ast }(t))=\end{array}K(t)\frac{P^{\ast }(t)}{P^{\ast }(t)}{Q}^{\ast }(t{)}^{\raisebox{1ex}{$\rho $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}Q(t{)}^{-\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$x+1$}\right.}=\\ \begin{array}{ll}& =\end{array}K(t)\frac{P(t)}{P^{\ast }(t)}{Q}^{\ast }(t{)}^{{\rho }^{\prime }}{Q}^{\ast }(t{)}^{-{\theta }^{\prime }}.\hfill \end{array}$$

(30)

In Formula (29), we will assume: the additional capital inflow that occurs with GDP growth correlates primarily with the growth of goods and services exports. There is sufficient stability of the member $\left(Q_t{}^{\frac{1}{x+1}}{Q}_{t-1}{}^{\frac{x}{x+1}}\right)$ in comparison with other financial and economic indicators. As a result, a strict increase in the internal functions $k_{E,l}\left(t\right)$ and $k_{K^{+},l}\left(t\right)$ in this case, guarantee a strict decrease of the introduced function K(t) in the Formula (30) by t.

One consequence deserves attention. Regroup in the Formula (30) and express the real exchange rate:

$$\begin{array}{cc}& e^R(t)=e(t)\raisebox{1ex}{$P^{\ast }(t)$}\!\left/ \!\raisebox{-1ex}{$P(t)$}\right.=\end{array}K(t)Q^{\ast }{(t)}^{{\rho }^{\prime }}{Q}^{\ast }{(t)}^{-{\theta }^{\prime }}.$$

(31)

The dynamic behavior of the function K(t) in (31) guarantees the strengthening of both the nominal and the real exchange rates in the long term compared to the medium-term equilibrium.

7. Conclusions, Discussion, and Results

The paper presents mathematical exchange rate modeling of two interconnected equal economies in the free-floating currency regime. Modeling is based on the further development of the author’s concept of International Flows Equilibrium Exchange Rate modeling (IFEER-modeling). This approach allows us to study the dynamics of the exchange rate of medium-term equilibrium and short- and long-term disequilibrium relatively. Developed discrete and integral variants are the core of the concept in this work.

The IFEER concept makes it possible to include the movement of capital as a determinant of the global economy in the structural mathematical modeling of the exchange rate. The internal functional dependencies of export-import operations and capital movements in the system of the main exchange rate determinants are mathematically determined and formalized.

The newly constructed structural models of the medium-, short- and long-term exchange rate dynamics and the new final structural dependencies of the exchange rate, based on the system of fundamental macroeconomic factors, are the main result of the work. This system includes aggregates of export-import operations and capital flows, competitive advantage index, consumer price index, actual export price index, real gross domestic product index, elasticity coefficients of foreign trade operations, intertemporal solutions of micro agents, etc.

The conducted modeling allowed the revealing of the structural pricing mechanism of the exchange rate dynamics from new positions.

A distinctive feature of the models is the emphasis on the mechanism of pricing formation in the consumer’s currency. This is typical for the pricing mechanism of Russian export products, based on prices in US dollars of the main world commodity exchanges.

Empirical studies of the exchange rate of the US dollar to the Russian ruble (USD/RUR), based on a systematic analysis of the exchange rate policy, are carried out during the financial and economic crises in recent Russian history.

Because of the conducted analysis in these periods, it is possible to single out the fall in export prices of oil and other energy products on international markets as the main reason for the fall in the Russian ruble exchange rate. This is due to the overwhelming predominance of mineral raw materials in the index of average actual export prices and the deterioration of the global market situation. At the same time, the growth of consumer prices within the country also had a significant impact on the results of the dynamics of the USD/RUR exchange rate. The impact of the fall in aggregate output in certain periods was also noticeable.

At the same time, in the last period, when the Bank of Russia completely switched to the floating exchange rate policy, the simulation results correlated much better with market data compared to previous periods.

The conducted modeling allows us to evaluate the short-term contribution to the crisis depreciation dynamics of the Russian ruble quantitatively.

The identification of the structural dependence of the exchange rate on its main factors makes it possible to simplify the development of sound management decisions on the exchange rate regulation in the system of macroeconomic management.

The modeling also allowed us to draw mathematical conclusions about the nominal and the real exchange rate dynamics in the long term under certain conditions. However, the economic interpretation of the long-term modeling results requires the further accumulation of the state statistics and may become a future study.