Monitoring of Linear Profiles Using Linear Mixed Model in the Presence of Measurement Errors
Abstract
1. Introduction
2. Methodology
2.1. Linear Mixed Measurement Error Model
2.2. Estimation of Random Effects
3. Proposed Control Charts
3.1. The Hotelling’s Control Chart
3.2. The MEWMA Control Chart
3.3. The MCUSUM Control Chart
3.4. Performance Measures
3.5. Searching UCLs
- Step 1:
- The initial values of lower and upper bounds are pre-specified, denoted as and . It is desirable that , where and are the corresponding ARL values of and , respectively.
- Step 2:
- Let and be the corresponding ARL value. If , then assign and . Otherwise, assign and .
- Step 3:
- Repeat Step 2 until is sufficiently small and then the desired is obtained.
4. Performance Study
| MEWMA | MCUSUM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.01 | 0.04 | 0.09 | 0.00 | 0.01 | 0.04 | 0.09 | 0.00 | 0.01 | 0.04 | 0.09 | |||||
| 0.0 | 1.2 | 67.6 | 72.2 | 80.5 | 87.7 | 84.7 | 92.4 | 95.8 | 102.7 | 93.0 | 101.3 | 101.1 | 110.2 | |||
| 1.4 | 29.8 | 32.6 | 38.0 | 43.0 | 44.8 | 50.5 | 53.5 | 59.1 | 52.3 | 59.2 | 59.6 | 64.5 | ||||
| 1.6 | 16.4 | 17.9 | 21.0 | 24.6 | 27.9 | 32.0 | 33.8 | 38.4 | 33.6 | 39.7 | 38.7 | 42.6 | ||||
| 1.8 | 10.5 | 11.4 | 13.6 | 15.4 | 19.5 | 22.0 | 23.4 | 26.6 | 23.8 | 27.8 | 27.5 | 30.1 | ||||
| 2.0 | 7.5 | 8.1 | 9.4 | 10.9 | 14.8 | 16.3 | 17.3 | 19.6 | 18.0 | 21.2 | 20.8 | 22.8 | ||||
| 2.2 | 5.8 | 6.1 | 7.1 | 8.2 | 11.4 | 12.7 | 13.6 | 15.3 | 14.4 | 16.9 | 16.3 | 18.1 | ||||
| 2.4 | 4.7 | 5.0 | 5.7 | 6.3 | 9.5 | 10.4 | 11.0 | 12.3 | 11.7 | 13.8 | 13.3 | 14.7 | ||||
| 2.6 | 4.0 | 4.3 | 4.7 | 5.3 | 7.9 | 8.7 | 9.2 | 10.3 | 10.0 | 11.6 | 11.3 | 12.2 | ||||
| 2.8 | 3.5 | 3.6 | 4.1 | 4.4 | 6.8 | 7.4 | 7.8 | 8.8 | 8.5 | 9.9 | 9.6 | 10.6 | ||||
| 3.0 | 3.1 | 3.2 | 3.6 | 3.9 | 5.9 | 6.6 | 6.8 | 7.7 | 7.5 | 8.7 | 8.5 | 9.0 | ||||
| AEQL | 39.6 | 42.0 | 47.9 | 53.8 | 74.5 | 82.5 | 87.2 | 97.8 | 92.2 | 107.2 | 104.8 | 114.2 | ||||
| 0.1 | 1.2 | 74.0 | 68.1 | 94.3 | 81.6 | 90.2 | 75.2 | 109.1 | 100.9 | 97.2 | 91.3 | 112.8 | 110.8 | |||
| 1.4 | 33.1 | 29.9 | 45.8 | 39.5 | 48.8 | 40.4 | 62.2 | 57.5 | 54.5 | 51.0 | 68.4 | 68.6 | ||||
| 1.6 | 18.4 | 16.7 | 25.3 | 22.2 | 30.0 | 24.5 | 39.3 | 37.0 | 35.6 | 33.3 | 45.1 | 46.2 | ||||
| 1.8 | 11.5 | 10.7 | 15.6 | 14.2 | 20.8 | 17.2 | 27.0 | 25.9 | 25.2 | 23.6 | 32.4 | 33.0 | ||||
| 2.0 | 8.2 | 7.7 | 10.8 | 10.0 | 15.3 | 12.6 | 19.9 | 19.5 | 19.3 | 17.7 | 24.4 | 25.3 | ||||
| 2.2 | 6.2 | 6.0 | 8.0 | 7.6 | 12.1 | 9.9 | 15.4 | 15.2 | 15.1 | 14.2 | 19.4 | 19.8 | ||||
| 2.4 | 5.0 | 4.8 | 6.3 | 6.1 | 10.0 | 8.2 | 12.5 | 12.1 | 12.4 | 11.5 | 15.6 | 16.4 | ||||
| 2.6 | 4.3 | 4.1 | 5.3 | 5.0 | 8.3 | 6.9 | 10.3 | 10.2 | 10.5 | 9.7 | 13.1 | 13.8 | ||||
| 2.8 | 3.6 | 3.5 | 4.4 | 4.3 | 7.1 | 5.9 | 8.8 | 8.7 | 9.0 | 8.4 | 11.4 | 11.9 | ||||
| 3.0 | 3.2 | 3.2 | 3.8 | 3.7 | 6.2 | 5.1 | 7.6 | 7.5 | 7.8 | 7.3 | 9.8 | 10.2 | ||||
| AEQL | 42.3 | 40.3 | 53.8 | 50.5 | 78.6 | 64.7 | 98.7 | 96.2 | 97.0 | 90.4 | 122.6 | 126.9 | ||||
| 0.5 | 1.2 | 70.6 | 70.9 | 79.3 | 90.2 | 87.7 | 88.3 | 89.8 | 109.7 | 92.7 | 95.5 | 90.9 | 116.0 | |||
| 1.4 | 31.7 | 31.3 | 37.4 | 44.1 | 46.4 | 47.2 | 49.4 | 64.0 | 51.7 | 54.3 | 53.1 | 71.9 | ||||
| 1.6 | 17.3 | 17.5 | 20.5 | 25.1 | 29.4 | 29.5 | 31.1 | 40.5 | 32.5 | 35.4 | 34.8 | 47.5 | ||||
| 1.8 | 11.1 | 11.2 | 13.0 | 15.9 | 19.9 | 20.3 | 21.5 | 28.0 | 23.0 | 25.0 | 24.5 | 34.1 | ||||
| 2.0 | 7.8 | 8.0 | 9.1 | 11.2 | 14.8 | 15.3 | 16.0 | 20.9 | 17.3 | 19.0 | 18.3 | 26.2 | ||||
| 2.2 | 6.1 | 6.1 | 6.9 | 8.2 | 11.8 | 12.0 | 12.6 | 16.2 | 13.7 | 15.2 | 14.6 | 20.5 | ||||
| 2.4 | 4.9 | 5.0 | 5.6 | 6.5 | 9.6 | 9.8 | 10.3 | 13.1 | 11.3 | 12.2 | 11.9 | 16.8 | ||||
| 2.6 | 4.1 | 4.2 | 4.6 | 5.3 | 7.9 | 8.2 | 8.7 | 10.9 | 9.5 | 10.5 | 9.9 | 13.9 | ||||
| 2.8 | 3.6 | 3.7 | 4.0 | 4.5 | 6.9 | 7.1 | 7.4 | 9.3 | 8.1 | 9.0 | 8.5 | 11.9 | ||||
| 3.0 | 3.2 | 3.2 | 3.5 | 3.9 | 6.1 | 6.2 | 6.6 | 8.0 | 7.1 | 7.9 | 7.6 | 10.4 | ||||
| AEQL | 41.1 | 41.6 | 46.8 | 54.8 | 75.9 | 77.6 | 81.9 | 103.3 | 88.3 | 96.7 | 93.0 | 129.8 | ||||
| 0.9 | 1.2 | 68.2 | 72.7 | 81.3 | 97.0 | 89.7 | 78.3 | 95.6 | 111.2 | 101.0 | 97.3 | 104.9 | 116.5 | |||
| 1.4 | 29.5 | 32.6 | 37.7 | 49.0 | 47.1 | 41.3 | 53.3 | 64.9 | 58.3 | 55.6 | 62.1 | 70.9 | ||||
| 1.6 | 16.2 | 17.7 | 20.5 | 27.6 | 29.3 | 25.5 | 33.2 | 41.7 | 37.5 | 36.0 | 40.3 | 47.5 | ||||
| 1.8 | 10.4 | 11.3 | 13.1 | 17.2 | 20.6 | 17.2 | 23.1 | 28.9 | 26.4 | 25.6 | 28.7 | 34.6 | ||||
| 2.0 | 7.5 | 8.0 | 9.3 | 12.0 | 15.2 | 12.8 | 17.2 | 21.3 | 20.0 | 19.4 | 21.9 | 25.7 | ||||
| 2.2 | 5.8 | 6.2 | 7.1 | 8.8 | 12.1 | 10.2 | 13.3 | 16.4 | 15.8 | 15.3 | 17.5 | 20.6 | ||||
| 2.4 | 4.7 | 4.9 | 5.6 | 7.0 | 9.8 | 8.3 | 11.0 | 13.3 | 13.1 | 12.6 | 14.3 | 16.8 | ||||
| 2.6 | 4.0 | 4.1 | 4.7 | 5.7 | 8.2 | 7.0 | 9.1 | 11.1 | 11.0 | 10.6 | 12.0 | 14.1 | ||||
| 2.8 | 3.5 | 3.6 | 4.0 | 4.8 | 7.1 | 6.0 | 7.8 | 9.5 | 9.5 | 9.2 | 10.3 | 12.2 | ||||
| 3.0 | 3.1 | 3.2 | 3.5 | 4.1 | 6.2 | 5.3 | 6.8 | 8.1 | 8.3 | 8.0 | 9.0 | 10.4 | ||||
| AEQL | 39.6 | 41.7 | 47.3 | 58.8 | 77.6 | 66.1 | 86.3 | 105.4 | 102.1 | 98.8 | 111.2 | 130.4 | ||||
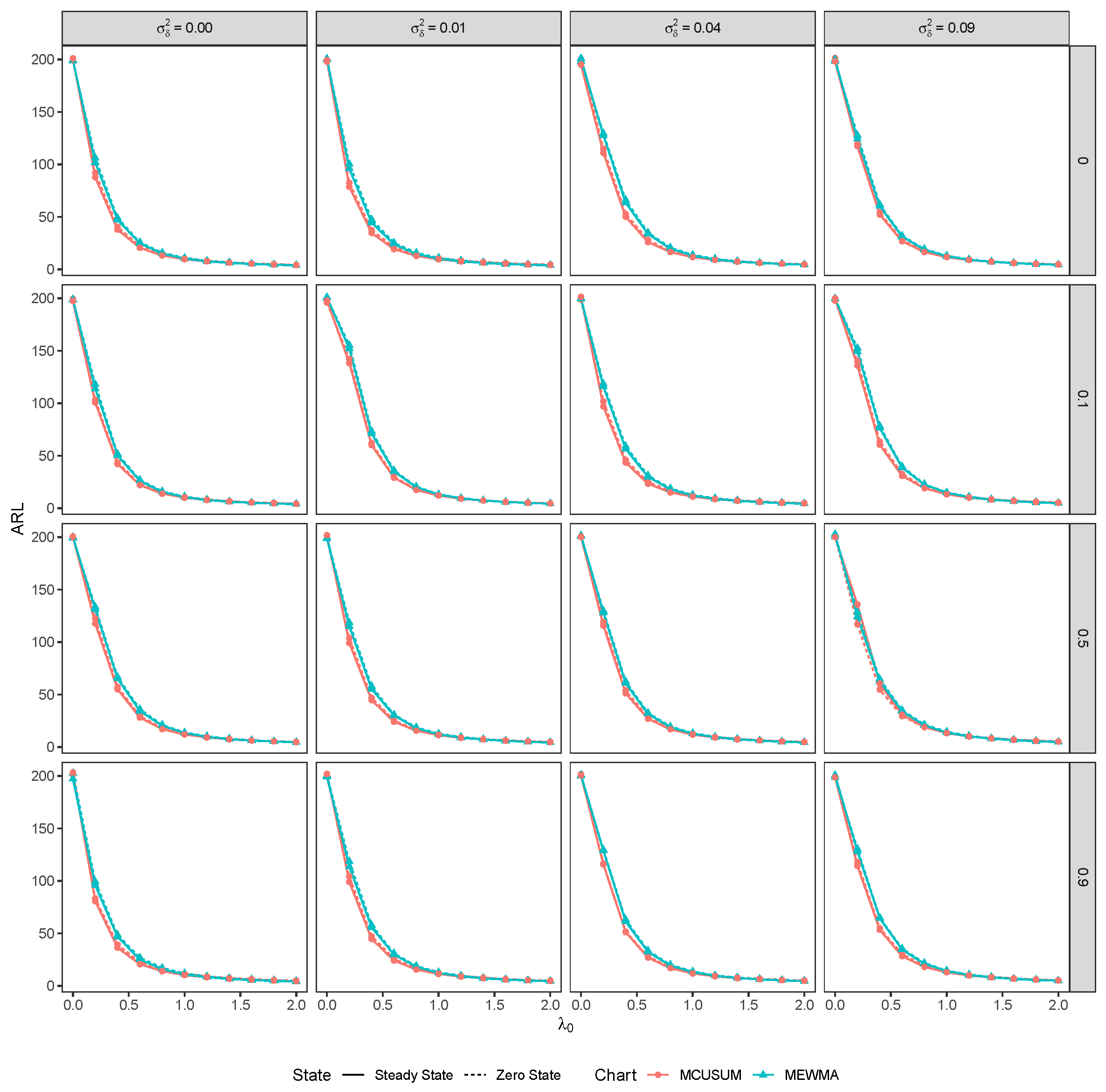
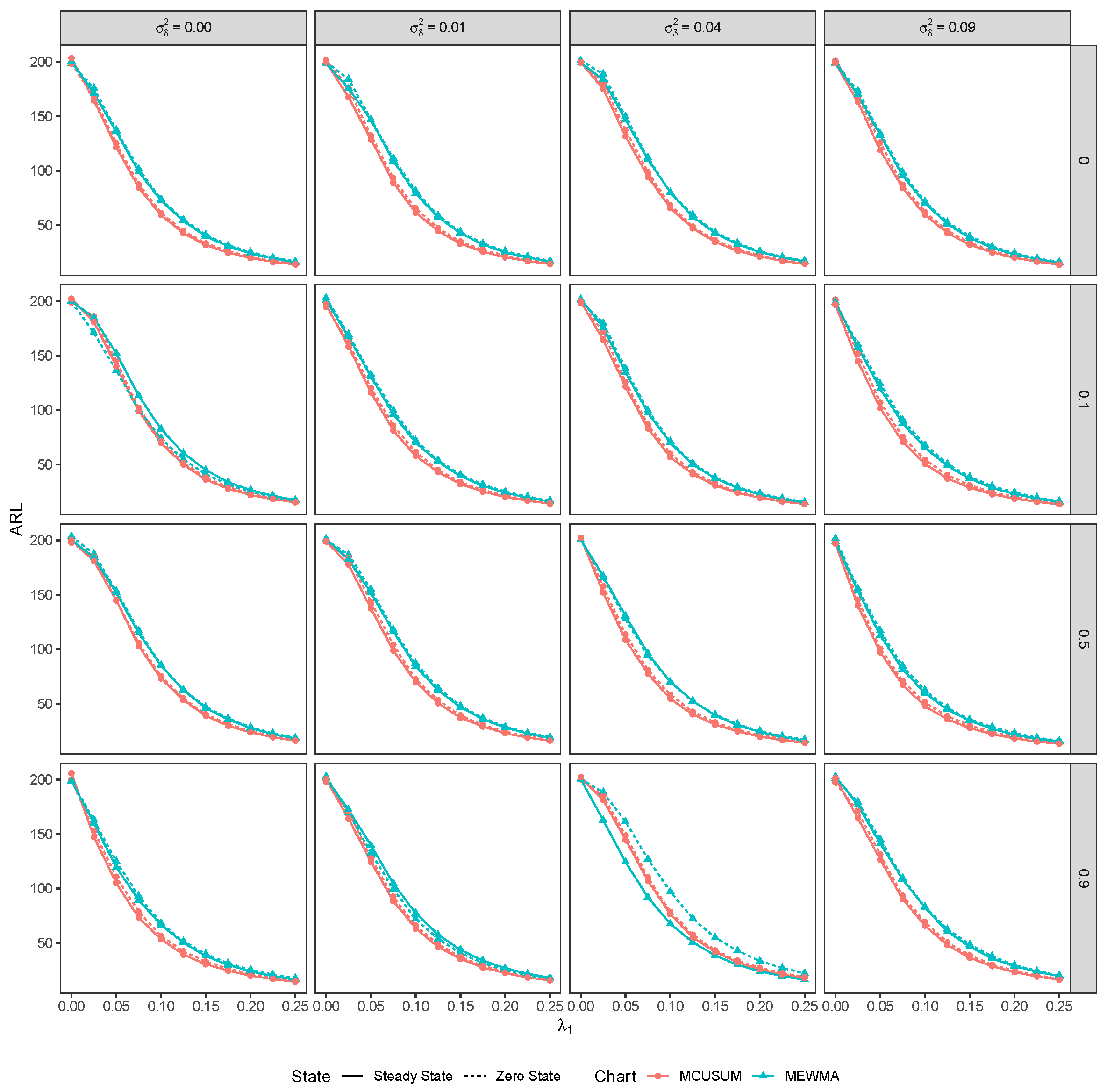
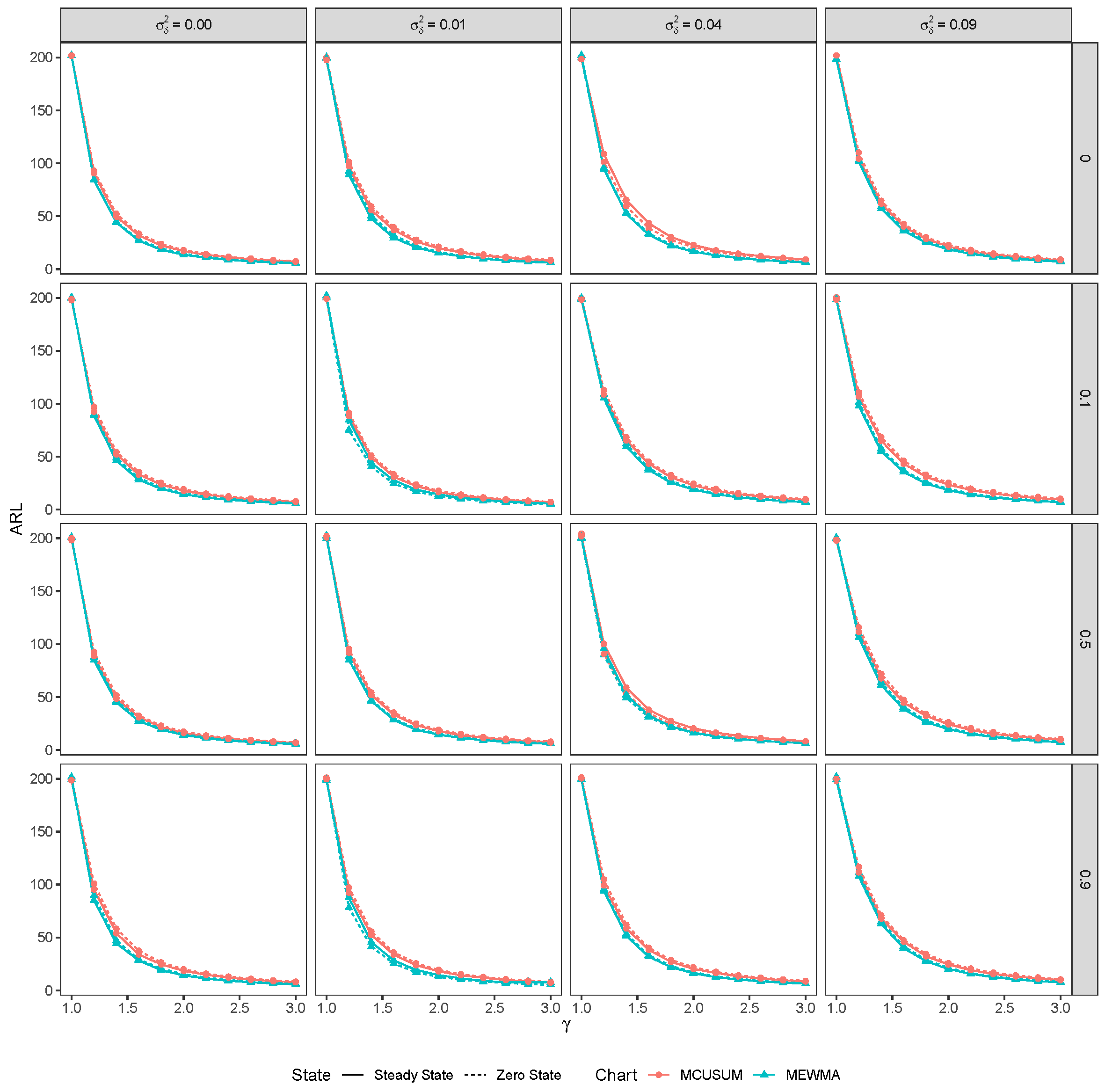
Effect of Ignoring Measurement Error and/or Random Effects
5. Case Study
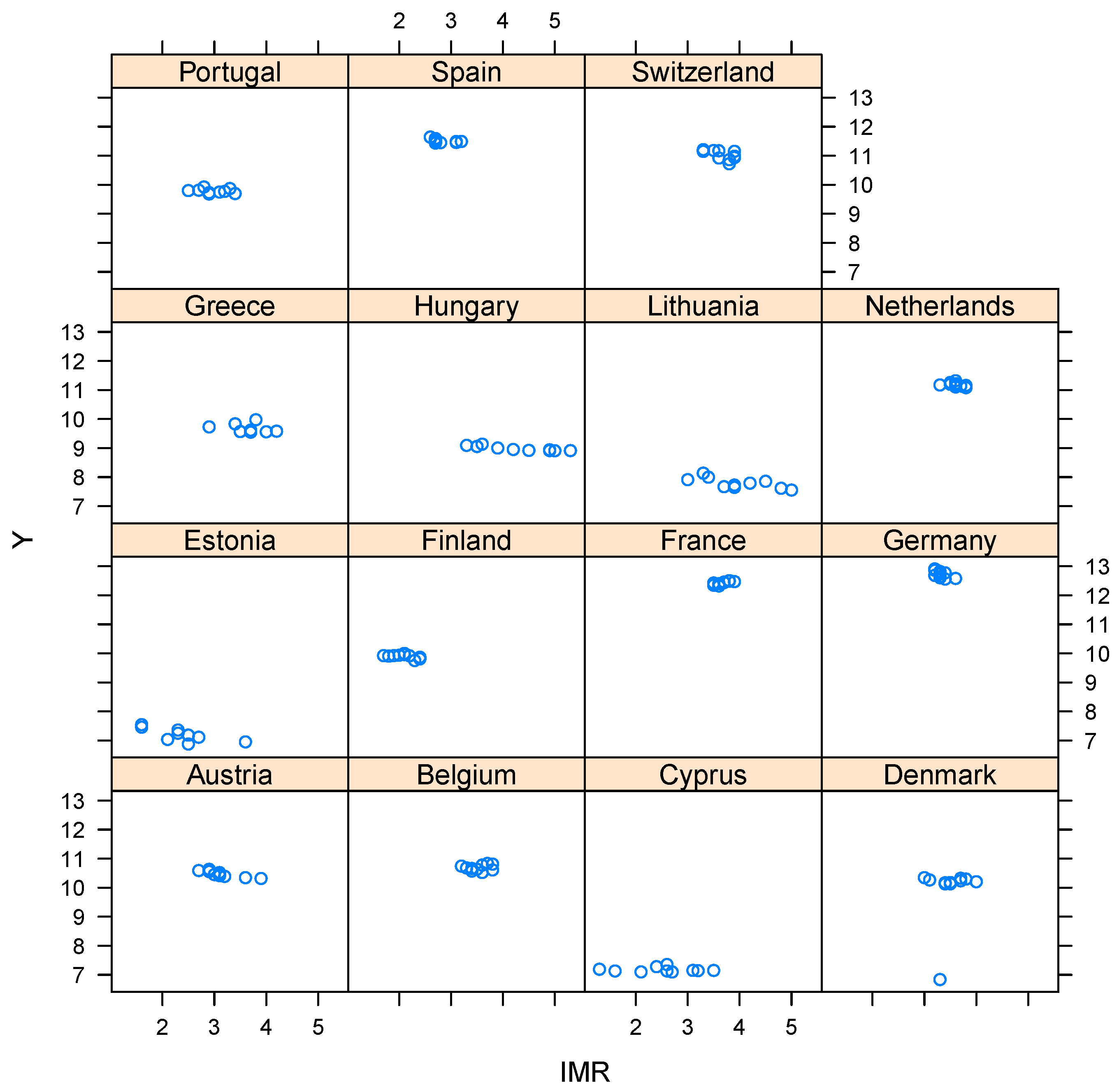
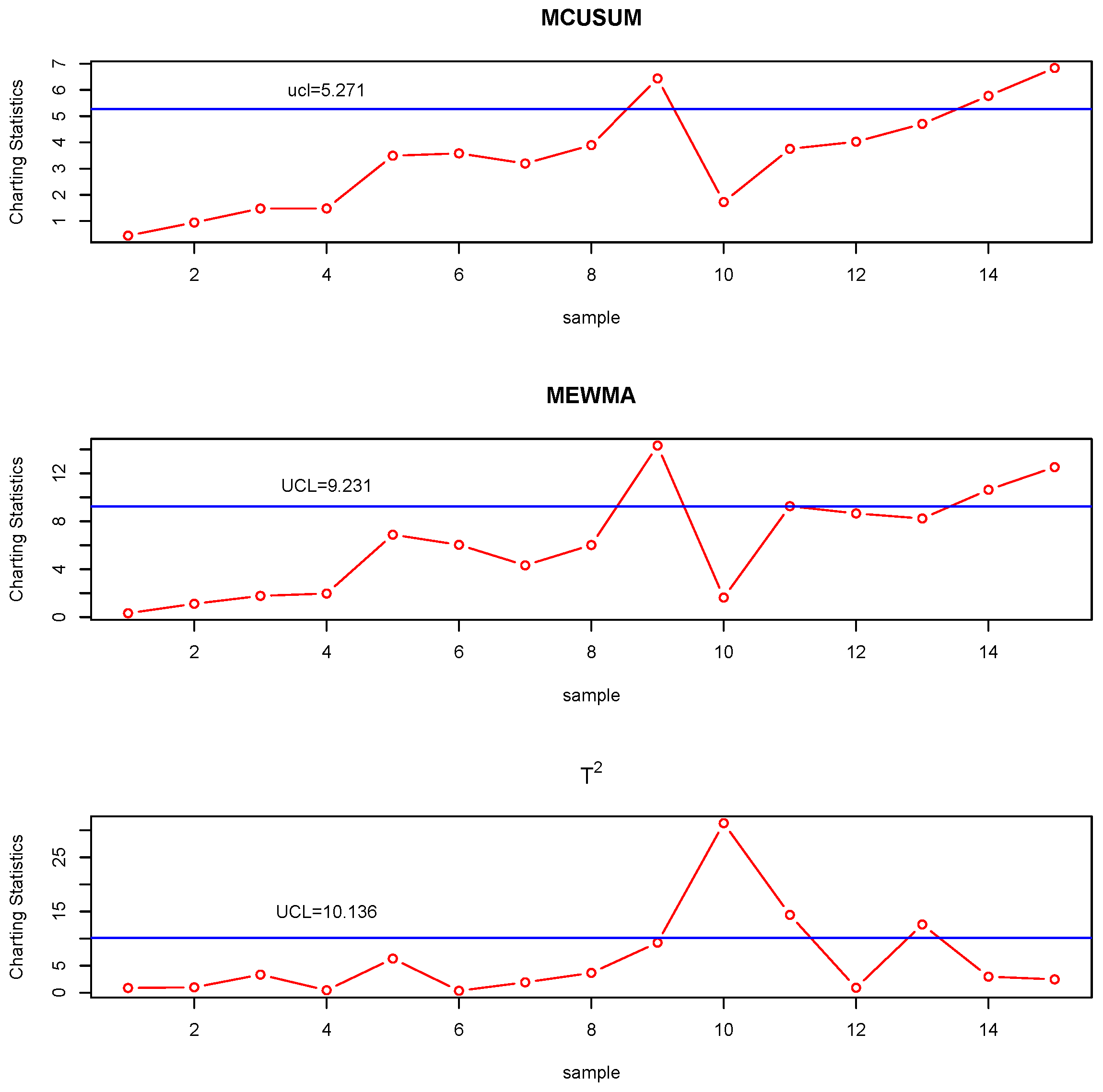
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Estimation of D and σ 2
- Step 1:
- Predict the residuals given for subject i,
- Step 2:
- Given , we can update the estimate of by
References
- Kang, L.; Albin, S.L. On-line monitoring when the process yields a linear profile. J. Qual. Technol. 2000, 32, 418–426. [Google Scholar] [CrossRef]
- Woodall, W.H.; Spitzner, D.J.; Montgomery, D.C.; Gupta, S. Using Control Charts to Monitor Process and Product Quality Profiles. J. Qual. Technol. 2004, 36, 309–320. [Google Scholar] [CrossRef]
- Maleki, M.R.; Amiri, A.; Castagliola, P. An overview on recent profile monitoring papers (2008–2018) based on conceptual classification scheme. Comput. Ind. Eng. 2018, 126, 705–728. [Google Scholar] [CrossRef]
- Stover, F.S.; Brill, R.V. Statistical quality control applied to ion chromatography calibrations. J. Chromatogr. A 1998, 804, 37–43. [Google Scholar] [CrossRef]
- Kim, K.; Mahmoud, M.A.; Woodall, W.H. On the monitoring of linear profiles. J. Qual. Technol. 2003, 35, 317–328. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; Woodall, W.H. Phase I analysis of linear profiles with calibration applications. Technometrics 2004, 46, 380–391. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, Y.; Wang, Z. A control chart based on a change-point model for monitoring linear profiles. IIE Trans. 2006, 38, 1093–1103. [Google Scholar] [CrossRef]
- Mahmoud, M.A.; Parker, P.A.; Woodall, W.H.; Hawkins, D.M. A change point method for linear profile data. Qual. Reliab. Eng. Int. 2007, 23, 247–268. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Wang, Z. Control chart based on likelihood ratio for monitoring linear profiles. Comput. Stat. Data Anal. 2009, 53, 1440–1448. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z. An exponentially weighted moving average scheme with variable sampling intervals for monitoring linear profiles. Comput. Ind. Eng. 2010, 59, 630–637. [Google Scholar] [CrossRef]
- Amiri, A.; Mehrjoo, M.; Pasek, Z.J. Modifying simple linear profiles monitoring schemes in phase II to detect decreasing step shifts and drifts. Int. J. Adv. Manuf. Technol. 2013, 64, 1323–1332. [Google Scholar] [CrossRef]
- Kazemzadeh, R.B.; Noorossana, R.; Amiri, A. Phase I monitoring of polynomial profiles. Commun. Stat. Theory Methods 2008, 37, 1671–1686. [Google Scholar] [CrossRef]
- Kazemzadeh, R.; Noorossana, R.; Amiri, A. Monitoring polynomial profiles in quality control applications. Int. J. Adv. Manuf. Technol. 2009, 42, 703–712. [Google Scholar] [CrossRef]
- Zou, C.; Tsung, F.; Wang, Z. Monitoring general linear profiles using multivariate exponentially weighted moving average schemes. Technometrics 2007, 49, 395–408. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Phase I analysis of multiple linear regression profiles. Commun. Stat. Simul. Comput. 2008, 37, 2106–2130. [Google Scholar] [CrossRef]
- Noorossana, R.; Eyvazian, M.; Vaghefi, A. Phase II monitoring of multivariate simple linear profiles. Comput. Ind. Eng. 2010, 58, 563–570. [Google Scholar] [CrossRef]
- Zi, X.; Zou, C.; Tsung, F. A distribution-free robust method for monitoring linear profiles using rank-based regression. IIE Trans. 2012, 44, 949–963. [Google Scholar] [CrossRef]
- Zou, C.; Ning, X.; Tsung, F. LASSO-based multivariate linear profile monitoring. Ann. Oper. Res. 2012, 192, 3–19. [Google Scholar] [CrossRef]
- Ding, Y.; Zeng, L.; Zhou, S. Phase I analysis for monitoring nonlinear profiles in manufacturing processes. J. Qual. Technol. 2006, 38, 199–216. [Google Scholar] [CrossRef]
- Moguerza, J.M.; Muñoz, A.; Psarakis, S. Monitoring nonlinear profiles using support vector machines. In Proceedings of the Progress in Pattern Recognition, Image Analysis and Applications, Valpariso, Chile, 13–16 November 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 574–583. [Google Scholar] [CrossRef]
- Williams, J.D.; Woodall, W.H.; Birch, J.B. Statistical monitoring of nonlinear product and process quality profiles. Qual. Reliab. Eng. Int. 2007, 23, 925–941. [Google Scholar] [CrossRef]
- Vaghefi, A.; Tajbakhsh, S.D.; Noorossana, R. Phase II monitoring of nonlinear profiles. Commun. Stat. Theory Methods 2009, 38, 1834–1851. [Google Scholar] [CrossRef]
- Fan, S.K.S.; Chang, Y.J.; Aidara, N. Nonlinear profile monitoring of reflow process data based on the sum of sine functions. Qual. Reliab. Eng. Int. 2013, 29, 743–758. [Google Scholar] [CrossRef]
- Xin, H.; Hsieh, W.J.; Lio, Y.; Tsai, T.R. Nonlinear Profile Monitoring Using Spline Functions. Mathematics 2020, 8, 1588. [Google Scholar] [CrossRef]
- Jensen, W.A.; Birch, J.B.; Woodall, W.H. Monitoring correlation within linear profiles using mixed models. J. Qual. Technol. 2008, 40, 167–183. [Google Scholar] [CrossRef]
- Jensen, W.A.; Birch, J.B. Profile monitoring via nonlinear mixed models. J. Qual. Technol. 2009, 41, 18–34. [Google Scholar] [CrossRef]
- Narvand, A.; Soleimani, P.; Raissi, S. Phase II monitoring of auto-correlated linear profiles using linear mixed model. J. Ind. Eng. Int. 2013, 9, 1–9. [Google Scholar] [CrossRef][Green Version]
- Soleimani, P.; Narvand, A.; Raissi, S. Online monitoring of auto correlated linear profiles via mixed model. Int. J. Manuf. Technol. Manag. 2013, 27, 238–250. [Google Scholar] [CrossRef]
- Maleki, M.R.; Amiri, A.; Castagliola, P. Measurement errors in statistical process monitoring: A literature review. Comput. Ind. Eng. 2017, 103, 316–329. [Google Scholar] [CrossRef]
- Linna, K.W.; Woodall, W.H. Effect of measurement error on Shewhart control charts. J. Qual. Technol. 2001, 33, 213–222. [Google Scholar] [CrossRef]
- Linna, K.W.; Woodall, W.H.; Busby, K.L. The performance of multivariate control charts in the presence of measurement error. J. Qual. Technol. 2001, 33, 349–355. [Google Scholar] [CrossRef]
- Maravelakis, P.; Panaretos, J.; Psarakis, S. EWMA chart and measurement error. J. Appl. Stat. 2004, 31, 445–455. [Google Scholar] [CrossRef]
- Tran, K.P.; Castagliola, P.; Celano, G. The performance of the Shewhart-RZ control chart in the presence of measurement error. Int. J. Prod. Res. 2016, 54, 7504–7522. [Google Scholar] [CrossRef]
- Chen, L.P.; Yang, S.F. A New p-Control Chart with Measurement Error Correction. arXiv 2022, arXiv:2203.03384. [Google Scholar] [CrossRef]
- Li, J.; Huang, S. Regression-based process monitoring with consideration of measurement errors. IIE Trans. 2009, 42, 146–160. [Google Scholar] [CrossRef]
- Wang, Y.H.T.; Huwang, L. On the monitoring of simple linear Berkson profiles. Qual. Reliab. Eng. Int. 2012, 28, 949–965. [Google Scholar] [CrossRef]
- Noorossana, R.; Zerehsaz, Y. Effect of measurement error on phase II monitoring of simple linear profiles. Int. J. Adv. Manuf. Technol. 2015, 79, 2031–2040. [Google Scholar] [CrossRef]
- Deaton, A. Panel data from time series of cross-sections. J. Econom. 1985, 30, 109–126. [Google Scholar] [CrossRef]
- Fuller, W.A. Measurement Error Models; Wiley: New York, NY, USA, 1987. [Google Scholar] [CrossRef]
- Cheng, C.L.; Van Ness, J.W. Statistical Regression with Measurement Error; Arnold: London, UK, 1999. [Google Scholar]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models: A Modern Perspective; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Buonaccorsi, J.P. Measurement Error: Models, Methods, and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X. Consistency of LS estimator in simple linear EV regression models. Acta Math. Sci. 2005, 25, 50–58. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, F.; Wang, K. Central limit theorems for LS estimators in the EV regression model with dependent measurements. J. Korean Stat. Soc. 2011, 40, 303–312. [Google Scholar] [CrossRef]
- Xu, S.; Li, N. Consistency for the LS estimator in the linear EV regression model with replicate observations. J. Korean Stat. Soc. 2013, 42, 451–458. [Google Scholar] [CrossRef]
- Harville, D.A. Maximum likelihood approaches to variance component estimation and to related problems. J. Am. Stat. Assoc. 1977, 72, 320–338. [Google Scholar] [CrossRef]
- Zhong, X.; Fung, W.; Wei, B. Estimation in linear models with random effects and errors-in-variables. Ann. Inst. Stat. Math. 2002, 54, 595–606. [Google Scholar] [CrossRef]
- Sullivan, J.H.; Woodall, W.H. A comparison of multivariate control charts for individual observations. J. Qual. Technol. 1996, 28, 398–408. [Google Scholar] [CrossRef]
- Fung, W.K.; Zhong, X.P.; Wei, B.C. On estimation and influence diagnostics in linear mixed measurement error models. AJMMS-Am. J. Math. Manag. Sci. 2003, 23, 37–59. [Google Scholar] [CrossRef]
- Zare, K.; Rasekh, A. Diagnostic measures for linear mixed measurement error models. SORT-Stat. Oper. Res. Trans. 2011, 35, 125–144. [Google Scholar]
- Maksaei, N.; Rasekh, A.; Babadi, B. Influence measures and outliers detection in linear mixed measurement error models with Ridge estimation. Commun. Stat. Simul. Comput. 2021, 4, 1–17. [Google Scholar] [CrossRef]
- Yavarizadeh, B.; Rasekh, A.; Ahmed, S.E.; Babadi, B. Ridge estimation in linear mixed measurement error models with stochastic linear mixed restrictions. Commun. Stat. Simul. Comput. 2022, 51, 3037–3053. [Google Scholar] [CrossRef]
- Lowry, C.A.; Woodall, W.H.; Champ, C.W.; Rigdon, S.E. A multivariate exponentially weighted moving average control chart. Technometrics 1992, 34, 46–53. [Google Scholar] [CrossRef]
- Crosier, R.B. Multivariate generalizations of cumulative sum quality-control schemes. Technometrics 1988, 30, 291–303. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Sun, Y.; Zhang, W.; Tong, H. Estimation of the covariance matrix of random effects in longitudinal studies. Ann. Stat. 2007, 35, 2795–2814. [Google Scholar] [CrossRef]



| MEWMA | MCUSUM | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.5 | 0.9 | 0.0 | 0.1 | 0.5 | 0.9 | 0.0 | 0.1 | 0.5 | 0.9 | |||
| 0.00 | 10.762 | 11.255 | 9.590 | 10.890 | 9.918 | 10.251 | 8.731 | 10.468 | 5.653 | 5.791 | 5.021 | 6.060 | ||
| 0.01 | 10.309 | 9.700 | 11.018 | 11.563 | 10.815 | 9.003 | 10.132 | 10.610 | 6.170 | 5.175 | 5.748 | 5.987 | ||
| 0.04 | 10.594 | 11.618 | 10.739 | 12.726 | 9.646 | 10.678 | 9.947 | 11.555 | 5.468 | 6.008 | 6.015 | 6.407 | ||
| 0.09 | 9.727 | 11.811 | 10.829 | 12.032 | 8.871 | 11.093 | 10.201 | 10.938 | 5.110 | 6.315 | 5.841 | 6.086 | ||
| MEWMA | MCUSUM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.01 | 0.04 | 0.09 | 0.00 | 0.01 | 0.04 | 0.09 | 0.00 | 0.01 | 0.04 | 0.09 | |||||
| 0.0 | 0.2 | 179.0 | 195.2 | 187.6 | 183.6 | 106.2 | 100.4 | 129.7 | 127.8 | 92.0 | 82.6 | 115.1 | 119.3 | |||
| 0.4 | 137.1 | 165.6 | 159.0 | 149.2 | 48.9 | 47.4 | 66.2 | 61.9 | 40.5 | 37.4 | 52.8 | 54.0 | ||||
| 0.6 | 99.5 | 121.6 | 124.5 | 106.7 | 25.8 | 25.4 | 35.0 | 32.0 | 22.2 | 21.1 | 28.0 | 28.1 | ||||
| 0.8 | 69.5 | 82.6 | 94.1 | 75.9 | 16.0 | 15.9 | 20.8 | 19.4 | 14.3 | 14.3 | 17.6 | 17.6 | ||||
| 1.0 | 47.9 | 55.4 | 68.1 | 54.3 | 11.0 | 11.1 | 13.9 | 13.1 | 10.6 | 10.7 | 12.5 | 12.4 | ||||
| 1.2 | 33.3 | 38.0 | 49.4 | 37.7 | 8.3 | 8.4 | 10.2 | 9.6 | 8.3 | 8.6 | 9.6 | 9.5 | ||||
| 1.4 | 23.3 | 26.0 | 35.1 | 26.7 | 6.7 | 6.7 | 7.9 | 7.6 | 6.8 | 7.1 | 7.9 | 7.6 | ||||
| 1.6 | 16.4 | 18.4 | 25.3 | 19.4 | 5.5 | 5.6 | 6.5 | 6.2 | 5.9 | 6.1 | 6.6 | 6.4 | ||||
| 1.8 | 11.9 | 13.0 | 18.5 | 14.3 | 4.7 | 4.8 | 5.5 | 5.3 | 5.1 | 5.3 | 5.7 | 5.6 | ||||
| 2.0 | 8.8 | 9.5 | 13.7 | 10.6 | 4.1 | 4.2 | 4.8 | 4.6 | 4.5 | 4.8 | 5.1 | 4.9 | ||||
| AEQL | 183.2 | 209.6 | 262.8 | 208.7 | 56.9 | 57.1 | 69.6 | 66.2 | 56.5 | 57.4 | 66.1 | 64.9 | ||||
| 0.1 | 0.2 | 180.4 | 190.9 | 181.0 | 191.3 | 118.1 | 155.3 | 118.5 | 152.6 | 103.1 | 142.3 | 101.8 | 140.1 | |||
| 0.4 | 136.2 | 156.8 | 148.2 | 160.0 | 51.7 | 73.3 | 59.0 | 78.3 | 43.7 | 62.2 | 46.0 | 63.6 | ||||
| 0.6 | 95.4 | 117.7 | 113.7 | 122.9 | 26.8 | 36.1 | 31.2 | 39.8 | 23.1 | 30.0 | 25.1 | 32.7 | ||||
| 0.8 | 65.3 | 82.9 | 82.3 | 88.7 | 16.1 | 20.6 | 18.9 | 23.0 | 14.7 | 18.1 | 16.4 | 20.1 | ||||
| 1.0 | 43.8 | 57.5 | 59.6 | 62.7 | 11.1 | 13.4 | 12.8 | 15.1 | 10.7 | 12.5 | 11.9 | 14.0 | ||||
| 1.2 | 29.8 | 39.8 | 41.9 | 44.2 | 8.3 | 9.8 | 9.6 | 11.0 | 8.4 | 9.5 | 9.3 | 10.8 | ||||
| 1.4 | 20.5 | 27.4 | 30.0 | 31.4 | 6.5 | 7.5 | 7.5 | 8.5 | 6.8 | 7.6 | 7.7 | 8.7 | ||||
| 1.6 | 14.8 | 19.4 | 21.7 | 22.6 | 5.4 | 6.1 | 6.2 | 6.9 | 5.8 | 6.3 | 6.5 | 7.3 | ||||
| 1.8 | 10.6 | 13.9 | 15.8 | 16.9 | 4.6 | 5.2 | 5.3 | 5.7 | 5.1 | 5.4 | 5.7 | 6.3 | ||||
| 2.0 | 7.9 | 10.3 | 11.8 | 12.4 | 4.1 | 4.5 | 4.6 | 5.0 | 4.5 | 4.8 | 5.0 | 5.5 | ||||
| AEQL | 168.1 | 216.4 | 228.7 | 242.4 | 56.9 | 68.6 | 65.2 | 75.7 | 57.1 | 66.0 | 63.4 | 73.9 | ||||
| 0.5 | 0.2 | 186.4 | 179.7 | 181.9 | 184.1 | 133.5 | 118.6 | 129.8 | 128.3 | 122.5 | 103.7 | 119.1 | 117.0 | |||
| 0.4 | 157.9 | 148.6 | 144.2 | 148.1 | 66.7 | 57.8 | 62.4 | 64.8 | 57.2 | 46.9 | 53.9 | 54.8 | ||||
| 0.6 | 122.8 | 110.1 | 104.9 | 109.6 | 35.9 | 30.9 | 32.6 | 35.1 | 29.5 | 25.4 | 28.3 | 29.6 | ||||
| 0.8 | 92.8 | 81.5 | 74.1 | 80.7 | 21.1 | 18.8 | 19.6 | 21.5 | 18.2 | 16.5 | 17.9 | 19.0 | ||||
| 1.0 | 66.4 | 58.3 | 51.2 | 57.7 | 13.9 | 12.8 | 13.3 | 14.6 | 12.8 | 12.0 | 12.6 | 13.6 | ||||
| 1.2 | 48.3 | 41.9 | 36.0 | 41.6 | 10.3 | 9.6 | 9.8 | 10.7 | 9.7 | 9.4 | 9.7 | 10.5 | ||||
| 1.4 | 34.1 | 29.9 | 25.6 | 29.9 | 8.0 | 7.6 | 7.7 | 8.4 | 7.9 | 7.6 | 7.9 | 8.5 | ||||
| 1.6 | 24.5 | 21.6 | 18.9 | 21.8 | 6.5 | 6.2 | 6.3 | 6.8 | 6.6 | 6.5 | 6.6 | 7.2 | ||||
| 1.8 | 18.0 | 15.8 | 13.6 | 16.3 | 5.5 | 5.3 | 5.3 | 5.8 | 5.7 | 5.7 | 5.7 | 6.2 | ||||
| 2.0 | 13.2 | 11.7 | 10.3 | 12.4 | 4.8 | 4.6 | 4.6 | 5.0 | 5.0 | 5.0 | 5.1 | 5.5 | ||||
| AEQL | 256.3 | 226.5 | 201.1 | 228.3 | 70.3 | 65.2 | 66.8 | 72.3 | 67.0 | 63.5 | 66.3 | 71.0 | ||||
| 0.9 | 0.2 | 172.9 | 178.4 | 183.8 | 183.6 | 99.2 | 118.6 | 129.7 | 130.6 | 83.3 | 104.3 | 116.6 | 117.7 | |||
| 0.4 | 134.2 | 142.6 | 147.3 | 148.1 | 48.5 | 57.8 | 63.0 | 65.0 | 39.3 | 47.3 | 51.7 | 55.0 | ||||
| 0.6 | 99.4 | 107.6 | 107.3 | 111.2 | 26.9 | 31.0 | 33.6 | 35.6 | 22.8 | 25.8 | 28.0 | 30.3 | ||||
| 0.8 | 70.8 | 77.9 | 76.2 | 82.2 | 17.1 | 18.9 | 20.1 | 21.8 | 15.4 | 16.8 | 17.9 | 19.0 | ||||
| 1.0 | 50.1 | 54.9 | 53.7 | 57.2 | 12.0 | 13.1 | 13.8 | 14.6 | 11.5 | 12.3 | 12.8 | 13.7 | ||||
| 1.2 | 36.0 | 39.4 | 38.0 | 41.5 | 9.1 | 9.7 | 10.0 | 10.8 | 9.2 | 9.5 | 9.9 | 10.5 | ||||
| 1.4 | 25.6 | 27.9 | 27.1 | 29.9 | 7.3 | 7.6 | 7.9 | 8.5 | 7.6 | 7.9 | 8.1 | 8.6 | ||||
| 1.6 | 18.8 | 20.4 | 20.0 | 21.9 | 6.1 | 6.3 | 6.5 | 6.9 | 6.5 | 6.6 | 6.9 | 7.2 | ||||
| 1.8 | 13.9 | 15.0 | 14.5 | 16.5 | 5.2 | 5.4 | 5.5 | 5.9 | 5.7 | 5.8 | 5.9 | 6.2 | ||||
| 2.0 | 10.3 | 11.2 | 11.1 | 12.5 | 4.6 | 4.7 | 4.8 | 5.1 | 5.1 | 5.1 | 5.2 | 5.5 | ||||
| AEQL | 198.0 | 215.2 | 211.0 | 229.5 | 61.3 | 65.7 | 68.6 | 73.2 | 61.4 | 64.6 | 67.6 | 71.3 | ||||
| MEWMA | MCUSUM | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.01 | 0.04 | 0.09 | 0.00 | 0.01 | 0.04 | 0.09 | 0.00 | 0.01 | 0.04 | 0.09 | |||||
| 0.0 | 0.025 | 197.7 | 203.9 | 198.4 | 195.0 | 176.0 | 184.3 | 188.8 | 173.7 | 167.4 | 176.1 | 180.6 | 168.9 | |||
| 0.050 | 187.5 | 197.9 | 192.5 | 184.8 | 137.5 | 147.2 | 149.7 | 134.1 | 125.4 | 132.4 | 137.5 | 125.9 | ||||
| 0.075 | 177.8 | 193.0 | 178.5 | 172.1 | 101.9 | 111.5 | 111.9 | 98.7 | 87.4 | 93.1 | 98.7 | 86.9 | ||||
| 0.100 | 163.5 | 178.7 | 165.8 | 156.7 | 73.8 | 81.6 | 80.2 | 71.7 | 61.3 | 65.5 | 68.6 | 62.3 | ||||
| 0.125 | 147.2 | 165.9 | 148.7 | 141.6 | 55.1 | 59.1 | 59.6 | 52.8 | 44.7 | 47.3 | 48.8 | 45.1 | ||||
| 0.150 | 130.5 | 149.2 | 131.4 | 124.0 | 41.5 | 43.8 | 43.8 | 40.0 | 33.3 | 35.1 | 36.5 | 34.2 | ||||
| 0.175 | 114.1 | 134.1 | 114.8 | 109.1 | 31.6 | 33.3 | 33.8 | 30.5 | 26.3 | 27.5 | 28.0 | 26.4 | ||||
| 0.200 | 100.2 | 116.6 | 99.1 | 93.6 | 25.4 | 26.3 | 26.0 | 24.5 | 21.2 | 22.1 | 22.4 | 21.3 | ||||
| 0.225 | 87.1 | 103.8 | 86.6 | 81.0 | 20.3 | 21.3 | 21.0 | 19.6 | 17.7 | 18.3 | 18.4 | 17.5 | ||||
| 0.250 | 76.4 | 87.9 | 74.6 | 69.6 | 16.8 | 17.4 | 17.4 | 16.4 | 14.9 | 15.5 | 15.4 | 15.0 | ||||
| AEQL | 100.6 | 115.9 | 100.3 | 94.6 | 30.5 | 32.3 | 32.2 | 29.5 | 25.8 | 27.1 | 27.7 | 26.0 | ||||
| 0.1 | 0.025 | 198.5 | 191.7 | 196.0 | 195.0 | 171.2 | 169.4 | 179.6 | 160.3 | 186.1 | 161.9 | 172.0 | 151.9 | |||
| 0.050 | 191.3 | 182.7 | 185.7 | 184.8 | 136.3 | 132.8 | 138.1 | 123.9 | 144.8 | 120.2 | 125.6 | 107.1 | ||||
| 0.075 | 179.2 | 171.9 | 167.9 | 172.1 | 100.4 | 99.5 | 99.5 | 91.2 | 102.1 | 85.6 | 86.7 | 75.5 | ||||
| 0.100 | 166.2 | 157.9 | 152.0 | 156.7 | 74.0 | 72.0 | 71.3 | 68.0 | 71.7 | 61.6 | 60.0 | 54.3 | ||||
| 0.125 | 148.5 | 141.4 | 134.6 | 141.6 | 54.6 | 53.9 | 51.2 | 50.7 | 51.5 | 44.9 | 43.1 | 40.2 | ||||
| 0.150 | 131.7 | 127.0 | 117.0 | 124.0 | 41.0 | 40.7 | 37.9 | 38.7 | 38.0 | 33.8 | 32.7 | 31.1 | ||||
| 0.175 | 114.8 | 114.3 | 99.8 | 109.1 | 31.5 | 31.7 | 29.4 | 30.2 | 29.3 | 26.8 | 25.2 | 24.7 | ||||
| 0.200 | 100.2 | 99.3 | 84.0 | 93.6 | 25.0 | 25.2 | 23.4 | 24.3 | 23.2 | 21.4 | 20.4 | 20.4 | ||||
| 0.225 | 86.5 | 86.5 | 72.9 | 81.0 | 20.2 | 20.5 | 18.9 | 19.8 | 19.0 | 18.0 | 17.0 | 17.1 | ||||
| 0.250 | 74.5 | 75.2 | 62.0 | 69.6 | 16.9 | 17.2 | 15.7 | 16.6 | 16.1 | 15.2 | 14.5 | 14.8 | ||||
| AEQL | 100.5 | 99.0 | 87.1 | 94.6 | 30.3 | 30.3 | 28.6 | 28.8 | 28.9 | 26.0 | 25.1 | 24.1 | ||||
| 0.5 | 0.025 | 197.4 | 197.8 | 190.6 | 191.7 | 187.7 | 186.9 | 165.8 | 156.0 | 185.3 | 184.1 | 157.8 | 145.6 | |||
| 0.050 | 189.8 | 192.0 | 181.5 | 181.2 | 153.5 | 155.1 | 127.7 | 117.2 | 145.0 | 143.8 | 113.6 | 100.5 | ||||
| 0.075 | 179.9 | 179.1 | 170.0 | 164.7 | 117.3 | 117.9 | 94.3 | 84.7 | 105.9 | 104.2 | 81.1 | 71.1 | ||||
| 0.100 | 165.1 | 166.5 | 155.1 | 147.0 | 85.6 | 87.2 | 70.2 | 62.5 | 75.2 | 72.4 | 58.4 | 51.1 | ||||
| 0.125 | 148.6 | 150.5 | 139.6 | 131.8 | 62.8 | 64.5 | 52.3 | 46.2 | 54.8 | 53.4 | 42.7 | 38.6 | ||||
| 0.150 | 132.3 | 136.5 | 126.2 | 116.9 | 47.1 | 48.0 | 40.1 | 35.7 | 40.3 | 39.4 | 32.9 | 30.0 | ||||
| 0.175 | 116.6 | 119.3 | 109.6 | 101.3 | 36.5 | 37.0 | 31.3 | 28.7 | 31.3 | 30.5 | 26.1 | 24.2 | ||||
| 0.200 | 102.7 | 105.8 | 95.6 | 88.0 | 28.5 | 29.0 | 25.0 | 23.1 | 24.8 | 24.4 | 21.3 | 19.9 | ||||
| 0.225 | 89.2 | 93.2 | 83.9 | 77.5 | 22.8 | 23.3 | 20.4 | 19.0 | 20.3 | 20.1 | 18.0 | 16.8 | ||||
| 0.250 | 76.9 | 80.5 | 73.9 | 66.6 | 18.8 | 19.4 | 17.2 | 16.0 | 17.0 | 16.9 | 15.4 | 14.5 | ||||
| AEQL | 102.3 | 105.3 | 96.6 | 89.5 | 34.6 | 35.3 | 29.8 | 27.1 | 30.5 | 30.0 | 25.4 | 23.3 | ||||
| 0.9 | 0.025 | 191.0 | 195.5 | 197.5 | 195.5 | 163.1 | 169.4 | 188.4 | 179.5 | 153.1 | 171.0 | 184.9 | 171.0 | |||
| 0.050 | 180.9 | 187.4 | 194.7 | 187.2 | 125.0 | 132.8 | 161.3 | 145.2 | 110.8 | 127.7 | 148.6 | 131.3 | ||||
| 0.075 | 168.1 | 177.5 | 182.3 | 177.6 | 93.3 | 99.5 | 127.1 | 109.5 | 78.8 | 92.5 | 110.3 | 93.3 | ||||
| 0.100 | 151.3 | 160.6 | 170.8 | 163.2 | 68.3 | 72.0 | 97.2 | 83.2 | 56.5 | 65.9 | 78.6 | 69.3 | ||||
| 0.125 | 136.6 | 144.8 | 157.7 | 150.4 | 51.5 | 53.9 | 72.6 | 62.6 | 42.3 | 48.8 | 57.7 | 50.5 | ||||
| 0.150 | 121.3 | 130.2 | 146.6 | 135.3 | 39.9 | 40.7 | 55.0 | 48.7 | 33.0 | 37.4 | 43.3 | 38.8 | ||||
| 0.175 | 106.9 | 115.2 | 130.0 | 120.6 | 31.4 | 31.7 | 42.9 | 37.7 | 26.4 | 29.0 | 33.8 | 29.9 | ||||
| 0.200 | 93.9 | 101.0 | 115.0 | 106.8 | 25.4 | 25.2 | 33.5 | 29.7 | 21.6 | 23.7 | 27.2 | 24.6 | ||||
| 0.225 | 82.3 | 87.6 | 102.9 | 94.7 | 21.0 | 20.5 | 27.0 | 24.4 | 18.3 | 19.5 | 22.3 | 20.3 | ||||
| 0.250 | 70.5 | 77.4 | 90.9 | 82.5 | 17.6 | 17.2 | 22.2 | 20.1 | 15.8 | 16.5 | 18.9 | 17.4 | ||||
| AEQL | 94.0 | 100.9 | 114.3 | 106.1 | 29.8 | 30.3 | 39.9 | 35.3 | 25.5 | 28.3 | 32.8 | 29.3 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Li, Z.; Wang, Z. Monitoring of Linear Profiles Using Linear Mixed Model in the Presence of Measurement Errors. Mathematics 2022, 10, 4641. https://doi.org/10.3390/math10244641
Liu W, Li Z, Wang Z. Monitoring of Linear Profiles Using Linear Mixed Model in the Presence of Measurement Errors. Mathematics. 2022; 10(24):4641. https://doi.org/10.3390/math10244641
Chicago/Turabian StyleLiu, Wenhui, Zhonghua Li, and Zhaojun Wang. 2022. "Monitoring of Linear Profiles Using Linear Mixed Model in the Presence of Measurement Errors" Mathematics 10, no. 24: 4641. https://doi.org/10.3390/math10244641
APA StyleLiu, W., Li, Z., & Wang, Z. (2022). Monitoring of Linear Profiles Using Linear Mixed Model in the Presence of Measurement Errors. Mathematics, 10(24), 4641. https://doi.org/10.3390/math10244641







