Reduce-Order Modeling and Higher Order Numerical Solutions for Unsteady Flow and Heat Transfer in Boundary Layer with Internal Heating
Abstract
1. Introduction
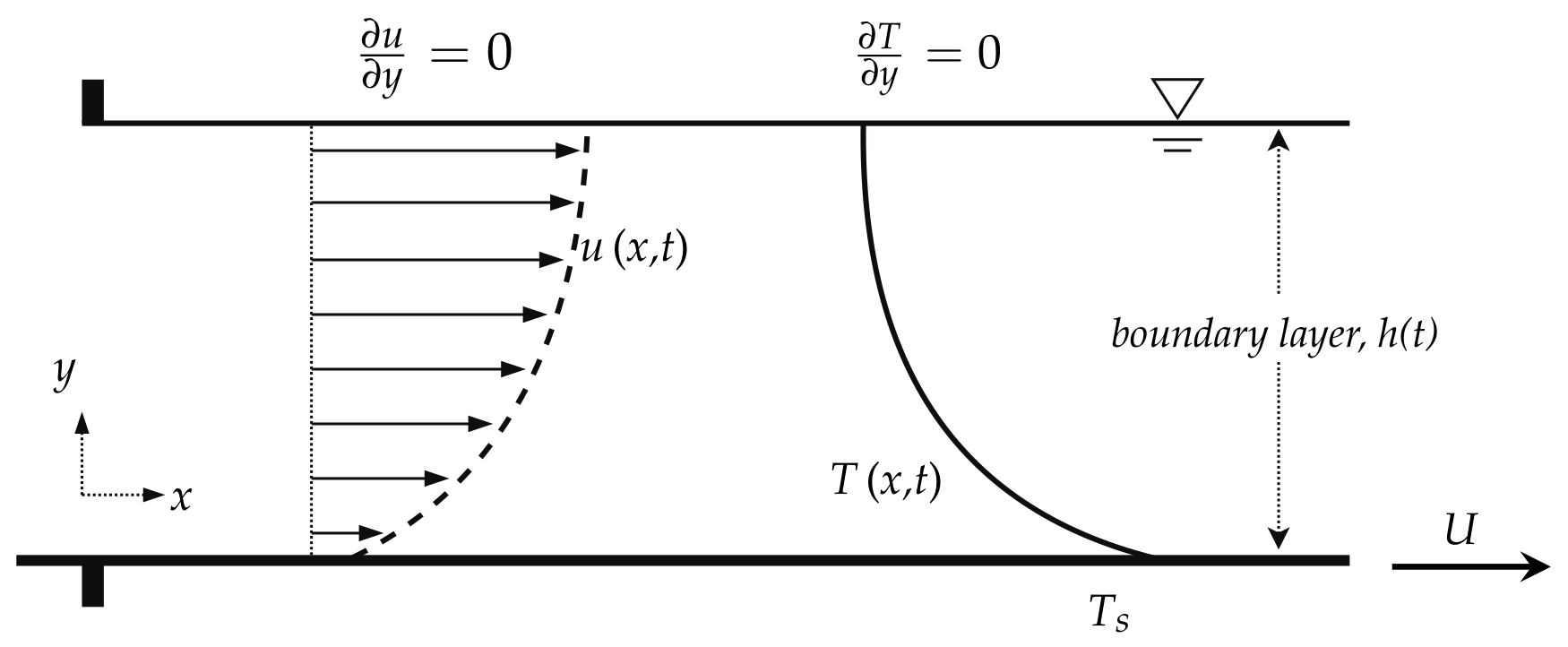
2. Mathematical Formulation, Lie Symmetries, Similarity Transformations and Reductions of Flow Equations
2.1. Lie Symmetries and Invariants
2.2. Double Reductions and Construction of Similarity Transformations
3. Numerical Solutions
4. Results
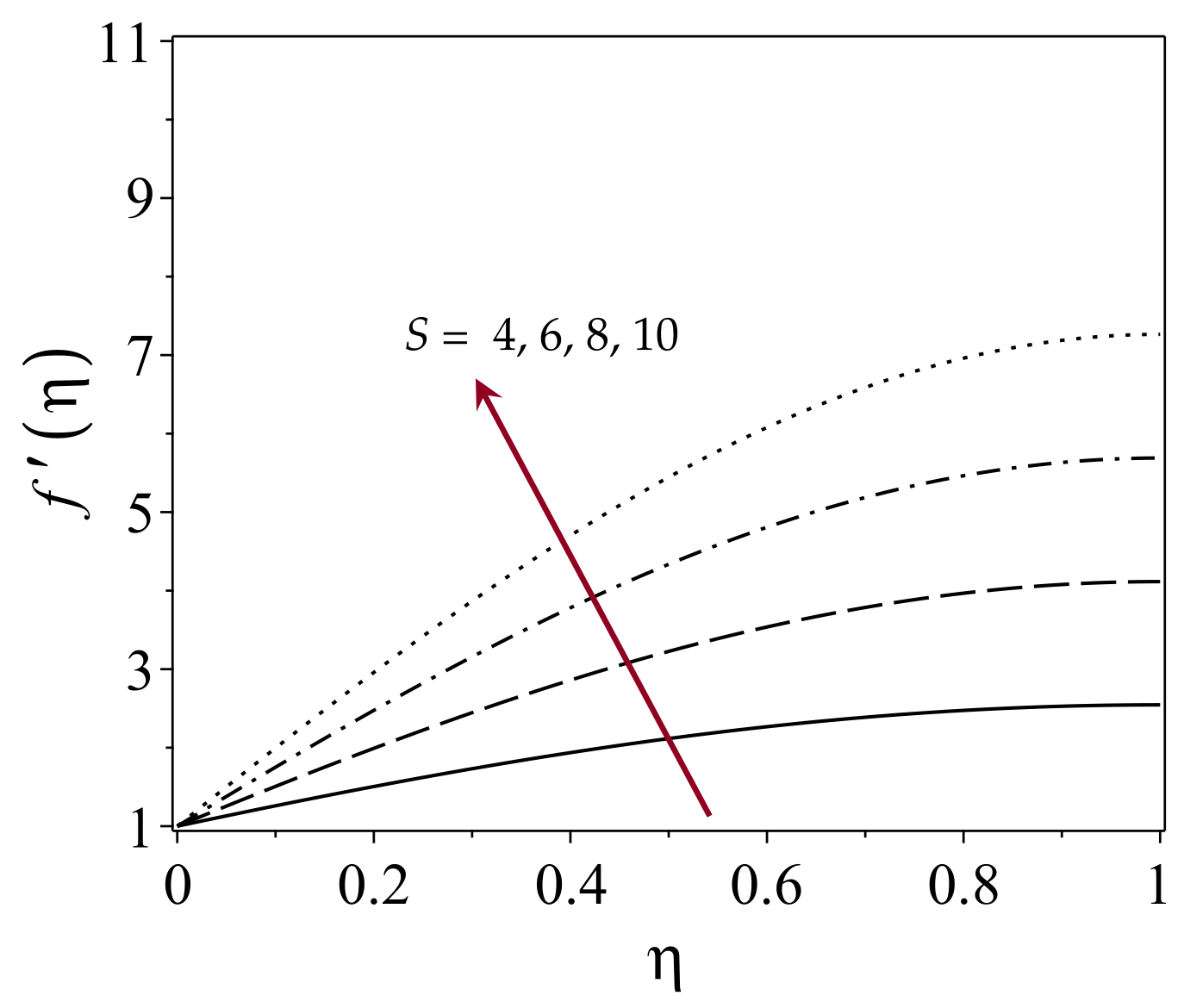
4.1. Effect of Unsteadiness on Film Thickness and Fluid Velocity
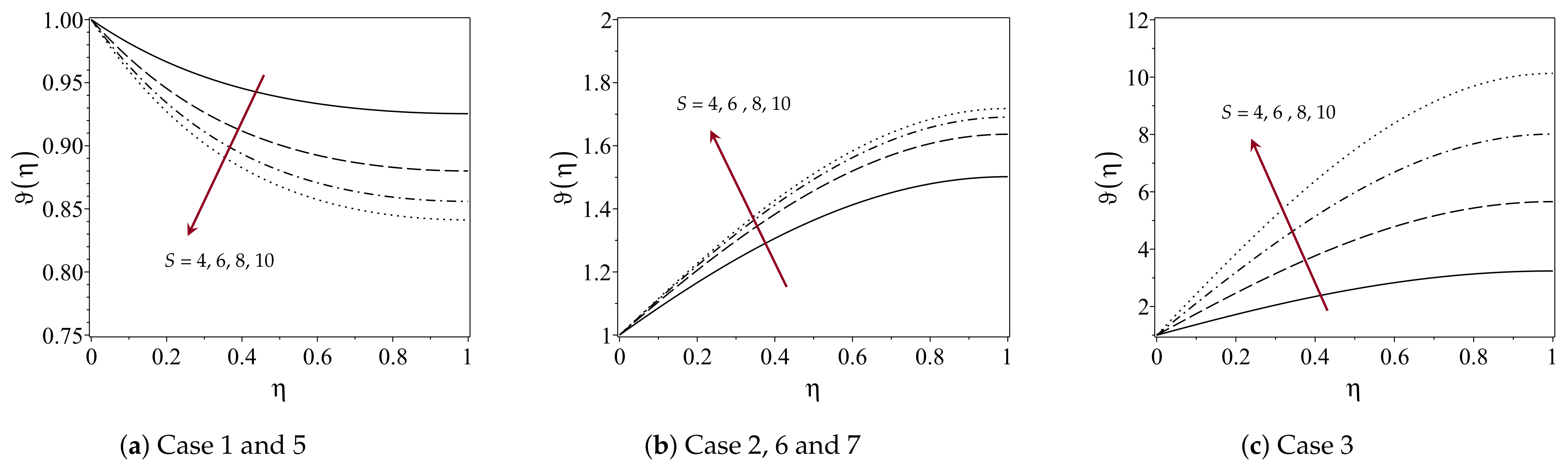
4.2. Effect of Unsteadiness on Temperature
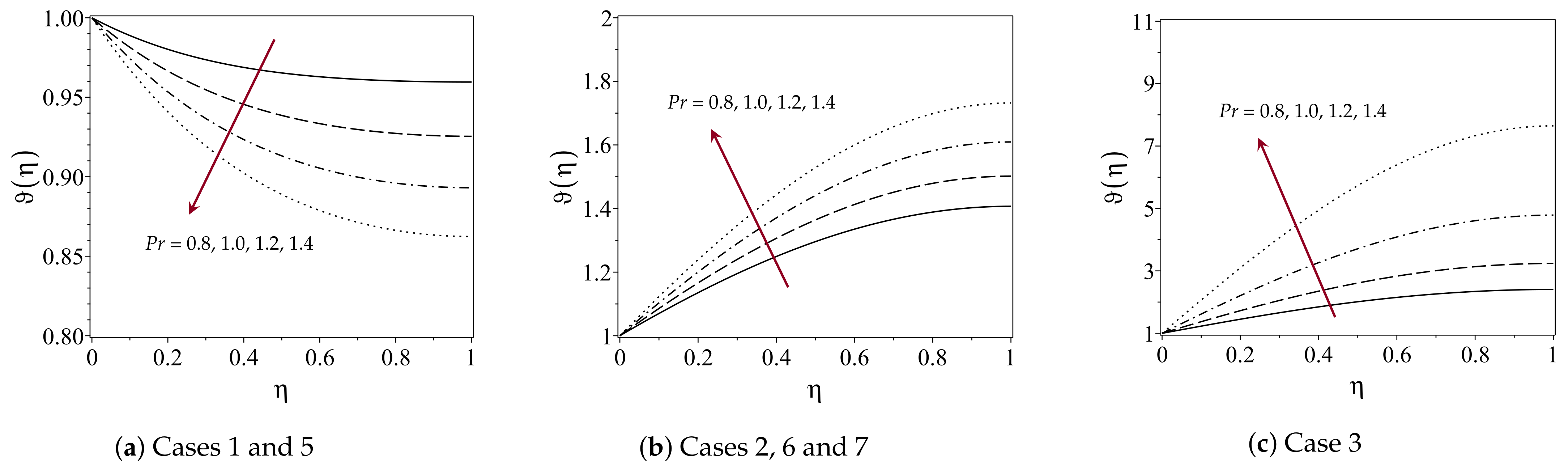
4.3. Effect of Prandtl Number on Temperature
4.4. Effect of Heat Generation/Absorption on Temperature
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ferziger, J.H.; Peric, M.; Leonard, A. Computational Methods for Fluid Dynamics; California Institute of Technology: Pasadena, CA, USA, 1997. [Google Scholar]
- Wang, C.Y. Liquid Film on an Unsteady Stretching Surface. Q. Appl. Math. 1990, 48, 601–610. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Und Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Andersson, H.I.; Aarseth, J.B.; Dandapat, B.S. Heat transfer in a liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Chen, C.H. Heat transfer in a power-law fluid film over a unsteady stretching sheet. Heat Mass Transf. 2003, 39, 791–796. [Google Scholar] [CrossRef]
- Dandapat, B.S.; Santra, B.; Andersson, H.I. Thermocapillarity in a liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2003, 46, 3009–3015. [Google Scholar] [CrossRef]
- Chen, C.H. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J. Non-Newton. Fluid Mech. 2006, 135, 128–135. [Google Scholar] [CrossRef]
- Dandapat, B.S.; Santra, B.; Vajravelu, K. The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet. Int. J. Heat Mass Transf. 2007, 50, 991–996. [Google Scholar] [CrossRef]
- Liu, I.C.; Andersson, H.I. Heat transfer in a liquid film on an unsteady stretching sheet. Int. J. Therm. Sci. 2008, 47, 766–772. [Google Scholar] [CrossRef]
- Abel, M.S.; Tawade, J.; Nandeppanavar, M.M. Effect of non-uniform heat source on MHD heat transfer in a liquid film over an unsteady stretching sheet. Int. J. Non-Linear Mech. 2009, 44, 990–998. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Hashim, I. Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2010, 53, 2044–2051. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I. Liquid film on unsteady stretching sheet with general surface temperature and viscous dissipation. Chin. Phys. Lett. 2010, 27, 110202. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I.; Abbasbandy, S. Effects of thermocapillarity and thermal radiation on flow and heat transfer in a thin liquid film on an unsteady stretching sheet. Math. Probl. Eng. 2012, 2012, 127320. [Google Scholar] [CrossRef]
- Liu, I.C.; Megahed, A.M. Numerical study for the flow and heat transfer in a thin liquid film over an unsteady stretching sheet with variable fluid properties in the presence of thermal radiation. J. Mech. 2012, 28, 291–297. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I.; Abbasbandy, S. Flow and heat transfer in a nanofluid thin film over an unsteady stretching sheet. Sains Malays. 2018, 47, 1599–1605. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Elementary Lie Group Analysis and Ordinary Differential Equations; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Hydon, P.E. Symmetry Methods for Differential Equations: A Beginner’s Guide; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 2000. [Google Scholar]
- Szatmari, S.; Bihlo, A. Symmetry analysis of a system of modified shallow-water equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 530–537. [Google Scholar] [CrossRef]
- Chesnokov, A.A. Symmetries of shallow water equations on a rotating plane. J. Appl. Ind. Math. 2010, 4, 24–34. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Momoniat, E.; Ferdows, M.; Basiriparsa, A. Lie group solution for free convective flow of a nanofluid past a chemically reacting horizontal plate in a porous media. Math. Probl. Eng. 2014, 2014, 239082. [Google Scholar] [CrossRef]
- Siriwat, P.; Kaewmanee, C.; Meleshko, S.V. Symmetries of the hyperbolic shallow water equations and the Green Naghdi model in Lagrangian coordinates. Int. J. Non-Linear Mech. 2016, 86, 185–195. [Google Scholar] [CrossRef]
- Xin, X.; Zhang, L.; Xia, Y.; Liu, H. Nonlocal symmetries and exact solutions of the (2+1)-dimensional generalized variable coefficient shallow water wave equation. Appl. Math. Lett. 2019, 94, 112–119. [Google Scholar] [CrossRef]
- Paliathanasis, A. Lie symmetries and similarity solutions for rotating shallow water. Z. Naturforschung-Sect. A J. Phys. Sci. 2019, 74, 869–877. [Google Scholar] [CrossRef]
- Meleshko, S.V. Complete group classification of the two-Dimensional shallow water equations with constant coriolis parameter in Lagrangian coordinates. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105293. [Google Scholar] [CrossRef]
- Paliathanasis, A. Shallow-water equations with complete Coriolis force: Group properties and similarity solutions. Math. Methods Appl. Sci. 2021, 44, 6037–6047. [Google Scholar] [CrossRef]
- Abd-El-malek, M.B.; Badran, N.A.; Amin, A.M.; Hanafy, A.M. Lie symmetry group for unsteady free convection boundary-layer flow over a vertical surface. Symmetry 2021, 13, 175. [Google Scholar] [CrossRef]
- Paliathanasis, A. Lie symmetries and similarity solutions for a family of 1+1 fifth-order partial differential equations. Quaest. Math. 2021, 45, 1099–1114. [Google Scholar] [CrossRef]
- Safdar, M.; Ijaz Khan, M.; Taj, S.; Malik, M.Y.; Shi, Q.H. Construction of similarity transformations and analytic solutions for a liquid film on an unsteady stretching sheet using lie point symmetries. Chaos Solitons Fractals 2021, 150, 111115–111121. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I.; Alomari, A.K. Thin film flow and heat transfer on an unsteady stretching sheet with internal heating. Meccanica 2011, 46, 349–357. [Google Scholar] [CrossRef]
- John, H.; Mathews, K.D.F. Numerical Methods Using MATLAB; Pearson Prentice Hall: Hoboken, NJ, USA, 2004. [Google Scholar]
- Wang, C. Analytic solutions for a liquid film on an unsteady stretching surface. Heat Mass Transf.- Und Stoffuebertragung 2006, 42, 759–766. [Google Scholar] [CrossRef]

| Symmetry | Invariants-Conserved Quantities |
|---|---|
| Case | Symmetry and Invariants | Corresponding Boundary Conditions |
|---|---|---|
| 1 | X + X | |
| 2 | X + X | |
| 3 | X + X | |
| 4 | X + X | |
| 5 | X + X | |
| 6 | X + X | |
| 7 | X + X | |
| Case | Symmetry Generator and Similarity Transformation | System of ODEs |
|---|---|---|
| 1 | X + X | |
| 2 | X + X | |
| 3 | X + X | |
| 4 | X + X | |
| 5 | X + X | |
| 6 | X + X | |
| 7 | X + X | |
| S | Present Study | Wang [32] | ||
|---|---|---|---|---|
| −f | −f | |||
| 1.2 | 1.1277809 | 1.4426253 | 1.127780 | 1.442631 |
| 1.3 | 0.9642181 | 1.2183196 | 0.964219 | 1.218322 |
| 1.4 | 0.8210322 | 1.0127802 | 0.821032 | 1.012784 |
| 1.5 | 0.6931444 | 0.8218421 | 0.693144 | 0.821842 |
| 1.6 | 0.5761730 | 0.6423970 | 0.576173 | 0.642397 |
| Pr | Present Study | Wang [32] | ||
|---|---|---|---|---|
| 0.01 | 0.9823314 | 0.0377342 | 0.982331 | 0.037734 |
| 0.1 | 0.8462218 | 0.3439312 | 0.843622 | 0.343931 |
| 1.0 | 0.2867165 | 1.9995915 | 0.286717 | 1.999590 |
| 2.0 | 0.1281219 | 2.9759051 | 0.128124 | 2.975450 |
| 3.0 | 0.0676448 | 3.7013202 | 0.067658 | 3.698830 |
| S | f | f | |
|---|---|---|---|
| 4.0 | 0.46222258 | 2.54527934 | 2.64859856 |
| 6.0 | 0.42256741 | 4.11506337 | 5.12669108 |
| 8.0 | 0.38196786 | 5.68906454 | 7.57845493 |
| 10.0 | 0.34939989 | 7.26442893 | 10.0221543 |
| S | Case 1 and 5 | Case 2, 6 and 7 | Case 3 | |||
|---|---|---|---|---|---|---|
| 4.0 | 0.9254323 | 0.2063995 | 1.5018941 | 0.8804902 | 3.2395043 | 3.7582109 |
| 6.0 | 0.8800376 | 0.3375851 | 1.6365029 | 1.0733105 | 5.6566690 | 7.5566639 |
| 8.0 | 0.8559376 | 0.4088891 | 1.6905412 | 1.1414694 | 8.0118998 | 11.224076 |
| 10 | 0.8412676 | 0.4528668 | 1.7180535 | 1.1725929 | 10.128307 | 14.510949 |
| Pr | Case 1 and 5 | Case 2, 6 and 7 | Case 3 | |||
|---|---|---|---|---|---|---|
| 0.8 | 0.9595775 | 0.1261086 | 1.4071290 | 0.7190225 | 2.4052188 | 2.3063102 |
| 1.0 | 0.9254323 | 0.2063995 | 1.5018941 | 0.8804902 | 3.2395043 | 3.7582109 |
| 1.2 | 0.8930815 | 0.2836747 | 1.6093876 | 1.0579964 | 4.7864442 | 6.2626166 |
| 1.4 | 0.8623943 | 0.3581463 | 1.7320289 | 1.2589990 | 7.6471113 | 10.783625 |
| G | Case 1 and 5 | Case 2, 6 and 7 | Case 3 | |||
|---|---|---|---|---|---|---|
| −2.0 | 0.6980416 | 0.6846427 | 1.0296499 | 0.0020397 | 1.7502717 | 1.3163411 |
| −1.0 | 0.7626680 | 0.5501907 | 1.1551679 | 0.2443599 | 2.0816556 | 1.8831544 |
| 0.0 | 0.8376079 | 0.3886397 | 1.3090560 | 0.5316521 | 2.5452882 | 2.6576106 |
| 1.0 | 0.9254323 | 0.2063995 | 1.5018941 | 0.8804902 | 3.2395043 | 3.7582109 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, M.; Safdar, M.; Taj, S.; Zafar, A.; Ali, M.U.; Lee, S.W. Reduce-Order Modeling and Higher Order Numerical Solutions for Unsteady Flow and Heat Transfer in Boundary Layer with Internal Heating. Mathematics 2022, 10, 4640. https://doi.org/10.3390/math10244640
Bilal M, Safdar M, Taj S, Zafar A, Ali MU, Lee SW. Reduce-Order Modeling and Higher Order Numerical Solutions for Unsteady Flow and Heat Transfer in Boundary Layer with Internal Heating. Mathematics. 2022; 10(24):4640. https://doi.org/10.3390/math10244640
Chicago/Turabian StyleBilal, Muhammad, Muhammad Safdar, Safia Taj, Amad Zafar, Muhammad Umair Ali, and Seung Won Lee. 2022. "Reduce-Order Modeling and Higher Order Numerical Solutions for Unsteady Flow and Heat Transfer in Boundary Layer with Internal Heating" Mathematics 10, no. 24: 4640. https://doi.org/10.3390/math10244640
APA StyleBilal, M., Safdar, M., Taj, S., Zafar, A., Ali, M. U., & Lee, S. W. (2022). Reduce-Order Modeling and Higher Order Numerical Solutions for Unsteady Flow and Heat Transfer in Boundary Layer with Internal Heating. Mathematics, 10(24), 4640. https://doi.org/10.3390/math10244640








