Robust Synchronization of Fractional-Order Chaotic System Subject to Disturbances
Abstract
:1. Introduction
2. Preliminaries and Problem Statements
3. Main Results
4. The Determination of IMM M
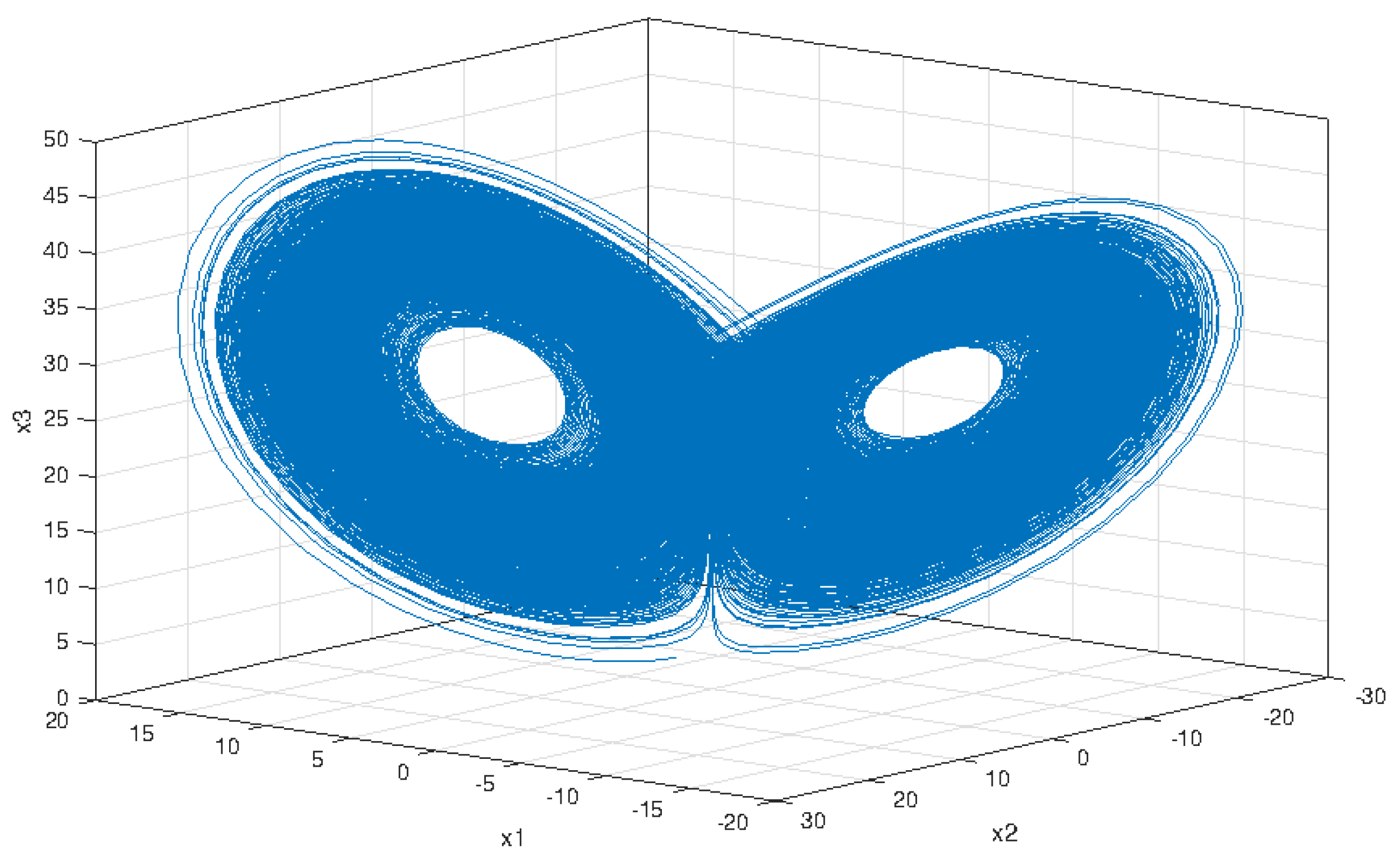
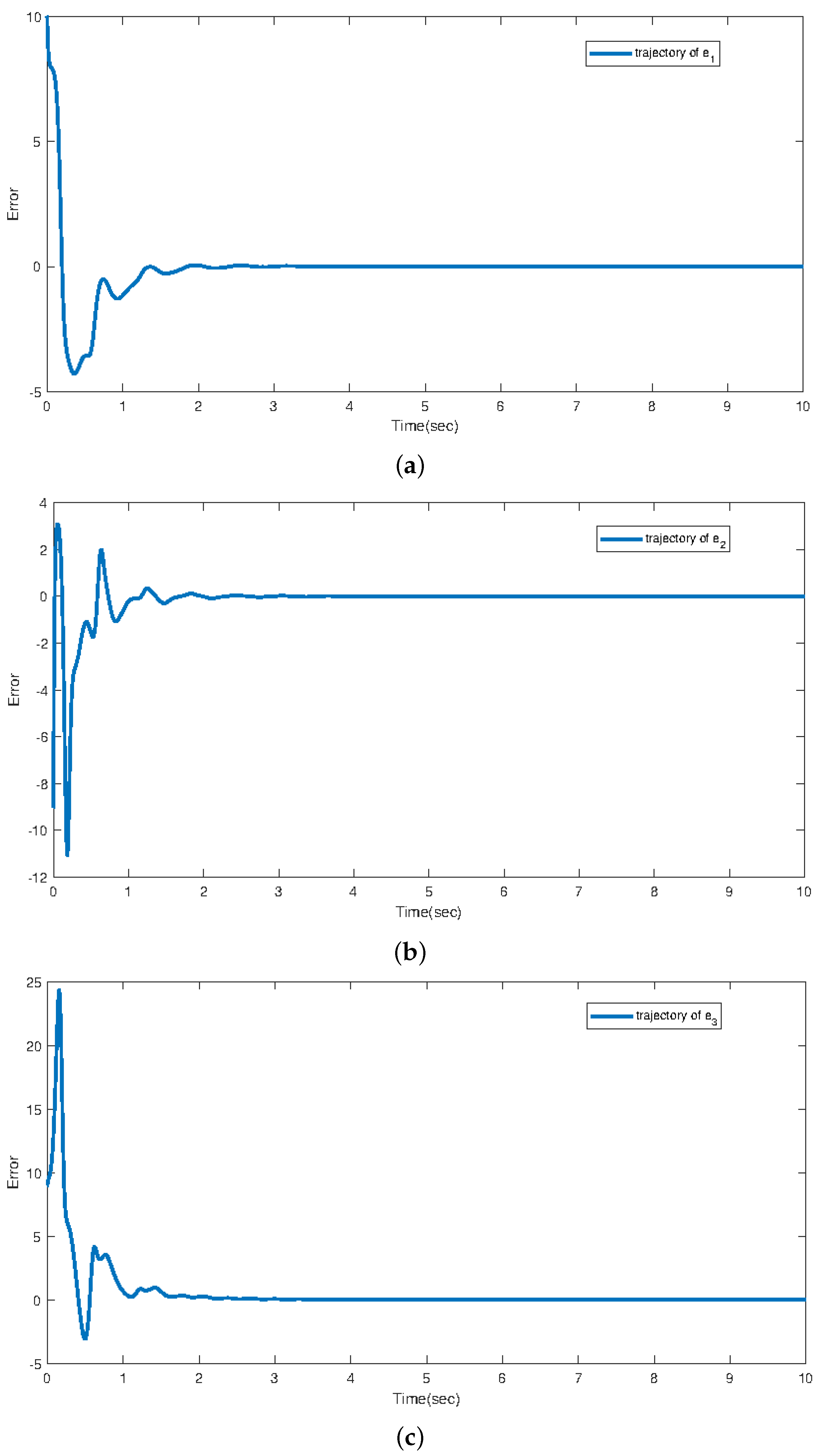
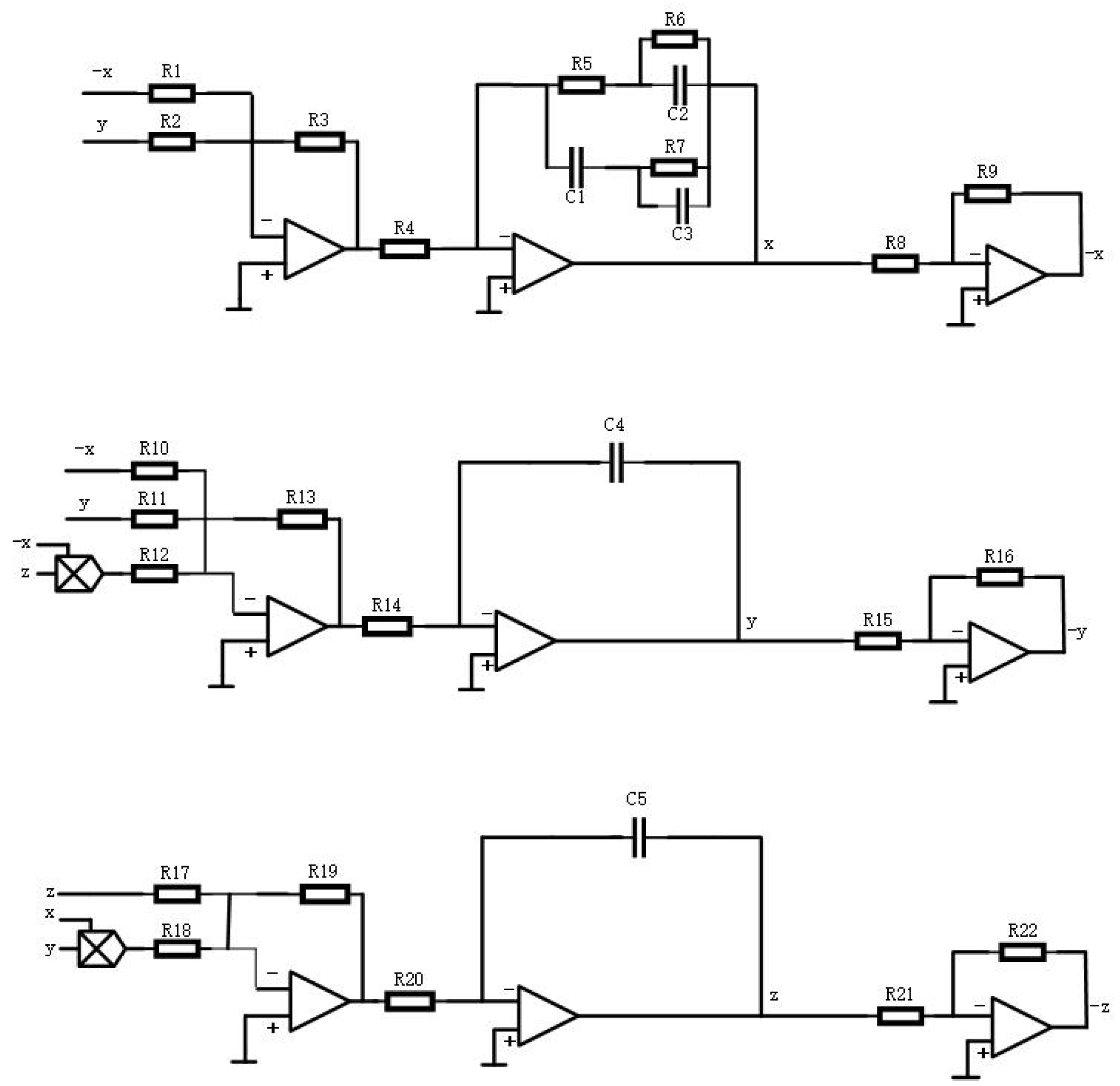
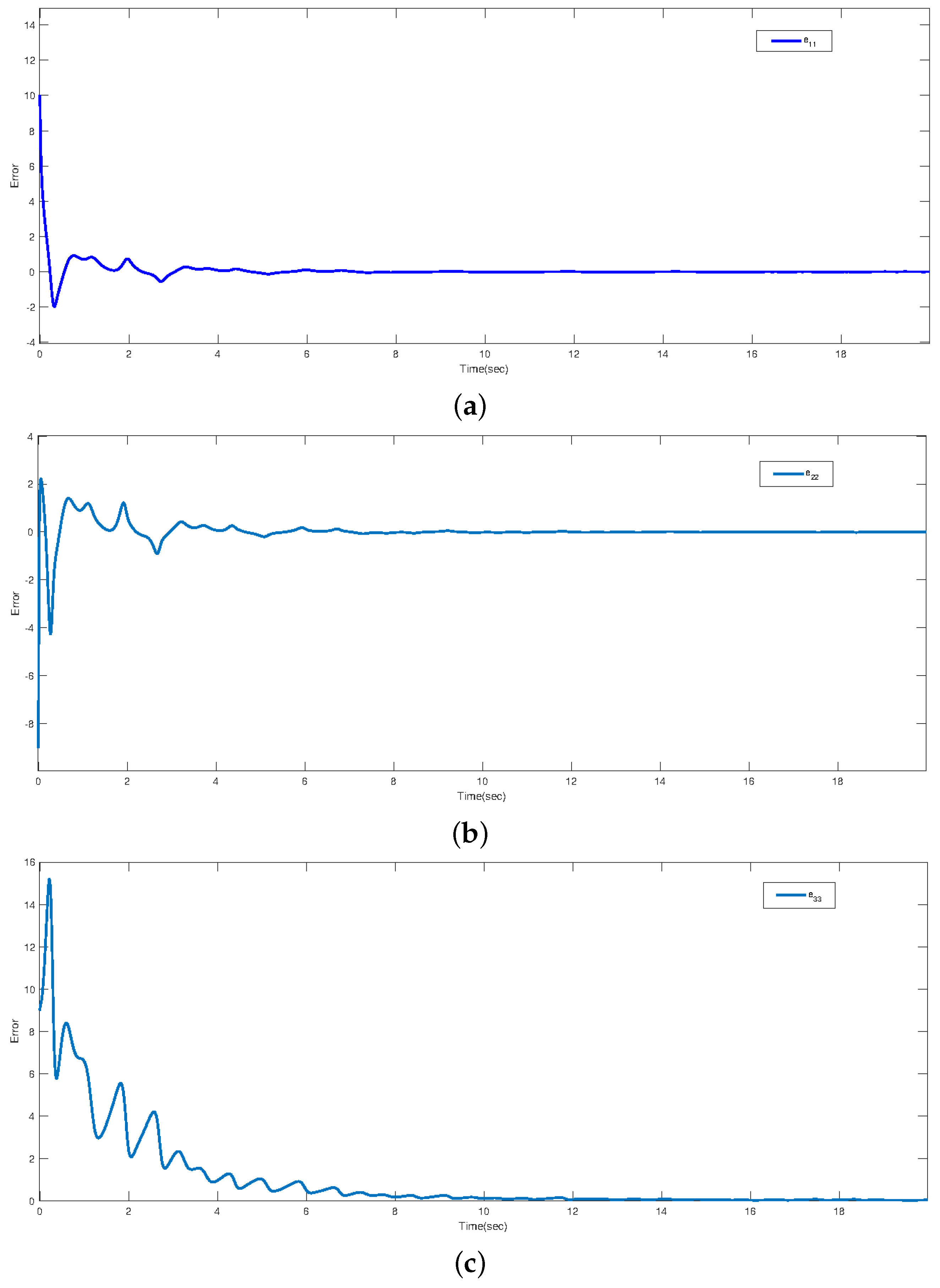
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Du, Y.; Duever, T.A.; Budman, H. Fault detection and diagnosis with parametric uncertainty using generalized polynomial chaos. Comput. Chem. Eng. 2015, 76, 63–75. [Google Scholar] [CrossRef]
- Potapov, A.; Ali, M. Robust chaos in neural networks. Phys. Lett. A 2000, 277, 310–322. [Google Scholar] [CrossRef]
- Cheng, C.J. Robust synchronization of uncertain unified chaotic systems subject to noise and its application to secure communication. Appl. Math. Comput. 2012, 219, 2698–2712. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Hybrid chaos synchronization of Liu and Lü systems by active nonlinear control. In Proceedings of the International Conference on Computational Science, Engineering and Information Technology, Tirunelveli, India, 23–25 September 2011; pp. 1–10. [Google Scholar]
- Ahn, C.K.; Jung, S.T.; Kang, S.K.; Joo, S.C. Adaptive H∞ synchronization for uncertain chaotic systems with external disturbance. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2168–2177. [Google Scholar] [CrossRef]
- Zhao, Z.; Lv, F.; Zhang, J.; Du, Y. H∞ synchronization for uncertain time-delay chaotic systems with one-sided lipschitz nonlinearity. IEEE Access 2018, 6, 19798–19806. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Olusola, O.I.; Vincent, E.; Njah, A.N.; Ali, E. Control and synchronization of chaos in biological systems via backsteping design. Int. J. Nonlinear Sci. 2011, 11, 121–128. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Shah, K.; Arfan, M.; Mahariq, I.; Ahmadian, A.; Salahshour, S.; Ferrara, M. Fractal-fractional mathematical model addressing the situation of corona virus in Pakistan. Results Phys. 2020, 19, 103560. [Google Scholar] [CrossRef]
- Raza, A.; Ahmadian, A.; Rafiq, M.; Salahshour, S.; Ferrara, M. An analysis of a nonlinear susceptible-exposed-infected-quarantine-recovered pandemic model of a novel coronavirus with delay effect. Results Phys. 2021, 21, 103771. [Google Scholar] [CrossRef] [PubMed]
- Udrişte, C.; Ferrara, M.; Zugrăvescu, D.; Munteanu, F. Controllability of a nonholonomic macroeconomic system. J. Optim. Theory Appl. 2012, 154, 1036–1054. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A note on the stability of fractional order systems. Math. Comput. Simul. 2009, 79, 1566–1576. [Google Scholar] [CrossRef]
- Li, M.; Li, D.; Wang, J.; Zhao, C. Active disturbance rejection control for fractional-order system. ISA Trans. 2013, 52, 365–374. [Google Scholar] [CrossRef]
- Zheng, S. Robust stability of fractional order system with general interval uncertainties. Syst. Control Lett. 2017, 99, 1–8. [Google Scholar] [CrossRef]
- Kamal, S.; Sharma, R.K.; Dinh, T.N.; Ms, H.; Bandyopadhyay, B. Sliding mode control of uncertain fractional-order systems: A reaching phase free approach. Asian J. Control 2021, 23, 199–208. [Google Scholar] [CrossRef]
- Agrawal, S.; Srivastava, M.; Das, S. Synchronization of fractional order chaotic systems using active control method. Chaos Solitons Fractals 2012, 45, 737–752. [Google Scholar] [CrossRef]
- Andrew, L.Y.T.; Xian-Feng, L.; Yan-Dong, C.; Hui, Z. A novel adaptive-impulsive synchronization of fractional-order chaotic systems. Chin. Phys. B 2015, 24, 100502. [Google Scholar] [CrossRef]
- N Doye, I.; Salama, K.N.; Laleg-Kirati, T.M. Robust fractional-order proportional-integral observer for synchronization of chaotic fractional-order systems. IEEE/CAA J. Autom. Sin. 2019, 6, 268–277. [Google Scholar] [CrossRef]
- Luo, R.; Su, H. The stability of impulsive incommensurate fractional order chaotic systems with Caputo derivative. Chin. J. Phys. 2018, 56, 1599–1608. [Google Scholar] [CrossRef]
- D’Alto, L.; Corless, M. Incremental quadratic stability. Numer. Algebra Control Optim. 2013, 3, 175–201. [Google Scholar] [CrossRef]
- Açıkmeşe, B.; Corless, M. Observers for systems with nonlinearities satisfying incremental quadratic constraints. Automatica 2011, 47, 1339–1348. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, W.; Su, H.; Yang, J. Observer-based synchronization of chaotic systems satisfying incremental quadratic constraints and its application in secure communication. IEEE Trans. Syst. Man Cybern. Syst. 2018, 1–12. [Google Scholar] [CrossRef]
- Xu, X.; Açıkmeşe, B.; Corless, M.J. Observer-Based Controllers for Incrementally Quadratic Nonlinear Systems With Disturbances. IEEE Trans. Autom. Control. 2021, 66, 1129–1143. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Derivatives and Integrals. In Fractional Differential Equations: An Introduction to Fractional Derivatives; Elsevier: Amsterdam, The Netherlands, 1998; pp. 41–80. [Google Scholar]
- Xiang, W.; Xiao, J.; Iqbal, M.N. Robust observer design for nonlinear uncertain switched systems under asynchronous switching. Nonlinear Anal. Hybrid Syst. 2012, 6, 754–773. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, J.; He, S. Fractional-Order Interval Observer for Multiagent Nonlinear Systems. Fractal Fract. 2022, 6, 355. [Google Scholar] [CrossRef]
- Li, D.; Lu, J.; Wu, X.; Chen, G. Estimating the bounds for the Lorenz family of chaotic systems. Chaos Solitons Fractals 2005, 23, 529–534. [Google Scholar] [CrossRef]
- Jia, H.; Tao, Q.; Chen, Z. Analysis and circuit design of a fractional-order Lorenz system with different fractional orders. Syst. Sci. Control Eng. Open Access J. 2014, 2, 745–750. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zhang, X.; Wang, S.; You, F. Robust Synchronization of Fractional-Order Chaotic System Subject to Disturbances. Mathematics 2022, 10, 4639. https://doi.org/10.3390/math10244639
Li D, Zhang X, Wang S, You F. Robust Synchronization of Fractional-Order Chaotic System Subject to Disturbances. Mathematics. 2022; 10(24):4639. https://doi.org/10.3390/math10244639
Chicago/Turabian StyleLi, Dongya, Xiaoping Zhang, Shuang Wang, and Fengxiang You. 2022. "Robust Synchronization of Fractional-Order Chaotic System Subject to Disturbances" Mathematics 10, no. 24: 4639. https://doi.org/10.3390/math10244639
APA StyleLi, D., Zhang, X., Wang, S., & You, F. (2022). Robust Synchronization of Fractional-Order Chaotic System Subject to Disturbances. Mathematics, 10(24), 4639. https://doi.org/10.3390/math10244639




