Abstract
Studies have shown that illuminance and correlated colour temperature (CCT) are strongly correlated with body responses such as circadian rhythm, alertness, and mood. It is worth noting that these responses show a complex and variable coupling, which needs to be solved using accurate mathematical models for the regulation of indoor light parameters. Therefore, in this study, by weighing the evaluations of visual comfort, alertness, valence, and arousal of mood, a multi-objective optimisation mathematical model was developed with constraints conducive to the healthy rhythm. The problem was solved with the multi-objective evolutionary algorithm based on the decomposition differential evolution (MOEA/D-DE) algorithm. Taking educational space as the analysis goal, a dual-parameter setting strategy for illuminance and CCT covering four modes was proposed: focused learning, comfortable learning, soothing learning, and resting state, which could provide a scientific basis for the regulation of the lighting control system. The alertness during class time reached 3.01 compared to 2.34 during break time, showing a good light facilitation effect. The proposed mathematical model and analysis method also have the potential for application in the lighting design and control in other spaces to meet the era of intelligent, highly flexible, and sustainable buildings.
Keywords:
mathematical modelling; multi-objective evolutionary algorithms; visual comfort; alertness and mood; lighting control strategy; illuminance; correlated colour temperature; colour rendering index MSC:
68T20
1. Introduction
With over 80% of time spent in buildings, the quality of the architectural environment has a crucial impact on human health and comfort. In this regard, light plays an essential role. Architectural light environment is usually designed and controlled according to the visual requirements of various standards, such as illuminance, glare or correlated colour temperature (CCT), and colour rendering index (CRI), to ensure that the relevant parameters support users in their visual tasks corresponding to their demands. In recent years, with the progressive development of biological effects driven by molecular mechanisms of circadian rhythms [1], more and more research has focused on the non-visual effects of light and its application to regulate human circadian rhythm, mental health, and operational performance. Among these, changes in illuminance and CCT of light parameters were strongly related to melatonin secretion and suppression, sleep/wake cycles, cognitive functions, alertness, and mood [2,3,4,5]. In terms of the melatonin suppression of non-visual effects, models that quantify the effectiveness of the spectrum and illuminance magnitude of a given light source have also been proposed, such as the equivalent melanopic lux [6,7], and circadian stimulus values [8,9]. In the domain of typical everyday life with regular schedules, these studies provide an effective way to consider non-visual effects for lighting control strategies. The creation of a healthy, efficient, and comfortable light environment for the users, taking into account visual comfort (visual effects), alertness, and mood as well as aspects of circadian rhythm (non-visual effects), is a research topic of extensive attention.
Mathematical modelling as a general approach has a wide range of applications in the field of lighting design and control. For example, Yin et al. solved the problem of alertness optimisation based on a mathematical model of a dynamic circadian system [10], and Papatsimpa et al. proposed a personalised office lighting system with adaptive rhythms by introducing a new algorithm to optimise the lighting schedule to match the individual circadian cycle [11]. Lighting control systems are regulated from the visual requirements or non-visual aspects, so accurate responses to the set targets are required [12], and the use of mathematical methods to characterise important evaluation indices is a prerequisite for quantitative regulation. For most scenarios, the users’ activities vary from time to time and the targets will change dynamically according to the demands [13]. For example, users prefer the relaxing light environment during rest time and the light environment to stay awake and focused during work time. When considering visual effects and non-visual effects in terms of alertness and mood at the same time, the problem of complex conflicts about user perceptions has not been addressed yet. Educational buildings are representative of this because the main users are students, whose behavioural activities are characterised by a fixed and long-term nature. Current frontend research focuses on cognitive-functional considerations [14], and the impact of low carbon and energy efficiency is also an important objective that has been highlighted [15]. Dynamic lighting control systems based on learning contexts have also been proposed [16], as well as the provision of variable illuminance and CCT levels according to different subject classifications [17]. However, these light parameters exhibit a variable and coupled relationship between their effects on human comfort, alertness, and mood. Currently, it remains a very interesting and important issue to develop accurate mathematical models for solving the trade-off between the users’ good visual comfort and alertness, valence, and arousal of mood.
This study contributed to research on mathematical models and dynamic strategies for the simultaneous regulation of the dual parameters: illuminance and CCT. The complex and coupled relationships of lighting perceptions (visual comfort, alertness, and mood) were transformed into a multi-objective optimisation problem with feasible solutions of illuminance and CCT based on constraints conducive to the healthy circadian rhythm. The conflicts of multiple objectives based on the behavioural and active characteristics of the users in educational spaces were balanced through an evolutionary algorithm. The main contributions are as follows:
- To address the higher-order and non-linear effects of light parameters on human comfort, alertness, and valence of mood, and the linear effects of light parameters on the arousal of mood, a mathematical model of the intrinsic rules for light effects was established with constraints conducive to the healthy rhythm, and the multi-objective optimisation problem was solved based on the multi-objective evolutionary algorithm based on the decomposition differential evolution (MOEA/D-DE) algorithm.
- Based on the obtained non-dominated solutions, a dual-parameter regulation strategy of illuminance and CCT applicable to different learning and resting needs in educational spaces was constructed. With regular learning activities as the analysis target, focused learning, comfortable learning, soothing learning, and resting states were distinguished, which effectively weighed the comfort, alertness, and mood of users and could help to positively motivate their learning effects. The proposed model and method also have the potential for application in the lighting control in other spaces to meet the era of intelligent, highly flexible, and sustainable buildings.
This paper is organised as follows. In Section 2, the optimisation problem of visual comfort, alertness, and mood with circadian rhythm constraints is proposed. In Section 3, the algorithm for solving the multi-objective optimisation problem is constructed. In Section 4, the solutions to the problem are demonstrated and the lighting regulation strategy for educational spaces is analysed. Finally, Section 5 draws conclusions and outlines future perspectives.
2. Multi-Objective Optimisation Model
Rational settings of illuminance and CCT are beneficial to human health and have been proven in medical research. The illuminance adjustment in lighting can alleviate visual fatigue [18], while the CCT adjustment can ease sleepiness and enhance comfort [19,20]. Here, a mathematical model of the effect of light parameters on human feelings is developed and formulated as a multi-objective optimisation problem (MOP) with constraints. Firstly, the MOP is described in Section 2.1. Secondly, the objective functions are introduced in Section 2.2, and finally the decision space under the constraint conditions is introduced in Section 2.3.
2.1. Problem Description
Trends in human perception of visual comfort, alertness, valence, and arousal of mood in the light environment with different illuminance and CCT levels are the prerequisite for the search of the optimal solutions for lighting control. We conducted a series of lighting experiments with the variables of illuminance and CCT. The participants voted for visual comfort, alertness, valence, and arousal of mood under each lighting condition. The mean voting scores were fitted using non-linear and linear regression methods to obtain polynomial functions, and the non-linear/linear functions of humans’ visual comfort, alertness, and mood with illuminance and CCT are used as the objective functions of MOP. Furthermore, light that is conducive to healthy circadian rhythms is considered the constraint to investigating the light parameter conditions. The non-dominated solutions obtained in a feasible domain with continuously varying parameters from the MOP, that satisfy high visual comfort, enhanced alertness, and positively motivated mood, can provide a research basis for the lighting control strategies. Without loss of generality, the mathematical expression of the above problem is shown in Equation (1).
Let D be the feasible domain of the above multi-objective optimisation problem,
where is a decision vector, F(x) is a K-dimensional objective vector, K is the number of the objective functions, gi(x) is an inequality constraint, and M is the number of the constraints.
2.2. Objective Functions
In our MOP, we focus on four dimensions of human perceptions under the light environment, visual comfort, alertness, valence, and arousal of mood. Visual comfort is defined by the European standard EN 12665 as “the subjective condition of visual health caused by the visual environment” [21]. Alertness is being awake, attentive, and ready to act or react. Mood can be represented by valence and arousal [22]. Valence is the degree of pleasantness and can be defined from negative to positive. Arousal is a level of autonomous activation that ranges from calm to excited. The averages of the voting scores of visual comfort, alertness, valence, and arousal of mood (see Table A2 in Appendix A) were fitted using non-linear and linear regression methods. According to the regression results, the functions of visual comfort fcom(x), alertness fale(x), and valence fval(x) of mood were binary cubic polynomials on illuminance (x1) and CCT (x2), which are shown in Equation (3). The arousal of mood function faro(x) was a binary linear regression on illuminance (x1) and CCT (x2). The specific parameters for the functions are shown in Table 1.

Table 1.
Specific parameters for the functions of visual comfort fcom(x), alertness fale(x), valence fval(x), and arousal faro(x) of mood.
Details of the objective functions are shown below.
- The visual comfort of users in the different light environments was graded as 0 uncomfortable, 1 less comfortable, 2 neutral, 3 a little comfortable, and 4 comfortable. fcom(x) was lowest at 300 lx, 3000 K, i.e., the least comfortable, and increased with both illuminance and CCT, with an extreme value at 673 lx, 4231 K and a maximum of 3. After that, fcom(x) decreased with both illuminance and CCT, but to a lesser extent with CCT. Maximisation was one of the objective functions.
- The alertness of users in the different light environments was graded as 0 sleepy, 1 a little sleepy, 2 neutral, 3 a little alert, and 4 alert. fale(x) was lowest at 300 lx, 3000 K, i.e., the most sleepy, and tended to increase with increasing illuminance and CCT, from sleepy to alert, with an extreme value at 733 lx, 5553 K, and a maximum of 3.4. The level of alertness was the same at 700 lx and 800 lx, and the same at 5000 K and 6000 K. Maximisation was one of the objective functions.
- The impact of the user’s valence in the different light environments was graded as 0 unpleased, 1 less pleased, 2 neutral, 3 a little pleased, and 4 pleased. fval(x) tended to arch upwards centrally in the two-dimensional effects of illuminance and CCT, from unpleased to a little pleased, with an extreme value at 665 lx, 4753 K, and a maximum of 2.98. After that, the degree of valence decreased with further increases in illuminance and CCT. Maximisation was one of the objective functions.
- The arousal dimension was graded as 0 calm, 1 a little calm, 2 neutral, 3 a little excited, and 4 excited. faro(x) tended to increase with both illuminance and CCT, gradually moving from calm to excited. As the goal was to make the arousal level close to neutral, maximisation was one of the objective functions.
2.3. Decision Space with Constraints
The variables involved in the MOP are x1: illuminance, x1 ∈ [300, 800] in the units of lux (lx), and x2: CCT, x2 ∈ [3000, 6000] in the units of Kelvin (K). Take classroom lighting as an example, according to the EU standard “Light and lighting—Lighting of work places—Part 1: Indoor work places” (EN 12464-1: 2021), the recommended illuminance of the task area is 500 lx [23]. According to the Chinese “Architectural Lighting Design Standard” (GB 50034-2013), the horizontal illuminance of the working surface should not be lower than 300 lx, and the recommended CCT range is 3000~5500 K [24]. In summary, we optimise the illuminance range to a minimum of 300 lx, taking into account energy-saving factors, i.e., lighting power density values, the maximum illuminance is 800 lx. The CCT takes values ranging from 3000 K (warm) to 6000 K (cold). When the illuminance and CCT vary, the CRI value is assumed not to be lower than 80, in accordance with the guidelines contained in the EN 12464-1:2021 Standard.
The constraint condition considers light that is conducive to a healthy circadian rhythm. Light plays a synchronising role in the body’s biological clock. In addition to changing the phase of circadian rhythms, it also regulates the timing and quality of human sleep. The international standard CIE S 026:2018 (CIE 2018) defined spectral sensitivity functions and quantification methods to describe the non-visual effects (melatonin suppression aspect) induced by stimulation of intrinsically photosensitive retinal ganglion cells (ipRGCs) containing melanopsin through retinal-mediated light radiation [25]. It is worth noting that the spectral characteristics at the eye level play an important role from the point of view of the influence of light on non-visual effects, and the spectral characteristics of the light source used in the lighting experiments should be taken into account. As more melanopsin-based photoreception during the day contributes to increased alertness, circadian rhythm, and good sleep quality, lower melanopsin-based photoreception at night facilitates faster sleep [26,27].
Equivalent Melanopic Lux (EML), which considers only the contribution of ipRGCs in non-visual effects, originated with Enezi’s team [6] and was subsequently improved by Lucas’ team [7]. Each equivalent α-opic illuminance (symbol Eα; unit: α-opic + lux, lx, lumen per square metre, lm·m−2) specifies a photometric quantity related to the spectral power distribution of irradiance Ee,λ(λ) by the following equation. The absolute sensitivity is identical to photopic illuminance for light with an equal-energy spectral power distribution.
where λ is the wavelength of the radiation. The maximum spectral luminous efficacy Km = 683.002 lm/W. V(λ) is the spectral luminous efficacy function for photopic vision. Ee,λ(λ) is the spectral power distribution. NZ(λ) is the α-opic sensitivity curve with arbitrary normalisation. α specifies the retinal photopigment for a given organism. For example, the five human variants are: cyanopic, relating to the s-cone photopigment; chloropic, relating to the m-cone photopigment; erythropic, relating to the l-cone photopigment; rhodopic, relating to rhodopsin; and melanopic, relating to melanopsin. As = 106.857 and = 1, Equation (4) can be simplified to an equivalent form to the calculations for photopic lux:
The Circadian Stimulus (CS) was proposed by Rea’s team, taking into account the blue-yellow spectral colour-blocking mechanism in the phototransduction pathway caused by S-type cone cells, and the method included two metrics, Circadian light (CLA) and CS [8,9]. The formulas are available as follows.
where 1548 is the constant, sets the normalization of CLA so that 2856 K blackbody radiation at 1000 lux has a CLA value of 1000. Mc(λ) is the melanopsin (corrected for crystalline lens transmittance). E(λ) is the light source spectral irradiance distribution. S(λ) is the S-cone fundamental. mpλ is the macular pigment transmittance. V(λ) and V′(λ) are the photopic and scotopic luminous efficiency functions, respectively. RodSat is the half-saturation constant for bleaching rods = 6.5 W/m2. ab−y = 0.70, arod = 0.70.
In our MOP, the thresholds of EML and CS suggested by relevant studies would be constructed as constraints. Details are shown below.
- The WELL Building Standard v2 recommends a minimum value of 150 EML for regularly occupied spaces in the vertical plane at eye level between 9 a.m. and 1 p.m. [28]. Therefore, EML 150 was one of the constraints.
- The lighting research centre proposed that at least one hour in the morning satisfying a CS greater than 0.3 is beneficial for enhancing human health and well-being, improving productivity, and reducing long-term health problems associated with circadian rhythm disturbances [29]. Therefore, CS 0.3 was one of the constraints.
The functions of EML and CS with illuminance (x1) and CCT (x2) can be fitted according to Table A1 in Appendix A. Feasibility laws were used to deal with the constraints of circadian lighting, and it can be calculated that the constraints on the decision space are to make x1 468 by solving the two inequalities. Thus, the lighting multi-objective optimisation problem can be formulated as maximising comfort, alertness, valence, and the gap between neutrality and arousal, and considering circadian lighting with x1 [468, 800], x2 [3000, 6000]. The mathematical model of the problem is shown below.
3. MOEA/D-DE Algorithm
In our MOP, when the values of objectives get larger, the user perceptions present higher comfort and alertness, and a more pleased and excited mood. There are conflicts between these objectives, e.g., an increase in alertness may lead to a decrease in visual comfort and valence. Therefore, a satisfactory trade-off between these conflicting objectives needs to be obtained. The optimal solutions appear in only a few regions, so an evolutionary algorithm (EA) with strong search capability at the global scale is required to solve the problem. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimisation problem play the role of individuals in a population, and the objective functions determine the quality of the solutions. The multi-objective evolutionary algorithm based on decomposition (MOEA/D) algorithm has the outstanding advantage of obtaining a set of widely distributed solutions that approximate the Pareto optimal front in a single iteration [30]. The combination of differential evolution (DE) as a crossover operator maintains excellent population diversity and is suitable for dealing with continuous multi-objective problems with complex sets of solutions. Thus, the MOEA/D-DE algorithm is constructed to solve the MOP in this paper. The framework of MOEA/D-DE [31] is as follows.
MOEA/D decomposes the multi-objective optimisation problem into several scalar subproblems and optimises all subproblems simultaneously using their neighbourhood information. In the case of the number of objective functions greater than 2, the penalty-based boundary intersection (PBI) approach is applied in the algorithm to obtain uniformly distributed solutions. Equation (8) can be converted to Equation (9) through the PBI approach:
where , , is the reference point and the weight vector satisfies , m is the number of the objective functions, θ is a predefined penalty parameter, which is used to balance the convergence and diversity, the larger θ is, the better-distributed individuals are selected, otherwise, the better-converged individuals are selected. In the conventional PBI aggregation function, the empirical θ value is generally taken as 5.
By using weight vectors, each subproblem is associated with a decomposition function. By optimising each subproblem, a set of solutions can be found. In the decomposition-based selection method, an individual is selected to survive to the next generation based on the decomposition value.
The DE operator and the polynomial variation operator are used to generate new solutions that maintain excellent population diversity. Defining the scope of the update and generating new individuals:
where δ1 denotes the probability of selecting the parent solution from the neighbourhood, rand is a random number within [0, 1], N is the size of the population, , and are the nearest T vectors of .
Using DE operator and polynomial mutation operator for generating new individuals:
In Equation (11), CR denotes the crossover probability and ranges 0–1, and F is a scalar number and ranges 0–1. Let r1 = i and r2 and r3 be chosen randomly from P and is generated using the DE operator; is the kth element in . Three individuals xr1, xr2, and xr3 are selected from their parents. is the kth element of . In Equations (12) and (13), pm is the mutation rate, is the distribution index, and are the lower and upper bound of the kth decision variable, respectively.
After selection of the mating pool, reproduction and repair, the reference point is updated, and solutions are replaced. When the counter gen is larger than the maximum generation or the stopping criterion is satisfied, the algorithm is stopped and can output a set of non-dominated solutions. The flowchart of the MOEA/D-DE algorithm [32] used for optimisation is shown in Figure 1. The set of non-dominated solutions and the corresponding objective values through the MOEA/D-DE algorithm can provide a good choice space for the decision-makers.
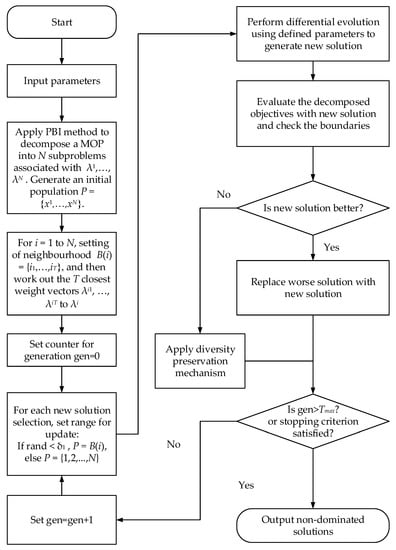
Figure 1.
The flowchart of the MOEA/D-DE algorithm used for MOP.
4. Experiment and Analysis
4.1. Results of Non-Dominated Solutions
The MOEA/D-DE algorithm was constructed to evaluate its effectiveness in the MOP for educational spaces where the light environment needs to be weighed against the effects of light parameters on the dimensions of comfort, alertness, and mood. The input parameters of the MOEA/D-DE algorithm are shown in Table 2 and the output is the non-dominated solutions obtained in the final generation.

Table 2.
The parameters of the MOEA/D-DE algorithm.
Table 3 shows the 18 solutions run out of the algorithm with a running time of 0.48 s. The non-dominated solutions correspond to a comfort value between 2.3 and 3, i.e., a little comfortable; an alertness value between 2.3 and 3.3, i.e., a neutral to alert level; a valence value between 2.4 and 3, i.e., a neutral bias towards a little pleased level; and an arousal value between 1.7 and 2.4, i.e., a neutral range between calm and excited. It can be observed that the median values of visual comfort, alertness, valence, and arousal of mood are 2.93, 2.98, 2.94, and 2.10, respectively, indicating a state of a little comfortable, alert, pleased, and neutral arousal. Figure 2 shows the histogram of the objective values in 4 dimensions corresponding to the 18 solutions. It can be seen that when solution i (i = 1, 2, …, 18) has an objective value greater than the other solutions, the remaining three objective values of this solution are all less than or equal to those of the other solutions, indicating the solutions are non-dominated. The results show that MOEA/D-DE has a reasonable degree of trade-off between the competing four objective functions, with good convergence and diversity in the solution set.

Table 3.
A set of non-dominated solutions and their corresponding objective functions and constraint values.
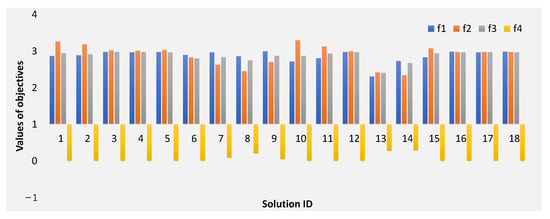
Figure 2.
Histogram of the objective values in 4 dimensions according to the non-dominated solutions (IDs: 1~18).
4.2. Regulation Strategy of Light Parameters for Educational Spaces
Taking the educational space as an example, the regulation of light parameters was investigated in this section. In the classroom, low illuminance puts the eyes in a state of fatigue and leads to poor vision, while too high illuminance puts the inner muscles of the eye in a state of high tension and causes discomfort. Through non-visual effects, high illuminance and CCT levels are positively correlated with students’ subjective alertness and are conducive to a positive mood. Therefore, classroom lighting should be a balance between visual comfort, alertness, and mood. In this study, the classroom schedule of Tongji University was used as an example, in the morning from 8:00 to 11:35, and in the afternoon from 13:30 to 17:05. Both the morning and the afternoon sessions were scheduled for 4 lessons of 45 min each, with a 5 min break between lessons 1 and 2, lessons 3 and 4, and a 25 min break between lessons 2 and 3, and the same schedule in the afternoon. The optimal solution to meet the needs of students would be selected from the 18 solutions according to the actual situation.
For different lesson time and rest time, the students’ lighting requirements vary [16,17], and the preference decisions of comfort, alertness, valence, and arousal are as follows. In lesson 1, a comfort learning mode should be applied to get students in a happy mood at the start of the day and to maintain a high level of arousal. In lessons 2 and 3, a focused learning mode should be applied to maintain a high level of alertness. In lesson 4, a soothing learning mode should be applied, where the primary aim is to focus on the students’ visual comfort after a long period of focused learning and to keep their arousal level calm and relaxed. Rest mode, a state of low arousal, should be applied during all rest time. In the afternoon, lessons 5 and 6 should use the focused learning mode, which positively motivates students’ alertness. In lesson 7, a comfortable learning mode should be applied, which maintains high arousal while first considering the students’ level of pleasure. Lesson 8, like lesson 4, should use a soothing learning mode with primary attention to students’ visual comfort.
Based on the descriptions of the four modes above, we can select an optimal solution for each mode from the 18 solutions in Table 3, depending on the requirements of the different modes. The mathematical definitions for the ranking (fcom, fale, fval) and numerical size of the four modes for the target values of comfort, alertness, valence, and arousal are as follows:
- Focused learning mode, rank: fale > fval > fcom, and faro > 2, high arousal, corresponding to solution IDs: 1, 2, 3, 4, 5, 10, 11, 15, 16, 17, 18. Among these solutions, ID 1 is the optimal solution since it has the largest fale value.
- Comfortable learning mode, rank: fcom > fale > fval, and faro > 2, high arousal, corresponding to solution ID: 6.
- Soothing learning mode, rank: fcom > fval > fale, and faro < 2, low arousal, corresponding to solution IDs: 7, 8, 9, 14. Among these solutions, ID 9 is the optimal solution since it has the largest fcom value.
- Rest mode, ID 14 is the optimal solution since it has the smallest fale value and faro value, rank: fcom > fval > fale, and faro < 2, low arousal.
A dual-parameter regulation strategy varying with time is composed, as shown in Table 4. The modes applied in different lesson times are listed based on optimal solutions, and the rank of objective functions according to the schedule are shown in the table. Figure 3 presents the diagram of the changes in illuminance and CCT. The application of each mode is shown in a different colour in the diagram (red: focused learning mode; manganese violet: comfortable learning mode; blue: soothing learning mode; green: rest mode).

Table 4.
A dual-parameter regulation strategy based on optimal solutions, and the rank of objective functions according to the schedule.
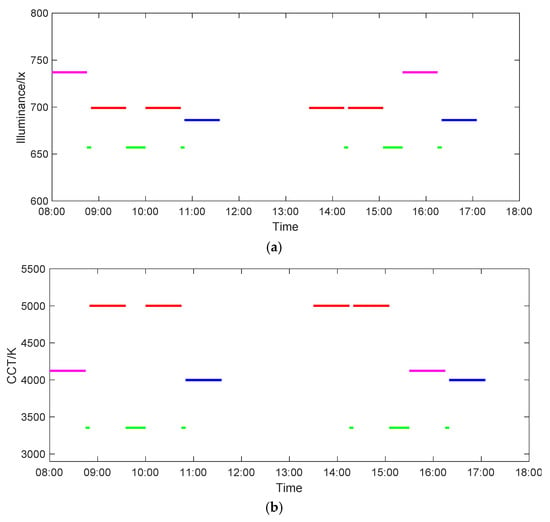
Figure 3.
The diagram of the changes in the dual-parameter regulation strategy varying with time. (a) The changes in illuminance. (b) The changes in CCT. The red lines correspond to the focused learning mode; the manganese violet lines correspond to the comfortable learning mode; the blue lines correspond to the soothing learning mode; and the green lines correspond to the rest mode.
The regulation strategy demonstrated that during class time, the comfort value reached 2.91 on average, the alertness value reached 3.01 on average, and the valence value reached 2.89 on average, indicating a positive effect on the students, and the arousal value was 2.15 on average, showing a neutral to excited (high arousal) state. During break time, the comfort value was 2.73, the alertness value was 2.34, the valence value was 2.67, and the arousal value was 1.72, showing a neutral to calm (low arousal) state. It can be seen that such a lighting control strategy could promote better perceptions to positively motivate learning outcomes during class time and moderate arousal to reduce visual fatigue during break time. In addition, the combination of light parameters during class time and break time resulted in an EML greater than 150, which was in line with the EML recommendation from the WELL Standard v2, and a CS greater than 0.3, too. The regulation strategy was conducive to reducing the problems associated with circadian rhythm disturbances.
5. Conclusions
A lighting control system aims to provide users with a flexible light environment that changes according to their demands. Different configurations of illuminance and CCT significantly affect circadian rhythm, operational efficiency, and mood, and the coupling between these effects is complex and variable. This paper investigated a dual-parameter light optimisation aimed at weighing users’ comfort, alertness, and mood. A mathematical model of the effects of illuminance and CCT on human comfort, alertness, valence, and arousal of mood, and the EML and CS values were used as constraints to limit decision space, and 18 non-dominated solutions were obtained based on the MOEA/D-DE algorithm. Taking the educational space as an example, a dual-parameter regulation strategy of illuminance and CCT suitable for students’ habits during the course time was proposed from the optimal solutions based on the different demand ranking of focused learning, comfortable learning, soothing learning, and resting state, which better weighed the conflict between alertness and comfort, and valence and arousal level. The results can provide a scientific basis for lighting control systems in educational spaces and help to create a healthy and efficient light environment for students, thereby positively stimulating learning. The proposed mathematical models and analysis methods have the potential for application in the lighting design and control in other types of building spaces. The next step in the research will be to apply the regulation strategy to intelligent lighting control systems, utilising the variable nature of daylight and the adjustable luminous flux and CCTs of LEDs under the consideration of a wider range (from 2700 K to 6500 K) to investigate the optimal combination of shading device actions and LED channel given commands to control the single or mixed light conditions within the mode settings. The correlation of the spectral characteristics with circadian rhythm, alertness, and mood is also a target to be considered in future work, to analyse the possibilities of improving the light quality of intelligent buildings.
Author Contributions
Conceptualization, H.C. and H.X.; methodology, H.C. and H.X.; validation, X.L.; investigation, Q.L. and H.L.; data curation, Q.L. and H.L.; writing—original draft preparation, H.C.; writing—review and editing, X.L. and H.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Shanghai Science and Technology Planning Project (20DZ2205900), Shanghai Municipal Commission of Science and Technology Project (19511132101), Shanghai Municipal Science and Technology Major Project (2021SHZDZX0100), and the Fundamental Research Funds for the Central Universities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The target and measured values of illuminance and CCT for experimental lighting conditions.
Table A1.
The target and measured values of illuminance and CCT for experimental lighting conditions.
| ID | Et/lx, CCTt/K | Working Surface | Eye Level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ework/lx | x | y | CCT/K | CRI | Eeye/lx | EML | CS | ||
| 1 | 300, 3000 | 301 | 0.4356 | 0.3993 | 2984 | 86 | 194 | 98 | 0.23 |
| 2 | 300, 4000 | 302 | 0.3788 | 0.3676 | 3976 | 88 | 193 | 133 | 0.17 |
| 3 | 300, 5000 | 302 | 0.3434 | 0.3476 | 5053 | 87 | 193 | 157 | 0.23 |
| 4 | 300, 6000 | 309 | 0.3223 | 0.3373 | 5972 | 85 | 196 | 176 | 0.26 |
| 5 | 400, 3000 | 408 | 0.4334 | 0.3987 | 3016 | 86 | 259 | 133 | 0.28 |
| 6 | 400, 4000 | 411 | 0.3807 | 0.3691 | 3935 | 88 | 262 | 178 | 0.21 |
| 7 | 400, 5000 | 407 | 0.3446 | 0.3487 | 5008 | 87 | 258 | 209 | 0.28 |
| 8 | 400, 6000 | 409 | 0.3224 | 0.3372 | 5965 | 85 | 260 | 232 | 0.32 |
| 9 | 500, 3000 | 508 | 0.4335 | 0.3990 | 3016 | 86 | 323 | 165 | 0.32 |
| 10 | 500, 4000 | 506 | 0.3803 | 0.3690 | 3945 | 88 | 325 | 222 | 0.25 |
| 11 | 500, 5000 | 505 | 0.3456 | 0.3496 | 4972 | 87 | 319 | 256 | 0.32 |
| 12 | 500, 6000 | 517 | 0.3235 | 0.3375 | 5913 | 85 | 326 | 290 | 0.36 |
| 13 | 600, 3000 | 592 | 0.4325 | 0.3986 | 3031 | 86 | 376 | 193 | 0.35 |
| 14 | 600, 4000 | 597 | 0.3793 | 0.3683 | 3967 | 88 | 377 | 258 | 0.28 |
| 15 | 600, 5000 | 602 | 0.3457 | 0.3493 | 4969 | 87 | 380 | 305 | 0.35 |
| 16 | 600, 6000 | 612 | 0.3231 | 0.3370 | 5931 | 85 | 386 | 343 | 0.39 |
| 17 | 700, 3000 | 698 | 0.4317 | 0.3979 | 3039 | 86 | 443 | 228 | 0.38 |
| 18 | 700, 4000 | 702 | 0.3800 | 0.3686 | 3950 | 88 | 444 | 301 | 0.31 |
| 19 | 700, 5000 | 711 | 0.3451 | 0.3488 | 4989 | 87 | 445 | 354 | 0.38 |
| 20 | 700, 6000 | 707 | 0.3232 | 0.3364 | 5929 | 85 | 446 | 396 | 0.42 |
| 21 | 800, 3000 | 809 | 0.4339 | 0.3994 | 3014 | 85 | 513 | 260 | 0.41 |
| 22 | 800, 4000 | 804 | 0.3788 | 0.3677 | 3976 | 88 | 509 | 348 | 0.34 |
| 23 | 800, 5000 | 811 | 0.3462 | 0.3492 | 4949 | 87 | 511 | 408 | 0.41 |
| 24 | 800, 6000 | 811 | 0.3230 | 0.3359 | 5942 | 85 | 510 | 455 | 0.45 |

Table A2.
The average of the voting scores from the participants in the lighting experiments.
Table A2.
The average of the voting scores from the participants in the lighting experiments.
| ID | Et/lx, CCTt/K | Visual Comfort | Alertness | Valence | Arousal |
|---|---|---|---|---|---|
| 1 | 300, 3000 | 0.83333333 | 1.25 | 1.33333333 | 0.91666667 |
| 2 | 300, 4000 | 1.5 | 1.16666667 | 1.66666667 | 1.25 |
| 3 | 300, 5000 | 2 | 2 | 2.08333333 | 1.91666667 |
| 4 | 300, 6000 | 1.58333333 | 1.91666667 | 1.75 | 1.75 |
| 5 | 400, 3000 | 1.41666667 | 1 | 1.83333333 | 1.08333333 |
| 6 | 400, 4000 | 1.75 | 1.83333333 | 2.08333333 | 1.5 |
| 7 | 400, 5000 | 2 | 2 | 2.41666667 | 1.75 |
| 8 | 400, 6000 | 1.66666667 | 2.58333333 | 2.08333333 | 2 |
| 9 | 500, 3000 | 1.58333333 | 1.25 | 2.08333333 | 1.16666667 |
| 10 | 500, 4000 | 2.5 | 1.83333333 | 2.33333333 | 1.83333333 |
| 11 | 500, 5000 | 2.33333333 | 2.5 | 2.58333333 | 2 |
| 12 | 500, 6000 | 2.25 | 2.33333333 | 2.25 | 2.66666667 |
| 13 | 600, 3000 | 2.33333333 | 2.25 | 2.33333333 | 1.41666667 |
| 14 | 600, 4000 | 3.08333333 | 2.66666667 | 3 | 2.08333333 |
| 15 | 600, 5000 | 2.83333333 | 3.25 | 2.91666667 | 2.41666667 |
| 16 | 600, 6000 | 2.41666667 | 3 | 2.58333333 | 2.41666667 |
| 17 | 700, 3000 | 2.5 | 2.66666667 | 2.58333333 | 2 |
| 18 | 700, 4000 | 2.75 | 2.5 | 2.83333333 | 1.91666667 |
| 19 | 700, 5000 | 2.91666667 | 2.91666667 | 3.08333333 | 2 |
| 20 | 700, 6000 | 2.33333333 | 3.25 | 2.5 | 2.66666667 |
| 21 | 800, 3000 | 1.75 | 2.16666667 | 2 | 2 |
| 22 | 800, 4000 | 2.83333333 | 2.66666667 | 2.66666667 | 1.75 |
| 23 | 800, 5000 | 2.08333333 | 3.33333333 | 2.25 | 2.66666667 |
| 24 | 800, 6000 | 2.41666667 | 3.25 | 2.5 | 2.33333333 |
References
- Berson, D.M.; Dunn, F.A.; Takao, M. Phototransduction by retinal ganglion cells that set the circadian clock. Science 2002, 295, 1070–1073. [Google Scholar] [CrossRef] [PubMed]
- Cajochen, C. Alerting effects of light. Sleep Med. Rev. 2007, 11, 453–464. [Google Scholar] [CrossRef] [PubMed]
- Chellappa, S.L.; Steiner, R.; Blattner, P.; Oelhafen, P.; Gotz, T.; Cajochen, C. Non-visual effects of light on melatonin, alertness and cognitive performance: Can blue-enriched light keep us alert? PLoS ONE 2011, 6, 11. [Google Scholar]
- Figueiro, M.G.; Steverson, B.; Heerwagen, J.; Kampschroer, K.; Hunter, C.M.; Gonzales, K.; Plitnick, B.; Rea, M.S. The impact of daytime light exposures on sleep and mood in office workers. Sleep Health 2017, 3, 204–215. [Google Scholar] [CrossRef]
- Xiao, H.; Cai, H.; Li, X. Non-visual effects of indoor light environment on humans: A review. Physiol. Behav. 2021, 228, 113195. [Google Scholar] [CrossRef]
- Enezi, J.; Revell, V.; Brown, T.; Wynne, J.; Schlangen, L.; Lucas, R. A “melanopic” spectral efficiency function predicts the sensitivity of melanopsin photoreceptors to polychromatic lights. J. Biol. Rhythms 2011, 26, 314–323. [Google Scholar] [CrossRef]
- Lucas, R.J.; Peirson, S.N.; Berson, D.M.; Brown, T.M.; Cooper, H.M.; Czeisler, C.A.; Figueiro, M.G.; Gamlin, P.D.; Lockley, S.W.; O’Hagan, J.B.; et al. Measuring and using light in the melanopsin age. Trends Neurosci. 2014, 37, 1–9. [Google Scholar] [CrossRef]
- Rea, M.S.; Figueiro, M.G.; Bierman, A.; Hamner, R. Modelling the spectral sensitivity of the human circadian system. Light. Res. Technol. 2012, 44, 386–396. [Google Scholar] [CrossRef]
- Rea, M.S.; Figueiro, M.G. Light as a circadian stimulus for architectural lighting. Light. Res. Technol. 2018, 50, 497–510. [Google Scholar] [CrossRef]
- Yin, J.W.; Julius, A.; Wen, J.T.; Wang, Z.; He, C.L.; Kou, L. Human Alertness Optimization with a Three-Process Dynamic Model. Mathematics 2022, 10, 1916. [Google Scholar] [CrossRef]
- Papatsimpa, C.; Linnartz, J.-P. Personalized Office Lighting for Circadian Health and Improved Sleep. Sensors 2020, 20, 4569. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, S.; Gao, Y. Application of healthful lighting: Research progress and prospects. Chin. Sci. Bull. 2020, 65, 300–310. [Google Scholar] [CrossRef]
- Schlangen, L.J.M. CIE Position Statement on Non-Visual Effects of Light—Recommending Proper Light at the Proper Time, 2nd ed.; CIE: Vienna, Austria, 2019. [Google Scholar]
- Llinares, C.; Castilla, N.; Higuera-Trujillo, J.L. Do Attention and Memory Tasks Require the Same Lighting? A Study in University Classrooms. Sustainability 2021, 13, 8374. [Google Scholar] [CrossRef]
- Sun, B.S.; Zhang, Q.L.; Cao, S. Development and Implementation of a Self-Optimizable Smart Lighting System Based on Learning Context in Classroom. Int. J. Environ. Res. Public Health 2020, 17, 1217. [Google Scholar] [CrossRef]
- Choi, K.; Suk, H.-J. Dynamic lighting system for the learning environment: Performance of elementary students. Opt. Express 2016, 24, A907–A916. [Google Scholar] [CrossRef]
- Lee, H.S.; Kwon, S.Y.; Lim, J.H. A Development of a Lighting Control System Based on Context-Awareness for the Improvement of Learning Efficiency in Classroom. Wirel. Pers. Commun. 2016, 86, 165–181. [Google Scholar] [CrossRef]
- Wu, H.; Wu, Y.; Sun, X.; Liu, J. Combined effects of acoustic, thermal, and illumination on human perception and performance: A review. Build. Environ. 2020, 169, 106593. [Google Scholar] [CrossRef]
- Manav, B. An experimental study on the appraisal of the visual environment at offices in relation to colour temperature and illuminance. Build. Environ. 2007, 42, 979–983. [Google Scholar] [CrossRef]
- Yu, H.; Akita, T. The effect of illuminance and correlated colour temperature on perceived comfort according to reading behaviour in a capsule hotel. Build. Environ. 2019, 148, 384–393. [Google Scholar] [CrossRef]
- EN 12665; Light and Lighting—Basic Terms and Criteria for Specifying Lighting Requirements. European Committee for Standardization: Brussels, Belgium, 2011.
- Russell, J.A. A circumplex model of affect. J. Pers. Soc. Psychol. 1980, 39, 1161–1178. [Google Scholar] [CrossRef]
- EN12464-1:2021; Light and Lighting—Lighting of Work Places. Part 1: Indoor Work Places. European Committee for Standardization: Brussels, Belgium, 2021.
- GB50034-2013; Standard for Lighting Design of Buildings. National Standards of the People’s Republic of China: Beijing, China, 2013. (In Chinese)
- CIE S 026/E:2018; CIE System for Metrology of Optical Radiation for ipRGC-Influenced Responses to Light. CIE: Vienna, Austria, 2018.
- Nowozin, C.; Wahnschaffe, A.; Rodenbeck, A.; de Zeeuw, J.; Hadel, S.; Kozakov, R.; Schopp, H.; Munch, M.; Kunz, D. Applying Melanopic Lux to Measure Biological Light Effects on Melatonin Suppression and Subjective Sleepiness. Curr. Alzheimer Res. 2017, 14, 1042–1052. [Google Scholar] [CrossRef]
- Souman, J.L.; Borra, T.; de Goijer, I.; Schlangen, L.J.M.; Vlaskamp, B.N.S.; Lucassen, M.P. Spectral Tuning of White Light Allows for Strong Reduction in Melatonin Suppression without Changing Illumination Level or Color Temperature. J. Biol. Rhythms 2018, 33, 420–431. [Google Scholar] [CrossRef]
- WELL v2. Available online: https://v2.wellcertified.com/en/v/light/feature/3 (accessed on 20 May 2022).
- Lighting Research Center. Available online: https://www.lrc.rpi.edu/cscalculator/img/CircadianEffectiveLight.pdf (accessed on 22 May 2022).
- Zhang, Q.F.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.F. Multiobjective Optimization Problems with Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Hsiao, J.C.; Shivam, K.; Chou, C.L.; Kam, T.Y. Shape Design Optimization of a Robot Arm Using a Surrogate-Based Evolutionary Approach. Appl. Sci. 2020, 10, 2223. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).