Abstract
The hybrid architecture of the driven qubit–photon–magnon system has recently emerged as a promising candidate for novel quantum technologies. In this paper, we introduce the effective wave-function of a superconducting single qubit and a magnon mode contained within a cavity resonator and an external field. The non-classicality of the magnon and resonator modes are investigated by using the negative values of the Wigner function. Additionally, we discuss the non-classicality of the qubit state via the Wigner–Yanase skew information. We find that the mixture angle of the qubit–resonator plays a controllable role in non-classicality. However, the strength of the magnon–photon increases the non-classical behaviour of the system.
MSC:
81P10; 81P13
1. Introduction
Hybrid quantum systems have provided an excellent experimental and theoretical platform for studying quantum computing [1], quantum information processing [2], and quantum state engineering [3,4,5,6,7]. Different components of hybrid quantum systems have been developed, such as strongly coupled magnons and cavity microwave photons [8], magnon–photon–phonons [9,10], magnon-superconducting qubits [11], and microwave optomechanical-magnetic systems [12]. One of the most attractive quantum systems is the hybrid qubit–photon–magnon quantum system because of its diversification [13,14]. It has opened a new avenue for exploring intermediate transitions through the Hamiltonian interaction between different components. It also has many attractive applications, including the generation of hybrid entangled states. Experimentally, the entanglement of a single hybrid qubit–photon–magnon has been realized [15]. Additionally, some theoretical studies have been devoted to illustrating the potential of quantum information in this system [2,16].
As is well known, study of driven qubit systems is the core of the primary discoveries of principal effects in both classical and quantum physics. An attractive example is the influence of an external classical field over a two-level quantum system [17]. Furthermore, the effect of the driven classical field on a two-level atom with some other medians such as the Kerr nonlinear [18], Stark shift [19], and vibrating graphene membrane [20] have been investigated. The effective simulation of a single classical drive in the Jaynes–Cummings model has been realized [21]. Moreover, the driven system of two identical superconducting qubits coupled simultaneously to a cavity field has been studied [22].
Furthermore, non-classicality is an essential characteristic of the quantum world, where it has many theoretical implications and practical applications [23]. Various meanings have been constructed for the non-classicality of quantum systems, such as quantumness [24], the negativity of Wigner functions [25,26], quantum entanglement [27,28], non-locality [29,30], discordance, and other quantum correlations [31,32,33,34]. In terms of atomic spin optical coherent states, the non-classicality of light has been quantified by virtue of the Wigner–Yanase skew information [35]. Additionally, the non-classicality of two atoms and the nondegenerate two-photon nonlinear Jaynes-–Cummings model has been investigated [36]. The Wigner–Yanase skew information has been identified as the amount of non-classicality of bosonic field states [37] and for a single and multi-qubit state [38,39]. It has also been used to indicate quantum entanglement [40], quantum coherence [41], and some non-local quantum correlations [42].
This study highlights the non-classicality of a hybrid qubit–photon–magnon system in the presence of an external classical field. The present system still needs more investigation, by opens a new avenue for more theoretical and applicable novel quantum technologies. The non-classicality of the photon–magnon subsystem is discussed in the quantum phase space by applying the two-mode Wigner distribution function. However, the non-classicality of the qubit subsystem is realized by using the atomic Wigner-Yanase skew information. In Section 2, we introduce our physical Hamiltonian component and drive the effective wave function in a dispersive-limit interaction. The mathematical form of the two-mode Wigner function is reconstructed in Section 3, where the quantumness of the magnon–photon in phase space is investigated. Section 4 presents the non-classicality of the qubit system in terms of skew information. Finally, we summarize the effect of different physical Hamiltonian components on the behaviour of non-classicality.
2. Physical Model
Let us consider a hybrid physical quantum system consisting of a superconducting qubit (single atom), a ferromagnetic crystal in the Kittle mode (magnon), and a resonator (photon). These physical components are driven by an external classical field. The magnon mode interacts with the resonator via the magnetic dipole interaction, while the single qubit is coupled to the resonator via a general Rabi model. The physical Hamiltonian of this system can be written as,
where , , and are the eigenfrequencies of the resonator, magnon, and qubit, respectively. and are the creation and annihilation operators of the resonator and magnon modes, respectively. and are the standard Pauli operators, which are labelled by the excited and the ground states as , and . , are the coupling strengths of the photon–magnon, qubit–photon, and the driven external field, respectively. The angle represents the transversal couplings and the mixture of the longitudinal between the qubit and the resonator.
By diagonalizing the driven classical field and non-interacted qubit terms using the following eigenstates [17,43], we have
with , In this case, the excited state and the ground state can be rotated into new excited and ground states; hence, one can redefine the Pauli spin operators and as,
where , . After applying the previous transformations with the rotating wave approximation, the Hamiltonian (1) can be rewritten as,
where , and . In the interaction picture, the physical Hamiltonian model (4) is,
in the dispersive interactions of the hybrid model, assuming that the coupling strengths and are much smaller than the transition frequencies and , where we use the condition . The effective Hamiltonian by the James method of the system takes the following form [44],
where , , , and with .
Now, we consider the case in which the qubit system is initially prepared in the new exited state , while the initial resonator and magnon modes are initially in coherent states. Thus, the initial state is given by,
According to the effective Hamiltonian (6), the temporal wave function associated with the initial state (7) is obtained by employing the Schrödinger equation as,
where
Consequentially, the final density operator of the total effective system is given by,
Hereafter, we will obtain the reduced quantum state of the resonator–magnon to recognize the non-classicality by employing the two-mode Wigner distribution. Furthermore, we will find the reduced qubit state to visualize the atomic non-classicality.
3. Wigner Function of a Two-Mode Field
The Wigner quasi-probability distribution in the quantum phase space for an arbitrary density operator of a single mode electromagnetic field is defined by [45],
where and satisfy the commutation relation . The generalized Wigner distribution functions of the two-mode electromagnetic field can be expressed by,
Using the fact of transition operator , the effect of the displacement operators in the state is,
Then, one can write,
Substituting in Equation (13), the integration form of the Wigner function reads,
Particularly, we use the Fock basis and parity operator to obtain the final form of the two-mode Wigner function,
In our discussion, we assume that , where i is related to the number mode field.
By studying the Wigner function of the resonator–magnon subsystem, one can trace out the qubit subsystem in Equation (10), where the final density operator of the resonator–magnon system is given by,
Substituting the density operator (13) into Equation (16), one may obtain the ultimate form of the Wigner function of the resonator–magnon as,
where
As is well known, the Wigner function is a two-fold measure, where negative values indicate the quantumness of a system and positive values indicate classicality or minimum uncertainty. We display the Wigner function to show the classicality and quantumness of the resonator–magnon subsystem and study the effect of the mixture angle with coupling parameters in the Wigner function. In Figure 1, Figure 2 and Figure 3, we set the scaled time equal to , where this time represents the middle of the collapse period in atomic inversion. The initial mean photon numbers are , (related to the resonator) and (related to the magnon mode).

Figure 1.
The behaviour of as a function of , where where (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .

Figure 2.
The behaviour of as a function of , where , where (a) , ; (b) , ; (c) , ; (d) , ; (e) , ; (f) , .

Figure 3.
The behaviour of as a function of , where , where (a) , ; (b) , ; (c) ,; (d) , ; (e) , ; (f) , .
In Figure 1, we displayed the general behaviour of the two-mode Wigner distribution with .The quantumness and classicality of the resonator–magnon system depend on the mixture angle, where the position of negative and positive values is changed according to the phase space. At and , Figure 1a shows that the function has negative fringes at , as well as an original positive peak at . This means that the quantumness of the system is limited around zero phase space, while the classicality of the system corresponds to the initial intensity of the coherent state. As displayed in Figure 1b, the position of classicality and non-classicality changes around at , while the non-classicality around is neglected. Moreover, the Wigner function shows that the classicality of the quantum system increases at Figure 1c. By regulating the qubit-resonator in the maximum mixture state with , the effects of the magnon–resonator, resonator–qubit, and driven field couplings are displayed in Figure 1d–f, respectively. Note that an increase in different couplings reduces and diffuses the maximum and lower bounds of the Wigner function. The decreasing rate induced by the coupling of the qubit–resonator system is less than that predicated in the other two couplings. From this figure, one can deduce that the qubit–resonator position decreases the quantum and classical correlation when the two mode fields are measured in the same phase space.
Figure 2 shows the general behaviour of the Wigner function according to the magnon–resonator system in the magnon phase space, where and . Figure 2a displays the Wigner function where the mixing angle is initially fixed at . The Wigner function predicts a maximum negative peak at , with some interference peaks at . On the other hand, the negative and positive behaviours of decrease at , while the negative behaviour increases at . Hence, the mixing angle has a noticeable influence on the behaviour of the Wigner function in the magnon phase space as shown in Figure 2c. Figure 2d illustrates the behaviour of the Wigner function where , increasing the strength of external classical field (). It is remarked that the non-classicality increases along compared to Figure 2b. This means that the strength of the external classical field increases the non-classicality along one side of phase space [18]. Additionally, as the strength of the qubit-resonator grows which displayed in Figure 2d–f, the non-classicality in the magnon phase increases, where the negative behaviour of is increased. Moreover, the increase of the coupling of the resonator–magnon reduces the classicality and non-classicality of the system. In this case, the general behaviour of the Wigner function is similar to the standard Schrödinger’s cat state [46]. From this figure, we can infer that the non-classicality of the driven qubit–photon–magnon system increases in the magnon phase space by handling the qubit–resonator in a pure state with and increasing the value of the coupling strength.
Different behaviour can be seen in Figure 3, where the behaviour of the Wigner function is displayed in cavity-mode phase space with . As shown in Figure 3a, the maximum bounds of the non-classical and classical correlation are depicted at , such that the qubit–photon–magnon reduces to a generalized Jaynes–Cummings Hamiltonian [47]. This justifies Wigner function’s similarity to its behaviour in the Fock state [48]. Further, Figure 3b,c show that the classical and non-classical correlations at are greater than those are depicted at . On the other hand, the increase of the classical field and qubit–resonator couplings diffuse and reduce the classicality and non-classicality.
4. Non-Classicality in Terms of Skew Information
This section will pursue the dynamics of the non-classicality of the qubit system from information-theoretic interpretations of the Wigner–Yanase skew information. If a conserved observable is not commuting with a reduced density operator , one can measure the information content of the pure or mixed quantum state skew to the observable by using the skew information [49],
This quantifier can be interpreted as a coherence of quantum state for the operator , the asymmetry of relating to , the uncertainty of in the state , and as a version of quantum Fisher information. For a single qubit state, the atomic non-classicality in terms of skew information is expressed as [38],
However, the non-classicality of a general mixed state can be defined as,
where , and .
Employing Equation (10), for the single qubit quantum state after tracing out the two-mode field and return to the original qubit basis and , one can obtain,
where
The components of the Bloch vector are given by,
The non-classical behaviour of the qubit subsystem is illustrated in Figure 4 with different values of coupling strengths, and mixture angels are taken into account. From Figure 4a, the behaviour of non-classicality at is effectively that formed at and . The super-mixed angle reduces the non-classicality of the qubit system. Further, Figure 4b exhibits the effect of different strengths of magnon–resonator couplings at a super-mixed angle. Clearly, as the strength of the magnon–resonator coupling increases, the qubit non-classicality vanishes. In Figure 4c, we show the influence of the qubit–resonator coupling on the function , where . Obviously, the interior Figure 4c shows that, as time increases, the coupling does not recreate the quantumness of the qubit system. Moreover, the effects of different values of classical field coupling are shown in Figure 4d at a super-mixed angle. The non-classicality is stable at the maximum value with , while it decreases at other values. Thus, it is better to know the influence of the classical field at a fixed time (). The black curve shows the non-classicality is maximum at . Then, it decays as the coupling of the classical field increases.
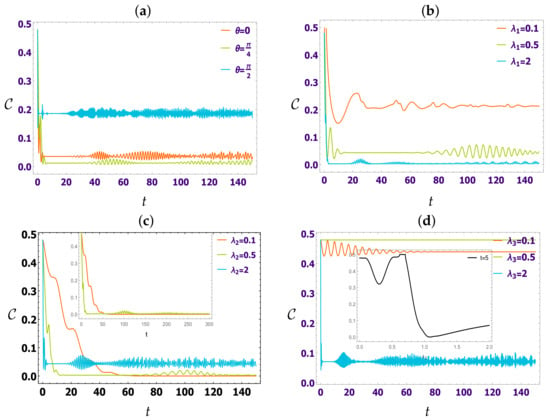
Figure 4.
The behaviour of qubit non-classicality through skew information , where . (a) ; (b) , ; (c) , ; (d) , .
5. Conclusions
This paper investigated the dynamical behaviour of non-classicality for a hybrid physical system consisting of the qubit–photon–magnon within an external classical field. The wave function in the dispersive regime of the hybrid model was obtained where the qubit is prepared initially in the excited state, while the resonator and magnon modes were prepared in the standard coherent state. The negative values of the two-mode Wigner function show the non-classicality of the magnon–resonator. The atomic spin skew information was employed to display the non-classicality of the qubit system.
Our results show that when the resonator and magnon are measured in the same phase space via the Wigner function, non-classical behaviour at a considerable strength of qubit–resonator coupling is generated, while a super-mixture angle reduces the non-classicality. By measuring the magnon–resonator in the magnon phase space, the non-classicality increases as the strength of the qubit–resonator coupling increases. In the resonator phase space, the coupling of the qubit–resonator increases the non-classicality. Overall, the coupling of the external field disperses and increases the non-classicality along one side of the phase space. When returning the hybrid system to a generalized Jaynes–Cummings Hamiltonian model via the mixture angle, the Wigner function depicted high non-classicality. On the other hand, atomic non-classicality is reduced as the magnon–resonator coupling increases, while the qubit–resonator coupling recreates the classicality of the qubit system. The behaviour of qubit non-classicality depends on the value of the external classical field.
Author Contributions
Formal analysis, M.F.A. and E.M.K.; Investigation, M.Y.A.-R. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institutional Fund Projects under grant IFPIP: 1584-130-1443. The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
The data used was generated from the relationship found in the manuscript.
Acknowledgments
This research was funded by the Institutional Fund Projects under grant IFPIP: 1584-130-1443. The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, W.; Tyberkevych, V.; Kwok, W.K.; Hoffmann, A.; Novosad, V. Hybrid magnonics: Physics, circuits, and applications for coherent information processing. J. App. Phys. 2020, 128, 130902. [Google Scholar] [CrossRef]
- Makhlin, Y.; Schön, G.; Shnirman, A. Quantum-state engineering with Josephson-junction devices. Rev. Mod. Phys. 2001, 73, 357–400. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Awschalom, D.D.; Du, C.; He, R.; Heremans, J.; Hoffmann, A.; Hou, J.; Kurebayashi, H.; Li, Y.; Liu, L.; Novosad, V.; et al. Quantum engineering with hybrid magnonics systems and materials. IEEE Trans. Quantum Eng. 2021, 2, 5500836. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The size-dependent thermoelastic vibrations of nanobeams subjected to harmonic excitation and rectified sine wave heating. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry 2020, 12, 1276. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, C.L.; Jiang, L.; Tang, H.X. Strongly Coupled Magnons and Cavity Microwave Photons. Phys. Rev. Lett. 2014, 113, 156401. [Google Scholar] [CrossRef]
- Li, J.; Zhu, S.Y.; Agarwal, G.S. Magnon-Photon-Phonon Entanglement in Cavity Magnomechanics. Phys. Rev. Lett. 2018, 121, 203601. [Google Scholar] [CrossRef]
- Zhang, L.; Bhatti, M.; Michaelides, E.E.; Marin, M.; Ellahi, R. Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field. Eur. Phys. J. Spec. Top. 2022, 231, 521–533. [Google Scholar] [CrossRef]
- Tabuchi, Y.; Ishino, S.; Noguchi, A.; Ishikawa, T.; Yamazaki, R.; Usami, K.; Nakamura, Y. Coherent coupling between a ferromagnetic magnon and a superconducting qubit. Science 2015, 349, 405–408. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X.; Chao, S.; Peng, R.; Li, C.; Zhou, L. Simultaneous blockade of a photon, phonon, and magnon induced by a two-level atom. Phys. Rev. A 2020, 101, 063838. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Tabuchi, Y.; Gloppe, A.; Usami, K.; Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 2019, 12, 070101. [Google Scholar] [CrossRef]
- Qi, S.f.; Jing, J. Generation of Bell and Greenberger-Horne-Zeilinger states from a hybrid qubit-photon-magnon system. Phys. Rev. A 2022, 105, 022624. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Wolski, S.P.; Tabuchi, Y.; Kono, S.; Usami, K.; Nakamura, Y. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 2020, 367, 425–428. [Google Scholar] [CrossRef]
- Kong, D.; Hu, X.; Hu, L.; Xu, J. Magnon-atom interaction via dispersive cavities: Magnon entanglement. Phys. Rev. B 2021, 103, 224416. [Google Scholar] [CrossRef]
- Solano, E.; Agarwal, G.S.; Walther, H. Strong-Driving-Assisted Multipartite Entanglement in Cavity QED. Phys. Rev. Lett. 2003, 90, 027903. [Google Scholar] [CrossRef]
- Abd-Rabbou, M.; Khalil, E.; Ahmed, M.; Obada, A.S. External classical field and damping effects on a moving two level atom in a cavity field interaction with Kerr-like medium. Int. J. Theor. Phys. 2019, 58, 4012–4024. [Google Scholar] [CrossRef]
- Al Naim, A.F.; Khan, J.Y.; Abdel-Khalek, S.; Khalil, E.M. Entanglement and physical attributes of the interaction between two SC-qubits and thermal field in the presence of a magnetic field. Microelectron. J. 2019, 86, 15–21. [Google Scholar] [CrossRef]
- Alotaibi, M.F.; Khalil, E.; Abdel-Khalek, S.; Abd-Rabbou, M.; Omri, M. Effects of the vibrating graphene membrane and the driven classical field on an atomic system coupled to a cavity field. Results Phys. 2021, 31, 105012. [Google Scholar] [CrossRef]
- Sánchez Muñoz, C.; Frisk Kockum, A.; Miranowicz, A.; Nori, F. Simulating ultrastrong-coupling processes breaking parity conservation in Jaynes–Cummings systems. Phys. Rev. A 2020, 102, 033716. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, S.p.; Yang, G.q.; Huang, G.m.; Li, G.X. Ultranarrow spectral line of the radiation in double qubit-cavity ultrastrong coupling system. Opt. Express 2021, 29, 23939–23952. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Luo, S.; Li, N.; Fu, S. Quantumness of quantum ensembles. Theor. Math. Phys. 2011, 169, 1724–1739. [Google Scholar] [CrossRef]
- Mari, A.; Kieling, K.; Nielsen, B.M.; Polzik, E.S.; Eisert, J. Directly Estimating Nonclassicality. Phys. Rev. Lett. 2011, 106, 010403. [Google Scholar] [CrossRef]
- Abd-Rabbou, M.Y.; Metwally, N.; Ahmed, M.; Obada, A.S. Wigner function of noisy accelerated two-qubit system. Quantum Inf. Process. 2019, 18, 367. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Mohamed, A.B.; Metwally, N. Nonclassical features of two SC-qubit system interacting with a coherent SC-cavity. Phys. E 2018, 102, 1–7. [Google Scholar] [CrossRef]
- Hu, M.L.; Wang, X.M.; Fan, H. Hierarchy of the nonlocal advantage of quantum coherence and Bell nonlocality. Phys. Rev. A 2018, 98, 032317. [Google Scholar] [CrossRef]
- Genovese, M.; Gramegna, M. Quantum correlations and quantum non-locality: A review and a few new ideas. Appl. Sci. 2019, 9, 5406. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef]
- Metwally, N.; Abdel-Aty, M. Quantum deficits and correlations of two superconducting charge qubits. Phys. C 2009, 469, 111–115. [Google Scholar] [CrossRef]
- Bang-Fu, D.; Xiao-Yun, W.; He-Ping, Z. Quantum and classical correlations for a two-qubit X structure density matrix. Chin. Phys. B 2011, 20, 100302. [Google Scholar]
- Gårding, E.R.; Schwaller, N.; Chan, C.L.; Chang, S.Y.; Bosch, S.; Gessler, F.; Laborde, W.R.; Hernandez, J.N.; Si, X.; Dupertuis, M.A.; et al. Bell Diagonal and Werner state generation: Entanglement, non-locality, steering and discord on the IBM quantum computer. Entropy 2021, 23, 797. [Google Scholar] [CrossRef]
- Dai, H.; Luo, S. Information-theoretic approach to atomic spin nonclassicality. Phys. Rev. A 2019, 100, 062114. [Google Scholar] [CrossRef]
- Ghorbani, M.; Faghihi, M.J.; Safari, H. Wigner function and entanglement dynamics of a two-atom two-mode nonlinear Jaynes–Cummings model. JOSA B 2017, 34, 1884–1893. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, Y. Quantifying nonclassicality via Wigner-Yanase skew information. Phys. Rev. A 2019, 100, 032116. [Google Scholar] [CrossRef]
- Dai, H.; Fu, S.; Luo, S. Atomic nonclassicality in the Jaynes-Cummings model. Phys. Lett. A 2020, 384, 126371. [Google Scholar] [CrossRef]
- Abd-Rabbou, M.; Metwally, N.; Ahmed, M.; Obada, A.S. Wigner distribution of accelerated tripartitew-state. Optik 2020, 208, 163921. [Google Scholar] [CrossRef]
- Chen, Z. Wigner-Yanase skew information as tests for quantum entanglement. Phys. Rev. A 2005, 71, 052302. [Google Scholar] [CrossRef]
- Yu, C.s. Quantum coherence via skew information and its polygamy. Phys. Rev. A 2017, 95, 042337. [Google Scholar] [CrossRef]
- Li, L.; Wang, Q.W.; Shen, S.Q.; Li, M. Measurement-induced nonlocality based on Wigner-Yanase skew information. EPL Europhys. Lett. 2016, 114, 10007. [Google Scholar] [CrossRef]
- Abdalla, M.S.; Khalil, E.; Obada, A.F. Exact treatment of the Jaynes–Cummings model under the action of an external classical field. Ann. Phys. 2011, 326, 2486–2498. [Google Scholar] [CrossRef]
- James, D.; Jerke, J. Effective Hamiltonian theory and its applications in quantum information. Can. J. Phys. 2007, 85, 625–632. [Google Scholar] [CrossRef]
- Wigner, E.P.; Yanase, M.M. Information contents of distributions. Proc. Natl. Acad. Sci. USA 1963, 49, 910–918. [Google Scholar] [CrossRef]
- Moya-Cessa, H. Decoherence in atom–field interactions: A treatment using superoperator techniques. Phys. Rep. 2006, 432, 1–41. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Fran ça Santos, M.; Solano, E.; de Matos Filho, R.L. Conditional Large Fock State Preparation and Field State Reconstruction in Cavity QED. Phys. Rev. Lett. 2001, 87, 093601. [Google Scholar] [CrossRef]
- Luo, S. Wigner-Yanase Skew Information and Uncertainty Relations. Phys. Rev. Lett. 2003, 91, 180403. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).