A Multi-Category Inverse Design Neural Network and Its Application to Diblock Copolymers

Abstract

In this work, we design a multi-category inverse design neural network to map ordered periodic structures to physical parameters. The neural network model consists of two parts, a classifier and Structure-Parameter-Mapping (SPM) subnets. The classifier is used to identify structures, and the SPM subnets are used to predict physical parameters for desired structures. We also present an extensible reciprocal-space data augmentation method to guarantee the rotation and translation invariant of periodic structures. We apply the proposed network model and data augmentation method to two-dimensional diblock copolymers based on the Landau–Brazovskii model. Results show that the multi-category inverse design neural network has high accuracy in predicting physical parameters for desired structures. Moreover, the idea of multi-categorization can also be extended to other inverse design problems.

1. Introduction

Material properties are mainly determined by microscopic structures. Therefore, to obtain satisfactory properties, how to find desired structures is very important in material design. The formation of ordered structures directly relies on physical conditions, such as temperature, pressure, molecular components, and geometry confinement. However, the relationship between ordered structures and physical conditions is extremely complicated and diversified. A traditional approach is a trial-and-error manner, i.e., passively finding ordered structures for given physical conditions. This approach, in terms of solving the direct problem, is time-consuming and expensive. A wise way is an inverse design that turns to find physical conditions for desired structures.

In this work, we are concerned about the theoretical development of the inverse design method for block copolymers. Block copolymer systems are important materials in industrial applications since they can self-assemble into innumerous ordered structures. There are many approaches for solving the direct problem of block copolymer systems, such as the first principle calculation [1], Monte Carlo simulation [2,3], molecular dynamics [4], dissipative particle dynamics [5,6], self-consistent field simulation [7], and density functional theory [8]. In the past decades, a directed self-assembly (DSA) method has been developed to invert design block copolymers. Liu et al. [9] presented an integration scheme of a block-copolymer-directed assembly with 193 nm immersion lithography, and provided a pattern quality that was comparable with existing double patterning techniques. Suh et al. [10] obtained nanopatterns via DSA of block copolymer films with a vapor-phase-deposited topcoat. Many DSA strategies have been also developed for the fabrication of ordered square patterns to satisfy the demand for lithography in semiconductors [11,12,13,14].

With the rise of data science and machine learning, many deep-learning inverse design methods have been developed to learn the mapping between structures and physical parameters [15,16,17,18]. These new techniques and methods are beginning to be used to study block copolymers. Yao et al. combined machine learning with self-consistent field theory (SCFT) to accelerate the exploration of parameter space for block copolymers [19]. Lin and Yu designed a deep learning solver inspired by physical-informed neural networks to tackle the inverse discovery of the interaction parameters and the embedded chemical potential fields for an observed structure [20]. Based on the idea of classifying first and fitting later, Katsumi et al. estimated Flory–Huggins interaction parameters of diblock copolymers from cross-sectional images of phase-separated structures [21]. The phase diagrams of block copolymers could be predicted by combining the deep learning technique and SCFT [22,23].

In this work, we propose a new neural network to address inverse design problem based on the idea of multi-categorization. We take the AB diblock copolymer system as an example to demonstrate the performance of our network. The training and test datasets are generated from the Landau–Brazovskii (LB) model [24]. The LB model is an effective tool to describe the phases and phase transition of diblock copolymers [25,26,27,28,29]. Let $\varphi \left(\mathit{r}\right)$ be the order parameter, a function of spatial position $\mathit{r}$, which represents the density distribution of diblock copolymers. The free energy functional of the LB model is

$$E\left(\varphi \left(\mathit{r}\right)\right)=\frac{1}{\left|\mathsf{\Omega }\right|}{\int }_{\mathsf{\Omega }}\left\{\frac{{\xi }^2}{2}{\left[(\Delta +1)\varphi \right]}^2+\frac{\tau }{2!}{\varphi }^2-\frac{\gamma }{3!}{\varphi }^3+\frac{1}{4!}{\varphi }^4\right\}d\mathit{r},$$

(1)

where $\varphi \left(\mathit{r}\right)$ satisfies the mass conservation $\frac{1}{\left|\mathsf{\Omega }\right|}{\int }_{\mathsf{\Omega }}\varphi \left(\mathit{r}\right)\mathrm{d}\mathit{r}=0$ and $\mathsf{\Omega }$ is the system volume. The model parameters in (1) are associated to physical conditions of diblock copolymers. Concretely, $\tau$ is a temperature-like parameter related to the Flory–Huggins interaction parameter, the degree of polymerization N, and the A monomer fraction f of each diblock copolymer chain. $\tau$ can control the onset of the order–disorder spinodal decomposition. The disordered phase becomes unstable at $\tau =0$. $\gamma$ is associated with f and N; it is nonzero only if the AB diblock copolymers chain is asymmetric. $\xi$ is the bare correlation length. Further relationships can be found in [25,26,27,28,29]. The stationary states of the LB free energy functional correspond to ordered structures.

The rest of the paper is organized as follows. In Section 2, we solve the LB model (1) to obtain datasets. In Section 3, we present the multi-category inverse design neural network and the reciprocal-space data augmentation method for periodic structures. In Section 4, we take the diblock copolymer system confined in two dimensions as an example to test the performance of our proposed inverse design neural network model. In Section 5, we draw a brief summary of this work.

2. Direct Problem

Solving the direct problem involves optimizing the LB free energy functional (1) to obtain stationary states corresponding to ordered structures:

$$\underset{\varphi \left(\mathit{r}\right)}{min}E\left(\varphi \left(\mathit{r}\right)\right),\mathrm{s}.\mathrm{t}.\frac{1}{\left|\mathsf{\Omega }\right|}{\int }_{\mathsf{\Omega }}\varphi \left(\mathit{r}\right)\mathrm{d}\mathit{r}=0.$$

(2)

Here, we only consider periodic structures. Therefore, we can apply the Fourier pseudospectral method to discretize the above optimization problem.

2.1. Fourier Pseudospectral Method

For a periodic order parameter $\varphi \left(\mathit{r}\right)$, $\mathit{r}\in \mathsf{\Omega }:={\mathbb{T}}^d={\mathbb{R}}^d/\mathit{A}{\mathbb{Z}}^d$, where $\mathit{A}=\left({\mathit{a}}_1,{\mathit{a}}_2,\dots ,{\mathit{a}}_d\right)$$\in {\mathbb{R}}^{d\times d}$ is the primitive Bravis lattice. The primitive reciprocal lattice $\mathit{B}=\left({\mathit{b}}_1,{\mathit{b}}_2,\dots ,{\mathit{b}}_d\right)\in {\mathbb{R}}^{d\times d}$, satisfying the dual relationship

$$\begin{array}{c}\hfill \mathit{A}{\mathit{B}}^T=2\pi \mathit{I}.\end{array}$$

(3)

The order parameter $\varphi \left(\mathit{r}\right)$ can be expanded as

$$\begin{array}{c}\hfill \varphi \left(\mathit{r}\right)=\sum _{\mathit{k}\in {\mathbb{Z}}^d}\widehat{\varphi }\left(\mathit{k}\right)e^{i{\left(\mathit{B}\mathit{k}\right)}^T\mathit{r}},\mathit{r}\in {\mathbb{T}}^d,\end{array}$$

(4)

where the Fourier coefficient

$$\begin{array}{c}\hfill \widehat{\varphi }\left(\mathit{k}\right)=\frac{1}{|{\mathbb{T}}^d|}{\int }_{{\mathbb{T}}^d}\varphi \left(\mathit{r}\right)e^{-i{\left(\mathit{B}\mathit{k}\right)}^T\mathit{r}}d\mathit{r},\end{array}$$

(5)

$|{\mathbb{T}}^d|$ is the volume of ${\mathbb{T}}^d$.

We define the discrete grid set as

$$\begin{array}{c}\hfill {\mathbb{T}}_N^d=\left\{(r_{1,j_1},r_{2,j_2},...,r_{d,j_d})=\mathit{A}{\left(j_1/N,j_2/N,...,j_d/N\right)}^T,0\le j_i<N,j_i\in \mathbb{Z},i=1,2,...,d\right\},\end{array}$$

(6)

where the number of elements of ${\mathbb{T}}_N^d$ is $M=N^d$. Denote the grid periodic function space ${\mathcal{G}}_N$ = {$f:{\mathbb{T}}_N^d\mapsto \mathbb{C}$, f is periodic}. For any periodic grid functions $F,G\in {\mathcal{G}}_N$, the ${\ell }^2$-inner product is defined as

$$\begin{array}{c}\hfill {\langle F,G\rangle }_N=\frac{1}{M}\sum _{{\mathit{r}}_j\in {\mathbb{T}}_N^d}F\left({\mathit{r}}_j\right)\overline{G}\left({\mathit{r}}_j\right).\end{array}$$

(7)

The discrete reciprocal space is

$$\begin{array}{c}\hfill {\mathbb{K}}_N^d=\left\{\mathit{k}={\left(k_j\right)}_{j=1}^d\in {\mathbb{Z}}^d:-N/2\le k_j<N/2\right\},\end{array}$$

(8)

and the discrete Fourier coefficients of $\varphi \left(\mathit{r}\right)$ in ${\mathbb{T}}_N^d$ can be represented as

$$\begin{array}{c}\hfill \widehat{\varphi }\left(\mathit{k}\right)={\langle \varphi \left({\mathit{r}}_j\right),e^{i{\left(\mathit{Bk}\right)}^T{\mathit{r}}_j}\rangle }_N=\frac{1}{M}\sum _{{\mathit{r}}_j\in {\mathbb{T}}_N^d}\varphi \left({\mathit{r}}_j\right)e^{-i{\left(\mathit{B}\mathit{k}\right)}^T{\mathit{r}}_j},\mathit{k}\in {\mathbb{K}}_N^d.\end{array}$$

(9)

For $\mathit{k}\in {\mathbb{Z}}^d$ and $\mathit{l}\in {\mathbb{Z}}^d$, we have the discrete orthogonality

$$\begin{array}{c}\hfill {\langle e^{i{\left(\mathit{Bk}\right)}^T{\mathit{r}}_{\mathit{j}}},e^{i{\left(\mathit{Bl}\right)}^T{\mathit{r}}_{\mathit{j}}}\rangle }_N=\left\{\begin{array}{cc}1,& \mathit{k}=\mathit{l}+N\mathit{m},\mathit{m}\in {\mathbb{Z}}^d,\\ 0,& otherwise.\end{array}\right.\end{array}$$

(10)

Therefore, the discrete Fourier transform of $\varphi \left({\mathit{r}}_{\mathit{j}}\right)$ is

$$\begin{array}{c}\hfill \varphi \left({\mathit{r}}_j\right)=\sum _{\mathit{k}\in {\mathbb{K}}_N^d}\widehat{\varphi }\left(\mathit{k}\right)e^{i{\left(\mathit{B}\mathit{k}\right)}^T{\mathit{r}}_j},{\mathit{r}}_j\in {\mathbb{T}}_N^d.\end{array}$$

(11)

The $N^d$-order trigonometric polynomial is

$$\begin{array}{c}\hfill I_N\varphi \left(\mathit{r}\right)=\sum _{\mathit{k}\in {\mathbb{K}}_N^d}\widehat{\varphi }\left(\mathit{k}\right)e^{i{\left(\mathit{B}\mathit{k}\right)}^T\mathit{r}},\mathit{r}\in {\mathbb{T}}^d.\end{array}$$

(12)

Then, for ${\mathit{r}}_j\in {\mathbb{T}}_N^d$, we have $\varphi \left({\mathit{r}}_j\right)\approx I_N\varphi \left({\mathit{r}}_j\right)$.

Due to the orthogonality (10), the LB energy functional $E\left(\varphi \right)$ can be discretized as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill E_h\left[\widehat{\mathsf{\Phi }}\right]& =\frac{{\xi }^2}{2}\sum _{{\mathit{h}}_1+{\mathit{h}}_2=\mathbf{0}}{\left[1-{\left(\mathit{B}{\mathit{h}}_1\right)}^T\left(\mathit{B}{\mathit{h}}_2\right)\right]}^2\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right)+\frac{\tau }{2!}\sum _{{\mathit{h}}_1+{\mathit{h}}_2=\mathbf{0}}\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right)\hfill \\ & -\frac{\gamma }{3!}\sum _{{\mathit{h}}_1+{\mathit{h}}_2+{\mathit{h}}_3=\mathbf{0}}\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right)\widehat{\varphi }\left({\mathit{h}}_3\right)\hfill \\ & +\frac{1}{4!}\sum _{{\mathit{h}}_1+{\mathit{h}}_2+{\mathit{h}}_3+{\mathit{h}}_4=\mathbf{0}}\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right)\widehat{\varphi }\left({\mathit{h}}_3\right)\widehat{\varphi }\left({\mathit{h}}_4\right),\hfill \end{array}\end{array}$$

(13)

where ${\mathit{h}}_i\in {\mathbb{K}}_N^d$, $i=1,2,3,4$, and $\widehat{\mathsf{\Phi }}={\left({\widehat{\varphi }}_1,{\widehat{\varphi }}_2,\dots ,{\widehat{\varphi }}_M\right)}^T\in {\mathbb{C}}^M$. The convolutions in the above expression can be efficiently calculated through the fast Fourier transform (FFT). Moreover, the mass conservation constraint $\frac{1}{\left|\mathsf{\Omega }\right|}{\int }_{\mathsf{\Omega }}\varphi \left(\mathit{r}\right)\mathrm{d}\mathit{r}=0$ is discretized as

$$\begin{array}{c}\hfill e^T\widehat{\mathsf{\Phi }}=0,\end{array}$$

(14)

where $e={(1,0,...,0)}^T\in {\mathbb{R}}^M$. Therefore, (2) reduces to a finite dimensional optimization problem

$$\begin{array}{c}\hfill \underset{\widehat{\mathsf{\Phi }}\in {\mathbb{C}}^{\mathrm{M}}}{min}{E}_h\left[\widehat{\mathsf{\Phi }}\right]=G_h\left[\widehat{\mathsf{\Phi }}\right]+F_h\left[\widehat{\mathsf{\Phi }}\right],\mathrm{s}.\mathrm{t}.e^T\widehat{\mathsf{\Phi }}=0,\end{array}$$

(15)

where $G_h$ and $F_h$ are the discretized interaction and bulk energies

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill G_{\mathit{h}}\left(\widehat{\mathsf{\Phi }}\right)& =\frac{{\xi }^2}{2}\sum _{{\mathit{h}}_1+{\mathit{h}}_2=\mathbf{0}}{\left[1-{\left(\mathit{B}{\mathit{h}}_1\right)}^T\left(\mathit{B}{\mathit{h}}_2\right)\right]}^2\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right),\hfill \\ \hfill F_{\mathit{h}}\left(\widehat{\mathsf{\Phi }}\right)& =\frac{\tau }{2!}\sum _{{\mathit{h}}_1+{\mathit{h}}_2=\mathbf{0}}\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right)-\frac{\gamma }{3!}\sum _{{\mathit{h}}_1+{\mathit{h}}_2+{\mathit{h}}_3=\mathbf{0}}\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right)\widehat{\varphi }\left({\mathit{h}}_3\right)\hfill \\ & +\frac{1}{4!}\sum _{{\mathit{h}}_1+{\mathit{h}}_2+{\mathit{h}}_3+{\mathit{h}}_4=\mathbf{0}}\widehat{\varphi }\left({\mathit{h}}_1\right)\widehat{\varphi }\left({\mathit{h}}_2\right)\widehat{\varphi }\left({\mathit{h}}_3\right)\widehat{\varphi }\left({\mathit{h}}_4\right).\hfill \end{array}\end{array}$$

(16)

In the work, we employ the adaptive APG method to solve (15).

2.2. Phase Diagram

Given parameters $[\gamma ,\tau ]$, we can obtain the stationary states by solving the free energy functional $\left(16\right)$. Due to the non-convexity of LB free energy functional, there are many, even infinite stationary states for given parameters. We need to determine the stationary state with the lowest energy, which corresponds to the most probable ordered structure observed in experiments. It requires comparing the energies of stationary states to obtain the stable structure and constructing a phase diagram. In the following, we consider disordered (DIS), cylindrical hexagonal (HEX), lamellar (LAM), body-centered cubic (BCC), and double gyroid (DG) phases as candidate structures. We use the AGPD software [30] to produce a $(\tau ,\gamma )$-plane phase diagram, as shown in Figure 1. The obtained phase diagram is consistent with previous work [29,31,32].

3. Inverse Design Neural Network

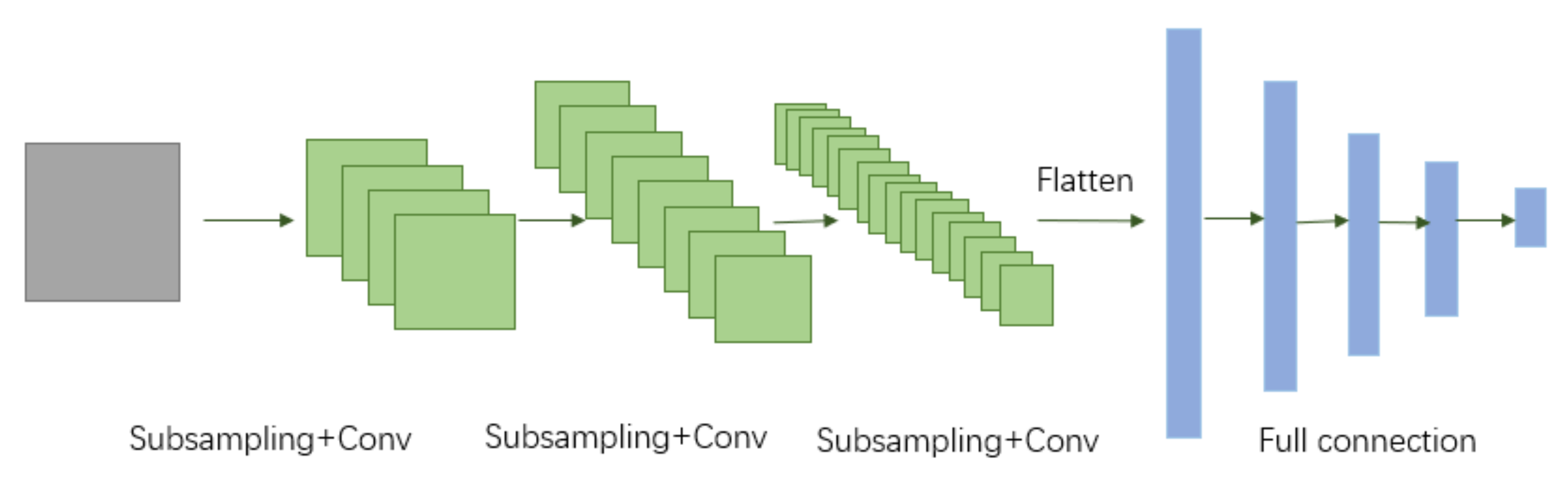
3.1. Multi-Category Inverse Design Network

The architecture of the multi-category inverse design network for predicting physical parameters for the desired periodic structure is shown in Figure 2. The neural network mainly consists of two modules: a classifier and SPM subnets. The former (orange block) identifies and classifies candidate structures, and the latter (blue block) including a family of subnets is a mapping connecting physical parameters and ordered structures.

According to the characteristics of the problem, we can design corresponding network architectures of classifier and SPM subnets. In this work, the classifier and each SPM subnet use the same network architecture as shown in Figure 3. Concretely, the network contains an input layer, three convolutional layers, three max-pooling layers, four fully connected layers, and an output layer. For the classifier network, the size of the output layer represents the number of categories, while for each subnet, it means the number of predicted physical parameters. The network architecture is a development of the Lenet-5 network [33].

3.2. Computational Complexity

In this subsection, we analyze the computational complexity of the network architecture of the classifier and each SPM subnet. As shown in Figure 3, the network consists of three parts:

• Convolution. The computational amount of a convolution layer is $O((2·C_{\mathrm{in}}·k^2-1)·H·W·C_{\mathrm{out}})$, where $k^2$ is the size of the convolution kernel. $C_{\mathrm{in}}$ and $C_{\mathrm{out}}$ represent the number of channels of the previous layer and the current layer. H and W are the height and width of the current layer.
• Max-pooling. The computational amount of a pooling layer is $O(C_{\mathrm{in}}·k^2·H·W·C_{\mathrm{out}})$, where $k^2$ is the size of the pooling kernel. $C_{\mathrm{in}}$ and $C_{\mathrm{out}}$ represent the number of channels of the previous layer and the current layer. H and W are the height and width of the current layer.
• Full connection. The computational amount of a fully connected layer is $O(2·N_{\mathrm{in}}·N_{\mathrm{out}})$, where $N_{\mathrm{in}}$ and $N_{\mathrm{out}}$ represent the dimensionality of the previous layer and the current layer.

3.3. Reciprocal-Space Data Augmentation (RSDA) Method

Generally, the ability of a network depends not only on its architecture, but also on the amount and properties of data. Due to the rotation and translation invariance of periodic structures, how to make the classifier recognize the invariance is very important. Here, we use a data augmentation method to increase the amount of data. Existing data augmentation methods, such as Swapping, Mixup, Insertion, and Substitution, are often used for classification tasks, see a recent review [34] and the references therein. However, as the dataset increases, these data augmentation approaches might become expensive, and it would be easy to use the wrong labels to train the network. For one-dimensional periodic phases, Yao et al. [19] used a Period-Filling method for data augmentation. However, this approach is difficult to extend to higher dimensions.

In this paper, we propose an extensible data augmentation method implemented in reciprocal space called the RSDA method. For a periodic structure, the primary wave vectors in the reciprocal space can describe the main features of the structure. The RSDA method uses the information of the primary wave vectors for data augmentation. We denote the fundamental domain of periodic structure $\varphi \left(\mathit{r}\right)$ as $\mathsf{\Omega }=\{{\sum }_{j=1}^d{\zeta }_j{\mathit{a}}_j,{\mathit{a}}_j\in {\mathbb{R}}^d,{\zeta }_j\in [0,1)\}$. For any translation $\mathit{t}\in {\mathbb{R}}^d$, $\mathit{t}/\mathit{A}{\mathbb{Z}}^d\in \mathsf{\Omega }$; therefore, we only need to consider the translation in the fundamental domain $\mathsf{\Omega }$. From the Fourier expansion $\left(12\right)$, and for rotation matrix $\mathit{R}\in SO\left(d\right)$, $\mathit{t}\in \mathsf{\Omega }$, we have

$$\begin{array}{cc}\hfill \varphi (\mathit{R}\mathit{r}+\mathit{t})& =\sum _{\mathit{h}\in {\mathbb{K}}_N^d}\widehat{\varphi }\left(\mathit{h}\right)e^{i{\left(\mathit{B}\mathit{h}\right)}^T(\mathit{R}\mathit{r}+\mathit{t})}\hfill \\ \hfill & =\sum _{\mathit{h}\in {\mathbb{K}}_N^d}\widehat{\varphi }\left(\mathit{h}\right)e^{i{\left(\mathit{B}\mathit{h}\right)}^T\mathit{t}}{e}^{i{\left(\tilde{\mathit{B}}\mathit{h}\right)}^T\mathit{r}}\hfill \\ \hfill & =\sum _{\mathit{h}\in {\mathbb{K}}_N^d}\tilde{\varphi }\left(\mathit{h}\right)e^{i{\left(\tilde{\mathit{B}}\mathit{h}\right)}^T\mathit{r}}\hfill \end{array}$$

(17)

where $\tilde{\mathit{B}}={\mathit{R}}^T\mathit{B}$ is a new reciprocal lattice by rotation transformation and $\tilde{\varphi }\left(\mathit{h}\right)=\widehat{\varphi }\left(\mathit{h}\right)e^{i{\left(\mathit{B}\mathit{h}\right)}^T\mathit{t}}$ is a new Fourier coefficient associated with translation transformation. Obviously, the RSDA method is easy to implement, and can be suitable for arbitrary dimensional periodic structures.

4. Application

In this section, we apply the multi-category network model to diblock copolymers confined on a two-dimensional plane to obtain the mapping from periodic structure to physical parameters. Besides, we compare the approximation accuracy and computational time of forecasting parameters. All the experiments in this section are conducted on a workstation equipped with two Intel(R) Xeon(R) Silver 4214 CPUs @ 2.20 GHz with 128 GB RAM. As the phase diagram shows, in two dimensions, only LAM and HEX phases are thermodynamic stable. Therefore, the SPM has two subnets, i.e., LAM and HEX subnets. As shown in Figure 4, the classifier is used to distinguish LAM or HEX phase after inputting the order parameter $\varphi$. For desired structures, LAM and HEX subnets are used to predict the physical parameters $({\tau }^{*},{\gamma }^{*})$. The dataset required for the classifier consists of ${\left\{({\varphi }_j,y_j)\right\}}_{j=1}^N$, where $y_j$ is the label, and for each SPM subnet, consists of ${\left\{({\varphi }_j,({\tau }_j^{*},{\gamma }_j^{*}))\right\}}_{j=1}^N$; N is the size of training data.

Table 1. Network parameters of classifier and each subnet. The notations of parameters in the table are as follows: in channels (i), out channels (o), kernel size (k), stride (s), padding (p), batch size (Nb).

Layer Type	Output Shape	Layer Type	Output Shape
Conv2d $(\mathrm{i}=1,\mathrm{o}=4,\mathrm{k}=5,\mathrm{p}=2,\mathrm{s}=1)$	$\left({\mathrm{N}}_{\mathrm{b}},4,40,40\right)$		Connect left
MaxPool2d $(\mathrm{k}=2,\mathrm{s}=2)$	$\left({\mathrm{N}}_{\mathrm{b}},4,20,20\right)$	Reshape	$\left({\mathrm{N}}_{\mathrm{b}},256\right)$
Conv2d $(\mathrm{i}=4,\mathrm{o}=8,\mathrm{k}=5,\mathrm{p}=2,\mathrm{s}=1)$	$\left({\mathrm{N}}_{\mathrm{b}},8,20,20\right)$	Fully connected	$\left({\mathrm{N}}_{\mathrm{b}},128\right)$
MaxPool2d $(\mathrm{k}=2,\mathrm{s}=2)$	$\left({\mathrm{N}}_{\mathrm{b}},8,10,10\right)$	Fully connected	$\left({\mathrm{N}}_{\mathrm{b}},64\right)$
Conv2d $(\mathrm{i}=8,\mathrm{o}=16,\mathrm{k}=5,\mathrm{p}=1,\mathrm{s}=1)$	$\left({\mathrm{N}}_{\mathrm{b}},16,8,8\right)$	Fully connected	$\left({\mathrm{N}}_{\mathrm{b}},10\right)$
MaxPool2d $(\mathrm{k}=5,\mathrm{s}=1)$	$\left({\mathrm{N}}_{\mathrm{b}},16,4,4\right)$	Fully connected	$\left({\mathrm{N}}_{\mathrm{b}},2\right)$

shows the network parameters of the classifier and SPM subnets. In all networks, the size of the output layer is 2. We adopt the ReLU function as the activation function and the Adam optimizer with a learning rate of ${10}^{-4}$ to train the neural network model. Kaiming_uniform [35] is used to initialize the network parameters both in tje classifier and subnets. We set the maximum epoch to be 20,000 and stop training if the error on the validation set decreases to ${10}^{-5}$ to prevent overfitting. For the classifier, the loss function is defined as

$$\begin{array}{c}\hfill L=\frac{1}{N}\sum _{i=1}^N-\left[y_i·log\left(p_i\right)+\left(1-y_i\right)·log\left(1-p_i\right)\right],\end{array}$$

(18)

where $y_i$ represents the label of the sample, LAM phase is 0, and HEX phase is 1. $p_i$ is the probability of identifying HEX phase. For each SPM subnet, the loss function is

$$\begin{array}{c}\hfill MSE=\frac{1}{N}\sum _{i=1}^N{\left({\mathit{u}}_i-{\tilde{\mathit{u}}}_i\right)}^2,\end{array}$$

(19)

where ${\mathit{u}}_i=({\tau }^{*},{\gamma }^{*})$ are the targeted parameters and ${\tilde{\mathit{u}}}_i=(\tau ,\gamma )$ are the predicted parameters.

It is well known that the LAM and HEX phases have 2- and 6-fold symmetries, respectively. As shown in Figure 5a,b, the fundamental domain ${\mathsf{\Omega }}_{LAM}$ of the LAM phase is a square, while the fundamental domain ${\mathsf{\Omega }}_{HEX}$ of the HEX phase is a parallelogram region due to the 6-fold rotational symmetry. Their corresponding primitive Bravis lattice is

$${\mathit{A}}_{LAM}={\lambda }_1\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],{\mathit{A}}_{HEX}={\lambda }_2\left[\begin{array}{cc}1& cos(\pi /3)\\ 0& sin(\pi /3)\end{array}\right].$$

Lattice constants ${\lambda }_1$ and ${\lambda }_2$ depend on the model parameters.

Now, we construct the dataset of the LAM phase. We discrete the $\tau$-$\gamma$ phase space of the stable LAM phase with step size $[\Delta \tau ,\Delta \gamma ]=[0.008,0.02]$ to form the dataset $S_{LAM}^1$ for training and validation, and with step size $[\Delta \tau ,\Delta \gamma ]=[0.003,0.015]$ to form $S_{LAM}^2$ for testing. We randomly choose 627 parameter pairs as a group $G_{LAM}^1$ from $S_{LAM}^1$ to construct training and validation sets, and 262 parameter pairs as a group $G_{LAM}^2$ from $S_{LAM}^2$ to build the test set. Then, we generate LAM phases by solving the direct problem with each selected parameter pair in $G_{LAM}^2$ and $G_{LAM}^2$.

We augment data by rotation and translation. The rotation matrix is

$$\begin{array}{c}\hfill \mathit{R}=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right],\end{array}$$

(20)

where $\theta$ is the rotation angle. LAM phases have 2-fold rotational symmetry; therefore, $\theta \in [0,\pi )$. Figure 5c gives a sketch plot of rotating LAM phase in the reciprocal space. Concretely, we rotate 627 LAM phases in $G_{LAM}^1$ with $\theta ={\{j\pi /60\}}_{j=1}^{60}$ and translate them with $\mathit{t}={(i,i)}^{\top }\in {\mathsf{\Omega }}_{LAM},i\in \{0,0.2,0.4,0.6,0.8\}$. The dataset we obtained includes 188,100 LAM phases. We randomly split these samples into a training set and a validation set at a ratio of 4:1. In the group $G_{LAM}^2$, 262 LAM phases are rotated by $\theta \in \{3^{°}$, 7°, 19°, 20°, 27°, 34°, 78°, 80°, 82°, ${114}^{°}\}$ and translated by $\mathit{t}={(i,i)}^{\top },i\in \{0.17$, $0.37$, $0.51$, $0.65$, $0.73\}$ to form the test set.

Similarly, we construct a dataset of the HEX phase. The $\tau$-$\gamma$ domain of the stable HEX phase is discretized with step size $[\Delta \tau ,\Delta \gamma ]=[0.008,0.02]$ to form $S_{HEX}^1$ for training and validation, and with step size $[\Delta \tau ,\Delta \gamma ]=[0.003,0.015]$ to form $S_{HEX}^2$ for testing. We randomly choose 1600 parameter pairs as a group $G_{HEX}^1$ from $S_{HEX}^1$ to construct training and validation sets, and 300 parameter pairs as a group $G_{HEX}^2$ from $S_{HEX}^2$ to build the test set. We still obtain HEX phases by solving the direct problem for selected parameters.

Then, we augment the dataset by rotation and translation operators. The HEX phase has 6-fold rotational symmetry; therefore, the rotation angle $\theta$ in (20) belongs to $[0,\pi /3)$. An illustration of rotating HEX phase in the reciprocal space is shown in Figure 5d. Concretely, we discretize rotation angle $\theta ={\{j\pi /60\}}_{j=1}^{20}$ and select translation vector $\mathit{t}={(i,i)}^{\top }$ in ${\mathsf{\Omega }}_{HEX}$, $i\in \{0,0.2,0.4,0.6,0.8\}$, for processing each sample in $G_{HEX}^1$. This results in 16,000 HEX phases. We randomly divide them into a training set and a validation set with a ratio of 4:1. The generated dataset of 300 in $G_{HEX}^2$ is rotated by $\theta \in \{3^{°}$, 11°, 24°, 27°, 38°, 40°, 52°, 54°, ${59}^{°}\}$ and translated by $\mathit{t}={(i,i)}^T$, $i\in \{0.17$, $0.37$, $0.51$, $0.65$, $0.73\}$ to form the test set.

Some LAM and HEX phases under rotation and translation transformation are visually illustrated in Figure 6. The sizes of training, validation, and test sets for the classifier are given in

Table 2. Amount of training, validation, and test data for the classifier.

	Training Set	Validation Set	Test Set
Classifier	278,480	69,620	26,600

.

Figure 7 shows the training and validation loss of the classifier. One can find that the training and validation losses reach ${10}^{-7}$ and ${10}^{-8}$ at epoch = 5, respectively. The accuracy is defined as $\alpha ={\sum }_i{\mathit{M}}_{i,i}/{\sum }_{i,j}{\mathit{M}}_{i,j}$, where $\mathit{M}$ is the confusion matrix [21]—a visual table layout that reflects the predictions of the network. As shown in

Table 3. The confusion matrix of classifier at epoch = 5.

	Identified LAM	Identified HEX
Certain LAM	13,100	0
Certain HEX	0	13,500

, ${\mathit{M}}_{ij}$ denotes the number of i identified to be j, and $i,j\in \left\{\mathrm{LAM},\mathrm{HEX}\right\}$. These results show that the classifier can identify structures with 100% success.

We classify the training and validation data by the classifier and obtain 188,100 LAM and 160,000 HEX phases. Then, we adopt them as the training and validation data for each subnet. For the test data onto each subnet, we only consider the data translated by $\mathit{t}={(0.17,0.17)}^{\top }$ in the test set.

Table 4. Amount of training, validation, and test data for LAM and HEX subnets.

	Training Data	Validation Data	Test Data
LAM subnet	150,480	37,620	2620
HEX subnet	128,000	32,000	2700

indicates the size of the dataset for each SPM subnet.

Figure 8 presents the training and validation losses of SPM networks. We can see that the training loss of the LAM (HEX) subnet is $5.75\times {10}^{-5}$ ($1.16\times {10}^{-5}$) and the validation loss is $1.89\times {10}^{-5}$ ($8.30\times {10}^{-6}$) at epoch = 700 (1200).

We define the relative error

$$\mathcal{E}=\frac{{∥\mathbf{u}-\tilde{\mathbf{u}}∥}_{{\ell }^2}}{{∥\mathbf{u}∥}_{{\ell }^2}},$$

and the average relative error

$${\mathcal{E}}_{\mathrm{average}}=\frac{1}{N_{test}}\sum _{k=1}^{N_{\mathrm{test}}}\frac{{∥{\mathbf{u}}^k-{\tilde{\mathbf{u}}}^k∥}_{{\ell }^2}}{{∥{\mathbf{u}}^k∥}_{{\ell }^2}},$$

where $N_{\mathrm{test}}$ is the size of test data. The predicted accuracy of single sample is $(1-\mathcal{E})\times 100\%$, while the average accuracy is $(1-{\mathcal{E}}_{\mathrm{average}})\times 100\%$. Figure 9 illustrates the test accuracy of the LAM and HEX subnets. Results indicate that the accuracy of parameters prediction for a single sample can achieve $80\%\sim 100\%$, and the average prediction accuracy of LAM subnet (blue dashed line) is 84%. For the HEX subnet (pink dashed line), the average prediction accuracy can reach 91%.

We randomly select two test samples in the test set and input them into the network to predict the corresponding parameters. Next, we obtain structures corresponding to the predicted parameters by solving the direct problem. Figure 10 shows LAM and HEX phases with targeted and predicted parameters, and the absolute errors between the targeted and predicted phases. From Figure 10c,f, we can see that the absolute error of the LAM phase is ${10}^{-2}$ and of the HEX phase is ${10}^{-3}$. This also reflects a good fitting effect of SPM subnets.

Table 5. Training and test time for the classifier and each SPM subnet.

	Classifier	LAM Subnet	HEX Subnet
Training time	11.5 min	11.6 h	20.0 h
Test time	0.0078 s	0.0034 s	0.0074 s

shows the training time of the classifier and each SPM subnet, and the online calculation time of these networks when identifying structures or predicting parameters with one sample in the test set.

5. Conclusions

In this paper, we propose a multi-category neural network for the inverse design of ordered periodic structures. The proposed network can construct the mapping between phases and physical parameters. For periodic phases, we provide an extensible RSDA approach to augment data. Then, we apply these methods to the two-dimensional diblock copolymer system. The dataset is produced by the LB free energy functional. Experimental results show that the structure recognition accuracy of the classifier can reach 100% based on 26,600 randomly selected test data. Moreover, on a dataset consisting of 5320 randomly selected test data, the parameter prediction accuracy of the LAM phase reaches 84% and the accuracy of the HEX phase reaches 91%. The network model and RSDA method are applied to a two-dimensional problem; however, they can be extended to higher-dimensional inverse design problems.