Solving a Class of High-Order Elliptic PDEs Using Deep Neural Networks Based on Its Coupled Scheme

Abstract

Deep learning—in particular, deep neural networks (DNNs)—as a mesh-free and self-adapting method has demonstrated its great potential in the field of scientific computation. In this work, inspired by the Deep Ritz method proposed by Weinan E et al. to solve a class of variational problems that generally stem from partial differential equations, we present a coupled deep neural network (CDNN) to solve the fourth-order biharmonic equation by splitting it into two well-posed Poisson’s problems, and then design a hybrid loss function for this method that can make efficiently the optimization of DNN easier and reduce the computer resources. In addition, a new activation function based on Fourier theory is introduced for our CDNN method. This activation function can reduce significantly the approximation error of the DNN. Finally, some numerical experiments are carried out to demonstrate the feasibility and efficiency of the CDNN method for the biharmonic equation in various cases.

1. Introduction

In this paper, we consider the numerical solution of the biharmonic equation

$$\left\{\begin{array}{c}{\Delta }^{2}u\left(\mathit{x}\right)=f\left(\mathit{x}\right),\mathrm{in}\Omega ,\hfill \\ {\displaystyle u\left(\mathit{x}\right)=g\left(\mathit{x}\right),\mathrm{on}\partial \Omega ,}\hfill \\ \Delta u\left(\mathit{x}\right)=h\left(\mathit{x}\right),\mathrm{on}\partial \Omega ,\hfill \end{array}\right.$$

(1)

where $\Omega$ is a polygonal or polyhedral domain in Euclidean space $R^d$ (d is the dimension) with a piecewise Lipschitz boundary that satisfies an interior cone condition, $f\left(\mathit{x}\right)\in L^2(\Omega )$ is a given function and $\Delta$ is a standard Laplace operator. The operators $\Delta u\left(\mathit{x}\right)$ and ${\Delta }^{2}u\left(\mathit{x}\right)$ are expressed as

$$\Delta u\left(\mathit{x}\right)=\sum _{i=1}^d\frac{{\partial }^{2}u}{\partial x_i^2}\mathrm{and}{\Delta }^{2}u\left(\mathit{x}\right)=\sum _{i=1}^d\frac{{\partial }^{4}u}{\partial x_i^4}+\sum _{i=1}^d\sum _{j=1}^d\frac{{\partial }^{4}u}{\partial x_i^2{x}_j^2},$$

respectively.

A biharmonic equation is a class of common high-order partial differential equations (PDEs) that stems from the field of physics and applied mathematics, especially in elasticity theory and Stokes flow problems; for instance, scattered data fitting with thin plate splines [1], fluid mechanics [2,3] and linear elasticity [4,5]. In the last few decades, many traditional numerical methods have been proposed for dealing with (1), and they can be classified into two categories: a direct (uncoupled) approach and coupled (splitting, mixed) approach.

In terms of the direct approach, there are the finite difference method (FDM) based on its uncoupled scheme [6,7,8,9], finite volume method (FVM) [10,11,12], finite element method (FEM) based on its variational formulation, such as non-conforming FEM [13,14,15], and conforming FEM [16,17]. The idea of the coupled approach is to introduce auxiliary variables and split the biharmonic equation into two coupled Poisson equations. Based on this coupled scheme, the finite difference technique [9,18,19], finite element technique and mixed element technique [20,21,22,23,24] are naturally used to solve the two second-order equations. In addition, the collocation method [25,26,27] and radial basis functions (RBF) method [28,29,30] are also approaches considered to solve (1).

However, the traditional methods will encounter the curse of an irregular domain and high dimension. Deep learning, especially deep neural networks (DNNs), have expressed a remarkable performance in solving mathematical problems in scientific computations and engineering applications based on its great potential in nonlinear approximation; for example, utilizing DNNs to solve partial differential equations [31,32,33,34], stochastic differential equations [35], inverse problems [36], molecular modeling [37], etc. Specially, the Deep Ritz method (DRM) [32] and physical information neural network (PINN) [36] have gained more and more attention in PDEs, and they have made wonderful grades for solving various PDEs. Within the architectures of DRM and PINN, some DNN-based methods have been proposed to directly deal with this biharmonic Equation (1) [38,39,40,41,42,43]. Since these DNN-based methods need to compute the second-order or fourth-order derivative of the solution in $\Omega$ and the second-order derivative of the solution in $\partial \Omega$, they may consume a large amount of time and computer resources when solving (1). In addition, the authors in [44] proposed a deep mixed residual method (MIM) to solve PDEs with high-order derivatives by splitting it into some first-order systems; however, the PDEs solution and its derivatives share nearly the same DNN and boundary conditions, are not consistent with the mechanism of PDEs and adversely affect the performance of MIM.

In this paper, we investigate addressing the high-order elliptic Equation (1) by combining the Deep Ritz method and the coupled scheme of the biharmonic equation, and then establish a coupled deep neural network architecture (CDNN). Motivated by double triangle series and Fourier expansion, a new activation function with sine and cosine are provided for our CDNN model; it will improve the capability of DNN for approximating a complex target because of it being smooth and local. The application of a trigonometric function as an activation function can also be found in [45,46]. The main contributions of this paper are as follows:

• Based on the coupled scheme of the fourth-order biharmonic Equation (1), we constructed a CDNN architecture for dealing with (1) by means of the Deep Ritz method used to solve variational problems; this architecture is composed of two independent DNNs. Compared with the existing DNN methods, the CDNN will reduce effectively the complexity of the algorithm, save the resources of the computer and make the neural networks easier to train. In the meantime, this model performs remarkably well and obtains considerable results.
• According to the property of spectral bias or frequency preference for the DNN, we introduced a Fourier mapping with sine and cosine as the activation function of the first layer for the DNN model; it can mitigate the pathology of the spectral bias of the DNN. In the viewpoint of function approximation, the DNN model with Fourier mapping mimics the Fourier expansion, in which, the first layer with Fourier mapping can be regarded as a series of Fourier basic functions and the output of the DNN is the (nonlinear) combination of those basis functions.
• By introducing some compared DRM models with different activation functions to solve the original form of the biharmonic equation, we show that our CDNN model performs better when solving (1) in various dimensional space.

The paper is structured as follows. In Section 2, we briefly introduce the framework of the deep neural network and the formulation of ResNet. Then, in Section 3, we construct the CDNN architecture to approximate the solution of the biharmonic equation based on its coupled scheme and provide the options of the activation function. In Section 4, some numerical examples are carried out to test the performance of the developed CDNN model. Section 5 discusses the merits and shortcomings of the CDNN, and provides the opportunity to address related works. Finally, some brief conclusions are made in Section 6.

2. Deep Neural Network and ResNet Architecture

In this section, the related concepts and mathematical formulation of the DNN are briefly introduced. At first, a standard neural unit of a DNN with an input $\mathit{x}\in {\mathbb{R}}^d$ and an output $\mathit{y}\in {\mathbb{R}}^m$ is in the form of

$$\begin{array}{c}\hfill \mathit{y}=\sigma \circ (\mathit{W}\mathit{x}+\mathit{b})\end{array}$$

(2)

where $\mathit{W}=\left(w_{ij}\right)\in {\mathbb{R}}^{d\times m}$ and $\mathit{b}\in {\mathbb{R}}^m$ are called a weight matrix and bias vector, respectively. Here and thereafter, $\sigma$ is a non-linear operator, commonly known as the activation function, and “∘” stands for the elementary-wise operation. Generally, the output of (2) will be transformed by a new weight and a new bias, and the new output will be fed into another activation function. Hence, (2) is also called the hidden layer of the DNN. In other word, the DNN is a nested composition of sequential single linear functions and nonlinear activation functions. Mathematically, the DNN with an input datum $\mathit{x}\in {\mathbb{R}}^d$ and an output $\mathit{y}(\mathit{x};\mathit{\theta })$ can be formulated as

$$\left\{\begin{array}{c}{\mathit{y}}^{\left[0\right]}=\mathit{x}\hfill \\ {\mathit{y}}^{\left[l\right]}=\sigma \circ ({\mathit{W}}^{\left[l\right]}{\mathit{y}}^{[l-1]}+{\mathit{b}}^{\left[l\right]}),\mathrm{for}l=1,2,3,\cdots \cdots ,L\hfill \\ \mathit{y}(\mathit{x};\mathit{\theta })={\mathit{y}}^{\left[L\right]}\hfill \end{array}\right.$$

(3)

where ${\mathit{W}}^{\left[l\right]}\in {\mathbb{R}}^{m_{l+1}\times m_l},{\mathit{b}}^{\left[l\right]}\in {\mathbb{R}}^{m_{l+1}}$ are the weight matrix and bias vector of the l-th hidden layer, respectively, $m_0=d$ and $m_L$ is the dimension of the output for the DNN. For convenience, we denote the parameter set $\left({\mathit{W}}^{\left[L\right]},\cdots {\mathit{W}}^{\left[1\right]},{\mathit{W}}^{\left[0\right]},{\mathit{b}}^{\left[L\right]},\cdots {\mathit{b}}^{\left[1\right]},{\mathit{b}}^{\left[0\right]}\right)$ by $\mathit{\theta }$ here and thereafter.

The residual neural network (ResNet) technique [47] has been widely used in deep neural networks for solving PDEs; it can not onl skilfully overcome the vanishing gradient problem of DNN in backpropagation, but can also well improve the capacity of the DNN to approximate the solution and high-order derivatives of PDEs [32,37]. The architecture of ResNet is depicted in the following Figure 1.

Mathematically, a ResNet block with a one-step connection produces a filtered version ${\mathit{y}}^{[\ell +1]}(\mathit{x};\mathit{\theta })$ for the input ${\mathit{y}}^{[\ell ]}(\mathit{x};\mathit{\theta })$, which is as follows:

$${\mathit{y}}^{[\ell +1]}(\mathit{x};\mathit{\theta })={\mathit{y}}^{[\ell ]}(\mathit{x};\mathit{\theta })+\sigma \circ ({\mathit{W}}^{[\ell +1]}{\mathit{y}}^{[\ell ]}(\mathit{x};\mathit{\theta })+{\mathit{b}}^{[\ell +1]}).$$

In this work, we also employed the strategy of a one-step skip connection for two consecutive layers in the DNN if they have the same number of neurons. For those consecutive layers with different neuron numbers, the skip connection step is omitted.

3. Unified coupled DNNs Architecture to Biharmonic Equation

Skilfully decoupling the biharmonic Equation (1) into two Poisson equations, traditional numerical methods such as FEM and FDM obtain a favorable performance with a small number of computing resources and a lower time complexity. By introducing an auxiliary variable $w=-\Delta u$, one can rewrite the fourth-order Equation (1) into a couple of second-order equations:

$$\left\{\begin{array}{c}-\Delta w=f,\mathrm{in}\Omega \hfill \\ w=h,\mathrm{on}\partial \Omega \hfill \end{array}\right.\mathrm{and}\left\{\begin{array}{c}-\Delta u=w,\mathrm{in}\Omega \hfill \\ u=g,\mathrm{on}\partial \Omega \hfill \end{array}\right..$$

(4)

Then, we searched a couple of functions $(w,u)$ instead of finding a solution for the original problem (1). Generally, the strong solutions of (4) may be non-existent; one can obtain their weak solutions in the given domain $\Omega$. The weak function pair $(w,u)$ should satisfy $u,w\in {\mathbb{H}}_0^1(\Omega )$ and

$${\int }_{\Omega }(\nabla u·\nabla v-wv)d\mathit{x}=0\mathrm{and}{\int }_{\Omega }(\nabla w·\nabla \psi -f\psi )d\mathit{x}=0\mathrm{for}\mathrm{all}v,\psi \in {\mathbb{H}}_0^1(\Omega ).$$

They are equivalent to the weak version of the Euler–Lagrange equation for the following variational problems:

$$w=\underset{\psi \in {\mathbb{H}}_0^1(\Omega )}{min}{\mathcal{J}}_1\left(\psi \right)=\frac{1}{2}{\int }_{\Omega }{|\nabla \psi |}^{2}d\mathit{x}-{\int }_{\Omega }f\psi d\mathit{x}$$

(5)

and

$$u=\underset{v\in {\mathbb{H}}_0^1(\Omega )}{min}{\mathcal{J}}_2\left(v\right)=\frac{1}{2}{\int }_{\Omega }{|\nabla v|}^{2}d\mathit{x}-{\int }_{\Omega }wvd\mathit{x},$$

(6)

respectively.

The Deep Ritz method based on a deep neural network is an efficient approach for solving variational problems that generally stem from PDEs [32]; it utilizes a parameterized neural network to replace the trial function and changes the original problems into the optimization of neural networks. In addition, some works concerning convergence analysis for DRM are proposed [48,49].

Based on the above results, we then suppose two ansatzes of DNN $y_1(:,{\mathit{\theta }}_1)$ and $y_2(:,{\mathit{\theta }}_2)$ as the functions $\psi$ and v, which minimize the variational problem (5) and (6), respectively, where ${\mathit{\theta }}_1\in \Theta$ and ${\mathit{\theta }}_2\in \Theta$ denote the parameters of underlying DNNs. Substituting $y_1(:,{\mathit{\theta }}_1)$ into (5) for $\psi$, we can firstly obtain the following equation:

$$w\left(\mathit{x}\right)=\underset{y_1(\mathit{x},{\mathit{\theta }}_1),{\mathit{\theta }}_1\in \Theta }{argmin}\left[\frac{1}{2}{\int }_{\Omega }{|\nabla y_1(\mathit{x},{\mathit{\theta }}_1)|}^{2}d\mathit{x}-{\int }_{\Omega }f\left(\mathit{x}\right)y_1(\mathit{x},{\mathit{\theta }}_1)d\mathit{x}\right]\mathrm{for}\mathit{x}\in \Omega .$$

(7)

Since the minimization problem (5) is related to w and $y_1(\mathit{x},{\mathit{\theta }}_1)$ is an approximation of w, then we obtain the following equation by replacing v and w with $y_2(\mathit{x},{\mathit{\theta }}_1)$ and $y_1(\mathit{x},{\mathit{\theta }}_2)$, respectively, in (6):

$$u\left(\mathit{x}\right)=\underset{y_2(\mathit{x},{\mathit{\theta }}_2),{\mathit{\theta }}_2\in \Theta }{argmin}\left[\frac{1}{2}{\int }_{\Omega }{|\nabla y_2(\mathit{x},{\mathit{\theta }}_2)|}^{2}d\mathit{x}-{\int }_{\Omega }{y}_1(\mathit{x},{\mathit{\theta }}_1)y_2(\mathit{x},{\mathit{\theta }}_2)d\mathit{x}\right]\mathrm{for}\mathit{x}\in \Omega .$$

(8)

Using the Monte Carlo method [50] to calculate the above integration in $\Omega$, we further have

$${\mathit{\theta }}_1^{*}=\underset{{\mathit{\theta }}_1\in \Theta }{argmin}{L}_{in1}(S_I;{\mathit{\theta }}_1)\mathrm{and}{\mathit{\theta }}_2^{*}=\underset{{\mathit{\theta }}_2\in \Theta }{argmin}{L}_{in2}(S_I;{\mathit{\theta }}_2)$$

(9)

with

$$L_{in1}(S_I;{\mathit{\theta }}_1)=\frac{1}{n_{in}}\sum _{i=1}^{n_{in}}\left[\frac{1}{2}|\nabla y_1({\mathit{x}}_I^i,{\mathit{\theta }}_1){|}^2-f\left({\mathit{x}}_I^i\right)y_1({\mathit{x}}_I^i,{\mathit{\theta }}_1)\right]\mathrm{for}{\mathit{x}}_I^i\in S_I$$

(10)

and

$$L_{in2}(S_I;{\mathit{\theta }}_2)=\frac{1}{n_{in}}\sum _{i=1}^{n_{in}}\left[\frac{1}{2}|\nabla y_2({\mathit{x}}_I^i,{\mathit{\theta }}_2){|}^2-y_1({\mathit{x}}_I^i,{\mathit{\theta }}_1)y_2({\mathit{x}}_I^i,{\mathit{\theta }}_2)\right]\mathrm{for}{\mathit{x}}_I^i\in S_I,$$

(11)

respectively; here, and thereafter, $S_I$ stands for the samples in $\Omega$ with probability density ${\rho }_I$.

Boundary conditions are important constraints for numerical methods such as FDM and FEM to solve PDEs, which ensure the uniqueness and accuracy of the solution for PDEs. Analogously, imposing boundary conditions is also an important issue in DNN representation. Under the boundary constraints of (4), the DNNs $y_1(\mathit{x},{\mathit{\theta }}_1)$ and $y_2(\mathit{x},{\mathit{\theta }}_2)$ on $\partial \Omega$ should satisfy

$$L_{bd1}(S_B;{\mathit{\theta }}_1)=\frac{1}{n_{bd}}\sum _{j=1}^{n_{bd}}[y_1\left({\mathit{x}}_B^j,{\mathit{\theta }}_1\right)-h\left({\mathit{x}}_B^j\right){]}^2\to 0\mathrm{for}{\mathit{x}}_B^j\in S_B$$

(12)

and

$$L_{bd2}(S_B;{\mathit{\theta }}_1)=\frac{1}{n_{bd}}\sum _{j=1}^{n_{bd}}[y_2\left({\mathit{x}}_B^j,{\mathit{\theta }}_2\right)-g\left({\mathit{x}}_B^j\right){]}^2\to 0\mathrm{for}{\mathit{x}}_B^j\in S_B,$$

(13)

here, and thereafter, $S_B$ stands for the samples on $\partial \Omega$ with probability density ${\rho }_B$.

To this end, two individual parameters of DNNs model are optimized by minimizing the following loss function:

$$L(S_I,S_B;{\mathit{\theta }}_1,{\mathit{\theta }}_2)=L_1(S_I,S_B;{\mathit{\theta }}_1)+L_2(S_I,S_B;{\mathit{\theta }}_2)$$

(14)

with

$$L_1(S_I,S_B;{\mathit{\theta }}_1)=L_{in1}(S_I,{\mathit{\theta }}_1)+\gamma L_{bd1}(S_B;{\mathit{\theta }}_1)and{L}_2(S_I,S_B;{\mathit{\theta }}_2)=L_{in2}(S_I,{\mathit{\theta }}_2)+\gamma L_{bd2}(S_B;{\mathit{\theta }}_2)$$

where $S_I={\left\{{\mathit{x}}_I^i\right\}}_{i=1}^{n_{in}}$ and $S_B={\left\{{\mathit{x}}_B^j\right\}}_{j=1}^{n_{bd}}$ represent the training data of $\Omega$ and $\partial \Omega$, respectively. In addition, we introduce a penalty parameter $\gamma$ to control the contribution of the boundary for the loss function; it increases gradually as the training process continues.

Our goal is to find two sets of parameters ${\mathit{\theta }}_1$ and ${\mathit{\theta }}_2$ such that the approximate functions $y_1(·,{\mathit{\theta }}_1)$ and $y_2(·,{\mathit{\theta }}_2)$ minimize the functions $L_1(S_I,S_B;{\mathit{\theta }}_1),L_2(S_I,S_B;{\mathit{\theta }}_2)$ and $L(S_I,S_B;{\mathit{\theta }}_1,{\mathit{\theta }}_2)$. If these loss functions are small enough, then $y_1(\mathit{x},{\mathit{\theta }}_1)$ and $y_2(\mathit{x},{\mathit{\theta }}_2)$ will be very close to the solution of (4), i.e.,

$${\mathit{\theta }}_1^{*},{\mathit{\theta }}_2^{*}=\left\{\begin{array}{c}\underset{{\mathit{\theta }}_1\in \Theta }{argmin}{L}_1(S_I,S_B;{\mathit{\theta }}_1)\hfill \\ \underset{{\mathit{\theta }}_2\in \Theta }{argmin}{L}_2(S_I,S_B;{\mathit{\theta }}_2)\hfill \\ \underset{{\mathit{\theta }}_1,{\mathit{\theta }}_2\in \Theta }{argmin}L(S_I,S_B;{\mathit{\theta }}_1,{\mathit{\theta }}_2)\hfill \end{array}\right.⟺w\left(\mathit{x}\right)=y_1(\mathit{x},{\mathit{\theta }}_1^{*})\mathrm{and}u\left(\mathit{x}\right)=y_2(\mathit{x},{\mathit{\theta }}_2^{*}).$$

(15)

Remark 1. 

In practical implementation, we bundled $L_1(S_I,S_B;{\mathit{\theta }}_1)$, $L_2(S_I,S_B;{\mathit{\theta }}_2)$ and $L(S_I,S_B;{\mathit{\theta }}_1,{\mathit{\theta }}_2)$ together and trained them by means of a neural network optimizer. These functions in form are related, but they can be trained in parallel.

Remark 2. 

By directly transforming the biharmonic Equation (1) into a variational problem, one can easily employ DRM to solve it. The corresponding loss is given by

$$L(S_I,S_B;\mathit{\theta })=L_{in}(S_I;\mathit{\theta })+\gamma L_{bd}(S_B;\mathit{\theta })$$

with

$$L_{in}(S_I;\mathit{\theta })=\frac{1}{n_{in}}\sum _{i=1}^{n_{in}}\left[\frac{1}{2}|\Delta y({\mathit{x}}_I^i;\mathit{\theta }){|}^2-f\left({\mathit{x}}_I^i\right)y({\mathit{x}}_I^i;\mathit{\theta })\right]\mathit{for}{\mathit{x}}_I^i\in S_I,$$

and

$$L(S_B;\mathit{\theta })=\frac{1}{n_{bd}}\sum _{j=1}^{n_{bd}}[y\left({\mathit{x}}_B^j;\mathit{\theta }\right)-g\left({\mathit{x}}_B^j\right){]}^2+\frac{1}{n_{bd}}\sum _{j=1}^{n_{bd}}[\Delta y\left({\mathit{x}}_B^j;\mathit{\theta }\right)-h\left({\mathit{x}}_B^j\right){]}^2\to 0\mathit{for}{\mathit{x}}_B^j\in S_B,$$

where $y(·;\mathit{\theta })$ stands for the output of DRM.

In order to obtain the ${\mathit{\theta }}_1^{*}$ and ${\mathit{\theta }}_2^{*}$, one can update the parameters ${\mathit{\theta }}_1$ and ${\mathit{\theta }}_2$ by means of gradient descent (GD) or stochastic gradient descent (SGD) techniques over the training samples at each iteration. Regarding implementation, SGD is the common optimization method used for deep learning; it only requires the gradient information of a DNN over one or a few samples. In this context, the SGD is given by:

$${\mathit{\theta }}^{k+1}={\mathit{\theta }}^k-{\alpha }_k{\nabla }_{{\mathit{\theta }}^k}L(\mathit{x};{\mathit{\theta }}^k),\mathit{x}\in S_I\mathrm{or}{S}_B,$$

where the “learning rate” ${\alpha }_k$ decreases with k increasing and $\mathit{\theta }=\{{\mathit{\theta }}_1,{\mathit{\theta }}_2\}$. Based on the above discussions, Figure 2 describes the schematic of the CDNN for solving biharmonic Equation (1).

Many experiments have shown that choosing a suitable activation function is crucial for DNNs in various fields. As we have learned, nonlinear activation functions such as $\mathrm{ReLU}\left(\mathit{z}\right)=max\{0,\mathit{z}\}$, $\mathrm{Sigmoid}\left(\mathit{z}\right)$ and $tanh\left(\mathit{z}\right)$ are the common choice for the DNN model; they will improve the capacity of DNN to deal with various nonlinear problems, such as nonlinear PDEs and classification. Due to the biharmonic equation in this work being a class of high-order PDEs, an activation function with a low-order derivative possibly has an unfavourable effect for DNN when it is used to solve (1). We then consider the activation function with a good regularity, such as tanh. Figure 3 depicts the curves of the tanh function with first-order and second-order derivatives, which shows that the range of derivatives for tanh is small and stable.

In the viewpoint of function approximation, the first layer with activation functions for the DNN can be regarded as a series of basic functions, and the output of the DNN is the (nonlinear) combination of those basis functions. Recently, the works [51,52] found the phenomenon of spectral bias or frequency preference for DNNs and show that the DNN will firstly capture the low-frequency component, and then some corresponding explanations are made by means of a neural tangent kernel (NTK) [45,53] and Fourier analysis [54,55]. Within this sense of spectral bias and Fourier approximation, a given real function $\mathcal{F}\left(x\right)$ can be expressed by the following sine and cosine expansions:

$$\mathcal{F}\left(x\right)=\sum _{n=1}^{\tilde{N}}(S(cos\left({\omega }_{n}x\right);\tilde{\mathit{\theta }})+T(sin\left({\omega }_{n}x\right);\overline{\mathit{\theta }})),$$

where $S(x,\tilde{\mathit{\theta }}),T(x,\overline{\mathit{\theta }})$ are fully connected DNNs or sub-modules of the DNN, respectively, $\{{\omega }_0,{\omega }_1,{\omega }_2,\cdots \}$ are the frequencies of interest in the target function and $\omega =0$ will always be included. Obviously, it mimics the Fourier expansion, and the remaining blocks of the DNN (except for the first layer) are used to learn the coefficients of Fourier basis functions.

Choosing a Fourier feature mapping with sine and cosine as the activation function for the DNN model is reasonable; it can mitigate the pathology of spectral bias and enable networks to learn the target function well [45,46]. It is

$$\sigma \left(\mathit{z}\right)=\left[\begin{array}{c}cos\left(2\mathit{\kappa }\pi \mathit{z}\right)\\ sin\left(2\mathit{\kappa }\pi \mathit{z}\right)\end{array}\right],$$

(16)

where $\mathit{\kappa }$ is a user-specified vector (it is not trainable) and is consistent with the number of neural units in the first hidden layer for the DNN. By performing the Fourier feature mapping for input points, the input points in $\Omega$ may be mapped to $[-1,1]$; then, the subsequent modules of the DNN with different activation functions can easily deal with the feature information, such as sigmoid, tanh and ReLU, etc.

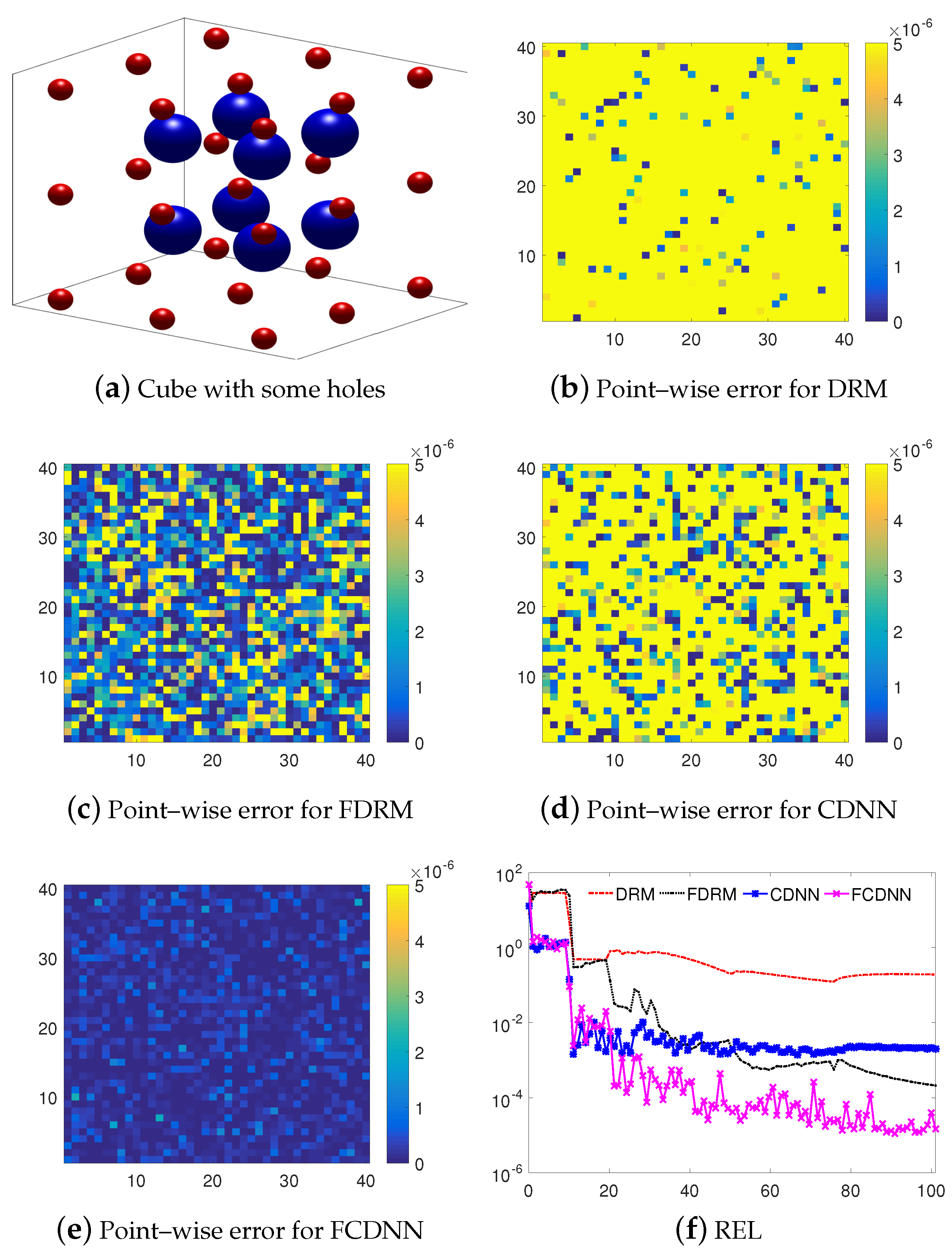
4. Numerical Experiments

4.1. Training Setup

In this section, we tested the performance of the CDNN model with the aforementioned activation functions (tanh and Fourier mapping) for solving the biharmonic equation in varying-dimensional spaces. In addition, two types of Deep Ritz methods with tanh and Fourier mapping were introduced to serve as the baseline. These compared methods and their setups are as follows:

• DRM: A normal DNN model with tanh being its activation function for all hidden layers and its output layer being linear.
• FDRM: A normal DNN model with Fourier mapping as the activation function for its first hidden layer, where its activation functions for the remainder hidden layers are chosen as tanh and its output layer is linear. The vector $\mathit{\kappa }$ as in (16) is set as $(0.25,0.5,0.75,1,\cdots ,9.75,10)$, and we will repeat it when the length of $\mathit{\kappa }$ is less than the number of neural units for the first hidden layer.
• CDNN: A coupled DNN model with tanh being its activation function for all hidden layers and its output layer being linear.
• FCDNN: A coupled DNN model with Fourier mapping as the activation function for its first hidden layer, where its activation functions for the remainder hidden layers are chosen as tanh and its output layer is linear. The vector $\mathit{\kappa }$ as in (16) is set as $(0.25,0.5,0.75,1,\cdots ,9.75,10)$, and we will repeat it when the length of $\mathit{\kappa }$ is less than the number of neural units for the first hidden layer.

We provide the following criteria to evaluate the above models:

$$\mathrm{REL}=\sum _{i=1}^{N^{\prime }}\frac{|\tilde{u}\left({\mathit{x}}^i\right)-u^{*}\left({\mathit{x}}^i\right){|}^2}{|u^{*}\left({\mathit{x}}^i\right){|}^2}$$

where $\tilde{u}\left({\mathit{x}}^i\right)$ and $u^{*}\left({\mathit{x}}^i\right)$ are the approximate solution of the DNN and exact solution, respectively, for testing points $\left\{{\mathit{x}}^i\right\}(i=1,2,\cdots ,N^{\prime })$, and $N^{\prime }$ represents the number of testing points.

In our numerical experiments, all training and test data were generated with uniform distribution in Euclidean space ${\mathbb{R}}^d$, and all networks were trained by an Adam optimizer. The initial learning rate was set as $2\times {10}^{-4}$ with a decay rate of $5\times {10}^{-5}$ for each training epoch.

For the sake of viewing the training process, we tested our models for every 1000 epochs in the training process and recorded the result at the end. In our codes, the $\gamma$ was set as

$$\gamma =\left\{\begin{array}{cc}\hfill {\gamma }_0,& \mathrm{if}{i}_{\mathrm{epoch}}<0.1T_{max},\hfill \\ \hfill 10{\gamma }_0,& \mathrm{if}0.1T_{max}<=i_{\mathrm{epoch}}<0.2T_{max},\hfill \\ \hfill 50{\gamma }_0,& \mathrm{if}0.2T_{max}<=i_{\mathrm{epoch}}<0.25T_{max},\hfill \\ \hfill 100{\gamma }_0,& \mathrm{if}0.25T_{max}<=i_{\mathrm{epoch}}<0.5T_{max},\hfill \\ \hfill 200{\gamma }_0,& \mathrm{if}0.5T_{max}<=i_{\mathrm{epoch}}<0.75T_{max},\hfill \\ \hfill 500{\gamma }_0,& \mathrm{otherwise},\hfill \end{array}\right.$$

(17)

where the ${\gamma }_0=5$ in all our tests, and $T_{max}$ represents the total number of epoch and was set as 100000 in our all experiments. We performed all neural network training and testing in TensorFlow (version 1.14.0) on a workstation (256-GB RAM, single NVIDIA GeForce GTX 2080Ti 12-GB).

4.2. Numerical Examples

Example 1. 

We solved the biharmonic Equation (1) on the unit square domain $\Omega =[0,1]\times [0,1]$. The exact solution and force-side are

$$u(x_1,x_2)=sin\left(\pi x_1\right)sin\left(\pi x_2\right)$$

and

$$f(x_1,x_2)=4{\pi }^{4}sin\left(\pi x_1\right)sin\left(\pi x_2\right),$$

respectively. The boundary conditions $g(x_1,x_2)=h(x_1,x_2)=0$ on $\partial \Omega$.

In the following tests, we obtained the solution of (1) by means of DRM, FDRM, CDNN and FCDNN, respectively. Their network size is (120, 60, 50, 50, 40), (60, 60, 50, 50, 40), (100, 50, 30, 30, 20) and (50, 50, 30, 30, 20), respectively. It is easy to know that the number of parameters for the methods is 14100, 10800, 14000 and 10000, respectively. At each training epoch, the training dataset was generated from $\Omega$ and $\partial \Omega$, which include 3000 interior points and 500 boundary points in $\Omega$, respectively. The testing dataset was uniformly sampled from $\Omega$ of mesh-size $h=1/129$. We plot the numerical results in Figure 4 and list the final error results in

Table 1. REL and running time of the aforementioned four models for Example 2.

	DRM	FDRM	CDNN	FCDNN
REL	$1.64\times {10}^{-4}$	$1.45\times {10}^{-4}$	$1.12\times {10}^{-4}$	$4.06\times {10}^{-6}$
Time	1.05 h	1.37 h	0.42 h	0.55 h

.

Based on the above results, we can see that the DRM, FDRM, CDNN and FCDNN are all able to approximate the solution of (1), in which, the FCDNN model performs best, and the performances of CDNN, DRM and FDRM are competitive. In terms of the overall errors, the CDNN is stable in all training processes, but the FCDNN is still descending with small oscillations. This means that the Fourier mapping activation function will improve the capability of the CDNN model. Table 1 shows that the CDNNs only cost approximately 0.5 h to solve Equation (1), but the DRMs cost more than 1.05 h. In summary, our CDNN methods not only have a high accuracy, but are also efficient.

Example 2. 

We solved the biharmonic Equation (1) on the hexagram domain Ω derived from $[0,1]\times [0,1]$. The exact solution and force-side are

$$u(x_1,x_2)=10x(1-2x_1^2+x_1^3)y(1-2x_2^2+x_2^3)$$

and

$$f(x_1,x_2)=240x_2(1-2x_2^2+x_2^3)+2880x_1(x_1-1)x_2(x_2-1)+240x(1-2x_1^2+x_1^3),$$

respectively. The functions $g(x_1,x_2)$ and $h(x_1,x_2)$ on $\partial \Omega$ are easy to obtain according to the exact solution; here, we omit it.

In this example, the setups for DRM, FDRM, CDNN and FCDNN are the same as Example 4. At each training epoch, the training dataset was sampled from $\Omega$ and $\partial \Omega$, which include 3000 interior points and 500 boundary points, respectively. The testing dataset was randomly sampled from the hexagon domain in $[0,1]\times [0,1]$. We plot the numerical results in Figure 5 and list the final error results in

Table 2. REL and running time of the aforementioned four models for Example 2.

	DRM	FDRM	CDNN	FCDNN
REL	$1.65\times {10}^{-4}$	$1.{0310}^{-4}$	$5.{7310}^{-5}$	$1.15\times {10}^{-5}$
Time	1.10 h	1.26 h	0.44 h	0.55 h

.

On the irregular domain, the CDNN and FCDNN are still able to obtain the solution of (1), and the performance of FCDNN is superior to that of DRM, FDRM and CDNN. In the meantime, the runtime of CDNNs is also approximately half of DRMs and the performance of FCDNN is still decreasing, with small oscillations when the other three methods become stable.

Example 3. 

We solved the biharmonic Equation (1) on a unit cubic domain $\Omega =[0,1]\times [0,1]\times [0,1]$ with some holes. The exact solution is given by

$$u(x_1,x_2,x_3)=10x_1(1-2x_1^2+x_1^3)x_2(1-2x_2^2+x_2^3)x_3(1-2x_3^2+x_3^3).$$

It will naturally induce the boundary conditions $g(x_1,x_2)$ and $h(x_1,x_2)$ on $\partial \Omega$. By careful calculations, one can obtain the force side; here, we omit it.

When the DRM, FDRM, CDNN and FCDNN are used to solve (1) in the three-dimension space, their network size is set as (200, 100, 80, 80, 60), (100, 100, 80, 80, 60), (100, 80, 60, 60, 40) and (50, 80, 60, 60, 40). The training data set, including 6000 interior points and 1000 boundary points, was randomly sampled from $\Omega$ and $\partial \Omega$. A testing dataset was given that includes 1600 random points distributed in $\Omega$. The testing results are plotted in Figure 6 and the final error results are listed in

Table 3. REL and running time of the aforementioned four models for Example 3.

	DRM	FDRM	CDNN	FCDNN
REL	0.192	$2.11\times {10}^{-4}$	$1.99\times {10}^{-3}$	$1.49\times {10}^{-5}$
Time	2.97 h	4.16 h	0.50 h	0.54 h

. For showing these results visually, we projected the point-wise error for the DRM, FDRM, CDNN and FCDNN evaluated on 1600 sample points into a rectangular region with mesh size $40\times 40$, respectively. Note that the mapping is only for the purpose of visualization and is independent of the actual coordinates of those points.

Based on the above results, we can see that the FCDNN still outperforms other models when solving the biharmonic problem (1) in a three-dimensional space, and that the performance of the CDNN becomes a bit weaker than the FDRM. In addition, the point-wise square error of the four models in Figure 6b,c, as well as the overall errors in Figure 6f, show that the performance of FCDNN is much better than that of the other three models. Compared with the case of 2D, the data in Table 3 show the run-time of CDNNs is almost kept unchanged, but the DRMs will cost more time.

Example 4. 

We solved the biharmonic Equation (1) on the unit higher-dimensional domain $\Omega ={[0,1]}^8$. The exact solution and force-side are

$$u(x_1,x_2,\dots ,x_8)=sin\left(\pi x_1\right)sin\left(\pi x_2\right)\cdots sin\left(\pi x_8\right)$$

and

$$f(x_1,x_2,\dots ,x_8)=64{\pi }^{4}sin\left(\pi x_1\right)sin\left(\pi x_2\right)\cdots sin\left(\pi x_5\right),$$

respectively. The boundaries of this problem satisfy $g(x_1,x_2,\dots ,x_8)=h(x_1,x_2,\dots ,x_8)=0$.

Since the DRM and FDRM needed a large amount of computing resources for this example, our station could not satisfy their requirements; as a result, we only employed the CDNN and FCDNN to solve the biharmonic Equation (1) in eight-dimensional space, where the sizes for the CDNN and FCDNN were set as (300, 200, 200, 100, 100) and (150, 200, 200, 100, 100), respectively. The training data set included 20000 interior points and 5000 boundary points randomly sampled from $\Omega$ and $\partial \Omega$. A testing dataset was given that included 1600 random points distributed in $\Omega$. The testing results are plotted in Figure 7 and the final error results are listed in

Table 4. REL and running time of the CDNN and FCDNN for Example 4.

	CDNN	FCDNN
REL	0.0793	0.00042
Time	3.57 h	4.03 h

. Additionally, the point-wise error for CDNN and FCDNN evaluated on 1600 sample points was projected into a rectangular region with mesh size $40\times 40$, respectively.

The results in Figure 7 show that the FCDNN still maintains its good performance to approximate the exact solution of (1) in eight-dimensional space; however, the CDNN model will become slightly degenerated. In addition, the relative error of the FCDNN is much smaller than that of the CDNN based on Table 4.

5. Discussion

Compared with the DRM algorithms, the proposed CDNN method can solve the fourth-order biharmonic equation well based on its coupled scheme. It not only effectively reduces the complexity of the DNN algorithm, but also save the resources of the computer. In the meantime, a novel activation function composed of sine and cosine is introduced; it will obviously improve the performance of DNNs in solving a complex target. In a lower dimensional space, the CDNN method costs the least time, and attains the best accuracy. Regarding a high dimensional space, the CDNN can still keep its favorable performance; however, the DRM method cannot work because of the tremendous computational burden. In addition, the idea of a coupled scheme can be extended to the PINN method; then, a coupled PINN method may be developed to solve the PDEs without a variational form or other high-order problems. In this paper, we considered the biharmonic equation with a Neumann boundary; it is suitable for our CDNN method. Thus, more complex boundary conditions, such as the Dirichlet boundary and Robin boundary or other mixed boundaries, may be considered. Different from the case of Neumann, the other boundaries will not naturally induce the boundaries for two networks; thus, it is necessary to carefully design the coupled framework and boundary constraints of the DNN. Further, the performance of the CDNN will be degenerated or even not convergent if all of the networks lack the appropriate boundary conditions. Finally, the first-order optimization methods of the DNN and the sampling technique of training points may have an unfavorable effect on the accuracy and efficiency of DNN; this is an important issue to be solved.

6. Conclusions

By means of a coupled scheme of the biharmonic equation, we proposed a coupled DNN framework to solve this high-order problem in the work. As a class of a meshless method, the CDNN method does not rely on the initial guess and can approximate the solution of the biharmonic equation with a low complexity well. Additionally, a mixed loss function was designed that will enhance the stability and robustness for our model. Furthermore, a novel activation function based on Fourier approximation was introduced for the input layer, and the subsequent hidden layers were chosen as a good regularity function, such as tanh; this strategy can improve the accuracy and convergence rate for the CDNN method. Computational results show that the proposed method is feasible and efficient in solving the (1) in a complex domain and various dimension space. In the future, work is in progress to extend the neural network models to solve other high-order partial differential equations.