Homogeneity Test of Multi-Sample Covariance Matrices in High Dimensions
Abstract
1. Introduction
2. Preliminaries
- (C1)
- As , for .
- (C2)
- As , and for arbitrary , and .
3. Main Results
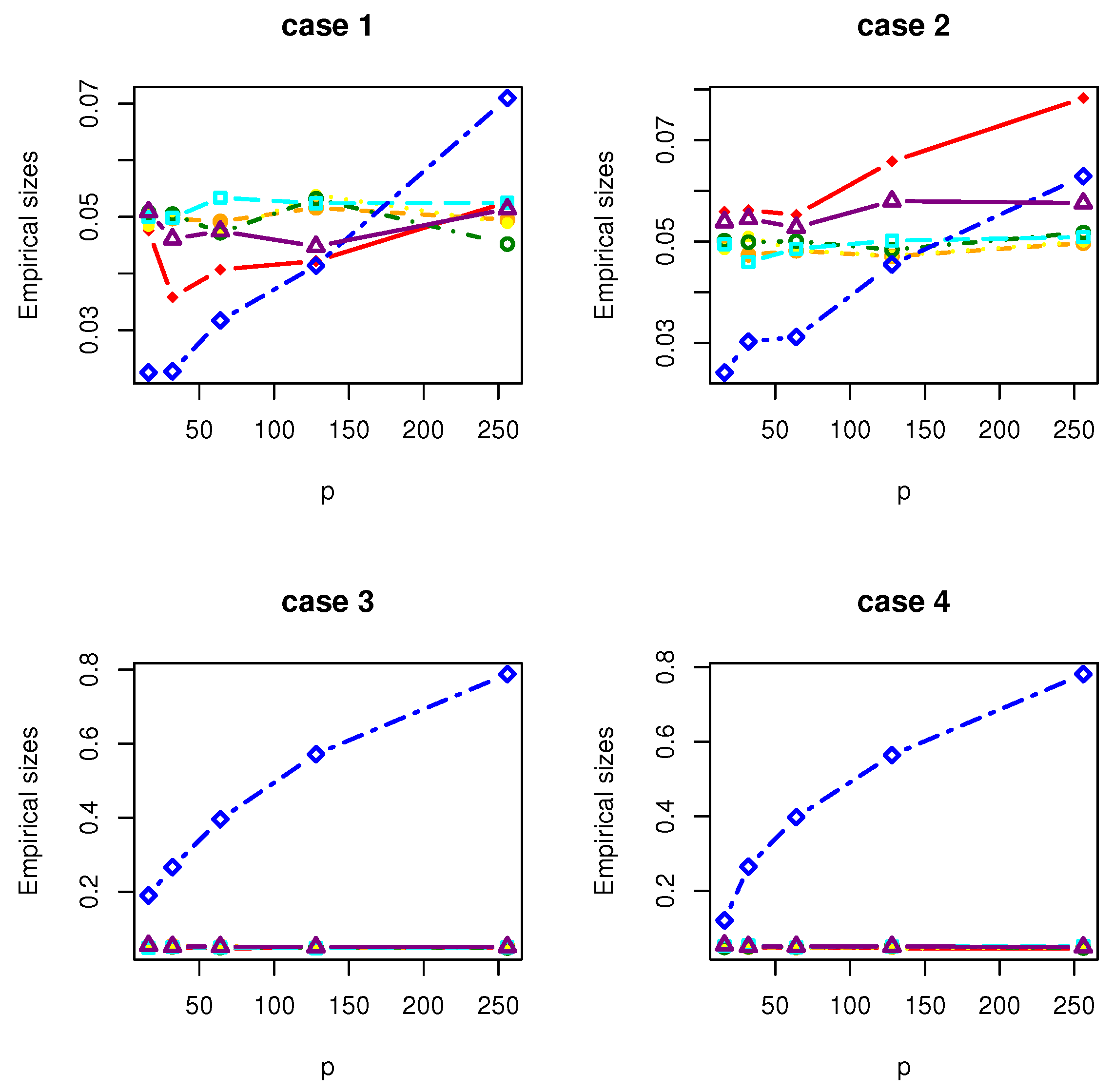
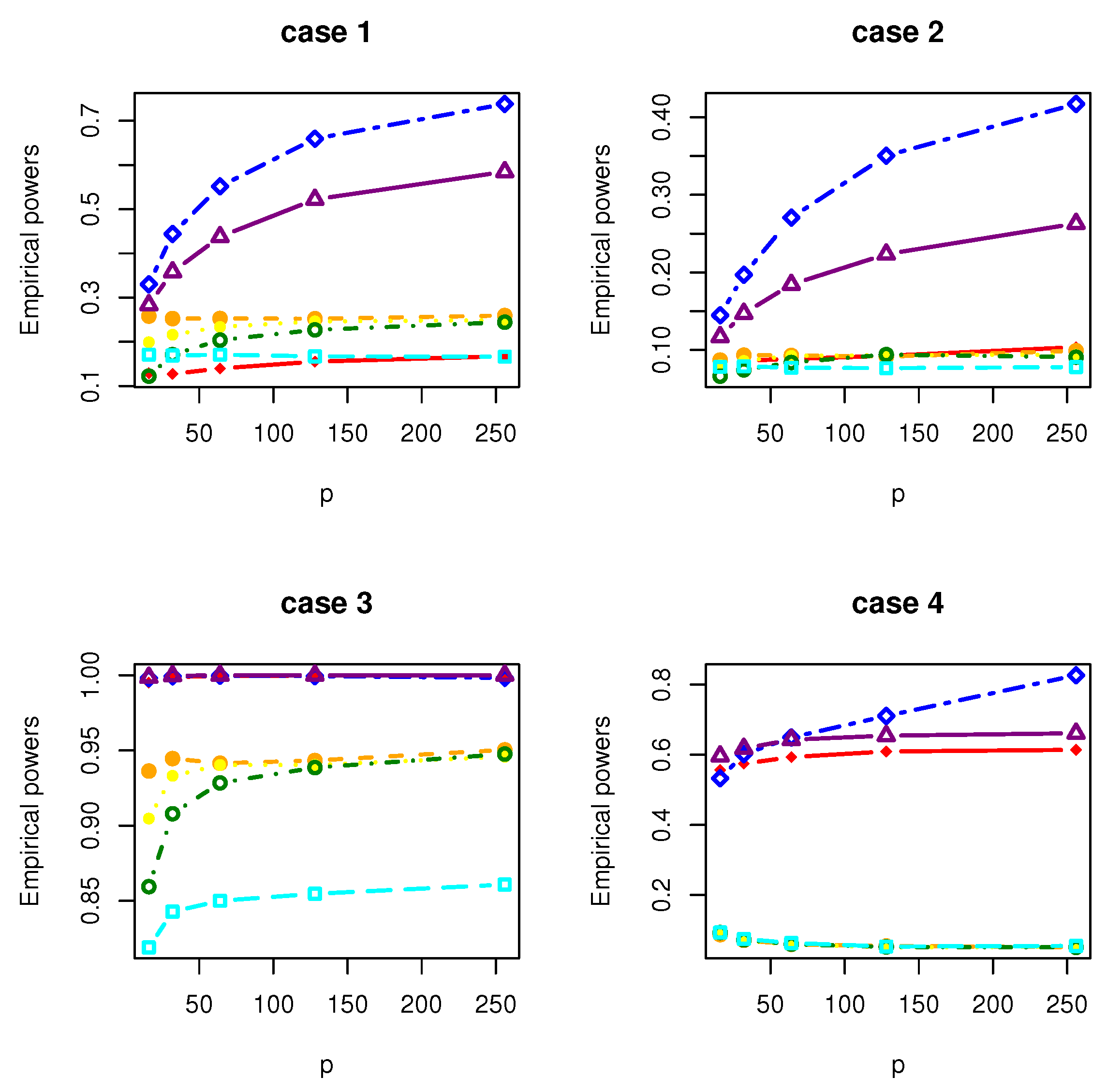
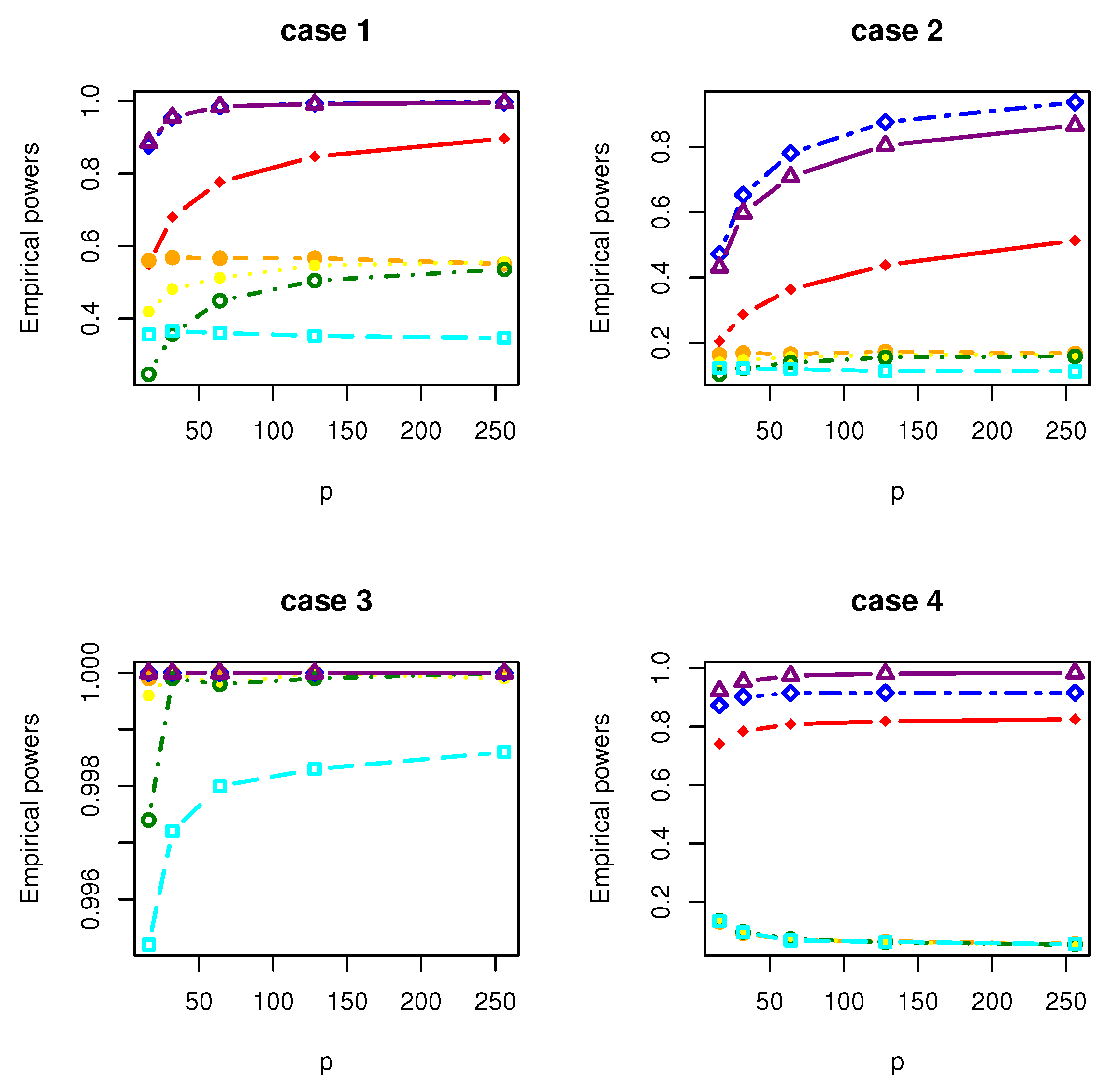
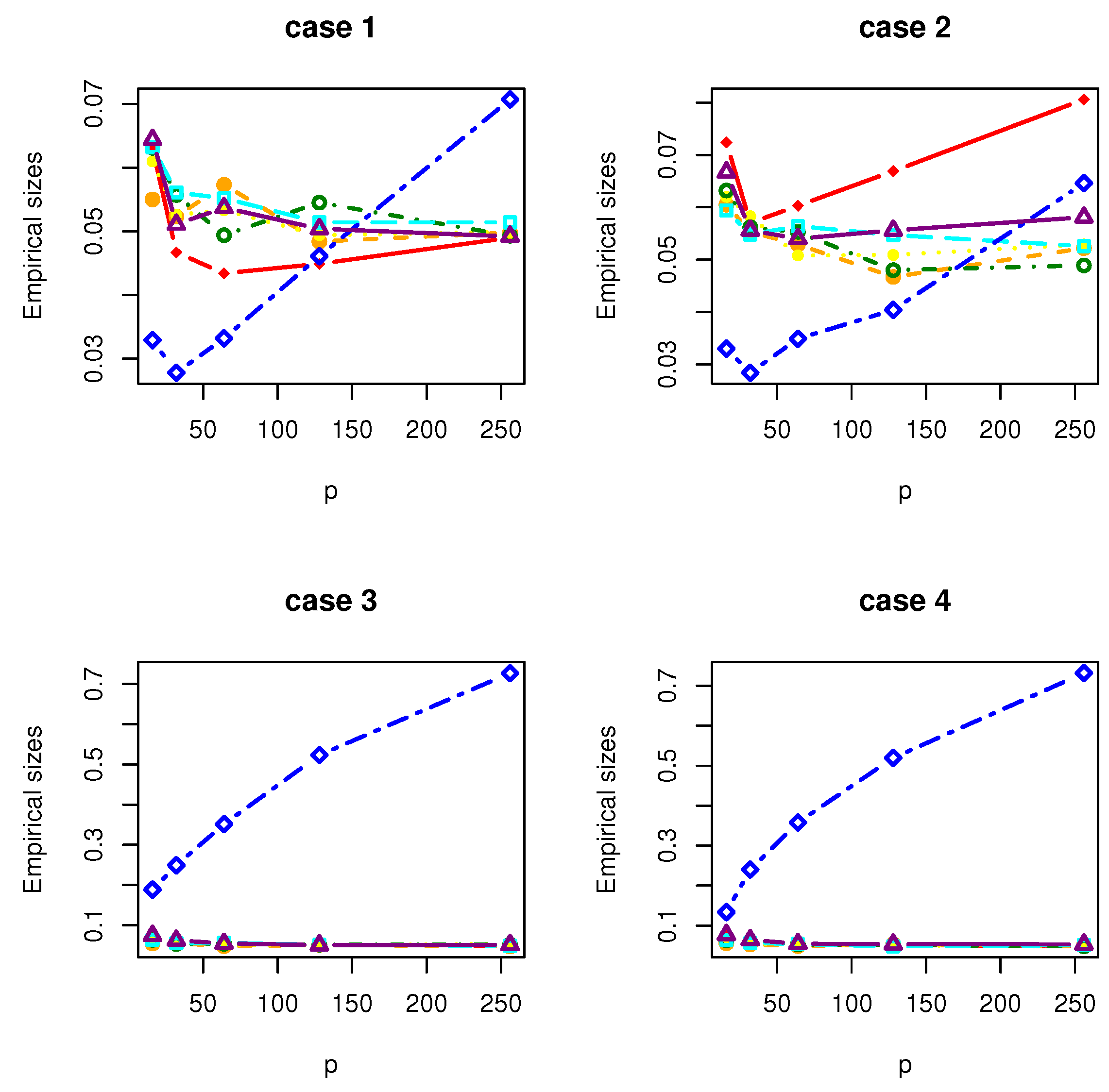
4. Simulation Studies
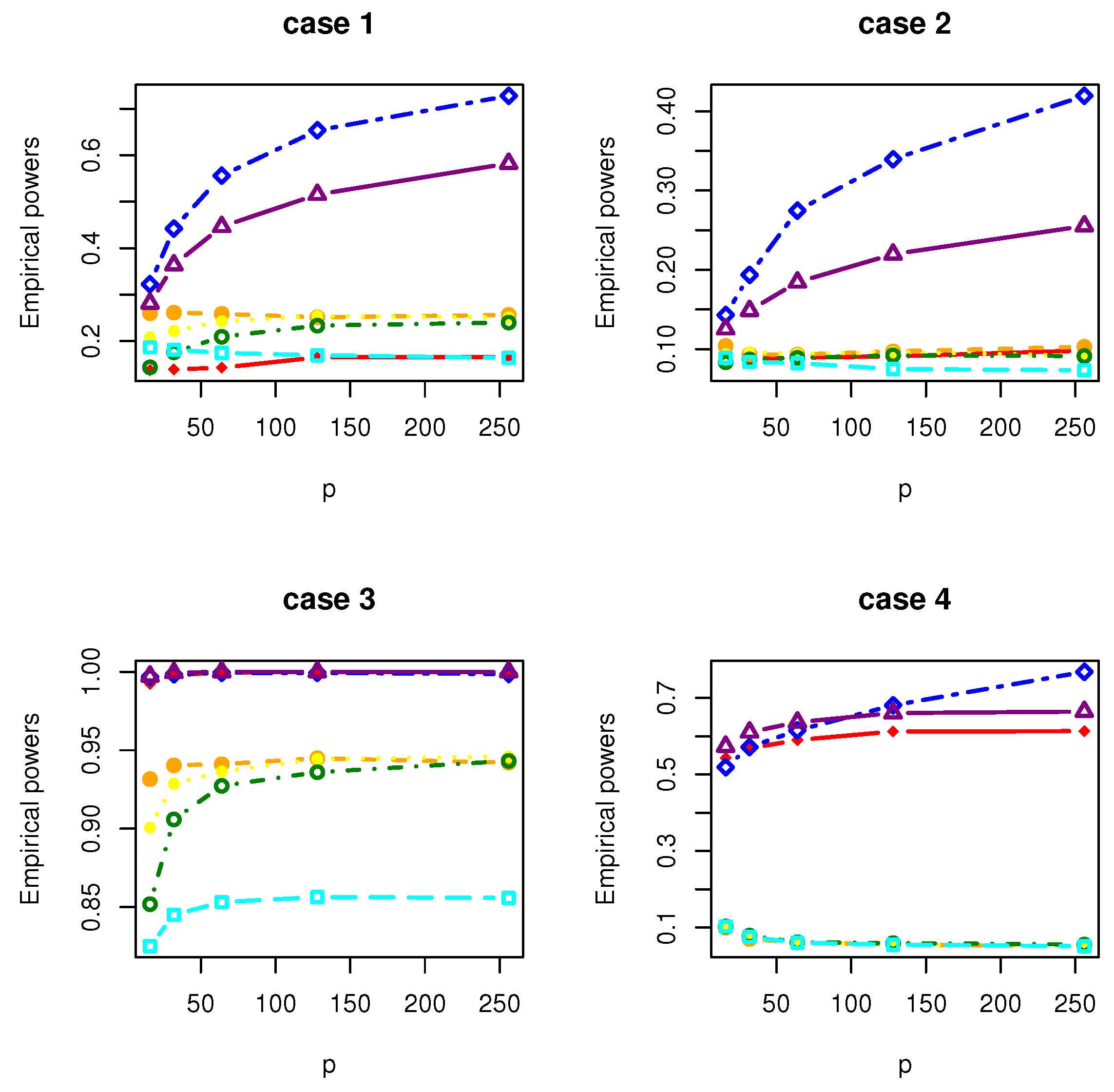
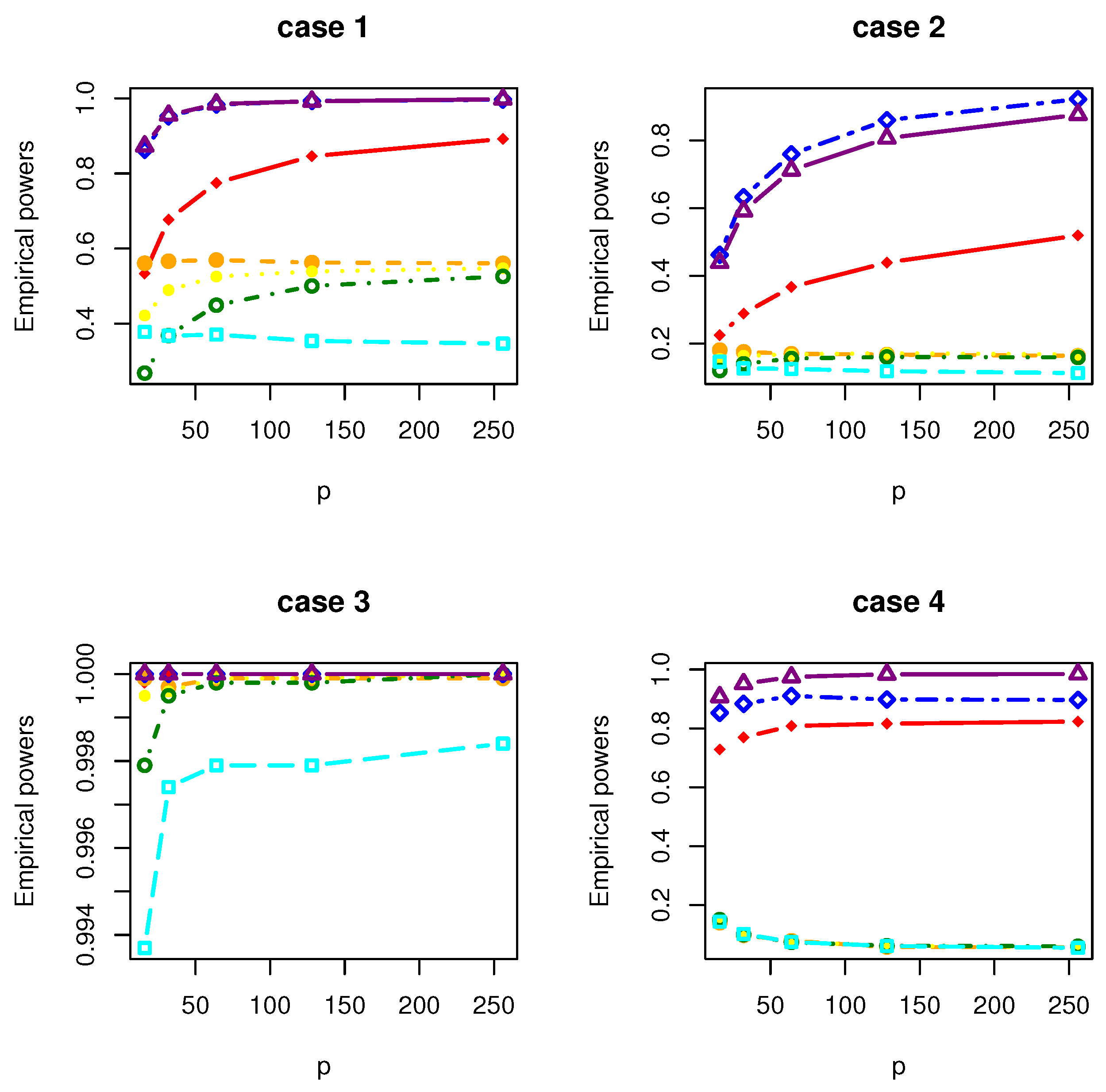
- Case 1: , where with and is a matrix with the th element being .
- Case 2: , where with and is a matrix with the th element being .
- Case 3: , where with . is a symmetric matrix with the th element being 1.01, the th elements being 0.1 and the rest being 0; is a symmetric matrix with the th element being 3, the th elements being 2, the th elements being 1 and the rest being 0.
- Case 4: where , where with , and is a matrix whose entries are independently generated from the normal distribution .
5. Real Data Analysis
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Some Lemmas
Appendix B. Proof of Theorem 1
References
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Muirhead, R.J. Aspects of Multivariate Statistical Theory; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Schmidt, M.; Böhm, D.; Törne, C.; Steiner, E.; Puhl, A.; Pilch, H.; Lehr, H.; Hengstler, J.; Kölbl, H.; Gehrmann, M. The humoral immune system has a key prognostic impact in node-negative breast cancer. Cancer Res. 2008, 68, 5405–5413. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.; Wei, J.S.; Ringner, M.; Saal, L.H.; Ladanyi, M.; Westermann, F.; Berthold, F.; Schwab, M.; Antonescu, C.R.; Peterson, C.; et al. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001, 7, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Ong, Y.S.; Dash, M. Markov blanket-embedded genetic algorithm for gene selection. Pattern Recognit. 2007, 49, 3236–3248. [Google Scholar] [CrossRef]
- Li, T.; Zhang, C.; Ogihara, M. A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics 2004, 20, 2429–2437. [Google Scholar] [CrossRef] [PubMed]
- Wilks, S.S. Sample criteria for testing equality of means, equality of variances, and equality of covariances in a normal multivariate distribution. Ann. Math. Stat. 1946, 17, 257–281. [Google Scholar] [CrossRef]
- Ahmad, M.R. Testing homogeneity of several covariance matrices and multi-sample sphericity for high-dimensional data under non-normality. Commun. Stat. Theory Methods 2017, 46, 3738–3753. [Google Scholar] [CrossRef]
- Schott, J.R.A. Test for the equality of covariance matrices when the dimension is large relative to the sample sizes. Comput. Stat. Data Anal. 2007, 51, 6535–6542. [Google Scholar] [CrossRef]
- Srivastava, M.S.; Yanagihara, H. Testing the equality of several covariance matrices with fewer observations than the dimension. J. Multivar. Anal. 2010, 101, 1319–1329. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, Z.; Hu, J.; Wang, C. Multi-sample test for high-dimensional covariance matrices. Commun. Stat. Theory Methods 2018, 47, 3161–3177. [Google Scholar] [CrossRef]
- Zhong, P.; Li, R.; Shanto, S. Homogeneity tests of covariance matrices with high-dimensional longitudinal data. Biometrika 2019, 106, 619–634. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Lin, R.; Guo, J.; Yin, G. Testing homogeneity of high-dimensional covariance matrices. Stat. Sin. 2020, 30, 35–53. [Google Scholar] [CrossRef]
- Qayed, A.; Han, D. Homogeneity test of several covariance matrices with high-dimensional data. J. Biopharm. Stat. 2021, 31, 523–540. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.P. A general distribution theory for a class of likelihood criteria. Biometrika 1949, 36, 317–346. [Google Scholar] [CrossRef]
- Li, J.; Chen, S. Two sample tests for high-dimensional covariance matrices. Ann. Stat. 2012, 40, 908–940. [Google Scholar] [CrossRef]
- Aoshima, M.; Yata, K. Two-sample tests for high-dimension, strongly spiked eigenvalue models. Stat. Sin. 2018, 28, 43–62. [Google Scholar] [CrossRef]
- Jiang, Y.; Wen, C.; Jiang, Y.; Wang, X.; Zhang, H. Use of Random Integration to Test Equality of High Dimensional Covariance Matrices. Stat. Sin. 2020. [Google Scholar] [CrossRef]
- Chen, S.; Qin, Y. A two-sample test for high-dimensional data with applications to gene-set testing. Ann. Stat. 2010, 38, 808–835. [Google Scholar] [CrossRef]


| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0476 | 0.0501 | 0.0484 | 0.0508 | 0.0500 | 0.0225 | 0.0509 |
| n = 45 | 32 | 0.0358 | 0.0497 | 0.0507 | 0.0505 | 0.0498 | 0.0227 | 0.0461 |
| 64 | 0.0407 | 0.0492 | 0.0471 | 0.0472 | 0.0534 | 0.0317 | 0.0475 | |
| 128 | 0.0422 | 0.0516 | 0.0539 | 0.0532 | 0.0524 | 0.0414 | 0.0448 | |
| 256 | 0.0526 | 0.0495 | 0.0489 | 0.0452 | 0.0525 | 0.0710 | 0.0514 | |
| n = 95 | 16 | 0.0633 | 0.0524 | 0.0535 | 0.0522 | 0.0512 | 0.0719 | 0.0601 |
| 32 | 0.0584 | 0.0488 | 0.0537 | 0.0515 | 0.0479 | 0.1230 | 0.0576 | |
| 64 | 0.0595 | 0.0518 | 0.0499 | 0.0472 | 0.0534 | 0.2814 | 0.0582 | |
| 128 | 0.0628 | 0.0477 | 0.0556 | 0.0499 | 0.0445 | 0.5641 | 0.0594 | |
| 256 | 0.0710 | 0.0478 | 0.0477 | 0.0534 | 0.0474 | 0.7692 | 0.0669 | |
| Power | 16 | 0.1291 | 0.2582 | 0.1991 | 0.1224 | 0.1710 | 0.3301 | 0.2837 |
| n = 45 | 32 | 0.1273 | 0.2526 | 0.2160 | 0.1709 | 0.1691 | 0.4441 | 0.3582 |
| 64 | 0.1398 | 0.2528 | 0.2337 | 0.2039 | 0.1710 | 0.5516 | 0.4377 | |
| 128 | 0.1552 | 0.2523 | 0.2462 | 0.2270 | 0.1671 | 0.6594 | 0.5222 | |
| 256 | 0.1676 | 0.2595 | 0.2490 | 0.2444 | 0.1665 | 0.7380 | 0.5847 | |
| n = 95 | 16 | 0.5490 | 0.5605 | 0.4198 | 0.2466 | 0.3561 | 0.8783 | 0.8870 |
| 32 | 0.6810 | 0.5684 | 0.4816 | 0.3566 | 0.3653 | 0.9559 | 0.9563 | |
| 64 | 0.7771 | 0.5669 | 0.5128 | 0.4494 | 0.3603 | 0.9861 | 0.9863 | |
| 128 | 0.8476 | 0.5670 | 0.5465 | 0.5048 | 0.3521 | 0.9946 | 0.9924 | |
| 256 | 0.8974 | 0.5509 | 0.5560 | 0.5359 | 0.3469 | 0.9974 | 0.9966 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0630 | 0.0550 | 0.0610 | 0.0631 | 0.0632 | 0.0329 | 0.0644 |
| n = 45 | 32 | 0.0467 | 0.0523 | 0.0526 | 0.0557 | 0.0561 | 0.0278 | 0.0511 |
| 64 | 0.0434 | 0.0573 | 0.0533 | 0.0494 | 0.0552 | 0.0332 | 0.0537 | |
| 128 | 0.0449 | 0.0484 | 0.0494 | 0.0545 | 0.0514 | 0.0461 | 0.0504 | |
| 256 | 0.0490 | 0.0498 | 0.0499 | 0.0493 | 0.0514 | 0.0707 | 0.0492 | |
| n = 95 | 16 | 0.0822 | 0.0560 | 0.0657 | 0.0699 | 0.0631 | 0.0851 | 0.0789 |
| 32 | 0.0741 | 0.0531 | 0.0610 | 0.0629 | 0.0594 | 0.1224 | 0.0698 | |
| 64 | 0.0619 | 0.0544 | 0.0535 | 0.0545 | 0.0540 | 0.2505 | 0.0617 | |
| 128 | 0.0638 | 0.0524 | 0.0540 | 0.0517 | 0.0477 | 0.5037 | 0.0627 | |
| 256 | 0.0686 | 0.0508 | 0.0493 | 0.0498 | 0.0517 | 0.7041 | 0.0668 | |
| Power | 16 | 0.1375 | 0.2602 | 0.2085 | 0.1437 | 0.1866 | 0.3225 | 0.2815 |
| n = 45 | 32 | 0.1392 | 0.2613 | 0.2221 | 0.1760 | 0.1815 | 0.4421 | 0.3639 |
| 64 | 0.1429 | 0.2587 | 0.2427 | 0.2094 | 0.1746 | 0.5561 | 0.4463 | |
| 128 | 0.1652 | 0.2513 | 0.2538 | 0.2334 | 0.1695 | 0.6536 | 0.5155 | |
| 256 | 0.1658 | 0.2565 | 0.2514 | 0.2401 | 0.1639 | 0.7279 | 0.5824 | |
| n = 95 | 16 | 0.5336 | 0.5610 | 0.4219 | 0.2685 | 0.3780 | 0.8629 | 0.8730 |
| 32 | 0.6772 | 0.5664 | 0.4895 | 0.3683 | 0.3681 | 0.9523 | 0.9551 | |
| 64 | 0.7749 | 0.5695 | 0.5256 | 0.4493 | 0.3709 | 0.9834 | 0.9849 | |
| 128 | 0.8460 | 0.5628 | 0.5391 | 0.5005 | 0.3540 | 0.9929 | 0.9923 | |
| 256 | 0.8922 | 0.5608 | 0.5477 | 0.5260 | 0.3470 | 0.9966 | 0.9978 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0559 | 0.0501 | 0.0485 | 0.0502 | 0.0495 | 0.0242 | 0.0539 |
| n = 45 | 32 | 0.0562 | 0.0474 | 0.0510 | 0.0499 | 0.0460 | 0.0303 | 0.0545 |
| 64 | 0.0553 | 0.0482 | 0.0483 | 0.0501 | 0.0486 | 0.0312 | 0.0528 | |
| 128 | 0.0658 | 0.0471 | 0.0472 | 0.0484 | 0.0502 | 0.0455 | 0.0580 | |
| 256 | 0.0783 | 0.0497 | 0.0500 | 0.0518 | 0.0509 | 0.0629 | 0.0576 | |
| n = 95 | 16 | 0.0724 | 0.0511 | 0.0499 | 0.0484 | 0.0494 | 0.0750 | 0.0656 |
| 32 | 0.0675 | 0.0492 | 0.0497 | 0.0486 | 0.0491 | 0.1132 | 0.0624 | |
| 64 | 0.0747 | 0.0532 | 0.0505 | 0.0483 | 0.0498 | 0.2468 | 0.0641 | |
| 128 | 0.0821 | 0.0479 | 0.0465 | 0.0473 | 0.0468 | 0.5114 | 0.0680 | |
| 256 | 0.0790 | 0.0514 | 0.0488 | 0.0514 | 0.0492 | 0.7645 | 0.0625 | |
| Power | 16 | 0.0838 | 0.0869 | 0.0804 | 0.0662 | 0.0781 | 0.1447 | 0.1170 |
| n = 45 | 32 | 0.0862 | 0.0933 | 0.0858 | 0.0743 | 0.0788 | 0.1969 | 0.1471 |
| 64 | 0.0883 | 0.0928 | 0.0923 | 0.0838 | 0.0771 | 0.2706 | 0.1844 | |
| 128 | 0.0924 | 0.0915 | 0.0933 | 0.0940 | 0.0765 | 0.3505 | 0.2235 | |
| 256 | 0.1035 | 0.0989 | 0.0937 | 0.0907 | 0.0779 | 0.4172 | 0.2631 | |
| n = 95 | 16 | 0.2053 | 0.1640 | 0.1405 | 0.1048 | 0.1238 | 0.4722 | 0.4314 |
| 32 | 0.2877 | 0.1693 | 0.1482 | 0.1220 | 0.1225 | 0.6532 | 0.5974 | |
| 64 | 0.3641 | 0.1659 | 0.1569 | 0.1405 | 0.1203 | 0.7805 | 0.7090 | |
| 128 | 0.4380 | 0.1740 | 0.1632 | 0.1559 | 0.1143 | 0.8758 | 0.8046 | |
| 256 | 0.5136 | 0.1680 | 0.1651 | 0.1595 | 0.1129 | 0.9364 | 0.8659 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0724 | 0.0605 | 0.0620 | 0.0632 | 0.0594 | 0.0330 | 0.0667 |
| n = 45 | 32 | 0.0570 | 0.0553 | 0.0583 | 0.0562 | 0.0548 | 0.0284 | 0.0556 |
| 64 | 0.0603 | 0.0529 | 0.0508 | 0.0553 | 0.0564 | 0.0349 | 0.0540 | |
| 128 | 0.0669 | 0.0467 | 0.0509 | 0.0480 | 0.0547 | 0.0404 | 0.0556 | |
| 256 | 0.0806 | 0.0522 | 0.0529 | 0.0489 | 0.0526 | 0.0646 | 0.0581 | |
| n = 95 | 16 | 0.0886 | 0.0556 | 0.0653 | 0.0660 | 0.0649 | 0.0865 | 0.0844 |
| 32 | 0.0792 | 0.0539 | 0.0554 | 0.0580 | 0.0580 | 0.1146 | 0.0718 | |
| 64 | 0.0794 | 0.0557 | 0.0550 | 0.0545 | 0.0555 | 0.2220 | 0.0696 | |
| 128 | 0.0774 | 0.0549 | 0.0524 | 0.0570 | 0.0490 | 0.4400 | 0.0658 | |
| 256 | 0.0855 | 0.0523 | 0.0504 | 0.0486 | 0.0505 | 0.7047 | 0.0691 | |
| Power | 16 | 0.0976 | 0.1041 | 0.0937 | 0.0834 | 0.0889 | 0.1430 | 0.1253 |
| n = 45 | 32 | 0.0882 | 0.0934 | 0.0961 | 0.0870 | 0.0839 | 0.1936 | 0.1486 |
| 64 | 0.0893 | 0.0931 | 0.0942 | 0.0890 | 0.0823 | 0.2746 | 0.1844 | |
| 128 | 0.0908 | 0.0972 | 0.0965 | 0.0922 | 0.0748 | 0.3395 | 0.2197 | |
| 256 | 0.0982 | 0.1029 | 0.0918 | 0.0913 | 0.0734 | 0.4195 | 0.2553 | |
| n = 95 | 16 | 0.2248 | 0.1807 | 0.1547 | 0.1205 | 0.1464 | 0.4621 | 0.4391 |
| 32 | 0.2886 | 0.1757 | 0.1641 | 0.1403 | 0.1267 | 0.6325 | 0.5913 | |
| 64 | 0.3671 | 0.1699 | 0.1681 | 0.1560 | 0.1253 | 0.7592 | 0.7119 | |
| 128 | 0.4392 | 0.1675 | 0.1715 | 0.1605 | 0.1184 | 0.8598 | 0.8064 | |
| 256 | 0.5194 | 0.1641 | 0.1682 | 0.1593 | 0.1129 | 0.9217 | 0.8760 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0530 | 0.0517 | 0.0478 | 0.0495 | 0.0484 | 0.1897 | 0.0545 |
| n = 45 | 32 | 0.0491 | 0.0539 | 0.0513 | 0.0514 | 0.0503 | 0.2663 | 0.0517 |
| 64 | 0.0463 | 0.0521 | 0.0498 | 0.0487 | 0.0491 | 0.3956 | 0.0513 | |
| 128 | 0.0490 | 0.0481 | 0.0503 | 0.0496 | 0.0475 | 0.5715 | 0.0508 | |
| 256 | 0.0492 | 0.0512 | 0.0491 | 0.0478 | 0.0501 | 0.7879 | 0.0511 | |
| n = 95 | 16 | 0.0455 | 0.0489 | 0.0516 | 0.0493 | 0.0496 | 0.2732 | 0.0520 |
| 32 | 0.0407 | 0.0484 | 0.0508 | 0.0493 | 0.0493 | 0.3462 | 0.0535 | |
| 64 | 0.0357 | 0.0471 | 0.0501 | 0.0516 | 0.0496 | 0.4335 | 0.0483 | |
| 128 | 0.0386 | 0.0483 | 0.0496 | 0.0465 | 0.0483 | 0.5736 | 0.0476 | |
| 256 | 0.0381 | 0.0497 | 0.0501 | 0.0532 | 0.0494 | 0.7541 | 0.0506 | |
| Power | 16 | 0.9951 | 0.9363 | 0.9047 | 0.8594 | 0.8190 | 0.9981 | 0.9986 |
| n = 45 | 32 | 0.9988 | 0.9446 | 0.9331 | 0.9079 | 0.8428 | 0.9993 | 0.9997 |
| 64 | 0.9996 | 0.9415 | 0.9403 | 0.9284 | 0.8500 | 0.9997 | 0.9999 | |
| 128 | 0.9998 | 0.9433 | 0.9404 | 0.9386 | 0.8547 | 0.9994 | 1.0000 | |
| 256 | 0.9999 | 0.9504 | 0.9458 | 0.9476 | 0.8608 | 0.9983 | 1.0000 | |
| n = 95 | 16 | 1.0000 | 0.9999 | 0.9996 | 0.9974 | 0.9952 | 1.0000 | 1.0000 |
| 32 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 0.9972 | 1.0000 | 1.0000 | |
| 64 | 1.0000 | 1.0000 | 0.9998 | 0.9998 | 0.9980 | 1.0000 | 1.0000 | |
| 128 | 1.0000 | 1.0000 | 1.0000 | 0.9999 | 0.9983 | 1.0000 | 1.0000 | |
| 256 | 1.0000 | 1.0000 | 0.9999 | 1.0000 | 0.9986 | 1.0000 | 1.0000 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0743 | 0.0540 | 0.0587 | 0.0633 | 0.0637 | 0.1885 | 0.0740 |
| n = 45 | 32 | 0.0599 | 0.0553 | 0.0544 | 0.0530 | 0.0551 | 0.2490 | 0.0622 |
| 64 | 0.0532 | 0.0476 | 0.0512 | 0.0536 | 0.0557 | 0.3514 | 0.0544 | |
| 128 | 0.0506 | 0.0508 | 0.0494 | 0.0511 | 0.0511 | 0.5232 | 0.0503 | |
| 256 | 0.0493 | 0.0471 | 0.0533 | 0.0516 | 0.0487 | 0.7273 | 0.0510 | |
| n = 95 | 16 | 0.0619 | 0.0526 | 0.0614 | 0.0679 | 0.0635 | 0.2469 | 0.0709 |
| 32 | 0.0441 | 0.0513 | 0.0565 | 0.0562 | 0.0501 | 0.3059 | 0.0553 | |
| 64 | 0.0430 | 0.0526 | 0.0537 | 0.0524 | 0.0558 | 0.3869 | 0.0521 | |
| 128 | 0.0368 | 0.0534 | 0.0500 | 0.0506 | 0.0511 | 0.5153 | 0.0478 | |
| 256 | 0.0365 | 0.0494 | 0.0463 | 0.0489 | 0.0523 | 0.7029 | 0.0445 | |
| Power | 16 | 0.9924 | 0.9316 | 0.9007 | 0.8519 | 0.8251 | 0.9968 | 0.9972 |
| n = 45 | 32 | 0.9978 | 0.9404 | 0.9286 | 0.9059 | 0.8451 | 0.9984 | 0.9994 |
| 64 | 0.9996 | 0.9411 | 0.9365 | 0.9273 | 0.8532 | 0.9994 | 1.0000 | |
| 128 | 0.9999 | 0.9449 | 0.9444 | 0.9360 | 0.8564 | 0.9993 | 1.0000 | |
| 256 | 1.0000 | 0.9421 | 0.9459 | 0.9432 | 0.8559 | 0.9986 | 1.0000 | |
| n = 95 | 16 | 0.9998 | 0.9999 | 0.9995 | 0.9979 | 0.9937 | 1.0000 | 1.0000 |
| 32 | 1.0000 | 0.9997 | 0.9996 | 0.9995 | 0.9974 | 1.0000 | 1.0000 | |
| 64 | 1.0000 | 0.9999 | 0.9999 | 0.9998 | 0.9979 | 1.0000 | 1.0000 | |
| 128 | 1.0000 | 0.9999 | 0.9999 | 0.9998 | 0.9979 | 1.0000 | 1.0000 | |
| 256 | 1.0000 | 0.9999 | 1.0000 | 1.0000 | 0.9984 | 1.0000 | 1.0000 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0517 | 0.0490 | 0.0514 | 0.0484 | 0.0522 | 0.1209 | 0.0548 |
| n = 45 | 32 | 0.0481 | 0.0496 | 0.0506 | 0.0507 | 0.0541 | 0.2649 | 0.0507 |
| 64 | 0.0487 | 0.0480 | 0.0495 | 0.0493 | 0.0487 | 0.3975 | 0.0512 | |
| 128 | 0.0459 | 0.0496 | 0.0459 | 0.0515 | 0.0510 | 0.5640 | 0.0511 | |
| 256 | 0.0455 | 0.0504 | 0.0483 | 0.0469 | 0.0520 | 0.7811 | 0.0493 | |
| n = 95 | 16 | 0.0450 | 0.0470 | 0.0522 | 0.0489 | 0.0550 | 0.2487 | 0.0513 |
| 32 | 0.0388 | 0.0504 | 0.0511 | 0.0514 | 0.0502 | 0.3486 | 0.0484 | |
| 64 | 0.0381 | 0.0504 | 0.0503 | 0.0488 | 0.0502 | 0.4379 | 0.0480 | |
| 128 | 0.0329 | 0.0530 | 0.0511 | 0.0487 | 0.0523 | 0.5704 | 0.0441 | |
| 256 | 0.0348 | 0.0498 | 0.0508 | 0.0514 | 0.0462 | 0.7527 | 0.0438 | |
| Power | 16 | 0.5566 | 0.0872 | 0.0922 | 0.0930 | 0.0933 | 0.5331 | 0.5965 |
| n = 45 | 32 | 0.5749 | 0.0710 | 0.0698 | 0.0724 | 0.0749 | 0.6018 | 0.6180 |
| 64 | 0.5935 | 0.0596 | 0.0591 | 0.0601 | 0.0633 | 0.6495 | 0.6432 | |
| 128 | 0.6095 | 0.0547 | 0.0507 | 0.0522 | 0.0532 | 0.7108 | 0.6546 | |
| 256 | 0.6142 | 0.0516 | 0.0527 | 0.0508 | 0.0552 | 0.8269 | 0.6615 | |
| n = 95 | 16 | 0.7418 | 0.1311 | 0.1361 | 0.1359 | 0.1338 | 0.8735 | 0.9232 |
| 32 | 0.7846 | 0.0923 | 0.0916 | 0.0966 | 0.0953 | 0.9024 | 0.9548 | |
| 64 | 0.8089 | 0.0680 | 0.0738 | 0.0735 | 0.0679 | 0.9151 | 0.9753 | |
| 128 | 0.8184 | 0.0650 | 0.0607 | 0.0615 | 0.0626 | 0.9166 | 0.9824 | |
| 256 | 0.8258 | 0.0560 | 0.0548 | 0.0533 | 0.0549 | 0.9161 | 0.9849 |
| p | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | 16 | 0.0776 | 0.0559 | 0.0589 | 0.0632 | 0.0641 | 0.1338 | 0.0773 |
| n = 45 | 32 | 0.0634 | 0.0526 | 0.0534 | 0.0584 | 0.0567 | 0.2403 | 0.0642 |
| 64 | 0.0532 | 0.0488 | 0.0527 | 0.0527 | 0.0540 | 0.3579 | 0.0546 | |
| 128 | 0.0520 | 0.0533 | 0.0500 | 0.0517 | 0.0480 | 0.5195 | 0.0534 | |
| 256 | 0.0483 | 0.0495 | 0.0506 | 0.0482 | 0.0512 | 0.7316 | 0.0530 | |
| n = 95 | 16 | 0.0674 | 0.0586 | 0.0605 | 0.0605 | 0.0668 | 0.2348 | 0.0729 |
| 32 | 0.0482 | 0.0528 | 0.0530 | 0.0586 | 0.0514 | 0.2945 | 0.0613 | |
| 64 | 0.0425 | 0.0511 | 0.0491 | 0.0551 | 0.0525 | 0.3839 | 0.0533 | |
| 128 | 0.0420 | 0.0523 | 0.0522 | 0.0491 | 0.0499 | 0.5164 | 0.0520 | |
| 256 | 0.0388 | 0.0456 | 0.0488 | 0.0519 | 0.0511 | 0.6998 | 0.0490 | |
| Power | 16 | 0.5435 | 0.0993 | 0.1039 | 0.1028 | 0.1026 | 0.5191 | 0.5735 |
| n = 45 | 32 | 0.5685 | 0.0697 | 0.0741 | 0.0787 | 0.0756 | 0.5717 | 0.6106 |
| 64 | 0.5901 | 0.0606 | 0.0601 | 0.0615 | 0.0602 | 0.6153 | 0.6368 | |
| 128 | 0.6124 | 0.0551 | 0.0552 | 0.0592 | 0.0551 | 0.6810 | 0.6606 | |
| 256 | 0.6133 | 0.0511 | 0.0512 | 0.0554 | 0.0510 | 0.7685 | 0.6645 | |
| n = 95 | 16 | 0.7283 | 0.1401 | 0.1468 | 0.1506 | 0.1438 | 0.8526 | 0.9070 |
| 32 | 0.7695 | 0.0973 | 0.0997 | 0.1000 | 0.1019 | 0.8832 | 0.9513 | |
| 64 | 0.8081 | 0.0790 | 0.0745 | 0.0738 | 0.0749 | 0.9100 | 0.9746 | |
| 128 | 0.8158 | 0.0577 | 0.0627 | 0.0621 | 0.0611 | 0.8980 | 0.9835 | |
| 256 | 0.8231 | 0.0570 | 0.0545 | 0.0601 | 0.0550 | 0.8966 | 0.9843 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Tang, Y.; Cao, M. Homogeneity Test of Multi-Sample Covariance Matrices in High Dimensions. Mathematics 2022, 10, 4339. https://doi.org/10.3390/math10224339
Sun P, Tang Y, Cao M. Homogeneity Test of Multi-Sample Covariance Matrices in High Dimensions. Mathematics. 2022; 10(22):4339. https://doi.org/10.3390/math10224339
Chicago/Turabian StyleSun, Peng, Yincai Tang, and Mingxiang Cao. 2022. "Homogeneity Test of Multi-Sample Covariance Matrices in High Dimensions" Mathematics 10, no. 22: 4339. https://doi.org/10.3390/math10224339
APA StyleSun, P., Tang, Y., & Cao, M. (2022). Homogeneity Test of Multi-Sample Covariance Matrices in High Dimensions. Mathematics, 10(22), 4339. https://doi.org/10.3390/math10224339






