Numerical Investigation of Heat Transfer Enhancement in a Microchannel with Conical-Shaped Reentrant Cavity
Abstract
1. Introduction
2. Mathematical Formulation and Numerical Methods
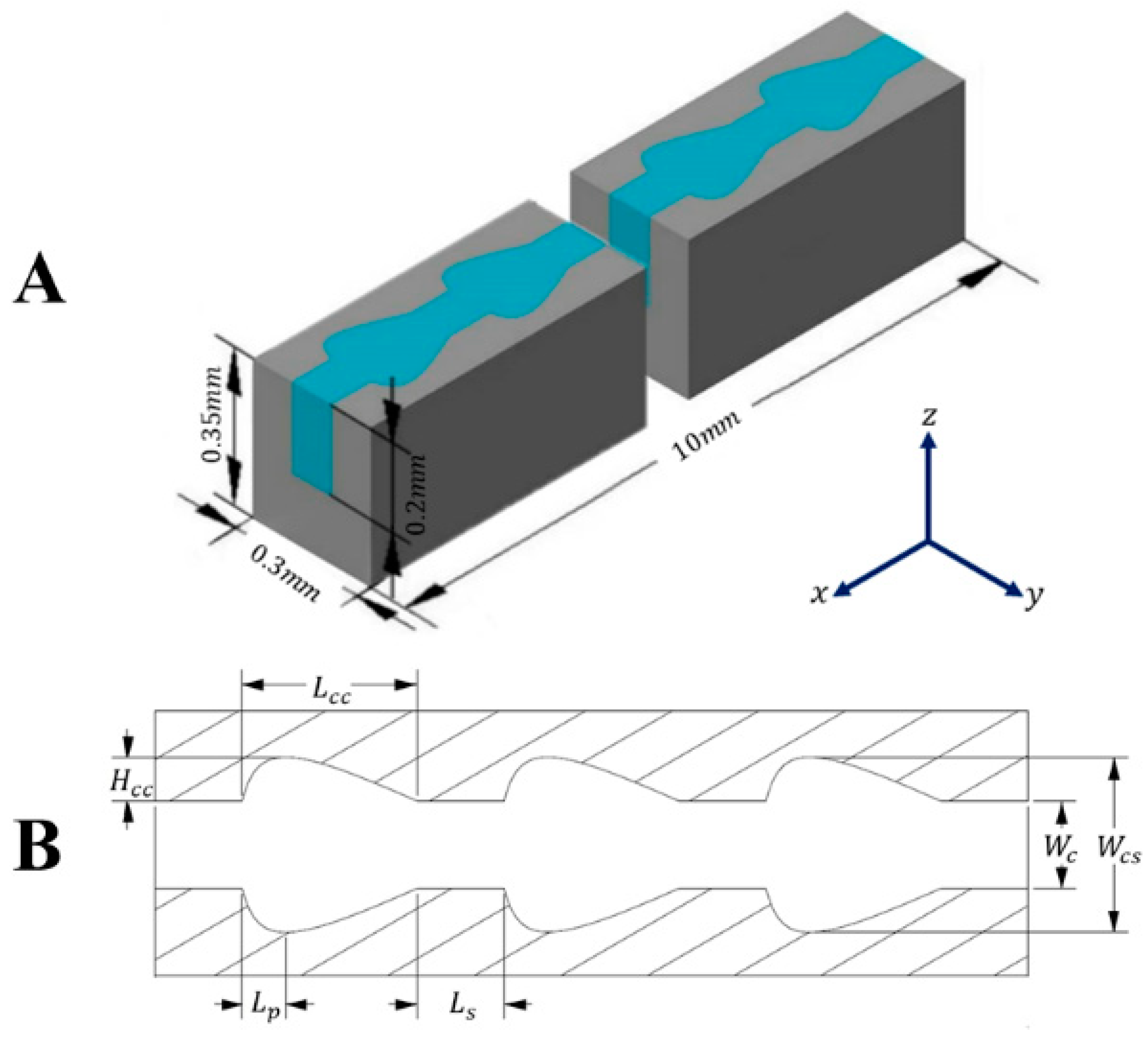
2.1. Physical Model and Assumptions
- The flow is 3-dimensional, steady-state, incompressible, laminar.
- Piecewise-linear dynamic viscosity of water temperature.
- Viscous dissipation is considered.
- Negligible gravity and radiation heat transfer.
2.2. Governing Equations
- For liquid:
- 2.
- For silicon substrate:
2.3. Boundary Conditions
| at the channel wall surface (no-slip and no-penetration); | |
| ; | |
| . |
- For liquid
| at | |
| at |
- 2.
- For silicon substrate by considering the solid region is without axial heat transfer.
| at and , | |
| at and | |
| at , | |
| at , |
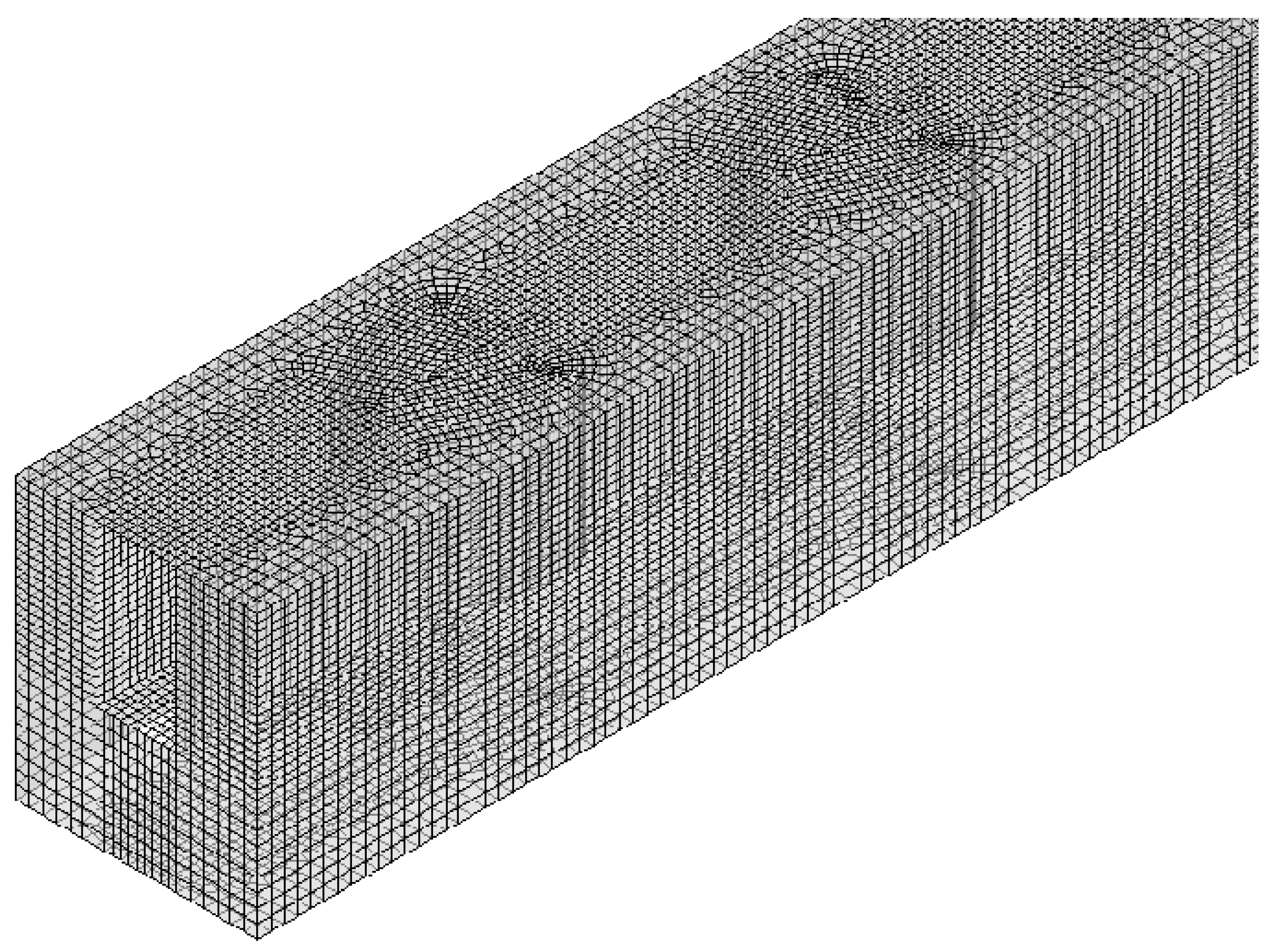
2.4. Mesh Precision Test
2.5. Numerical Implementation
3. Results and Discussion
3.1. Numerical Validation
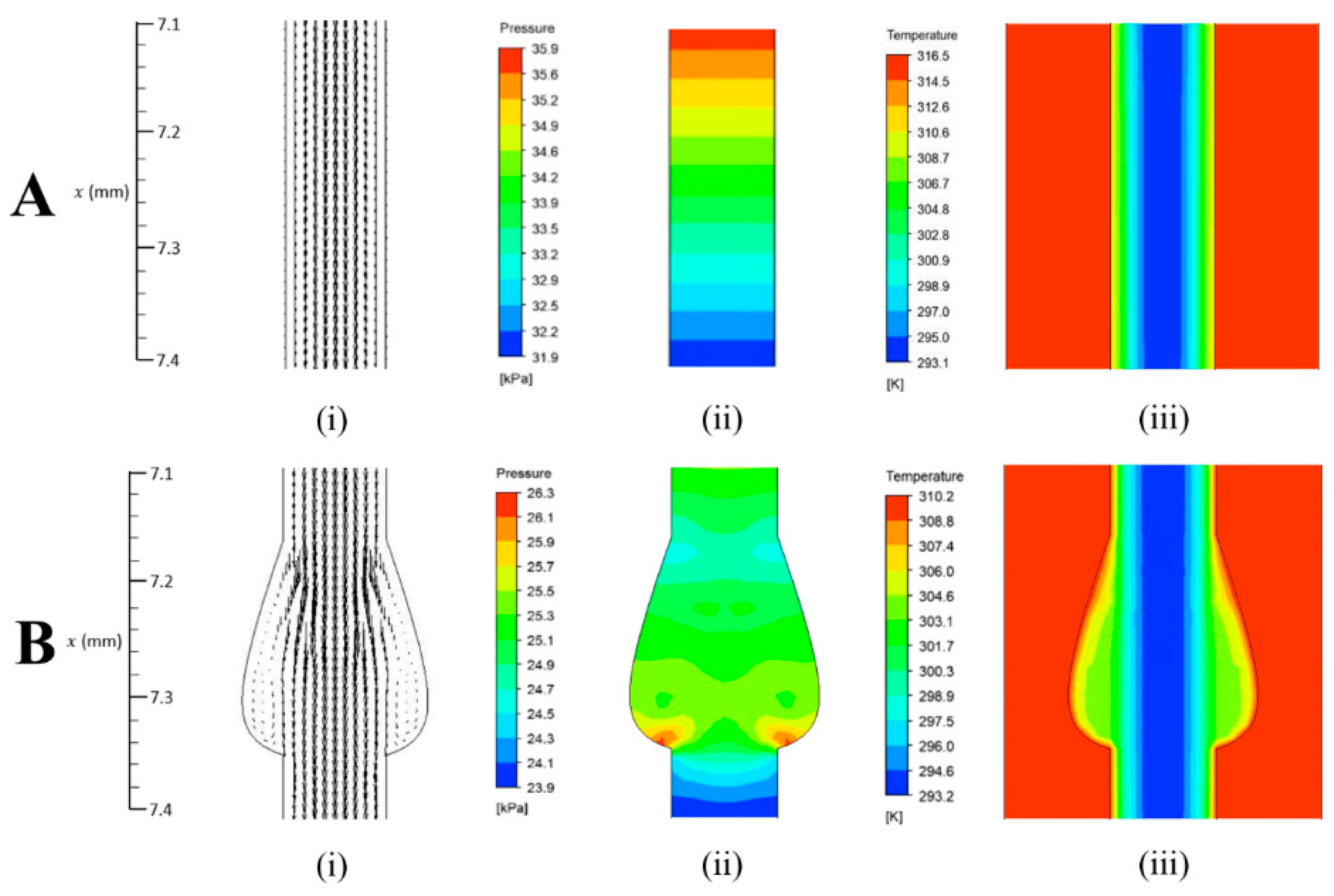
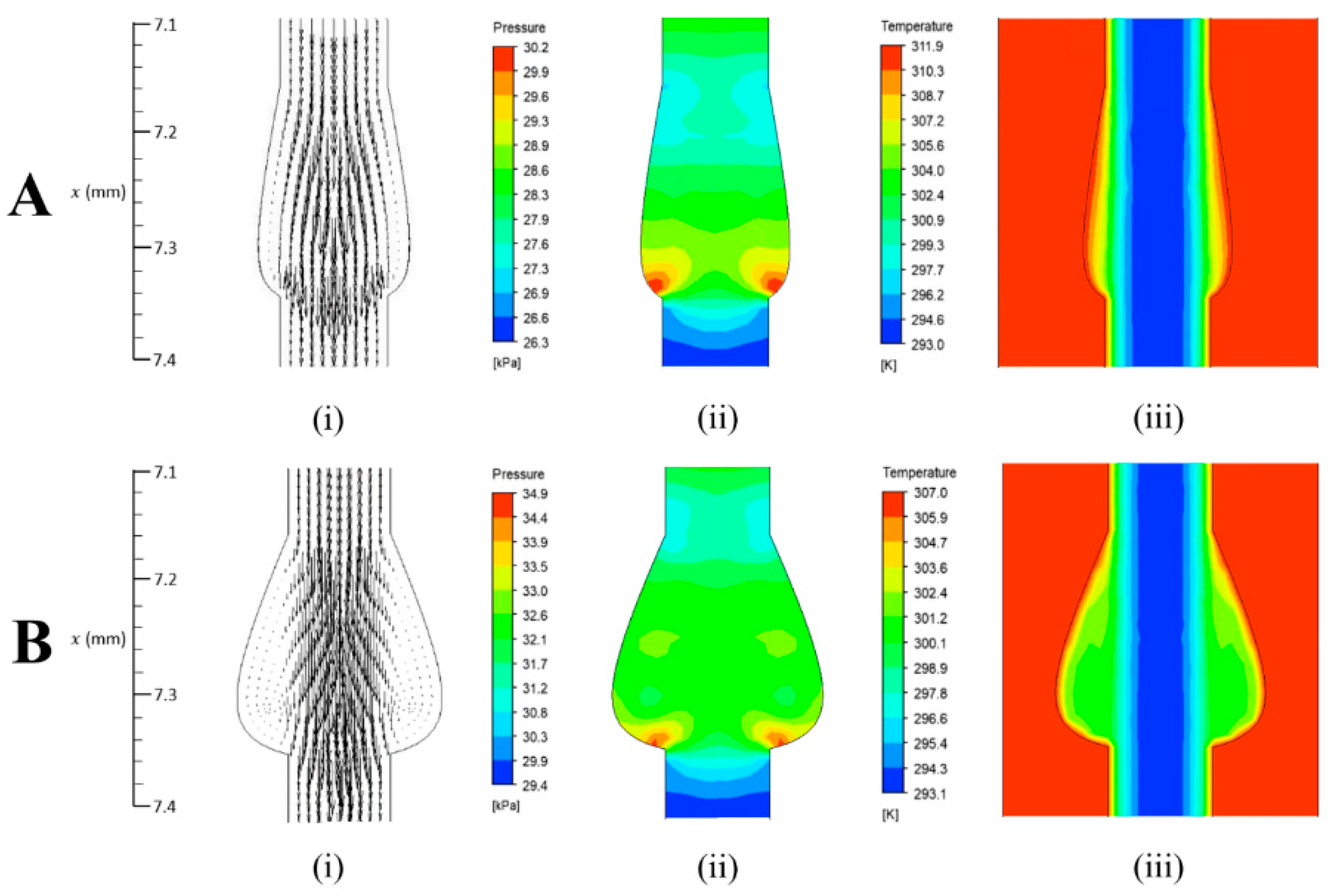
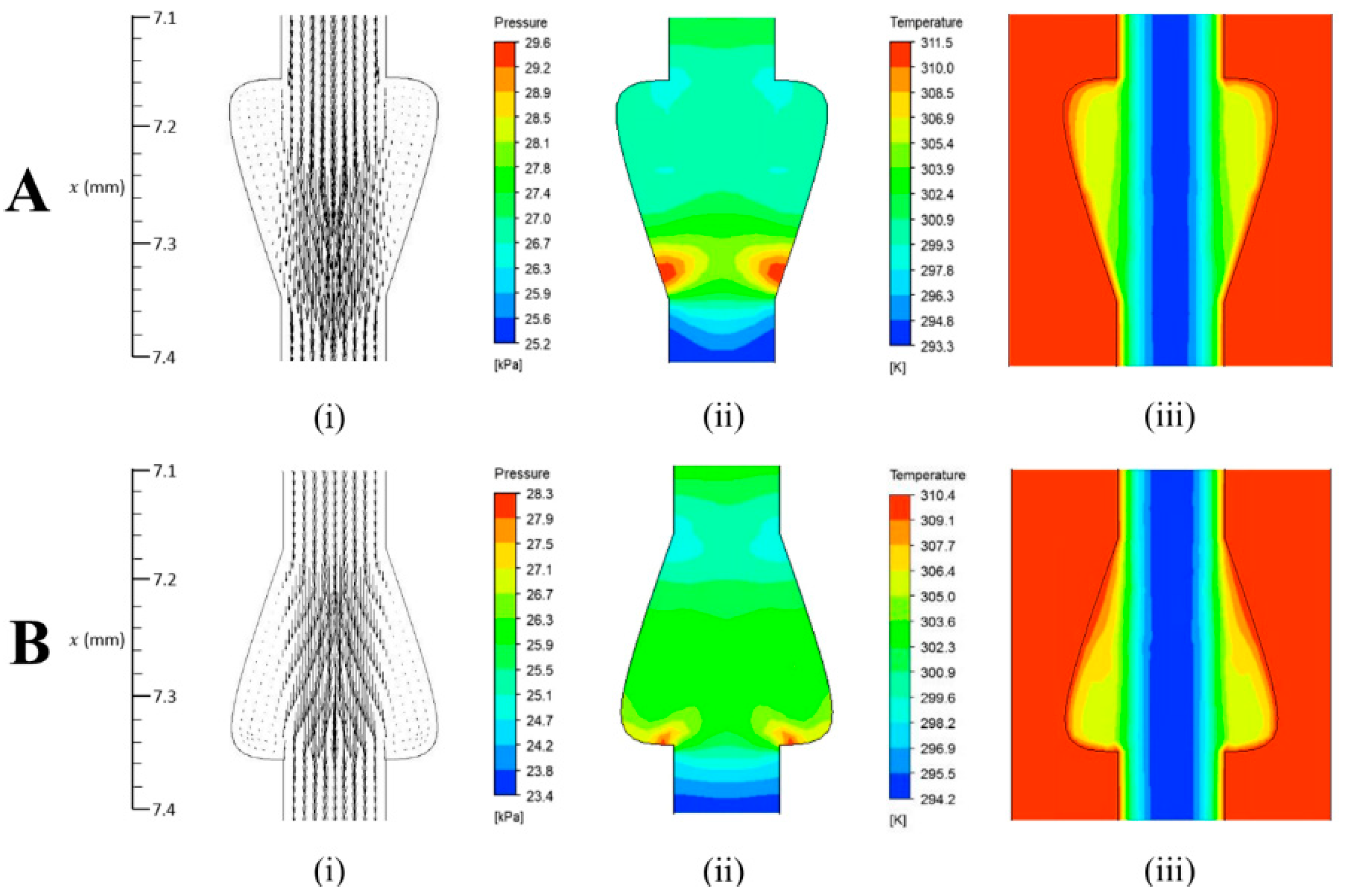
3.2. Flow Field Analysis of Conical-Shaped Microchannel Heat Sink
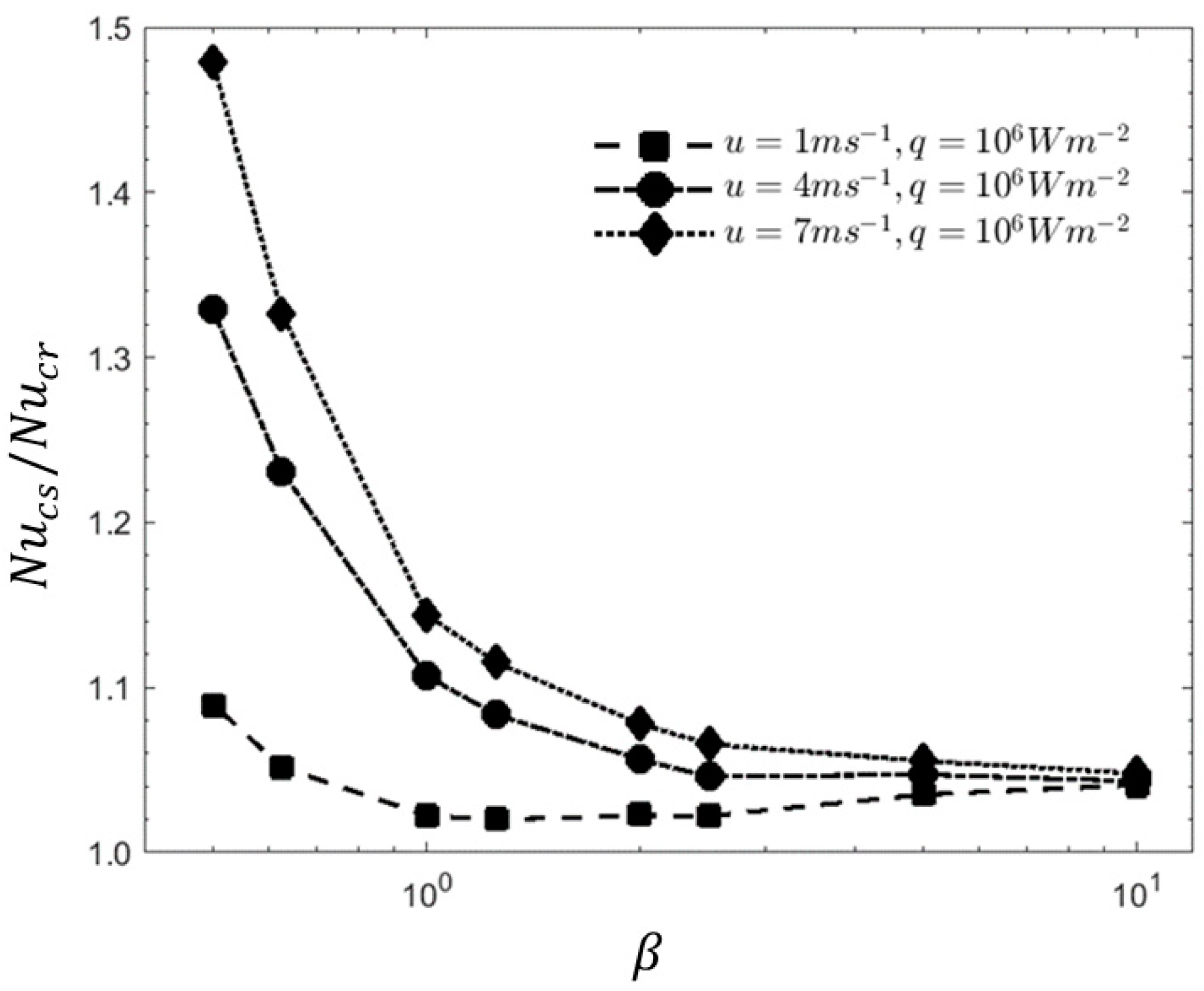
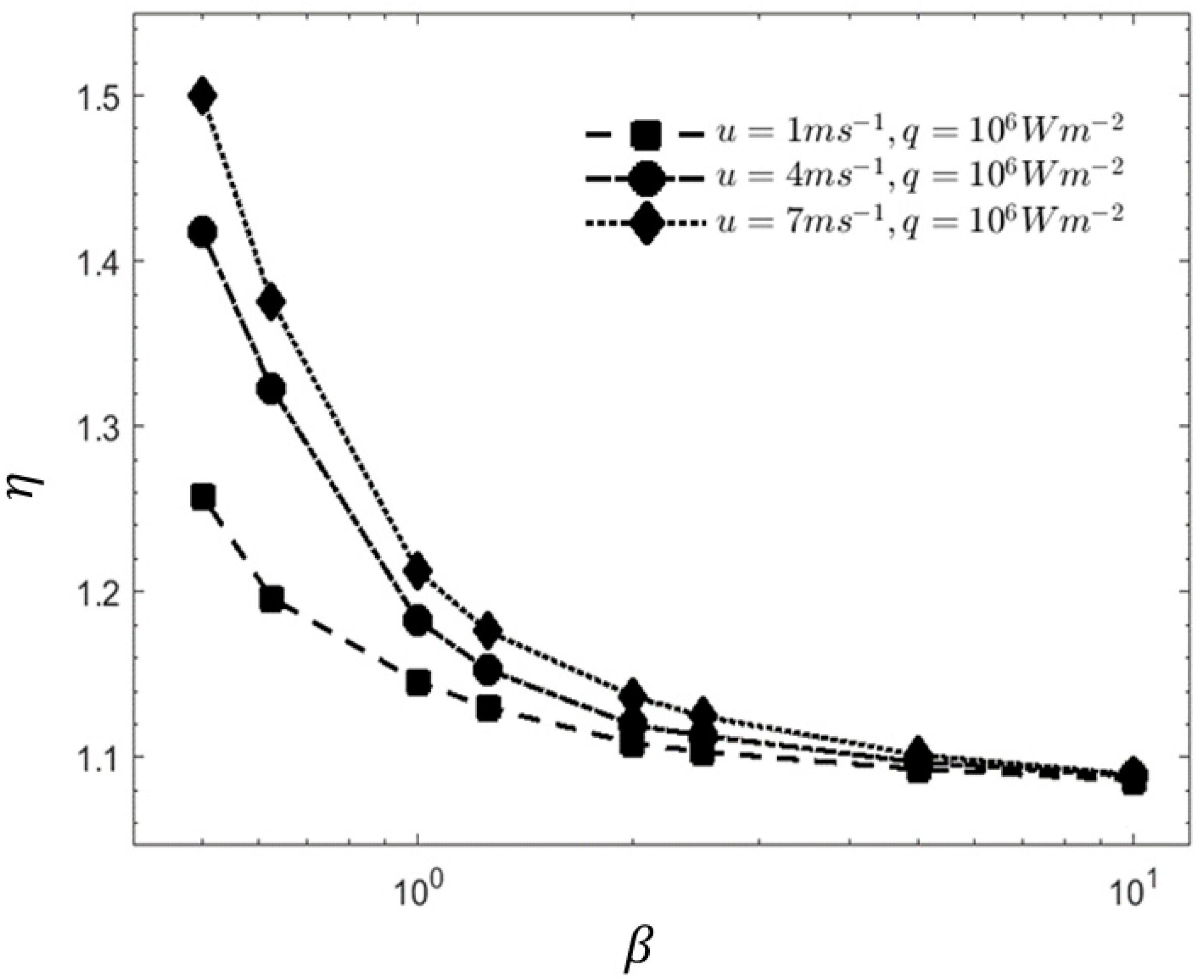
3.3. Influence of Cavity Number (β)
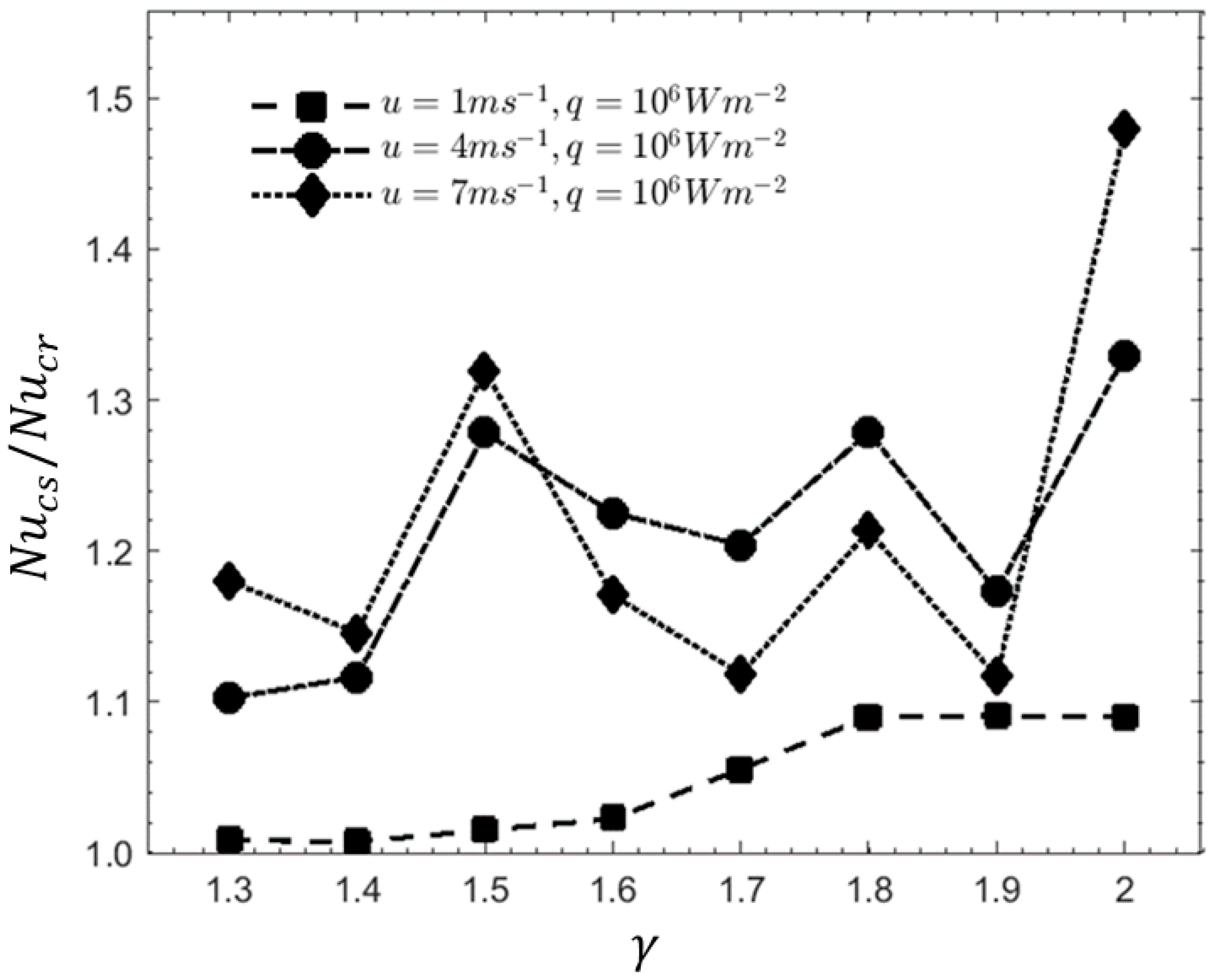
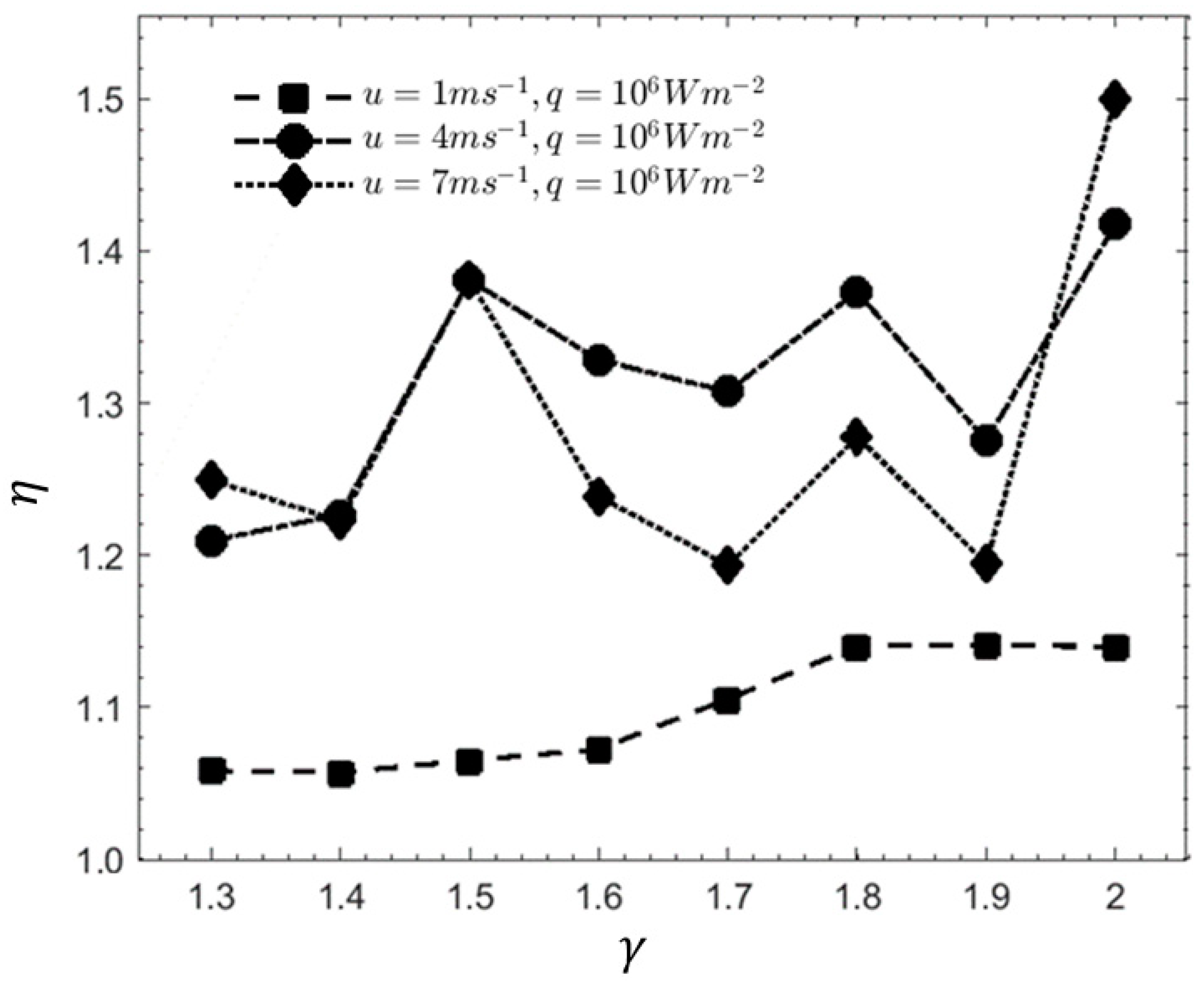
3.4. Influence of Cavity Width (γ)
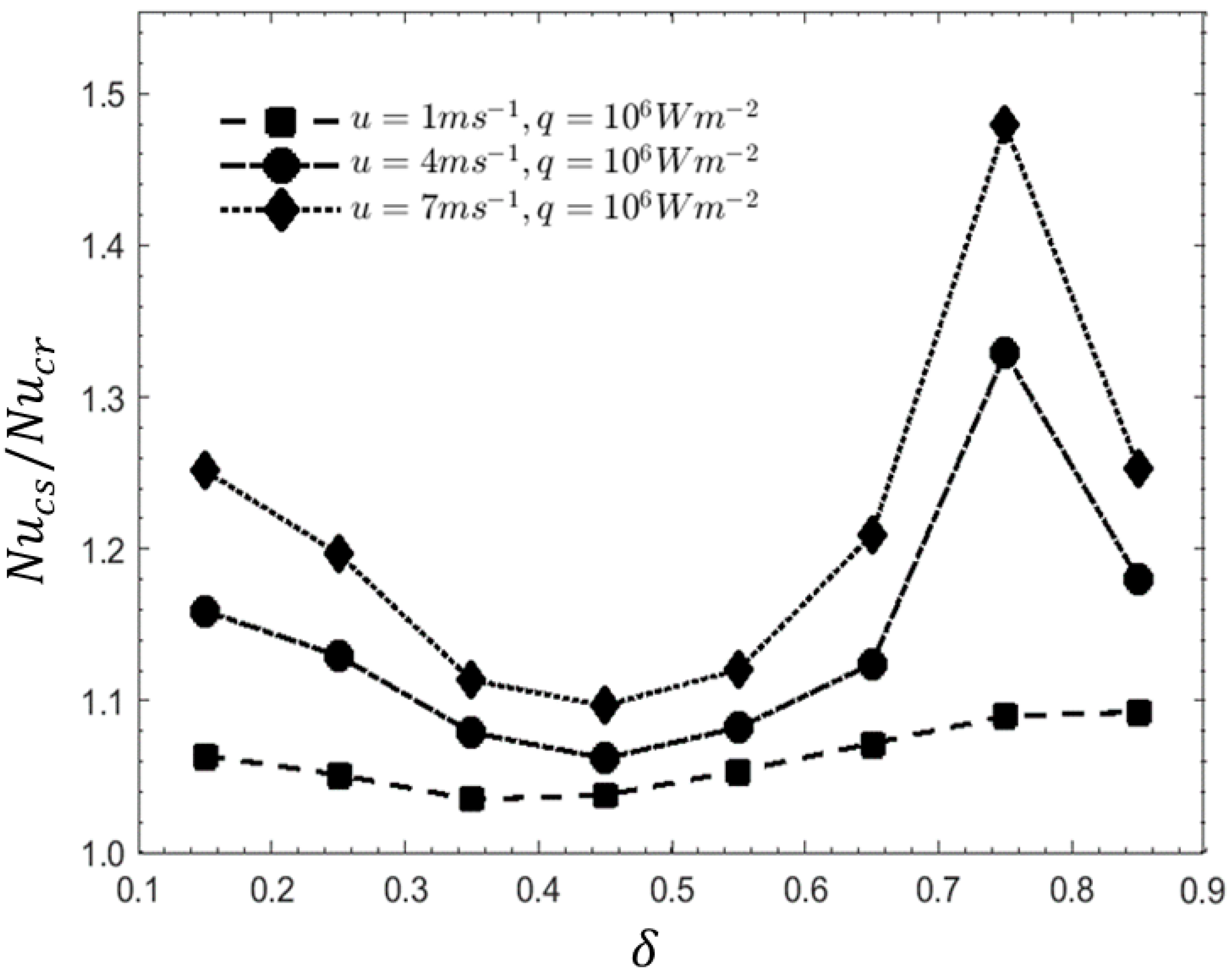
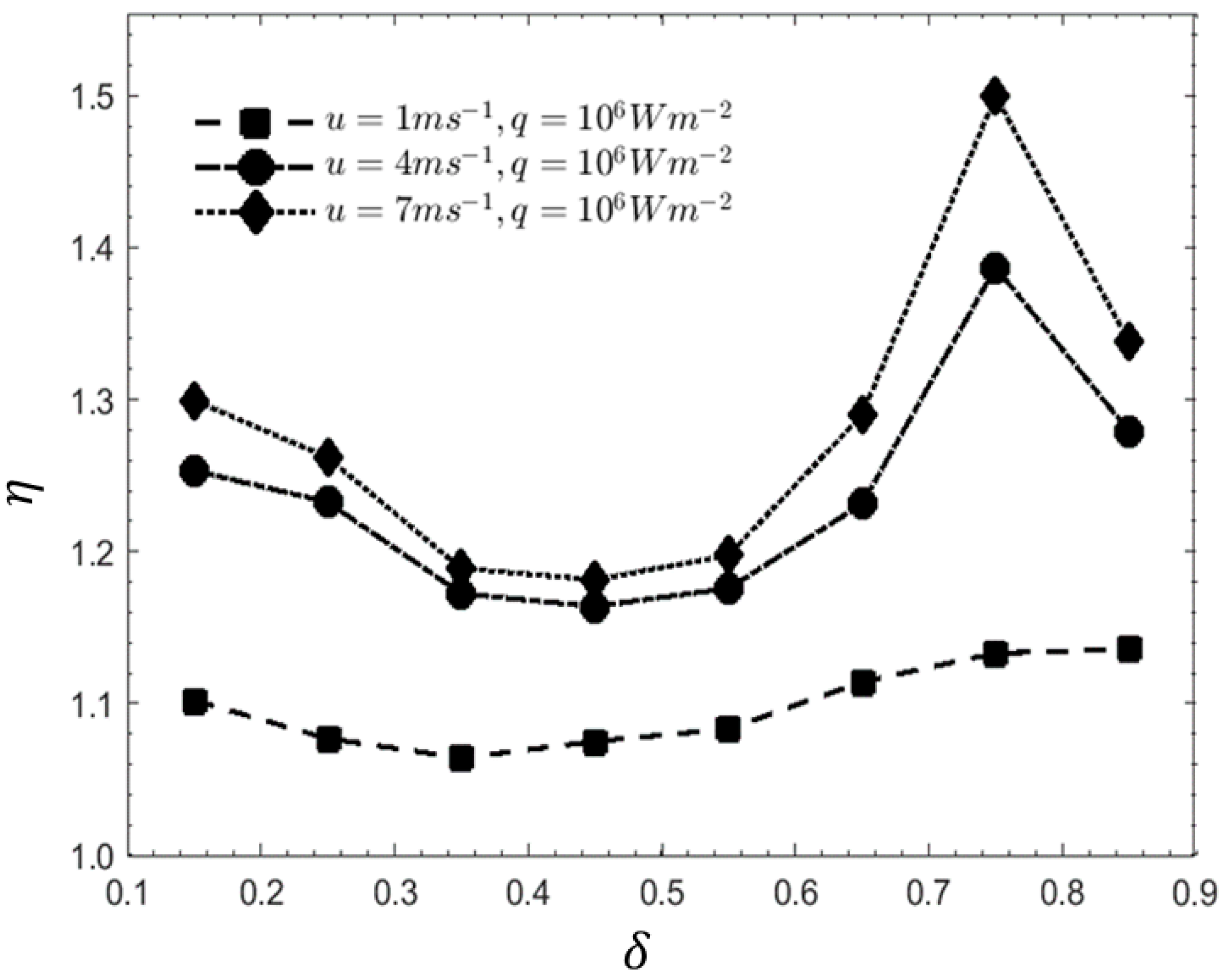
3.5. Influence of Peak Distance from the Entrance of Each Cavity (δ)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Contact surface area between water and silicon | ||
| Aspect ratio | - | |
| local coordinate normal to the wall | - | |
| Specific heat capacity | ||
| Hydraulic diameter | ||
| Friction factor | - | |
| Height of the microchannel | ||
| Heat transfer coefficient | ||
| Hagenbach factor | - | |
| Length of the microchannel | ||
| Number of cavities | - | |
| Nusselt number | - | |
| Pressure | ||
| Projected heat flux on the bottom of the microchannel | ||
| Reynolds number | - | |
| Temperature | ||
| Velocity | ||
| Total width of microchannel plus lateral wall | ||
| Dimensionless Cartesian coordinate | - | |
| Greek letters | ||
| Ratio of the total length of the channel respective to the number of cavities introduced | - | |
| Ratio of the largest width of the conical cavities side wall with the constant cross-section | - | |
| Ratio of the peak distance from the entrance of each cavity with the total length of the conic cavity | - | |
| Performance evaluation criterion | - | |
| Thermal conductivity | ||
| Dynamic viscosity | ||
| Density | ||
| Wall shear stress | ||
| Subscript | ||
| Average | ||
| Channel | ||
| Conic cavity | ||
| Conventional rectangular | ||
| Conic shape | ||
| Fluid | ||
| direction of Cartesian coordinate | ||
| Inlet | ||
| Mean | ||
| Outlet | ||
| Peak | ||
| Silicon | ||
| Space between cavity | ||
References
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Mohamad Noh, N.H.; Che Sidik, N.A. Numerical Simulation of Nanofluids for Improved Cooling Efficiency in Microchannel Heat Sink. Appl. Mech. Mater. 2014, 695, 403–407. [Google Scholar] [CrossRef]
- Peng, X.F.; Peterson, G.P. Convective heat transfer and flow friction for water flow in microchannel structures. Int. J. Heat Mass Transf. 1996, 39, 2599–2608. [Google Scholar] [CrossRef]
- Adams, T.M.; Abdel-Khalik, S.I.; Jeter, S.M.; Qureshi, Z.H. An experimental investigation of single-phase forced convection in microchannels. Int. J. Heat Mass Transf. 1998, 41, 851–857. [Google Scholar] [CrossRef]
- Tao, W.Q.; He, Y.L.; Wang, Q.W.; Qu, Z.G.; Song, F.Q. A unified analysis on enhancing single phase convective heat transfer with field synergy principle. Int. J. Heat Mass Transf. 2002, 45, 4871–4879. [Google Scholar] [CrossRef]
- Steinke, M.E.; Kandlikar, S.G. Single-phase heat transfer enhancement techniques in microchannel and minichannel flows. In Proceedings of the Second International Conference on Microchannels and Minichannels, Rochester, NY, USA, 17–19 June 2004; pp. 141–148. [Google Scholar]
- Gunnasegaran, P.; Mohammed, H.A.; Shuaib, N.H.; Saidur, R. The effect of geometrical parameters on heat transfer characteristics of microchannels heat sink with different shapes. Int. Commun. Heat Mass Transf. 2010, 37, 1078–1086. [Google Scholar] [CrossRef]
- Alfaryjat, A.A.; Mohammed, H.A.; Adam, N.M.; Ariffin, M.K.A.; Najafabadi, M.I. Influence of geometrical parameters of hexagonal, circular, and rhombus microchannel heat sinks on the thermohydraulic characteristics. Int. Commun. Heat Mass Transf. 2014, 52, 121–131. [Google Scholar] [CrossRef]
- Xia, G.; Chai, L.; Zhou, M.; Wang, H. Effects of structural parameters on fluid flow and heat transfer in a microchannel with aligned fan-shaped reentrant cavities. Int. J. Therm. Sci. 2011, 50, 411–419. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.; Zhou, M.; Li, J. Numerical simulation of fluid flow and heat transfer in a microchannel heat sink with offset fan-shaped reentrant cavities in sidewall. Int. Commun. Heat Mass Transf. 2011, 38, 577–584. [Google Scholar] [CrossRef]
- Xia, G.; Chai, L.; Wang, H.; Zhou, M.; Cui, Z. Optimum thermal design of microchannel heat sink with triangular reentrant cavities. Appl. Therm. Eng. 2011, 31, 1208–1219. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.; Wang, L.; Zhou, M.; Cui, Z. Heat transfer enhancement in microchannel heat sinks with periodic expansion-constriction cross-sections. Int. J. Heat Mass Transf. 2013, 62, 741–751. [Google Scholar] [CrossRef]
- Abouali, O.; Baghernezhad, N. Numerical Investigation of Heat Transfer Enhancement in a Microchannel With Grooved Surfaces. J. Heat Transf. 2010, 132, 041005. [Google Scholar] [CrossRef]
- Kuppusamy, N.R.; Mohammed, H.A.; Lim, C.W. Numerical investigation of trapezoidal grooved microchannel heat sink using nanofluids. Thermochim. Acta 2013, 573, 39–56. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Ahmed, M.I. Optimum thermal design of triangular, trapezoidal and rectangular grooved microchannel heat sinks. Int. Commun. Heat Mass Transf. 2015, 66, 47–57. [Google Scholar] [CrossRef]
- Li, Y.F.; Xia, G.D.; Ma, D.D.; Jia, Y.T.; Wang, J. Characteristics of laminar flow and heat transfer in microchannel heat sink with triangular cavities and rectangular ribs. Int. J. Heat Mass Transf. 2016, 98, 17–28. [Google Scholar] [CrossRef]
- Ghani, I.A.; Kamaruzaman, N.; Sidik, N.A.C. Heat transfer augmentation in a microchannel heat sink with sinusoidal cavities and rectangular ribs. Int. J. Heat Mass Transf. 2017, 108, 1969–1981. [Google Scholar] [CrossRef]
- Lin, L.; Zhao, J.; Lu, G.; Wang, X.D.; Yan, W.M. Heat transfer enhancement in microchannel heat sink by wavy channel with changing wavelength/amplitude. Int. J. Therm. Sci. 2017, 118, 423–434. [Google Scholar] [CrossRef]
- Alfellag, M.A.; Ahmed, H.E.; Fadhil, O.T.; Kherbeet, A.S. Optimal hydrothermal design of microchannel heat sink using trapezoidal cavities and solid/slotted oval pins. Appl. Therm. Eng. 2019, 158, 113765. [Google Scholar] [CrossRef]
- Gu, W.Z.; Shen, J.Y.; Ma, C.F. Heat Transfer Enhancement; Science Press: Beijing, China, 1990. [Google Scholar]
- Steinke, M.E.; Kandlikar, S.G. Single-phase liquid friction factors in microchannels. Int. J. Therm. Sci. 2006, 45, 1073–1083. [Google Scholar] [CrossRef]
- Sui, Y.; Teo, C.J.; Lee, P.S.; Chew, Y.T.; Shu, C. Fluid flow and heat transfer in wavy microchannels. Int. J. Heat Mass Transf. 2010, 53, 2760–2772. [Google Scholar] [CrossRef]

| Number of Cavities | 1 | 2 | 4 | 5 |
| 10 | 5 | 2.5 | 2 | |
| Number of Cavities | 8 | 10 | 16 | 20 |
| 1.25 | 1 | 0.625 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzhaimey, S.S.S.; Ghazali, N.N.N.; Zainon, M.Z.; Badruddin, I.A.; Hussien, M.; Kamangar, S.; Ahammad, N.A. Numerical Investigation of Heat Transfer Enhancement in a Microchannel with Conical-Shaped Reentrant Cavity. Mathematics 2022, 10, 4330. https://doi.org/10.3390/math10224330
Muzhaimey SSS, Ghazali NNN, Zainon MZ, Badruddin IA, Hussien M, Kamangar S, Ahammad NA. Numerical Investigation of Heat Transfer Enhancement in a Microchannel with Conical-Shaped Reentrant Cavity. Mathematics. 2022; 10(22):4330. https://doi.org/10.3390/math10224330
Chicago/Turabian StyleMuzhaimey, Syarif Syahrul Syazwan, Nik Nazri Nik Ghazali, Mohd Zamri Zainon, Irfan Anjum Badruddin, Mohamed Hussien, Sarfaraz Kamangar, and N. Ameer Ahammad. 2022. "Numerical Investigation of Heat Transfer Enhancement in a Microchannel with Conical-Shaped Reentrant Cavity" Mathematics 10, no. 22: 4330. https://doi.org/10.3390/math10224330
APA StyleMuzhaimey, S. S. S., Ghazali, N. N. N., Zainon, M. Z., Badruddin, I. A., Hussien, M., Kamangar, S., & Ahammad, N. A. (2022). Numerical Investigation of Heat Transfer Enhancement in a Microchannel with Conical-Shaped Reentrant Cavity. Mathematics, 10(22), 4330. https://doi.org/10.3390/math10224330





