New Delay-Partitioning LK-Functional for Stability Analysis with Neutral Type Systems
Abstract
1. Introduction
2. Related Works
3. Main Results
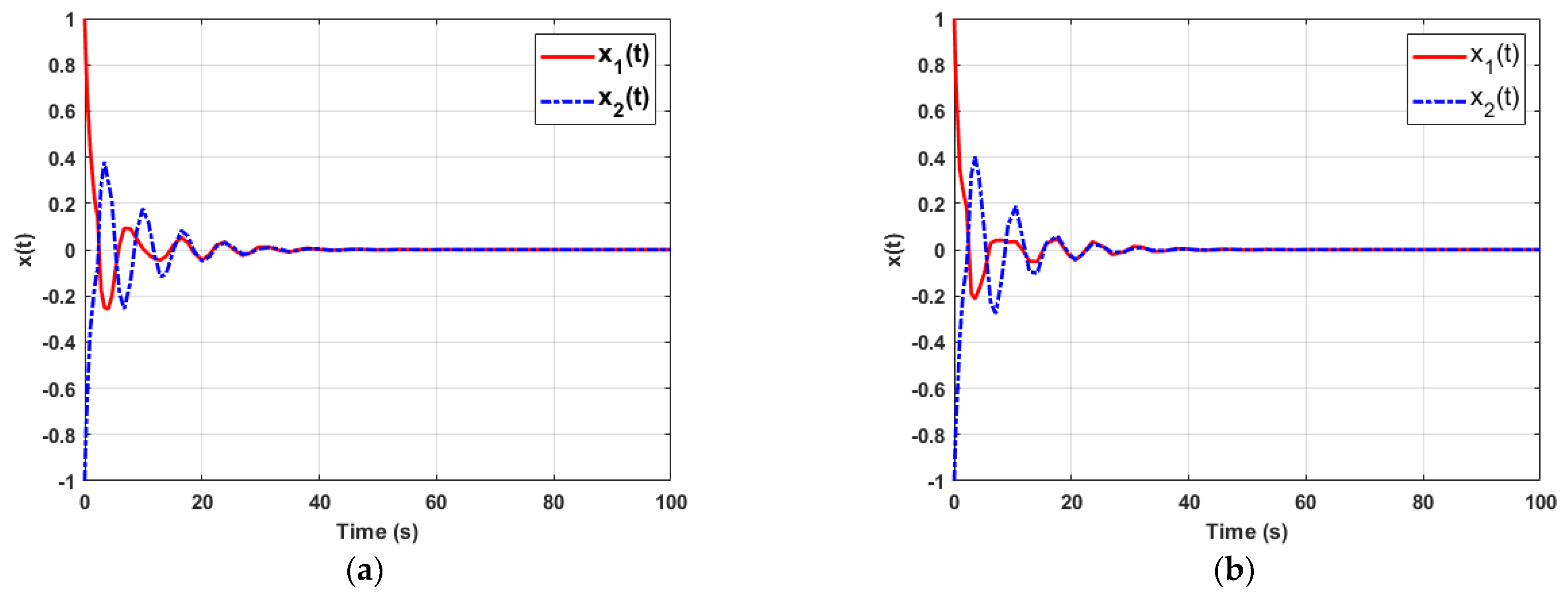
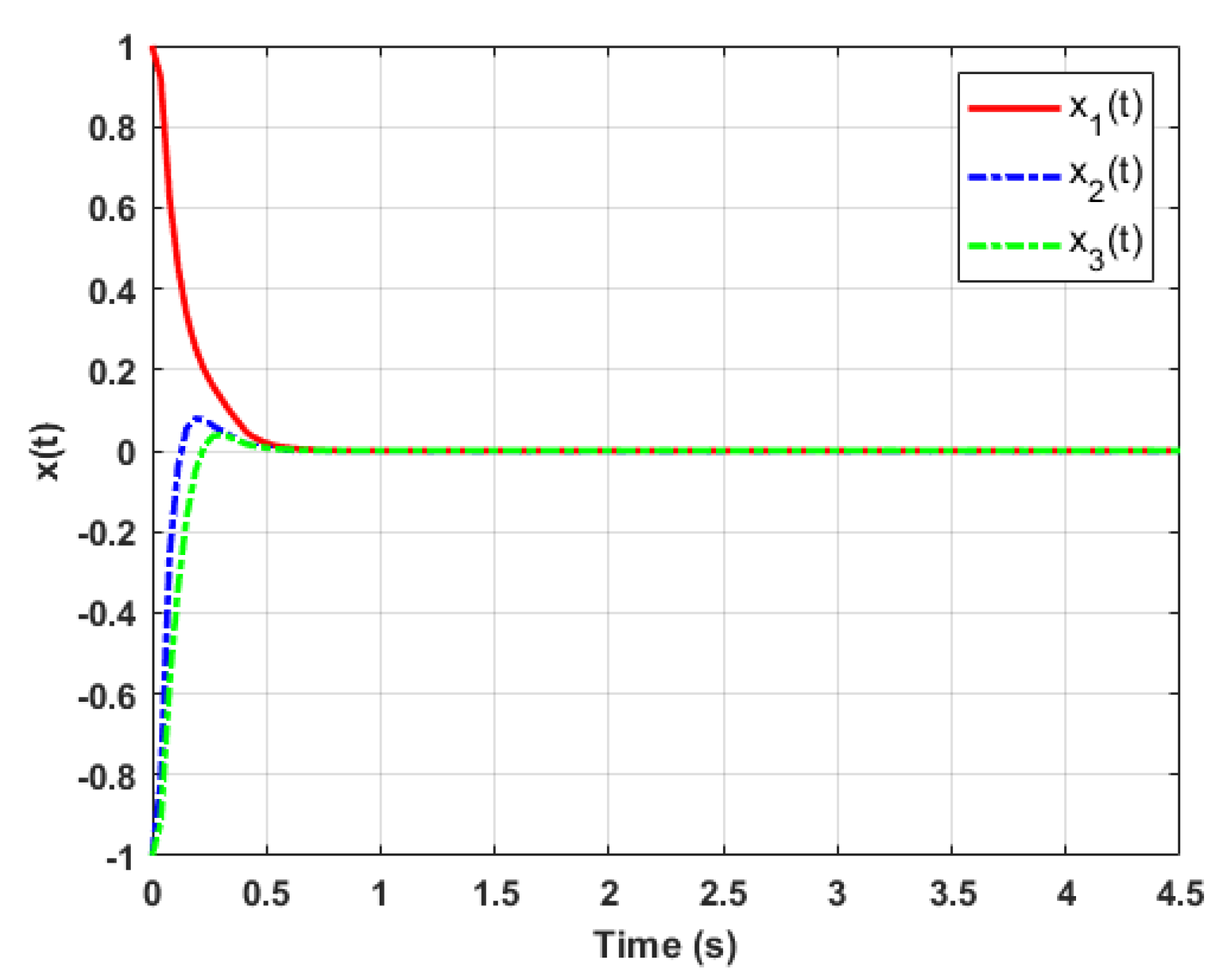
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, M.; He, Y.; She, J.H. Stability Analysis and Robust Control of Time-Delay Systems; Springer: Berlin, Germany, 2010. [Google Scholar]
- Park, J.H.; Lee, T.H.; Liu, Y.J.; Chen, J. Dynamic Systems with Time Delays: Stability and Control; Springer: Singapore, 2019. [Google Scholar]
- Kolmanovskii, V.B.; Myshkis, A. Applied Theory of Functional Differential Equations; Kluwer Academic Publishers: Boston, MA, USA, 1992. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: Boston, MA, USA, 1993. [Google Scholar]
- Ding, L.M.; He, Y.; Wu, M.; Wang, Q.G. New Augmented Lyapunov-Krasovskii Functional for Stability Analysis of Systems with Additive Time-Varying Delays. Asian J. Control 2018, 20, 1663–1670. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.Y.; Chen, W.M.; Zhang, B.Y.; Ma, Q.; Zou, Y. Two general integral inequalities and their applications to stability analysis for systems with time-varying delay. Int. J. Robust Nonlinear Control 2016, 26, 4088–4103. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.Y.; Zhang, B.Y. Single/Multiple Integral Inequalities with Applications to Stability Analysis of Time-Delay Systems. IEEE Trans. Autom. Control 2017, 62, 3488–3493. [Google Scholar] [CrossRef]
- Gu, K.; Niculescu, S. Survey on recent results in the stability and control of time-delay systems. Trans. ASME J. Dyn. Syst. Meas. Control 2003, 125, 158–165. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Seuret, A.; Gouaisbaut, F.; He, Y. Overview of recent advances in stability of linear systems with time-varying delays. IET Control Theory Appl. 2019, 13, 1–16. [Google Scholar] [CrossRef]
- He, Y.; Wu, M.; She, J.H.; Liu, G.P. Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays. Syst. Control Lett. 2004, 51, 57–65. [Google Scholar] [CrossRef]
- Liu, X.G.; Wu, M.; Martin, R.; Tang, M.L. Stability analysis for neutral systems with mixed delays. J. Comput. Appl. Math. 2007, 202, 478–497. [Google Scholar] [CrossRef]
- Qian, W.; Liu, J.; Sun, Y.; Fei, S. A less conservative robust stability criteria for uncertain neutral systems with mixed delays. Math. Comput. Simulat. 2010, 80, 1007–1017. [Google Scholar] [CrossRef]
- Chen, Y.G.; Fei, S.M.; Gu, Z.; Li, Y.M. New mixed-delay-dependent robust stability conditions for uncertain linear neutral systems. IET Control Theory Appl. 2014, 8, 606–613. [Google Scholar] [CrossRef]
- Ding, L.M.; He, Y.; Wu, M.; Ning, C.Y. Improved mixed-delay-dependent asymptotic stability criteria for neutral systems. IET Control Theory Appl. 2015, 9, 2180–2187. [Google Scholar] [CrossRef]
- Idrissi, S.; Tissir, E.H.; Boumhidi, I.; Chaibi, N. New delay dependent robust stability criteria for T-S fuzzy systems with constant delay. Int. J. Control Autom. Syst. 2013, 11, 885–892. [Google Scholar] [CrossRef]
- Yang, J.; Luo, W.P.; Wang, Y.H.; Duan, C.S. Improved stability criteria for TS fuzzy systems with time-varying delay by delay-partitioning approach. Int. J. Control Autom. Syst. 2015, 13, 1521–1529. [Google Scholar] [CrossRef]
- Idrissi, S.; Tissir, E.H.; Boumhidi, I.; Chaibi, N. Robust H∞ control for uncertain TS fuzzy systems via delay partitioning approach. Int. J. Ecol. Dev. 2014, 28, 96–108. [Google Scholar]
- Li, T.; Tang, X.L.; Qian, W.; Fei, S.M. Mixed-delay-dependent stability for time-delay neutral system: An improved dynamic Lyapunov method. IET Control Theory Appl. 2019, 9, 869–877. [Google Scholar] [CrossRef]
- Yue, D.; Han, Q.L. A delay-dependent stability criterion of neutral systems and its applicaiton to a partial element equivalent cricuit model. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Sun, J.; Liu, G.P. On improved delay-dependent stability criteria for neutral time-delay systems. Eur. J. Control 2009, 15, 613–623. [Google Scholar] [CrossRef]
- Xiong, L.L.; Cheng, J.; Liu, X.Z.; Wu, T. Improve conditions for neutral delay systems with novel inequlities. J. Nonlinear Sci. Appl. 2017, 10, 2309–2317. [Google Scholar] [CrossRef]
- Kharitonov, V.; Plischke, E. Lyapunov matrices for time-delay systems. Syst. Control Lett. 2006, 55, 697–706. [Google Scholar] [CrossRef]
- Han, Q.L. A new delay-dependent absolute stability criterion for a class of nonlinear systems. Automatica 2008, 44, 272–277. [Google Scholar] [CrossRef]
- He, Y.; Wang, Q.G.; Lin, C.; Wu, M. Augmented Lyapunov functional and delay-dependent stability criteria for neutral systems. Int. J. Robust Nonlinear Control 2019, 7, 104655–104666. [Google Scholar] [CrossRef]
- Duan, W.; Li, Y.; Chen, J. Further stability analysis for time-delayed neural networks based on an augmented Lyapunov functional. IEEE Access 2018, 355, 5957–5967. [Google Scholar] [CrossRef]
- Mahto, S.C.; Elavarasan, R.M.; Ghosh, S.; Saket, R.K.; Hossain, E.; Nagar, S.K. Improved Stability Criteria for Time-Varying Delay System Using Second and First Order Polynomials. IEEE Access 2020, 8, 210961–210969. [Google Scholar] [CrossRef]
- Ding, L.M.; He, Y.; Wu, M.; Zhang, Z.M. A novel delay partitioning method for stability analysis of interval time-varying delay systems. J. Frankl. Inst. 2017, 354, 1209–1219. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, J.H. A novel lyapunov functional for stability of time-varying delay systems via matrix-refined-function. Automatica 2017, 80, 239–242. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, G. Stability analysis of delayed neural networks based on a relaxed delay-product-type lyapunov functional. Neurocomputing 2021, 439, 340–347. [Google Scholar] [CrossRef]
- Mahto, S.C.; Ghosh, S.; Saket, R.K. Shyam Krishna Nagar, Stability analysis of delayed neural network using new delay-product based functionals. Neurocomputing 2020, 417, 106–113. [Google Scholar] [CrossRef]
- Udhayakumar, K.; Rihan, F.A.; Rakkiyappan, R.; Cao, J.D. Fractional-order discontinuous systems with indefinite lkfs: An application to fractional-order neural networks with time delays. Neural Netw. 2021, 145, 319–330. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; She, J.H. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay. IEEE Trans. Autom. Control 2015, 60, 2768–2772. [Google Scholar] [CrossRef]
- Park, P.; Lee, W.I.; Lee, S.Y. Auxiliary function-based integral/summation inequalities: Application to continuous/discrete time-delay systems. Int. J. Control Autom. Syst. 2016, 14, 3–11. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using Bessel-Legendre inequalities. IEEE Trans. Autom. Control 2018, 63, 225–232. [Google Scholar] [CrossRef]
- Huang, Y.B.; He, Y.; An, J.Q.; Wu, M. Polynomial-type Lyapunov-Krasovskii functional and Jacobi-Bessel inequality: Further results on stability analysis of time-delay systems. IEEE Trans. Autom. Control 2021, 66, 2905–2912. [Google Scholar] [CrossRef]
- Zhao, N.; Lin, C.; Chen, B.; Wang, Q.G. A new double integral inequlity and application to stability test for time-delay systems. Appl. Math. Lett. 2017, 65, 26–31. [Google Scholar] [CrossRef]
- Tian, J.K.; Ren, Z.R.; Zhong, S.M. A new integral inequality and application to stability of time-delay systems. Appl. Math. Lett. 2020, 101, 106058. [Google Scholar] [CrossRef]
- Jin, L.; He, Y.; Jiang, L. A novel integral inequality and its application to stability analysis of linear system with multiple delays. Appl. Math. Lett. 2022, 124, 107648. [Google Scholar] [CrossRef]
- Park, P.G.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Zhang, C.K.; He, Y.; Jiang, L.; Wu, M.; Wang, Q.G. An extended reciprocally convex matrix inequality for stability analysis of systems with time-varying delay. Automatica 2017, 85, 481–485. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Seuret, A.; Gouaisbaut, F. An improved reciprocally convex inequality and an augmented Lyapunov-Krasovskii functional for stability of linear systems with time-varying delay. Automatica 2017, 84, 221–226. [Google Scholar] [CrossRef]
- Seuret, A.; Liu, K.; Gouaisbaut, F. Generalized reciprocally convex combination lemmas and its application to time-delay systems. Automatica 2018, 95, 488–493. [Google Scholar] [CrossRef]
- Zeng, H.B.; Lin, H.C.; He, Y.; Teo, K.L.; Wang, W. Hierarchical stability conditions for time-varying delay systems via an extended reciprocally convex quadratic inequality. J. Frankl. Inst. 2020, 357, 9930–9941. [Google Scholar] [CrossRef]
- Kim, J.H. Further improvement of Jensen inequality and application to stability of time-delayed systems. Automatica 2016, 64, 121–125. [Google Scholar] [CrossRef]
- Zhang, C.K.; Long, F.; He, Y.; Yao, W.; Jiang, L.; Wu, M. A relaxed quadratic function negative-determination lemma and its application to time-delay systems. Automatica 2020, 113, 108764. [Google Scholar] [CrossRef]
- De Oliveira, F.S.; Souza, F.O. Further refinements in stability conditions for time-varying delay systems. Appl. Math. Comput. 2020, 369, 124866. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, X.M.; Park, J.H.; Xu, S.Y. Improved stability criteria for delayed neural networks using a quadratic function negative-definiteness approach. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1348–1354. [Google Scholar] [CrossRef] [PubMed]
| Method | 0.1 | 0.5 | 1 | ||
|---|---|---|---|---|---|
| [10] | 1.7100 | 1.6781 | 1.6543 | 114 | |
| [11] | 1.7884 | 1.7495 | 1.7201 | 129 | |
| [12] | 1.8307 | 1.7755 | 1.7213 | 96 | |
| [13], Theorem 3 (N = 5) | 2.2137 | 2.3210 | 2.3588 | 113 | |
| [14], Theorem 2 (N = 5) | 2.2181 | 2.3331 | 2.3636 | 120 | |
| [21], Theorem 3.1 | 2.2961 | 2.3491 | 2.3773 | 268 | |
| = 0.75 | 2.2950 | 2.3478 | 2.3759 | 893 | |
| = 0.6 | 2.2963 | 2.3481 | 2.3775 | 893 | |
| Analytical bounds | 2.2963 | 2.3491 | 2.3775 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, L.; Chen, L.; He, D.; Xiang, W. New Delay-Partitioning LK-Functional for Stability Analysis with Neutral Type Systems. Mathematics 2022, 10, 4119. https://doi.org/10.3390/math10214119
Ding L, Chen L, He D, Xiang W. New Delay-Partitioning LK-Functional for Stability Analysis with Neutral Type Systems. Mathematics. 2022; 10(21):4119. https://doi.org/10.3390/math10214119
Chicago/Turabian StyleDing, Liming, Liqin Chen, Dajiang He, and Weiwei Xiang. 2022. "New Delay-Partitioning LK-Functional for Stability Analysis with Neutral Type Systems" Mathematics 10, no. 21: 4119. https://doi.org/10.3390/math10214119
APA StyleDing, L., Chen, L., He, D., & Xiang, W. (2022). New Delay-Partitioning LK-Functional for Stability Analysis with Neutral Type Systems. Mathematics, 10(21), 4119. https://doi.org/10.3390/math10214119







