Computational Scheme for the First-Order Linear Integro-Differential Equations Based on the Shifted Legendre Spectral Collocation Method
Abstract
1. Introduction
2. Approximation Scheme Design
2.1. System Formulating
2.2. Approximation Theory
2.3. Approximation Scheme Design
3. Approximation Scheme Convergence
3.1. The Trotter-Kato Theorem
- (A1)
- , , where and are independent of N;
- (A2)
- as , for all ;
- (A3)
- , where is the identity operator on .
- (a)
- There exists a such that, for all ,
- (b)
- for every and ,uniformly on bounded t-intervals.
- (C1)
- There exists a subset such that and for a ;
- (C2)
- For all there exists a sequence with such that
3.2. Convergence for the Scheme
- (A1)
- , , where and are independent of N;
- (A2)
- as , for all ;
- (A3)
- , where is the n-dimensional identity operator on .
4. Scheme Application
4.1. Approximation Algorithm
- Step 1: Inputting system parameters. Input the system parameters for the system operator and boundary operator . Input T as the upper boundary value of the transient rate function. Input N as the number of discrete nodes to approximation.
- Step 3: Decompositing the system operator. By definded the integral operator , differential operator and boundary operator , we decompose the system operator into , and , which are defined as in Section 2.3, and
- Step 4: Constructing an approximating operator. Based on Step 1, Step 2 and Step 3, we construct an approximating operator aswhere , and are defined in Section 2.3, ⊗ is the Kronecker product and is the n-dimensional identity matrix.
4.2. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.J. General Fractional Derivatives: Theory, Methods and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019; pp. 52–85. ISBN 978-04-2928-408-3. [Google Scholar]
- Shiri, B. A note on using the Differential Transformation Method for the Integro-Differential Equations. Appl. Math. Comput. 2013, 219, 7306–7309. [Google Scholar] [CrossRef]
- Hariharan, G.; Kannan, K. Review of wavelet methods for the solution of reaction-diffusion problems in science and engineering. Appl. Math. Model. 2014, 38, 799–813. [Google Scholar] [CrossRef]
- Iannelli, M.; Milner, F. The Basic Approach to Age-Structured Population Dynamics, 1st ed.; Springer: Dordrecht, The Netherlands, 2017; pp. 10–250. ISBN 978-94-0241-146-1. [Google Scholar]
- Shortle, J.F.; Thompson, J.M.; Gross, D.; Harris, C.M. Fundamentals Of Queueing Theory, 3rd ed.; John Wiley and Sons: New York, NY, USA, 2018; pp. 25–75. ISBN 978-71-1556-998-1. [Google Scholar]
- Ascher, H.; Feingold, H. Repairable Systems Reliability: Modeling, Inference, Misconceptions, and Their Causes; Wiley Online Library: Hoboken, NJ, USA, 1985; pp. 119–223. ISBN 0-8247-7276-8. [Google Scholar]
- Sharma, G.; Rai, R.N. Reliability modeling and analysis of environmental control and life support systems of space stations: A literature survey. Acta Astronaut. 2018, 155, 238–246. [Google Scholar] [CrossRef]
- Cox, D. The analysis of non-Markovian stochastic processes by the inclusion of supplementary variables. Math. Proc. Camb. 1955, 51, 433–441. [Google Scholar] [CrossRef]
- Li, Y.; Meng, X.Y. Reliability analysis of a warm standby repairable system with priority in use. Appl. Math. Model. 2011, 35, 4295–4303. [Google Scholar] [CrossRef]
- Huo, H.; Xu, H.; Chen, Z. Modelling and dynamic behaviour analysis of the software rejuvenation system with periodic impulse. Math. Comp. Model. Dyn. 2021, 27, 522–542. [Google Scholar] [CrossRef]
- Zheng, F.; Xu, S.S.; Li, X. Numerical solution of the steady-state probability and reliability of a repairable system with three unites-ScienceDirect. Appl. Math. Comput. 2015, 263, 251–267. [Google Scholar] [CrossRef]
- Nazarov, A.; Melikov, A.; Pavlova, E. Analyzing an M/M/N Queueing System with Feedback by the Method of Asymptotic Analysis. Cybern. Syst. Anal. 2021, 57, 57–65. [Google Scholar] [CrossRef]
- Yuan, L.; Guan, J. An optimal repair–replacement policy for a cold standby system with use priority. Appl. Math. Model. 2013, 35, 1222–1230. [Google Scholar] [CrossRef]
- Zong, S.; Chai, G.; Zhe, G. Optimal replacement policy for a deteriorating system with increasing repair times. Appl. Math. Model. 2013, 37, 9768–9775. [Google Scholar] [CrossRef]
- Gupur, G. Functional Analysis Methods for Reliability Models; Springer: Basel, Switzerland, 2011; pp. 59–133. ISBN 978-3-0348-0101-0. [Google Scholar]
- Pazy, A. Semigroups of Linear Operator and Applications to Partial Differential Equations; Springer: New York, NY, USA, 1983; pp. 8–22. ISBN 978-01-4612-5563-8. [Google Scholar]
- Xu, H.; Yu, J.; Zhu, G. Asymptotic property of a reparable multi-state device. Quart. Appl. Math. 2005, 63, 779–789. [Google Scholar] [CrossRef][Green Version]
- Hu, W. Differentiability and compactness of the C0-semigroup generated by the reparable system with finite repair time. J. Math. Anal. Appl. 2016, 433, 1614–1625. [Google Scholar] [CrossRef]
- Wang, W.L.; Xu, G.Q. Stability analysis of a complex standby system with constant waiting and different repairman criteria incorporating environmental failure. Appl. Math. Model. 2009, 33, 724–743. [Google Scholar] [CrossRef]
- Rhodes, C.A.; House, T. The rate of convergence to early asymptotic behaviour in age-structured epidemic models. Theor. Popul. Biol. 2013, 85, 58–62. [Google Scholar] [CrossRef]
- Fu, Z.; Zhu, G.; Chao, G. Well-posedness and stability of the repairable system with N failure modes and one standby unit. J. Math. Anal. Appl. 2011, 375, 174–184. [Google Scholar] [CrossRef][Green Version]
- Funaro, D. Polynomial Approximation of Differential Equations; Springer: New York, NY, USA, 1992; ISBN 3-540-55230-8. [Google Scholar]
- Mastroianni, G.; Milovanovic, G. Interpolation Processes; Springer: New York, NY, USA, 2008; pp. 48–68. ISBN 978-35-4068-346-9. [Google Scholar]
- Jie, S.; Tao, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer: New York, NY, USA, 2011; pp. 47–105. ISBN 978-3-540-71041-7. [Google Scholar]
- Dzhumabaev, D.S. On one approach to solve the linear boundary value problems for Fredholm integro-differential equations. J. Comput. Appl. Math. 2016, 294, 342–357. [Google Scholar] [CrossRef]
- Dzhumabaev, D.S. New general solutions to linear Fredholm integro-differential equations and their applications on solving the boundary value problems. J. Comput. Appl. Math. 2018, 327, 79–108. [Google Scholar] [CrossRef]
- Dzhumabaev, D.S. Computational methods of solving the boundary value problems for the loaded differential and Fredholm integro-differential equations. Math. Methods Appl. 2018, 41, 1439–1462. [Google Scholar] [CrossRef]
- Rahmoune, A. Spectral collocation method for solving Fredholm integral equations on the half-line. Appl. Math. Comput. 2013, 219, 9254–9260. [Google Scholar] [CrossRef]
- Al-Ahmad, S.; Sulaiman, I.B.; Nawi, M.A.A.; Mamat, M.; Ahmad, M.Z. Analytical solution of systems of Volterra integro-differential equations using modified differential transform method. J. Math. Comput. Sci. 2022, 26, 1–9. [Google Scholar] [CrossRef]
- Xu, M.M.; Sulaiman, J.; Ali, L.H. Half-sweep SOR iterative method using linear rational finite difference approximation for first-order Fredholm integro-differential equations. Int. J. Math. Comput. Sci. 2021, 16, 1555–1570. [Google Scholar]
- Dawood, L.A.; Hamoud, A.A.; Mohammed, N.M. Laplace discrete decomposition method for solving nonlinear Volterra-Fredholm integro-differential equations. J. Math. Comput. Sci. 2020, 2, 158–163. [Google Scholar] [CrossRef]
- Iskandarov, S. Estimate and asymptotic smallness of solutions of a weakly nonlinear implicit Volterra integro-differential equation of the first order on the semiaxis. Lobachevskii J. Math. 2021, 42, 3645–3651. [Google Scholar] [CrossRef]
- Xu, H.; Hu, W. Analysis and approximation of a reliable model. Appl. Math. Model. 2013, 37, 3777–3788. [Google Scholar] [CrossRef]
- Xu, H.; Hu, W. Modelling and analysis of repairable systems with preventive maintenance. Appl. Math. Comput. 2013, 224, 46–53. [Google Scholar] [CrossRef]
- Boardman, N.; Hu, W.; Mishra, R. Optimal Maintenance Design for a Simple Reparable System. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 3098–3103. [Google Scholar] [CrossRef]
- Guo, B.Y.; Wang, Z.Q. Legendre-Gauss collocation methods for ordinary differential equations. Adv. Comput. Math. 2009, 30, 249–280. [Google Scholar] [CrossRef]
- Lax, P.D.; Richtmyer, R.D. Survey of the stability of linear finite differential equations. Commun. Pure Appl. Math. 1956, 9, 267–293. [Google Scholar] [CrossRef]
- Ito, K.; Kappel, K. The Trotter-Kato theorem and approximation of PDEs. Math. Comput. 1998, 67, 21–44. [Google Scholar] [CrossRef]
- Issa, M.B.; Hamoud, A.; Ghadle, K. Numerical solutions of fuzzy integro-differential equations of the second kind. J. Math. Comput. Sci. 2021, 23, 67–74. [Google Scholar] [CrossRef]
- Ghanbari, M. A new computational method for solving the first order linear fuzzy Fredholm integro-differential equations. J. Interpolat. Approx. Sci. Comput. 2013, 13, 89–101. [Google Scholar]



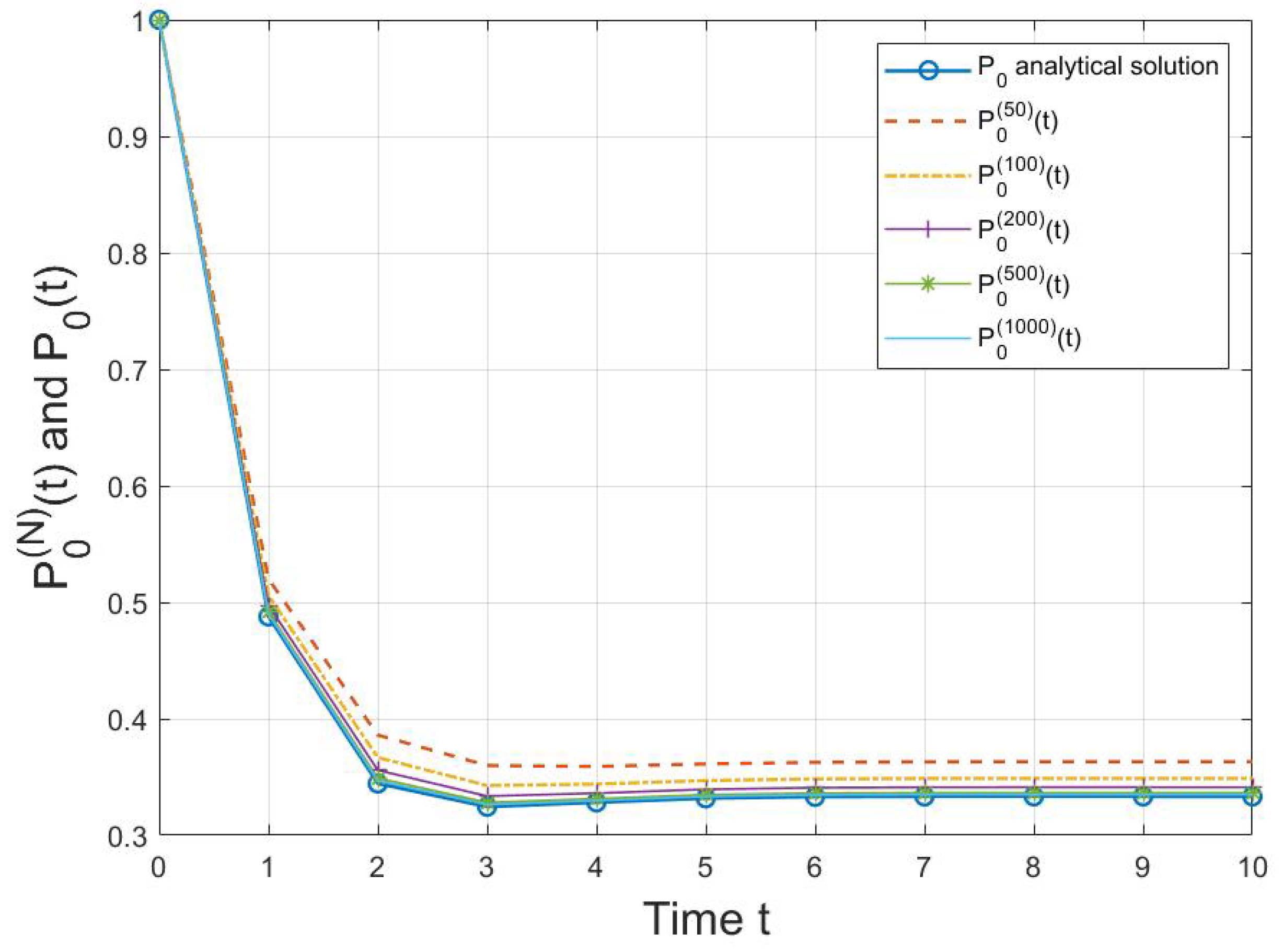
| Analytical Solution | Approximation Solutions Derived by (30) | ||||||
|---|---|---|---|---|---|---|---|
| Value | Value | Error | Value | Error | Value | Error | |
| Analytical Solution | Approximation Solutions by Finite-Differences Method | ||||||
|---|---|---|---|---|---|---|---|
| Value | Value | Error | Value | Error | Value | Error | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xu, H.; Huo, H. Computational Scheme for the First-Order Linear Integro-Differential Equations Based on the Shifted Legendre Spectral Collocation Method. Mathematics 2022, 10, 4117. https://doi.org/10.3390/math10214117
Chen Z, Xu H, Huo H. Computational Scheme for the First-Order Linear Integro-Differential Equations Based on the Shifted Legendre Spectral Collocation Method. Mathematics. 2022; 10(21):4117. https://doi.org/10.3390/math10214117
Chicago/Turabian StyleChen, Zhuoqian, Houbao Xu, and Huixia Huo. 2022. "Computational Scheme for the First-Order Linear Integro-Differential Equations Based on the Shifted Legendre Spectral Collocation Method" Mathematics 10, no. 21: 4117. https://doi.org/10.3390/math10214117
APA StyleChen, Z., Xu, H., & Huo, H. (2022). Computational Scheme for the First-Order Linear Integro-Differential Equations Based on the Shifted Legendre Spectral Collocation Method. Mathematics, 10(21), 4117. https://doi.org/10.3390/math10214117






