3.1. Validity Demonstration Example: Fracking in West Virginia
To illustrate the validity of our method with real data, we turn to data on fracking in West Virginia. Methodologically, this example is ideal, because the data consist of approximately 2000 observations: this is small enough that a Bayesian kriging model still can be estimated over the full dataset, yet large enough that reasonably-sized bootstrap samples can be drawn from the data. This allows us to show how closely the bootstrap results resemble results gathered from the real data.
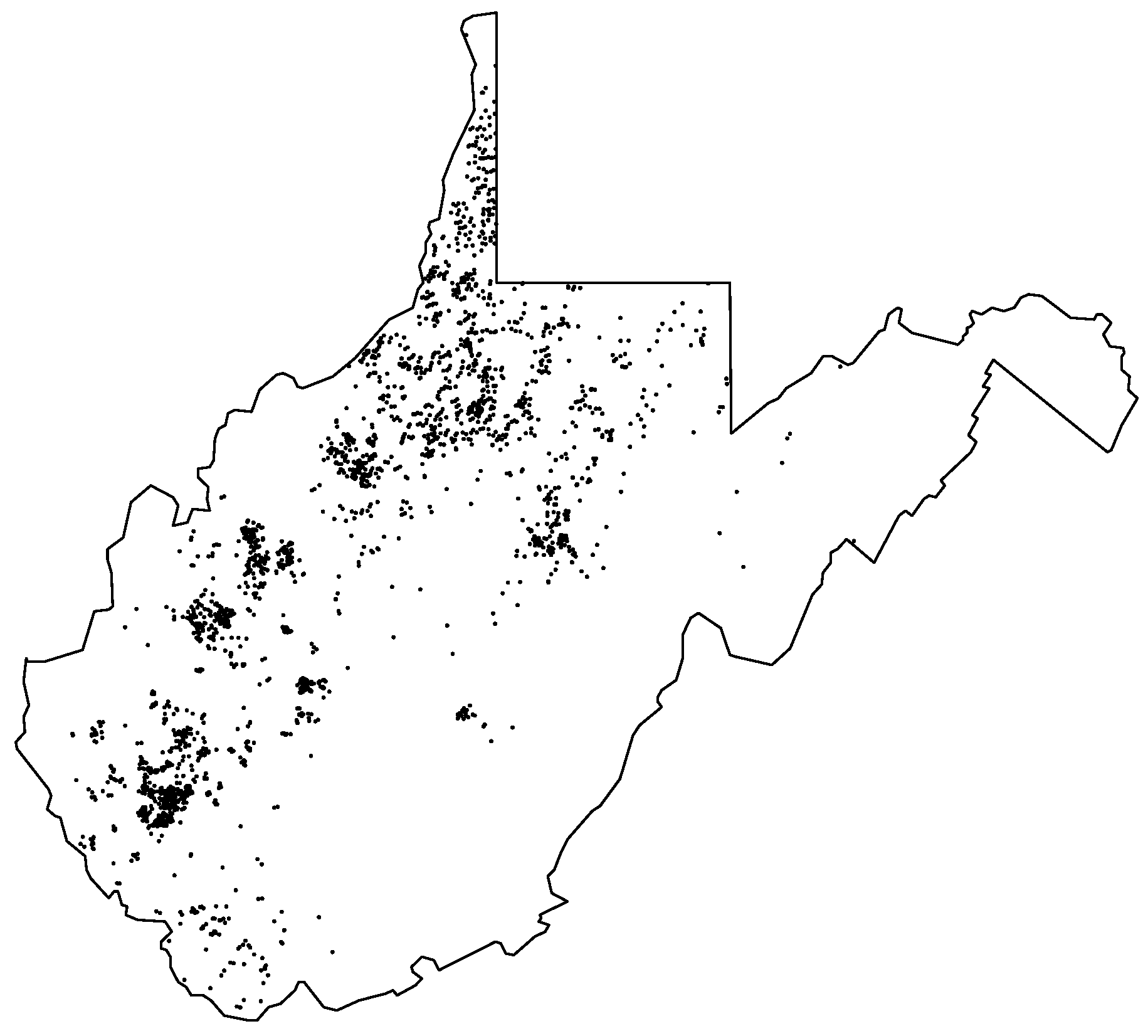
Figure 2 illustrates our data with the locations of 2474 natural gas wells in the state (Data accessed 25 March 2019 from FracTracker:
https://www.fractracker.org/map/us/west-virginia). This example is in line with the original development of kriging techniques by D.W. Krige, who sought to predict the value of minerals that could be extracted from a new borehole given information about yields from past boreholes. Fracking certainly poses a number of risks—not only accidents to workers but also the possible induction of seismic activity. However, using natural gas to supply electricity emits far less carbon dioxide into the atmosphere than any other fossil fuel [
32]. So there can be significant profits, jobs, and environmental effects from a large yield of natural gas to weigh against the risks. Ultimately, a good model that can forecast where the high yields are would help assess where the balance of environmental gains versus risks might be in favor of fracking.
3.1.1. Fracking Model: Full Data versus Bootstrap
For each site, we observe gas production in 2012 in thousands of cubic feet (Mcf). Most wells produced little or no gas in this year in West Virginia, with a median output of 0 Mcf. However, some yielded substantial output, bringing the mean up to 83,140 Mcf. The highest output in 2012 was 2,144,000 Mcf coming from a well operated by Hall Drilling, LLC (Ellenboro, WV, USA) that was located near the northern end of the state, on the Allegheny Plateau in Harrison County. In order to demonstrate how our BRSS kriging method operates, compared to how the Bayesian kriging model with the full data set behaves, we focus on productive gas wells in 2012 and model the logarithm of natural gas production as our outcome variable.
We have two predictors pertaining to gas production. First, we consider the elevation of the well. Geological features have the potential to affect outputs, and wells in West Virginia ranged from 565 feet above sea level to 3700 feet above sea level. Meng [
33] and Meng and Ashby [
34] found a correlation between the elevation of the land, from sea level, and the location of natural gas well sites in Pennsylvania. Second, we consider the formation rock pressure at the surface in pounds per square inch (PSI), which ranges from 0 PSI to 7390 PSI, with an average of 842.5 PSI. The formation rock pressure at the surface is tied directly to the amount of pressure that must be used when applying the fracturing liquid to the earth’s surface [
35] (p. 56).
When modeling the logged gas production, we predict it with just these two covariates. Additionally, our error term follows an exponential semivariogram kriging structure. As described, this error pattern requires that, holding both predictors constant, more proximate wells are expected to bear similar yields in gas production. We estimate this model with an illustration of a model using the BRSS (without replacement), BRSS (with replacement) jittered, and with a model fitted over the full data to compare the results (For further discussion of the BRSS (without replacement) and the BRSS (with replacement) jittered, please see the supplemental materials in
Appendix A). In all three cases the prior distributions for regression parameters are diffuse normals centered at zero and the prior distributions for variance parameters are gammas with long tails.
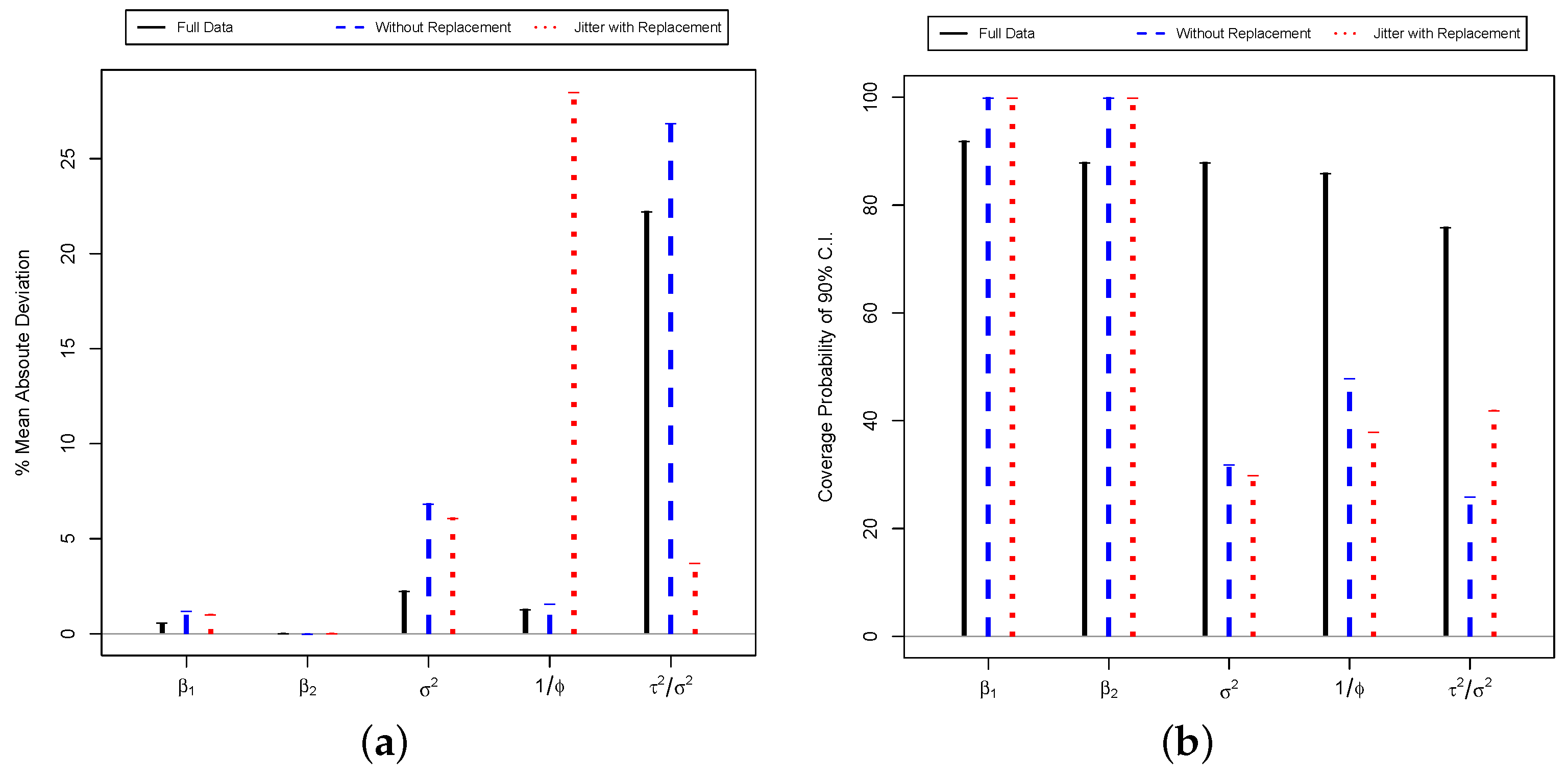
Table 1 shows a comparison between a full-data model, a bootstrapped (without replacement) model, and a bootstrapped (with replacement) jittered model. Once the data are cleaned, we have 1949 wells in the dataset. The BRSS models were estimated using 100 bootstrap samples of 500 randomly drawn natural gas wells each, applying the Bayesian kriging model to each sample and recording the mean estimate in each iteration (All samples were estimated utilizing 1 cpu core with 10 gb of memory. The full model took approximately 15 min to execute, with the BRSS and BRSS with jitter taking 54 and 59 min, respectively).
Recall, to obtain our estimates we take a random sample of the data as well as a random sample of the cases. With each round of the bootstrap, we create an unbiased approximation of both parameter estimates from the model and forecasts of the selected predictive observations. At the end, we pool the sample values of parameter estimates in order to summarize the marginal posterior distributions of each model parameter.
Turning to the results of
Table 1, the estimates from the three models are largely similar. The estimates from the BRSS models tend to have more uncertainty than those from the model with the full data set—as our result from (
22) would imply. Across all three models, both the intercept and the partial coefficient for pressure are similar in coefficient size, direction, and robustness. From either model, we would draw the conclusion that, holding elevation and location constant, on average higher pressure leads to higher expected gas yields. The only major loss we get from inference is the effect of elevation: The median value of the coefficient is comparable across the three models, which would indicate greater yields at higher elevations in West Virginia, on average an all else equal. However, in the full data model, we conclude that the probability of a positive relationship exceeds 95%, whereas with the BRSS models we cannot draw such a robust conclusion. For the variance terms of the partial sill (
), the range (
), and the ratio of the nugget to the partial sill (
), we get similarly-scaled terms in
Table 1, again with a larger spread in the credible interval for the BRSS (without replacement) model.
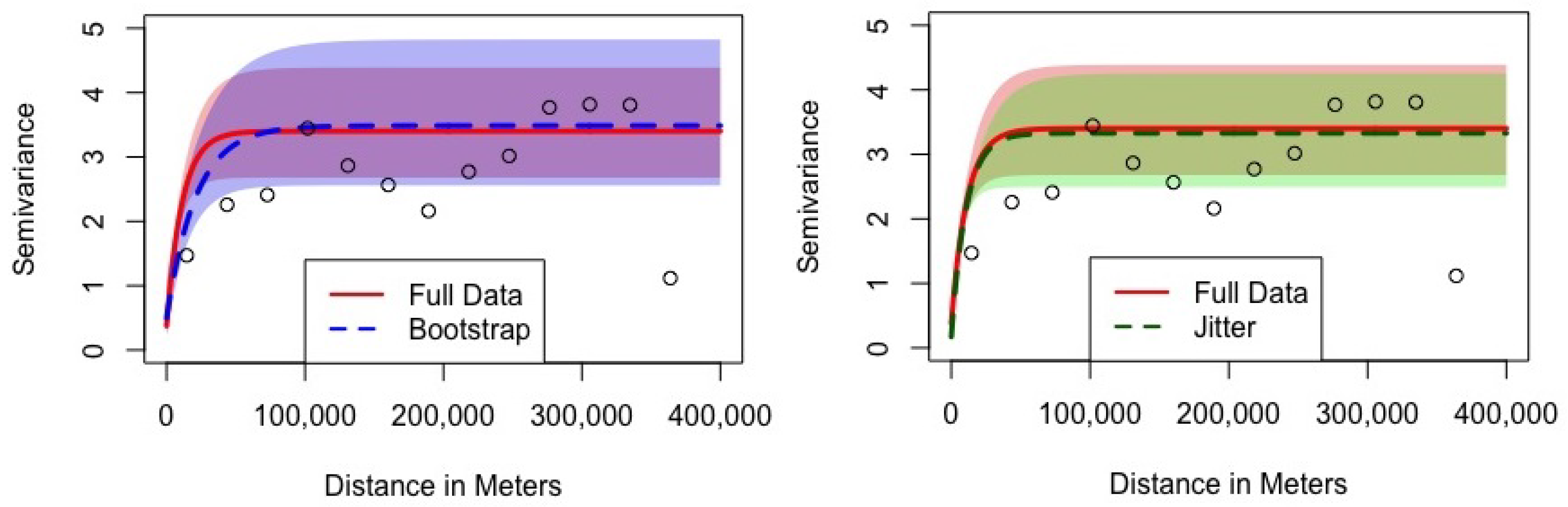
To truly gauge what these variance terms mean, though, the best technique is to turn to a visual representation of the semivariogram, shown in
Figure 3. In this figure, the horizontal axis represents the distance between wells in meters. The vertical axis represents the semivariance for the error terms of wells separated by this distance. The semivariance has two interpretations: it is half the variance of the difference in residuals for wells separated by a given distance, or the full variance of residuals when wells at a given separation distance are pooled together. The points on the graph represent the empirically observed semivariance of the residuals when observations at an approximate distance are pooled together. The solid red line is the estimated exponential semivariogram for the full dataset, as implied by the first numerical column of
Table 1. The shaded pink area is the 90% credible interval for the full-data semivariogram. The dashed blue (green) line is the estimated exponential semivariogram for the BRSS models, as implied by the third and fourth numerical columns of
Table 1. The shaded light blue (green) area is the 90% credible interval for the BRSS semivariograms.
In
Figure 3, both of the estimated parametric models successfully thread through the empirical semivariogram points estimated from the raw data. The nugget of a semivariogram is the portion of the unexplained variance that cannot be attributed to geospatial factors, which is the semivariance at a distance of zero meters. In the BRSS figure (left), we can see that both models have a closely sized nugget term, with semivariances of 0.38 and 0.50, respectively. Additionally, for the BRSS with jitter (right), the semivariances are 0.38 and 0.17, respectively. The range term describes how quickly or slowly spatial association dissipates. When the semivariance is low, observations are highly spatially correlated (as is expected for physically proximate values), and when the semivariance is high, there is little correlation. With a smaller range term, the semivariance approaches its upper bound quickly and spatial association dissipates. As this figure shows, the full data model does have a smaller range term, with the solid red line reaching its asymptote a little more quickly than the blue dashed line for the BRSS model. These positions are close on the scale of the data, though. With distances as long as 400,000 m in the data, both models approach the top variance well before 100,000 m. Finally, the sill is the sum of the nugget and the partial sill, and it represents the maximum semivariance reached when a sufficient distance is reached. The sill, thus, is the asymptotic variance the semivariogram approaches, seen as the approximate values taken when the lines flatten-out. The solid red line’s asymptotic variance is 3.40 for the full data model, while the blue and green dashed line’s sill is 3.48 and 3.33 for the BRSS and BRSS with jitter models. Again, these are similar maxima.
It should be noted that with fracking, geological processes produce natural gas. Because similar processes are in proximate places, nearby wells are likely to produce similar outputs. This is the fundamental goal of a kriging model—unobserved processes generate similar data in similar locations. Additionally, the relationship in the semivariogram is non-linear. We would expect heavy correlation in a cluster of proximate wells, but getting out of a cluster the correlation will drop away substantially more. Hence, by 100,000 m the correlation has basically disappeared.
Examining these lines in
Figure 3, the variance structure of the two models is nearly the same. In fact, the wider 90% credible interval for the BRSS model includes nearly all of the credible interval of the full data model, including the median-level estimate of the semivariogram. The small difference in the median estimates of the semivariograms is because these are variance components and the BRSS process adds slightly more uncertainty through the multistage generation and combination process. The median estimates of the semivariogram do cross, largely because a larger range term in the BRSS model offsets in part the larger partial sill term from that model. Again, we note that the credible intervals show that there is not a robust difference between these two models. This is an example of our point that big data statistical procedures generally impose compromises on the researcher versus analogous standard procedures on more modest sized data.
3.1.2. A Performance Experiment
Under what circumstances does our BRSS models perform the best? To answer this, we expanded the comparison from
Table 1 to consider performance when we manipulate the number of iterations in the bootstrap as well as the resample size in each bootstrap iteration. Thus, we have two different treatments: The first treatment is to manipulate the number of iterations of the bootstrap, ranging from 1 to 50. The second treatment is to manipulate how large the resample size is per bootstrap iteration, using resample sizes of 50, 250, and 500. For each combination of treatments, we compare the results from BRSS to those of the full data model shown in
Table 1. We computed the percent mean absolute deviance between the BRSS results and the full data model. Ideally, these percentages will be as small as possible, indicating that BRSS is recovering estimates closer to what would be obtained from a full data model, in cases where estimating the full data model would be feasible.
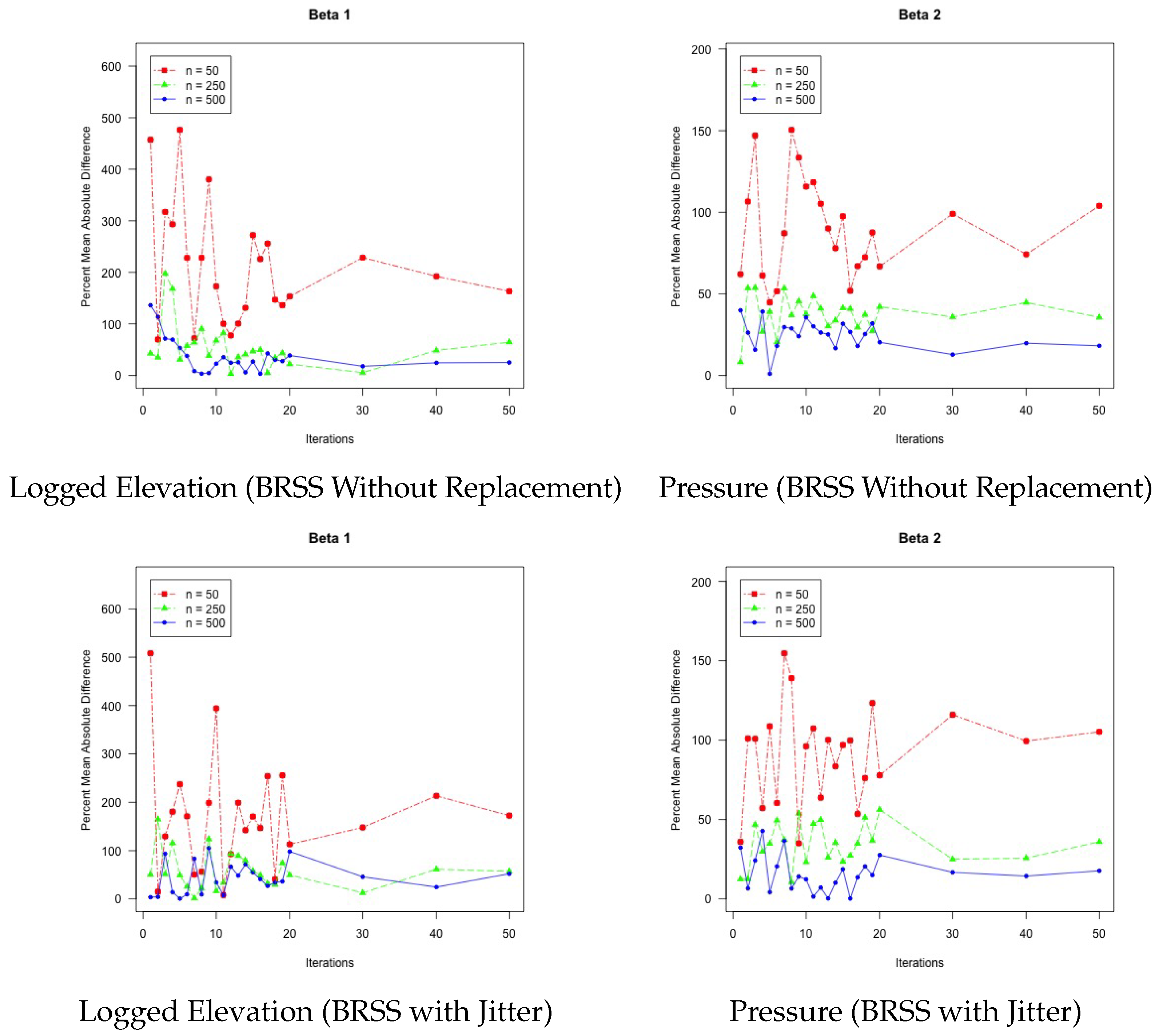
Figure 4 shows the findings from our experiment. Each of the four panels in the figure represents the two primary coefficients from the two BRSS models. In each panel, the horizontal axis represents the number of iterations used in the bootstrap. Experiments were run for all iteration counts from 1–20, as well as 30, 40, and 50. The vertical axis represents the percent mean absolute difference, or the percentage difference between the BRSS estimates and the model estimated over the full data. Each panel contains three lines: a red dot-dash line with square characters to represent the treatment of 50 observations per bootstrap resample, a green dashed line with triangle characters to represent the 250 observation treatment, and a blue solid line with dot characters to represent the 500 observation treatment.
From this analysis of gas production in West Virginia, we have learned several important facets of the BRSS model. First, in instances in which it is computationally impossible to estimate a model over the full data, BRSS offers an estimable alternative that provides estimates that fairly approximate the results that would be obtained if a single model could be fitted over the full data. Second, BRSS does perform better with larger bootstrap sample sizes and more iterations of the bootstrap. There is greater benefit with increasing the bootstrap resample size than the number of iterations to bringing the results in line with the full data model. Of course, the challenge that estimating a kriging model is in computational complexity remains with bootstrap samples. This means that a researcher can improve results by increasing sample size per iteration, yet cannot increase the sample size too much before the problem becomes intractable again. Having learned these features of the model, we now apply these lessons to another example in which estimating a model over all of the data is entirely impossible.
3.2. Application with Big Data: Campaign Contributions in California
The fracking data were useful to illustrate how well the BRSS method works whenever we still have few enough observations to estimate the model over all data. In this way we were able to compare the results of the model with the full data to the results when we use BRSS. We also learned that relatively large bootstrap samples and more bootstrap iterations improve the results. Now we turn to an example of data which are too big for us to estimate the full model, thereby inducing the need for us to turn to BRSS. In this way, we show the applied researcher how to implement our strategy when managing a large dataset.
This big data problem is increasingly common as campaigns and consultants scrape massive datasets on voters, donors, and consumers. To illustrate this, we analyze data that have been shared by the consulting firm
∅ptimus (a right-of-center firm that collects and integrates government and corporate produced data). Their dataset consists of over 19 million residents of California, with 475 variables about them. We specifically were interested in campaign donation behavior, so we focused on residents who had donated to a left- or right-of-center campaign from 2011–2018. This reduced the data to 199,626 donors on the left and 77,566 donors on the right.
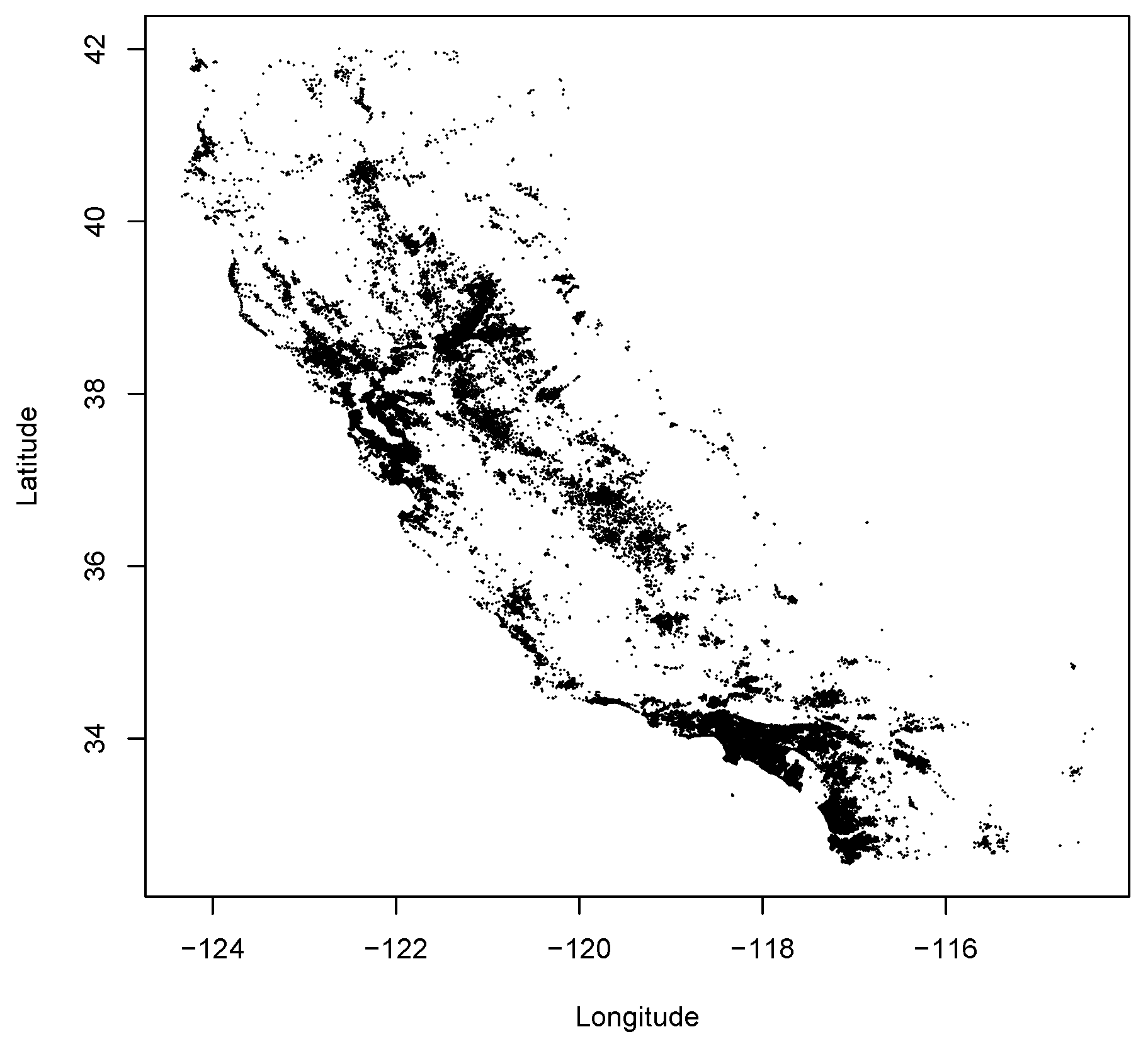
Figure 5 shows a map of the 277,192 Californians who donated enough money in this time-frame to be reported by the Federal Election Commission. Each point on the map represents the donor’s location, geocoded based on his or her address.
Our Bayesian model is fashioned after [
36] analysis of campaign contributions to Rick Perry’s 2006 gubernatorial reelection campaign, which was not Bayesian but similar features. In that paper, they estimated an ordinary kriging model and showed that values of contributions to the Perry campaign did have a tendency to cluster together. (The implication of this finding is that certain areas could be more profitable to seek donations from.) We would like to repeat this ordinary kriging analysis, and we also want to consider whether clustering is present in the context of linear predictors in a Bayesian universal kriging model. However, a model of 77,566 right-of-center donors (much less 199,626 left-of-center donors) cannot be readily estimated due to the computational questions involved. Thus, we have no choice but to use the BRSS algorithm to understand patterns in California political donor behavior.
Monogan and Gill [
2] argue that kriging models are appropriate when analyzing political responses (of which campaign donations are a clear example) because local factors are likely to make neighbors more like-minded. Gimpel and Schuknecht note that there are compositional and contextual reasons that neighbors are politically similar [
37] (pp. 2–4). Compositional reasons are that neighbors are likely to share similar economic interests, social structure, religion, and socioeconomic factors. Since it is impossible to include all of these factors in a model, we need to account for similarity among neighbors somehow, and the error term from a kriging structure is one way to do this. The contextual reasons for similarity are that proximate residents are likely to share the same information sources through media outlets and are likely to even speak with each other such that ideas and information will spread through local networks. This, too, cannot be easily modeled and calls for a spatial error term like we specify. Hence, there are several reasons that nearby citizens will be politically similar.
As a first look at the patterns in these data from
∅ptimus, we present contour maps of running local averages of logged donations levels in
Figure 6. In each panel of this figure, the horizontal axis represents donors’ locations in eastings, while the vertical axis represents donors’ locations in northings. By rescaling longitude and latitude to eastings and northings, all distances on the graph can be evenly scaled with kilometer-based distances. The left panel shows patterns for donors whose largest contribution was to a left-of-center campaign while the right panel shows patterns for donors whose largest contribution was to a right-of-center campaign. In each panel, darker spots indicate a higher average contribution relative to other places on the panel. Contour lines also illustrate particular levels of the logged value of donations.
As
Figure 6 shows, local averages of contributions behave as would be expected. On the left panel of left-of-center donations, on the northern coast, there tends to be a high average, indicated by fairly consistent patterns of dark gray. The southern coast, by contrast, is more checkered. The more rural inland east is shaded lighter, indicating that relatively fewer left-of-center contributions come from this area. Meanwhile, the right-hand panel shows the patterns for right-of-center contributions. This, too, behaves as might be expected: The highest levels of right-of-center contributions tend to be scattered in a checkered pattern in coastal areas. Meanwhile, the rural inland east is a consistent cluster for right-of-center donations. In both panels, it does appear that there is noticeable clustering, which suggests that geographical space is worthwhile when considering where donations can emerge. Based on the figures, it might appear that there is endogeneity based on the placement of donors in the state of California. Based on [
2] we are confident that these concerns are alleviated.
To this end, we proceed to estimate kriging models for the larger left-of-center dataset. We have to use BRSS because the full dataset is simply too large to estimate the full model.
Table 2 presents two models of the logged value of left-of-center donations. These two models are an ordinary kriging model in which levels of donations are entirely a function of a spatial error process, and a universal kriging model in which logged donations are a linear function of several predictors and the errors of the model have a spatial error process. Each row of the table represents another parameter from the model. The first three numerical columns of the table show the median and 90% credible interval of parameter estimates from the ordinary kriging model. The last three numerical columns of the table show the median and 90% credible interval of parameter estimates from the universal kriging model. Medians and percentiles are all computed from BRSS with 50 iterations and 1000 observations drawn per iteration. In this way, we follow the recommendations from the previous section to estimate the model with a large number of iterations and a resample size that is large enough for reliable results but still feasible on a computing cluster. (Utilizing 1 cpu core with 10 gb of memory, it took approximately 6 h to estimate the ordinary kriging model. Additionally, utilizing the same machine metrics, it took approximately 17 h to estimate the universal kriging model. While this is time-consuming, it is feasible, whereas a full-data model is not even feasible at present).
As
Table 2 shows, the ordinary kriging model confirms substantial clustering in contributions. The partial still term (
) is the portion of the variance that is attributable to spatial causes, and the posterior median of this term is approximately 1.4. Meanwhile the nugget effect (
) is the portion of the variance that is independent from geographic space—individually idiosyncratic variance. We parameterize the nugget relative to the value of the partial sill, and we get a posterior median of this ratio of approximately 2.2. This tells us that, at the median parameter values, we would estimate that approximately 31% of the variance can be explained by spatial clustering (This calculation is based on the calculation
, which can easily be computed with the model-estimated ratio if rewritten as
). The range term (
) indicates how persistent spatial correlation is in the observations, with higher values indicating more persistence. From the range, we can mathematically deduce the effective range, which is the distance at which spatial correlation among values drops to a negligible level. The effective range of this ordinary kriging model is approximately 1150 km (The effective range is typically defined as the distance at which spatially-based correlations drop below 0.05 [
4] (p. 27). We can compute this using the formula:
. For the median estimates of
and
, the effective range approximates to 1150 km).
Does geospatial correlation in donations persist even in the context of linear predictors? The universal kriging model of the last three columns of
Table 2 show us that it does. While the partial sill (
) does appear smaller with a posterior median of approximately 1.3, this drop can largely be attributed to the fact that this variance is now reflective of residual variance in a model, as opposed to total variance. The ratio of the nugget to the partial sill (
) increased a slight fraction, and in the universal kriging model we still at the posterior median would estimate that approximately 31% of the unexplained variance is geospatial in nature. Hence, adding the predictive model did not effectively alter the share of spatial to idiosyncratic variance. In fact, the larger range term (
) implies that residual correlation in the universal kriging model is actually more persistent than observational correlations over the raw data in the ordinary kriging model. In this case, the effective range is 1304 km, which is greater than California’s north-south length of 1240 km. So spatial correlation persists strongly in this case.
Meanwhile, the predictors from the universal kriging model in
Table 2 offer a sense of which left-of-center donors are most likely to donate more, holding their location constant. There are robust effects in this table that, on average and ceteris paribus, women donors on average donate less, higher-income donors give more, and Latino donors donate less than non-Latino whites. Note again that the population is of people who donate to left-of-center campaigns. This model speaks less to who would choose to donate in the first place, but rather to how much individuals will contribute if they are the donating type. It is also worth noting that the estimates of these coefficients benefit from efficiency gains relative to estimation with ordinary least squares: The universal kriging model accounts for the spatial correlation of errors while estimating these coefficients, whereas OLS would ignore this important feature of the data.
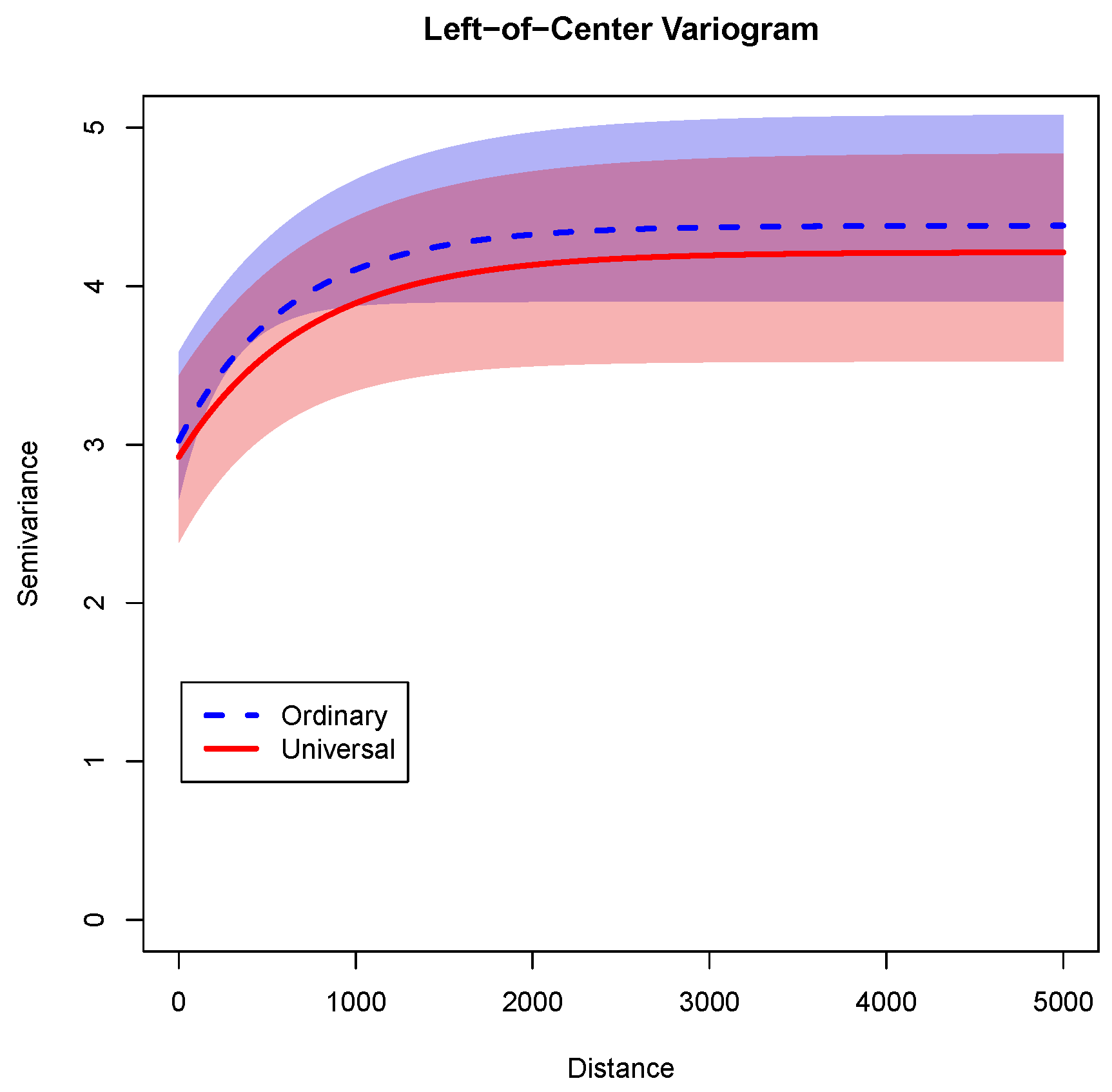
As a final illustration of the variance properties from these two models,
Figure 7 shows the semivariance functions implied by the two models of
Table 2. In this figure, the horizontal axis represents the distance in kilometers. The vertical axis is the semivariance for observations separated by that distance. The semivariance can be interpreted in two ways: For observations separated by a certain distance (say, 1000 km) it is half of the variance of the differences between these observations, or alternatively if all of the observations are pooled it is the variance of the pooled observations. In this graph, the exponential semivariogram function for the ordinary kriging model is shown with a blue dashed line, and its 90% credible interval is shown by the shaded light blue area. The semivariogram function for the universal kriging model is shown with a red solid line, and its 90% credible interval is shown by the shaded pink area.
As
Figure 7 shows, the semivariance for both models is at its lowest in short distances, which is expected because variances are lower for observations that are highly correlated. As the distance increases, the semivariance increases because there is more spread (and less correlation) among more separated observations. For any given distance, the semivariance for the universal kriging model is lower than for the ordinary kriging model. This pattern makes sense because the linear model explains some of the variance in the universal kriging model. Finally, for both models, the curve flattens-out between 1000 and 2000 km. This fits with the expected ranges of 1150 and 1304 km for the ordinary and universal kriging models, respectively. When the correlation among spatial observations becomes minimal, the variance finds an asymptotic upper bound. Also notably, there is substantial overlap between the credible intervals. Therefore adding predictors does not appear to have altered dramatically the implied variance structure.
With this illustration, we show how scholars or campaign strategists can simultaneously take advantage of geospatial statistical methods while working with big datasets. In this model, we had information for 199,626 donors, which is simply too big of a dataset to estimate a kriging model with. However, using BRSS with 50 iterations and 1000 observations per sample, we were able to describe the level of clustering in the data and how predictors affect contribution levels even when holding geospatial location constant.