Improved Estimation of the Inverted Kumaraswamy Distribution Parameters Based on Ranked Set Sampling with an Application to Real Data

Abstract

The ranked set sampling (RSS) methodology is an effective technique of acquiring data when measuring the units in a population is costly, while ranking them is easy according to the variable of interest. In this article, we deal with an RSS-based estimation of the inverted Kumaraswamy distribution parameters, which is extensively applied in life testing and reliability studies. Some estimation techniques are regarded, including the maximum likelihood, the maximum product of spacing’s, ordinary least squares, weighted least squares, Cramer–von Mises, and Anderson–Darling. We demonstrate a simulation investigation to assess the performance of the suggested RSS-based estimators via accuracy measures relative to simple random sampling. On the basis of actual data regarding the waiting times between 65 consecutive eruptions of Kiama Blowhole, additional conclusions have been drawn. The outcomes of simulation and real data application demonstrated that RSS-based estimators outperformed their simple random sampling counterparts significantly based on the same number of measured units.

1. Introduction

In some investigations, cost-effective sampling is a key concern, particularly when the measurement of the characteristic of interest is expensive, uncomfortable, or time-consuming. In order to increase the accuracy achieved per unit of the sample, the ranked set sampling (RSS) approach is an excellent tool for achieving observational economy. Reference [1] proposed the RSS technique as an alternative to the frequently used simple random sample (SRS) methodology for increasing the efficiency of the sample mean. In RSS, the population is divided into q sets of q units each by randomly selecting q² units from it. Without taking actual measurements, the q units in each set are ranked with respect to the study variable. For actual quantification, the lowest-ranked unit from the first set of q units is chosen. The second smallest ranked unit is measured from the second set of q units. The process is repeated; say h times until the greatest rated unit from the last set is determined. To obtain an RSS sample of size $n^{\circ }$ = qh, the entire process can be replicated a number of times, say h times. The following matrix notation is considered to express the RSS design.

$$\begin{array}{c}Initial\hspace{0.17em}Observations\\ \left(\begin{array}{cccc}{X}_{(1:1)}& X_{(1:2)}& \dots & X_{(1:q)}\\ X_{(2:1)}& X_{(2:2)}& \dots & X_{(2:q)}\\ ⋮& ⋮& \ddots & ⋮\\ X_{(q:1)}& X_{(q:2)}& \dots & X_{(q:q)}\end{array}\right)\end{array}\Rightarrow \begin{array}{c}Ranked\hspace{0.17em}Observations\\ \left(\begin{array}{cccc}\boxed{X_{11}}& X_{21}& \dots & X_{q1}\\ X_{12}& \boxed{X_{22}}& \dots & X_{q2}\\ ⋮& ⋮& \ddots & ⋮\\ X_{1q}& X_{2q}& \dots & \boxed{X_{qq}}\end{array}\right)\end{array}\Rightarrow \begin{array}{c}RSS\hspace{0.17em}\hspace{0.17em}(h=1)\\ \boxed{X_{11},X_{22},\dots ,X_{qq}}\end{array}$$

The mathematical foundation of RSS was initially created in reference [2]. In statistical inference, the parametric estimate approach employing the RSS sampling strategy is of utmost importance. A large number of studies have recently been conducted on the issue of RSS-based estimate for a variety of parametric models. For example, refeference [3] used the data from the RSS technique to calculate the population variance. In subsequent years, RSS was employed to estimate the statistical distribution’s involved parameters. Reference [4] used RSS to estimate the exponential distribution parameters, while reference [5] investigated the estimator of the Cauchy distribution’s location parameter. Reference [6] looked at estimating normal and exponential distribution parameters based on RSS. Reference [7] investigated estimators for the logistic distribution’s location and scale parameters, whereas reference [8] considered the RSS to get the geometric parameter estimators. Reference. [9] succeeded in estimating the parameters of the half-logistic distribution, while reference. [10] investigated estimators of logistic distribution parameters using RSS. Reference [11] achieved estimating modified Weibull distribution parameters. Reference [12] used RSS to derive maximum likelihood (ML) and Bayesian estimators for generalized exponential model. Reference [13] handled with parameter estimators of Pareto distribution using RSS. The parameter estimator of the Rayleigh distribution was regarded in [14] using different methods of estimations and ranking designs. Within the framework of RSS, reference [15] examined the approach of the ML for the shape and scale parameters of the generalized Rayleigh distribution. Reference [16] considered estimation of the new Weibull-Pareto distribution parameters using RSS. Reference [17] discussed the parameter estimators of Zubair Lomax distribution using RSS. Reference [18] investigated efficient estimation of the generalized quasi-Lindley distribution parameters under RSS. For recent results and references, see [19,20,21,22,23,24,25,26,27].

The Kumaraswamy distribution (KD) was offered in [28], which is one of the most significant lifetime distributions with a range of [0,1]. It cannot, however, be utilized for most lifetime data sets that theoretically have limitless support. It is regarded as a viable alternative to beta distribution since they both share the same characteristics such as being uni-modal, decreasing, increasing, or constant. The KD’s probability density function (PDF) with two positive shape parameters is defined by:

$$f(x;\tau ,\upsilon )=\tau \upsilon x^{\tau -1}{\left(1-x^{\tau }\right)}^{\upsilon -1};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\tau ,\upsilon >0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<x<1.$$

(1)

Reference [29] proposed the inverted KD distribution (IKD) with the goal of providing a new flexible lifetime distribution for analyzing real data sets in the best situation. The following are indeed the principles of the IKD: It’s the distribution of the random variable Z = 1/X − 1, where X is a random variable following the KD in Equation (1). The PDF and cumulative distribution function (CDF) of the IKD are, respectively, characterized by:

$$f(z;\tau ,\upsilon )=\tau \upsilon {(1+z)}^{-\tau -1}{\left[1-{\left(1+z\right)}^{-\tau }\right]}^{\upsilon -1};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}z,\tau ,\upsilon >0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(2)

$$F(z;\tau ,\upsilon )={\left[1-{\left(1+z\right)}^{-\tau }\right]}^{\upsilon };\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}z,\tau ,\upsilon >0.\hspace{0.17em}$$

(3)

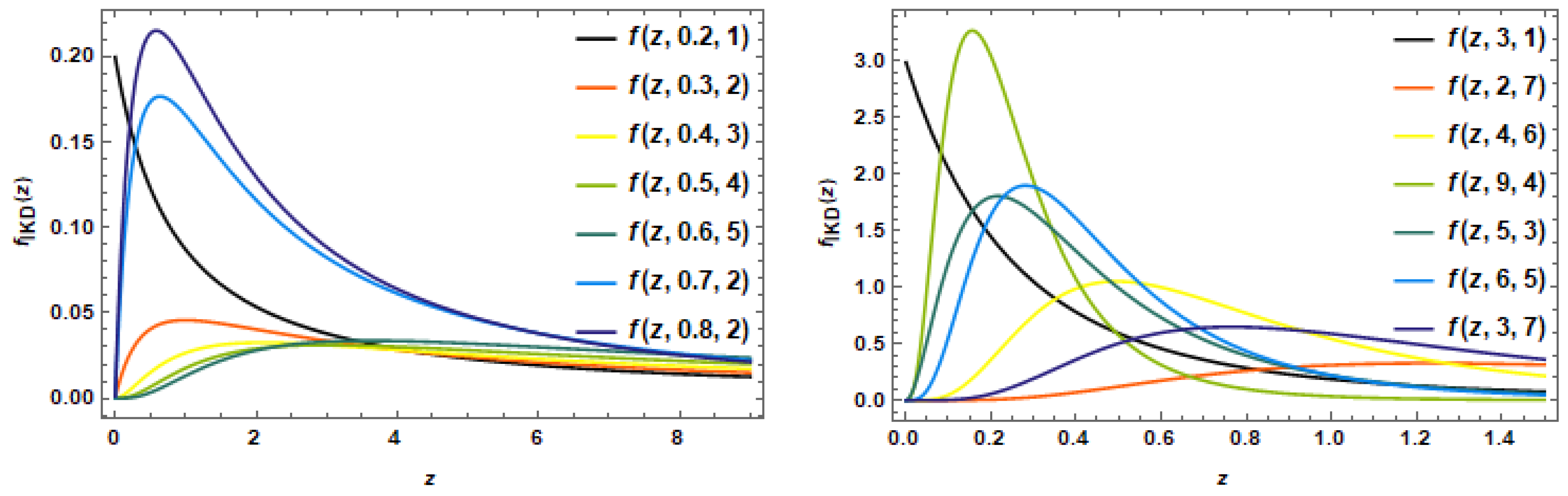
Figure 1 presents some possible PDF plots of the IKD for some selected distribution parameters. It is clear that the distribution is skewed to the right.

The CDF (3) comprises several well-known distributions, including (i) the Lomax distribution for $\upsilon =1,$ (ii) the beta type II (inverted beta) distribution for $\tau =1,$ (iii) log-logistic distribution for $\tau =\upsilon =1,$ (iv) the inverse Weibull distribution as $\upsilon \to \infty ,$ and the generalized exponential distribution when $\tau \to \infty .$ According to reference [29], the IKD has a long right tail, and when compared to other distributions, the IKD gives optimistic forecasts of uncommon events happening in the right tail.

To our knowledge, there have been no published works that have utilized the RSS to estimate IKD parameters. In this study, we assumed that the ranking is perfect and we focus on several classical estimations of the IKD parameters using RSS and SRS. The considered methods are the ML, maximum product of spacing (MPS), least squares (LS), weighted least squares (WLS), Cramer–von Mises (CvM), and Anderson–Darling (AD). A simulation study compares the suggested RSS based estimators to the basic SRS based on some criteria measures.

The following is the paper’s configuration: we provide the ML estimators (MLEs) and MPS estimators (MPSEs) of the IKD parameters in Section 2. Section 3 obtains the IKD parameter estimators using LS and WLS approaches. Using the AD and CvM methodologies, we obtain the IKD parameter estimators in Section 4. Section 5 and Section 6 describe, respectively, simulation research as well as its application to real-world situations, and comparing RSS estimators to SRS equivalents. The paper comes to a close with main findings in Section 7.

2. ML and MPS Methods of Estimation

The ML and MPS estimation methods are examined in this section for estimating the IKD parameters. First, we’ll go through the RSS framework methodology, and then obtain the estimators from SRS.

2.1. ML Estimators

Let $\{Z_{ct},c=1,2,\dots ,q,\hspace{0.17em}\hspace{0.17em}t=1,2,\dots ,h\}$ denote cth order statistics (OS) in the tth cycle, where h is the number of cycles and q is the set size. The data in RSS are all mutually independent, and the data are distributed identically for each $c=1, 2,\dots ,q$. The distribution of the cth data, for each $c=1, 2,\dots , q$, is identical to the distribution of the cth OS of the random sample X₁, X₂, …, X_q, that is;

$$f_{Z_{ct}}(z_{ct})=\frac{q!}{(c-1)!(q-c)!}f(z_{ct}){\left[F(z_{ct})\right]}^{c-1}{\left[1-F(z_{ct})\right]}^{q-c},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\infty \hspace{0.17em}<z<\infty .\hspace{0.17em}$$

(4)

Substituting Equations (2) and (3) in Equation (4), then we have:

$$f_{Z_{ct}}(z)=\frac{(q)!\tau \upsilon }{(c-1)!(q-c)!}{(1+z_{ct})}^{-\tau -1}{\left[1-{\left(1+z_{ct}\right)}^{-\tau }\right]}^{\upsilon c-1}{\left[1-{\left[1-{\left(1+z_{ct}\right)}^{-\tau }\right]}^{\upsilon }\right]}^{q-c},\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}<\hspace{0.17em}{z}_{ct}<\infty .$$

(5)

The likelihood function of IKD using RSS $\{Z_{ct},c=1,2,\dots ,q,\hspace{0.17em}t=1,2,\dots ,h\}$, where $n^{\circ }=qh$ is the sample size, is as follows:

$$l_{\Re \mathbb{S}\mathbb{S}}(z)={\displaystyle \prod _{c=1}^q{\displaystyle \prod _{t=1}^h\frac{(q)!\tau \upsilon }{(c-1)!(q-c)!}}}{(1+z_{ct})}^{-\tau -1}{\left[1-{(1+z_{ct})}^{-\tau }\right]}^{\upsilon c-1}{\left[1-{\left[1-{\left(1+z_{ct}\right)}^{-\tau }\right]}^{\upsilon }\right]}^{q-c}.$$

The log-likelihood function of IKD, denoted by $l_{\Re \mathbb{S}\mathbb{S}}^{*}$ is as follows:

$$l_{\Re \mathbb{S}\mathbb{S}}^{*}\propto qh\ln (\tau \upsilon )-(\tau +1){\displaystyle \sum _{c=1}^q{\displaystyle \sum _{t=1}^h\ln ({\xi }_{ct})+(\upsilon c-1){\displaystyle \sum _{c=1}^q{\displaystyle \sum _{t=1}^h\ln (1-{\left({\xi }_{ct}\right)}^{-\tau })}}+(q-c){\displaystyle \sum _{c=1}^q{\displaystyle \sum _{t=1}^h\ln \left[1-{\left[1-{\left({\xi }_{ct}\right)}^{-\tau }\right]}^{\upsilon }\right]}}}},$$

where ${\xi }_{ct}=(1+z_{ct}).$ The MLEs of $\tau ,$ and $\upsilon ,$ denoted by ${\widehat{\tau }}_{\mathrm{ML}},$ and ${\widehat{\upsilon }}_{\mathrm{ML}},$ of the IKD using RSS are produced by solving the nonlinear equations

$$\partial l_{\Re \mathbb{S}\mathbb{S}}^{*}/\partial \tau =0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{and} \partial l_{\Re \mathbb{S}\mathbb{S}}^{*}/\partial \upsilon =0.$$

(6)

Let $Z_1,Z_2,\dots ,Z_{n^{\circ }}$ be a SRS of size $n^{\circ }$ from a IKD with PDF (2) and CDF (3). The log-likelihood function, say $l_{SRS}^{*},$ for $\tau$ and $\upsilon$ is given by:

$$l_{SRS}^{*}=n^{\circ }\ln \tau +n^{\circ }\ln \upsilon -(\tau +1){\displaystyle \sum _{i=1}^{n^{\circ }}\ln }\left(1+z_i\right)+(\upsilon -1){\displaystyle \sum _{i=1}^{n^{\circ }}\ln }\left(1-{\left(1+z_i\right)}^{-\tau }\right).$$

The MLEs for $\tau$ and $\upsilon ,$ say ${\tilde{\tau }}_{ML}$ and ${\tilde{\upsilon }}_{ML},$ are given as the solution of the following equations:

$$\partial l_{SRS}^{*}/\partial \tau =0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{and} \partial l_{SRS}^{*}/\partial \upsilon =0.$$

(7)

Using numerical technique in Equation (7), we obtain the MLEs of $\tau$ and $\upsilon ,$ denoted by ${\tilde{\tau }}_{\mathrm{ML}}$ and ${\tilde{\upsilon }}_{\mathrm{ML}}$.

2.2. MPS Estimators

For estimating the population parameters of continuous distributions, reference [30] presented a powerful alternative approach known as MPS. Consider the ordered items $Z_{(1:n^{\circ })},Z_{(2:n^{\circ })},\dots ,Z_{(n^{\circ }:n^{\circ })}$ constitute a RSS of size $n^{\circ }=qh$, $q$ is set size and $h$ is the cycle numbers drawn from a distribution Equation (3). Hence, the uniform spacing’s are defined by $D_c(\tau ,\upsilon )=F\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)-F\left(z_{(c-1:n^{\circ })}\left|\tau ,\upsilon \right.\right),c=1,2,\dots ,n^{\circ }+1,$ with $F\left(z_{(0:n^{\circ })}\left|\tau ,\upsilon \right.\right)=0,$ $F\left(z_{(n^{\circ }+1:n^{\circ })}\left|\tau ,\upsilon \right.\right)=1,$ such that ${\displaystyle \sum _{c=1}^{n^{\circ }+1}{D}_c(\tau ,\upsilon )}=1.$ The MPSEs, represented by ${\widehat{\tau }}_{\mathrm{MPS}},{\widehat{\upsilon }}_{\mathrm{MPS}}$, are obtained by maximizing the geometric mean of the spacing $\mathrm{GM}(\tau ,\upsilon ),$ where

$$\mathrm{GM}(\tau ,\upsilon )={\left\{{\displaystyle \prod _{c=1}^{n^{\circ }+1}{D}_c(}\tau ,\upsilon )\right\}}^{1/(n^{\circ }+1)}.$$

(8)

The logarithm of (8), denoted by ${\mathrm{GM}}^{\ast }(\tau ,\upsilon ),$ is

$${\mathrm{GM}}^{\ast }(\tau ,\upsilon )=\frac{1}{n^{\circ }+1}{\displaystyle \sum _{c=1}^{n^{\circ }+1}\ln }\left\{{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-{\left[1-{\left(1+z_{(c-1:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }\right\}.$$

The MPSEs; ${\widehat{\tau }}_{\mathrm{MPS}},{\widehat{\upsilon }}_{\mathrm{MPS}}$ can also be obtained by solving the nonlinear equations numerically:

$$\frac{\partial {\mathrm{GM}}^{\ast }(\tau ,\upsilon )}{\partial \upsilon }=\frac{1}{n^{\circ }+1}{\displaystyle \sum _{c=1}^{n^{\circ }+1}\frac{1}{D_c\left(\tau ,\upsilon \right)}}\left\{{\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)-{\mathsf{{\rm Y}}}_1\left(z_{(c-1:n^{\circ })}\left|\tau ,\upsilon \right.\right)\right\}=0,$$

(9)

$$\frac{\partial {\mathrm{GM}}^{\ast }(\tau ,\upsilon )}{\partial \tau }=\frac{1}{n^{\circ }+1}{\displaystyle \sum _{c=1}^{n^{\circ }+1}\frac{1}{D_c\left(\tau ,\upsilon \right)}}\left\{{\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)-{\mathsf{{\rm Y}}}_2\left(z_{(c-1:n^{\circ })}\left|\tau ,\upsilon \right.\right)\right\}=0,$$

(10)

where

$${\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=\frac{\partial }{\partial \upsilon }{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }={\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }\ln \left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right],$$

(11)

$${\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=\frac{\partial }{\partial \tau }{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }=\upsilon {\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon -1}{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\ln \left(1+z_{(c:n^{\circ })}\right).$$

(12)

Based on SRS, let $Z_{(1)},Z_{(2)},\dots ,Z_{(n^{\circ })}$ be the OS from a sample of size $n^{\circ }$ from Equation (3). Hence, the uniform spacing’s in this case are defined by $D_i^{\ast }(\tau ,\upsilon )=F\left(z_{(i)}\left|\tau ,\upsilon \right.\right)-F\left(z_{(i-1)}\left|\tau ,\upsilon \right.\right),$ $i=1,2,\dots ,n^{\circ }+1$ with $F\left(z_{(0)}\left|\tau ,\upsilon \right.\right)=0,F\left(z_{(n^{\circ }+1)}\left|\tau ,\upsilon \right.\right)=1,$ such that ${\displaystyle \sum _{i=1}^{n^{\circ }+1}{D}_i^{\ast }(\tau ,\upsilon )}=1.$ The MPSEs, represented by ${\tilde{\tau }}_{\mathrm{MPS}},{\tilde{\upsilon }}_{\mathrm{MPS}}$, are obtained by maximizing the geometric mean of the spacing ${\mathrm{GM}}_{SRS}(\tau ,\upsilon ),$ where

$${\mathrm{GM}}_{SRS}(\tau ,\upsilon )={\left\{{\displaystyle \prod _{i=1}^{n^{\circ }+1}{D}_i^{\ast }(}\tau ,\upsilon )\right\}}^{1/(n^{\circ }+1)}.$$

(13)

The logarithm of Equation (13), denoted by ${\mathrm{GM}}_{SRS}^{\ast }(\tau ,\upsilon ),$ is

$${\mathrm{GM}}_{SRS}^{\ast }(\tau ,\upsilon )=\frac{1}{n^{\circ }+1}{\displaystyle \sum _{i=1}^{n^{\circ }+1}\ln }\left\{{\left[1-{\left(1+z_{(i)}\right)}^{-\tau }\right]}^{\upsilon }-{\left[1-{\left(1+z_{(i-1)}\right)}^{-\tau }\right]}^{\upsilon }\right\}.$$

The MPSEs; ${\widehat{\tau }}_{\mathrm{MPS}},{\widehat{\upsilon }}_{\mathrm{MPS}}$ can also be obtained by solving the following nonlinear equations numerically:

$$\frac{\partial {\mathrm{GM}}_{SRS}^{\ast }(\tau ,\upsilon )}{\partial \upsilon }=\frac{1}{n^{\circ }+1}{\displaystyle \sum _{i=1}^{n^{\circ }+1}\frac{1}{D_i^{\ast }\left(\tau ,\upsilon \right)}}\left\{{\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)-{\mathsf{{\rm Y}}}_1\left(z_{(i-1)}\left|\tau ,\upsilon \right.\right)\right\}=0,$$

(14)

$$\frac{\partial {\mathrm{GM}}_{SRS}^{\ast }(\tau ,\upsilon )}{\partial \tau }=\frac{1}{n^{\circ }+1}{\displaystyle \sum _{i=1}^{n^{\circ }+1}\frac{1}{D_{{}_i}^{\ast }\left(\tau ,\upsilon \right)}}\left\{{\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)-{\mathsf{{\rm Y}}}_2\left(z_{(i-1)}\left|\tau ,\upsilon \right.\right)\right\}=0,$$

(15)

where, ${\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)$ and ${\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)$ have the same expressions as Equations (11) and (12) by replacing $z_{(c:n^{\circ })}$ with $z_{(i)}$.

3. LS and WLS Methods

The LS and WLS methods for estimating unknown parameters are well established in reference [31]. Here, the LS estimators (LSEs) and WLS estimators (WLSEs) of $\tau ,$ and $\upsilon$ are examined using SRS and RSS design. We’ll go over the RSS framework technique first, and then obtain these estimators using SRS.

Let the ordered items $Z_{(1:n^{\circ })},Z_{(2:n^{\circ })},\dots ,Z_{(n^{\circ }:n^{\circ })}$ constitute a RSS of size $n^{\circ }=qh$, from the IKD has the CDF given by Equation (3). The LSEs and WLSEs of $\tau ,$ and $\upsilon ,$ are derived by minimizing the following functions with respect to population parameters:

$$\mathbb{Q}={\displaystyle \sum _{c=1}^{n^{\circ }}{\left[F\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)-\frac{c}{n^{\circ }+1}\right]}^2}={\displaystyle \sum _{c=1}^{n^{\circ }}{\left[{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{c}{n^{\circ }+1}\right]}^2},$$

(16)

$$\Im ={\displaystyle \sum _{c=1}^{n^{\circ }}\mathbb{N}(c,n^{\circ }){\left[F\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)-\frac{c}{n^{\circ }+1}\right]}^2}={\displaystyle \sum _{c=1}^{n^{\circ }}\mathbb{N}(c,n^{\circ })}\hspace{0.17em}\hspace{0.17em}{\left[{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{c}{n^{\circ }+1}\right]}^2,$$

(17)

where $\mathbb{N}(c,n^{\circ })=\frac{{(n^{\circ }+1)}^2(n^{\circ }+2)}{c(n^{\circ }-c+1)}.$ As an alternative to Equation (16), the following nonlinear equations can be used to yield the LSEs of $\tau ,$ and $\upsilon ,$ denoted by ${\widehat{\tau }}_{\mathrm{LS}},$ and ${\widehat{\upsilon }}_{\mathrm{LS}},$ respectively, as below:

$$\frac{\partial \mathbb{Q}}{\partial \upsilon }=2{\displaystyle \sum _{c=1}^{n^{\circ }}\left[{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{c}{n+1}\right]{\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=0,}$$

(18)

$$\frac{\partial \mathbb{Q}}{\partial \tau }=2{\displaystyle \sum _{c=1}^{n^{\circ }}\left[{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{c}{n+1}\right]{\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=0.}$$

(19)

Similarly, as an alternative to Equation (17), the following nonlinear equations can be used to obtain the WLSEs of $\tau ,$ and $\upsilon ,$ respectively, denoted by ${\widehat{\tau }}_{\mathrm{WLS}},$ and ${\widehat{\upsilon }}_{\mathrm{WLS}},$ as below:

$$\frac{\partial \Im }{\partial \upsilon }=2{\displaystyle \sum _{c=1}^{n^{\circ }}\mathbb{N}(c,n^{\circ })\left[{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{c}{n+1}\right]{\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=0,}$$

(20)

$$\frac{\partial \Im }{\partial \tau }=2{\displaystyle \sum _{c=1}^{n^{\circ }}\mathbb{N}(c,n^{\circ })\left[{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{c}{n+1}\right]{\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=0,}$$

(21)

where ${\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)$ and ${\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)$ are defined in Equations (11) and (12).

Additionally, the LSEs and WLEs, of ordered SRS $Z_{(1)},Z_{(2)},\dots ,Z_{(n^{\circ })}$ of sizes n^º, for $\tau ,$ and $\upsilon ,$ denoted by ${\tilde{\tau }}_{\mathrm{LS}},{\tilde{\upsilon }}_{\mathrm{LS}}$ and ${\tilde{\tau }}_{\mathrm{WLS}},{\tilde{\upsilon }}_{\mathrm{WLS}}$ are obtained, by solving numerically the following nonlinear equations

$$\frac{\partial {\mathbb{Q}}_{SRS}}{\partial \upsilon }=2{\displaystyle \sum _{i=1}^{n^{\circ }}\left[{\left[1-{\left(1+z_{(i)}\right)}^{-\tau }\right]}^{\upsilon }-\frac{i}{n+1}\right]{\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)=0,}$$

(22)

$$\frac{\partial {\mathbb{Q}}_{SRS}}{\partial \tau }=2{\displaystyle \sum _{i=1}^{n^{\circ }}\left[{\left[1-{\left(1+z_{(i)}\right)}^{-\tau }\right]}^{\upsilon }-\frac{i}{n+1}\right]{\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)=0,}$$

(23)

$$\frac{\partial {\Im }_{SRS}}{\partial \upsilon }=2{\displaystyle \sum _{i=1}^{n^{\circ }}\frac{{(n^{\circ }+1)}^2(n^{\circ }+2)}{i(n^{\circ }-i+1)}\left[{\left[1-{\left(1+z_{(i)}\right)}^{-\tau }\right]}^{\upsilon }-\frac{i}{n+1}\right]{\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)=0,}$$

(24)

$$\frac{\partial {\Im }_{SRS}}{\partial \tau }=2{\displaystyle \sum _{i=1}^{n^{\circ }}\frac{{(n^{\circ }+1)}^2(n^{\circ }+2)}{i(n^{\circ }-i+1)}\left[{\left[1-{\left(1+z_{(i)}\right)}^{-\tau }\right]}^{\upsilon }-\frac{i}{n+1}\right]{\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)=0,}$$

(25)

where, ${\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)$ and ${\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)$ have the same expressions as Equations (11) and (12) by replacing $z_{(c:n^{\circ })}$ with z_(i), where z_(i) is the ordered SRS of size $n^{\circ }$ with CDF of IKD presented in Equation (3).

4. AD and CvM Methods

We employ two estimating methods that are based on the minimization of two well-known goodness-of-fit statistics. The two techniques are the CvM and AD, both of which are based on the difference between the CDF and empirical distribution function estimations. The CvM estimators (CvMEs) and AD estimators (ADEs) of the IKD are explored using SRS and RSS designs.

Suppose that $Z_{(1:n^{\circ })},Z_{(2:n^{\circ })},\dots ,Z_{(n^{\circ }:n^{\circ })}$ are OS items constitute a RSS of size $n^{\circ }=qh$, from IKD. The CvMEs and ADEs of $\tau ,$ and $\upsilon ,$ are derived by minimizing the following functions with respect to population parameters

$$\mathfrak{A}=\frac{1}{12n^{\circ }}+\frac{1}{n^{\circ }}{\displaystyle \sum _{c=1}^{n^{\circ }}{\left\{F\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)-\frac{2c-1}{2n^{\circ }}\right\}}^2}\hspace{0.17em},$$

(26)

$$\mathfrak{M}=-n^{\circ }-\frac{1}{n^{\circ }}{\displaystyle \sum _{c=1}^{n^{\circ }}(2c-1)\left\{\log F\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)+\log \overline{F}\left(z_{(n^{\circ }-c+1:n^{\circ })}\left|\tau ,\upsilon \right.\right)\right\}}\hspace{0.17em}.$$

(27)

As an alternative to Equation (26), the following nonlinear equations can be used to get the CvMEs of $\tau ,$ and $\upsilon ,$ denoted by ${\widehat{\tau }}_{\mathrm{CM}},$ and ${\widehat{\upsilon }}_{\mathrm{CM}},$ as below:

$$\frac{\partial \mathfrak{A}}{\partial \upsilon }=\frac{2}{n^{\circ }}{\displaystyle \sum _{c=1}^{n^{\circ }}\left\{{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{2c-1}{2n^{\circ }}\right\}}{\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=0\hspace{0.17em},$$

(28)

$$\frac{\partial \mathfrak{A}}{\partial \tau }=\frac{2}{n^{\circ }}{\displaystyle \sum _{c=1}^{n^{\circ }}\left\{{\left[1-{\left(1+z_{(c:n^{\circ })}\right)}^{-\tau }\right]}^{\upsilon }-\frac{2c-1}{2n^{\circ }}\right\}}{\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)=0\hspace{0.17em},$$

(29)

where ${\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)$ and ${\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)$ are defined in Equations (11) and (12). Similarly, as an alternative to Equation (27), the following nonlinear equations can be used to obtain the ADEs of $\tau ,$ and $\upsilon ,$ denoted by ${\widehat{\tau }}_{\mathrm{AD}},$ and ${\widehat{\upsilon }}_{\mathrm{AD}},$ as below:

$$\frac{\partial \mathfrak{M}}{\partial \upsilon }=\frac{-1}{n^{\circ }}{\displaystyle \sum _{c=1}^{n^{\circ }}(2c-1)\left\{\frac{{\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)}{F\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)}-\frac{{\mathsf{{\rm Y}}}_1\left(z_{(n^{\circ }-c+1:n^{\circ })}\left|\tau ,\upsilon \right.\right)}{\overline{F}\left(z_{(n^{\circ }-c+1:n^{\circ })}\left|\tau ,\upsilon \right.\right)}\right\}}=0,$$

(30)

$$\frac{\partial \mathfrak{M}}{\partial \tau }=\frac{-1}{n^{\circ }}{\displaystyle \sum _{c=1}^{n^{\circ }}(2c-1)\left\{\frac{{\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)}{F\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)}-\frac{{\mathsf{{\rm Y}}}_2\left(z_{(n^{\circ }-c+1:n^{\circ })}\left|\tau ,\upsilon \right.\right)}{\overline{F}\left(z_{(n^{\circ }-c+1:n^{\circ })}\left|\tau ,\upsilon \right.\right)}\right\}=0},$$

(31)

where ${\mathsf{{\rm Y}}}_1\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)$ and ${\mathsf{{\rm Y}}}_2\left(z_{(c:n^{\circ })}\left|\tau ,\upsilon \right.\right)$ are defined in Equations (11) and (12).

Furthermore, the ADs of $\tau ,$ and $\upsilon ,$ denoted by ${\tilde{\tau }}_{\mathrm{CM}},$ and ${\tilde{\upsilon }}_{\mathrm{CM}},$ based on ordered SRS $Z_{(1)},Z_{(2)},\dots ,Z_{(n^{\circ })}$ of sizes n^º are obtained by solving numerically the following equations

$$\frac{\partial {\mathfrak{A}}_{SRS}}{\partial \upsilon }=\frac{2}{n^{\circ }}{\displaystyle \sum _{i=1}^{n^{\circ }}\left\{{\left[1-{\left(1+z_{(i)}\right)}^{-\tau }\right]}^{\upsilon }-\frac{2i-1}{2n^{\circ }}\right\}}{\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)=0\hspace{0.17em},$$

(32)

$$\frac{\partial {\mathfrak{A}}_{SRS}}{\partial \tau }=\frac{2}{n^{\circ }}{\displaystyle \sum _{i=1}^{n^{\circ }}\left\{{\left[1-{\left(1+z_{(i)}\right)}^{-\tau }\right]}^{\upsilon }-\frac{2i-1}{2n^{\circ }}\right\}}{\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)=0\hspace{0.17em},$$

(33)

where ${\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)$ and ${\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)$ are defined in Equations (11) and (12) with ordered samples $Z_{(1)},Z_{(2)},\dots ,Z_{(n^{\circ })}.$

Similarly, the CvMEs of $\tau ,$ and $\upsilon ,$ denoted by ${\tilde{\tau }}_{\mathrm{CM}},$ and ${\tilde{\upsilon }}_{\mathrm{CM}},$ based on ordered SRS $Z_{(1)},Z_{(2)},\dots ,Z_{(n^{\circ })}$ of sizes n^º, are obtained by solving the following non-linear equations:

$$\frac{\partial {\mathfrak{M}}_{SRS}}{\partial \upsilon }=\frac{-1}{n^{\circ }}{\displaystyle \sum _{i=1}^{n^{\circ }}(i-1)\left\{\frac{{\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)}{F\left(z_{(i)}\left|\tau ,\upsilon \right.\right)}-\frac{{\mathsf{{\rm Y}}}_1\left(z_{(n^{\circ }-i+1)}\left|\tau ,\upsilon \right.\right)}{\overline{F}\left(z_{(n^{\circ }-i+1)}\left|\tau ,\upsilon \right.\right)}\right\}},$$

(34)

$$\frac{\partial {\mathfrak{M}}_{SRS}}{\partial \tau }=\frac{-1}{n^{\circ }}{\displaystyle \sum _{i=1}^{n^{\circ }}(2i-1)\left\{\frac{{\mathsf{{\rm Y}}}_2\left(z_{(i)}\left|\tau ,\upsilon \right.\right)}{F\left(z_{(i)}\left|\tau ,\upsilon \right.\right)}-\frac{{\mathsf{{\rm Y}}}_2\left(z_{(n^{\circ }-i+1)}\left|\tau ,\upsilon \right.\right)}{\overline{F}\left(z_{(n^{\circ }-i+1)}\left|\tau ,\upsilon \right.\right)}\right\}},$$

(35)

where ${\mathsf{{\rm Y}}}_1\left(z_{(i)}\left|\tau ,\upsilon \right.\right)$ and ${\mathsf{{\rm Y}}}_2\left(z_{(n^{\circ }-i+1)}\left|\tau ,\upsilon \right.\right)$ are defined in Equations (11) and (12) with ordered samples $Z_{(1)},Z_{(2)},\dots ,Z_{(n^{\circ })}.$

5. Numerical Evaluation

A simulation study is undertaken here to evaluate the performance of the estimation methods under SRS and RSS. The random samples were produced using IKD for different values of $\upsilon$ and $\tau .$ The following is the simulation algorithm:

• Generate n^º SRS from IKD using the quantile function $z_i={\left(1-{(u)}^{1/\upsilon }\right)}^{-1/\tau }-1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<u<1,$ i = 1, 2,…, $n^{\circ }$, where u is the uniform random variable.
• Select q random samples via SRS each set of size q from the IKD, then rank the units within each set.
• Choose a sample for actual quantification by including the smallest ranked unit in the first set, the second smallest ranked unit in the second set, the process continues in this way until the largest ranked unit is selected from the last set.
• Repeat steps 2 and 3 for h cycles to obtain a sample of sizes $n^{\circ }=qh,$ where the set size q = 3, 4, 5 with cycles number h = 5 and 10.
• The sample sizes of SRS are selected as $n^{\circ }$ = 15, 20, 25, 30, 40, and 50. The sample sizes of RSS are selected as $n^{\circ }=qh,$ where the set size q = 3, 4, 5 with cycles number h = 5 and 10.
• The parameter values are selected as $(\upsilon ,\tau )$ = (0.5, 0.8), (0.5, 1.2), (1.2, 0.8) and (1.5, 1.5).
• Obtain the ML estimates under RRS and SRS, respectively, by solving numerically Equations (6) and (7).
• The MPS estimates of $\tau ,$ and $\upsilon ,$ are produced by solving Equations (9) and 10 for RSS, while solving Equations (14) and (15) in case of SRS.
• The LS and WLS estimates of $\tau ,$ and $\upsilon ,$ are computed by solving numerically Equations (18)–(21) for RSS and solving Equations (22)–(25) in case of SRS.
• The CvM and AD estimates of $\tau ,$ and $\upsilon ,$ are computed by solving numerically Equations (28)–(31) in case of SRS, while solving Equations (32)–(35) in case of SRS.
• Repeat the pervious steps from 1 to 10 N times representing different samples, where N = 1000. The criteria for comparison include mean squared errors (MSEs) for all parameter estimates (PEs) and efficiency (Eff), which are obtained using the following relations:

  $$\mathrm{MSE}(\widehat{\vartheta })=\frac{1}{1000}{\displaystyle \sum _{c=1}^{1000}{\left(\hspace{0.17em}{\widehat{\vartheta }}_c-\vartheta \right)}^2,}\hspace{0.17em}\mathrm{Eff}(\widehat{\vartheta })=\frac{{\mathrm{MSE}}_{\mathrm{SRS}}(\tilde{\vartheta })}{{\mathrm{MSE}}_{\Re \mathbb{S}\mathbb{S}}(\widehat{\vartheta })},\hspace{0.17em}\hspace{0.17em}\widehat{\vartheta }=\widehat{\tau },\widehat{\upsilon }.$$

The PE, MSE, and the Eff are all presented in

Table 1. MSE values for all parameter estimates of IKD under SRS.

${\mathit{n}}^{\circ }$	True Value	ML		MPS		LS		WLS		CvM		AD
		PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
15	$\upsilon =0.5$	0.585	0.190	0.461	0.090	0.514	0.167	0.529	0.175	0.589	0.255	0.437	0.107
	$\tau =0.8$	1.007	0.728	0.716	0.299	0.847	0.633	0.866	0.616	1.043	1.058	0.777	0.532
20	$\upsilon =0.5$	0.564	0.160	0.466	0.088	0.505	0.131	0.521	0.137	0.571	0.196	0.453	0.102
	$\tau =0.8$	0.959	0.621	0.726	0.298	0.838	0.588	0.862	0.557	0.993	0.885	0.787	0.497
25	$\upsilon =0.5$	0.545	0.138	0.464	0.082	0.506	0.122	0.517	0.124	0.556	0.164	0.472	0.104
	$\tau =0.8$	0.924	0.504	0.728	0.260	0.828	0.432	0.849	0.432	0.946	0.608	0.802	0.420
30	$\upsilon =0.5$	0.543	0.133	0.472	0.085	0.511	0.115	0.518	0.118	0.549	0.145	0.472	0.102
	$\tau =0.8$	0.912	0.466	0.742	0.259	0.838	0.418	0.854	0.430	0.933	0.557	0.792	0.388
40	$\upsilon =0.5$	0.530	0.120	0.474	0.083	0.506	0.108	0.513	0.110	0.534	0.128	0.470	0.096
	$\tau =0.8$	0.873	0.381	0.739	0.233	0.813	0.340	0.829	0.344	0.881	0.425	0.768	0.322
50	$\upsilon =0.5$	0.527	0.116	0.479	0.085	0.512	0.109	0.516	0.110	0.534	0.125	0.474	0.099
	$\tau =0.8$	0.858	0.352	0.746	0.230	0.820	0.330	0.830	0.331	0.873	0.396	0.767	0.313

,

Table 2. MSE values for all parameter estimates of IKD under RRS.

q	h	True Value	ML		MPS		LS		WLS		CvM		AD
			PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
3	5	$\upsilon =0.5$	0.557	0.029	0.444	0.020	0.489	0.037	0.492	0.030	0.570	0.070	0.510	0.025
		$\tau =0.8$	0.936	0.170	0.670	0.121	0.772	0.217	0.785	0.193	0.964	0.365	0.824	0.153
	10	$\upsilon =0.5$	0.535	0.008	0.460	0.010	0.494	0.015	0.501	0.014	0.530	0.020	0.506	0.012
		$\tau =0.8$	0.226	0.336	0.709	0.059	0.789	0.095	0.805	0.086	0.877	0.121	0.818	0.071
4	5	$\upsilon =0.5$	0.539	0.016	0.449	0.015	0.486	0.025	0.494	0.026	0.542	0.038	0.505	0.017
		$\tau =0.8$	0.892	0.077	0.680	0.073	0.766	0.161	0.786	0.166	0.900	0.229	0.809	0.079
	10	$\upsilon =0.5$	0.512	0.004	0.465	0.007	0.493	0.010	0.498	0.008	0.520	0.012	0.502	0.008
		$\tau =0.8$	0.188	0.377	0.713	0.039	0.776	0.054	0.789	0.043	0.841	0.064	0.799	0.041
5	5	$\upsilon =0.5$	0.529	0.001	0.451	0.010	0.489	0.014	0.493	0.012	0.533	0.020	0.502	0.010
		$\tau =0.8$	0.862	0.049	0.684	0.055	0.762	0.081	0.775	0.067	0.868	0.107	0.798	0.053
	10	$\upsilon =0.5$	0.495	0.003	0.467	0.005	0.491	0.006	0.496	0.005	0.511	0.007	0.499	0.005
		$\tau =0.8$	0.167	0.402	0.723	0.028	0.774	0.035	0.787	0.029	0.825	0.039	0.796	0.027

,

Table 3. MSE values for all parameter estimates of IKD under SRS.

${\mathit{n}}^{\circ }$	True Value	ML		MPS		LS		WLS		CvM		AD
		PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
15	$\upsilon =0.5$	0.598	0.062	0.471	0.029	0.533	0.065	0.537	0.062	0.644	0.292	0.516	0.050
	$\tau =1.2$	1.537	0.787	1.095	0.390	1.281	0.715	1.292	0.637	1.596	1.211	1.310	0.704
20	$\upsilon =0.5$	0.566	0.031	0.468	0.018	0.525	0.041	0.509	0.024	0.564	0.042	0.518	0.018
	$\tau =1.2$	1.419	0.393	1.078	0.232	1.246	0.445	1.205	0.246	1.397	0.457	1.244	0.206
25	$\upsilon =0.5$	0.550	0.023	0.469	0.015	0.514	0.027	0.520	0.024	0.560	0.039	0.513	0.024
	$\tau =1.2$	1.379	0.278	1.090	0.177	1.241	0.394	1.264	0.339	1.411	0.551	1.260	0.283
30	$\upsilon =0.5$	0.538	0.019	0.467	0.014	0.511	0.024	0.516	0.019	0.551	0.031	0.508	0.021
	$\tau =1.2$	1.333	0.197	1.083	0.139	1.229	0.285	1.274	0.263	1.401	0.389	1.266	0.249
40	$\upsilon =0.5$	0.529	0.012	0.473	0.009	0.502	0.014	0.509	0.012	0.530	0.017	0.505	0.014
	$\tau =1.2$	1.306	0.138	1.106	0.105	1.211	0.162	1.234	0.140	1.312	0.199	1.231	0.148
50	$\upsilon =0.5$	0.527	0.010	0.479	0.008	0.511	0.012	0.515	0.010	0.533	0.014	0.505	0.013
	$\tau =1.2$	1.290	0.100	1.120	0.079	1.234	0.136	1.247	0.116	1.315	0.165	1.229	0.131

,

Table 4. MSE values all parameter estimates of IKD under RSS.

q	h	True Value	ML		MPS		LS		WLS		CvM		AD
			PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
3	5	$\upsilon =0.5$	0.558	0.032	0.447	0.022	0.488	0.034	0.493	0.032	0.568	0.059	0.514	0.028
		$\tau =1.2$	1.390	0.319	1.003	0.242	1.144	0.417	1.161	0.378	1.432	0.715	1.237	0.321
	10	$\upsilon =0.5$	0.525	0.011	0.458	0.010	0.496	0.016	0.499	0.013	0.532	0.020	0.506	0.012
		$\tau =1.2$	1.308	0.132	1.071	0.122	1.187	0.194	1.206	0.173	1.321	0.248	1.231	0.141
4	5	$\upsilon =0.5$	0.541	0.018	0.448	0.014	0.495	0.025	0.499	0.022	0.552	0.038	0.508	0.017
		$\tau =1.2$	1.356	0.198	1.027	0.169	1.179	0.276	1.175	0.243	1.384	0.398	1.239	0.200
	10	$\upsilon =0.5$	0.517	0.007	0.463	0.007	0.488	0.010	0.495	0.008	0.514	0.012	0.499	0.008
		$\tau =1.2$	1.254	0.072	1.068	0.082	1.145	0.113	1.172	0.096	1.240	0.129	1.189	0.084
5	5	$\upsilon =0.5$	0.529	0.010	0.452	0.010	0.484	0.013	0.490	0.011	0.527	0.018	0.501	0.010
		$\tau =1.2$	1.309	0.130	1.037	0.129	1.144	0.178	1.168	0.152	1.301	0.232	1.209	0.142
	10	$\upsilon =0.5$	0.514	0.004	0.466	0.005	0.492	0.006	0.496	0.005	0.512	0.006	0.499	0.004
		$\tau =1.2$	1.247	0.051	1.081	0.060	1.162	0.075	1.180	0.060	1.238	0.085	1.190	0.055

,

Table 5. MSE values for all parameter estimates of IKD under SRS.

${\mathit{n}}^{\circ }$	True Value	ML		MPS		LS		WLS		CvM		AD
		PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
15	$\upsilon =1.5$	1.915	1.204	1.381	0.445	1.661	1.138	1.670	1.029	2.102	2.710	1.707	0.805
	$\tau =1.5$	1.739	0.362	1.356	0.229	1.542	0.409	1.556	0.370	1.803	0.655	1.601	0.300
20	$\upsilon =1.5$	1.759	0.528	1.359	0.251	1.598	0.710	1.604	0.618	1.882	1.504	1.624	0.405
	$\tau =1.5$	1.652	0.238	1.349	0.178	1.498	0.269	1.515	0.238	1.678	0.366	1.549	0.207
25	$\upsilon =1.5$	1.715	0.443	1.379	0.234	1.605	0.372	1.623	0.333	1.816	0.631	1.613	0.278
	$\tau =1.5$	1.615	0.171	1.361	0.141	1.495	0.132	1.521	0.175	1.634	0.253	1.536	0.156
30	$\upsilon =1.5$	1.709	0.341	1.413	0.189	1.598	0.372	1.614	0.339	1.769	0.561	1.626	0.300
	$\tau =1.5$	1.629	0.151	1.402	0.115	1.536	0.192	1.554	0.172	1.654	0.243	1.567	0.149
40	$\upsilon =1.5$	1.600	0.171	1.376	0.124	1.523	0.227	1.543	0.203	1.638	0.297	1.550	0.177
	$\tau =1.5$	1.567	0.096	1.387	0.088	1.491	0.124	1.512	0.112	1.576	0.143	1.522	0.101
50	$\upsilon =1.5$	1.587	0.127	1.398	0.097	1.530	0.172	1.546	0.150	1.622	0.218	1.548	0.130
	$\tau =1.5$	1.563	0.076	1.410	0.069	1.508	0.100	1.525	0.088	1.577	0.115	1.530	0.078

,

Table 6. MSE values for all parameter estimates of IKD under RSS.

q	h	True Value	ML		MPS		LS		WLS		CvM		AD
			PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
3	5	$\upsilon =1.5$	1.779	0.665	1.302	0.328	1.519	0.951	1.529	0.802	1.880	1.903	1.593	0.660
		$\tau =1.5$	1.673	0.248	1.300	0.202	1.437	0.326	1.459	0.289	1.672	0.450	1.524	0.234
	10	$\upsilon =1.5$	1.652	0.191	1.381	0.147	1.527	0.285	1.550	0.245	1.686	0.418	1.576	0.222
		$\tau =1.5$	1.586	0.094	1.369	0.100	1.473	0.139	1.498	0.121	1.587	0.165	1.521	0.109
4	5	$\upsilon =1.5$	1.690	0.317	1.315	0.228	1.500	0.456	1.525	0.422	1.750	0.784	1.558	0.323
		$\tau =1.5$	1.608	0.142	1.305	0.156	1.438	0.198	1.461	0.178	1.611	0.251	1.500	0.151
	10	$\upsilon =1.5$	1.582	0.109	1.364	0.098	1.493	0.166	1.504	0.132	1.606	0.220	1.521	0.120
		$\tau =1.5$	1.543	0.057	1.366	0.070	1.460	0.088	1.475	0.071	1.545	0.099	1.491	0.064
5	5	$\upsilon =1.5$	1.610	0.168	1.310	0.152	1.455	0.224	1.478	0.203	1.639	0.340	1.513	0.179
		$\tau =1.5$	1.567	0.097	1.318	0.119	1.432	0.130	1.453	0.121	1.568	0.154	1.485	0.106
	10	$\upsilon =1.5$	1.557	0.068	1.375	0.072	1.474	0.103	1.494	0.085	1.561	0.125	1.505	0.074
		$\tau =1.5$	1.539	0.041	1.388	0.053	1.467	0.064	1.486	0.053	1.534	0.069	1.496	0.048

,

Table 7. MSE values for all parameter estimates of IKD under SRS.

${\mathit{n}}^{\circ }$	True Value	ML		MPS		LS		WLS		CvM		AD
		PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
15	$\upsilon =1.2$	1.494	0.663	1.098	0.245	1.337	1.17	1.332	0.822	1.65	2.245	1.345	0.476
	$\tau =0.8$	0.926	0.114	0.712	0.072	0.812	0.133	0.822	0.117	0.952	0.203	0.848	0.095
20	$\upsilon =1.2$	1.469	0.367	1.15	0.156	1.314	0.42	1.325	0.37	1.541	0.906	1.350	0.278
	$\tau =0.8$	0.928	0.091	0.752	0.055	0.828	0.099	0.84	0.088	0.935	0.146	0.863	0.08
25	$\upsilon =1.2$	1.359	0.225	1.109	0.126	1.252	0.229	1.261	0.200	1.406	0.365	1.281	0.189
	$\tau =0.8$	0.867	0.058	0.724	0.046	0.800	0.063	0.810	0.056	0.88	0.081	0.823	0.052
30	$\upsilon =1.2$	1.305	0.159	1.093	0.104	1.227	0.225	1.239	0.179	1.348	0.317	1.248	0.150
	$\tau =0.8$	0.846	0.043	0.722	0.038	0.793	0.055	0.804	0.047	0.859	0.067	0.813	0.042
40	$\upsilon =1.2$	1.291	0.094	1.119	0.066	1.231	0.124	1.245	0.108	1.318	0.166	1.250	0.092
	$\tau =0.8$	0.842	0.031	0.740	0.027	0.801	0.038	0.811	0.034	0.849	0.045	0.816	0.031
50	$\upsilon =1.2$	1.274	0.079	1.129	0.059	1.234	0.106	1.246	0.093	1.303	0.134	1.247	0.081
	$\tau =0.8$	0.837	0.025	0.751	0.023	0.807	0.034	0.817	0.0300	0.846	0.039	0.819	0.027

,

Table 8. MSE values for all parameter estimates of IKD under RSS.

q	h	True Value	ML		MPS		LS		WLS		CvM		AD
			PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE	PE	MSE
3	5	$\upsilon =1.2$	1.422	0.372	1.056	0.170	1.224	0.452	1.225	0.358	1.514	1.070	1.272	0.259
		$\tau =0.8$	0.896	0.077	0.687	0.062	0.772	0.103	0.778	0.083	0.910	0.155	0.813	0.068
	10	$\upsilon =1.2$	1.304	0.109	1.099	0.086	1.218	0.157	1.238	0.151	1.335	0.223	1.252	0.126
		$\tau =0.8$	0.846	0.034	0.724	0.037	0.789	0.048	0.802	0.046	0.854	0.058	0.813	0.039
4	5	$\upsilon =1.2$	1.335	0.177	1.059	0.133	1.178	0.229	1.197	0.206	1.358	0.381	1.234	0.175
		$\tau =0.8$	0.868	0.048	0.700	0.047	0.766	0.065	0.780	0.059	0.864	0.083	0.805	0.050
	10	$\upsilon =1.2$	1.257	0.058	1.094	0.057	1.190	0.089	1.205	0.077	1.275	0.117	1.214	0.064
		$\tau =0.8$	0.831	0.019	0.731	0.023	0.787	0.029	0.798	0.025	0.836	0.034	0.805	0.021
5	5	$\upsilon =1.2$	1.289	0.090	1.058	0.077	1.153	0.104	1.168	0.090	1.287	0.153	1.203	0.078
		$\tau =0.8$	0.842	0.028	0.703	0.032	0.757	0.037	0.768	0.031	0.834	0.044	0.791	0.028
	10	$\upsilon =1.2$	1.233	0.036	1.095	0.044	1.185	0.059	1.195	0.048	1.250	0.072	1.201	0.042
		$\tau =0.8$	0.813	0.013	0.728	0.018	0.781	0.020	0.788	0.016	0.818	0.022	0.792	0.015

,

Table 9. Eff values for all estimates.

q	h	True Value	ML	MPS	LS	WLS	CvM	AD
3	5	$\upsilon =0.5$	6.552	4.500	4.514	5.833	3.643	4.280
		$\tau =0.8$	4.282	2.471	2.917	3.192	2.899	3.477
	10	$\upsilon =0.5$	16.220	8.500	7.667	8.429	7.250	8.500
		$\tau =0.8$	1.387	4.390	4.400	5.000	4.603	5.465
4	5	$\upsilon =0.5$	10.000	5.867	5.240	5.269	5.158	6.000
		$\tau =0.8$	8.065	4.082	3.652	3.355	3.865	6.291
	10	$\upsilon =0.5$	28.571	11.690	10.800	13.253	10.667	12.468
		$\tau =0.8$	1.011	5.974	6.296	8.000	6.641	7.854
5	5	$\upsilon =0.5$	138.000	8.200	8.714	10.333	8.200	10.722
		$\tau =0.8$	10.286	4.727	5.333	6.448	5.682	7.925
	10	$\upsilon =0.5$	44.615	17.000	17.302	21.195	17.361	20.625
		$\tau =0.8$	0.876	8.214	9.429	11.414	10.154	11.593

,

Table 10. Eff values for all estimates.

q	h	True Value	ML	MPS	LS	WLS	CvM	AD
3	5	$\upsilon =0.5$	1.938	1.318	1.912	1.938	4.949	1.786
		$\tau =1.2$	2.467	1.612	1.715	1.685	1.694	2.193
	10	$\upsilon =0.5$	1.727	1.400	1.500	1.462	1.550	1.750
		$\tau =1.2$	1.492	1.139	1.469	1.520	1.569	1.766
4	5	$\upsilon =0.5$	1.722	1.286	1.640	1.091	1.105	1.059
		$\tau =1.2$	1.985	1.373	1.612	1.012	1.148	1.030
	10	$\upsilon =0.5$	1.739	1.292	1.400	1.379	1.417	1.842
		$\tau =1.2$	1.917	1.280	1.434	1.458	1.543	1.762
5	5	$\upsilon =0.5$	2.300	1.546	2.077	2.182	2.167	2.400
		$\tau =1.2$	2.138	1.372	2.213	2.230	2.375	1.993
	10	$\upsilon =0.5$	2.310	1.531	2.143	2.128	2.188	3.023
		$\tau =1.2$	1.961	1.317	1.813	1.933	1.941	2.382

,

Table 11. Eff values for all estimates.

q	h	True Value	ML	MPS	LS	WLS	CvM	AD
3	5	$\upsilon =1.5$	1.811	1.357	1.197	1.283	1.424	1.220
		$\tau =1.5$	1.460	1.134	1.255	1.280	1.456	1.282
	10	$\upsilon =1.5$	1.785	1.286	1.305	1.384	1.342	1.351
		$\tau =1.5$	1.606	1.150	1.381	1.421	1.473	1.367
4	5	$\upsilon =1.5$	1.666	1.101	1.557	1.464	1.918	1.254
		$\tau =1.5$	1.676	1.141	1.359	1.337	1.458	1.371
	10	$\upsilon =1.5$	1.569	1.265	1.367	1.538	1.350	1.475
		$\tau =1.5$	1.684	1.257	1.409	1.577	1.444	1.578
5	5	$\upsilon =1.5$	2.637	1.539	1.661	1.640	1.856	1.553
		$\tau =1.5$	1.763	1.185	1.015	1.446	1.643	1.472
	10	$\upsilon =1.5$	1.868	1.347	1.670	1.765	1.744	1.757
		$\tau =1.5$	1.854	1.302	1.563	1.660	1.667	1.625

and

Table 12. Eff values for all estimates.

q	h	True Value	ML	MPS	LS	WLS	CvM	AD
3	5	$\upsilon =1.2$	1.782	1.441	2.588	2.296	2.098	1.838
		$\tau =0.8$	1.481	1.161	1.291	1.410	1.310	1.397
	10	$\upsilon =1.2$	1.459	1.209	1.433	1.185	1.422	1.190
		$\tau =0.8$	1.265	1.027	1.146	1.022	1.155	1.077
4	5	$\upsilon =1.2$	2.073	1.173	1.834	1.796	2.378	1.589
		$\tau =0.8$	1.896	1.170	1.523	1.492	1.759	1.600
	10	$\upsilon =1.2$	1.621	1.158	1.393	1.403	1.419	1.438
		$\tau =0.8$	1.632	1.174	1.310	1.360	1.324	1.476
5	5	$\upsilon =1.2$	2.500	1.636	2.202	2.222	2.386	2.423
		$\tau =0.8$	2.071	1.438	1.703	1.806	1.841	1.857
	10	$\upsilon =1.2$	2.194	1.341	1.797	1.938	1.861	1.929
		$\tau =0.8$	1.923	1.278	1.700	1.875	1.773	1.800

. One can draw the following conclusions from the simulation findings.

▪

All estimates based on RSS are more efficient than their competitors based on SRS in most of the situations (see Table 9, Table 10, Table 11 and Table 12).

▪

All estimates under RSS generally exhibit lower MSE than those under SRS for different sample sizes.

▪

As the cycles number increase, the Eff value of estimates increases in most of the cases (Table 9, Table 10, Table 11 and Table 12).

▪

In most of the cases, as seen in Figure 2 and Figure 3, the MSEs of all estimates decrease as the set size increases. Also, the MSE of ${\widehat{\upsilon }}_{\mathrm{CM}}$ and ${\widehat{\tau }}_{\mathrm{CM}}$ has the highest values, while the MSE of ${\widehat{\upsilon }}_{\mathrm{MPS}},{\widehat{\upsilon }}_{\mathrm{ML}},$ ${\widehat{\tau }}_{\mathrm{MPS}}$ and ${\widehat{\tau }}_{\mathrm{ML}}$ has the smallest values.

Figure 2. MSE of $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ in RSS.

Figure 2. MSE of $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ in RSS.

Figure 3. MSE of $\tau$ estimates at $(\upsilon ,\tau )$ $=(0.5,0.8)$ in RSS.

Figure 3. MSE of $\tau$ estimates at $(\upsilon ,\tau )$ $=(0.5,0.8)$ in RSS.

▪

In most of the cases, the MSEs of all estimates decrease as $n^{\circ }$ increases in both SRS and RSS (see Figure 3 and Figure 4).

▪

The MSE of ${\widehat{\upsilon }}_{\mathrm{MPS}},$ and ${\widehat{\tau }}_{\mathrm{MPS}},$ take the least values at $(\upsilon ,\tau )=(0.5,0.8)$ for sample sizes = 15, 20 and 25 (see Figure 4 and Figure 5).

▪

The MSE of ${\widehat{\upsilon }}_{\mathrm{CM}},$ and ${\widehat{\tau }}_{\mathrm{CM}},$ get the largest values at $(\upsilon ,\tau )=(0.5,0.8)$ for sample sizes = 15, 20 and 25 in both sampling methods (see Figure 2, Figure 3, Figure 4 and Figure 5).

Figure 4. MSE of $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ in SRS.

Figure 4. MSE of $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ in SRS.

Figure 5. MSE of $\tau$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ in SRS.

Figure 5. MSE of $\tau$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ in SRS.

▪

The MSEs of $\upsilon$ and $\tau$ estimates for all methods of estimation in RSS are smaller than the others via SRS (Figure 6 and Figure 7).

▪

The MSEs of ${\tilde{\upsilon }}_{\mathrm{MPS}}$ and ${\widehat{\upsilon }}_{\mathrm{MPS}}$ get the smallest values in both SRS and RSS schemes. While, the MSEs of ${\tilde{\upsilon }}_{\mathrm{CM}}$ and ${\widehat{\upsilon }}_{\mathrm{CM}}$ get the highest values in both SRS and RSS in majority of situations.

Figure 6. MSE of $\upsilon$ estimates at $(\upsilon ,\tau )=$ $(0.5,0.8)$ for (q, h) = (3,5).

Figure 6. MSE of $\upsilon$ estimates at $(\upsilon ,\tau )=$ $(0.5,0.8)$ for (q, h) = (3,5).

Figure 7. MSE of $\tau$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ for (q, h) = (3,10).

Figure 7. MSE of $\tau$ estimates at $(\upsilon ,\tau )=(0.5,0.8)$ for (q, h) = (3,10).

▪

Figure 8 shows that AD is the most Eff method for $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,1.2),$ and h = 10 for different set sizes. Also, we conclude that the MPS is the least Eff method for $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,1.2),$ and h = 10 for different set sizes.

▪

Figure 9 demonstrates that MPS is the least Eff method for $\tau$ estimates at $(\upsilon ,\tau )=(0.5,1.2),$ and h = 10 for different set sizes. Also, we conclude that AD is the most efficient method for $\tau$ estimates at $(\upsilon ,\tau )=(0.5,1.2),$ and h = 10 at different set sizes, except at sample size 40.

▪

Efficiency of all estimates increases as the set size increases (Figure 8 and Figure 9).

Figure 8. Eff of $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,1.2)$ for different set sizes at h = 10.

Figure 8. Eff of $\upsilon$ estimates at $(\upsilon ,\tau )=(0.5,1.2)$ for different set sizes at h = 10.

Figure 9. Eff of $\tau$ estimates at $(\upsilon ,\tau )=(0.5,1.2)$ for different set sizes at h = 10.

Figure 9. Eff of $\tau$ estimates at $(\upsilon ,\tau )=(0.5,1.2)$ for different set sizes at h = 10.

▪

The MSE always decreases as sample size increases, indicating that the estimates are all consistent.

▪

The estimates get more accurate as the sample size increases, indicating that they are asymptotically unbiased.

▪

In general, for fixed $\upsilon$ and $\tau$ as the sample size increases the suggested estimates of $\upsilon$ and $\tau$ approach their real values.

6. Real Data Application

In order to demonstrate the utility of the suggested estimators, a real data set was taken into consideration and carefully thoroughly explained in this part. The information is based on the times between 64 consecutive eruptions of Kiama Blowhole in 1998. A popular tourist destination is the Kiama Blowhole, which is around 120 km south of Sydney. The water is forced into a cliff’s gap by the ocean’s surging. The water then bursts forth via an opening, typically dousing everyone close. Since 12 July 1998, there have been 1340 h’ worth of eruption data collected. These are the data set’s details:

83	51	87	60	28	95	8	27	15	10
18	16	29	54	91	8	17	55	10	35
47	77	36	17	21	36	18	40	10	7
34	27	28	56	8	25	68	146	89	18
73	69	9	37	10	82	29	8	60	61
61	18	169	25	8	26	11	83	11	42
17	14	9	12

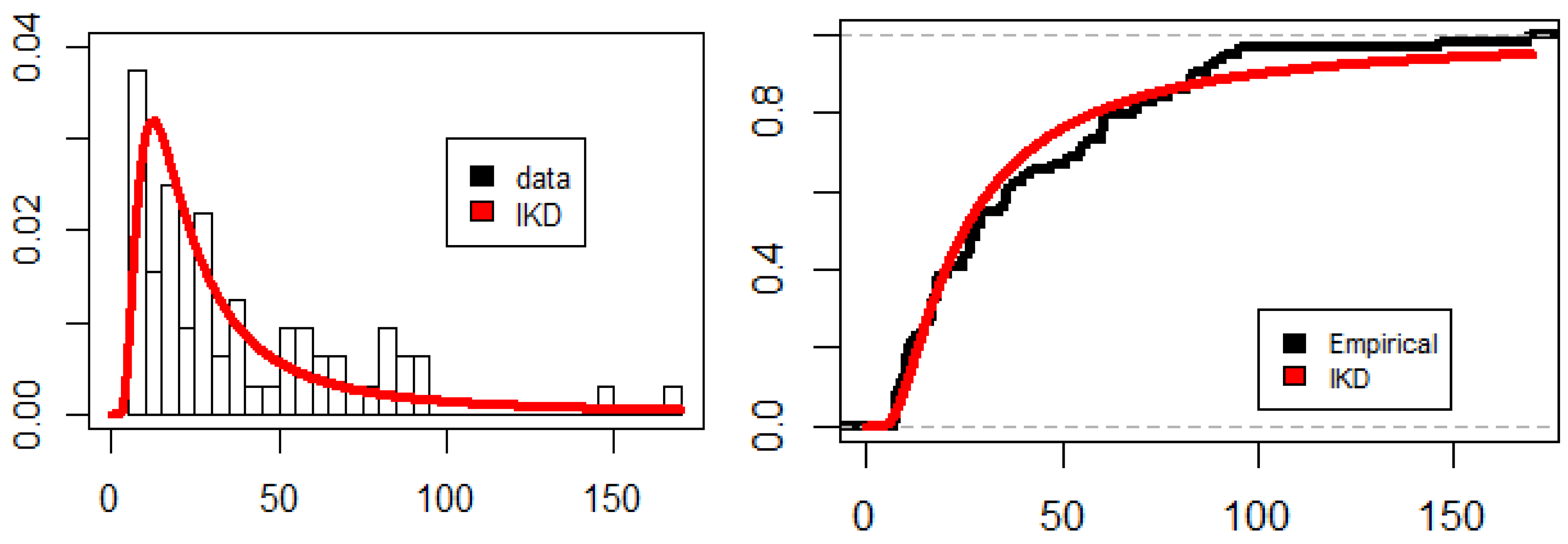
Using the Kolmogorov-Smirnov (K–S) test, the data set is checked for such a fitted model and the estimates are obtained using the ML method. With a p-value (PV) of 0.591, the K–S distance is 0.409. As a result, it is obvious that the IKD is a suitable model for fitting these data. Data’s estimated PDF and CDF are displayed in Figure 10. According to this graph, the IKD seems to be a suitable model for fitting the data.

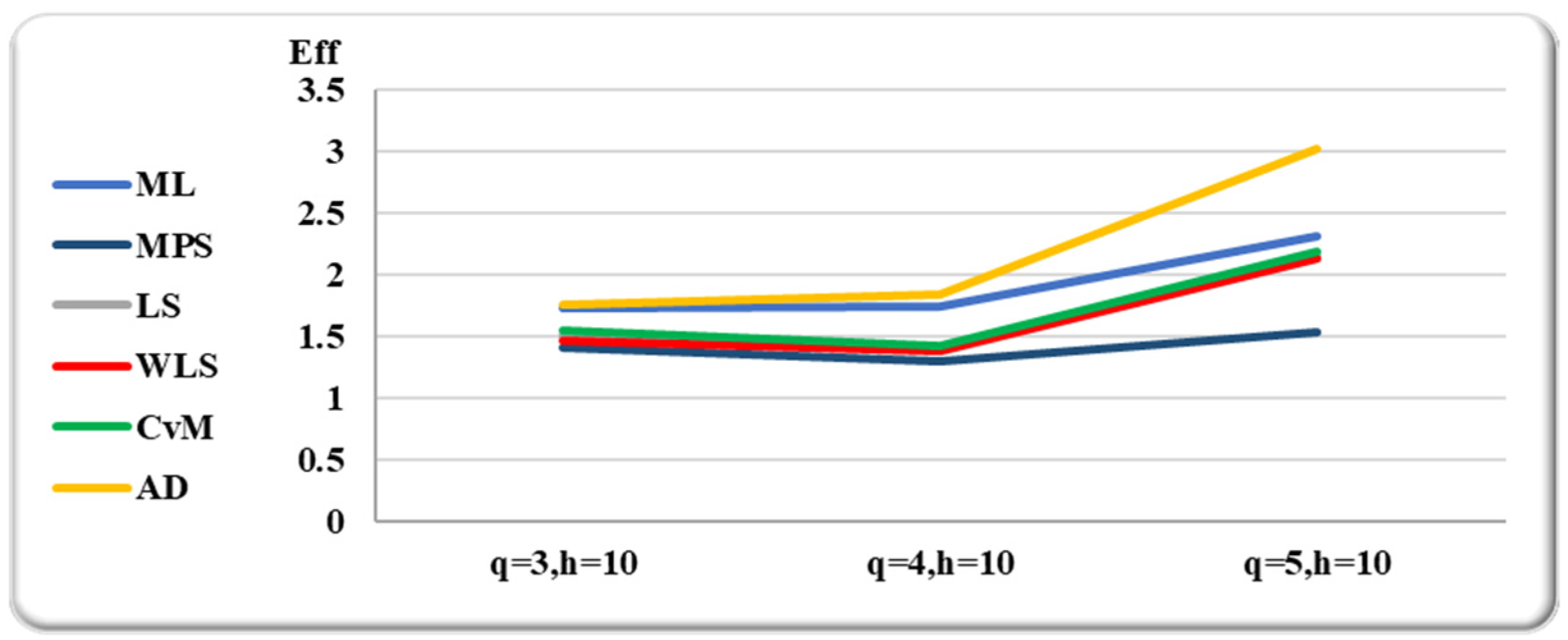
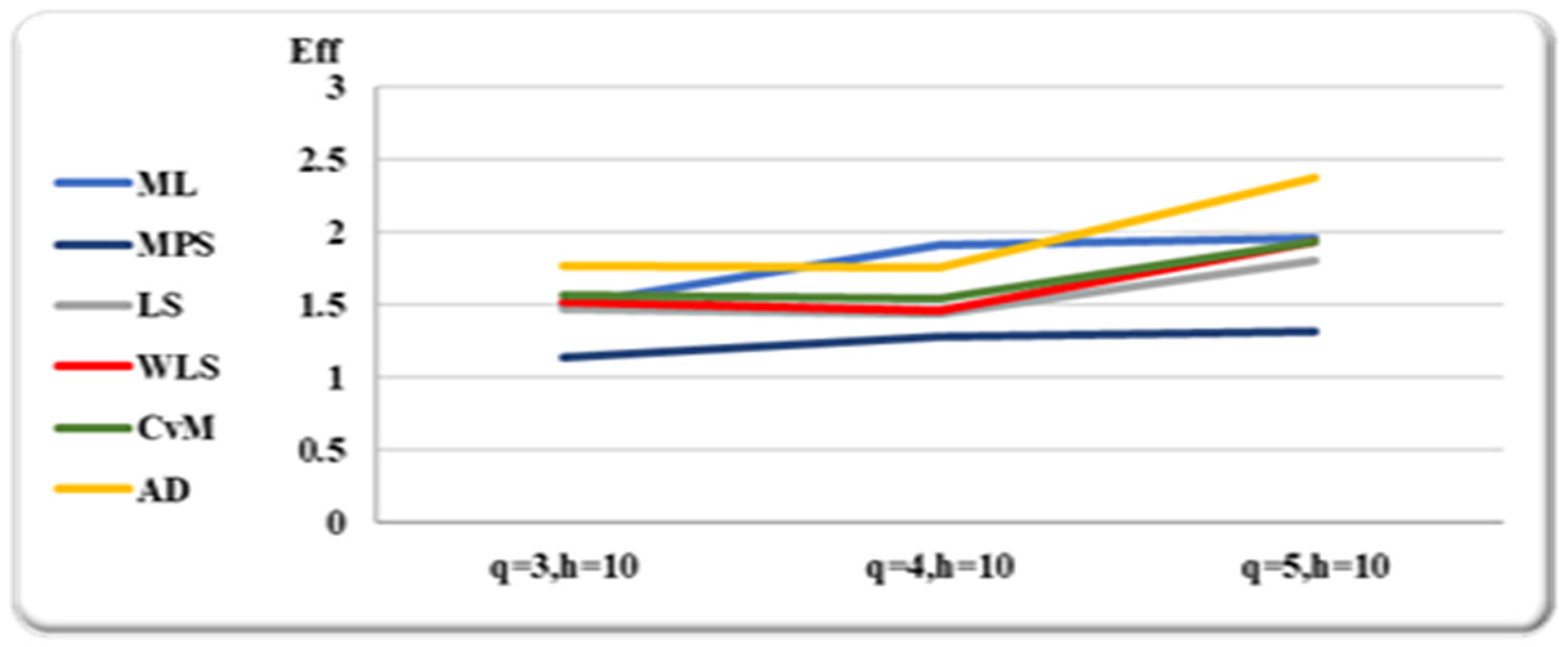
Based on the aforementioned theoretical results, actual data sets are checked using the RSS and SRS sampling techniques. The SRS and RSS estimators from the IKD are shown in

Table 13. SRS estimates of the data set based on different estimation methods.

n		ML	MPS	LS	WLS	CvM	AD
15	$\upsilon$	52.759	28.766	22.742	27.786	32.434	34.004
	$\tau$	1.29	1.107	1.024	1.092	1.127	1.147
20	$\upsilon$	61.707	37.744	362.488	566.907	646.151	49.261
	$\tau$	1.232	1.098	1.623	1.749	1.771	1.146
25	$\upsilon$	46.967	31.391	41.129	47.972	54.742	38.924
	$\tau$	1.196	1.082	1.123	1.185	1.2	1.124
30	$\upsilon$	89.6	59.695	52.938	67.719	65.581	66.906
	$\tau$	1.426	1.306	1.249	1.336	1.31	1.326
40	$\upsilon$	65.611	48.335	87.959	117.002	109.634	59.715
	$\tau$	1.284	1.198	1.322	1.42	1.381	1.237

and

Table 14. RSS estimates of the data set based on different estimation methods.

q	h		ML	MPS	LS	WLS	CvM	AD
3	5	$\upsilon$	30.92	22.378	13.259	18.47	17.111	20.176
		$\tau$	1.159	1.059	0.889	0.996	0.963	1.02
	10	$\upsilon$	40.778	32.993	19.161	29.912	22.273	26.569
		$\tau$	1.294	1.228	1.046	1.192	1.092	1.153
4	5	$\upsilon$	49.991	32.709	23.525	30.568	29.35	31.467
		$\tau$	1.286	1.167	1.049	1.138	1.114	1.144
	10	$\upsilon$	64.691	46.637	46.466	71.757	53.781	45.476
		$\tau$	1.311	1.228	1.194	1.354	1.235	1.203
5	5	$\upsilon$	56.251	56.251	43.076	33.266	44.666	38.693
		$\tau$	1.33	1.33	1.26	1.159	1.272	1.204

for various set sizes under five and ten cycles utilizing different estimating techniques. The R-package is used to generate the RSS and SRS observations.

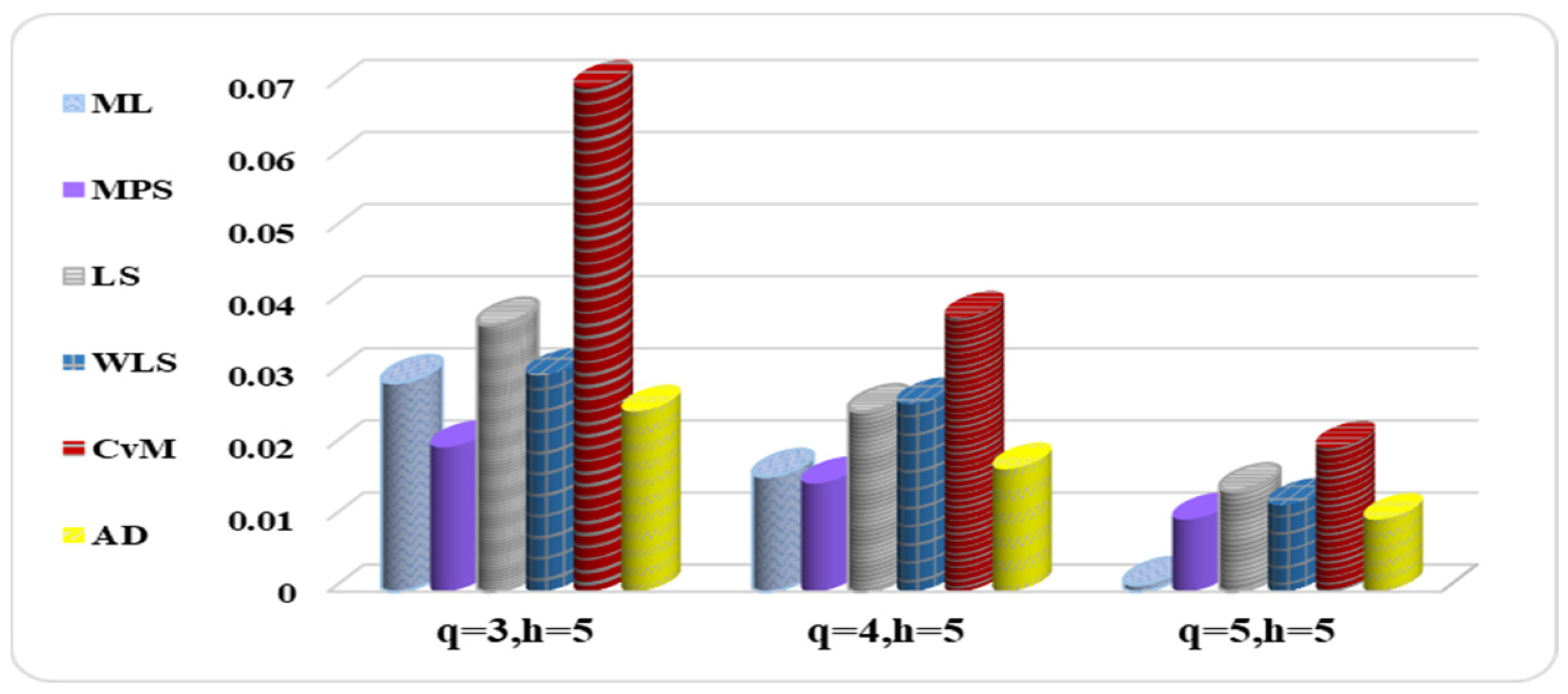
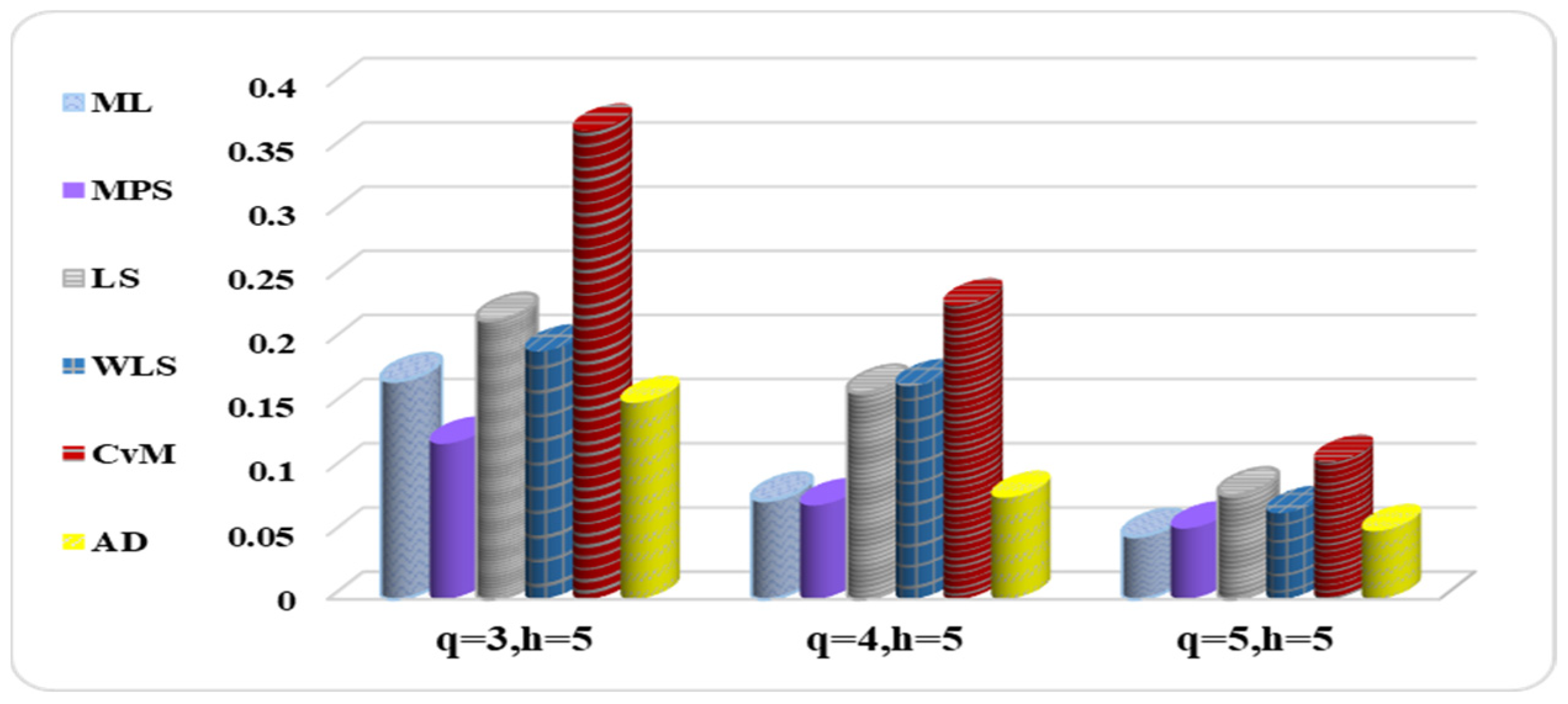
We considered the K–S test for quantifying the distance between the empirical distribution function of the real data and the CDF using the estimators’ parameters in each design, based on the choices of q and h, in order to demonstrate the superiority of RSS over the SRS using various estimation methods considered in this study. Be aware that we have substituted the K–S for the mean squared in this case. Obviously, estimators that outperform the other competitors have larger PVs (greater than 5%) and lower K–S values. Remember that for data, the MLEs based on SRS are regarded as the true population parameters.

The SRS design is considered for this dataset and for each estimation method, where the estimators are obtained using a sample of size qh = 40. Using the RSS with sample of sizes q = 4 and h = 10 is considered for calculating the estimators. We compare the SRS and RSS designs in terms of the K–S distance value and PVs results given in

Table 15. The PEs, KS and PV in SRS and RSS designs for the dataset at sample size for n^º = qh = 40.

Method	$\mathit{\upsilon }$		$\mathit{\tau }$		K–S		PV
	SRS	RSS	SRS	RSS	SRS	RSS	SRS	RSS
ML	65.611	58.035	1.284	1.365	0.128	0.096	0.525	0.858
MPS	48.335	61.198	1.198	1.382	0.135	0.098	0.461	0.838
LS	87.959	38.497	1.322	1.225	0.140	0.106	0.411	0.761
WLS	117.002	52.336	1.420	1.326	0.114	0.087	0.674	0.924
CvM	109.634	44.232	1.381	1.267	0.591	0.099	0.409	0.826
AD	59.715	50.793	1.237	1.316	0.132	0.089	0.489	0.911

, and the corresponding fittings are displayed in Figure 11 and Figure 12. Due to the smallest values of the K–S and the corresponding largest PVs, the RSS is more efficient than the SRS based on the same number of measured units for all estimators.

7. Conclusions

This article considered the problem of RSS-based estimation for the IKD parameters using some estimation techniques; such as, the maximum likelihood, the maximum product of spacing, the ordinary and weighted least squares, the Cramer-von Mises, and the Anderson-Darling. With the aid of a simulation study and the use of a real dataset, the performance results of the proposed estimators are contrasted with those of their SRS equivalents based on the same number of measured units. The numerical simulation results show that for all outcomes shown in the tables with the same sample sizes, the proposed RSS estimators are superior to their SRS counterparts in terms of the smallest MSE. The estimates are asymptotically unbiased because their accuracy improves with sample size. The results of the real dataset also showed that the RSS design is superior to the SRS design due to the largest values for its P-values. As future research the IKD parameters can be estimated using other modifications of RSS as modified robust extreme ranked set sampling [32], neoteric RSS [33] and varied RSS [34]. Also, the process performance index of the IKD can be obtained in future [35,36].