cpd: An R Package for Complex Pearson Distributions
Abstract
1. Introduction
2. Complex Pearson Distributions
2.1. Brief Description and Properties
2.2. Maximum Likelihood Estimation
3. Using the cpd Package
3.1. Overview
R> install.packages(“cpd”)
R> library(cpd)
The package is open-source, so it is also available from GitHub (https://github.com/ujaen-statistics/cpd, accessed on 1 September 2022), where updates and comments can be submitted.
dcbp(x, b, gamma)
pcbp(q, b, gamma, lower.tail = TRUE)
qcbp(p, b, gamma, lower.tail = TRUE)
where x is a vector of the non-negative integer values, q is a vector of the quantiles, p is a vector of the probabilities and b and gamma are the parameters of the distribution. In the pcbp and qcbp functions, the argument lower.tail has to be specified to consider (if it is TRUE ) or (if it is FALSE ). It is also possible to generate n random numbers from a CBP distribution with parameters b and gamma using the rcbp function, whose sentence is rcbp(n, b, gamma).
dctp(x, a, b, gamma)
pctp(q, a, b, gamma, lower.tail = TRUE)
qctp(p, a, b, gamma, lower.tail = TRUE)
rctp(n, b, gamma)
debw(x, alpha, gamma, rho)
pebw(q, alpha, gamma, rho, lower.tail = TRUE)
qebw(p, alpha, gamma, rho, lower.tail = TRUE)
rebw(n, alpha, gamma, rho)
fitcbp(x, bstart = NULL, gammastart = NULL, method = “L-BFGS-B”,
+ control = list(), …),
for the CTP distribution
fitctp(x, astart = NULL, bstart = NULL, gammastart = NULL,
+ method = “L-BFGS-B”, control = list(), …)
as well as for the EBW distribution
fitebw(x, alphastart = NULL, gammastart = NULL, rhostart = NULL,
+ method = “L-BFGS-B”, control = list(), …)
3.2. Examples
3.2.1. Probability Mass, Distribution, Quantile and Random Generation Functions
R> library(cpd)
R> cpd::dcbp(c(0, 1, 2), 3, 2.5)
[1] 0.02985882 0.10749176 0.15355965
The following sentences allow for computing , and :
R> cpd::pcbp(c(3, 5), 3, 2.5)
[1] 0.4387825 0.6528353
R> cpd::pcbp(c(2), 3, 2.5, lower.tail = FALSE)
[1] 0.7090898
To obtain the quartiles of X and the 95th percentile, the sentence and the R output are
R> cpd::qcbp(c(0.25, 0.5, 0.75, 0.95), 3, 2.5)
[1] 2 4 7 17
Finally, to generate 300 numbers from X, we type
R> set.seed(123)
R> x <- cpd::rcbp(300, 3, 2.5)
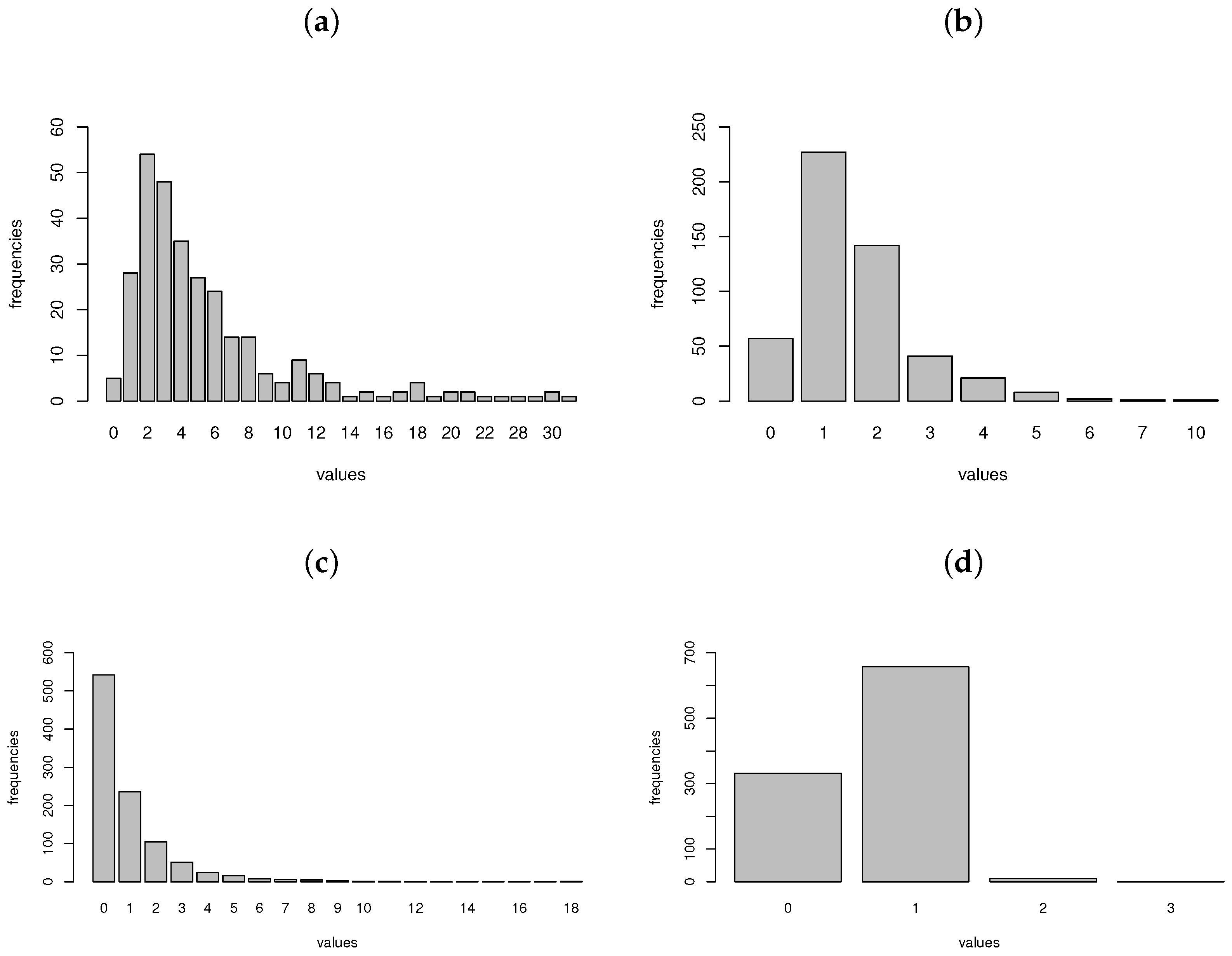
R> table(x)
x
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 26
5 28 54 48 35 27 24 14 14 6 4 9 6 4 1 2 1 2 4 1 2 2 1 1
28 29 30 45
1 1 2 1
Figure 1a shows the bar plot of the random generated data which is obtained with the code
R> barplot(table(x), xlab = “values”, ylab = “frequencies”)
R> cpd::dctp(c(0:3),−1.5, 2, 2)
[1] 0.1331089 0.4159654 0.2946422 0.1043524
Now, the cumulative probabilities and are
R> cpd::pctp(c(1,3), −1.5, 2, 2)
[1] 0.5490744 0.9480690
R> cpd::pctp(1, −1.5, 2, 2, lower.tail = FALSE)
[1] 0.4509256
The quartiles and 95th percentile are obtained as follows:
R> cpd::qctp(c(0.25, 0.5, 0.75, 0.95), −1.5, 2, 2)
[1] 1 1 2 4
To generate 500 random values from Y, we use the code
R> set.seed(123)
R> y <- cpd::rctp(500, -1.5, 2, 2)
The frequency table is
R> table(y)
y
0 1 2 3 4 5 6 7 10
57 227 142 41 21 8 2 1 1
R> cpd::debw(c(0:4), 2, rho = 5)
[1] 0.53571429 0.23809524 0.10714286 0.05194805 0.02705628
R> cpd::debw(c(0:4), −1.2, gamma = 0.75)
[1] 0.3396452713 0.6521189210 0.0074527877 0.0005781556 0.0001248816
The cumulative probabilities , and are obtained as follows:
R> cpd::pebw(c(2,4), 2, rho = 5)
[1] 0.8809524 0.9599567
R> cpd::pebw(2, 2, rho = 5, lower.tail = FALSE)
[1] 0.1190476
R> cpd::pebw(c(2,4), −1.2, gamma = 0.75)
[1] 0.9981288 0.9998974
R> cpd::pebw(3, −1.2, gamma = 0.75, lower.tail = FALSE)
[1] 0.0002048643
The corresponding quartiles and 99th percentile are given by
R> cpd::qebw(c(0.25, 0.5, 0.75, 0.99), 2, rho = 5)
[1] 0 0 1 8
R> cpd::qebw(c(0.25, 0.5, 0.75, 0.99), −1.2, gamma = 0.75)
[1] 0 1 1 1
To generate 1000 random values of and , we type the code
R> set.seed(123)
R> x1 <- cpd::rebw(1000, 2, rho = 5)
R> x2 <- cpd::rebw(1000, -1.2, gamma = 0.75)
The respective frequency tables are
R> table(x1)
x1
0 1 2 3 4 5 6 7 8 9 10 11 18
542 236 105 51 25 16 8 6 5 3 1 1 1
R> table(x2)
x2
0 1 2 3
332 657 10 1
3.2.2. Fitting Functions
R> fireoutbreaks.cbp <- cpd::fitcbp(fireoutbreaks)
b gamma
1.486206 1.494944
(0.08849089) (0.12183708)
Using the summary method, the output is more complete. The argument grouping = TRUE is the setting for grouping in classes with an expected frequency greater than or equal to five in the goodness of fit test, since the default value is FALSE:
R> summary(fireoutbreaks.cbp, grouping = TRUE)
Parameters:
Estimate Std. Error z-value Pr(>|z|)
b 1.486206 0.08849089 16.79502 2.654186 × 10−63
gamma 1.494944 0.12183708 12.27003~1.312062 × 10−34
Loglikelihood: −1637.21 AIC: 3278.43 BIC: 3287.5
Goodness-of-fit tests:
Chi-2: 60.05902 (p-value: 5.11525627536094 × 10−7)
Kolmogorov-Smirnov: 0.04732388 (p-value: 0.033)
Correlation Matrix:
b gamma
b 1.0000000 0.9296264
gamma 0.9296264 1.0000000
The AIC for the CBP fit is lower than the AIC related to an usual NB fit for these data:
R> library(MASS)
R> fireoutbreaks.nb <- MASS::fitdistr(fireoutbreaks, “negative binomial”)
R> fireoutbreaks.nb
size mu
0.80061445 3.52752644
(0.05537946) (0.16624492)
R> AIC(fireoutbreaks.nb)
[1] 3292.707
|
R> fireoutbreaks.ctp <- cpd::fitctp(fireoutbreaks)
Error in fitctp(fireoutbreaks) :
The method of moments does not provide any estimates. Enter
initial values for the~parameters.
R> fireoutbreaks.ctp <- cpd::fitctp(fireoutbreaks, astart = 0, bstart = 1,
+ gammastart = 2.1)
R> summary(fireoutbreaks.ctp, grouping = TRUE)
Parameters:
Estimate Std. Error z-value Pr(>|z|)
a 1.880214 0.8151401 2.306615 0.021076319
b 1.579993 0.5102531 3.096489 0.001958269
gamma 6.441561 2.1065484 3.057874~0.002229130
Loglikelihood: −1623.73 AIC: 3253.45 BIC: 3260.53
Goodness-of-fit tests:
Chi-2: 23.21167 (p-value: 0.0569114065884523)
Kolmogorov-Smirnov: 0.01796262 (p-value: 0.746)
Correlation Matrix:
a b gamma
a 1.0000000 −0.9502083 0.9952855
b −0.9502083 1.0000000 −0.9193242
gamma 0.9952855 −0.9193242 1.0000000
|
R> fireoutbreaks.ebw <- cpd::fitctp(fireoutbreaks)
R> summary(fireoutbreaks.ebw, grouping = TRUE)
Parameters:
Estimate Std. Error z-value Pr(>|z|)
alpha 2.749528 0.1621672 16.954903 1.770541× 10−64
rho 3.139183 0.3171861 9.896977 4.290494 × 10−23
gamma 8.638240 0.6293458 13.725746~7.119262 × 10−43
Loglikelihood: −1624.12 AIC: 3252.25 BIC: 3261.32
Goodness-of-fit tests:
Chi-2: 24.05791 (p-value: 0.0641165517298056)
Kolmogorov-Smirnov: 0.01778027 (p-value: 0.773)
Correlation Matrix:
alpha rho
alpha 1.0000000 0.9247998
rho 0.9247998 1.0000000
This is the most accurate of the four fits using the AIC. Moreover, the goodness-of-fit tests show that the EBW distribution is a reasonable model for the fire outbreak data. Figure 2 includes the observed and expected frequencies, CDFs and PP plots for this fit obtained with the following sentences:
R> plot(fireoutbreaks.ebw)
R> plot(fireoutbreaks.ebw, plty = “CDF”)
R> plot(fireoutbreaks.ebw, plty = “PP”)
R> cpd::varcomp(fireoutbreaks.ebw)
Value Ratio
Randomness 3.534015 0.1019654
Liability 11.631922 0.3356107
Proneness 19.493035 0.5624239
The results indicate that 10.1965% of the variability in fire outbreaks was due to ramdomness, 33.5611% was due to liability (which refers to the general and external conditions of the municipality), and 56.2424% was due to proneness (related to the specific and internal characteristics of the municipality).
R> table(cs_schools)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 18 20
201 437 67 31 17 6 6 2 3 2 2 1 2 1 1 1~1
26 28 47 48
1 1 1 1
First, we fit an NB model:
R> schools.nb <- MASS::fitdistr(cs_schools, “negative binomial”)
R> schools.nb
size mu
1.19336385 1.43057377
(0.10212557) (0.06330097)
R> AIC(schools.nb)
2584.456
As expected, the results for the CTP fit (with initial values and ) improved remarkably with respect to the previous ones:
R> schools.ctp <- cpd::fitctp(schools, astart = 0, bstart = 1,
+ gammastart = 0.5)
R> summary(schools.ctp)
Parameters:
Estimate Std. Error z-value Pr(>|z|)
a −0.5141782 0.03519091 −14.611108 2.386050 × 10−48
b 0.4165253 0.09994774 4.167431 3.080518 × 10−5
gamma 0.2020829 0.05620251 3.595620~3.236198 × 10−4
Loglikelihood: −1058.91 AIC: 2123.81 BIC: 2131.14
Goodness-of-fit tests:
Chi-2: 40.81333 (p-value: 0.649840570375861
Kolmogorov-Smirnov: 0.007734697 (p-value: 0.932)
Correlation Matrix:
a b gamma
a 1.0000000 −0.8066776 −0.7935876
b −0.8066776 1.0000000 0.9637505
gamma −0.7935876 0.9637505 1.0000000
The goodness-of-fit tests also support the adequacy of the model fitted. Figure 3 includes the observed and expected frequencies, CDFs and PP plots for the CTP fit obtained with the code sentences
R> plot(schools.ctp)
R> plot(schools.ctp, plty = “CDF”)
R> plot(schools.ctp, plty = “PP”)
R> syllables.ctp <- cpd::fitctp(syllables)
R> summary(syllables.ctp)
and the output
Parameters:
Estimate Std. Error z-value Pr(>|z|)
a −5.7319721810 0.8127761 −7.0523387550 1.759352 × 10−12
b 0.0008637403 6.0264402 0.0001433251 9.998856 × 10−1
gamma 6.9298746437 3.3472112 2.0703428298~3.842025 × 10−2
Loglikelihood: −159.33 AIC: 324.67 BIC: 328.19
Goodness-of-fit tests:
Chi-2: 0.6018625 (p-value: 0.437868271837147)
Kolmogorov-Smirnov: 0.01181905 (p-value: 0.994)
Correlation Matrix:
a b gamma
a 1.000000000 0.002883042 −0.970588862
b 0.002883042 1.000000000 −0.001203176
gamma −0.970588862 −0.001203176 1.000000000
R> syllables.ebw <- cpd::fitebw(syllables)
R> summary(syllables.ebw)
Parameters:
Estimate Std. Error z-value Pr(>|z|)
alpha −5.731882 0.812740 −7.052541 1.756792 × 10−12
gamma 6.929558 3.347026 2.070363~3.841840 × 10−2
Loglikelihood: −159.33 AIC: 322.67 BIC: 328.19
Goodness-of-fit tests:
Chi-2: 0.6019236 (p-value: 0.74010605961245)
Kolmogorov-Smirnov: 0.01181588 (p-value: 0.994)
Correlation Matrix:
alpha gamma
alpha 1.0000000 −0.9705887
gamma −0.9705887 1.0000000
R> plot(syllables.ebw)
R> plot(syllables.ebw, plty = “CDF”)
R> plot(syllables.ebw, plty = “PP”)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnson, N.L.; Kemp, A.W.; Kotz, S. Univariate Discrete Distributions, 3rd ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Irwin, J.O. The generalized Waring distribution. Part I. J. R. Stat. Soc. Ser. A 1975, 138, 18–31. [Google Scholar] [CrossRef]
- Rodríguez-Avi, J.; Conde-Sánchez, A.; Sáez-Castillo, A.J.; Olmo-Jiménez, M.J. A new generalization of the Waring distribution. Comput. Stat. Data Anal. 2007, 51, 6138–6150. [Google Scholar] [CrossRef]
- Joe, H.; Zhu, R. Generalized Poisson Distribution: The Property of Mixture of Poisson and Comparison with Negative Binomial Distribution. Biom. J. 2005, 45, 219–229. [Google Scholar] [CrossRef] [PubMed]
- Vieira, A.M.C.; Hinde, J.P.; Demetrio, C.G.B. Zero-inflated proportion data models applied to a biological control assay. J. Appl. Stat. 2000, 27, 373–389. [Google Scholar] [CrossRef]
- Conceição, K.S.; Louzada, F.; Andrade, M.G.; Helou, E.S. Zero-modified power series distribution and its Hurdle distribution version. J. Stat. Comput. Simul. 2017, 87, 1842–1862. [Google Scholar] [CrossRef]
- Sáez-Castillo, A.J.; Conde-Sánchez, A. Detecting over- and under-dispersion in zero inflated data with the hyper-Poisson regression model. Stat. Pap. 2017, 58, 19–33. [Google Scholar] [CrossRef]
- da Silva, W.B.; Ribeiro, A.M.T.; Conceição, K.S.; Andrade, M.G.; Neto, F.L. On Zero-Modified Poisson-Sujatha Distribution to Model Overdispersed Count Data. Austrian J. Stat. 2018, 47, 1–19. [Google Scholar] [CrossRef]
- Bonat, W.H.; Jørgensen, B.; Kokonendji, C.C.; Hinde, J.; Demétrio, C.G.B. Extended Poisson–Tweedie: Properties and regression models for count data. Stat. Model. 2018, 18, 24–49. [Google Scholar] [CrossRef]
- Satheesh Kumar, C.; Harisankar, S. On some aspects of a general class of Yule distribution and its applications. Commun. Stat.-Theory Methods 2019, 49, 1–11. [Google Scholar] [CrossRef]
- Rodríguez-Avi, J.; Conde-Sánchez, A.; Sáez-Castillo, A.J.; Olmo-Jiménez, M.J. A triparametric discrete distribution with complex parameters. Stat. Pap. 2004, 45, 81–95. [Google Scholar] [CrossRef]
- Olmo-Jiménez, M.J.; Rodríguez-Avi, J.; Cueva-López, V. A review of the CTP distribution: A comparison with other over- and underdispersed count data models. J. Stat. Comput. Simul. 2018, 88, 2684–2706. [Google Scholar] [CrossRef]
- Rodríguez-Avi, J.; Conde-Sánchez, A.; Sáez-Castillo, A.J. A new class of discrete distributions with complex parameters. Stat. Pap. 2003, 44, 67–88. [Google Scholar] [CrossRef]
- Rodríguez-Avi, J.; Olmo-Jiménez, M.J. A regression model for overdispersed data without too many zeros. Stat. Pap. 2017, 58, 749–773. [Google Scholar] [CrossRef]
- Cueva-López, V.; Olmo-Jiménez, M.J.; Rodríguez-Avi, J. EM algorithm for an extension of the Waring distribution. Comput. Math. Methods 2019, 1, e1046. [Google Scholar] [CrossRef]
- Cueva-López, V.; Olmo-Jiménez, M.J.; Rodríguez-Avi, J. An over- and underdispersed biparametric extension of the Waring distribution. Mathematics 2021, 9, 170. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Sellers, K.F.; Borle, S.; Shmueli, G. The COM-Poisson model for count data: A survey of methods and applications. Appl. Stoch. Model. Bus. Ind. 2012, 28, 104–116. [Google Scholar] [CrossRef]
- Sáez-Castillo, A.J.; Conde-Sánchez, A. A hyper-Poisson regression model for overdispersed and underdispersed count data. Comput. Stat. Data Anal. 2013, 61, 148–157. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Conover, W.J. A Kolmogorov goodness-of-fit test for discontinuous distributions. J. Am. Stat. Assoc. 1972, 67, 591–596. [Google Scholar] [CrossRef]
- Gleser, L.J. Exact power of goodness-of-fit tests of Kolmogorov type for discontinuous distributions. J. Am. Stat. Assoc. 1985, 80, 954–958. [Google Scholar] [CrossRef]
- Wimmer, G.; Kohler, R.; Grotjahn, R.; Altmann, G. Toward a theory of word length distributions. J. Quant. Ling. 1994, 1, 98–106. [Google Scholar] [CrossRef]
- DjurasErnst, G.; Stadlober, S. Text and Language: Structures Function Interrelations Quantitative Perspectives; Chapter Modeling Word Length Frequencies by the Singh-Poisson Distribution; Praesens Verlag: Wien, Austria, 2010; pp. 37–46. [Google Scholar]



| Min | Max | ||||||
|---|---|---|---|---|---|---|---|
| Fire outbreaks | 3.528 | 28.964 | 1 | 2 | 4.75 | 0 | 56 |
| Schools | 1.431 | 10.3807 | 0 | 1 | 1 | 0 | 48 |
| Syllables | 1.889 | 0.910 | 1 | 2 | 2 | 0 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olmo-Jiménez, M.J.; Vílchez-López, S.; Rodríguez-Avi, J. cpd: An R Package for Complex Pearson Distributions. Mathematics 2022, 10, 4101. https://doi.org/10.3390/math10214101
Olmo-Jiménez MJ, Vílchez-López S, Rodríguez-Avi J. cpd: An R Package for Complex Pearson Distributions. Mathematics. 2022; 10(21):4101. https://doi.org/10.3390/math10214101
Chicago/Turabian StyleOlmo-Jiménez, María José, Silverio Vílchez-López, and José Rodríguez-Avi. 2022. "cpd: An R Package for Complex Pearson Distributions" Mathematics 10, no. 21: 4101. https://doi.org/10.3390/math10214101
APA StyleOlmo-Jiménez, M. J., Vílchez-López, S., & Rodríguez-Avi, J. (2022). cpd: An R Package for Complex Pearson Distributions. Mathematics, 10(21), 4101. https://doi.org/10.3390/math10214101





