Fast Algorithms for Estimating the Disturbance Inception Time in Power Systems Based on Time Series of Instantaneous Values of Current and Voltage with a High Sampling Rate

Abstract

The study examines the development and testing of algorithms for disturbance inception time estimation in a power system using instantaneous values of current and voltage with a high sampling rate. The algorithms were tested on both modeled and physical data. The error of signal extremum forecast, the error of signal form forecast, and the signal value at the so-called joint point provided the basis for the suggested algorithms. The method of tuning for each algorithm was described. The time delay and accuracy of the algorithms were evaluated with varying tuning parameters. The algorithms were tested on the two-machine model of a power system in Matlab/Simulink. Signals from emergency event recorders installed on real power facilities were used in testing procedures. The results of this study indicated a possible and promising application of the suggested methods in the emergency control of power systems.

1. Introduction

The development of modern power systems is related to the global trend toward digitalization of all primary processes: generation, distribution, and consumption of power. A considerable emphasis is given to the design and application of digital devices of protection and control based on phasor measurement units (PMU). Time-synchronized instantaneous values of voltages and currents from power system objects can be obtained using these devices. This kind of data opens completely new possibilities for using adaptive emergency control systems based on steady-state measurements [1].

The following parameters of power systems operation are critical to maintaining required levels: stability of parallel operation of synchronous generators, voltage levels at buses, the current flowing through transmission lines and transformers, the operational state of grid equipment, and the cost-efficiency of operation. All mentioned problems are solved by the dispatch control of power system operation. The short duration of transients, the complexity of grid topology, and the difficulty of analyzing the operational states of a power system make the problem of emergency control impossible to be solved manually. As a result, the control of power systems to ensure stable operation is based on special devices for emergency control.

Emergency control, which is aimed at preserving both small signal stability and transient stability, is widely used in systems with relatively long distances between generation and load, large synchronous generators, and significantly constrained transmission lines. The power systems of the Russian Federation, the People’s Republic of China, the USA, and Canada have such features. In the United Power System (UPS) of Russia, emergency control systems are divided into local and centralized systems. Local systems maintain the stability of specific, load buses or regions. Centralized systems have the same purpose but for whole power systems of a larger scale. Algorithms of local emergency control systems (algorithms of the second type) are generally based on the open-loop principle (preventive algorithms): the control actions are designed using offline power flow and transient analysis of the existing power system model with the most probable disturbances being considered. The same principle is applied to centralized control systems (algorithms of the first type), although control actions are designed based on repetitive simulations of the existing power system model considering the most probable disturbances. These principles of emergency control find wide application in the dispatch control of the UPS of Russia.

There are several features of these algorithms:

• Control actions are designed for priori-selected disturbances. It may result in unstable operation of a power system in the case of unplanned disturbance or several consecutive disturbances;
• The design of control action is carried out based on power system models that are different from the real ones, which may decrease the accuracy of emergency control;
• Considering the worst emergency scenarios may lead to the excessive triggering of control actions.
• The drawbacks of conventional emergency control systems are negated by the redundancy and backup structure of emergency control.

The current stage of power systems development is followed by changes in structure, transient nature, and concepts of emergency control. There are new emerging aspects of power systems operation, which are considered non-typical for conventional power systems with fossil fuel-based generation. Emergency control operation is affected by the following features of development and tools of analysis:

• Increasing penetration of renewable sources of energy results in a decreased total inertia of power systems through fewer numbers of rotating masses and increased irregular interconnection fluctuations of active power due to the stochastic nature of generation;
• PMU-based estimation of power systems parameters receives more attention, and it allows obtaining estimation results with minimal time delay (once per utility frequency period for conventional PMUs, once per 5–10 ms for experimental units) and high accuracy;
• Increasingly efficient methods of digital signal processing in combination with PMU data make it possible to estimate parameters of power system models using measurements directly, improving the overall adaptability and accuracy of emergency control;
• The higher efficiency and processing speed of modern computer systems enable maximally fast analysis of power system operation.

The drawbacks of the existing emergency control systems can be overcome with the further development of tools for monitoring, accessing, and analysis of power systems. Significant contributions can be made by implementing the closed-loop type of algorithms (corrective algorithms). This type of algorithm arranges emergency control based on actual models of power systems and online measurements just after a disturbance. PMU data of proper accuracy and time response can be used as input signals. The first designs of these corrective algorithms appeared in the early 2000s. Most suggested algorithms have in their core methods of machine learning and total energy indices of a power system. The implementation of these algorithms was limited by the insufficient efficiency of computing systems and the lack of widely used PMUs [2].

The major problem of transition to corrective online emergency control is to come up with adaptive and fast algorithms for the detection of disturbance inception time using instantaneous values of voltage and current. The possible solution may significantly reduce the time response of emergency control algorithms, as well as improve their efficiency and adequacy.

2. Related Works

The following methods are used to solve the problem of measurement assessment for disturbance detection:

• Fourier transform;
• Gabor transform;
• Kalman filter;
• Hilbert–Huang transform;
• Wavelet transform;
• S transform;
• Methods based on artificial intelligence (AI).

The Fourier transform is used in the analysis of a stationary signal in quasi-steady states. Here, a signal is transformed into an aggregate of sine waves of various frequencies. The obtained frequency spectrum can be used in the evaluation of power quality, although without any time dependence. The short-time Fourier transform (STFT) is used to find out when and which frequency component varies over time [3,4]. According to this method, a non-stationary signal is divided into smaller segments with the following analysis of this signal as a stationary one [5]. STFT was applied in [6] to detect voltage deviations. The characteristic curves were obtained for events related to voltage changes (connecting the transformer to a grid, connecting the capacitor to a grid, and converter operation) in [7]. In this study, the STFT was used to detect it. Except for the drawback connected with the consideration of the frequency spectrum time dependence being difficult, [8] underlines the low-frequency change sensitivity of FT. To overcome this obstacle, authors developed a new version of FT—generalized discrete FT (GDFT). In particular, the paper proposes to reconfigure the comb filter according to the specific harmonic patterns of the input signal for improving the dynamic responses and system flexibility. It was noticed in the mentioned studies that the selection of proper window width was the main issue.

Unlike the traditional Fourier transform the Gabor transform can be used to determine frequency components over time [9]. Because of this, this method was applied to solving the problem of detecting short-time disturbances, as was conducted in [10]. Another notable example is an application of the Gabor transform combined with a neural network to detect arcing faults [11]. In this specific case, the filter eliminates noise and keeps essential signal changes at the same time, allowing for the detection of a disturbance. A trained neural network makes it possible to generalize the features of arcing faults. Such an algorithm can be used in the automatic reclosing of transmission lines when the reclosing is blocked if there is a non-clearing fault on a line. In [12] the modified Gabor–Winger transform is used to analyze disturbances.

The Kalman filter is another approach to the analysis of measurement signals for disturbance detection. According to this method, dimensions are presented as two sets of interconnected equations: equations of states and observations. The method was used together with the discrete wavelet transform to analyze a signal of voltage measurement in the study [13]. Then the processed data are used together with fuzzy logic to detect disturbances. A hybrid solution was also suggested in [14], where the Kalman filter and the S transform combined. The latter is used to detect and trace signals that are typical for short-time disturbances, while the former is used magnitude, phase, and frequency of a signal for the obtained data. The particle swarm optimization was applied to find optimal parameters of the Kalman filter in [15]. Such a solution can improve the accuracy and time response of the detection process.

The problem of identification and classification of disturbances based on measurement data can also be solved using the Hilbert–Huang Transform (HHT). It combines signal decomposition into intrinsic mode functions with the further application of the Hilbert transform to the obtained components [16,17,18]. Unlike other methods, such as STFT or wavelet, the HHT extracts base functions, thus making this method an adaptive one. The literature analysis has shown that the method finds its widest use in conjunction with AI-based models as a tool of signal processing. The HHT was used for signal processing with further events classification in [19,20,21,22,23], with the support vector machine (SVM) and probabilistic neural network (PNN) being used as well. These studies have demonstrated the use of the HHT in the problem of voltage drop identification; however, the range of its application does not end there. For example, in [20], the pattern of voltage surges, oscillations, harmonic distortion, voltage flicker, etc. The modification of HHT with the segmentation of the signal under analysis, which is aimed at accuracy improvement, was used in [21] to find the time of a voltage drop. In turn, [22] demonstrates the high efficiency of empirical-mode decomposition and HHT techniques being applied in combination. Based on a computational experiment, this solution returns better results than S-transform. Finally, in [24,25] HHT is used to find highly correlated mono-component modes of oscillations in terms of the signal processing procedure. Results then lay the basis for the implementation of a class-specific weighted random vector functional link network applied for the classification of power system transients.

The wavelet transform based on the method of Multi-resolution analysis (MRA) is often used in solving the problem of disturbance detection [26]. Following this method, a signal is decomposed using a mother wavelet for different resolutions. What makes it different from the Fourier transform is that in this type of transform there is a relation between signal frequencies and time of occurrence. Besides, this method can decompose the parameters of the initial signal (magnitude, standard deviation, mean value, etc.), which tells about its usability not only for extraction of signal attributes but also for data compression and noise reduction (although these problems are not considered further). The volume of studies covering the subject of wavelet transformation is vast and its literature analysis may require more research. Therefore, only a number of the most relevant studies are considered. In [5,27,28] one of the first examples of its application in events detection was presented. Wavelets were used in the analysis of electromagnetic transients in [5]. In this study, transients and sources of oscillations were identified using the MRA. The multi-resolution signal decomposition (MSD) of measurements was used in the detection and localization of disturbances based on the wavelet transform [28]. The hybrid discrete wavelet transforms, which have in their basis, mother wavelets of the 2-nd and 8-th order were sued in the detection of voltage surges in [29]. In [30] Wavelet Energy Entropy (WEE) and Wavelet Entropy Weight (WEW) were suggested to classify transients following faults and switching operations. The combination of the discrete wavelet transforms and the STFT was applied in the processing of measurement signals in [31]. The results were analyzed using fuzzy logic to classify events in a system. Studies [32,33] were aimed at the development of the online wavelet transform. The wavelet-based neural network, comprising wavelet transform and PNN, was described in [34]. Such a solution ensures adaptability and short time-response in disturbance detection. Another study [35] provides a PQ disturbances identification and classification methodology based on tunable-Q wavelet transform. In the first step, the low-frequency interharmonics are fined and then the wavelet is tuned in order to decompose signals and identify the presence of PQ events. The classification of these events is completed using multiclass support vector machines.

Another method of detection and analysis of disturbances is the S transform (ST), which is the advancement of the wavelet transform and the STFT, but with additional phase correction. The application of this method originated in studies [36,37], where the ST is combined with a neural network for the classification of events related to voltage deviations. Study [38] describes the joint use of the ST and the system based on fuzzy logic and particle swarm to process measurement signals. The fast version of the ST with alternative observation windows was proposed in [39]. The accuracy of identification was improved using the modified method of differential evolution and fuzzy decisions tree. The Fast Dyadic ST as described in [40,41] and was also based on fuzzy logic and fuzzy decisions tree. Authors of [42] propose to apply ST and SVM to identify and classify phase-to-phase and phase-to-ground faults in stator windings of induction motors. In turn, research [43] demonstrates improved approaches to detect so-called broken bar faults or rotor winding faults in induction motors. The proposed solution is based on a combination of the ST and adaptive time–frequency filter. Article [44] describes the methodology for the identification and classification of the grid-connected wind system faults which implies the usage of discrete wavelet transform and ST. The last method could be applied to detect short circuits in voltage source converter-interfaced DC systems, as shown in [45]. Finally, article [46] presents a possible way to use a combination of ST and HHT to implement the protection systems of distribution feeders basing current signals.

Recently neural networks and algorithms based on machine learning have become essential in addressing the problem of disturbance detection. It has already been noticed that up-to-date research often tends to suggest techniques based on combinations of, first, various transforms, the purpose of which is to process a signal and estimate its parameters, and, second, neural networks, the purpose of which is to classify an event. However, machine learning is not uncommon to be used as a stand-alone tool. The model for the detection and classification of events that can be trained on real data had been developed in [47]. Measurements of voltage, current and frequency at the facilities of the Western interconnection system (USA) were analyzed for cases of years 2016 and 2017 with sampling rates of 30 and 60 measurements per second. The following approaches to labeling and classification were considered in the study: decision tree (DT), multinomial logistic regression (MLR), Feedforward neural network (FFNN), single-channel convolutional neural networks (SC-CNN), and multi-channel convolutional neural networks (MC-CNN). In [48] the training with localized instance transfer (LocIT) was implemented to detect emergency events in conditions of a small training dataset and PMUs are allocated throughout a system. The real data were used to create a model. The deep learning neural network was used to detect and classify events online in [49]. The regularization algorithm (deep learning implementation) is described. The trained network detects events and groups them into the following categories: no disturbance, line switching, generator switching, and generator oscillations. The complex and efficient machine learning model is complemented by the experimental part of the research: the model was tested on two-year-long measurements of frequency, power, current and voltage from 187 PMUs installed on the facilities of the Eastern interconnection (USA). Training takes more than three hours, although online detection takes only 0.085 s. The study [50] presents the complex structural model of a deep learning neural network with the objective of the detection and localization of disturbances in a power system with further classification. Events were detected using an autoencoder. The continuous PMU data flow was used as the test dataset. The model was able to re-train and adapt to changes in operational conditions. The model was tested on systems IEEE-14, IEEE-68 and a 9-bus model of a real power system with the actual measurements with a sampling rate of 60 points per second. The accuracy of detection was about 97% for synthetic models. The classification of faults in a distribution grid was addressed in [51]. A huge number of types of classification can be noticed. In particular, 34 types of events are distinguished, including 11 types of faults, disconnection from source and load. Events were classified using machine learning algorithms k-NN, SVM, NN and LDA. The training was carried out on PMU measurements before, after and during a disturbance: current magnitudes and phases, positive, negative and zero sequences. The problem of emergency control based on machine learning was considered in [52]. The problem itself boiled down to insufficient datasets for training in real power systems. The LocIT algorithm was suggested, as well as using two models of a grid: the base model (with excessive training data) and the target model (varying number of PMUs installed). Hence, it was hypothesized that an algorithm trained on the test model can be used for classification in other power systems. In this case, the average accuracy of classification was about 81,7%.

Based on the laconic literature review presented above and obtained results of other studies [53,54] one could identify several typical benefits and drawbacks of each considered method. These specific features are briefly summarized in Table 1.

Table 1. Comparison of existing measurement assessment techniques.

Method	References	Merits	Drawbacks
FT	[3,4,5,6,7,8]	Simple implementation for stationary signals	Inability to consider time dependence of harmonics directly Low sensitivity for frequency deviations
GT	[9,10,11,12]	High time-frequency resolution	Can hardly be used for high frequency disturbances
KT	[13,14,15]	High signal-to-noise ratio	The decomposition of a signal cannot be provided both in time and frequency domains
HHT	[16,17,18,19,20,21,22,23,24,25]	High time-frequency resolution	Useful only for short-term disturbances
WT	[26,27,28,29,30,31,32,33,34,35]	High time-frequency resolution	High computational burden Inability to analyze noised signals
ST	[36,37,38,39,40,41,42,43,44,45,46]	High time-frequency resolution High accuracy of PQ events recognition	Cannot be applied to analyze harmonics
AI	[47,48,49,50,51,52]	Capability to extract complex features High accuracy	Dependence on training data set High computational difficulty

The purpose of this work is to develop simple and efficient algorithms for the adaptive detection of a disturbance time from the values of instantaneous current and voltage. The developed algorithms are aimed at application in the emergency control of power systems, which imposes higher requirements for speed, accuracy, and simplicity of implementation.

3. Description of the Algorithms of Disturbance Time Estimation Using Currents and Voltages

The three algorithms for estimation of the disturbance time using current and voltage values have been developed. These algorithms are based on a statistical analysis of the forecast error, signal shape, and difference of derivatives in joint points.

3.1. Algorithm 1

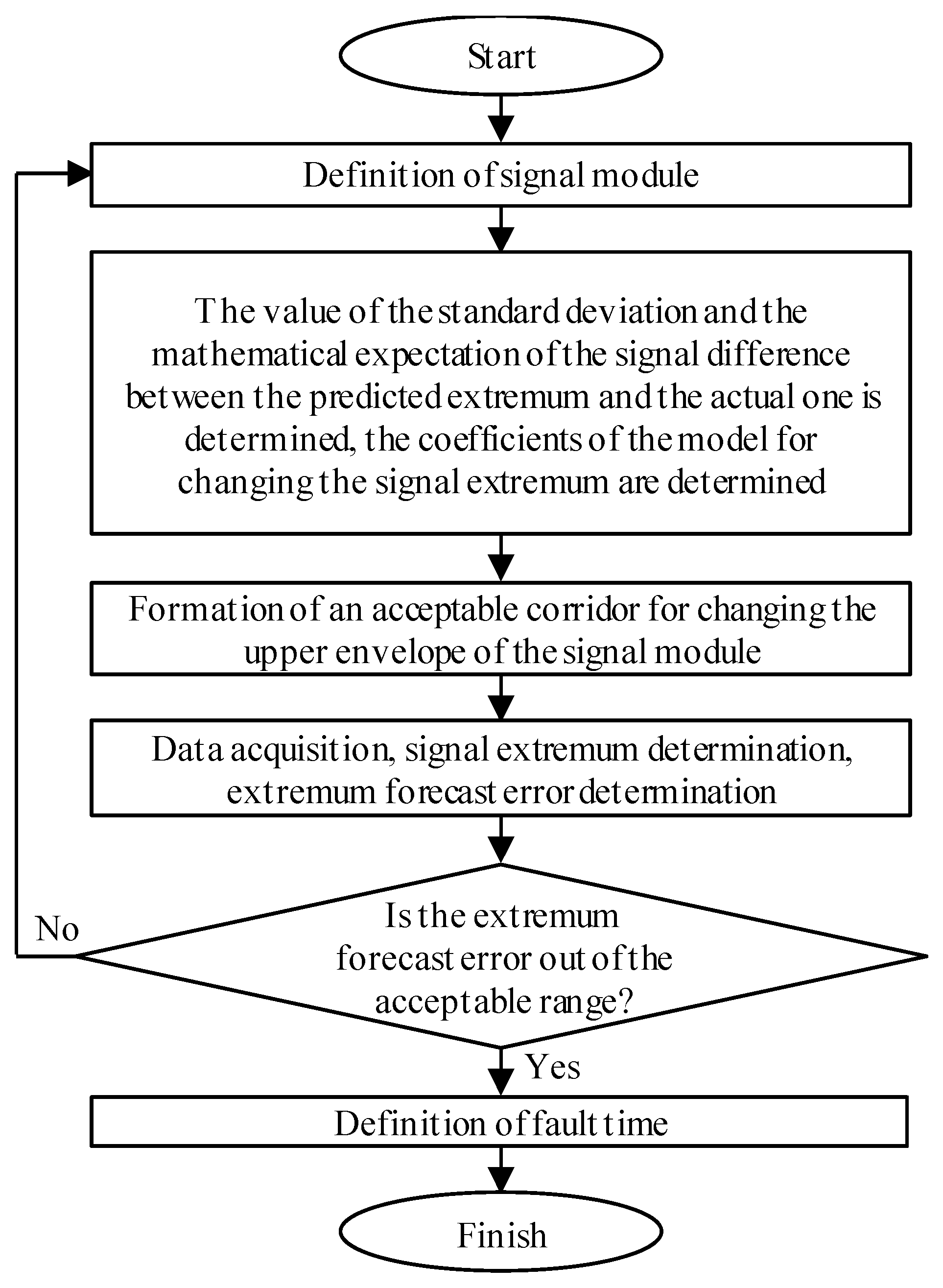
The block diagram in Figure 1 describes algorithm 1 of disturbance time estimation.

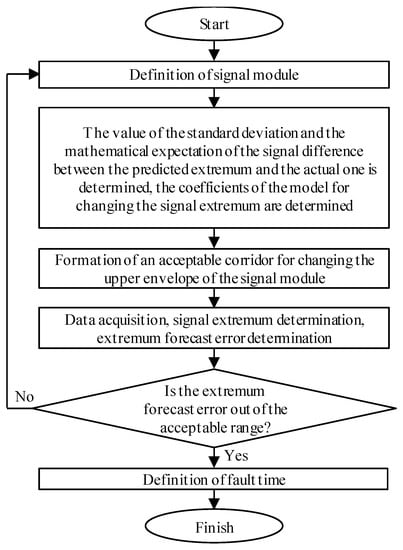
Figure 1. The block diagram of algorithm 1.

Signal extremum analysis is used in algorithm 1, the operation of which can be described as follows:

• For the selected training interval, the signal extremum is predicted;
• The difference between the actual extremum and the predicted one is found;
• The mathematical expectation and the standard deviation of the series of the difference between the actual and forecast extremes are determined;
• As a result of the execution of point 4, according to the three sigmas (3-σ) rule, the permissible range of change in the extremum forecast error is determined;
• For the prediction interval, an extremum is estimated;
• The difference between the actual value of the extremum and the predicted value is performed;
• If the difference between the actual value of the extremum and the predicted value is outside the allowable range, then the disturbance time is captured.

The following parameters were used as adjustable ones: the number of extremums on the learning stage and the number of forecast extremums of an absolute signal. Signal extremum estimation is based on the method of sliding parabolas [2].

3.2. Algorithm 2

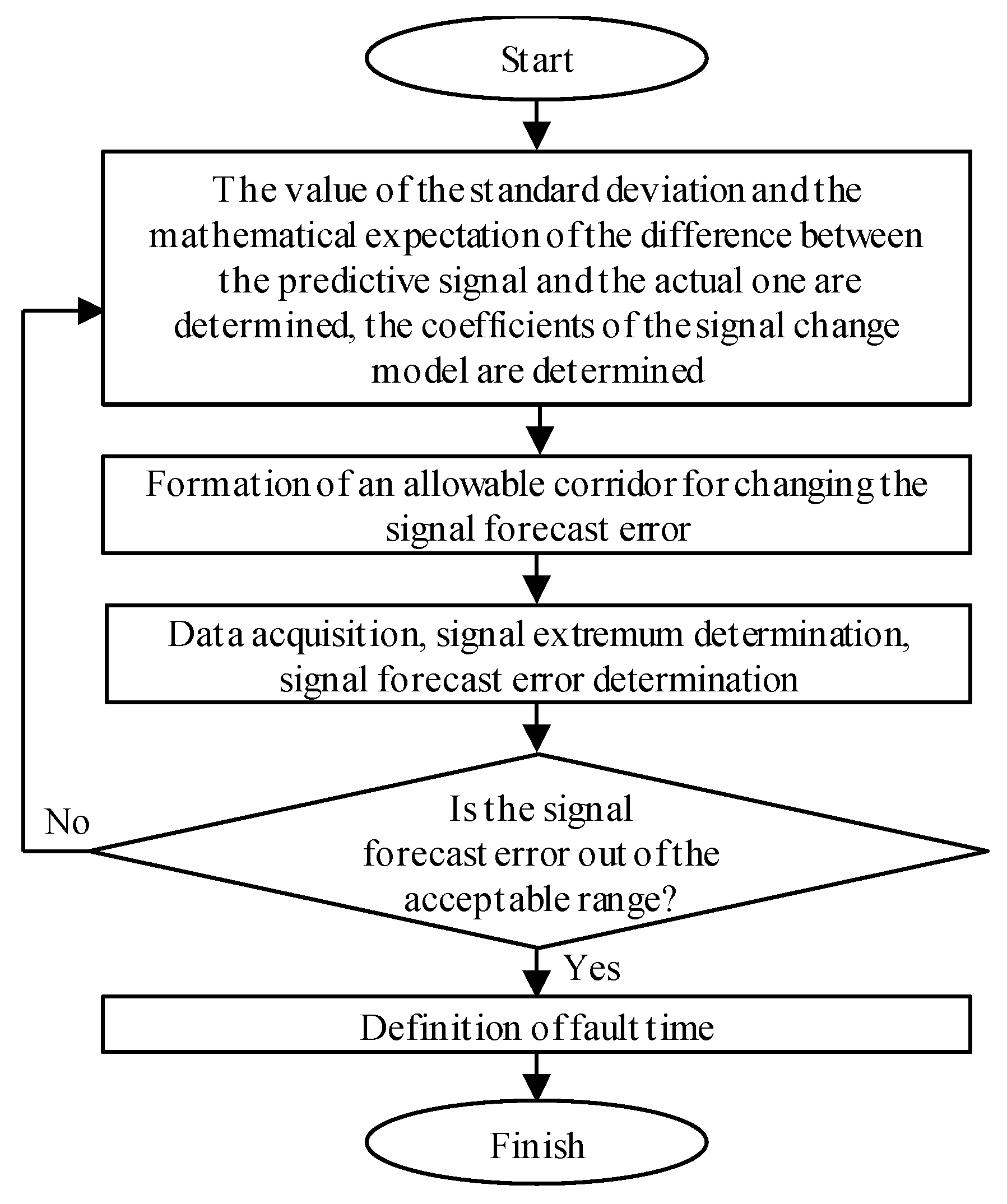
The block diagram in Figure 2 describes algorithm 2 of disturbance time estimation.

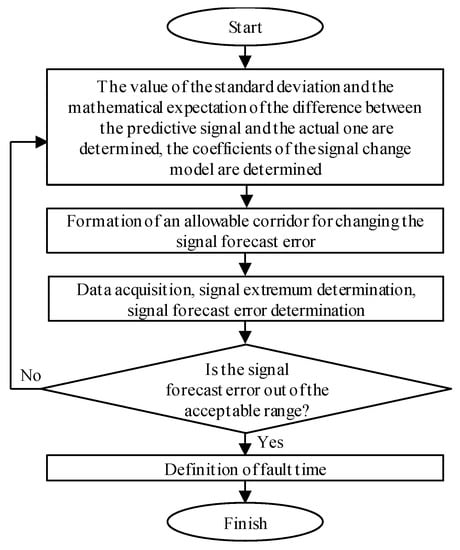
Figure 2. The block diagram of the algorithm 2.

Algorithm 2 is based on estimating the signal forecast error on the forestall interval. A polynomial is used to forecast a signal, it is a sum of the three first elements of the Fourier series. In the learning stage, the algorithm estimates the difference between the forecast signal and the original one. After that, the algorithm determines the mean and standard deviation of the signal forecast error. Assuming that forecast error follows a normal distribution, the algorithm forms a 3-σ corridor based on the rule of three sigmas. After data acquisition, the algorithm compares the forecast signal and the actual one after the new data are acquired. If the signal forecast error is out of the acceptable range, the algorithm detects the disturbance inception.

The following parameters were used as adjustable: training dataset size and prediction interval size.

3.3. Algorithm 3

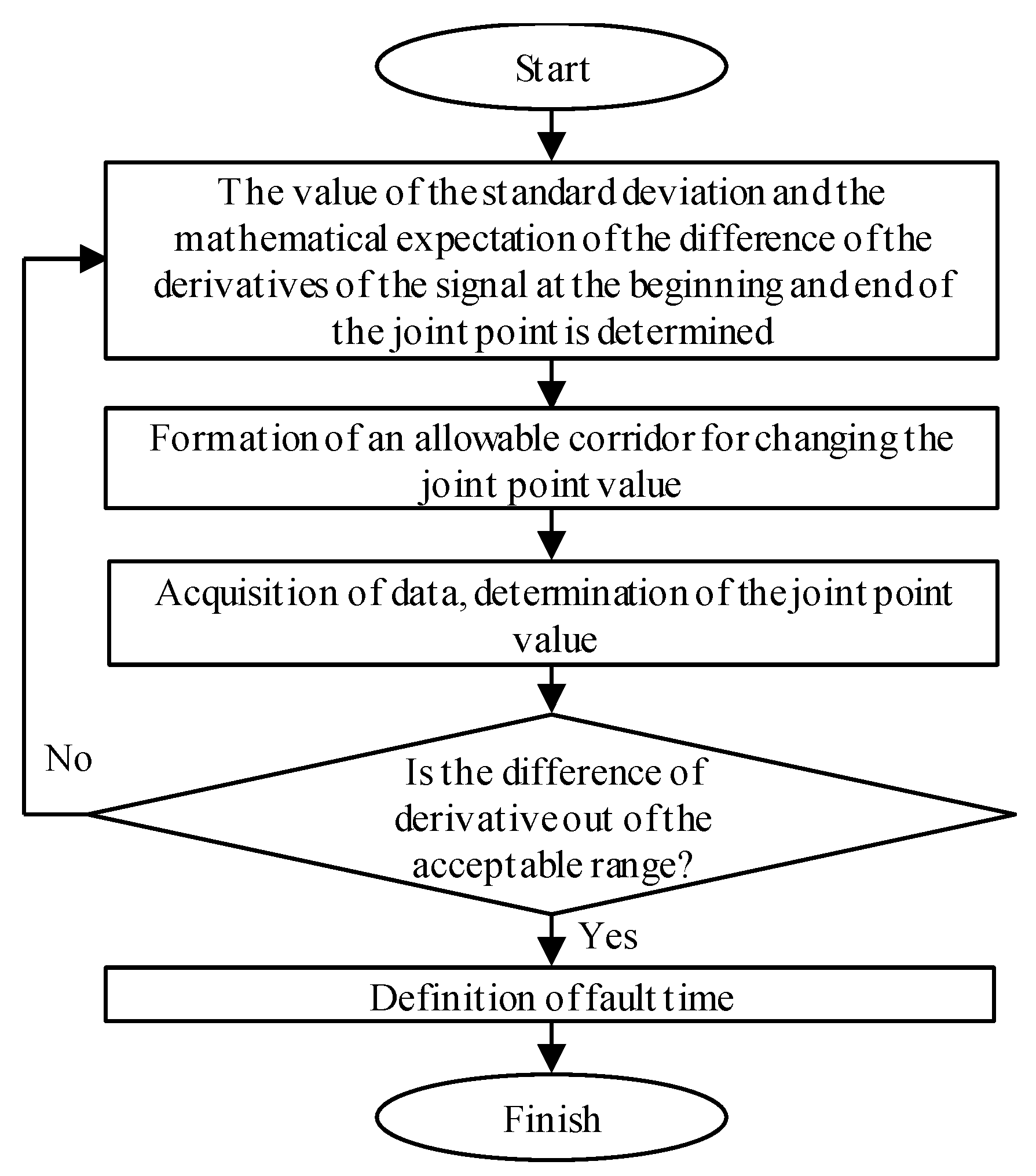
The block diagram in Figure 3 describes algorithm 3 of disturbance time estimation.

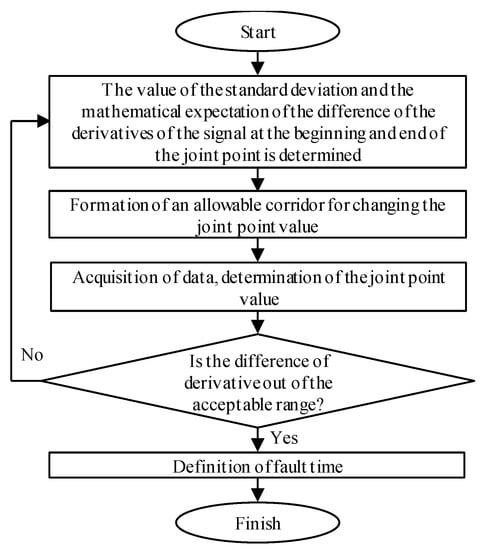
Figure 3. The block diagram of the algorithm 3.

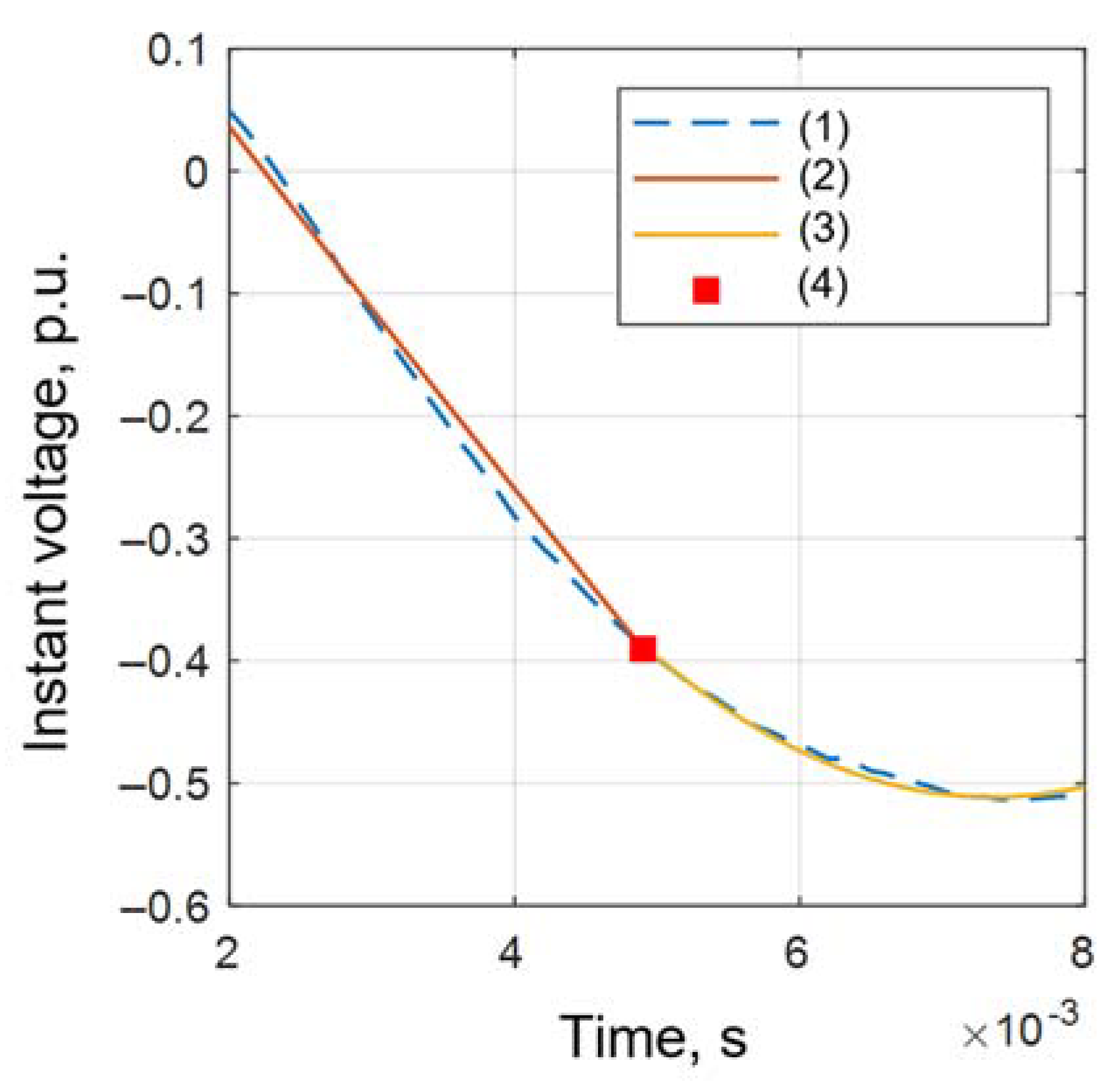
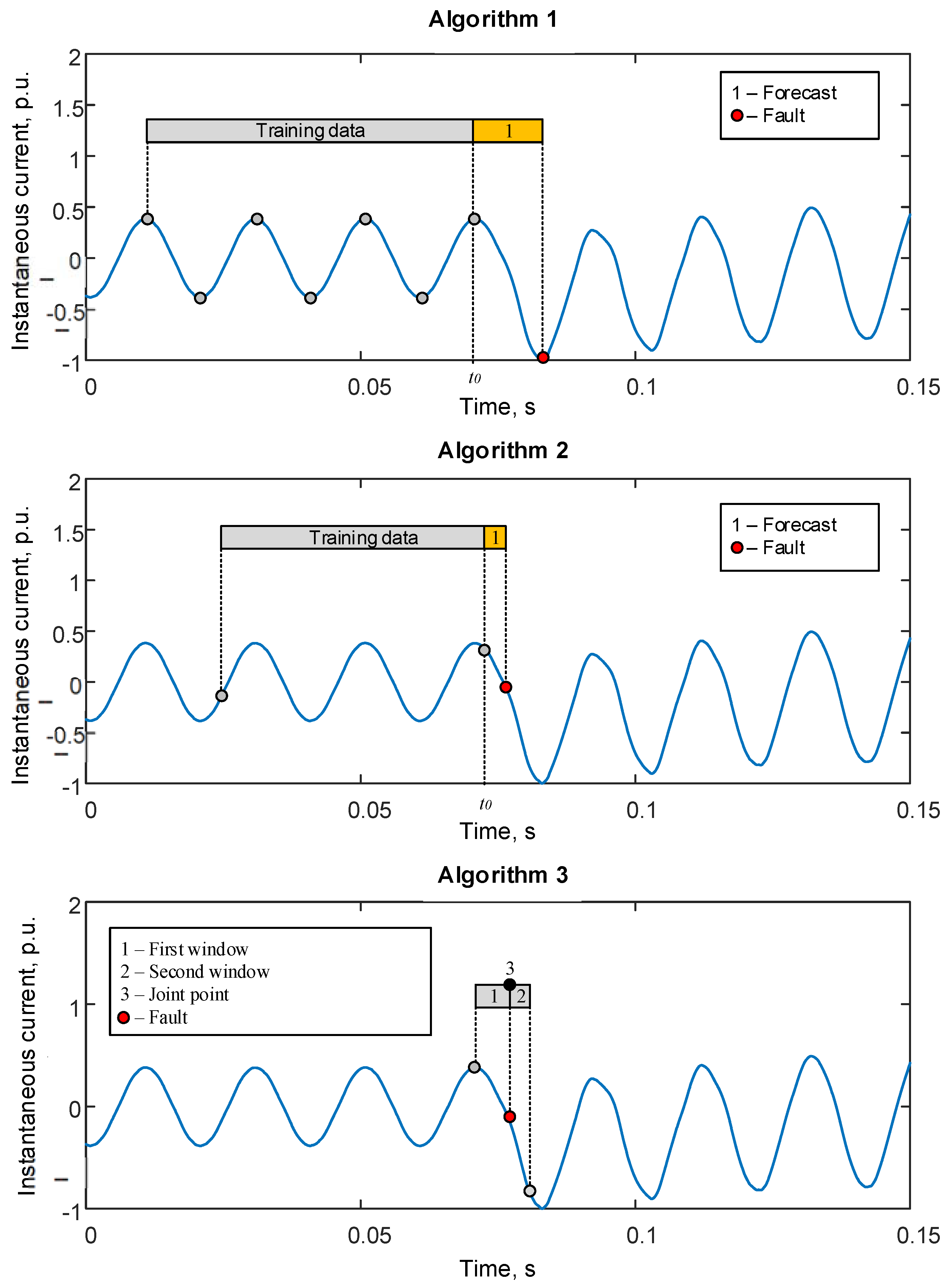
The second-order approximation is used to estimate the disturbance time in instantaneous values of sine current and voltage. Figure 4 describes an example of the joint point modulation, (1)—measurements, (2)—first window, (3)—second window, and (4)—joint point.

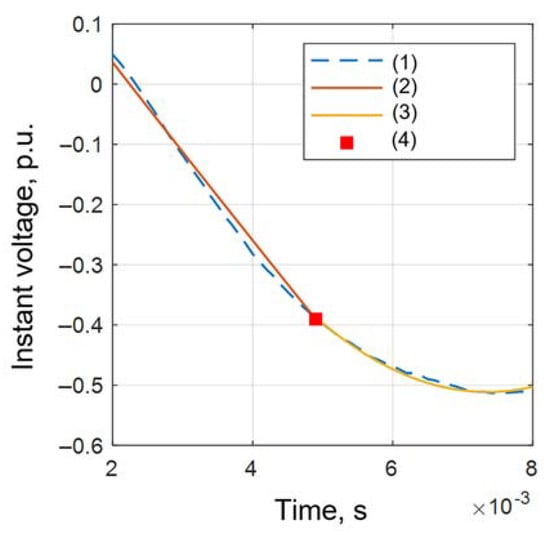
Figure 4. An example of joint point forming.

In this study, ‘a joint point’ means a point that is common for both first and second-order polynomials, obtained as a result of approximating instantaneous values of current/voltage on the pre-selected windows.

In the learning stage, the algorithm estimates the difference between derivatives of the signal from the first and second windows. Then, the mean and standard deviation of the resultant series are calculated. Assuming that forecast error follows a normal distribution, the algorithm forms a 3-σ corridor based on the rule of three sigmas. The algorithm estimates the value at the joint point after the new data are acquired. If the value is out of the acceptable range, the algorithm detects the disturbance inception.

Seizes of the first and second windows are used as adjustable parameters.

For algorithms 1 and 2 upper and lower limits are found as follows:

$$Bound{s}_{1,2}=M{E}_{1,2}\pm 3\times ST{D}_{1,2},$$

(1)

where Bounds_1,2 are acceptable bounds for algorithms 1 and 2, ME_1,2 are mean values of the forecast error for the signal extremum or value, and STD_1,2 are standard deviations of the measured extremum or signal from the forecast one on the learning stage.

For the algorithms, 3 upper and lower limits are found as:

$$Bound{s}_3=M{E}_3\pm 3\times ST{D}_3,$$

(2)

where Bounds₃ are acceptable bounds for algorithm 3, ME₃ is the mean value of the difference between derivatives of a signal between the first and the second window, and STD₃ is the standard deviation of signal derivatives difference between the first and the second window.

Values Bounds_1,2 of Bounds₃ are found on the pre-selected learning interval and are specified on each time cycle.

3.4. Comparison of Algorithms Time Delays

Figure 5 describes comparison delays of the algorithms’ time delays using the data of instantaneous values of current and voltage.

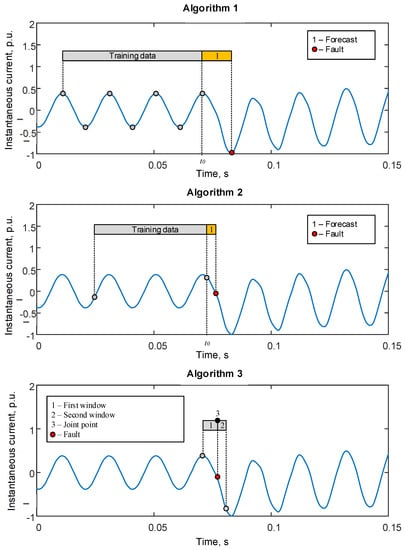
Figure 5. The algorithms time delays for methods of disturbance inception estimation.

Algorithm 1 makes it possible to find disturbance time within the first extremum of a transient, which leads to lower accuracy in comparison with algorithms 2 and 3. Algorithms 2 and 3 show similar accuracy. From the point of view of emergency control, one of the basic requirements is low time-response of signal digital processing. At the same time, the full-time delay of the algorithm is a sum of the algorithm delay and the delay of the apparatus part. For algorithms 1 and 2, the orange rectangle highlights the forecast stage and the gray one highlights the stage of acquisition of the coefficients of the changing signal model. The red circle highlights a point of disturbance inception. Figure 5 describes the first and second windows, marked as gray rectangles, forming the base for the joint point, the red circle highlights a point of disturbance inception. For algorithm 3 a time delay corresponds to the size of the first window. Algorithm 1 has the highest algorithm time delay and the lowest accuracy, which makes it difficult to use this emergency control. Algorithms 2 and 3 have similar accuracy in finding a time of disturbance inception. The time delay of algorithm 3 could be significantly reduced by using the express method of approximation with a second-order polynomial [45].

3.5. Method of Algorithm Parameters Selection

The selection of algorithm parameters is carried out with consideration to maintaining a balance between accuracy and time response.

In this study, the algorithms are tuned using the procedure of consecutive changing of parameters with tracing the forecast error of inception detection. The signals in use are obtained after a series of transient simulations of the power system model that describes the actual level of noise and distortion.

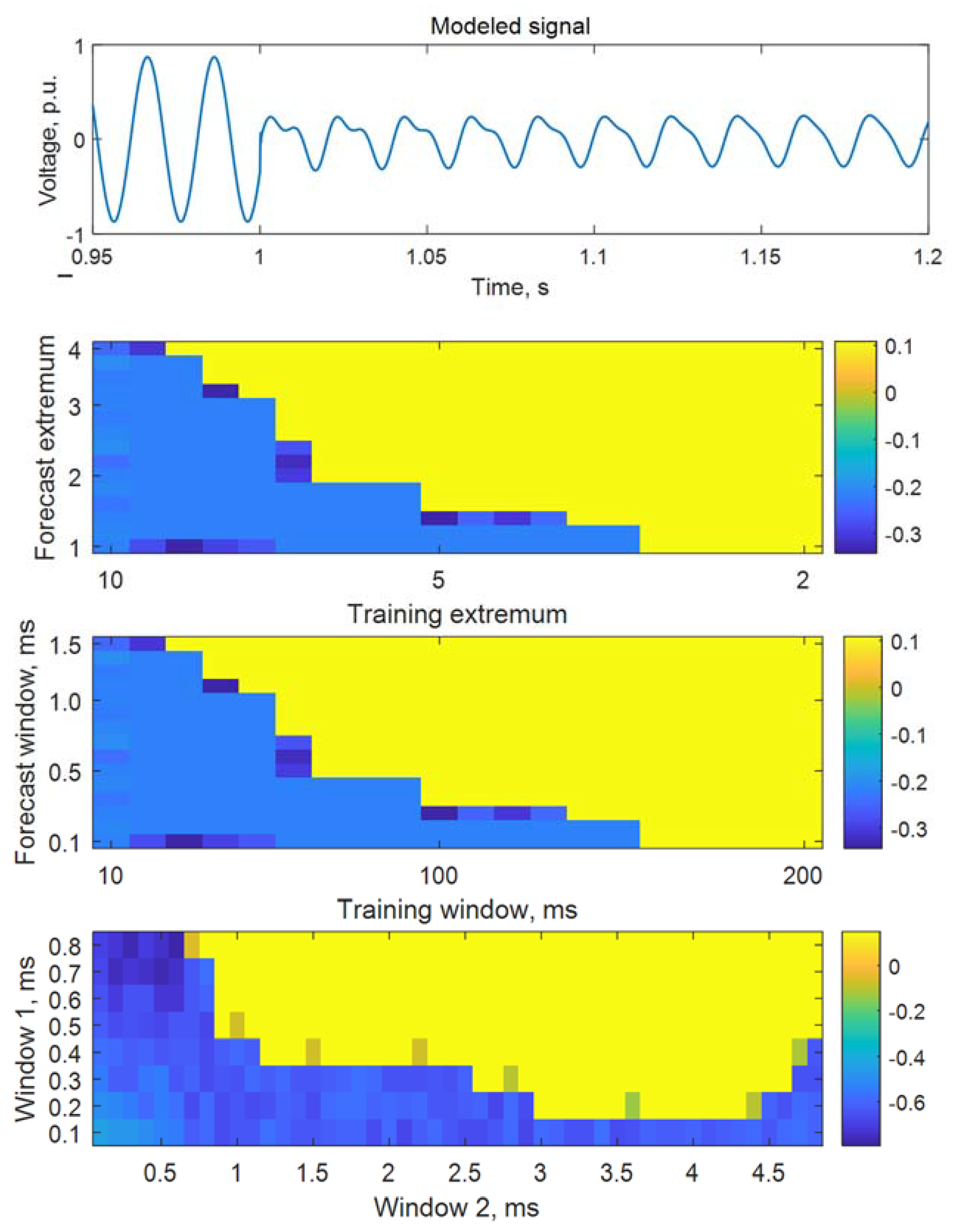
Figure 6 describes an example of settings for each algorithm for the modeled signal. The colored line shows the forecast error of disturbance inception estimation, the first sub-plot describes the actual signal, the second one—results after tuning algorithm 1, the third—results after tuning algorithm 2, and the fourth—results after tuning algorithm 3. The color in Figure 6 shows the values of the error in determining the disturbance time. Algorithm settings are selected by determining the range of acceptable error values for determining the disturbance time. The abscissa and ordinate axes of the subplots 2–4 of Figure 6 show the variable settings of the developed algorithms.

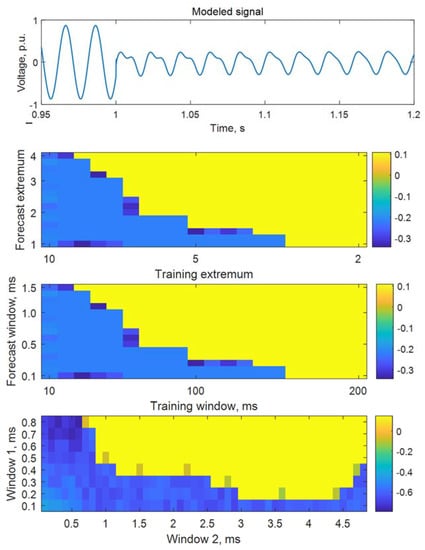
Figure 6. Results of algorithms tuning.

The following tuning parameters were used to estimate disturbance inception time for both modeled and physical signals:

• Algorithm 1: retrospective extremum—5 ms, forecast extremum—2 ms;
• Algorithm 2: training interval—60 ms, forecast interval—1 ms;
• Algorithm 3: first window—0.5 ms, second window—1.5 ms.

4. Testing the Algorithms of Disturbance Inception Estimation on Modeled and Physical Data

This section describes a comparison of the results of disturbance inception estimation between a modeled signal and a physical one with an initial sampling rate of 10 kHz.

The suggested algorithms are using the tracing of an index exceeding its acceptable corridor. The index of algorithm 1 is the extremum forecast error on the set prediction interval. The index of algorithm 2 is the forecast error on the set prediction interval. The index of algorithm 3 is the difference between the signal derivatives between the first and the second window in the joint point. The acceptable range in index variation is found on the pre-set sliding window.

4.1. Modelled Signal

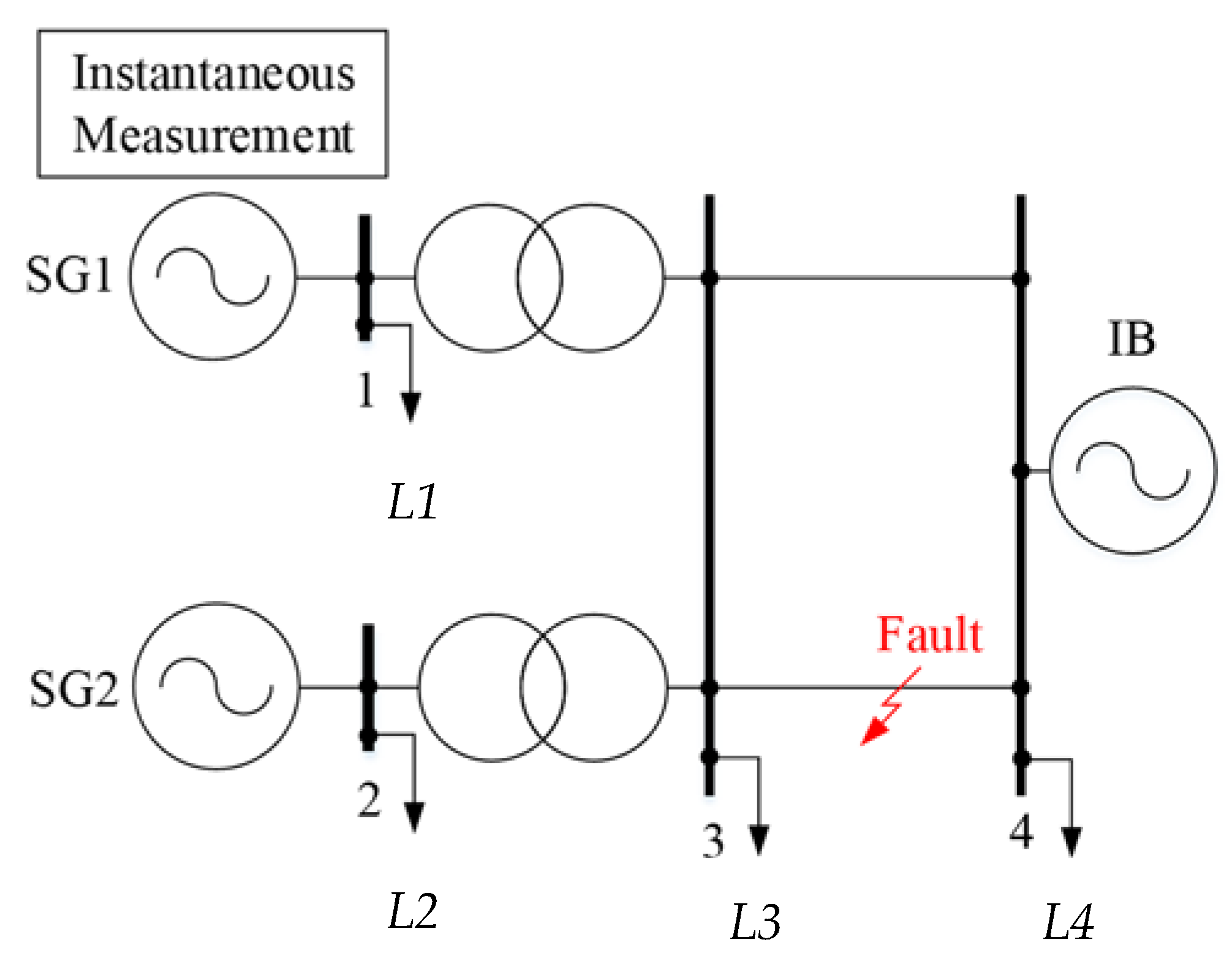
The two-machine model of a power system with a slack bus was used to simulate a transient. The model is shown in Figure 7. The simulation was conducted in Matlab/Simulink software using standard blocks of the library Simscape Electrical™.

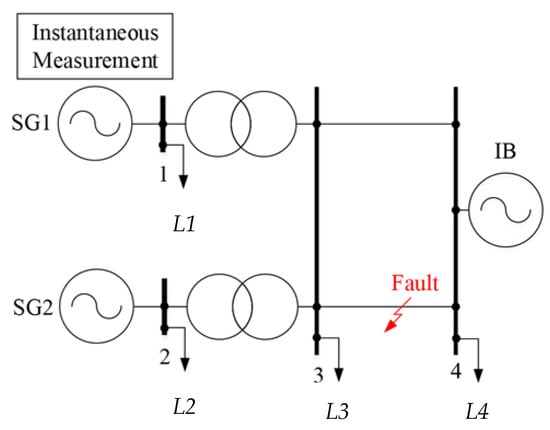
Figure 7. The power system model.

A three-phase fault on one of two parallel transmission lines 3–4 was considered a disturbance. The parameters of the model in use are shown in Table 2.

Table 2. Parameters of the two-machine power system model.

Element	Parameters
Synchronous generators	Prat = 300 MW, xd = 610 Ohm, xd′ = 186 Ohm, xd″ = 75 Ohm, TJ = 4 s
Load	L1 = L2 = 5 MW, L3 = L4 = 200 MW
Transformer	x = 28.3 Ohm, kU = 11.5/330 kV
Transmission line	r + jx = 2.75 + j43.23 Ohm, x0 = 108.06 Ohm, b = 444.3 μS
Instantaneous Measurement	fADC = 10 kHz
Fault	tstart = 10.0 s, tfinish = 10.20 s
Infinite bus (IB)	U = 330 kV

P_rat is the rated active power capacity of the synchronous generator, x_d is the reactance of a synchronous generator, x_d^′ is the transient reactance of a synchronous generator, x_d^″ is the sub-transient reactance of a synchronous generator, T_J is the time constant of a turbine and a synchronous generator, k_U is tap ratio of a transformer, x₀ zero-sequence reactance of a transmission line, b is susceptance of a transmission line, f_ADC is the sampling rate of an A/D, t_start is disturbance inception time, t_finish is disturbance ending time, x is reactance, r is resistance, j is the imaginary unit, and U is slack bus voltage.

Each synchronous generator is equipped with standard models of AVR and governor control. Loads L1, L2, L3, and L4 are modeled by constant active power extraction, independent of the voltage level and the frequency of the alternating current.

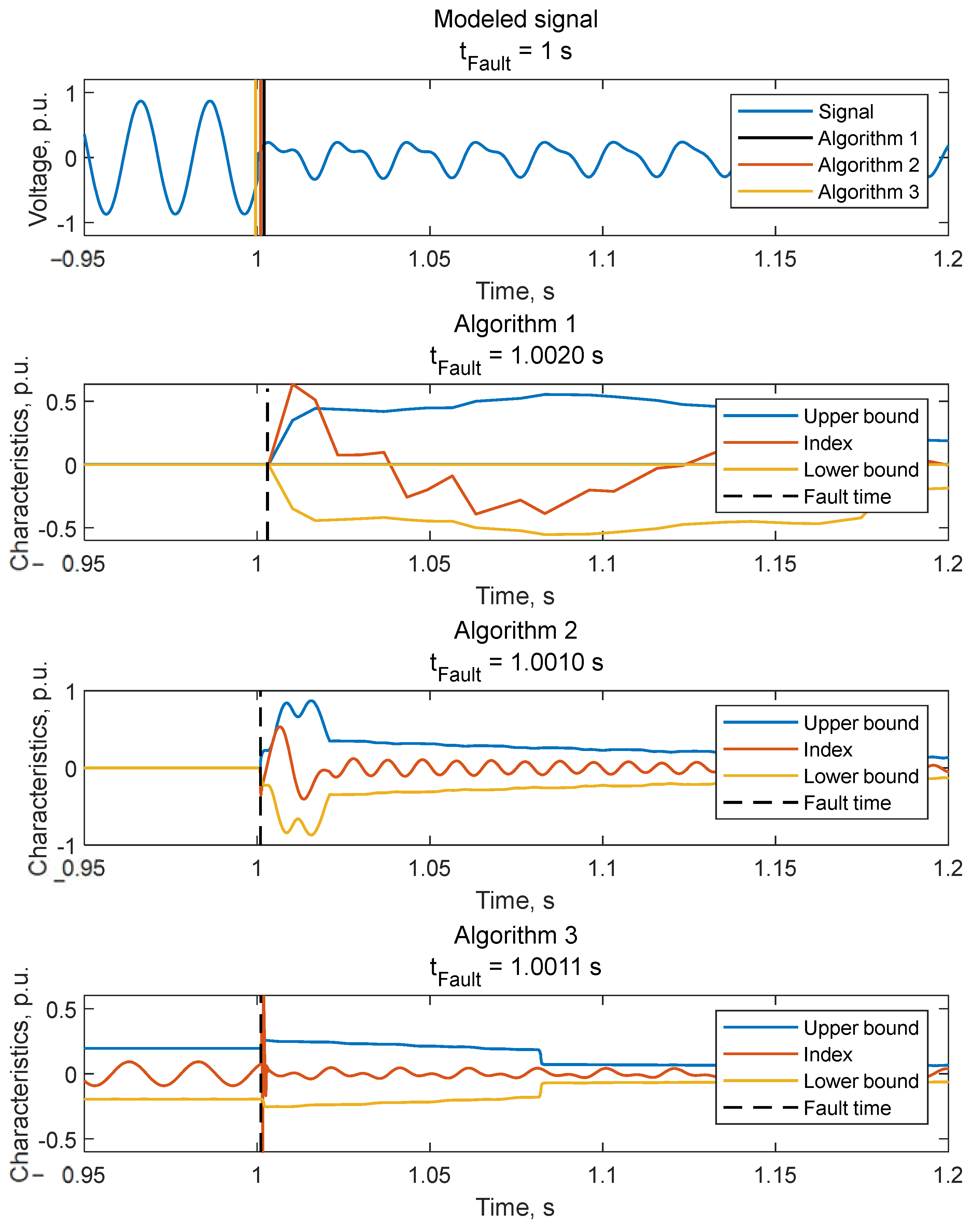
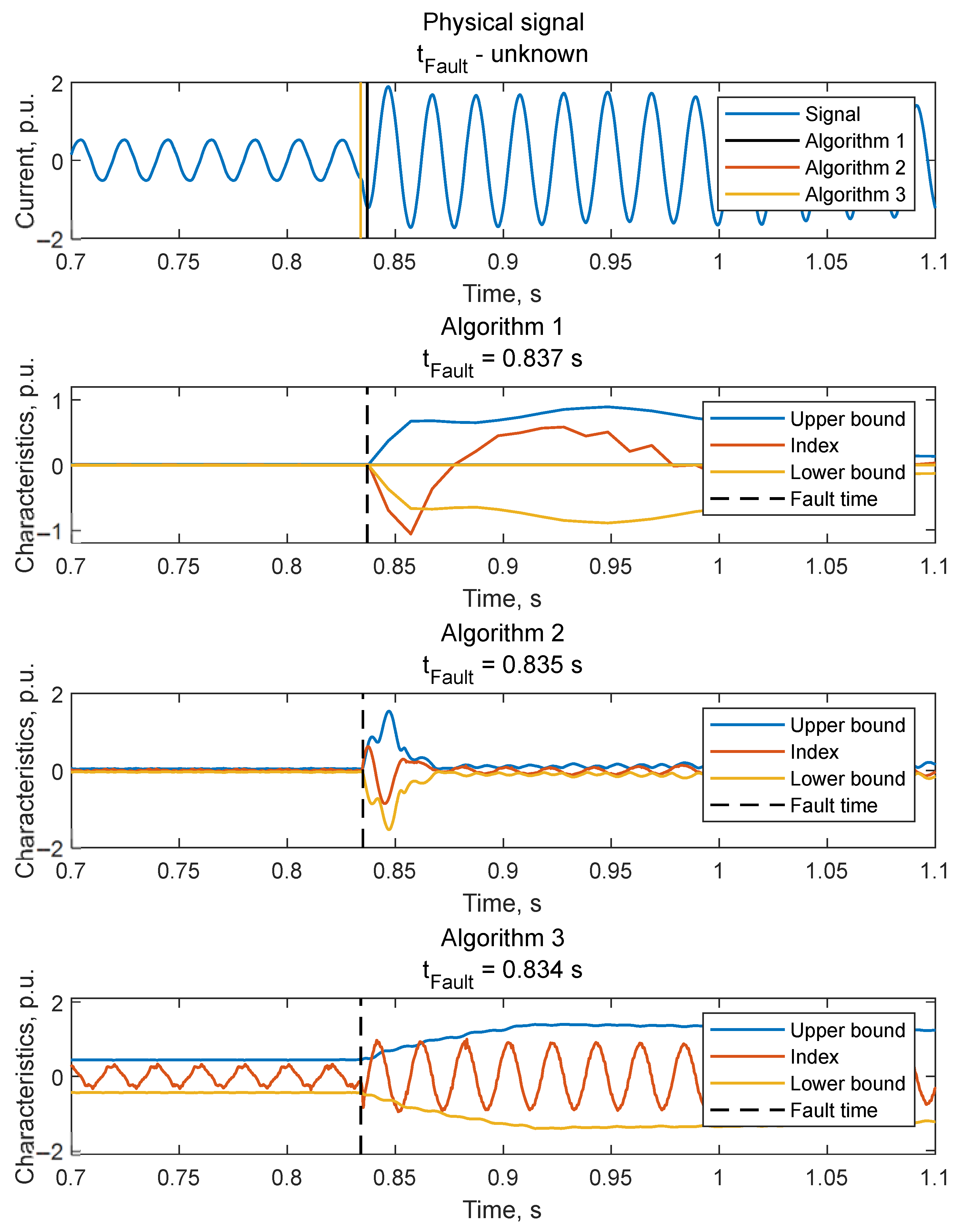
The results of the disturbance inception detection by the suggested algorithms are shown in Figure 8 and Table 3.

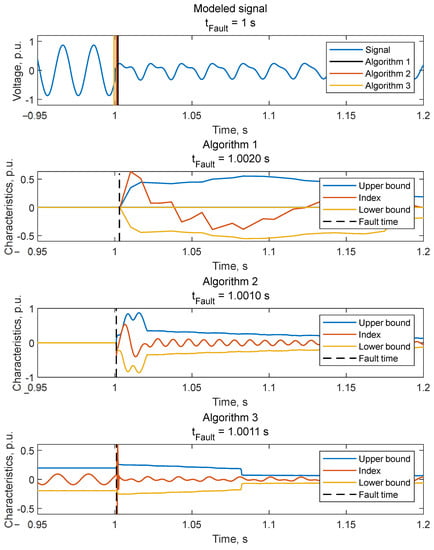
Figure 8. Results of inception time detection for the modeled signal.

Table 3. Results of inception time estimation for the modeled signal.

Parameter	Algorithm 1	Algorithm 2	Algorithm 3
Estimated time of disturbance inception, s	1.0020	1.0010	1.0011
Deviation from reference value%	0.20	0.10	0.11

4.2. Physical Signal

The physical signal was obtained as a result of recording by the emergency event recorder installed at the real power facility, with a sampling rate of 10 kHz. Figure 9 and Table 4 show the obtained results of estimating the disturbance inception time by the suggested algorithms. The discrete wavelet transform [55] was used to find the reference disturbance inception time. As a result, the value of 0.8342 s was obtained.

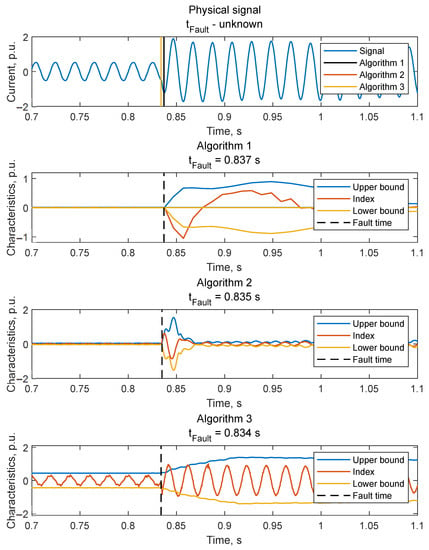
Figure 9. Results of inception time detection for the physical signal.

Table 4. Results of inception time estimation for the physical signal.

Parameter	Algorithm 1	Algorithm 2	Algorithm 3
Estimated time of disturbance inception, s	0.8374	0.8352	0.8341
Deviation from reference value%	0.3836	0.1198	0.0119

Algorithm 3 shows the minimal error in estimating the disturbance inception time for the considered signal.

4.3. Method of Improving the Accuracy of Suggested Algorithms

The accuracy of estimating the disturbance inception time can be improved using the simultaneous use of instantaneous values of phase current and phase voltage:

$$t_{Fault}=\min \left(t_{Ua};t_{Ub};t_{Uc};t_{Uab};t_{Ubc};t_{Uca};t_{Ia};t_{Ib};t_{Ic};t_{Iab};t_{Ibc};t_{Ica}\right),$$

(3)

where t_Fault is resultant disturbance time, t_Ua, t_Ub, t_Uc are disturbance inception times found using instantaneous phase voltages, t_UaB, t_UbC, t_UcA are disturbance inception times found using instantaneous line voltages, t_Ia, t_Ib, t_Ic are disturbance inception times found using instantaneous phase currents, t_Iab, t_Ibc, t_Ica are disturbance inception times found using instantaneous line currents.

The results of using (3) for algorithm 1 are shown in Figure 10 and Table 5.

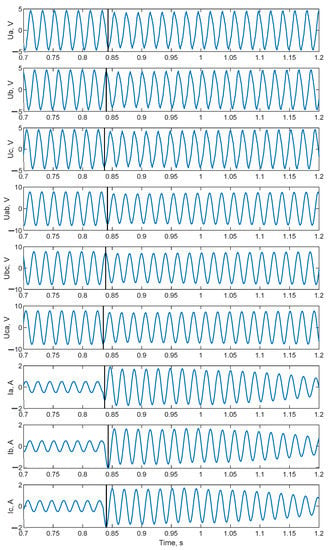
Figure 10. Results of accuracy improvement for algorithm 1.

Table 5. Comparison of the results for algorithm 1 after accuracy improvement.

Signal under Consideration	Disturbance Inception Time, s
Ua	0.843
Ub	0.840
Uc	0.837
Uab	0.842
Ubc	0.839
Uca	0.835
Ia	0.837
Ib	0.842
Ic	0.840

Considering (1) the disturbance inception time of a transient is 0.835 s, which is 0.09% different from the reference value.

5. Comparison of Estimating the Disturbance Inception Time in Power Systems Developed Algorithms with Existing Ones

Table 6 compares estimating the disturbance inception time in power systems developed algorithms with existing ones described in [55]. In Table 6, the abbreviation “rms” stands for root-mean-square. The following criteria were selected for comparing algorithms: type of input data, accuracy, and total delay.

Table 6. Comparison of developed algorithms with existing ones.

Algorithm	Input Data	Accuracy	Delay, ms
Threshold rms voltage	1-phase, rms	low	40.0
Waveform Envelope	1-phase, instantaneous	medium	10.0
Discrete Wavelet Transform	1-phase, instantaneous	high	40.0
Missing Voltage	1-phase, instantaneous	medium	20.0
d-q Transformation	3-phase, instantaneous	low	20.0
Numerical Matrix	1-phase, instantaneous	low	20.0
Peak Detector	1-phase, instantaneous	low	20.0
Algorithm 1	1-phase, instantaneous	medium	10.0
Algorithm 2	1-phase, instantaneous	high	1.0
Algorithm 3	1-phase, instantaneous	high	1.5

The developed algorithms 2 and 3 have a minimum delay in comparison with the considered methods. In addition, the accuracy of algorithms 2 and 3 can be assessed as high. Algorithm 1 has an average accuracy and a total delay of 10 ms.

6. Conclusions

Modern power systems have a high degree of digitalization and automation of the processes of generation, transmission, and distribution of power. There is an active implementation of PMUs, which perform measurements of instantaneous values of current and voltage with a high sampling rate (up to 10 kHz). These features of modern power systems make the prerequisites for the development of adaptive emergency control systems for normal and emergency operating conditions. The key step in the development of these algorithms is to find the time of disturbance inception.

This study presents three adaptive algorithms for detecting the disturbance time based on the instantaneous values of current and voltage. The algorithms are based on a statistical analysis of the forecast error of the signal extremum, the signal itself, and the difference between the derivatives of two sliding windows at the joint point. An evaluation of the algorithmic time delay of each algorithm was performed, which has shown that algorithm 3 has a minimal time delay. The study provides a method for selecting the parameters of each of the algorithms.

The numerical experiment was performed on a two-machine test model of a power system implemented in Matlab/Simulink. The model includes the AVR, PSS, and governor control. As a result of the application of the developed algorithms for fault detection in the test model, it was found that the biggest error (0.2%) corresponds to algorithm 1; algorithms 2 and 3 give similar error values of 0.1% and 0.11%, respectively.

In the case of the physical signal test, a transient record was used. It was obtained from an emergency event recorder installed on one of the real power system facilities. The calculated values of the disturbance inception time were compared with the reference method that uses the discrete Wavelet transform described in [39]. For a physical signal, algorithm 3 demonstrates the smallest deviation from the reference value.

The method of simultaneous analysis of six signals was proposed to increase the accuracy of the disturbance time detection, the instantaneous values of phase and line currents, and the instantaneous values of phase and line voltages.

The developed algorithms can be used in parallel. In this case, the backup algorithm is algorithm 1 due to its greater resistance to the noise of the input signal.

Further development of the research will be aimed at testing the algorithms online to assess the possibility of their application for emergency control. The second direction of development of the proposed algorithms relates to the creation of a procedure for the automatic selection and correction of configuration parameters.