Representation of Lipschitz Maps and Metric Coordinate Systems

Abstract

Here, we prove some general results that allow us to ensure that specific representations (as well as extensions) of certain Lipschitz operators exist, provided we have some additional information about the underlying space, in the context of what we call enriched metric spaces. In this conceptual framework, we introduce some new classes of Lipschitz operators whose definition depends on the notion of metric coordinate system, which are defined by specific dominance inequalities involving summations of distances between certain points in the space. We analyze “Pietsch Theorem inspired factorizations" through subspaces of ${\ell }_{\infty }$ and $L^1$, which are proved to characterize when a given metric space is Lipschitz isomorphic to a metric subspace of these spaces. As an application, extension results for Lipschitz maps that are obtained by a coordinate-wise adaptation of the McShane–Whitney formulas, are also given.

1. Introduction

The natural context in which Lipschitz operators make sense is that of metric spaces, and no additional structure in the spaces involved is needed in principle to give the definition and analyze their basic properties. However, in most cases some additional structure (algebraic relations, geometric properties, etc.) is needed, for example, to represent a linear endomorphism on a finite dimensional normed space from the image of a basis of the space, the linear structure is obviously necessary.

In the setting of extension of Lipschitz maps, two (deeply related but) different abstract notions make sense.

• The first one regards the classical extension problem, that consists on when, given a metric subspace S of a metric space M and a Lipschitz map $T:S\to N$ acting in it, T can be extended to the whole space M preserving the Lipschitz constant. We call it an extension of $T.$
• The second one regards the idea of reconstruction. Given a Lipschitz operator $T:M\to N$ and a subspace $S\subseteq M,$ when there exists an extension rule that allows to determine T using only ${T|}_S$ and the additional information that is known on the space $M.$ We call it a representation of $T.$

Both issues are studied and combined in the present paper. They are classical topics in analysis and general topology, and some authors have paid attention to both of them. Some specific developments have been recently published in several related topics. Since the foundational paper by Farmer and Johnson ([1], 2009), there has been a growing interest in the Lipschitz version of operator ideals theory (see, for example, [2,3,4,5,6,7] and the references therein). Such ideals are often characterized by means of factorization theorems, some of them connected to the results of the present paper. On the other hand, the classical topic of the extension of Lipschitz maps is also of current interest, both from a theoretical and applied point of view (see, for example, [8,9]), and is also used today as a theoretical tool for the foundations of new methods in Machine Learning ([10,11]).

In this paper, we present a new unified context to understand how these matters are related, and we also show as applications some concrete new results on the structure of metric spaces and the existence of constructive extensions of Lipschitz maps. First, we develop the general framework for understanding when a representation of a Lipschitz operator is possible, using the notion of representation tool. We also introduce the notion of enriched metric space in order to give a formal definition of when additional information on the metric space is available. Some of the ideas that are further developed in the present paper were already introduced in [12]. We show some applications for the case of normed spaces, in which the algebraic linear structure constitutes a fundamental support.

Thus, the first part of the paper is devoted to characterize the conditions under which a restriction of a given Lipschitz map T to a metric subspace can be extended (by using some extension rule) to the entire space to give exactly the original map T. This is explained in Section 2. As an application, we give in Proposition 1 and Theorem 1 the particular result for the case of Euclidean spaces. As it is shown in Section 2, the existence of an extension rule that allow to reconstruct an operator using only its values in a fixed subset S of its domain, X, is related with the possibility of distinguish any point $x\in X$ using only the known relations of x with the points in S. This is the starting point of the results of Section 3, in which the notion of metric generating system for a metric space is introduced. Metric $\infty -$ bounded and metric summing maps are also studied as technical tools to find new results in two directions: (1) representation of metric spaces as metric subspaces of the Banach spaces ${\ell }_{\infty }$ and $L^1\left(\mu \right)$ (Section 3.1), and (2) extension theorems for maps acting in metric generating systems, mimicking the linear extension of operators from their values on a basis of a finite dimensional normed space (Section 3.2).

We use standard notions and results on metric spaces and Lipschitz maps. Definitions and fundamental results will be introduced through the paper when needed. Recall that a metric on a set M is a symmetric and transitive function $d:M\times M\to {\mathbb{R}}^{+}$ such that $d(a,b)=0$ if and only if $a=b,$$a,b\in M.$ If $(M,d)$ and $(D,q)$ are metric spaces, we say that a map $T:M\to D$ is a Lipschitz operator if there is a constant $K>0$ such that $q\left(T\right(x),T(y\left)\right)\le K·d(x,y)$ for all $x,y\in M$. We write $Lip\left(T\right)$ for the infimum of all such constants K; this is called the Lipschitz constant of T. We will denote by $Lip(M,D)$ the class of Lipschitz maps from M to D. Since some of the notions introduced in the paper are new, we have made a special effort to show many examples and counterexamples.

2. Representation of Lipschitz Operators on Enriched Metric Spaces

The construction of a representation procedure is based on the determination of some kind of connection between the data available on the Lipschitz map and the extension method itself that allows the operator to be reconstructed. Within this concern, we have first to fix a general setting which allows to establish the minimal requirements for an extension to exist. So, we are interested in providing a characterization of when there is a constructive rule such that, given a restriction ${T|}_S$ of a Lipschitz map T to a subspace S, we can define an extension to the whole space using only the known relations between S and M (distances, and relations, that could include, for example, algebraic equalities), such that it coincides with the original map T.

In order to analyze this problem, let us now introduce several technical tools that will be necessary to develop the ideas in the present work. Essentially, we have to consider two types of information regarding the relations among the subset S and all the elements of $M.$

2.1. Representation of Enriched Metric Spaces

The following definition formalizes the notion of representability of a given space in terms of a subset of it. To use it, we assume that the metric space M has some additional relational structure, which we denote by $\mathcal{R}.$ We write $(M,d,\mathcal{R})$ for the resulting space, and call it an enriched metric space. In the next part, we will focus our attention on Euclidean spaces, but other examples could be considered, such as topological groups in which the topology is defined by a metric, or pure metric spaces, which have null additional relations between their elements, that is, $\mathcal{R}=\varnothing .$

We use the next formal notation. Let $S\subset M$ and $a\in M.$ We write:

• $Dist(S,a)$ for all the distances $d(s,a)$ among the elements of S and a. These relations can be represented as a one-side restriction of the distance function $d:S\times M\to {\mathbb{R}}^{+}$ (write it as $d(S,·)$), and
• $Rel(S,a)$ for the set of relations that exist on the metric space: algebraic equalities that hold among the elements of S and $a,$ order properties among the elements of $M,$ and any relation can be established in M. These sets, considered for each $a\in M,$ define $\mathcal{R}.$ For example, the equations as $a={\lambda }_1·s_1+{\lambda }_2·s_2$ constitutes $Rel(S,a)$ if $\mathcal{R}$ is defined by the linear relations in a 2-dimensional normed space, $\{s_1,s_2\}$ defines a basis and a is any element of $E.$

Definition 1.

Consider an enriched metric space $(M,d,\mathcal{R})$ and a subset $S\subseteq M.$ We say that M is S-representable if the information contained in $d(S,·)$ and $\mathcal{R}$ is sufficient to distinguish between any two elements of $M.$ In other words, for any two different elements $a,b\in M,$ we have that $Dist(S,a)\ne Dist(S,b)$ or $Rel(S,a)\ne Rel(S,b).$

For enriched metric spaces that are S-representable, we can define an index set $Re{p}_S\left(M\right)$ using the information provided by $d(S,·)$ and $\mathcal{R}$ that allows to distinguish between any two points of $M.$ This index set can be identified with the set M, and so there is a representation map $I:M\to Re{p}_S\left(M\right)$ that separates points, that is, the following statements are equivalent for every two elements $a,b\in M$:

• $I\left(a\right)\ne I\left(b\right),$
• $Dist(S,a)\ne Dist(S,b)orRel(S,a)\ne Rel(S,b),$
• $a\ne b.$

Thus, there is an inverse for $I.$ In terms of maps, this property can be characterized as the existence of a factorization scheme for the identity map through the representation $Re{p}_S\left(M\right)$ as

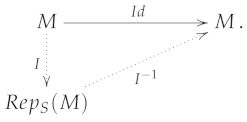
Of course, the set of relations that are considered in $\mathcal{R}$ has to be fixed for the Definition of the representation.

In the case that the information contained in $d(S,·)$ and $\mathcal{R}$ is not enough to provide a complete representation for the space $M,$ we can also consider a partial representation as follows. For every $a\in M,$ consider its equivalence class with respect to $d(S,·)$ and $\mathcal{R}$ provided by

$$\left[a\right]:=\left\{b\in M:d(S,a)=d(S,b)\mathrm{and}Rel(S,a)=Rel(S,b)\right\}.$$

Write $q:M\to \left[M\right]$ for the corresponding quotient map. The quotient space $\left[M\right]$ can then play the role of M instead, in such a way that we can define a representation $Re{p}_S\left(\left[M\right]\right)$ for it and a representation map $\left[I\right]:\left[M\right]\to Re{p}_S\left(\left[M\right]\right),$ that is injective. Since $Rep\left(\right[M\left]\right)$ is still giving a(n) (“incomplete”) representation of the space, we still use the notation $Rep\left(M\right)$ for it. The representation map $I:M\to Re{p}_S\left(M\right)$ can always be defined as

$$I=\left[I\right]\circ q:M\to \left[M\right]\to Re{p}_S\left(\left[M\right]\right)=Rep\left(M\right),$$

but it is not necessarily injective. Thus, for each element $a\in M$ we obtain a representation $I\left(a\right),$ but it may happen that there are two different elements $a,b\in M$ such that $I\left(a\right)=I\left(b\right).$

Example 1.

Consider a finitely generated group G (multiplicative notation) with generating system, that we take as the subset $S.$ Write $S^{-1}$ as the set of inverse elements of S. We define the length function ℓ associated to S as $\ell \left(1\right)=0$ and

$$\ell \left(g\right):=min\left\{n\in \mathbb{N}|\mathit{there}\mathit{are}{s}_1,..,s_n\in S\cup S^{-1}:g=s_1\cdots s_n\right\},$$

for any $g\ne 1$. Then, the word metric $d_S$ is given by $d_S(g,h):=\ell \left(g^{-1}h\right),$$g,h\in G.$ Take the set of relations $\mathcal{R}$ as the set of all equations of the group that give the representations of each $g\in G$ as $g=s_1\cdots s_n.$ So we consider the enriched metric space $(G,d_S,\mathcal{R}).$

In this case, the generating system S provides a representation of the space as follows. Every element $g\in G$ can be written as $g=s_1\cdots s_k,$$s_1,\dots ,s_k\in S$. Choose one of such decompositions for each $g,$ and consider the representation $Rep\left(G\right)$ given by the ordered set of the elements of S appearing in each of these decompositions. The map $I:G\to Rep\left(G\right)$ given by $g\mapsto I\left(g\right)=\{s_1,\dots ,s_k\}\in Rep\left(G\right)$ plays the role of a full representation of $G,$ and I satisfies a factorization scheme as the one given above. Clearly, it is an injective map, so the inverse operator $I^{-1}$ can be defined and the corresponding factorization $Id=I^{-1}\circ I$ commutes. Therefore, G is S-representable.

2.2. Representations and Extension Rules for Lipschitz Operators

Once we have defined when a metric space M is representable from a subspace $S,$ we are in position to analyze when a given operator T can be always extended from its restriction to $S.$ In this case, we will say that T is S-representable.

Thus, as we explained in the Introduction, the aim of this paper is to give a formal framework and explicit results on the existence of suitable extensions rules (ER) for Lipschitz operators that allow the representation of such operators as extensions of their restriction to a subset $S\subseteq M.$ An ER is a procedure for extending a Lipschitz map from a subspace of an enriched metric space to the whole space. So, we want to answer the following question:

If we have a Lipschitz operator T acting on M and we consider its restriction ${T|}_S$ to $S\subseteq M,$ is there a method $ER$ such that gives T when applied to ${T|}_S$?

In other words, we have to find an extension rule $ER$ to be applied to the restriction ${T|}_S$ to obtain $ER\left(T{|}_S\right)=T.$ In this case, $ER\left(T{|}_S\right)$ can be considered a representation of T based on the subspace $S.$ Let us give a formal definition of extension rule.

Definition 2.

Let $(M,d)$ be a metric space, $(S,d)$ a subspace of $(M,d)$, and let $(D,q)$ be another metric space. An extension rule is a map $ER:Lip(S,D)\to Lip(M,D)$ that preserves the Lipschitz constant, that is $Lip\left(T\right)=Lip\left(ER\right(T\left)\right)$ for all $T\in Lip(S,D).$

In case we have some additional structure on the space D, more can be said about such a map $ER$. For example, if D is a Banach space, then both $Lip(S,D)$ and $Lip(M,D)$ are linear spaces with $Lip(·)$ a semi-norm, that could become a norm if functions that differ by a constant are identified; the norms of T and $ER\left(T\right)$ coincide for all $T\in Lip(S,D).$

The rules $ER$ can be of different nature, but all of them have to define a map $ER\left(T\right):M\to D$ using the available information on the subspace $S.$ A lot is known about the problem of defining such an extension of a Lipschitz map, that is a classical topic in functional analysis. Let us mention the McShane–Whitney extension theorem for Lipschitz forms $T:(S,d)\to (\mathbb{R},|·\left|\right),$ (where S is a subspace of a metric space M), that establishes that we can always find an extension $T:M\to \mathbb{R}$ preserving the Lipschitz norm (see e.g., ([13], Ch. 4), and the original papers [14,15]). Other fundamental result in this direction is Kirszbraun’s theorem, that states that if S is a subset of some Hilbert space H, K is another Hilbert space and $T_0:S\to K$ is a Lipschitz map, we can always define an extension of $T_0$ to H with the same Lipschitz constant. The interested reader can find the original result in [16] and the excellent explanation by Fremlin in [17].

Definition 3.

Let $(M,d,\mathcal{R})$ be an enriched metric space. Consider a subset $S\subseteq M$ and a representation $Re{p}_S\left(M\right)$ defined by S. We say that a Lipschitz map $T:M\to M$ is S-symmetric (under the representation $R_S\left(M\right)$ with representation map I) if $T\left(x\right)=T\left(y\right)$ whenever $I\left(x\right)=I\left(y\right).$

Example 2.

Consider the metric group $(G,·,\ell )$ explained in Example 1 and a representation provided by the generating system $S\subset G.$ Take an element $h\in G$ and consider the map $T_h:G\to G$ given by $g\mapsto h·g.$

Note that this map is Lipschitz with Lipschitz constant equal to 1; a look to the expression of the metric ℓ makes clear that $\ell (g_1,g_2)=\ell (h·g_1,h·g_2),$ since ${(h·g_1)}^{-1}·(h·g_2)=g_1^{-1}·h^{-1}·h·g_2=g_1^{-1}·g_2.$ On the other hand, the representation provided by S is complete, in the sense that the associated map I is injective. Thus, $I\left(g_1\right)=I\left(g_2\right)$ implies $g_1=g_2.$ Therefore, $T_h$ is obviously S-symmetric.

Moreover, note that we can define the extension rule $ER$ for $T_h{|}_S$ provided by a representation as the one explained in Example 1. If $g\in G,$ we choose a decomposition in terms of the elements of S as $g=s_1\cdots s_n,$$s_1,\dots ,s_n\in S.$ As explained, the finite sequences as $\{s_1,\dots ,s_n\}$ associated to each $g\in G$ (one of them for each set of element of the group), give a representation $Re{p}_S\left(G\right)$.

Write $\prod \{s_1,\dots ,s_n\}:=s_1\cdots s_n.$ The representation map $I:G\to Re{p}_S\left(G\right)$ is then given by $I\left(g\right)=\{s_1,\dots ,s_n\},$ where the elements of S in this representation are given by the chosen particular decomposition of each g. An extension rule can then be given by

$$ER\left(T_h{|}_S\right)\left(g\right):=h·\prod I\left(g\right)=h·s_1\cdots s_n=T_h\left(s_1\right)·s_2\cdots s_n.$$

We clearly have $ER\left(T_h{|}_S\right)=T_h$ for all the elements of $G.$

Remark 1.

For particular metric spaces, requirements for the existence of extension rules to reconstruct the original map could be very restrictive. Essentially, it depends on how rich the structure of the space is and on the information that is considered to define the representation $Re{p}_S\left(M\right).$ Let $(D,\rho )$ be a discrete metric space, that is, $\rho (a,b)=1$ if $a\ne b$, and $\rho (a,b)=0$ if $a=b.$ Suppose that there is no complementary relations structure, that is, $\mathcal{R}=\varnothing .$ Let $T:D\to D$ be a map; it can be easily seen that such a T is always Lipschitz. However, the result concerning the characterization of when there is an extension rule is very restrictive: the following statements are equivalent for a subset $D_0\subseteq D.$

(1) 

For every $T:D\to D,$ there is an extension rule $ER$ such that

$$ER\left(T{|}_{D_0}\right)=T.$$

(2) 

$D\backslash \left\{c\right\}\subseteq D_0$ for a certain $c\in D.$

Proof .

The proof of this equivalence is immediate. In this case, the only information available for the representation of D is the one provided by $Dist.$ For $\left(1\right)\Rightarrow \left(2\right),$ suppose that there are two different points $b,c\in D$ that are not in $D_0,$ and take a map $T:D\to D$ such that $T\left(b\right)\ne T\left(c\right).$ The only information we have is that the distance from any other point to them is $1,$ and so these points are indiscernible if we can only use the information available to us: when we try to write them using the metric information, both of them are described by $d(a,b)=1$ for all $a\in D_0,$ and $d(a,c)=1$ for all $a\in D_0.$ The values of ${T|}_{D_0}$ do not provide any information about the values of $T\left(b\right)$ and $T\left(c\right).$ This means that we cannot define a map $f:\{b,c\}\to D$ such that $f\left(b\right)\ne f\left(c\right)$ through the description of b and c with the available metric information about them, since they coincide in this description. However, $T\left(b\right)\ne T\left(c\right),$ so there is no extension rule such that $ER\left(T{|}_{D_0}\right)=T.$ This proves $\left(1\right)\Rightarrow \left(2\right).$ For $\left(2\right)\Rightarrow \left(1\right)$, note that we only have to define $ER\left(T{|}_{D_0}\right)$ in c. The unique element that is described by $d(a,c)=1$ for all $a\in D_0$ is c, so we can define an extension as $c\mapsto ER\left(T{|}_{D_0}\right)\left(c\right)$ just by $c\mapsto T\left(c\right).$ With this extension we obviously have $ER\left(T{|}_{D_0}\right)=T,$ as required. □

However, if we center our attention on a given operator, conditions can be given for the existence of an extension rule for it. Fix a subset $D_0\subset D.$ The representation $Re{p}_{D_0}\left(D\right)$ provided by the metric only allows to distinguish among the elements that are in $D_0$ and the rest of the elements. Therefore, the associated map $I:D\to D$ leaves $D_0$ to $D_0$ and the rest of the elements to a unique element, since all the elements of $D\backslash D_0$ are the same one in $Re{p}_{D_0}\left(D\right).$ Thus, T is $D_0$-symmetric if and only if $T\left(x\right)=T\left(y\right)$ for all $x,y\in D\backslash D_0.$ And, in this case, there is an extension rule for T given by $ER\left(T{|}_{D_0}\right)\left(a\right)=T\left(a\right)$ if $a\in D_0$ and $ER\left(T{|}_{D_0}\right)\left(b\right)=c$ if $b\in D\backslash D_0$ for a fixed $c\in D.$ This is the motivation of the characterization of the existence of a representation for an operator T that is given in the next section for the case of Euclidean spaces.

2.3. An Application: Representation of Lipschitz Endomorphisms on Euclidean Spaces

Now, we focus attention on the case of finite dimensional Euclidean spaces $E={\mathbb{R}}^n$. The linear structure of these spaces allows us to avoid the problems that appears in the case of the general metric space shown in Remark 1. The result makes it clear that similar arguments could be used for general finite dimensional normed spaces; but recall that all the norms are equivalent in a finite-dimensional space. We give both relations and metric characterizations.

In this case, the metric properties needed to define $Dist$ are given by the Euclidean norm ${\parallel ·\parallel }_2$. The Lipschitz condition of the operators involved are just given to assure boundedness and relate the results with the linear counterparts. The relations properties to define $\mathcal{R}$ are the ones coming from both the linear structure and the projections provided by the scalar product. All the equalities relating the subset S and the rest of the elements of the space to define $Alg$ consist of linear combinations and projections on subsets of S. Recall that we are only considering real normed spaces.

Proposition 1.

Let $(E,\parallel ·{\parallel }_2,\mathcal{R})$ be the (enriched) n-dimensional Euclidean space and consider a subset $E_0\subseteq E.$ The following statements are equivalent.

(i) 

There is an extension rule $ER$ such that for any Lipschitz map $T:E\to E$, $ER\left(T{|}_{E_0}\right)=T$.

(ii) 

$E_0$ contains a basis of $E.$

(iii) 

The convex hull $co(E_0\cup \left\{0\right\})$ contains a ball.

Proof. 

Let us prove first (i) ⇒ (ii). In order to do it, suppose that $E_0$ does not contain a basis, and write $S_0$ for the subspace generated by $E_0$. Consider a norm one vector $v_0$ belonging to the orthogonal subspace $S_0^{\perp }.$ Recall that the only information available about $v_0$ is given by the metric structure of $E,$ the values of $x\mapsto T\left(x\right)$ for all $x\in E_0$ and the values of the distance $d(v_0,x)={\parallel v_0-x\parallel }_2$ for all $x\in E_0.$ Due to the lack of further known structure for T besides of being Lipschitz, the information on T is not useful at this step. Take $v_0$ and $-v_0.$ Fix an orthogonal basis $e_1,\dots ,e_k$ for $S_0.$ Then we have that for every $x={\sum }_{i=1}^k{\lambda }_i{e}_i\in S_0,$

$$\parallel x-v_0{\parallel }^2=\sum _{i=1}^k{\lambda }_i^2+\parallel -v_0{\parallel }^2=\sum _{i=1}^k{\lambda }_i^2+\parallel v_0{\parallel }^2={\parallel x+v_0\parallel }^2.$$

Consequently, there is no way of distinguishing $v_0$ and $-v_0$ to define an extension that includes a map $\{v_0,-v_0\}\mapsto E.$

For (ii) ⇒ (iii), take the basis $e_1,\dots ,e_n$ of E that belongs to $E_0$ and consider the vectors $x_r=r·{\sum }_{i=1}^n{e}_i/n,$ that belongs to $co(E_0\cup \left\{0\right\})$ for every $0\le r\le 1$ and belongs to the interior of $co(E_0\cup \left\{0\right\})$ for a fixed $0<r<1$, so there is an $\epsilon >0$ such that $B_{\epsilon }\left(x_r\right)\subset co(E_0\cup \left\{0\right\}).$

Finally, to show (iii) ⇒ (i) consider a ball $B_{\epsilon }\left(x_0\right)\subset co(E_0\cup \left\{0\right\}).$ Fix an orthogonal basis $\{e_1,\dots ,e_n\}$ of the space E; the elements $x_i:=\epsilon ·e_i+x_0$ belong to $co(E_0\cup \left\{0\right\})$ as well as $x_0.$ So, each of these points can be written as a (finite) convex combination of elements of $E_0.$ Therefore, each $e_i$ can be written as $(x_i-x_0)/\epsilon ,$ that is, as a (fixed) finite addition of real numbers multiplied by elements of $E_0.$ On the other hand, any vector x of E can be written as a linear combination of $e_1,\dots ,e_n$, which finally allows to write each x univocally using finite sums of elements of $E_0$ multiplied by real numbers that are univocally determined. Let us write $rep\left(x\right)$ for this representation (the ordered set of the involved vectors of $E_0$ and the corresponding scalars), and note that for every different elements $x,y\in E,$ we have that $rep\left(x\right)\ne rep\left(y\right).$ Thus, the map $x\mapsto rep\left(x\right)\mapsto T\left(x\right)$ can be defined and gives a suitable extension for ${T|}_{E_0}$ to all $E.$ This is the required extension rule. □

Proposition 1 is the extreme case of a situation that is fixed in the next theorem. It gives a general characterization of when an extension is possible for a Lipschitz endomorphism on an Euclidean space. Recall that, given a subspace S, the projection operator on S is denoted by $P_S.$

For the particular case of the Lipschitz endomorphism on Euclidean spaces, we can give a more explicit description of what an $E_0$-symmetric operator is. We say that a Lipschitz map $T:E\to E$ is $E_0$-symmetric, for $E_0\subseteq E,$ if, for the representation provided by the following $Dist$ and $Alg$,

1.

$Dist$ contains all the distances $\{d(x,y):y\in E_0\},$ and

2.

$Alg$ contains all the equations for the vectors that are linear combinations of the elements of $E_0$, and all the projections $P_S\left(x\right)$ for all $x\in E,$ where S is the subspace generated by $E_0,$

Here, we have that $T\left(x\right)=T\left(y\right)$ if x and y are indiscernible with respect to the equations in $Dist\cup Alg$; using the notation introduced in the previous section, $T\left(x\right)=T\left(y\right)$ if $I\left(x\right)=I\left(y\right).$

So, in this case, to be $E_0$-symmetric can be written as follows. T is $E_0$-symmetric if for every $x,y\in E$ such that

• $d(x,z)=d(y,z)$ for all $z\in E_0$, and
• $P_S\left(x\right)=P_S\left(y\right),$

we have that $T\left(x\right)=T\left(y\right).$

Recall that the distance $d(x,S)$ of a point x to a subspace S is defined by

$$d(x,S)=inf\{\parallel x-y\parallel :y\in S\}.$$

Theorem 1.

Let $T:E\to E$ be a Lipschitz map on the n-dimensional Euclidean space $(E,\parallel ·{\parallel }_2).$ Consider a subset $E_0\subseteq E$ and write S for its linear hull. The following statements are equivalent.

(i) 

T is $E_0$-symmetric.

(ii) 

For $x,y\in E,$ if $d(x,S)=d(y,S)$ and $P_S\left(x\right)=P_S\left(y\right),$ then $T\left(x\right)=T\left(y\right).$

(iii) 

There is an extension rule $ER$ such that $ER\left(T{|}_{E_0}\right)=T.$

Proof. 

The arguments are a refinement of those that prove Proposition 1. For (i) ⇒ (ii), fix $x\in E.$ Since T is $E_0$-symmetric, all the distances $d(x,y)$, $y\in E_0$, are known, and also the projection $P_S\left(x\right)$ on the linear hull S of $E_0$. On the other hand, assume that $P_S\left(x\right)=P_S\left(y\right)$ and $d(x,S)=d(y,S).$ Take an element $z\in E_0.$ Then, using Pythagorean Theorem, we get

$$d{(x,z)}^2={\parallel x-z\parallel }^2=d{(x,S)}^2+\parallel P_S{\left(x\right)-z\parallel }^2=d{(y,S)}^2+{\parallel P_S\left(y\right)-z\parallel }^2=d{(y,z)}^2.$$

Thus, since T is $E_0$-symmetric we obtain $T\left(x\right)=T\left(y\right),$ as we wanted to prove. The converse (ii) ⇒ (i) is also a consequence of the same argument: we have to prove that $P_S\left(x\right)=P_S\left(y\right)$ and $d(x,z)=d(y,z)$ for all $z\in E_0$ implies $d(x,S)=d(y,S).$ Take $x,y\in E,$ and suppose that $d(x,z)=d(y,z)$ for all $z\in E_0.$ Then, again, Pythagorean Theorem gives

$$d(x,S)=\sqrt{d{(x,z)}^2-{\parallel P_S\left(x\right)-z\parallel }^2}=\sqrt{d{(y,z)}^2-{\parallel P_S\left(y\right)-z\parallel }^2}=d(y,S).$$

Thus, we obtain $T\left(x\right)=T\left(y\right)$ by (ii), and we obtain the result.

For (i) ⇒ (iii), let us explicitly define the extension. Any extension rule is given by the map $E{\to }_{I}Re{p}_S\left(E\right){\to }_{R}E$ for a certain operator $R,$ and the composition has to obtain the values $x\mapsto ER\left(T\right)\left(x\right)=R\circ I\left(x\right)=T\left(x\right),$ and so for $x,y\in X,$$I\left(x\right)=I\left(y\right)$ has to imply $T\left(x\right)=T\left(y\right).$ But this is provided by the requirement of being $E_0$-symmetric. Indeed, following the definition of representation of the space, $I\left(x\right)=I\left(y\right)$ means that x and y are indiscernible, that is, $d(x,z)=d(y,z)$ for all $z\in E_0$, and $P_S\left(x\right)=P_S\left(y\right).$ But then the $E_0$-symmetry implies $T\left(x\right)=T\left(y\right).$

Finally, let us see that (iii) ⇒ (i). The existence of an extension rule implies a factorization through the representation provided for T. Then we have that $T\left(x\right)$ has to be equal to $T\left(y\right)$ for every $x,y\in E$ such that all the equalities contained in $Dist$ and $Alg$ for x and y are the same for both of them, that is $d(x,z)=d(y,z)$ for all $z\in E_0$ and $P_S\left(x\right)=P_S\left(y\right).$ That is, T is $E_0$-symmetric. □

Example 3.

Suppose that $T:E\to E$ is a (not necessarily linear) “diagonalizable" operator in the sense that there exists a basis $\mathcal{B}=\{x_1,x_2,\dots ,x_n\}$ of E such that $T({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)=(f_1\left({\alpha }_1\right),f_2\left({\alpha }_2\right),\dots ,f_n\left({\alpha }_n\right))$ in coordinates of the basis. Let $E_0=\{\alpha x_i:\alpha \in \mathbb{R},1\le i\le n\}$ be the “axis" set, since it contains the basis $\mathcal{B}$, T is $E_0$-symmetric (Proposition 1 and Theorem 1). Note that an extension rule can be provided by “linearity", if $x={\sum }_{i=1}^n{\alpha }_i{x}_i\in E$,

$$ER\left(T{|}_{E_0}\right)\left(x\right)=\sum _{i=1}^n{f}_i\left({\alpha }_i\right)x_i.$$

This extension rule allows to reconstruct the original operator T, that is $ER\left(T{|}_{E_0}\right)=T$. Observe that only the linear information of the space E is used in this extension rule, and none of its metric properties are used.

3. Metric Coordinates and Extension of Lipschitz Functions

In this section, we show a concrete setting in which the general philosophy explained in the previous section is applied. We introduce the notion of metric generating system for a metric space and two different summability requirements based on such systems. In the next step we show two representation results, that allow to write a metric space satisfying any of these summability properties as a metric subspace ${\ell }_{\infty }$ or $L^1\left(\mu \right)$ for a certain probability measure $\mu .$ We prove also that, using these results, we can obtain a new class of extension theorems for general Lipschitz maps. It is well-known that, in general, we cannot assure the existence of Lipschitz extensions of metric-space-valued Lipschitz functions. As an exception, we have the Kiszbraun Theorem for extension of Lipschitz endomorphisms on subsets of Hilbert spaces, that states that, if H and L are Hilbert spaces, $S\subseteq H,$ and $T:S\to L$ is a Lipschitz map, there is an extension $\widehat{T}:H\to L$ of T preserving the Lipschitz constant (see, for example, [16,17]). However, the main result on extensions that is relevant for the present paper is the McShane–Whitney Theorem ([14,15]), which estates that any real Lipschitz map acting in a subspace of a metric space can be extended to the whole space preserving the Lipschitz constant.

In this section, we show some results for Lipschitz maps between metric spaces using the idea of metric coordinates, in the general context that we have outlined in the preceding sections. Some basic ideas on extension of Lipschitz maps on metric spaces using the notion of metric coordinate system has been already used in ([18], Sec. 6). We are interested in going further in this direction. Therefore, in the rest of the paper we will study Lipschitz extensions of Lipschitz maps defined on pure metric spaces, that is, metric spaces without any further algebraic structure, which however are enriched by a certain representation tool, that gives in this case the set $\mathcal{R},$ in our notation.

The main idea underlying the notion of “metric coordinate system”, which has been studied by Calcaterra, Boldt and Green in [18], fits well with the framework that we have presented in the previous section. In this case, the existence of a metric generating system provides the “extra" information that is required to obtain reconstructions and extensions of Lipschitz maps. Let us introduce some technical concepts, that are straightforward adaptations of the notion of basis and associated definitions that appear in linear algebra.

Let $(M,d)$ be a metric space and consider a non-empty subset $C\subseteq M,$ we can always define a map $m:M\to {\mathbb{R}}^C$ by

$$M\ni x\mapsto m\left(x\right)={\left(m_c\left(x\right)\right)}_{c\in C}={\left(d(c,x)\right)}_{c\in C}\in {\mathbb{R}}^C.$$

Using the notation of the previous section, $m\left(x\right)$ is the information in $d(C,x)$. Moreover, consider the Banach space ${\ell }_{\infty }\left(C\right).$ If C is pointwise bounded, that is ${sup}_{c\in C}d(x,c)\in \mathbb{R}$ for every $x\in M,$ the map m can be defined to take values on ${\ell }_{\infty }\left(C\right).$

Definition 4.

We say that a subset $C\subset M$ is a metric generating system for M if m is injective, that is, for every $x,y\in M,$

$${\left(d(x,c)\right)}_{c\in C}={\left(d(y,c)\right)}_{c\in C}\mathit{implies}x=y.$$

Using the notation of the previous section, C is a metric generating system for M if $(M,d)$ (as a pure metric space, $\mathcal{R}=\varnothing$) is S-representable.

We say that a subset $C\subset M$ is a metric basis (or a metric generating independent system) for M if C is a metric generating system, and for every $c\in C,$$C\backslash \left\{c\right\}$ is not a metric generating system for $M.$ Thus, it is a “minimal" metric generating system for M.

As will be shown later on, in this paper, we are mainly concerned with the notion of metric generating system. Since we are going to use properties associated to summability of series in the metric spaces, we impose that these systems have to be be countable. However, this requirement is not fundamental for the definition and could be removed in a more general analysis: for compact metric spaces countable systems will be enough.

Some examples of metric basis and metric generating systems are provided in ([18], Sec. 2). Let us show now some other examples more connected with our concrete setting.

Example 4.

1. 

Consider the n-dimensional Euclidean space ${\mathbb{R}}^n,$ studied regarding the topic of the present paper in [18]. Then any orthogonal basis $\{a_1,\dots ,a_n\}$ together with the vector 0 is a metric generating system for it. Indeed, for any point x we only need to use the equations that allows to compute the projection of x in each of the subspaces generated by every $a_i$ by means of the distances from x to $a_i$ and from x to 0. For a fixed i, this can be easily done using the Pythagorean Theorem. For example, fix $i=1$ and write $r_1$ for the distance $\parallel x-x_1{a}_1\parallel .$ Then, by the Pythagorean Theorem we have that

$$x_1^2+r_1^2={\parallel x\parallel }^2,(x_1-\parallel a_1{\parallel )}^2+r_1^2={\parallel x-a_1\parallel }^2.$$

Consequently, $2x_1\parallel a_1\parallel -\parallel a_1{\parallel }^2={\parallel x\parallel }^2-{\parallel x-a_1\parallel }^2$. From these equations, we can easily compute the value of $x_1$ using only the information about $d(x,0)=\parallel x\parallel$ and $d(x,a_i)=\parallel x-a_1\parallel$. The same simple geometric arguments give the result for the other intervals. Using the same idea for all $x_2,\dots ,x_n,$ we obtain the result. Clearly, it is also a basis.

2. 

For the metric space $\left(\right[0,+\infty ),|·\left|\right)$ the element 0 clearly gives a metric basis.

3. 

Consider the (finite) cyclic groups ${\mathbb{Z}}_n=\mathbb{Z}/n\mathbb{Z}=G_n=\{1,g,g^2,\dots ,g^{n-1}\},$$n\in \mathbb{N},n\ge 2,$ endowed with the minimal path distance, that is,

$$\begin{array}{cc}\hfill d(g_j,g_k)=min\{& \{0\le r<n:g_k=g_j·g^r\},\hfill \\ & \{0\le r<n:g_k·g^r=g_j\}\},\hfill \end{array}$$

where $g^r$ indicates the $r-$ times product of the group $g·g\cdots g.$ It can be easily seen that $\{g^r,g^m\}\subset G_n$ ($0\le r,m<n$) is basis for $G_n$ if and only if $|r-m|\ne \frac{n}{2}$. No single-element set can be a metric generating system, and all sets of three elements are metric generating systems, but not basis.

4. 

Consider the graph $(G,d)$ with 7 elements defined as a tree with 3 branches, each of them containing 3 vertices, where d is the shortest path distance in the graph. Then no set containing just one element is a metric generating system. However, a subset with two different elements is a metric basis if and only if it does not contain the initial and the two elements does not belong to the same branch. Moreover, every subset containing 3 elements without the initial vertex is a metric generating system, but not a metric independent system.

5. 

Let $(H,⟨·,·⟩)$ be a separable Hilbert space with its usual distance $d_H(x,y)=\sqrt{⟨x-y,x-y⟩}$. Let $\mathcal{B}$ be an orthonormal basis, it is shown in [18] that $\mathcal{B}\cup \left\{0\right\}$ is a metric generating system for H.

It is also possible to show straightforward examples of spaces not having metric generating systems.

Example 5.

Take I to be an uncountable index set, and consider the space ${\ell }^1\left(I\right)$ of all sequences with support in I such that the sum of the absolute value of its components is convergent, and recall that all its elements have countable support. Suppose that such a space has a (countable) generating system, $\mathcal{G}.$ The union S of the supports of all its elements is countable, so there are two elements $i,j\in I\backslash S.$ Clearly, $\parallel a_i-e_i{\parallel }_{{\ell }^1\left(I\right)}={\parallel a_i-e_j\parallel }_{{\ell }^1\left(I\right)}$ for all $a_i\in \mathcal{G},$ where $e_i$ and $e_j$ are the canonical sequence which coefficientes equal 1 at the positions $i,j\in I,$ respectively. Therefore, $\mathcal{G}$ is not a generating system for ${\ell }^1\left(I\right).$

This example suggests the following result, that indeed provides a constructive method for obtaining metric generating systems.

Remark 2.

A separable metric space has always a metric generating system. In fact, any countable dense set is a metric generating system.

Proof. 

Let $(M,d)$ be a metric space, and let S be a countable dense set on it. Let us take two distinct elements $x_1,x_2\in M$ and write $\epsilon :=d(x_1,x_2).$ Then there is an element $s\in S$ such that $d(x_1,s)<\epsilon /3,$ and hence $d(x_1,s)\ge 2\epsilon /3.$ Consequently, we find an element in S that distinguishes $x_1$ and $x_2$ by distance, so S is a generating system. □

However, this is not the only way of getting a metric generating system for a metric space; easier systems are often available, as the following example shows.

Example 6.

The set $\left\{0\right\}$ is a metric basis for the metric space composed by $[0,1]$ endowed with the Euclidean distance, while Remark 2 would give a countable generating system.

Fix now other subset $S\subseteq M$, where $(M,d)$ and $(N,\rho )$ are metric spaces, and consider a K-Lipschitz function $T:S\to M.$ For every $c\in C,$ we will consider the next McShane type extension formulas involving all the maps $m_c:M\to \mathbb{R},$$m_c\left(x\right)=d(x,c),$ that is,

$${\widehat{T}}_c\left(x\right)=\underset{a\in S}{sup}\left(m_c\left(T\left(a\right)\right)-K·d(x,a)\right)=\underset{a\in S}{sup}\left(d\left(T\right(a),c)-K·d(x,a)\right).$$

At the end of the paper, we will expose similar extension formulas.

3.1. ∞-Bounded and Metric Summing Lipschitz Maps

In the case that we suppose some compactness property (the space or the metric generating system is compact), better information on metric representation of the space is available. We will show that an equivalent metric based on the metric coordinates can be sometimes obtained. In fact, we present a characterization of when an equivalent distance can be found, and explicit formulas for them are given.

Recall that by the Borel–Lebesgue Theorem (see, for example, Section 3.6 in [19]), a metric space is compact if and only if it is complete and totally bounded; a metric space M is totally bounded if for every $\epsilon >0$ there are finitely many $x_1,x_2,...,x_n\in M$ such that that $\{B_{\epsilon }\left(x_i\right):1\le i\le n\}$ is an open cover of $M.$

Lemma 1.

Let $(K,d)$ be a compact metric space. Let $T:(K,d)\to (N,\rho )$ be a Lipschitz map. Then there is a countable metric generating system $\mathcal{G}$ for $K,$ and $T\left(\mathcal{G}\right)$ is a metric generating system for $T\left(K\right).$

Proof. 

Since K is compact, by the Borel–Lebesgue theorem it is in particular totally bounded. Consider the sequence defined by choosing the centers of the open covers provided by the total boundedness of K associated when the $\epsilon$’s are taken to be $1/2^n.$ This clearly gives a dense countable set, so we apply Remark 2 to obtain the result. As a consequence of T being Lipschitz, $T\left(\mathcal{G}\right)$ is a dense subset of $T\left(K\right)$, and a metric generating system. □

The aim of the section is to show that, under some reasonable requirements, sometimes we can obtain a metric that is computed by means of the metric coordinates, and is (Lipschitz) equivalent to the metric $d.$

Although we will obtain other possible formulae, let us start by providing the “∞-type” metric based on the metric coordinates that could be equivalent to the initial metric $d.$

Definition 5.

Let $T:(M,d)\to (N,\rho )$ be a Lipschitz map and consider a countable metric generating system $\mathcal{G}$ of $M.$ We say that T is metric ∞-bounded (with respect to $\mathcal{G}$) if there is a constant $Q>0$ such that

$$\rho (T\left(x\right),T\left(y\right))\le Q\underset{a\in \mathcal{G}}{sup}|d(x,a)-d(y,a)|,x,y\in M.$$

This definitions follows from the idea of considering in M the map

$$\begin{array}{cc}\hfill m^{\infty }:(M,d)& \to {\ell }_{\infty }\left(\mathcal{G}\right)\hfill \\ \hfill x& \mapsto m^{\infty }\left(x\right)={\left(m_a^{\infty }\left(x\right)\right)}_{a\in \mathcal{G}}={\left(d(x,a)\right)}_{a\in \mathcal{G}}\hfill \end{array}$$

and the function on $M\times M$

$$d_{\infty }(x,y):=\underset{a\in \mathcal{G}}{sup}|d(x,a)-d(y,a)|=d_{{\ell }_{\infty }\left(\mathcal{G}\right)}(m^{\infty }\left(x\right),m^{\infty }\left(y\right)).$$

Note that, by the triangular inequality, the supremum always exists and $d_{\infty }(x,y)\le d(x,y)$ for all $x,y\in M,$ so $m^{\infty }$ is a 1-Lipschitz function. Moreover, the fact that $\mathcal{G}$ is a metric generating system implies that $d_{\infty }$ is a metric in M.

Next result is a straightforward rewriting of the definition of metric ∞-bounded operator.

Remark 3.

Let $T:M\to N$ be an operator, the following statements are equivalent.

1. 

T is is metric $\infty -$ bounded.

2. 

There is a Lipschitz factorization for T as

where R given by $R\left(m^{\infty }\left(x\right)\right)=T\left(x\right)$ is also a Lipschitz map.

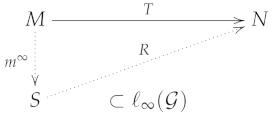
3. 

T is a Lipschitz map from $(M,d_{\infty })$ to $(N,\rho )$.

In this case, the Lipschitz constant of R coincides with the one of $T:(M,d_{\infty })\to (N,\rho )$ and the metric $\infty -$ bounded constant of $T.$

Observe that the metrics d and $d_{\infty }$ coincide in $\mathcal{G}$, since for any $a,b\in \mathcal{G}$

$$d(a,b)=|d(a,b)-d(b,b)|\le \underset{c\in \mathcal{G}}{sup}|d(a,c)-d(b,c)|=d_{\infty }(a,b)\le d(a,b).$$

So, a map $T:(\mathcal{G},d)\to (N,\rho )$ is ∞-bounded if and only if is a Lipschitz map.

In the particular case when the identity map $id:M\to M$ is metric $\infty -$ bounded, $d_{\infty }$ is a metric on M, Lipschitz equivalent to d and $(M,d)$ is Lipschitz isomorphic to a metric subspace of ${\ell }_{\infty }$. Moreover, in this case any Lipschitz map $T:M\to N$ is metric $\infty -$ bounded.

Some of the examples provided before are also examples of operators (the identity map) that are metric ∞-bounded. It is also easy to show examples of operators that are not. We center the attention on spaces in which the identity map satisfies the property.

Example 7.

Take the compact set defined by the convergent sequence together with its limit $K=\{x_n=1/2^n{e}_n:n\in \mathbb{N}\}\cup \left\{0\right\}\subset {\ell }_2,$ where $e_i$ are the elements of the normalized canonical basis of ${\ell }_2.$ Clearly, the set $\mathcal{G}=\{a=e_1\}$ gives a metric generating system for it. Suppose that there is a constant $Q>0$ such that

$$d(x,y)\le Q\underset{a\in \mathcal{G}}{sup}|d(x,a)-d(y,a)|=|d(x,e_1)-d(y,e_1)|,x,y\in K.$$

This gives a contradiction. Indeed, take the sequences $x_n=1/2^n{e}_n,$$y_n=0,$$n\in \mathbb{N}.$ Then

$$0<\frac{1}{Q}\le \underset{n}{lim}\frac{\sqrt{\frac{1}{2^{2n}}+1}-1}{1/2^n}=\underset{n}{lim}\left(\sqrt{1+2^{2n}}-2^n\right)=0,$$

a contradiction. So, the identity map on K is not metric ∞-bounded.

The following notion is a relevant tool for the rest of the paper. It allows to characterize when a given metric generating system provides also a metric q for the space that is equivalent to the original one d (in the sense that $q(x,y)\le d(x,y)\le Qq(x,y)$ for a certain $Q>0$ for all $x,y\in N$) and satisfies that it can be computed as a certain (generalized) convex combination of the coordinate functions associated to a certain metric generating system. This gives the “1-bounded” version of the equivalent metric that completes the picture, together with the ∞-bounded case.

Definition 6.

Let $T:(M,d)\to (N,\rho )$ be a Lipschitz map and consider a countable metric generating system $\mathcal{G}$ of $M.$ We say that T is metric summing if there is a constant $Q>0$ such that for every finite set $x_1,\dots ,x_n,y_1,\dots ,y_n\in M,$

$$\sum _{i=1}^n\rho \left(T\left(x_i\right),T\left(y_i\right)\right)\le Q\underset{a\in \mathcal{G}}{sup}\sum _{i=1}^n|d(x_i,a)-d(y_i,a)|.$$

Notice that a map that satisfies the previous definition is always a Lipschitz 1-summing using the notion introduced by Farmer and Johnson in [1]. However, the set on which the supremum is calculated in our case (and thus the measure that finally provides the domination theorem) has a very particular mathematical meaning, different from that in the classical case of summing maps. Our result provides a domination by what is “almost a convex combination” of distance evaluations on relevant elements, consistent with the idea of what is a metric generating system.

Examples are easy to find. Let us provide some of them regarding metric spaces in which the identity map (which of course is a Lipschitz map) is metric summing.

Example 8.

1. 

A basic example is given by a finite discrete space. Take a finite set $D=\{x_1,\dots ,x_n\}$ and consider the discrete metric space $(D,d).$ Consider the metric generating system for it given by D itself. Take a double finite sequence $x_1,\dots ,x_m,y_1,\dots y_m$ in $D.$ Assume that $x_i\ne y_i$ for all i and note that there is an element $x_0$ such that the element $x_0$ appears at least r times amont the $x_i$’s of the sequence, where $r\in \mathbb{N}$ is such that $m/n\le r.$ Then

$$\begin{array}{cc}\hfill \sum _{i=1}^{m}d(x_i,y_i)& =\sum _{i:x_i\ne y_i}d(x_i,y_i)\le m=n·\frac{m}{n}\le n·r\hfill \\ \hfill & =n·\sum _{i:x_i=x_0}|d(x_i,x_0)-d(y_i,x_0)|\hfill \\ \hfill & \le n·\underset{x\in D}{sup}\sum _{i=1}^m|d(x_i,x)-d(y_i,x)|.\hfill \end{array}$$

Consequently, the identity map is metric summing. Obviously, the space is compact.

These calculations cannot be extended to obtain an infinite (countable) version of this example; along with this fact, we also have that the space is not compact in the infinite case. However, this is not a general rule: later we will show in another example that there are compact spaces in which the identity map is not metric summing.

2. 

Consider the disjoint union $M_2$ of the interval $[0,1/2]$ with itself, that is, $M_2=I_1\cup I_2,$$I_1=I_2=[0,1/2].$ We write $r_i$ for the elements of the $i-$th copy of the interval $I_i,$$i=1,2.$ Consider the function $q:M_2\times M_2\to R^{+}\cup \left\{0\right\}$ given by

$$q(r_i,s_j)=\left\{\begin{array}{cc}|r_i-s_j|\hfill & \mathrm{if}i=j\hfill \\ 1\hfill & \mathrm{if}i\ne j,\hfill \end{array}\right.i,j\in \{1,2\}.$$

It can be easily seen that this function defines a metric on $M_2.$ The set $\{0_1,0_2\},$ where $0_i$ is the element 0 in the interval $I_i,$ is a metric basis for the space $(M_2,q).$ It can be also easily seen that $(M_2,q)$ is a compact space.

Consider now the identity map $id:M_2\to M_2,$ and let us show that it is a metric summing map. Take $x_1,\dots ,x_m,y_1,\dots ,y_m\in M_2.$ Let us divide the couples $(x_i,y_i)$ in three sets, $A_1=\{(x_i,y_i):x_i,y_i\in I_1\},$$A_2=\{(x_i,y_i):x_i,y_i\in I_2\},$ and

$$B=\{(x_i,y_i):x_i\in I_1,y_i\in I_2,\mathrm{or}{x}_i\in I_2,y_i\in I_1\}.$$

Clearly, these sets are disjoint and $|A_1\cup A_2\cup B|=m.$ Now compare the quantities

$$a_1:=\sum _{A_1}|x_i-y_i|\mathrm{and}{a}_2:=\sum _{A_2}|x_i-y_i|,$$

and write $j_0$ for the index 1 or 2 for which $max\{a_1,a_2\}$ is attained. We have that

$$\sum _{A_1\cup A_2}q(x_i,y_i)=a_1+a_2\le 2\sum _{A_{j_0}}|x_i-y_i|=2\sum _{A_{j_0}}|q(x_i,0_{j_0})-q(y_i,0_{j_0})|.$$

On the other hand, ${\sum }_{B}q(x_i,y_i)={\sum }_{B}1=\left|B\right|,$ and so

$$\left|B\right|=2\sum _B|1-1/2|\le 2\sum _B|q(x_i,0_{j_0})-q(y_i,0_{j_0})|.$$

Summing up the computations above, we get

$$\sum _{i=1}^{m}q(x_i,y_i)\le 2\sum _{A_{i_0}\cup B}|q(x_i,0_{i_0})-q(y_i,0_{i_0})|\le 2\underset{0\in \{0_1,0_2\}}{sup}\sum _{i=1}^m|q(x_i,0)-q(y_i,0)|.$$

So the identity map is metric summing.

Examples of Lipschitz operators that are not metric summing are also easy to find, even when the space in which it is defined is compact. Let us show one of them in the next example.

Example 9.

A compact space in which the identity map is not metric summing. Fix $r\in \mathbb{N}.$ Let us consider the compact subset W of the Hilbert space ${\ell }_2$ defined as

$$W=\left(\bigcup _{i=1}^r\left[0,\frac{1}{i}{e}_i\right]\right)\cup \left\{\frac{1}{i}{e}_i:i=r+1,r+2,\dots \right\}.$$

where $[a,b]$ represents the set between a and b and $e_i$ is the $i-$th element of the canonical basis of ${\ell }_2.$ So we take the compact metric space $(W,\parallel ·{\parallel }_2)$, where ${\parallel ·\parallel }_2$ is the Hilbert space norm of ${\ell }_2.$

First we claim that the sequence of vectors $\mathcal{G}=\{a_i=e_i/i:i=1,\dots ,r\}$ defines a metric generating for $W.$ If $x=e_s/s\in W$ with $s>r$, then, $d(e_i/i,x)>1/i$ for all $e_i/i\in \mathcal{G}$ and s is determined, for example, by $d(e_1,x)=\sqrt{1+1/s^2}$. If $x\in W$ is in a set of the form $[0,e_j/j]$ with $j\le r$, then $d(x,e_i/i)\ge 1/j$ for all $i=1,2,\dots ,r$, $i\ne j$ and $d(x,e_j/j)$ determines the point x.

Let us show that a metric summing type inequality cannot be reached for the identity map $id:W\to W.$ Take the vectors $x_i=e_i/i$ and $y_i=0$ for all $i\in \mathbb{N}$, then

$$\begin{array}{cc}\hfill \sum _{i=1}^n|d(x_i,a_k)-d(y_i,a_k)|& =1/k+\sum _{i=1,i\ne k}^n|\sqrt{1/i^2+1/k^2}-1/k|\hfill \\ \hfill & \le 1+\sum _{i=1}^n{\displaystyle \frac{1/i^2+1/k^2-1/k^2}{\sqrt{1/i^2+1/k^2}+1/k}}\hfill \\ \hfill & \le 1+\sum _{i=1}^n{\displaystyle \frac{1/i^2}{2/k}}\hfill \\ \hfill & =1+k/2\sum _{i=1}^n{\displaystyle \frac{1}{i^2}}.\hfill \end{array}$$

Consequently, since $\mathcal{G}$ is finite,

$$\underset{n\to \infty }{lim}\underset{a_k\in \mathcal{G}}{sup}\sum _{i=1}^n|d(x_i,a_k)-d(y_i,a_k)|\le \underset{n\to \infty }{lim}\underset{a_k\in \mathcal{G}}{sup}1+k/2\sum _{i=1}^n{\displaystyle \frac{1}{i^2}}<\infty .$$

However, ${\sum }_{i=1}^{n}d(x_i,y_i)={\sum }_{i=1}^{n}1/i$ diverges when $n\to \infty$, so the metric summing inequality does not hold for any $Q>0$.

Next proposition is inspired by the Pietsch domination theorem for Lipschitz p-summing maps ([1]), that is in turn inspired in the result for absolutely summing (linear) operators (see, for example, ([20], Ch. 2)). As we announced, it gives a characterization of when a metric computed by means of the coordinate functions, which is equivalent to the original metric, can be obtained.

Theorem 2.

Let $(M,d),(N,\rho )$ be two metric spaces and K a compact subset of M. Let $T:M\to N$ a mapping and $C>0$, the following statements are equivalent:

1. 

For any $n\in \mathbb{N}$, $x_1,x_2,\dots ,x_n,y_1,y_2,\dots ,y_n\in M$,

$$\sum _{i=1}^n\rho (T{x}_i,T{y}_i)\le C\underset{w\in K}{sup}\sum _{i=1}^n|d(x_i,w)-d(y_i,w)|.$$

2. 

There exists a Borel regular probability measure μ on K such that for any $x,y\in M$

$$\rho (Tx,Ty)\le C{\int }_K|d(x,w)-d(y,w)|d\mu \left(w\right)\left(\le Cd(x,y)\right).$$

Proof. 

The proof can also be directly obtained as a consequence of the abstract Pietsch domination theorem presented in [21]. However, for the aim of completeness and to underline that our result is essentially an application of the fundamental Hahn–Banach Theorem, we prefer to present the straightforward proof based on it. Let us first recall a basic argument that extend the requirement to the case of inequalities in which coefficients $a_i\ne 1$ affecting the terms of the inequalities for all $i=1,\dots ,n,$ are allowed. It seems to be due to Mendel and Schechtman (see ([1], p. 2989)). Since it is allowed that the elements $x_i,y_i$ appear several times in the inequalities in (1), we can use approximation by rational numbers to show that, in fact, this requirement is equivalent to: for any $n\in \mathbb{N}$, $x_1,x_2,\dots ,x_n,y_1,y_2,\dots ,y_n\in M$ and $a_1,a_2\dots ,a_n\ge 0$,

$$\sum _{i=1}^n{a}_i\rho (T{x}_i,T{y}_i)\le C\underset{w\in K}{sup}\sum _{i=1}^n{a}_i|d(x_i,w)-d(y_i,w)|.$$

Let us show the proof.

For the $\left(2\right)\Rightarrow \left(1\right)$ implication, it is enough to replace the function to integrate by its supremum. Suppose that such $\mu$ exists and apply $\left(2\right)$ on the first inequality,

$$\begin{array}{cc}\hfill \sum _{i=1}^n{a}_i\rho (T{x}_i,T{y}_i)& \le \sum _{i=1}^n{a}_{i}C{\int }_K|d(x_i,w)-d(y_i,w)|d\mu \left(w\right)\hfill \\ \hfill & =C{\int }_K\left(\sum _{i=1}^n{a}_i|d(x_i,w)-d(y_i,w)|\right)d\mu \left(w\right)\hfill \\ \hfill & \le C{\int }_K\left(\underset{t\in K}{sup}\sum _{i=1}^n{a}_i|d(x_i,t)-d(y_i,t)|\right)d\mu \left(w\right)\hfill \\ \hfill & =C\underset{t\in K}{sup}\sum _{i=1}^n{a}_i|d(x_i,t)-d(y_i,t)|.\hfill \end{array}$$

For the converse, consider for any finite set

$$A=\{(x_1,y_1,a_1),(x_2,y_2,a_2),\dots ,(x_n,y_n,a_n)\}\subseteq M\times M\times [0,+\infty [,$$

the function $f_A:K\to \mathbb{R}$ given by

$$w\mapsto \sum _{i=1}^n{a}_i\left(\rho (T{x}_i,T{y}_i)-C|d(x_i,w)-d(y_i,w)|\right).$$

This function is continuous (in fact, Lipschitz continuous) since for any $w,t\in K$,

$$\begin{array}{cc}\hfill |f_A\left(w\right)-f_A\left(t\right)|& \le \sum _{i=1}^n{a}_{i}C\left|\right|d(x_i,w)-d(y_i,w)|-|d(x_i,t)-d(y_i,t)\left|\right|\hfill \\ \hfill & \le \sum _{i=1}^n{a}_{i}C|d(x_i,w)-d(y_i,w)-d(x_i,t)+d(y_i,t)|\hfill \\ \hfill & \le \sum _{i=1}^n{a}_{i}C\left(|d(x_i,w)-d(x_i,t)|+|d(y_i,w)-d(y_i,t)|\right)\hfill \\ \hfill & \le \sum _{i=1}^n{a}_{i}C\left(d(w,t)+d(w,t)\right)\hfill \\ \hfill & =2C\left(\sum _{i=1}^n{a}_i\right)d(w,t).\hfill \end{array}$$

Consider the Banach space $(\mathcal{C}\left(K\right),\parallel ·{\parallel }_{\infty })$. The set of functions $F=\{f_A:A\subseteq M\times M\times [0,+\infty \left[\mathrm{finite}\right\}$ is a subset of $\mathcal{C}\left(K\right)$. Clearly, for any $f_A,f_B\in F$, $f_A+f_B=f_{A\cup B}\in F$ and if $\lambda \ge 0$, then $\lambda f_A$ is also in F so, in particular, F is a convex set.

Consider now the set $G=\{g\in \mathcal{C}(K):g(w)>0\forall w\in K\}$, which is also convex. Since K is compact, any function in G attains its minimum, which is positive, so G is a open set. We claim that $F\cap G=\varnothing$. Indeed, consider $f_A\in G$,

$$f_A\left(w\right)=\sum _{i=1}^n{a}_i\left(\rho (T{x}_i,T{y}_i)-C|d(x_i,w)-d(y_i,w)|\right),$$

the continuity of $f_A$ and the compactness of K implies that $f_A$ attains its minimum, and the hypothesis $\left(1\right)$ shows that $inf\{f_A\left(w\right):w\in K\}=f_A\left(w_0\right)\le 0$, so $f_A\notin G$.

By the geometric version of the Hahn–Banach theorem, there exists $\mu \in \mathcal{C}{\left(K\right)}^{\ast }=\mathcal{M}\left(K\right)$ a Borel regular measure and $\xi \in \mathbb{R}$ such that

$${\int }_K{f}_{A}d\mu \le \xi <{\int }_{K}gd\mu$$

for all $f_A\in F$, $g\in G$.

Let us see that $\xi =0$. Since the zero function $0=f_{(x,x,1)}$ (for $x\in M$) is an element of G, $\xi \ge {\int }_{K}0d\mu =0$. For any $\lambda >0$, the constant function with value $\lambda$, $\lambda \mathbf{1}:K\to \mathbb{R}$ is in F, so $\xi \le inf\{{\int }_K\lambda \mathbf{1}d\mu :\lambda >0\}=\mu \left(K\right)inf\{\lambda :\lambda >0\}=0$.

Moreover, $\mu$ is a positive measure. Indeed, any $f\ge 0$ is a limit in $\mathcal{C}\left(K\right)$ of functions ${\left(f_n\right)}_n\in F$ (for example $f_n=f+\frac{1}{n}\mathbf{1}$), and ${\int }_K{f}_{n}d\mu >0$. So, by the continuity of $\mu$ on $\mathcal{C}\left(K\right)$,

$${\int }_{K}fd\mu =\underset{n\to \infty }{lim}{\int }_K{f}_n\ge 0.$$

As $\mu \left(K\right)<+\infty$, we can assume (multiplying by a constant if is needed) that $\mu \left(K\right)=1$, and $\mu$ is a Borel regular probability measure.

Let now $x,y\in M$, consider the function $f_A\in F$ with $A=\left\{\right(x,y,1\left)\right\}$. Since ${\int }_K{f}_A\le 0$,

$$\rho (Tx,Ty)={\int }_K\rho (Tx,Ty)d\mu \left(w\right)\le C{\int }_K|d(x,w)-d(y,w)|d\mu \left(w\right).$$

□

As in the metric ∞-bounded case (Remark 3), there is natural factorization counterpart of the domination given in Theorem 2. It is one of our main results, and shows that any metric summing map factors through a subset of an $L^1$-space. This recalls the classical domination/factorization that holds for the cases of linear operators (see ([20], Ch. 2)) and Lipschitz maps ([1]).

In the rest of the paper, we fix a compact generating system $\mathcal{G}$ that will play the role of the compact set $K.$ We implicitly refer to such a system $\mathcal{G}$ when we introduce metric $\infty -$ bounded and metric summing operators, sometimes without explicitly mentioning it.

Observe that any Borel regular probability measure $\mu$ on $\mathcal{G}$ induces the map

$$\begin{array}{cc}\hfill m^{\mu }:(M,d)& \to L^1\left(\mu \right)\hfill \\ \hfill x& \mapsto m_{(·)}^{\mu }\left(x\right)=d(x,·)\hfill \end{array}$$

and then the function on $M\times M$

$$d_{\mu }(x,y):={\int }_{\mathcal{G}}|d(x,a)-d(y,a)|d\mu \left(a\right)=d_{L^1\left(\mu \right)}(m^{\mu }\left(x\right),m^{\mu }\left(y\right))$$

for $x,y\in M$. The triangular inequality shows that the integral is finite and that $m^{\mu }$ is a 1-Lipschitz function. Note that $d_{\mu }$ is a pseudo-metric (it could not be a metric), but a sufficient condition for it to be a metric is to satisfy that $\mu \left(a\right)>0$ for all $a\in \mathcal{G}$.

Corollary 1.

Let $T:M\to N$ be an operator, the following statements are equivalent.

1. 

T is metric summing.

2. 

There is a probability (regular Borel) measure μ, a subset $S\subseteq L^1\left(\mu \right)$ and a Lipschitz factorization for T as

where the map R given by $R\left(m^{\mu }\left(x\right)\right)=T\left(x\right)$ is a Lipschitz map.

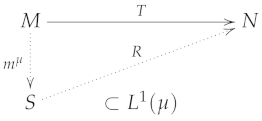
3.

There is a probability (regular Borel) measure μ such that T is Lipschitz from $(M,d_{\mu })$ to $(N,\rho )$.

In this case, the Lipschitz constant of R coincides with the one of $T:(M,d_{\mu })\to (N,\rho ),$ that is, the metric summing constant of $T.$

Together with Theorem 2, we obtain the next

Corollary 2.

Let $(M,d)$ be a metric space and a metric generating system $\mathcal{G}$ of M that is closed. Then, $id:M\to M$ is metric summing if and only if there is a constant $C>0$ and a Borel regular probability measure μ on $\mathcal{G}$ such that for any $x,y\in M,$

$$d(x,y)\le C{\int }_{\mathcal{G}}|d(x,w)-d(y,w)|d\mu \left(w\right).$$

Consequently, in this case, d and $d_{\mu }$ are Lipschitz equivalent metrics and $(M,d)$ is Lipschitz isomorphic to a metric subspace of an $L^1$-space.

Taking into account the properties of the integral with respect to a probability measure, we directly obtain the next result.

Corollary 3.

Let $T:(M,d)\to (N,\rho )$ a Lipschitz map. If T is metric summing, then it is metric $\infty -$ bounded, and in this case there is a constant $Q>0$ and a probability (regular Borel) measure μ such that

$$\rho (T\left(x\right),T\left(y\right))\le Q{d}_{\mu }(x,y)\le Q{d}_{\infty }(x,y)\le Qd(x,y),x,y\in M.$$

In particular, if the identity map in a given space is metric summing for a certain metric generating system, then we can obtain two equivalent formulas that allow to compute the (Lipschitz equivalent) distance(s) by only using the coordinates of the points of the metric space.

Remark 4.

Note that the equivalences of norms provided by the previous results give strong metric relations. However, the construction provides also weaker topological equivalences if we assume compactness on the metric space.

Consider a compact metric space $(K,d)$ and a countable (or finite) metric generating system $\mathcal{G}$ for K. Then we have that the map

$$\begin{array}{cc}\hfill \phi :(K,d)& \to (L^1\left(\mu \right),\parallel ·{\parallel }_1)\hfill \\ \hfill x& \mapsto d(x,·):\mathcal{G}\to \mathbb{R}.\hfill \end{array}$$

satisfies that $d_{\mu }(x,y)={\parallel \phi \left(x\right)-\phi \left(y\right)\parallel }_1.$ Clearly, φ is a 1-Lipschitz function, so it is continuous. Suppose that φ is one-to-one, ($\mu \left(\right\{a\left\}\right)>0$ for all $a\in \mathcal{G}$). Then, as $L^1\left(\mu \right)$ is Hausdorff, ${\phi }^{-1}:\phi \left(K\right)\to K$ is continuous, so $x_n\to x$ in $d_{\mu }$ implies that $x_n\to x$ in d. Then, the topological space generated by d is the same as the one generated by $d_{\mu }$. However, this could happen even in the metric space is not compact, as we show in the next example.

Example 10.

Let us give some (in a sense canonical) examples of the kind of equivalent metric that can be defined as an integral with respect to a probability measure (an average).

1. 

Consider the case of the Euclidean space ${\mathbb{R}}^N,$$N\in \mathbb{N},$ that was studied in [18] and in Example 4. Observe that it is not a compact space. We can choose as a metric basis the set $\mathcal{G}=\{0,e_1,e_2,\dots ,e_N\},$ where $e_i$ are the elements of the canonical basis. So we can define the new metric on ${\mathbb{R}}^N$ by the measure on $\mathcal{G}$ given by

$$\mu ={\displaystyle \frac{1}{N+1}}\left({\delta }_0+\sum _{i=1}^N{\delta }_{e_i}\right),$$

where ${\delta }_x$ is as usual the Dirac’s delta at the point $x.$ Then, we consider

$$d_{\mu }(x,y)={\displaystyle \frac{1}{N+1}}\left({|\parallel x\parallel }_2-{\parallel y\parallel }_2|+\sum _{i=1}^N|\parallel x-e_i{\parallel }_2-{\parallel y-e_i\parallel }_2|\right).$$

As $\mathcal{G}$ is a metric generating system, $d_{\mu }$ is also a metric.

We claim that the metrics d and $d_{\mu }$ provide the same topology on the Euclidean space ${\mathbb{R}}^N$ for $N\ge 2$, but are not Lipschitz equivalent.

It is clear that $d_{\mu }(x,y)\le d(x,y)$. To show that the corresponding topologies are in fact the same, suppose the sequence ${\left(x_n\right)}_n$ is convergent to x in $d_{\mu }$; we have to show that $x_n\to x$ in d. As $\left(x_n\right)$ is convergent, it is bounded (in $d_{\mu }$), so there exists $M>0$ such that $d_{\mu }(x_n,0)<M$ for all $n\in \mathbb{N}$. Then, it is also bounded in d, since

$$d(x_n,0)=|\parallel x_n{\parallel }_2-{\parallel 0\parallel }_2|\le (N+1)d_{\mu }(x_n,0)<(N+1)M.$$

Let $X={\overline{B}}_{{\mathbb{R}}^N}(0,(N+1)M),$ and let us consider now the function $\phi :(X,d)\to ({\mathbb{R}}^{N+1},\parallel ·{\parallel }_1),$ $z\mapsto {\left(d(z,w)\right)}_{w\in \mathcal{G}}.$ It is a continuous function since

$${\parallel \phi \left(z\right)-\phi \left(y\right)\parallel }_1=(N+1)d_{\mu }(z,y)\le (N+1)d(z,y).$$

As in Remark 4, since $(X,d)$ is compact, $({\mathbb{R}}^{N+1},\parallel ·{\parallel }_1)$ Hausdorff and φ is one-to-one ($\mathcal{G}$ is a metric generating system), ${\phi }^{-1}:\phi \left(X\right)\to X$ is also continuous.Note that $\parallel \phi \left(x_n\right)-\phi \left(x\right){\parallel }_1=(N+1)d_{\mu }(x_n,x)\to 0$ when $n\to \infty$, $\phi \left(x_n\right)\to \phi \left(x\right)$ in ${\parallel ·\parallel }_1$. By the continuity of ${\phi }^{-1}$, $x_n\to x$ in d.

To show that d and $d_{\mu }$ are not Lipschitz equivalent, consider the elements $x_n=(n+1)e_1+n{e}_2$ and $y_n=n{e}_1+(n+1)e_2$. We calculate now $d_{\mu }(x_n,y_n)$.

$$d(x_n,0)=\sqrt{{(n+1)}^2+n^2}=d(y_n,0),$$

$$d(x_n,e_1)=\sqrt{n^2+n^2}=\sqrt{2}n,$$

$$d(y_n,e_1)=\sqrt{{(n-1)}^2+{(n+1)}^2}=\sqrt{2}\sqrt{n^2+1},$$

$$d(x_n,e_2)=\sqrt{{(n+1)}^2+{(n-1)}^2}=\sqrt{2}\sqrt{n^2+1},$$

$$d(y_n,e_2)=\sqrt{n^2+n^2}=\sqrt{2}n,$$

$$d(x_n,e_m)=\sqrt{{(n+1)}^2+n^2+1}=d(y_n,e_m),\mathrm{for}m\ge 2.$$

Then, $d_{\mu }(x_n,y_n)=\frac{2\sqrt{2}}{N+1}\left(\sqrt{n^2+1}-n\right)\to 0$ as $n\to \infty$. Instead, $d(x_n,y_n)=\sqrt{2}$, so there is no $C>0$ such that $d(x_n,y_n)\le C{d}_{\mu }(x_n,y_n)$ for all $n\in \mathbb{N}$.

2. 

The infinite dimensional version of the example above is provided by the case when $(X,d)$ is an (infinite dimensional) separable Hilbert space. Let $\{e_i:i\in \mathbb{N}\}$ be an orthonormal basis. It is also shown in [18] that $\mathcal{G}=\left\{0\right\}\cup \{e_i:i\in \mathbb{N}\}$ is a metric generating system. We can use the measure on $\mathcal{G}$ given by

$$\mu =\frac{1}{2}{\delta }_0+\sum _{i=1}^{\infty }\frac{1}{2^{i+1}}{\delta }_{e_i},$$

so the new metric in X is

$$\begin{array}{cc}\hfill d_{\mu }(x,y)& ={\int }_{\mathcal{G}}|d(x,a)-d(y,a)|d\mu \hfill \\ \hfill & =\frac{1}{2}|\parallel x\parallel -\parallel y\parallel |+\sum _{i=1}^{\infty }\frac{1}{2^{i+1}}|d(x,e_i)-d(y,e_i)|.\hfill \end{array}$$

3.2. Applications: Metric Coordinates-Based Extensions of Lipschitz Operators

Let us show how the results on metric coordinates systems can be applied to obtain explicit formulas for Lipschitz extension of Lipschitz maps.

Let us recall the context we have fixed in the previous section. Suppose $\mathcal{G}$ is a compact metric generating system for a metric space M, and $\mu \in \mathcal{M}\left(\mathcal{G}\right)=\mathcal{C}{\left(\mathcal{G}\right)}^{\ast }$ a probability measure. Recall that

(1)

$d_{\infty }(x,y)={sup}_{a\in \mathcal{G}}|d(x,a)-d(y,a)|,x,y\in M,$

(2)

$d_{\mu }(x,y)={\int }_{\mathcal{G}}|d(x,a)-d(y,a)|d\mu \left(a\right),x,y\in M.$

According to the characterization theorems for metric $\infty -$ bounded and metric $1-$ summing Lipschitz maps, when the identity map satisfies any of the inequalities that characterize both clases of maps the information on ${\left(d(x,a)\right)}_{a\in \mathcal{G}}$ is enough to determine the point $x\in M$. We have already shown that, if the identity map is metric summing, we have for a probability measure $\mu$ and a certain constant $R>0,$

$$Rd(x,y)\le d_{\mu }(x,y)\le d_{\infty }(x,y)\le d(x,y),x,y\in M.$$

This fact implies that if the identity map $id:M\to M$ is ∞-bounded (metric summing), any Lipschitz map from M to another metric space, $T:M\to N$, is ∞-bounded (metric summing).

The question now is: given a metric space $(M,d)$ with a compact metric generating system $\mathcal{G},$ a Lipschitz map $T:(\mathcal{G},d)\to (N,\rho )$, can we obtain an extension $\widehat{T}:(M,d)\to (N,\rho )$ that is ∞-bounded or metric summing?

Following the idea in Lemma 1, we consider $T\left(\mathcal{G}\right)$ as a metric generating system of $T\left(M\right)$.

Lemma 2.

Let $(M,d)$ be a metric space and $\mathcal{G}$ a compact metric generating system for it. Let $\mu \in \mathcal{M}\left(\mathcal{G}\right)$ be a probability measure. Then the operators

$$\begin{array}{cc}\hfill m_T^{\infty }:T\left(\mathcal{G}\right)& \to {\ell }_{\infty }\left(\mathcal{G}\right)\hfill \\ \hfill T\left(b\right)& \mapsto m_T^{\infty }\left(T\left(b\right)\right)={\left(m_{T,a}^{\infty }\left(T\left(b\right)\right)\right)}_{a\in \mathcal{G}}={\left(\rho \left(T\right(b),T(a\left)\right)\right)}_{a\in \mathcal{G}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill m_T^{\mu }:T\left(\mathcal{G}\right)& \to L^1\left(\mu \right)\hfill \\ \hfill T\left(b\right)& \mapsto m_{T,(·)}^{\mu }\left(T\left(b\right)\right)=\rho (T\left(b\right),T(·))\hfill \end{array}$$

are well-defined and Lipschitz, with constant less or equal to $1.$

Proof. 

First note that the definitions depends only on $T\left(b\right)$ and not on b, so there is no problem of wrong definition if there are different $b,c\in \mathcal{G}$ such that $T\left(b\right)=T\left(c\right).$ Now, since $\mathcal{G}$ is a compact set and the function $a\mapsto \rho \left(T\right(a),T(b\left)\right)$ is continuous for each fixed $b\in \mathcal{G},$ these functions are all of them bounded. So, both $m_T^{\infty }\left(T\left(b\right)\right)$ and $m_T^{\mu }\left(T\left(b\right)\right)$ are well-defined (to see this for the second case, note also that these functions are integrable, since they are continuous functions and $\mu \in C{\left(\mathcal{G}\right)}^{\ast }$).

Now, take $b_1,b_2\in \mathcal{G}.$ Then

$$\begin{array}{cc}\hfill \parallel m_T^{\infty }\left(T\left(b_1\right)\right)-m_T^{\infty }\left(T\left(b_2\right)\right){\parallel }_{\infty }& =\underset{c\in \mathcal{G}}{sup}|\rho (T\left(c\right),T\left(b_1\right))-\rho (T\left(c\right),T\left(b_2\right))|\hfill \\ \hfill & \le \rho (T\left(b_1\right),T\left(b_2\right))\hfill \end{array}$$

On the other hand,

$$\parallel m_T^{\mu }\left(T\left(b_1\right)\right)-m_T^{\mu }\left(T\left(b_2\right)\right){\parallel }_{L^1\left(\mu \right)}={\int }_{\mathcal{G}}|\rho (T\left(b_1\right),T\left(c\right))-\rho (T\left(b_2\right),T\left(c\right))|d\mu \left(c\right)$$

$$\le {\int }_{\mathcal{G}}\rho (T\left(b_1\right),T\left(b_2\right))d\mu \left(c\right)=\rho (T\left(b_1\right),T\left(b_2\right))\mu \left(\mathcal{G}\right)=\rho (T\left(b_1\right),T\left(b_2\right)).$$

Consequently, both functions are $1-$ Lipschitz. □

Let $(M,d)$ be a metric space with a compact generating system $\mathcal{G}$ and H a subset of M (notice that $\mathcal{G}$ is also a metric generating system of H). Given a Lipschitz map $T:(H,d)\to (N,\rho )$, if T is ∞-bounded with constant Q, for a fixed $a\in \mathcal{G}$ we define the McShane type formula

$${\widehat{m}}_{T,a}^{\infty }\left(x\right):=\underset{b\in H}{sup}\left\{\rho (T\left(a\right),T\left(b\right))-Q\underset{c\in \mathcal{G}}{sup}|d(b,c)-d(x,c)|\right\},x\in M.$$

If T is metric summing with constant C, for a fixed $a\in \mathcal{G}$ we consider also the formula

$${\widehat{m}}_{T,a}^{\mu }\left(x\right):=\underset{b\in H}{sup}\left\{\rho (T\left(a\right),T\left(b\right))-C{\int }_{\mathcal{G}}|d(b,c)-d(x,c)|d\mu \left(c\right)\right\},x\in M.$$

Note that in these formulas (as in the rest of the section) not all the metric information on $(M,d)$ is used, but only the related to its metric generating system: using the notation of Section 2, $Dist=\left\{d\right(a,x):a\in \mathcal{G},x\in M\}.$

Let us prove first that these functions provide well-defined extensions ${\widehat{m}}_{T,a}^{\infty }:M\to \mathbb{R}$ and ${\widehat{m}}_{T,a}^{\mu }:M\to \mathbb{R}$.

Lemma 3.

Let $(M,d)$ be a metric space with a compact generating system $\mathcal{G}$, H a subset of M and $T:(H,d)\to (N,\rho )$ a Lipschitz map.

1. 

If T is ∞-bounded with constant Q, then for each $a\in \mathcal{G},$${\widehat{m}}_{T,a}^{\infty }$ is well defined, and

(a) 

for every $b\in H,$ ${\widehat{m}}_{T,a}^{\infty }\left(b\right)=\rho (T\left(a\right),T\left(b\right)),$

(b) 

for every $x,y\in M$

$$|{\widehat{m}}_{T,a}^{\infty }\left(x\right)-{\widehat{m}}_{T,a}^{\infty }\left(y\right)|\le Q\underset{c\in \mathcal{G}}{sup}|d(b,c)-d(x,c)|\le Qd(x,y).$$

2. 

If T is metric summing with constant C and associated measure $\mu ,$ then for each $a\in \mathcal{G}$, ${\widehat{m}}_{T,a}^{\mu }$ is well defined, and

(a) 

for every $b\in H,$ ${\widehat{m}}_{T,a}^{\mu }\left(b\right)=\rho (T\left(a\right),T\left(b\right)),$

(b) 

for every $x,y\in M,$

$$|{\widehat{m}}_{T,a}^{\mu }\left(x\right)-{\widehat{m}}_{T,a}^{\mu }\left(y\right)|\le C{\int }_{\mathcal{G}}|d(b,c)-d(x,c)|d\mu \left(c\right)\le Cd(x,y).$$

Proof. 

The proofs of these inequalities are given by standard computations. For the aim of completeness let us show some of them.

(1) To show that ${\widehat{m}}_{T,a}^{\infty }$ is well-defined, it is enough to prove that for a fixed $x\in M$, the set $\{\rho (T\left(a\right),T\left(b\right))-Q{sup}_{c\in \mathcal{G}}|d(b,c)-d(x,c)|:b\in H\}$ is upper bounded. As T is ∞-bounded, for any $b\in H$,

$$\begin{array}{cc}\hfill \rho \left(T\right(a),T(b\left)\right)-& Q\underset{c\in \mathcal{G}}{sup}|d(b,c)-d(x,c)|\hfill \\ \hfill & \le Q\underset{c\in \mathcal{G}}{sup}|d(a,c)-d(b,c)|-Q\underset{c\in \mathcal{G}}{sup}|d(b,c)-d(x,c)|\hfill \\ \hfill & \le Q\underset{c\in \mathcal{G}}{sup}|d(a,c)-d(x,c)|\le d(a,x)<+\infty \hfill \end{array}$$

Let us prove (a). Fix $b\in H,$ Then

$$\begin{array}{cc}\hfill \rho \left(T\right(a),T(b\left)\right)& =\rho (T\left(a\right),T\left(b\right))-Q\underset{c\in \mathcal{G}}{sup}|d(b,c)-d(b,c)|\hfill \\ \hfill & \le \underset{b_0\in H}{sup}\left\{\rho (T\left(a\right),T\left(b_0\right))-Q\underset{c\in \mathcal{G}}{sup}|d(b_0,c)-d(b,c)|\right\}.\hfill \end{array}$$

On the other hand, for $b_0\in \mathcal{G},$

$$\begin{array}{cc}\hfill \rho (T\left(a\right),T\left(b_0\right)& \le \rho (T\left(a\right),T\left(b\right))+\rho (T\left(b_0\right),T\left(b\right))\hfill \\ \hfill & \le \rho (T\left(a\right),T\left(b\right))+Q\underset{c\in \mathcal{G}}{sup}|d(b_0,c)-d(b,c)|,\hfill \end{array}$$

and so ${\widehat{m}}_{T,a}^{\infty }\left(b\right)\le \rho (T\left(a\right),T\left(b\right)).$

Now let us show the proof of (b) for the function ${\widehat{m}}_{T,a}^{\mu }$. Let $x,y\in M.$ Then

$$\begin{array}{cc}\hfill |{\widehat{m}}_{T,a}^{\mu }\left(x\right)& -{\widehat{m}}_{T,a}^{\mu }\left(y\right)|\le \underset{b\in \mathcal{G}}{sup}|\rho (T\left(a\right),T\left(b\right))-\rho (T\left(a\right),T\left(b\right))\hfill \\ \hfill & -Q{\int }_{\mathcal{G}}|d(b,c)-d(x,c)|d\mu \left(c\right)+Q{\int }_{\mathcal{G}}|d(b,c)-d(y,c)|d\mu \left(c\right)|\hfill \\ \hfill & \le Q{\int }_{\mathcal{G}}\left|\right|d(b,c)-d(x,c)|-|d(b,c)-d(y,c)\left|\right|d\mu \left(c\right)\hfill \\ \hfill & \le Q{\int }_{\mathcal{G}}|d(x,c)-d(y,c)|d\mu \left(c\right).\hfill \end{array}$$

□

Observe that the bounds on the statement $\left(b\right)$ of Lemma 2 are uniform on $a\in \mathcal{G}$. This fact will allow us to consider all these functions together (for all such elements $a\in \mathcal{G}$) taking values on ${\ell }_{\infty }\left(\mathcal{G}\right)$ or $L^1\left(\mu \right)$, depending on the case.

Theorem 3.

Let $(M,d)$ be a metric space with a compact generating system $\mathcal{G}$, H a subset of M and $T:(H,d)\to (N,\rho )$ a Lipschitz map.

1. 

If T is ∞-bounded, then there exists a ∞-bounded extension ${\widehat{T}}_{\infty }$ of $m_T^{\infty }\circ T$ preserving its Lipschitz constant and such that the following diagram commute

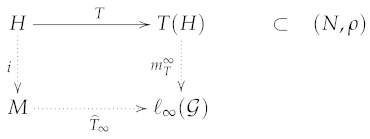
2. 

If T is metric summing, then there exists a metric summing extension ${\widehat{T}}_{\mu }$ of $m_T^{\mu }\circ T$ preserving its Lipschitz constant and such that the following diagram commute

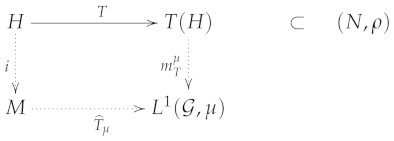
Moreover, the formulas below can be used for the extensions:

$${\widehat{T}}_{\infty }\left(x\right):={\left({\widehat{m}}_{T,a}^{\infty }\left(x\right)\right)}_{a\in \mathcal{G}}\in {\ell }_{\infty }\left(\mathcal{G}\right),{\widehat{T}}_{\mu }\left(x\right):={\widehat{m}}_{T,(·)}^{\mu }\left(x\right)\in L^1(\mathcal{G},\mu ).$$

Proof. 

Lemma 2 gives that both the maps $m_T^{\infty }\circ T$ (and $m_T^{\mu }\circ T$) preserve the ∞-bounded (and metric summing) condition of T.

By the construction we have shown in the previous lemmas, we have that

$$m_T^{\infty }\left(T\left(b\right)\right)={\left(\rho \left(T\right(a),T(b\left)\right)\right)}_{a\in \mathcal{G}}={\widehat{T}}_{\infty }\left(b\right)$$

(part (1) of Lemma 3), and

$$m_{T,(·)}^{\mu }\left(T\left(b\right)\right)=\rho (T\left(b\right),T(·))={\widehat{m}}_{T,(·)}^{\mu }\left(b\right)={\widehat{T}}_{\mu }\left(b\right)$$

for each $b\in \mathcal{G}$ (part (2) of Lemma 3). Therefore, the diagram commutes.

On the other hand, it has been proved in Lemma 3 that the pointwise components of the sequence/function that appear in ${\widehat{T}}_{\infty }\left(x\right)$ or ${\widehat{T}}_{\mu }\left(x\right)$ satisfy the boundedness requirements that are needed. Indeed, using the inequalities given there, we obtain for every $x,y\in M,$

$$\parallel {\widehat{T}}_{\infty }\left(x\right)-{\widehat{T}}_{\infty }{\left(y\right)\parallel }_{\infty }=\underset{a\in \mathcal{G}}{sup}|{\widehat{m}}_{T,a}^{\infty }\left(x\right)-{\widehat{m}}_{T,a}^{\infty }\left(y\right)|\le Qd(x,y)$$

and

$$\parallel {\widehat{T}}_{\mu }\left(x\right)-{\widehat{T}}_{\mu }{\left(y\right)\parallel }_{L^1\left(\mu \right)}={\int }_{\mathcal{G}}|{\widehat{m}}_{T,a}^{\mu }\left(x\right)-{\widehat{m}}_{T,a}^{\mu }\left(y\right)|d\mu \left(a\right)\le Cd(x,y).$$

Therefore, the extensions preserve the Lipschitz constants. □

These factorizations recall similar situations in the linear setting. For example, integral operators are characterized in the context of the (linear) operator ideals by a factorization of the canonical extension of the original operator to $L^{\infty }$ (see, for example, ([20], Ch. 5), see also [7]).

When the metric space $(N,\rho )$ is $({\ell }_{\infty },\parallel ·\parallel )$ (or $(L^1\left(\mu \right),\parallel ·\parallel )$) we obtain direct extension results. Let us finish the paper by writing the corresponding corollaries.

Corollary 4.

Let $(M,d)$ be a metric space with a compact generating system $\mathcal{G}$ and H a subset of M. Given a ∞-bounded map $T:(H,d)\to ({\ell }_{\infty },\parallel ·{\parallel }_{\infty }),$ there exists a ∞-bounded extension ${\widehat{T}}_{\infty }:M\to {\ell }_{\infty }$ preserving the Lipschitz constant.

Corollary 5.

Let $(M,d)$ be a metric space with a compact generating system $\mathcal{G}$ and H a subset of M. Given a metric summing map $T:(H,d)\to (L^1\left(\mu \right),\parallel ·\parallel ),$ there exists a metric summing extension ${\widehat{T}}_{\mu }:M\to L^1\left(\mu \right)$ preserving the Lipschitz constant.

4. Conclusions

We have introduced a new framework for the conceptualization of extensions and representations of Lipschitz maps, based on the notion of enriched metric space, which considers any additional structures that are added to the metric space (e.g., algebraic relations and graph structures). In the first part of the article, together with other examples, we have shown how our results apply in the case of Lipschitz operators on Euclidean spaces.

In the second part of the paper, we focus on how Lipschitz operators can be extended and represented under the assumption of the existence of a metric coordinate system, which we formalize by the notion of a metric generating system. We mimic the ideas underlying the representation of linear maps over finite dimensional spaces by means of their bases. Under some boundedness or summability requirements, we show that the related Lipschitz operators allow some factorization and extension results, which can be understood as representation theorems. Thus, once a certain domination inequality (defined for a metric-generating system) holds for a Lipschitz operator, we show that the Lipschitz inequality can be improved with a ${\ell }^{\infty }-$ norm or an $L^1-$ norm instead of the original distance. When these dominations hold for the identity map, this provides Lipschitz isomorphisms from the metric space to a metric subspace of ${\ell }^{\infty }$ or $L^1.$