Abstract
Left-truncated and right-censored data are widely used in lifetime experiments, biomedicine, labor economics, and actuarial science. This article discusses how to resolve the problems of statistical inferences on the unknown parameters of the exponentiated half-logistic distribution based on left-truncated and right-censored data. In the beginning, maximum likelihood estimations are calculated. Then, asymptotic confidence intervals are constructed by using the observed Fisher information matrix. To cope with the small sample size scenario, we employ the percentile bootstrap method and the bootstrap-t method for the establishment of confidence intervals. In addition, Bayesian estimations under both symmetric and asymmetric loss functions are addressed. Point estimates are computed by Tierney–Kadane’s approximation and importance sampling procedure, which is also applied to establishing corresponding highest posterior density credible intervals. Lastly, simulated and real data sets are presented and analyzed to show the effectiveness of the proposed methods.
Keywords:
Bayesian estimation; credible intervals; bootstrap method; exponentiated half-logistic distribution; importance sampling; maximum likelihood estimation; Tierney–Kadane’s approximation MSC:
62F10; 62N02
1. Introduction
1.1. Exponentiated Half-Logistic Distribution
The exponentiated half-logistic distribution is applied in life testing and reliability analysis far and wide. It has raised great interest in scholars in the past decades. Kang et al. [1] derived the maximum likelihood estimators and approximate maximum likelihood estimators of the scale parameter based on progressive Type II censored data. Rastogi et al. [2] studied Bayes estimates of the exponentiated half-logistic distribution. Gadde et al. [3] applied the exponentiated half-logistic distribution to the truncated life test and proposed acceptance sampling for the percentiles of the distribution. Seo et al. [4] showed that the exponentiated half-logistic distribution can be a substitute for the two-parameter family of distributions, such as the gamma distribution and the exponentiated exponential distribution. Gui [5] obtained a suitable condition for the existence of maximum likelihood estimates of the parameters in the exponentiated half-logistic distribution.
When the shape parameter equals one, the exponentiated half-logistic distribution is reduced to half-logistic distribution. The half-logistic distribution is highly suitable for the survival analysis of censored data. Based on progressively type-II censored samples, Balakrishnan et al. [6] derived the maximum likelihood estimator of the scale parameter in the half-logistic distribution. Based on the results of previous studies, Gile [7] conducted an in-depth study on the bias of the maximum likelihood estimator. Wang [8] derived an exact confidence interval for the scale parameter in scaled half-logistic distribution based on a progressively Type II censored sample. Rosaiah et al. [9] developed a reliability test plan for the half-logistic distribution.
In this article, it is assumed that the lifetime of units follows the exponentiated half-logistic distribution. The probability density function (PDF) has the form of:
where is the scale parameter and is the shape parameter.
The cumulative distribution function (CDF) is written as:
Based on the PDF and CDF, the reliability function and failure rate function are derived:
Figure 1 shows the PDF and CDF of the exponentiated half-logistic distribution. The PDF is right-skewed and unimodal when , while it is decreasing monotonically when . The PDF becomes more fat-tailed when the is larger. When it comes to CDF, the smaller and are, the faster the rising rate becomes.
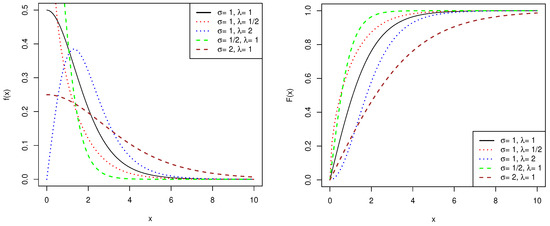
Figure 1.
PDF (left) and CDF (right) of the exponentiated half-logistic distribution.
Based on L’Hospital’s rule, the failure rate function approaches when x approaches infinity as Figure 2 shows. According to [10], gamma distribution and exponentiated half-logistic distribution have the same attributes as the PDF and behaviors of the failure rate function when shape parameters are larger than one. However, the CDF, reliability, and failure rate functions of the gamma distribution do not have a closed form when the shape parameter is not an integer. Thus, the exponentiated half-logistic distribution, whose overall distribution has a closed structure, performs better than the gamma distribution.
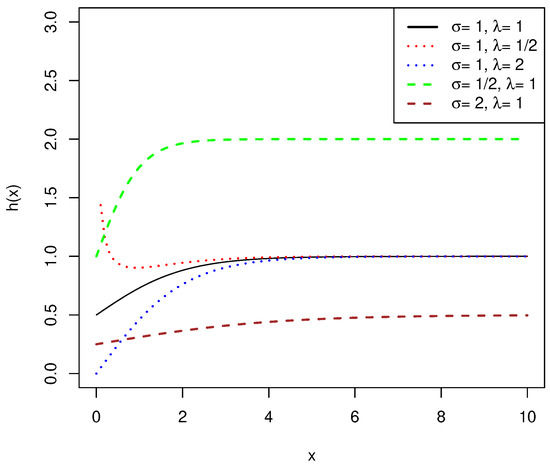
Figure 2.
Failure rate function of exponentiated half-logistic distribution.
1.2. Left-Truncated and Right-Censored Data
As for data collection, it is impractical to collect the entire lifetimes of all units with limited time and cost. For example, waiting until all the units have failed in the lifetime test of light bulbs is infeasible. Researchers may only collect partial observations and stop the experiment when a predetermined time has elapsed or when the amount of observations has reached a pre-specified number, which gives rise to type I censoring and type II censoring. In this paper, type I censoring is further discussed.
On the other hand, truncation arises when the observation information is available only if its value is within a specific range. Data out of the predetermined range are not considered. Truncation includes left and right truncations, and only left truncation is discussed in this paper. Each unit is observable only if its lifetime exceeds left-truncated time .
Left truncation and right censoring naturally occur in engineering, asset management, maintenance of instruments, reliability, and survival analysis studies. Hong et al. [11] proposed a famous and authentic example of left-truncated right-censored data. The data set consists of the lifetime data of approximately high-voltage power transformers from a specific energy company, collected from 1980 to 2008. The transformers were installed at different times in the past, and failure times were random. The information on lifetime is available only if the transformers failed after 1980. In [11], a parametric model was built to explain lifetime distribution. Balakrishnan et al. [12] applied the lognormal, Weibull, gamma, and generalized gamma distributions to mimic the lifetime distribution and provided a more detailed analysis. They used the expectation maximization algorithm to calculate maximum likelihood estimations of unknown parameters. Kundu et al. [13] solved the problem from a Bayesian perspective and involved competing risks in parametric analysis. In [14], another illustrative example of left truncation and right censoring, the Channing House data, is analyzed. The data set consists of 97 men and 365 women covered by a health care program in a retirement center in California. Data were collected from 1964 to 1975 to study the differences in the survival of genders. There is a restriction that only people who are 60 or older have permission to enter the center. Thus all the data are left-truncated. At the same time, the lifetime data of people who survived until 1975 or exited before the experiment stopped are right-censored.
Motivated by the previous work above, this paper discusses parametric estimations of left-truncated and right-censored data under an exponentiated half-logistic distribution. The rest of the paper is organized as follows: In Section 2, the maximum likelihood estimates of parameters are computed. Asymptotic confidence intervals are constructed by using the observed Fisher information matrix. In Section 3, the percentile bootstrap method and bootstrap-t method are proposed to build confidence intervals in case of a small sample size. In Section 4, Bayesian estimates are provided. Point estimates are carried out by Tierney–Kadane’s approximation and importance sampling procedure. The importance sampling procedure is also applied to build the highest posterior density credible intervals. In Section 5, simulations are carried out. Comparisons between estimators from different methods are also presented for illustrative purposes. An authentic data set, the Channing House data set, is analyzed to show the effectiveness of proposed methods in Section 6, and Section 7 concludes the paper.
2. Maximum Likelihood Estimation
In this section, point estimates and asymptotic confidence intervals are derived by using maximum likelihood estimation. Assuming there are totally n observable units in the lifetime test, namely . The random variable denotes the lifetime of the i-th unit with the value of . The order of units is random, and units are put to the test at different times. For the i-th unit, there is a predetermined left-truncation time point and a right-censoring time point (), which may be differentiated between units. It is important to note that the unit that fails before is not considered in this paper. This means that all of n observable units are put on test before and live till or put on test after . Units that fail after have the possibility to be censored at . In this paper, type I right censoring is discussed. The right-censoring time for each units is fixed on the same time point .
Moreover, we introduce a truncation indicator and a censoring indicator , which are defined as follows:
2.1. Point Estimates
In this paper, we assume that the lifetimes follow the exponentiated half-logistic distribution . Based on the observations , the PDF and the CDF, the likelihood function can be expressed by:
where denotes data .
The PDF and CDF have been displayed in Functions (1) and (2), respectively. Therefore, the likelihood function is transformed into:
The corresponding log-likelihood function can be written as:
To compute maximum likelihood estimations (MLE) of and , the first partial derivatives are set to zero:
where , , .
Then the MLEs of and are the roots of Equations (8) and (9), written as and . However, it is not easy to find the analytic roots due to the nonlinearity and non-closed forms of the equations. Thus, the Newton—Raphson method, one of the numerical methods, is applied to approximately solve the equations and then obtain MLEs, which can be achieved by R software.
2.2. Asymptotic Confidence Intervals
To derive the asymptotic confidence intervals of and , we further discuss the variance-covariance matrix. When the sample size is large, and asymptotically follow normal distributions. In this way, we can obtain asymptotic confidence intervals from the variance-covariance matrix, also known as the inverse of the Fisher information matrix. The Fisher information matrix is a vectorized definition of Fisher information which shows the average amount of information about the state parameters that a sample of random variables can provide in a certain sense.
2.2.1. Expected Fisher Information Matrix
The expected Fisher information matrix can be calculated by taking the expectation of the negative second derivative of the log-likelihood function:
Here, the second partial derivatives are as follows:
where
and .
2.2.2. Observed Fisher Information Matrix
To simplify the calculation, the observed Fisher information matrix obtained by samples is employed to approximate the expected Fisher information matrix. The observed Fisher information matrix is the value of the Fisher information matrix at the point of
where and are the MLEs, respectively.
The variances of and can be obtained by computing the inverse matrix of the observed Fisher information matrix:
where and are the variances of and , and and are the covariances of and .
Thus, asymptotic confidence intervals of two parameters can be constructed as
and
where denotes the upper -th quantile of the standard normal distribution.
3. Bootstrap Confidence Intervals
When the sample size is small, classical theory on constructing confidence intervals may not work well. The bootstrap methods are introduced to deal with a small sample size by resampling. The two widely used bootstrap methods are the percentile bootstrap method (boot-p) and the bootstrap-t method (boot-t). The boot-p method presents the distribution of the bootstrap sample statistics, rather than the original sample, to establish confidence intervals. The boot-t method converts the bootstrap sample statistics to the corresponding t statistics. The algorithms are demonstrated as follows:
3.1. Percentile Bootstrap Confidence Intervals
From Algorithm 1, we can obtain the ascending sequence of MLEs and . Thus, percentile bootstrap confidence intervals of and are and , where , and operator is rounding down to the nearest integer.
| Algorithm 1 Establishing percentile bootstrap confidence intervals. |
|
|
|
|
|
3.2. Bootstrap-t Confidence Intervals
From Algorithm 2, we can obtain ascending sequences of t-statistics for and , respectively. Thus, bootstrap-t confidence intervals of and can be constructed as
and
where and .
| Algorithm 2 Establishing bootstrap-t confidence intervals. |
|
|
|
|
|
4. Bayesian Estimates
Classical statistical analysis provides us with statistics such as MLE and credible intervals based on the information derived from samples. To promote the practical application of analysis in real-life cases, we propose to compute Bayesian estimates, which combine prior distributions determined by real experience with sample information.
The selections of prior distributions have a great influence on the consequences of Bayesian estimates. However, finding a conjugate prior distribution is difficult when the two parameters are unknown. The results in [15] show that the prior distributions adopted by them work well under . It is plausible to use the same prior distributions as Xiong et al. [15]: assuming that follows the inverse gamma distribution () and follows the gamma distribution (), where , , , are hyperparameters. We also suppose that two parameters are independent for the simplicity of calculation. The PDFs of prior distributions for and can be written as:
Therefore, the PDF of joint prior distribution is the multiple of two prior distributions:
Based on the theories of Bayes, the posterior distribution can be described as the ratio of the joint distribution of the samples and unknown parameters to the marginal distribution of the samples:
where denotes the data.
4.1. Loss Functions
Loss functions are employed to assess the intensity of inconsistency between parameter estimations and the true values. Symmetric loss functions, for example, the square error loss function (SELF), are classical. Overestimation causes the same loss as underestimation in symmetric loss functions. Asymmetric loss functions such as the linex loss function (LLF) fit in the condition of inequality. In this subsection, both symmetric loss function, SELF, and asymmetric loss function, LLF, are in further discussion.
4.1.1. Squared Error Loss Function
Squared error loss function is introduced in [16]. As the name suggests, squared error loss function is the square of the distance between predicted value and target variable. The form of function is defined as:
where is the target variable and is the predicted value of .
The Bayesian estimate for under SELF can be described as:
where is the density of . Thus, Bayesian estimates for unknown parameter and can be written as:
4.1.2. Linex Loss Function
Linex (linear exponential) loss function was originally introduced by Zellar [17]. The loss of one side of 0 increases exponentially while the other increases linearly. The linex loss function corresponds to:
where s is the linex parameter. LLF alters exponentially in the negative direction and linearly in the positive direction when , and in the opposite when . The larger s is, the more heavily punishment intensity is. The function tends to be symmetric when the absolute value of s approaches 0.
The Bayesian estimate for under LLF is:
Thus, Bayesian estimates for unknown parameter and are given as:
4.2. Tierney-Kadane’s Approximation
In this subsection, Tierney–Kadane’s (TK) approximation is used to compute Bayesian estimates of unknown parameters. Let denote the target parametric function about and , which takes two different forms under SELF and LLF. According to the TK approximation formula, the associated Bayesian estimate, as well as the posterior expectation of , can be written as:
where and . Note that is the log-likelihood function and is the prior distribution of unknown parameters.
and are the determinants of inverse Hessians of and at and , respectively, where and are the corresponding MLEs of and under and :
It can be observed that , and have no relation with . Using Expression (7), transforms into:
Then, can be computed by finding the roots of the equations, letting first-order partial derivatives of be equal to zero:
where , , .
With , can be obtained easily. As , we need to find out the second-order partial derivatives of at point . The second-order partial derivatives can be described as:
where .
Then, is gained by bringing into Expressions (34)–(36). On the other hand, , and is related to . The difference conditions of under SELF and LLF are discussed in detail as follows.
4.2.1. Squared Error Loss Function
Here, we take for example. According to Function (21), the Bayesian estimates for should be the conditional expectation of under sample data. Thus, let . Therefore, takes the form of:
Thus,
Similar to , and the second-order partial derivatives of are as below:
where , and are the same as Expressions (34)–(36).
Thus, the Bayesian estimate of under SELF can be derived:
For , we let , and the following steps are similar to . The Bayesian estimates of under SELF is given by:
4.2.2. Linex Loss Function
Additionally, we take for example. According to Function (25), the Bayesian estimates for should be the conditional expectation of under sample data. Thus, we take . Hence, takes the form of:
where s is the parameter of LLF.
Then, is computed by finding the roots of:
Thus,
The second-order partial derivatives of turn out to be the same as the second-order partial derivatives of h; then, has the form of:
Thus, the Bayesian estimate of under LLF is yielded:
Similarly, with , the Bayesian estimates of under LLF can be expressed as:
4.3. Importance Sampling Procedure
Importance sampling is a significant technique in Monte Carlo methods, which can greatly reduce the number of sample points drawn in a simulation. It is widely used in computing point estimates and interval estimates. According to (19), the joint posterior distribution can be described as:
where
It can be obviously seen that and are the PDFs of and , respectively.
To obtain point estimates and interval estimates by importance sampling procedure, samples need to be generated first. By executing Algorithm 3, and are generated.
| Algorithm 3 Generating importance sampling procedure samples. |
|
|
|
|
Then, point estimates and interval estimates can be acquired as follows.
4.3.1. Point Estimates
According to the principles of the importance sampling procedure, the Bayesian estimates of and under SELF can be written as:
Similarly, the Bayesian estimates of and under LLF can be written as:
4.3.2. Interval Estimates
Highest posterior density (HPD) regions are especially useful in Bayesian statistics [18]. The HPD credible interval is the interval that contains the required mass such that all points within the interval have a higher probability density than points outside the interval. Chen et al. [19] developed a Monte Carlo method to compute HPD credible intervals. In this paper, HPD credible intervals are obtained from samples generated by Algorithm 3.
Suppose that
it is obvious that . Display and q as . Then rearrange them in ascending order of into:. Note that and are produced in the same round of iteration. Define as:
In order to establish a HPD interval, needs to be computed first. Then, credible intervals can be expressed as , , which indicates that the length of each is near to . Finally, the interval with the shortest length turns out to be the HPD credible interval . This means for all .
5. Simulation Study
In this subsection, we carry out a Monte Carlo simulated data set, which is determined to mimic the lifetime data of the electronic transformers proposed in [11]. The details of the transformers’ data set can be found in Section 1.2. R software was employed to run all of the simulations. The evaluation indicators for point estimation were mean squared error (MSE) and estimation value, while for interval estimation, the evaluation indicators were average length (AL) and coverage rate (CR).
Left-truncated and right-censored data were generated as follows: The parameters we chose for lifetime distribution were . The sample size n was chosen as 80, 100 and 120. The left-truncated time for all units was set to 1980. Note that the item fails before 1980 were not considered, which means they were discarded and replaced by a new observation. The proportion of truncation was fixed: two different truncation percentages () were chosen as and for comparison, which was the same as [13]. Left-truncated samples were installed in the time range of with an equal possibility () attached to each year. The remaining units were installed in with an equal possibility () for each year.
The lifetime of all units were simulated from the . The year of failure was the installation year plus the lifetime. The censoring year for all units was set to 1998 and 2002 for comparison purposes. The data of observations that failed after the censoring year were right-censored.
To compute the maximum likelihood estimation, the L-BFGS-B method was applied, which is one of the most successful quasi-Newton algorithms. Relevant functions were provided in R software. Asymptotic confidence intervals and bootstrap confidence intervals at confidence level were also conducted. The bootstrap confidence intervals were computed with bootstrap samples. To calculate Bayesian estimates, not only non-informative priors but also informative priors were discussed. Four parameters , , and of prior distributions for and were set differently in different occasions. For non-informative priors, we set to minimize the impact brought by prior distribution. For informative priors, the parameters were chosen as , , , . The TK method under two loss functions was employed to compute Bayesian point estimation. For LLF, the linex parameter s was set as and . The importance sampling procedure was established for Bayesian point estimates and HPD intervals at the credible level.
For point estimates, the results of MLEs of and are shown in Table 1, while the results of non-informative and informative Bayesian estimates are presented in Table A1, Table A2, Table A3 and Table A4 in Appendix A. For interval estimates at the confidence level, the results of ACI, boot-p, boot-t and HPD intervals are provided in Table A5 and Table A6 in Appendix B.

Table 1.
The simulation results of MLEs for and .
From Table 1, the following conclusions can be drawn:
- (1)
- As the size of sampling n increases, the mean square error (MSE) of both and declines.
- (2)
- The smaller truncation percentage is, the lower the MSEs of both two parameters are. Censoring at a later year (2002) also leads to a lower MSE. This is reasonable because data under lower truncation and censoring percentages are closer to the unedited true data.
- (3)
- The MLEs of perform better than those of , but the estimation values of the two parameters are about the same distance from the true values.
- (1)
- Bayesian estimates with informative priors are more accurate than MLEs, while non-informative Bayesian estimates resemble MLEs. It proves that the results would have an essential leap in accuracy with suitable prior distribution and hyperparameters selection.
- (2)
- For non-informative Bayesian estimates, point estimates obtained by both Tierney–Kadane’s approximation and importance sampling procedure resemble MLEs. For informative Bayesian estimates, the importance sampling method overperforms TK approximation. MSEs of two parameters stay at low values no matter how the scheme varies, and estimation values are closer to true values using the importance sampling method.
- (3)
- As for loss functions, the estimates of under LLF perform better than SELF, while for , SELF is slightly better. For , setting linex parameter is better than , indicating that the positive error should have heavy punishment. For , there is little difference under and . Estimates gained by TK approximation are more sensitive to the change of loss function, while lit does not make an obvious difference for importance sampling.
- (4)
- The results under truncation percentage and censored at 2002 perform the best for both and .
- (1)
- Average lengths of intervals become narrower, and coverage rates rise as n increases.
- (2)
- Boot-p, boot-t, and HPD intervals all overperform asymptotic confidence intervals. Among all methods, informative HPD credible intervals have the shortest ALs, while boot-t intervals have the largest CRs. ALs of boot-p intervals are shorter, and CRs are larger than those of ACIs. The results of non-informative HPD credible intervals resemble ACIs. Although informative HPD credible intervals have the shortest ALs, their CRs are the lowest. Among all of the interval estimates, boot-t intervals perform the best.
- (3)
- For , the performance of intervals seems to have no clear relationship with . However, when it comes to , CRs of all intervals under the truncation percentage are obviously smaller than in other cases. Presumably, the reason is that excessive truncation percentage interferes with these methods to obtain the principles of data. As for the censoring year, it seems to have no relationship with CRs of both and , but the later the censoring year is, the smaller ALs of intervals are.
6. Real Data Analysis
The famous Channing House data set is analyzed in this section. The data set can be acquired in R software(the `channing’ data frame in package `boot’ [20]). The study investigated 97 men and 365 women from the opening of the Channing House retirement community (1964) in Palo Alto, California, until their death or the end of the study (July 1, 1975). The data set provides information on gender, age (months) of entry, age (months) of death or exit, and the censoring indicator. Here, the age of death or exit is the data we analyze. People are above 60 years old (720 months) when they enter the community, which indicates that the entire lifetime data in this study are left-truncated at 720 (months). The data of a person’s lifetime is right-censored if he/she lives till the end of the study or leaves the center before the end. The censoring indicator b shows whether the data is right-censored. Some characteristics of the data are shown in Table 2.

Table 2.
Basic statistics of the Channing House data.
At the beginning, we consider the problem whether the distribution fits the data set well. As many scholars mentioned, the complete data set should pass criteria examining goodness of fit, such as Kolmogorov-–Smirnov (K-S) statistics with its p-value, Bayesian information criterion (BIC), and Akaike information criterion (AIC). However, Channing House data are already truncated and censored. Therefore, we use a simulated data set to show the goodness of fit.
6.1. Fitness Test
The dataset is simulated in a manner that mimics the data collection process described in Section 5. Shang et al. [21] discussed the parameter estimation for the generalized gamma distribution based on left-truncated and right-censored data. We use the same data generation method in [21]. The sample size n is 200, and truncation percentage is . The left-truncated time is set to 1980. The year of installation () is simulated based on the following distributions:
For truncated observations,
For not truncated observations,
The lifetimes of 200 units are simulated from the with and . The right censoring year is set to 2014.
MLEs of and are computed with the L-BFGS-B method. We plot the true PDF (the PDF of ), the fitted PDF (the PDF with parameters set to MLEs) and the density of a simulated data set in Figure 3. The values of the log-likelihood for the simulated data set are also presented.
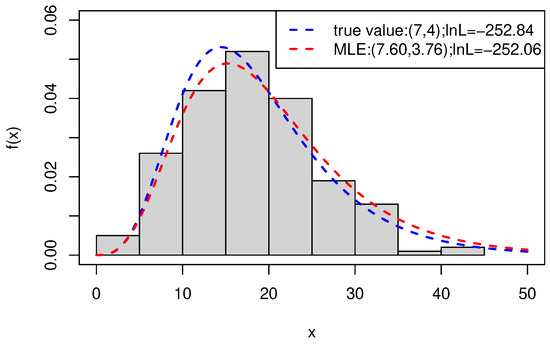
Figure 3.
The true and fitted PDFs, and the density of a simulated data set.
Figure 3 shows that the true and fitted PDFs are similar, indicating that exponentiated half-logistic distribution fits left-truncated and right-censored data well.
6.2. Data Processing and Analysis
For lifetime data in the Channing House data set, we subtract and divide by to each unit’s lifetime to obtain different truncation and censoring schemes. This operation does not affect data inference [14]. The schemes subtracted 720 and 620 are labeled as subtraction type I and II, respectively, while the schemes divided by 10, 30, 50 are labeled as division type i, ii, iii.
Point estimates are calculated using the maximum likelihood method, TK approximation, and the importance sampling procedure. Since an informative prior cannot be obtained, a non-informative prior is applied, and two loss functions, SELF and LLF, are considered for Bayesian estimates. The parameter s of LLF is set to and 1. ACI, boot-p, boot-t, and HPD intervals are established at the confidence/credible level. The results are presented in Table A7, Table A8, Table A9, Table A10 and Table A11 in Appendix C.
Seo et al. [4] proposed methods to derive moment estimation of unknown parameters in an EHL distribution. The first moment and the second moment can be obtained as
and variance can be derived by . In order to approximate the summation of infinite terms in Formulas (63) and (64), we ignore the items smaller than the precision value () since the summation term is monotonically decreasing.
In the Channing House data set scenario, the expectation and variance estimate the average lifespan and dispersion of the population lifetime sample. Expectations and variances obtained by MLEs in Table A7 are presented in Table A12 in Appendix C.
From Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12 in Appendix C, we can conclude that:
- (1)
- The estimates of parameter for males tend to be slightly larger than those for females, while the estimates of parameter for males turn out to be much smaller than those for females.
- (2)
- The Bayesian estimates for both and gained by the TK method are generally larger and closer to MLEs than the ones gained by the importance sampling procedure.
- (3)
- The estimates for both two parameters decrease as the number of divisions increases from 10 to 50. As the number of substractions declines from 720 to 620, the estimates for slightly decrease, while those increase sharply for .
- (4)
- The average lengths of interval estimates of is larger for males than those for females. However, interval estimates of are the opposite.
- (5)
- The ALs of boot-p, boot-t, and HPD credible intervals are all shorter than ALs of asymptotic confidence intervals. Among them, boot-t intervals have the shortest ALs.
- (6)
- For parameter , ALs become smaller as the number of divisions increases from 10 to 50. The rising number of substractions also leads to a decrease in ALs. However, the interval estimates have no apparent connection with different truncation and censoring schemes for parameter .
- (7)
- Expectations and variances of the distribution have slight differences due to different subtraction types.
- (8)
- The approximate average lifespan of males is 1079 (months), and the approximate average lifespan for females is (months). The distribution variances are more significant for males than for females, indicating that the lifespan lengths of females are more concentrated than males.
7. Conclusions
The paper investigates both classical and Bayesian inference of the exponentiated half-logistic parameters based on left-truncated and right-censored data. Point estimations are discussed using the maximum likelihood method. Two loss functions, SELF and LLF, are considered for Bayesian estimation. Tierney–Kadane’s approximation and importance sampling are employed to compute the value. Meanwhile, confidence and credible intervals of unknown parameters are also established. Asymptotic confidence intervals are constructed with the help of the observed Fisher information matrix. Bootstrap methods are applied to handle the problem of small sample sizes. The HPD credible intervals are established using the importance sampling procedure.
Two data sets, a simulated one and a real one, are analyzed to show the performance of different methods. Mean squared error and estimation value are obtained to show the performance of point estimation. For interval estimation, mean length and coverage rate are calculated. As for simulation results, Bayesian estimates with suitable informative priors overperform MLEs. Furthermore, the results gained by the importance sampling procedure are better than those gained by TK approximation. Bayesian estimates under LLF perform better than SELF for , and the difference between different loss functions for is not apparent. Regarding interval estimates, boot-p, boot-t, and HPD credible intervals make more sense than asymptotic confidence intervals. Informative HPD credible intervals have the shortest mean lengths, while boot-t intervals have the largest coverage rates. Among all of the interval estimates, boot-t intervals perform the best.
In reality, the parameter estimation of exponentiated half-logistic distribution for left-truncated and right-censored data is practical for survival analysis. For future research, competing risks can be combined with the model. Furthermore, more flexible truncation and censoring schemes can also be explored.
Author Contributions
Investigation, X.S. and Z.X.; Supervision, W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Project 202210004001 which was supported by National Training Program of Innovation and Entrepreneurship for Undergraduates. Wenhao’s work was partially supported by the Fund of China Academy of Railway Sciences Corporation Limited (No. 2020YJ120).
Data Availability Statement
The data presented in this study are openly available in R software (the `channing’ data frame in package ‘boot’ [20]).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Results of Bayesian Estimates Based on Simulated Data Set

Table A1.
The results of non-informative Bayesian estimates for using TK approximation and importance sampling.
Table A1.
The results of non-informative Bayesian estimates for using TK approximation and importance sampling.
| n | Trunc.p | Method | SELF | LLF | ||||
|---|---|---|---|---|---|---|---|---|
| s = 0.5 | s = 1 | |||||||
| VALUE | MSE | VALUE | MSE | VALUE | MSE | |||
| censored at 1998 | ||||||||
| 80 | 10 | TK | 5.1237 | 0.3908 | 5.0310 | 0.3380 | 4.9506 | 0.3104 |
| Importance sampling | 5.0766 | 0.3346 | 5.0428 | 0.3501 | 5.0144 | 0.3547 | ||
| 30 | TK | 5.2744 | 0.4886 | 5.1696 | 0.3967 | 5.0797 | 0.3407 | |
| Importance sampling | 5.0433 | 0.3591 | 5.0060 | 0.3619 | 4.9748 | 0.3810 | ||
| 100 | 10 | TK | 5.1435 | 0.3373 | 5.0689 | 0.2947 | 5.0024 | 0.2688 |
| Importance sampling | 5.0990 | 0.3283 | 5.0764 | 0.3210 | 5.0571 | 0.3189 | ||
| 30 | TK | 5.2288 | 0.3607 | 5.1478 | 0.3033 | 5.0761 | 0.2661 | |
| Importance sampling | 5.1195 | 0.3195 | 5.0956 | 0.3026 | 5.0753 | 0.2957 | ||
| 120 | 10 | TK | 5.1129 | 0.2483 | 5.0523 | 0.2223 | 4.9972 | 0.2063 |
| Importance sampling | 5.2318 | 0.2518 | 5.2159 | 0.2409 | 5.2019 | 0.2489 | ||
| 30 | TK | 5.2154 | 0.2984 | 5.1489 | 0.2563 | 5.0889 | 0.2273 | |
| Importance sampling | 5.1845 | 0.2478 | 5.1674 | 0.2417 | 5.1525 | 0.2491 | ||
| censored at 2002 | ||||||||
| 80 | 10 | TK | 5.0847 | 0.3190 | 5.0038 | 0.2862 | 4.9321 | 0.2704 |
| Importance sampling | 5.4596 | 0.3241 | 5.4439 | 0.3178 | 5.4307 | 0.2948 | ||
| 30 | TK | 5.1773 | 0.3606 | 5.0879 | 0.3065 | 5.0094 | 0.2754 | |
| Importance sampling | 5.3999 | 0.3409 | 5.3814 | 0.3226 | 5.3659 | 0.3082 | ||
| 100 | 10 | TK | 5.0702 | 0.2331 | 5.0063 | 0.2131 | 4.9484 | 0.2031 |
| Importance sampling | 5.5900 | 0.2691 | 5.5809 | 0.2418 | 5.5731 | 0.2405 | ||
| 30 | TK | 5.1811 | 0.3077 | 5.1100 | 0.2672 | 5.0460 | 0.2411 | |
| Importance sampling | 5.5086 | 0.2716 | 5.4971 | 0.2616 | 5.4874 | 0.2606 | ||
| 120 | 10 | TK | 5.0537 | 0.2014 | 5.0014 | 0.1877 | 4.9532 | 0.1805 |
| Importance sampling | 5.7301 | 0.1780 | 5.7241 | 0.1937 | 5.7188 | 0.1964 | ||
| 30 | TK | 5.1637 | 0.2379 | 5.1056 | 0.2099 | 5.0524 | 0.1911 | |
| Importance sampling | 5.6487 | 0.2080 | 5.6416 | 0.2104 | 5.6355 | 0.2297 | ||

Table A2.
The results of non-informative Bayesian estimates for using TK approximation and importance sampling.
Table A2.
The results of non-informative Bayesian estimates for using TK approximation and importance sampling.
| n | Trunc.p | Method | SELF | LLF | ||||
|---|---|---|---|---|---|---|---|---|
| s = 0.5 | s = 1 | |||||||
| VALUE | MSE | VALUE | MSE | VALUE | MSE | |||
| censored at 1998 | ||||||||
| 80 | 10 | TK | 1.8331 | 0.1383 | 1.8065 | 0.1398 | 1.7815 | 0.1431 |
| Importance sampling | 1.7091 | 0.1213 | 1.7009 | 0.1259 | 1.6924 | 0.1308 | ||
| 30 | TK | 1.5525 | 0.2733 | 1.5316 | 0.2878 | 1.5118 | 0.3025 | |
| Importance sampling | 1.5524 | 0.2546 | 1.5424 | 0.2634 | 1.5322 | 0.2725 | ||
| 100 | 10 | TK | 1.7936 | 0.1212 | 1.7735 | 0.1256 | 1.7544 | 0.1307 |
| Importance sampling | 1.5285 | 0.1184 | 1.5217 | 0.1246 | 1.5149 | 0.1311 | ||
| 30 | TK | 1.5469 | 0.2639 | 1.5304 | 0.2761 | 1.5146 | 0.2884 | |
| Importance sampling | 1.5134 | 0.2616 | 1.5066 | 0.2682 | 1.4996 | 0.2750 | ||
| 120 | 10 | TK | 1.7822 | 0.1082 | 1.7658 | 0.1129 | 1.7501 | 0.1180 |
| Importance sampling | 1.6107 | 0.1183 | 1.6073 | 0.1109 | 1.6038 | 0.1136 | ||
| 30 | TK | 1.5359 | 0.2588 | 1.5225 | 0.2696 | 1.5096 | 0.2804 | |
| Importance sampling | 1.4771 | 0.2423 | 1.4721 | 0.2476 | 1.4669 | 0.2730 | ||
| censored at 2002 | ||||||||
| 80 | 10 | TK | 1.8327 | 0.1246 | 1.8075 | 0.1268 | 1.7838 | 0.1305 |
| Importance sampling | 1.5791 | 0.1247 | 1.5734 | 0.1395 | 1.5674 | 0.1344 | ||
| 30 | TK | 1.5747 | 0.2470 | 1.5542 | 0.2608 | 1.5347 | 0.2750 | |
| Importance sampling | 1.4516 | 0.2483 | 1.4447 | 0.2657 | 1.4376 | 0.2733 | ||
| 100 | 10 | TK | 1.8013 | 0.1112 | 1.7821 | 0.1153 | 1.7638 | 0.1201 |
| Importance sampling | 1.5466 | 0.1080 | 1.5429 | 0.1114 | 1.5392 | 0.1148 | ||
| 30 | TK | 1.5487 | 0.2619 | 1.5330 | 0.2735 | 1.5178 | 0.2852 | |
| Importance sampling | 1.4279 | 0.2599 | 1.4228 | 0.2657 | 1.4177 | 0.2715 | ||
| 120 | 10 | TK | 1.8110 | 0.0892 | 1.7950 | 0.0932 | 1.7795 | 0.0978 |
| Importance sampling | 1.4952 | 0.0810 | 1.4925 | 0.0887 | 1.4898 | 0.1065 | ||
| 30 | TK | 1.5557 | 0.2432 | 1.5425 | 0.2532 | 1.5298 | 0.2633 | |
| Importance sampling | 1.3931 | 0.2559 | 1.3898 | 0.2598 | 1.3865 | 0.2639 | ||

Table A3.
The results of informative Bayesian estimates for using TK approximation and importance sampling.
Table A3.
The results of informative Bayesian estimates for using TK approximation and importance sampling.
| n | Trunc.p | Method | SELF | LLF | ||||
|---|---|---|---|---|---|---|---|---|
| s = 0.5 | s = 1 | |||||||
| VALUE | MSE | VALUE | MSE | VALUE | MSE | |||
| censored at 1998 | ||||||||
| 80 | 10 | TK | 5.0933 | 0.3426 | 5.0023 | 0.3000 | 4.9255 | 0.2800 |
| Importance sampling | 4.8494 | 0.0896 | 4.8317 | 0.0931 | 4.8155 | 0.0969 | ||
| 30 | TK | 5.2073 | 0.4247 | 5.1083 | 0.3525 | 5.0243 | 0.3101 | |
| Importance sampling | 4.7967 | 0.1112 | 4.7805 | 0.1163 | 4.7659 | 0.1216 | ||
| 100 | 10 | TK | 5.0933 | 0.2886 | 5.0218 | 0.2544 | 4.9602 | 0.2345 |
| Importance sampling | 5.2850 | 0.1499 | 5.2718 | 0.1416 | 5.2599 | 0.1344 | ||
| 30 | TK | 5.1708 | 0.3032 | 5.0924 | 0.2591 | 5.0253 | 0.2168 | |
| Importance sampling | 5.2452 | 0.1268 | 5.2329 | 0.1201 | 5.2219 | 0.1145 | ||
| 120 | 10 | TK | 5.0983 | 0.2331 | 5.0385 | 0.2109 | 4.9872 | 0.1947 |
| Importance sampling | 5.1783 | 0.1261 | 5.1658 | 0.1198 | 5.1547 | 0.1147 | ||
| 30 | TK | 5.1636 | 0.2430 | 5.0987 | 0.2110 | 5.0431 | 0.1896 | |
| Importance sampling | 5.0976 | 0.0958 | 5.0847 | 0.0917 | 5.0733 | 0.0885 | ||
| censored at 2002 | ||||||||
| 80 | 10 | TK | 5.0630 | 0.3023 | 4.9826 | 0.2742 | 4.9158 | 0.2615 |
| Importance sampling | 5.1148 | 0.0976 | 5.1070 | 0.0955 | 5.1001 | 0.0937 | ||
| 30 | TK | 5.1418 | 0.3164 | 5.0565 | 0.2721 | 4.9812 | 0.2506 | |
| Importance sampling | 5.0316 | 0.0871 | 5.0230 | 0.0863 | 5.0153 | 0.0858 | ||
| 100 | 10 | TK | 5.0844 | 0.2260 | 5.0237 | 0.2081 | 4.9662 | 0.1990 |
| Importance sampling | 5.2561 | 0.1509 | 5.2511 | 0.1479 | 5.2466 | 0.1453 | ||
| 30 | TK | 5.1311 | 0.2581 | 5.0615 | 0.2288 | 5.0010 | 0.2104 | |
| Importance sampling | 5.2013 | 0.1217 | 5.1965 | 0.1194 | 5.1922 | 0.1173 | ||
| 120 | 10 | TK | 5.0244 | 0.1833 | 4.9726 | 0.1740 | 4.9271 | 0.1699 |
| Importance sampling | 5.1305 | 0.0945 | 5.1274 | 0.0936 | 5.1246 | 0.0928 | ||
| 30 | TK | 5.1270 | 0.2074 | 5.0710 | 0.1862 | 5.0203 | 0.1716 | |
| Importance sampling | 5.0651 | 0.0781 | 5.0619 | 0.0776 | 5.0590 | 0.0771 | ||

Table A4.
The results of informative Bayesian estimates for using TK approximation and importance sampling.
Table A4.
The results of informative Bayesian estimates for using TK approximation and importance sampling.
| n | Trunc.p | Method | SELF | LLF | ||||
|---|---|---|---|---|---|---|---|---|
| s = 0.5 | s = 1 | |||||||
| VALUE | MSE | VALUE | MSE | VALUE | MSE | |||
| censored at 1998 | ||||||||
| 80 | 10 | TK | 1.8272 | 0.1201 | 1.7997 | 0.1234 | 1.7759 | 0.1279 |
| Importance sampling | 1.8788 | 0.0326 | 1.8728 | 0.0339 | 1.8666 | 0.0352 | ||
| 30 | TK | 1.5725 | 0.2532 | 1.5517 | 0.2638 | 1.5331 | 0.2757 | |
| Importance sampling | 1.7702 | 0.0691 | 1.7640 | 0.0718 | 1.7577 | 0.0745 | ||
| 100 | 10 | TK | 1.8053 | 0.1111 | 1.7827 | 0.1187 | 1.7641 | 0.1210 |
| Importance sampling | 1.7319 | 0.0867 | 1.7282 | 0.0886 | 1.7243 | 0.0905 | ||
| 30 | TK | 1.5687 | 0.2396 | 1.5492 | 0.2502 | 1.5357 | 0.2614 | |
| Importance sampling | 1.6337 | 0.1482 | 1.6295 | 0.1512 | 1.6253 | 0.1541 | ||
| 120 | 10 | TK | 1.7895 | 0.1023 | 1.7707 | 0.1057 | 1.7562 | 0.1095 |
| Importance sampling | 1.6605 | 0.1312 | 1.6573 | 0.1333 | 1.6541 | 0.1355 | ||
| 30 | TK | 1.5620 | 0.2373 | 1.5482 | 0.2461 | 1.5360 | 0.2553 | |
| Importance sampling | 1.5398 | 0.2316 | 1.5355 | 0.2354 | 1.5311 | 0.2394 | ||
| censored at 2002 | ||||||||
| 80 | 10 | TK | 1.8243 | 0.1171 | 1.7997 | 0.1205 | 1.7766 | 0.1249 |
| Importance sampling | 1.8066 | 0.0585 | 1.8021 | 0.0601 | 1.7976 | 0.0618 | ||
| 30 | TK | 1.5877 | 0.2390 | 1.5663 | 0.2537 | 1.5419 | 0.2591 | |
| Importance sampling | 1.6949 | 0.1154 | 1.6900 | 0.1183 | 1.6850 | 0.1212 | ||
| 100 | 10 | TK | 1.8101 | 0.1043 | 1.7918 | 0.1080 | 1.7736 | 0.1124 |
| Importance sampling | 1.7339 | 0.0878 | 1.7308 | 0.0894 | 1.7276 | 0.0911 | ||
| 30 | TK | 1.5871 | 0.2273 | 1.5695 | 0.2365 | 1.5546 | 0.2470 | |
| Importance sampling | 1.6360 | 0.1481 | 1.6325 | 0.1506 | 1.6290 | 0.1532 | ||
| 120 | 10 | TK | 1.8104 | 0.0887 | 1.7926 | 0.0921 | 1.7784 | 0.0962 |
| Importance sampling | 1.7429 | 0.0846 | 1.7402 | 0.0859 | 1.7374 | 0.0872 | ||
| 30 | TK | 1.5628 | 0.2344 | 1.5501 | 0.2426 | 1.5381 | 0.2521 | |
| Importance sampling | 1.6406 | 0.1478 | 1.6372 | 0.1502 | 1.6338 | 0.1526 | ||
Appendix B. The Results of Interval Estimates Based on Simulated Data Set

Table A5.
The simulation results of five intervals for at confidence/credible level.
Table A5.
The simulation results of five intervals for at confidence/credible level.
| n | Trunc.p | ACI | Bootstrap | HPD | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| boot-p | boot-t | Non-Info | Informative | ||||||||
| AL | CR | AL | CR | AL | CR | AL | CR | AL | CR | ||
| censored at 1998 | |||||||||||
| 80 | 10 | 1.9175 | 0.9112 | 1.8633 | 0.9116 | 1.9125 | 0.9436 | 1.9133 | 0.9140 | 1.8384 | 0.8612 |
| 30 | 2.0034 | 0.9211 | 1.8472 | 0.9285 | 1.9949 | 0.9317 | 2.0049 | 0.9237 | 1.9139 | 0.9042 | |
| 100 | 10 | 1.7184 | 0.9075 | 1.6645 | 0.9155 | 1.7167 | 0.9071 | 1.7179 | 0.9044 | 1.6599 | 0.8577 |
| 30 | 1.7905 | 0.9264 | 1.6537 | 0.9270 | 1.7848 | 0.9543 | 1.7898 | 0.9232 | 1.5698 | 0.8962 | |
| 120 | 10 | 1.5791 | 0.9073 | 1.5157 | 0.9092 | 1.5617 | 0.9343 | 1.5788 | 0.9054 | 1.4818 | 0.8722 |
| 30 | 1.6395 | 0.9249 | 1.5029 | 0.9253 | 1.6284 | 0.9407 | 1.6356 | 0.9250 | 1.4977 | 0.9149 | |
| censored at 2002 | |||||||||||
| 80 | 10 | 1.8040 | 0.9101 | 1.7546 | 0.9108 | 1.7906 | 0.9131 | 1.8019 | 0.9114 | 1.7286 | 0.8735 |
| 30 | 1.8835 | 0.9192 | 1.7626 | 0.9261 | 1.8648 | 0.9373 | 1.8785 | 0.9214 | 1.6254 | 0.8929 | |
| 100 | 10 | 1.6106 | 0.9020 | 1.5616 | 0.9068 | 1.6063 | 0.9137 | 1.6153 | 0.9017 | 1.5167 | 0.8992 |
| 30 | 1.6794 | 0.9074 | 1.5642 | 0.9108 | 1.6604 | 0.9222 | 1.6794 | 0.9044 | 1.5498 | 0.8749 | |
| 120 | 10 | 1.4767 | 0.9109 | 1.4306 | 0.9160 | 1.4679 | 0.9131 | 1.4760 | 0.9117 | 1.4256 | 0.8793 |
| 30 | 1.5469 | 0.9107 | 1.4399 | 0.9144 | 1.5408 | 0.9288 | 1.5518 | 0.9136 | 1.4064 | 0.8701 | |

Table A6.
The simulation results of five intervals for at confidence/credible level.
Table A6.
The simulation results of five intervals for at confidence/credible level.
| n | Trunc.p | ACI | Bootstrap | HPD | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| boot-p | boot-t | Non-Info | Informative | ||||||||
| AL | CR | AL | CR | AL | CR | AL | CR | AL | CR | ||
| censored at 1998 | |||||||||||
| 80 | 10 | 1.0264 | 0.7718 | 1.0773 | 0.7775 | 1.0177 | 0.7823 | 1.0285 | 0.7688 | 0.9299 | 0.7597 |
| 30 | 0.9375 | 0.6673 | 1.1971 | 0.6696 | 0.9198 | 0.6938 | 0.9328 | 0.6659 | 0.9062 | 0.6328 | |
| 100 | 10 | 0.9058 | 0.7344 | 0.9508 | 0.7415 | 0.9047 | 0.7425 | 0.9087 | 0.7351 | 0.8167 | 0.7087 |
| 30 | 1.0756 | 0.7181 | 1.0582 | 0.7238 | 1.0680 | 0.7331 | 1.0774 | 0.7175 | 1.0496 | 0.6770 | |
| 120 | 10 | 0.8209 | 0.6994 | 0.8569 | 0.7073 | 0.8036 | 0.7267 | 0.8250 | 0.7012 | 0.7465 | 0.6526 |
| 30 | 0.7481 | 0.6169 | 0.7124 | 0.6248 | 0.7359 | 0.6242 | 0.7474 | 0.6148 | 0.6945 | 0.6033 | |
| censored at 2002 | |||||||||||
| 80 | 10 | 1.0166 | 0.7794 | 1.0385 | 0.7797 | 1.0073 | 0.7959 | 1.0193 | 0.7813 | 0.9837 | 0.7775 |
| 30 | 0.9169 | 0.6732 | 1.0983 | 0.6811 | 0.8988 | 0.6998 | 0.9199 | 0.6732 | 0.8701 | 0.6291 | |
| 100 | 10 | 0.8959 | 0.7356 | 0.9700 | 0.7442 | 0.8802 | 0.7529 | 0.8910 | 0.7351 | 0.8584 | 0.7275 |
| 30 | 0.8226 | 0.7192 | 0.9127 | 0.7263 | 0.8109 | 0.7267 | 0.8204 | 0.7211 | 0.7577 | 0.6966 | |
| 120 | 10 | 0.8143 | 0.7206 | 0.8237 | 0.7294 | 0.8137 | 0.7337 | 0.8119 | 0.7237 | 0.7906 | 0.6766 |
| 30 | 0.7415 | 0.6728 | 0.8677 | 0.6776 | 0.7222 | 0.6826 | 0.7438 | 0.6746 | 0.6419 | 0.6585 | |
Appendix C. The Estimation Results Based on Real Data Set

Table A7.
The results of MLEs for and .
Table A7.
The results of MLEs for and .
| Substraction Type | Division Type | Male | Female | ||
|---|---|---|---|---|---|
| I | i | 12.4113 | 5.0859 | 10.6868 | 8.9206 |
| ii | 4.1380 | 5.0832 | 3.5622 | 8.9206 | |
| iii | 2.4822 | 5.0859 | 2.1373 | 8.9206 | |
| II | i | 12.0584 | 12.6146 | 10.5961 | 23.5695 |
| ii | 4.0194 | 12.6146 | 3.5320 | 23.5693 | |
| iii | 2.4116 | 12.6145 | 2.1192 | 23.5692 | |

Table A8.
The results of Bayesian estimates for using TK approximation and importance sampling.
Table A8.
The results of Bayesian estimates for using TK approximation and importance sampling.
| Substraction Type | Division Type | Method | Male | Female | ||||
|---|---|---|---|---|---|---|---|---|
| SELF | LLF | SELF | LLF | |||||
| s = 0.5 | s = 1 | s = 0.5 | s = 1 | |||||
| I | i | TK | 12.5600 | 12.1079 | 11.7509 | 10.7044 | 10.5934 | 10.4898 |
| Importance sampling | 12.1078 | 12.0853 | 12.0654 | 10.4471 | 10.4455 | 10.4439 | ||
| ii | TK | 4.1867 | 4.1310 | 4.0815 | 3.5682 | 3.5555 | 3.5431 | |
| Importance sampling | 4.0531 | 4.0505 | 4.0481 | 3.4804 | 3.4802 | 3.4800 | ||
| iii | TK | 2.5120 | 2.4912 | 2.4724 | 2.1409 | 2.1363 | 2.1318 | |
| Importance sampling | 2.4291 | 2.4281 | 2.4272 | 2.0880 | 2.0879 | 2.0879 | ||
| II | i | TK | 12.0646 | 11.6936 | 11.3897 | 10.5721 | 10.4703 | 10.3745 |
| Importance sampling | 12.2527 | 12.2487 | 12.2453 | 10.0916 | 10.0909 | 10.0902 | ||
| ii | TK | 4.0216 | 3.9769 | 3.9361 | 3.5242 | 3.5125 | 3.5012 | |
| Importance sampling | 4.0862 | 4.0858 | 4.0854 | 3.3661 | 3.3660 | 3.3660 | ||
| iii | TK | 2.4129 | 2.3965 | 2.3811 | 2.1145 | 2.1103 | 2.1061 | |
| Importance sampling | 2.4610 | 2.4608 | 2.4607 | 2.0197 | 2.0196 | 2.0196 | ||

Table A9.
The results of Bayesian estimates for using TK approximation and importance sampling.
Table A9.
The results of Bayesian estimates for using TK approximation and importance sampling.
| Substraction Type | Division Type | Method | Male | Female | ||||
|---|---|---|---|---|---|---|---|---|
| SELF | LLF | SELF | LLF | |||||
| s = 0.5 | s = 1 | s = 0.5 | s = 1 | |||||
| I | i | TK | 5.2321 | 4.9233 | 4.6730 | 9.0788 | 8.6490 | 8.2902 |
| Importance sampling | 5.1161 | 5.1096 | 5.1023 | 8.4163 | 8.4150 | 8.4138 | ||
| ii | TK | 5.2323 | 4.9232 | 4.6730 | 9.0781 | 8.6490 | 8.2902 | |
| Importance sampling | 5.0783 | 5.0720 | 5.0649 | 8.4251 | 8.4239 | 8.4226 | ||
| iii | TK | 5.2323 | 4.9233 | 4.6730 | 9.0783 | 8.6490 | 8.2902 | |
| Importance sampling | 5.0626 | 5.0561 | 5.0489 | 8.4335 | 8.4323 | 8.4310 | ||
| II | i | TK | 13.5821 | 10.8797 | 9.4551 | 24.5404 | 20.2862 | 17.8998 |
| Importance sampling | 12.3958 | 12.3612 | 12.3200 | 23.7676 | 23.7580 | 23.7470 | ||
| ii | TK | 13.5810 | 10.8796 | 9.4550 | 24.5401 | 20.2862 | 17.8999 | |
| Importance sampling | 12.3872 | 12.3534 | 12.3125 | 23.7005 | 23.6914 | 23.6809 | ||
| iii | TK | 13.5805 | 10.8793 | 9.4539 | 24.5404 | 20.2862 | 17.8999 | |
| Importance sampling | 12.3609 | 12.3243 | 12.2795 | 23.7410 | 23.7321 | 23.7219 | ||

Table A10.
The results of four intervals for at confidence/credible level.
Table A10.
The results of four intervals for at confidence/credible level.
| Subtraction Type | Division Type | ACI | Bootstrap | HPD | |||||
|---|---|---|---|---|---|---|---|---|---|
| boot-p | boot-t | ||||||||
| Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | ||
| Male | |||||||||
| I | i | 10.1601 | 14.6626 | 10.1634 | 14.6965 | 10.1668 | 14.6530 | 10.1643 | 14.6666 |
| ii | 3.3867 | 4.8875 | 3.3902 | 4.9091 | 3.4018 | 4.8726 | 3.3869 | 4.8794 | |
| iii | 2.0320 | 2.9325 | 2.0363 | 2.9679 | 2.0424 | 2.9206 | 2.0368 | 2.9269 | |
| II | i | 9.9908 | 14.1260 | 9.9906 | 14.1410 | 9.9939 | 14.1167 | 10.0004 | 14.1241 |
| ii | 3.3303 | 4.7087 | 3.3312 | 4.7272 | 3.3363 | 4.6997 | 3.3400 | 4.7118 | |
| iii | 1.9982 | 2.8252 | 2.0042 | 2.8593 | 2.0055 | 2.8137 | 2.0059 | 2.8238 | |
| Female | |||||||||
| I | i | 9.5815 | 11.7921 | 9.5777 | 11.7956 | 9.5999 | 11.7726 | 9.5908 | 11.7860 |
| ii | 3.1938 | 3.9307 | 3.1989 | 3.9677 | 3.2147 | 3.9251 | 3.2051 | 3.9276 | |
| iii | 1.9163 | 2.3584 | 1.9117 | 2.3977 | 1.9312 | 2.3474 | 1.9262 | 2.3597 | |
| II | i | 9.5308 | 11.6615 | 9.5293 | 11.7048 | 9.5432 | 11.6419 | 9.5371 | 11.6565 |
| ii | 3.1769 | 3.8872 | 3.1749 | 3.9281 | 3.1936 | 3.8762 | 3.1830 | 3.8794 | |
| iii | 1.9062 | 2.3323 | 1.9028 | 2.3683 | 1.9142 | 2.3271 | 1.9168 | 2.3242 | |

Table A11.
The results of four intervals for at confidence/credible level.
Table A11.
The results of four intervals for at confidence/credible level.
| Subtraction Type | Division Type | ACI | Bootstrap | HPD | |||||
|---|---|---|---|---|---|---|---|---|---|
| boot-p | boot-t | ||||||||
| Lower | Upper | Lower | Upper | Lower | Upper | Lower | Upper | ||
| Male | |||||||||
| I | i | 3.2317 | 6.9401 | 3.2272 | 6.9843 | 3.2513 | 6.9321 | 3.2383 | 6.9350 |
| ii | 3.2319 | 6.9401 | 3.2312 | 6.9803 | 3.2421 | 6.9335 | 3.2337 | 6.9354 | |
| iii | 3.2319 | 6.9401 | 3.2354 | 6.9563 | 3.2511 | 6.9327 | 3.2356 | 6.9452 | |
| II | i | 6.5424 | 18.6869 | 6.5416 | 18.7190 | 6.5541 | 18.6863 | 6.5540 | 18.6902 |
| ii | 6.5423 | 18.6870 | 6.5430 | 18.7159 | 6.5605 | 18.6777 | 6.5429 | 18.6886 | |
| iii | 6.5424 | 18.6868 | 6.5439 | 18.6946 | 6.5623 | 18.6776 | 6.5525 | 18.6869 | |
| Female | |||||||||
| I | i | 6.7172 | 11.1242 | 6.7231 | 11.1330 | 6.7406 | 11.1159 | 6.7222 | 11.1282 |
| ii | 6.7172 | 11.1242 | 6.7206 | 11.1567 | 6.7418 | 11.1055 | 6.7187 | 11.1286 | |
| iii | 6.7172 | 11.1242 | 6.7131 | 11.1314 | 6.7182 | 11.1175 | 6.7228 | 11.1325 | |
| II | i | 15.7819 | 31.3572 | 15.7838 | 31.3858 | 15.8027 | 31.3522 | 15.7925 | 31.3622 |
| ii | 15.7819 | 31.3569 | 15.7847 | 31.3579 | 15.7874 | 31.3424 | 15.7884 | 31.3522 | |
| iii | 15.7818 | 31.3567 | 15.7796 | 31.3721 | 15.8064 | 31.3411 | 15.7896 | 31.3637 | |

Table A12.
The expectations and variances of EHL distributions obtained by MLEs in Table A7.
Table A12.
The expectations and variances of EHL distributions obtained by MLEs in Table A7.
| Substraction Type | Division Type | Male | Female | ||
|---|---|---|---|---|---|
| I | i | 1080.2536 | 154,839.6810 | 1089.7549 | 18,721.4480 |
| ii | 1080.2724 | 154,857.3300 | 1089.7551 | 18,721.4760 | |
| iii | 1080.2532 | 154,831.9750 | 1089.7551 | 18,721.4925 | |
| II | i | 1078.8222 | 234,413.5690 | 1089.2238 | 18,524.9650 |
| ii | 1078.8227 | 234,413.9550 | 1089.2240 | 18,525.0240 | |
| iii | 1078.8225 | 234,413.9075 | 1089.2240 | 18,525.0675 | |
References
- Kang, S.B.; Seo, J.I. Estimation in an Exponentiated Half Logistic Distribution under Progressively Type-II Censoring. J. Korean Data Inf. Sci. Soc. 2011, 18, 5253–5261. [Google Scholar] [CrossRef]
- Rastogi, M.K.; Tripathi, Y.M. Parameter and reliability estimation for an exponentiated half-logistic distribution under progressive Type-II censoring. J. Stat. Comput. Simul. 2014, 84, 1711–1727. [Google Scholar] [CrossRef]
- Gadde, S.R.; Ch, R.N. An Exponentiated Half Logistic Distribution to Develop a Group Acceptance Sampling Plans with Truncated Time. J. Stat. Manag. Syst. 2015, 18, 519–531. [Google Scholar]
- Seo, J.I.; Kang, S.B. Notes on the exponentiated half logistic distribution. Appl. Math. Model. 2015, 39, 6491–6500. [Google Scholar] [CrossRef]
- Gui, W. Exponentiated half logistic distribution: Different estimation methods and joint confidence regions. Commun. Stat. Simul. Comput. 2017, 46, 4600–4617. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Asgharzadeh, A. Inference for the Scaled Half-Logistic Distribution Based on Progressively Type-II Censored Samples. Commun. Stat. Theory Methods 2005, 34, 73–87. [Google Scholar] [CrossRef]
- Giles, D.E. Bias Reduction for the Maximum Likelihood Estimators of the Parameters in the Half-Logistic Distribution. Commun. Stat. Theory Methods 2012, 41, 212–222. [Google Scholar] [CrossRef]
- Wang, B. Interval Estimation for the Scaled Half-Logistic Distribution Under Progressive Type-II Censoring. Commun. Stat. Theory Methods 2008, 38, 364–371. [Google Scholar] [CrossRef]
- Rosaiah, K.; Kantam, R.; Rao, B.S. Reliability Test Plan for Half Logistic Distribution. Calcutta Stat. Assoc. Bull. 2009, 61, 183–196. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized exponential distributions. Aust. N. Z. J. Stat. 1999, 41, 173. [Google Scholar] [CrossRef]
- Hong, Y.; Meeker, W.Q.; Mccalley, J.D. Prediction of Remaining Life of Power Transformers Based on Left Truncated and Right Censored Lifetime Data. Ann. Appl. Stat. 2009, 3, 857–879. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Mitra, D. Left truncated and right censored Weibull data and likelihood inference with an illustration. Comput. Stat. Data Anal. 2012, 56, 4011–4025. [Google Scholar] [CrossRef]
- Kundu, D.; Mitra, D.; Ganguly, A. Analysis of left truncated and right censored competing risks data. Comput. Stat. Data Anal. 2016, 108, 12–26. [Google Scholar] [CrossRef]
- Kundu, D.; Mitra, D. Bayesian inference of Weibull distribution based on left truncated and right censored data. Comput. Stat. Data Anal. 2016, 99, 38–50. [Google Scholar] [CrossRef]
- Xiong, Z.; Gui, W. Classical and Bayesian Inference of an Exponentiated Half-Logistic Distribution under Adaptive Type II Progressive Censoring. Entropy 2021, 23, 1558. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Zellner, A. Bayesian estimation and prediction using asymmetric loss functions. J. Am. Stat. Assoc. 1986, 81, 446–451. [Google Scholar] [CrossRef]
- Hoa, L.; Uyen, P.; Phuong, N.; Pham, T.B. Improvement on Monte Carlo estimation of HPD intervals. Commun. Stat. Simul. Comput. 2020, 49, 2164–2180. [Google Scholar] [CrossRef]
- Chen, M.; Shao, Q. Monte Carlo Estimation of Bayesian Credible and HPD Intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar] [CrossRef]
- Canty, A.; Ripley, B.D. boot: Bootstrap R (S-Plus) Functions; R package Version 1.3-25; R Archive Network: Vienna, Austria, 2020. [Google Scholar]
- Shang, X.; Ng, H.K.T. On parameter estimation for the generalized gamma distribution based on left-truncated and right-censored data. Comput. Math. Methods 2021, 3, e1091. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).