Development of a Robust Data-Driven Soft Sensor for Multivariate Industrial Processes with Non-Gaussian Noise and Outliers
Abstract
1. Introduction
- A robust soft-sensing algorithm that integrates Huber’s M-estimation with double regularised MLP is proposed. The resistance to non-Gaussian noise and outliers in the measured data is substantially improved compared with previous algorithms;
- MIC is used to evaluate the penalty degree of the input variables and design adaptive operators for the L1-regularisation of the input layer of MLP. This adaptive mechanism makes it easier to obtain unbiased model estimates;
- The superiority of the proposed data-driven soft sensor is verified through a normal artificial dataset and its contaminated version with outliers. Then, it is utilised to predict the octane number (RON) of the S-Zorb unit in an actual gasoline treatment process. Compared with state-of-the-art methods, the proposed algorithm exhibits better accuracy and robustness.
2. Background Theories
2.1. LASSO Regularisations for MLP
2.2. Maximal Information Coefficient (MIC)
2.3. Huber’s M-Estimation
3. Proposed Methodology
3.1. Robust dLASSO-MLP with Adaptive Input Variable Selection
3.2. Design of the Adaptive Operator
3.3. Determination of Hyperparameters
- Model performance criterion: The Bayesian information criterion (BIC) is applied as the evaluation criterion for model selection among a finite model set. BIC was proposed by [36] and adopted as a measure of the trade-off between the model’s accuracy and complexity. It is given as follows:where n denotes the number of observations and the number of selected variables.
- Grid search: Compared to experiential adjustments, the grid search method performs hyperparameter tuning exhaustively within the possible hyperparameter combinations. After generating all possible combinations, it is reliable to select the best combination by means of CV. The bound domain of is [0.01,10], and the bound domain of and is [] in this study, where is set as zero and is a sufficiently large value that depends on the dimension of the dataset. Subsequently, a list consisting of every possible combination of , , and is generated. The determination of the hyperparameters includes two loops, in which the CV was taken as the inner loop. In the outer loop, each possible combination of hyperparameters was enumerated and performed using a CV procedure.
- Cross-validation: CV is considered one of the simplest and most widely used model-validation approaches. First, the given dataset D is equally divided into K subsets, one of which is considered the validation set, and the others are taken as the training set. Then, the BIC of the current validation set is evaluated using Equation (15). The procedures are repeated K times until each subset is used as the validation set exactly once. Finally, the BIC values are averaged to evaluate the performance of hyperparameter combinations. Combining the above steps, the approach for determining hyperparameter combinations is presented; its pseudocode is outlined in Algorithm 1.
Algorithm 1. Determination of and via K-fold CV. Input: dataset
Output: the optimal combination of (, , )
Begin algorithm
Generate possible combinations of (, , ) within the parameter space;
Divide the initial dataset into k disjoint subsets ;
for each possible combination
for 1: K
Take as validation set and the others as training set;
Train an initial MLP with the current training set;
Integrate robust estimation and adaptive L1-regularisation to the MLP;
Solve Equations (11) or (12) and get the magnitude coefficient ;
Obtain a new MLP model by replacing with ;
Calculate for the current parameter combination through Equation (15);
End for
CV_BIC ;
End for
Return the optimal combination of (, , ) with the minimum CV_BIC.
End algorithm
3.4. Overall Procedure of the Proposed Algorithm
- Calculate the MIC correlation index and adaptive operator using Equations (9) and (14);
- Divide the initial dataset into training and testing datasets;
- Implement Algorithm 1 and obtain the optimal hyperparameter combination of (, , );
- Train a new MLP and obtain the optimal by solving Equation (11) using and ;
- Update the input weights of the MLP and select the input variables;
- Obtain the optimal by solving Equation (12) with and ;
- Optimise the structure of the MLP with ;
- Output the simplified dataset and optimised MLP model.
4. Simulations and Results on Artificial Datasets
4.1. Model Evaluation Criteria
- Coefficient of determination (): This statistic measures the fitness between the predicted and the actual observation of y, where is the average of y:
- Mean square error (MSE): This is the MSE between the predicted and measured y, and is formulated as follows:
- Mean absolute error (MAE): This is the average absolute residual between the predicted and the actual observation of y:
4.2. Experimental Setup
4.3. Simulation Results on Artificial Dataset
4.3.1. Artificial Dataset with Normal Distribution
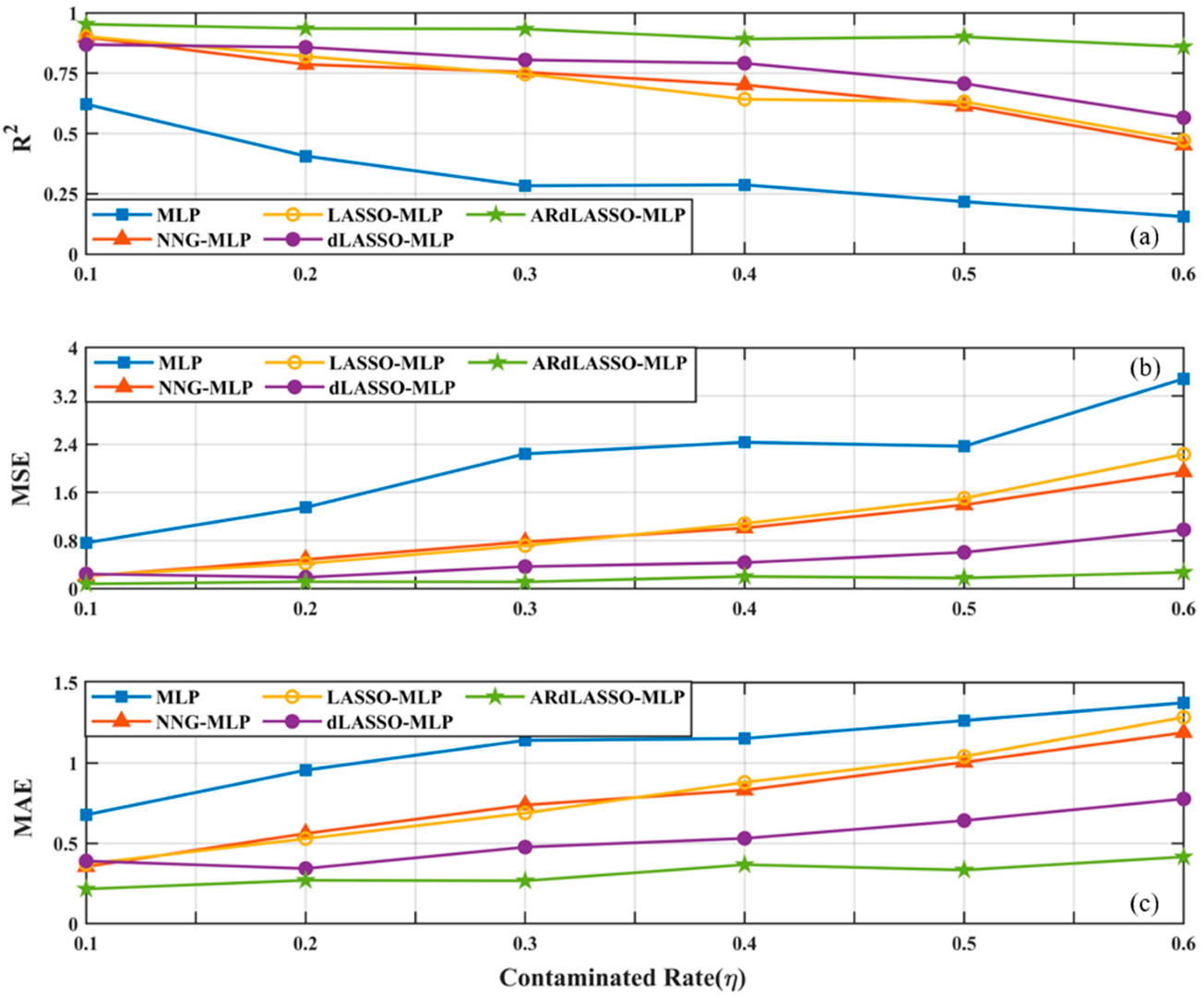
4.3.2. Artificial Dataset with Non-Gaussian Noise and Outliers
5. Application to RON Estimation in S-Zorb Plant
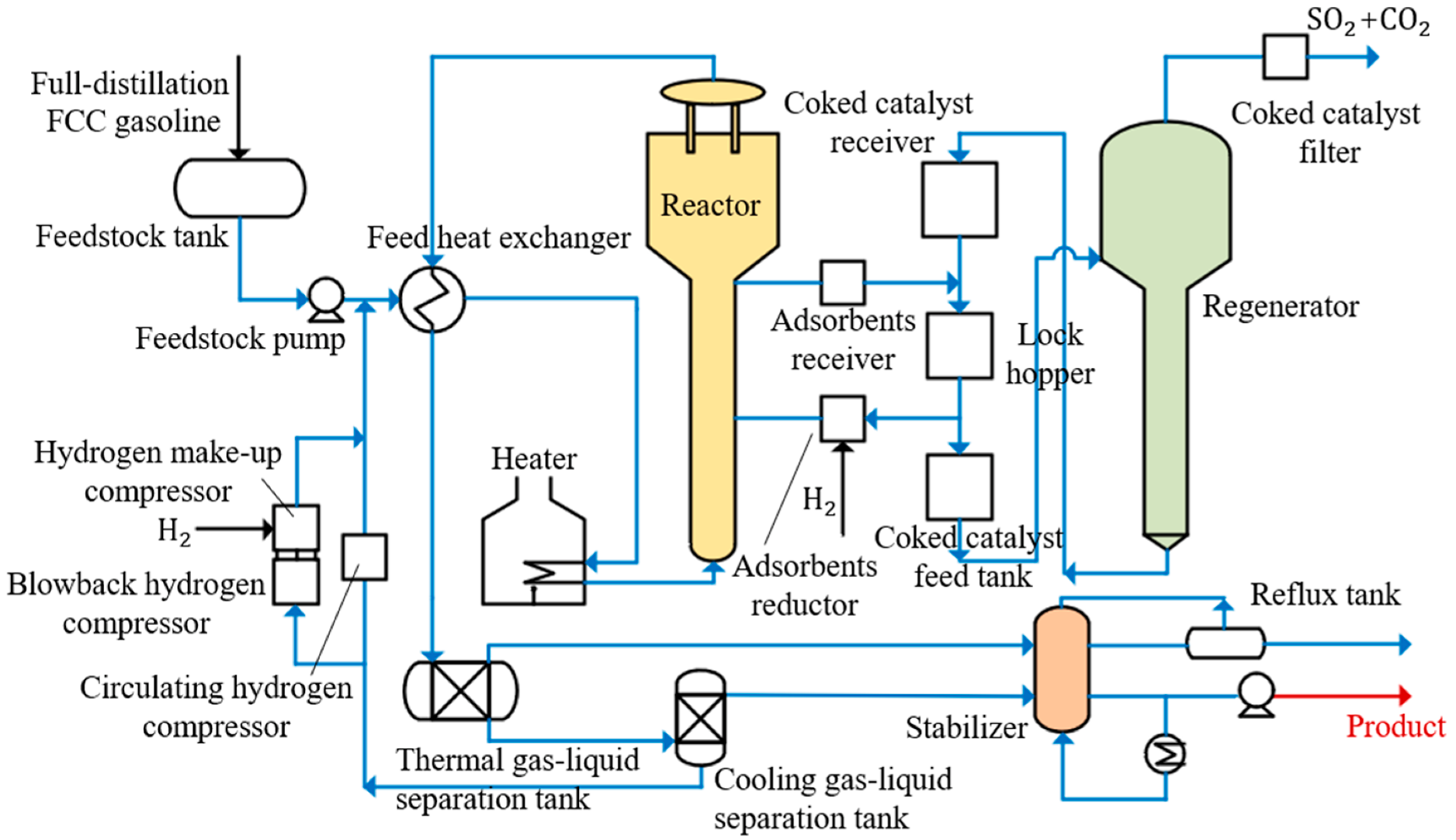
5.1. Overview of the S-Zorb Desulphurisation Plant
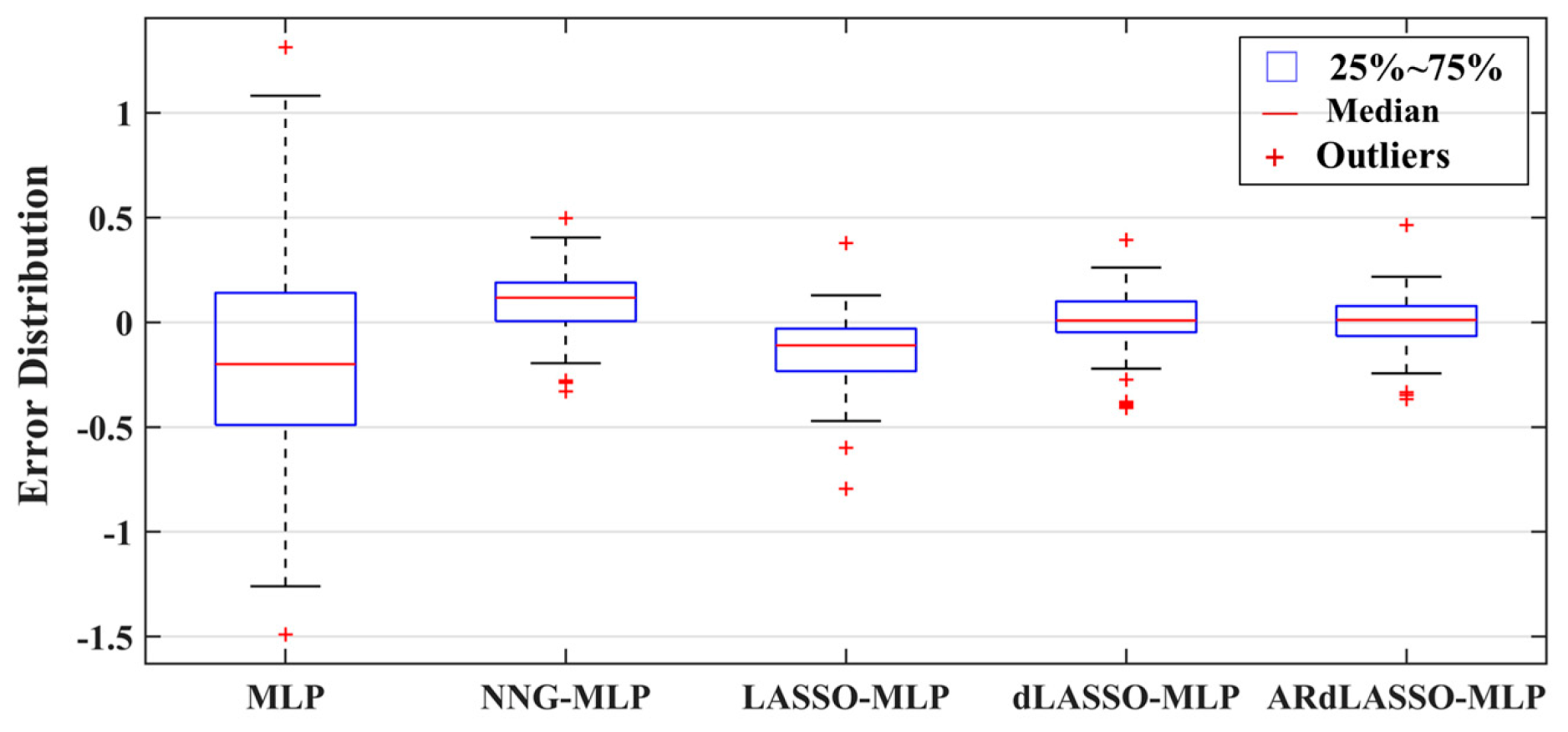
5.2. Simulations and Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Curreri, F.; Patanè, L.; Xibilia, M.G. Soft sensor transferability: A Survey. Appl. Sci. 2021, 11, 7710. [Google Scholar] [CrossRef]
- Cheng, T.; Harrou, F.; Sun, Y.; Leiknes, T. Monitoring influent measurements at water resource recovery facility using data-driven soft sensor approach. IEEE Sens. J. 2019, 19, 342–352. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Xia, Y.; Liao, Q. Bayesian aerosol retrieval-based PM2. 5 estimation through hierarchical Gaussian process models. Mathematics 2022, 10, 2878. [Google Scholar] [CrossRef]
- Muravyov, S.V.; Khudonogova, L.I.; Emelyanova, E.Y. Interval data fusion with preference aggregation. Measurement 2018, 116, 621–630. [Google Scholar] [CrossRef]
- Lu, B.; Chiang, L. Semi-supervised online soft sensor maintenance experiences in the chemical industry. J. Process Control 2018, 67, 23–34. [Google Scholar] [CrossRef]
- Song, X.; Han, D.; Sun, J.; Zhang, Z. A data-driven neural network approach to simulate pedestrian movement. Phys. A 2018, 509, 827–844. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Montes, F.; Ner, M.; Gernaey, K.V.; Sin, G. Model-based evaluation of a data-driven control strategy: Application to Ibuprofen Crystallization. Processes 2021, 9, 653. [Google Scholar] [CrossRef]
- Wang, C.C.; Chang, H.T.; Chien, C.H. Hybrid LSTM-ARMA demand-forecasting model based on error compensation for integrated circuit yray manufacturing. Mathematics 2022, 10, 2158. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, Y.; Huang, G.; Liu, L.; Hao, X. A soft sensor model based on long&short-term memory dual pathways convolutional gated recurrent unit network for predicting cement specific surface area. ISA Trans. 2022. [Google Scholar] [CrossRef]
- Lama, R.K.; Kim, J.I.; Kwon, G.R. Classification of Alzheimer’s disease based on core-large scale brain network using multilayer extreme learning machine. Mathematics. 2022, 10, 1967. [Google Scholar] [CrossRef]
- Sun, K.; Sui, L.; Wang, H.; Yu, X.; Jang, S.S. Design of an adaptive nonnegative garrote algorithm for multi-layer perceptron-based soft sensor. IEEE Sens. J. 2021, 21, 21808–21816. [Google Scholar] [CrossRef]
- Lv, J.; Tang, W.; Hosseinzadeh, H. Developed multiple-layer perceptron neural network based on developed search and rescue optimizer to predict iron ore price volatility: A case study. ISA Trans. 2022. [Google Scholar] [CrossRef]
- Saki, S.; Fatehi, A. Neural network identification in nonlinear model predictive control for frequent and infrequent operating points using nonlinearity measure. ISA Trans. 2020, 97, 216–229. [Google Scholar] [CrossRef]
- Pham, Q.B.; Afan, H.A.; Mohammadi, B.; Ahmed, A.N.; Linh, N.T.T.; Vo, N.D.; Moazenzadeh, R.; Yu, P.S. Hybrid model to improve the river streamflow forecasting utilizing multi-layer perceptron-based intelligent water drop optimization algorithm. Soft Comput. 2020, 24, 18039–18056. [Google Scholar] [CrossRef]
- Zoljalali, M.; Mohsenpour, A.; Amiri, E.O. Developing MLP-ICA and MLP algorithms for investigating flow distribution and pressure drop changes in manifold microchannels. Arab. J. Sci. Eng. 2022, 47, 6477–6488. [Google Scholar] [CrossRef]
- Min, H.; Ren, W.; Liu, X. Joint mutual information-based input variable selection for multivariate time series modeling. Eng. Appl. Artif. Intell. 2015, 37, 250–257. [Google Scholar]
- Romero, E.; Sopena, J.M. Performing feature selection with multilayer perceptrons. IEEE Trans. Neural Netw. 2008, 19, 431–441. [Google Scholar] [CrossRef]
- Sun, K.; Huang, S.H.; Wong, D.S.H.; Jang, S.S. Design and application of a variable selection method for multilayer perceptron neural network with LASSO. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1386–1396. [Google Scholar] [CrossRef]
- Sun, K.; Liu, J.; Kang, J.L.; Jang, S.S.; Wong, D.S.H.; Chen, D.S. Development of a variable selection method for soft sensor using artificial neural network and nonnegative garrote. J. Process Control 2014, 24, 1068–1075. [Google Scholar] [CrossRef]
- Muravyov, S.V.; Khudonogova, L.I.; Ho, M.D. Analysis of heteroscedastic measurement data by the self-refining method of interval fusion with preference aggregation—IF&PA. Measurement 2021, 183, 109851. [Google Scholar]
- Cui, C.H.; Wang, D.H. High dimensional data regression using Lasso model and neural networks with random weights. Inf. Sci. 2016, 372, 505–517. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wang, H.; Sui, L.; Zhang, M.; Zhang, F.; Ma, F.; Sun, K. A novel input variable selection and structure optimization algorithm for multilayer perceptron-based soft sensors. Math. Probl. Eng. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Fan, Y.; Tao, B.; Zheng, Y. A data-driven soft sensor based on multilayer perceptron neural network with a double LASSO approach. IEEE Trans. Instrum. Meas. 2019, 69, 3972–3979. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Jiang, G. Robust regression shrinkage and consistent variable selection through the LAD-LASSO. J. Bus. Econ. Stat. 2007, 25, 347–355. [Google Scholar] [CrossRef]
- De Menezes, D.Q.F.; Prata, D.M.; Secchi, A.R.; Pinto, J.C. A review on robust M-estimators for regression analysis. Comput. Chem. Eng. 2021, 147, 107254. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, J. Robust regression estimation based on low-dimensional recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5935–5946. [Google Scholar] [CrossRef]
- Wang, J.G.; Cai, X.Z.; Yao, Y.; Zhao, C.; Yang, B.H.; Ma, S.W. Statistical process fault isolation using robust nonnegative garrote. J. Taiwan Inst. Chem. Eng. 2020, 107, 24–34. [Google Scholar] [CrossRef]
- Gijbels, I.; Vrinssen, I. Robust nonnegative garrote variable selection in linear regression. Comput. Stat. Data Anal. 2015, 85, 1–22. [Google Scholar] [CrossRef]
- Zou, H. The adaptive Lasso and its oracle properties. J. Am. Stat. Assoc. 2012, 101, 1418–1429. [Google Scholar] [CrossRef]
- Alhamzawi, R.; Ali, H. The Bayesian adaptive lasso regression. Math. Biosci. 2018, 303, 75–82. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar]
- Lin, Y.J. Explaining critical clearing time with the rules extracted from a multilayer perceptron artificial neural network. Int. J. Electr. Power Energy Syst. 2010, 32, 873–878. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Schwarz, G. Estimating the dimension of a Model. Ann. Stat. 1978, 6, 461–4646. [Google Scholar] [CrossRef]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics; Kotz, S., Johnson, N.L., Eds.; Springer Science & Business Media: New York, NY, USA, 1992; pp. 492–518. [Google Scholar]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Solntsev, S.; Nocedal, J.; Byrd, R. An algorithm for quadratic ℓ1-regularized optimization with a flexible active-set strategy. Optim. Methods Softw. 2015, 30, 1213–1237. [Google Scholar] [CrossRef]
- Pukelsheim, F. The three Sigma rule. Am. Stat. 1994, 48, 88–91. [Google Scholar]
- Pham-Gia, T.; Hung, T. The mean and median absolute deviations. Math. Comput. Model. 2001, 34, 921–936. [Google Scholar] [CrossRef]





| Hyperparameter | Value |
|---|---|
| Hidden layers | 1 |
| Hidden neurons | 5 |
| Learning rate | 0.001 |
| Maximum number of iterations | 1000 |
| Model | MSE | MAE | Time Cost | ||||
|---|---|---|---|---|---|---|---|
| Mean | Best | Mean | Best | Mean | Best | ||
| MLP | 0.9330 | 0.9414 | 0.1206 | 0.1014 | 0.2192 | 0.2084 | 0.4357 |
| NNG-MLP | 0.9460 | 0.9491 | 0.0933 | 0.0880 | 0.2004 | 0.1909 | 5.1777 |
| LASSO-MLP | 0.9477 | 0.9510 | 0.0904 | 0.0847 | 0.1940 | 0.1819 | 5.3589 |
| dLASSO-MLP | 0.9471 | 0.9510 | 0.0929 | 0.0848 | 0.2157 | 0.1969 | 4.3865 |
| RAdLASSO-MLP | 0.9524 | 0.9548 | 0.0849 | 0.0786 | 0.1926 | 0.1858 | 2.6466 |
| Model | MSE | MAE | Time Cost | ||||
|---|---|---|---|---|---|---|---|
| Mean | Best | Mean | Best | Mean | Best | ||
| MLP | 0.8732 | 0.9235 | 0.1665 | 0.1310 | 0.2977 | 0.2687 | 0.4405 |
| NNG-MLP | 0.9496 | 0.9528 | 0.0838 | 0.0781 | 0.2171 | 0.2091 | 92.9382 |
| LASSO-MLP | 0.9508 | 0.9526 | 0.0888 | 0.0788 | 0.2206 | 0.2134 | 40.3202 |
| dLASSO-MLP | 0.9523 | 0.9567 | 0.0859 | 0.0760 | 0.2245 | 0.2077 | 19.9748 |
| RAdLASSO-MLP | 0.9545 | 0.9598 | 0.0799 | 0.0691 | 0.2038 | 0.1888 | 13.0524 |
| Model | MSE | MAE | Time Cost | ||||
|---|---|---|---|---|---|---|---|
| Mean | Best | Mean | Best | Mean | Best | ||
| MLP | 0.2834 | 0.3474 | 2.2393 | 1.9411 | 1.1407 | 1.1041 | 0.4916 |
| NNG-MLP | 0.7543 | 0.9049 | 0.7802 | 0.5192 | 0.7382 | 0.6186 | 53.0698 |
| LASSO-MLP | 0.7461 | 0.8245 | 0.7176 | 0.4925 | 0.6881 | 0.5893 | 47.8459 |
| dLASSO-MLP | 0.8052 | 0.9252 | 0.3685 | 0.1260 | 0.4763 | 0.2666 | 45.1171 |
| RAdLASSO-MLP | 0.9333 | 0.9495 | 0.1139 | 0.0833 | 0.2669 | 0.2289 | 35.1392 |
| Model | MSE | MAE | Time Cost | ||||
|---|---|---|---|---|---|---|---|
| Mean | Best | Mean | Best | Mean | Best | ||
| MLP | 0.0219 | 0.0236 | 5.3199 | 1.9544 | 1.4170 | 0.3874 | 0.5618 |
| NNG-MLP | 0.4861 | 0.8596 | 0.1496 | 0.0352 | 0.2797 | 0.1538 | 135.9702 |
| LASSO-MLP | 0.6051 | 0.8866 | 0.1638 | 0.0254 | 0.2257 | 0.1114 | 74.3032 |
| dLASSO-MLP | 0.8828 | 0.8753 | 0.0254 | 0.0194 | 0.1196 | 0.1072 | 47.2796 |
| RAdLASSO-MLP | 0.9353 | 0.9465 | 0.0123 | 0.0101 | 0.0789 | 0.0731 | 46.0341 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yu, X.; Zhao, J.; Pan, C.; Sun, K. Development of a Robust Data-Driven Soft Sensor for Multivariate Industrial Processes with Non-Gaussian Noise and Outliers. Mathematics 2022, 10, 3837. https://doi.org/10.3390/math10203837
Liu Y, Yu X, Zhao J, Pan C, Sun K. Development of a Robust Data-Driven Soft Sensor for Multivariate Industrial Processes with Non-Gaussian Noise and Outliers. Mathematics. 2022; 10(20):3837. https://doi.org/10.3390/math10203837
Chicago/Turabian StyleLiu, Yongshi, Xiaodong Yu, Jianjun Zhao, Changchun Pan, and Kai Sun. 2022. "Development of a Robust Data-Driven Soft Sensor for Multivariate Industrial Processes with Non-Gaussian Noise and Outliers" Mathematics 10, no. 20: 3837. https://doi.org/10.3390/math10203837
APA StyleLiu, Y., Yu, X., Zhao, J., Pan, C., & Sun, K. (2022). Development of a Robust Data-Driven Soft Sensor for Multivariate Industrial Processes with Non-Gaussian Noise and Outliers. Mathematics, 10(20), 3837. https://doi.org/10.3390/math10203837






