A Double-Penalized Estimator to Combat Separation and Multicollinearity in Logistic Regression

Abstract

When developing prediction models for small or sparse binary data with many highly correlated covariates, logistic regression often encounters separation or multicollinearity problems, resulting serious bias and even the nonexistence of standard maximum likelihood estimates. The combination of separation and multicollinearity makes the task of logistic regression more difficult, and a few studies addressed separation and multicollinearity simultaneously. In this paper, we propose a double-penalized method called lFRE to combat separation and multicollinearity in logistic regression. lFRE combines the logF-type penalty with the ridge penalty. The results indicate that compared with other penalty methods, lFRE can not only effectively remove bias from predicted probabilities but also provide the minimum mean squared prediction error. Aside from that, a real dataset is also employed to test the performance of the lFRE algorithm compared with several existing methods. The result shows that lFRE has strong competitiveness compared with them and can be used as an alternative algorithm in logistic regression to solve separation and multicollinearity problems.

1. Introduction

In many clinical research areas, logistic regression is frequently used to develop a predictive model based upon binary data to predict the likelihood of a patient’s health status, such as health or disease. In breast cancer research, for example, models can be developed to predict the likelihood of developing breast cancer. Predictions based on these models and the logistic regression framework assist physicians and patients in making joint decisions about future treatment options. Logistic regression, on the other hand, frequently suffers from severe estimation problems due to separation or multicollinearity, limiting its implementation and potentially leading to unreliable conclusions about the estimated model. Separation and multicollinearity are not insignificant issues, and they can be aggravating when they occur frequently at the same time.

The existence, finiteness, and uniqueness of maximum likelihood estimation, which has been extensively studied, determines whether the logistic regression model can draw valid conclusions. Silvapulle (1981) took a step in that direction by demonstrating that a certain degree of overlap is both a necessary and sufficient condition for the existence of maximum likelihood estimates for the binomial response model [1]. Albert and Anderson demonstrated the existence theorems of the maximum likelihood estimates (MLEs) for the multinomial logistic regression model by considering three possible patterns for the sample points: complete separation, quasi-complete separation, and overlap [2]. Albert and Anderson defined separation as one or more predictors having strong effects on the response and thus (almost) precisely predicting the outcome of interest (complete separation or quasi-complete separation) [2]. In small-to medium-sized datasets, Allison found that separation happens frequently when the regression coefficient of at least one covariate value becomes infinite [3]. Sparse data or separated data occur when the response variable is completely separated by a single covariate or linear combination of variables [4]. Additionally, an infinite estimate can also be regarded as exceedingly inaccurate, resulting in Wald confidence intervals with infinite widths [5]. Separation can occur even if the underlying model parameter has a low absolute value, according to Heinze and Schemper [6]. They also showed how the sample sizes, the number of dichotomous covariates, the magnitude of the odds ratios, and the degree of balance in their distribution all affected the probability of separation [6]. Furthermore, advanced but computationally costly techniques were exploited for detecting separation [7,8]. However, according to Agresti, monitoring the variance in the iteration process or supervising the iterative convergence is sufficient to proclaim separation [9].

The majority of the papers in this field are devoted to proposing new parameter estimates that would exist and have good theoretical properties if the data were already known to be in complete or quasi-complete separation. Penalized approaches for logistic regression models have gained popularity as a means of overcoming the separation problem. They produce fewer skewed estimates and, in general, more accurate inferences. In this case, Firth’s penalized method is an alternative to the standard logistic regression approach [10]. This method eliminates the first-order term ($O\left(n^{-1}\right)$) in the asymptotic bias expansion of the MLEs of the regression parameters by modifying the score equation with a penalty term known as the Jeffreys invariant prior. Heinze and Schemper applied Firth’s method to the solution of the separation problem in the logistic regression [6]. However, one of the criticisms leveled at the Firth-type penalty in recent studies is that it is based on observed covariate data, which can result in artifacts such as estimates that fall outside the prior median and the maximum likelihood estimation (MLE) range [11,12]. Firth’s logistic regression diminishes bias in maximum likelihood coefficient estimates while producing bias in the predicted probabilities. The more the outcome variables are imbalanced, the greater the bias [13]. As an alternative to this, Greenland and Mansournia proposed the log F(1, 1) and log F(2, 2) priors as default priors for logistic regression [11,12]. According to the authors, the proposed log-F(m, m) priors are reasonable, transparent, and computationally straightforward for logistic regression. Emmanuel modeled the prediction of the default probability using the penalized regression models and found that the log-F prior methods are preferred [14]. Note that other methods imposing shrinkage on the regression coefficients can also overcome the separation issue. For example, to address the issue of point separation, Rousseeuw and Christmann presented a hidden logistic regression model [15].

According to one assumption of binary logistic regression, explanatory variables should not be strongly correlated. Logistic regression models need to meet certain assumptions in order to produce reliable results. When the number of covariates is relatively large or the covariates are highly correlated, multicollinearity is likely to arise. One way to deal with this problem in linear regression models is called ridge regression, which was first introduced by Hoerl and Kennard [16,17]. The author proved that there is a non-zero ridge parameter value which makes the mean square error (MSE) of the slope parameter of the ridge regression smaller than the variance of the ordinary least squares (OLS) estimate of the corresponding parameter. Schaefer applied the ridge parameters proposed by Hoerl and Kennard in logistic regression and created a ridge-type estimator that will have a smaller total mean squared error than the maximum likelihood estimator when the independent variables are severely collinear [18]. Furthermore, the ridge parameter, whose size is determined by the number and collinearity of covariates, controls the amount of shrinkage [18]. Lee and Silvapulle showed that it is advised to employ ridge tracing as a diagnostic tool in logistic regression analysis, since it offers additional insight and readily draws attention to particular characteristics of the data model. They observed that a ridge type estimator is at least as good as and often much better than the standard logistic regression estimator in terms of the total and predicted mean squared error criteria in a Monte Carlo study [19]. In their study, Le Cessie and Van Houwellingen used the ridge regression method to improve the parameter estimates and decrease prediction errors in logistic regression [20]. Inan and Erdogan were the first to use the Liu-type estimator in the logistic regression model [21]. For the first time, Guoping Zeng and Emily Zeng investigated the relationship between multicollinearity and separation, proving analytically that multicollinearity implies quasi-complete separation as well as the absence of a finite solution for maximum likelihood estimation [22]. Senaviratna et al. also examined the four primary strategies for detecting multicollinearity before moving on to statistical inference, which are the tolerance, variance inflation factor (VIF), condition index, and variance proportions [23].

Separation and multicollinearity, on the other hand, are nearly never discussed together in the literature. Methods for addressing separation and multicollinearity at the same time have received little attention. To begin, Shen and Gao introduced a double-penalized likelihood estimator, which solves these two problems concurrently by combining Firth’s penalized likelihood equation with a ridge parameter in the logistic regression model [24]. Here, the separation problem is solved using Firth’s penalized likelihood equation, and the multicollinearity problem is solved using the ridge parameter. Nonetheless, Firth’s penalty has several unignorable flaws. Because Firth’s penalty incorporates the penalization’s intercept, it provides a bias in the average predicted probability that is much greater than that created by logistic regression [11]. Furthermore, as Firth noted [10], it does not minimize the MSE. Then, there’s the logF-type penalty, which is a popular alternative to Firth-type penalization that performs better in many ways. The following are the advantages of the logF-type penalty in further detail. First, the logF-type penalty avoids penalizing the intercept, causing an average predicted probability equal to the proportion of observed events. Next, the logF-type penalty is independent of the data. The logF-type penalty, unlike the Jeffreys prior (Firth-type penalty), does not result in correlations between explanatory variables. In particular, the logF-type penalty will minimize the MSE of efficient estimates while also providing more stable estimates. Thus, in this paper, we modify Shen and Gao’s approach and propose a more appealing double-penalized likelihood estimator (lFRE) for logistic regression models that combines a logF-type penalized likelihood approach with a ridge penalty term.

The rest of this paper is organized as follows. We consider logistic regression, Firth’s logistic regression [6], logistic regression with penalization by log-F(m, m) [11], and Shen and Gao’s double-penalized likelihood estimator [24] as the comparison methods. These methods are reviewed in Section 2. Then, in Section 3, we propose the estimator that combines the logF-type penalized likelihood approach with a ridge penalty term (lFRE), and we discuss the algorithm implementation of coefficient estimates and the selection of ridge parameters in this model. In Section 4, we offer two detailed simulation studies comparing the performance of lFRE to that of previous logistic regression-based approaches presented for both prediction and effect estimation in rare event and small dataset conditions. The predictive performance of the methods under investigation is demonstrated in Section 5 of the research for predicting the existence of breast cancer. Section 6 concludes with the discussion and conclusions.

2. Materials and Methods

2.1. Logistic Regression (LR)

Given the values of (a subset of) p candidate predictors, we define a logistic regression model for estimating the probability of an event occurring ($Y=1$) versus not occurring ($Y=0$). Let $Y_i$ be a binary response (0/1) for the ith subject with the probability ${\pi }_i=P(Y=1|{\mathbf{x}}_i)=1-P(Y=0|{\mathbf{x}}_i)$, $i=1,\dots ,n$, which follows a Bernoulli distribution. Let ${\mathbf{x}}_i={(1,x_{i1},\dots ,x_{ip})}^T$ be the covariate for the ith observation, where it is a $p+1$-dimensional row vector. Furthermore, the design matrix is denoted by ${\mathbf{X}}^T=({\mathbf{x}}_1,\dots ,{\mathbf{x}}_n)$ with an order $n\times (p+1)$. Then, we consider the following logistic regression model:

$$P(Y=1|{\mathbf{x}}_i)={\pi }_i=\frac{1}{1+\exp (-{{\mathbf{x}}_i}^T\mathbf{\beta })},$$

(1)

where $\mathbf{\beta }={({\beta }_0,{\beta }_1,\dots ,{\beta }_p)}^T$ is the $(p+1)$-dimensional parameter vector of the unknown parameters corresponding to the covariates. The log-likelihood for this model is written as

$$\ell \left(\mathbf{\beta }\right)=\sum _{i=1}^n\{Y_i\log {\pi }_i+(1-Y_i)\log (1-{\pi }_i)\},$$

(2)

The corresponding score function is

$$U\left(\mathbf{\beta }\right)=\sum _{i=1}^n(Y_i-{\pi }_i){\mathbf{x}}_i.$$

(3)

This method, however, is dependent on the existence of MLEs. Separation may occur in small to medium datasets. Although the likelihood converges, at least one parameter estimate is infinite in this case. MLE regression estimates produce large mean squared errors in the presence of multicollinearity. When separation occurs, Heinze and Schemper suggested Firth’s logistic regression as an alternative to the MLE [6].

2.2. Ridge Logistic Regression (Ridge)

The punishment term employed by Le Cessie and Van Houwelingen is ${\lambda \parallel \mathbf{\beta }\parallel }^2$. The ridge regression method minimizes the mean squared error of the predictions by introducing some bias to the estimation of the regression coefficients. The ridge log-likelihood is defined as

$${\ell }^{Ridge}\left(\mathbf{\beta }\right)=\ell \left(\mathbf{\beta }\right)-\lambda {\parallel \mathbf{\beta }\parallel }^2,$$

(4)

where $\parallel \mathbf{\beta }\parallel ={\left({\sum }_{j=1}^p{\beta }_j^2\right)}^{1/2}$, the norm of the parameter vector $\mathbf{\beta }$, and $\lambda$ is a tuning parameter that helps control the trade-off between the likelihood term and the penalty term, which is typically chosen to be a data-driven procedure such as cross-validation.

Hence, the corresponding score function is

$$U^{Ridge}\left(\mathbf{\beta }\right)=U\left(\mathbf{\beta }\right)-2\lambda \beta .$$

(5)

The ridge was initially created to address issues brought on by multicolinearity. However, it reduces the regression coefficient to almost zero, making it effective for reducing overfitting in risk prediction when there are linked predictors.

2.3. Firth’s Logistic Regression (Firth)

Firth proposed a method for removing the well-known small sample bias in maximum likelihood estimation [10]. Firth’s method involves introducing a bias term into the standard likelihood function, which itself becomes zero as $n\to +\infty$, but that will offset the existing $O\left(n^{-1}\right)$ for small n. The model likelihood is penalized by ${\left|\mathit{I}\left(\mathbf{\beta }\right)\right|}^{1/2}$ in Firth’s penalized likelihood logistic regression model, where $\mathit{I}\left(\mathbf{\beta }\right)$ is Fisher’s information matrix assessed at $\mathbf{\beta }$, $\mathit{I}\left(\mathbf{\beta }\right)={\mathbf{X}}^{\mathbf{T}}\mathbf{WX}$, and W is the diagonal matrix $\mathrm{diag}\left\{{\pi }_i(1-{\pi }_i)\right\}$. The corresponding Firth’s penalized log-likelihood function can be expressed as

$${\ell }^{Firth}\left(\mathbf{\beta }\right)=\ell \left(\mathbf{\beta }\right)+\frac{1}{2}\log \left|\mathit{I}\left(\mathbf{\beta }\right)\right|,$$

(6)

The corresponding score function is

$$U^{*}\left(\mathbf{\beta }\right)=U\left(\mathbf{\beta }\right)+\frac{1}{2}\mathrm{trace}\left\{{\mathit{I}\left(\mathbf{\beta }\right)}^{-1}\left[\frac{\partial \mathit{I}\left(\mathbf{\beta }\right)}{\partial \mathbf{\beta }}\right]\right\},$$

(7)

where $\mathbf{X}$ represents the observed covariate (design) matrix, $\ell \left(\mathbf{\beta }\right)$ is the log-likelihood function in Equation (2), $U\left(\mathbf{\beta }\right)$ denotes the standard score equation, and $\left|\mathit{I}\left(\mathbf{\beta }\right)\right|$ represents the determinant of the Fisher information matrix for $\ell \left(\mathbf{\beta }\right)$. The penalty term $\frac{1}{2}\log \left|\mathit{I}\left(\mathbf{\beta }\right)\right|$ is referred to as the Jeffreys invariant prior.

The Firth-type penalty is applicable in logistic regression. It prevents infinite estimates caused by separation problems by removing the $O\left(n^{-1}\right)$ bias of $\mathbf{\beta }$. The Firth-type penalty does, in fact, have the following flaws, which have been identified in the literature. Greenland and Mansournia pointed out that there are several serious practical flaws in the Jeffreys prior [11]. First, Firth’s penalty is dependent on the data because it is proportional to $\frac{1}{2}\log \left|\mathit{I}\left(\mathbf{\beta }\right)\right|$, where $\mathit{I}\left(\mathbf{\beta }\right)$ consists of the design matrix of the observed covariates. As a result, the majority of design matrices will generate correlations in the Jeffreys priors and coefficient estimates. Secondly, it is unclear how the penalty can be turned into a prior for odds ratios in general. Furthermore, the mean squared error (MSE) is not minimized. Therefore, when applied to small or sparse data, it can provide incredible estimates when contrasted to potentially stronger but still contextually weak penalties such as log-F priors. Finally, as model covariates are added or removed, the marginal prior for a given $\mathbf{\beta }$ could be altered in mysterious ways. Additionally, Puhr et al. demonstrated that a post hoc adjustment of the intercept in Firth’s logistic regression increases bias toward one half in the predicted probability [25]. They also demonstrated that the greater the imbalance of the outcome, the more substantial the bias in the predicted probabilities [25]. Accordingly, Greenland and Mansournia proposed a logF-type penalty as an alternative to Firth’s penalty in logistic regression when separation exists to avoid the concerns discussed above [11].

2.4. Logistic Regression with a log-F Prior Penalty (LF)

Greenland and Mansournia developed a family of penalty functions $r\left(\mathbf{\beta }\right)=\log \left(\right|{\mathit{I}\left(\mathbf{\beta }\right)}^{-m}\left|\right)$ indexed by $m\ge 0$, which yields the MLE ($m=0$) and Halane–Firth estimator ($m=1$) as special instances in an important paper [11]. By transforming each expected coefficient penalty into a pseudo-data record, log-F penalties are simple to implement in any logistic regression package, and this avoids penalizing the intercept in order to ensure that the mean predicted probability is the same as the proportion of events. Generally speaking, in a log-Fprior, the prior degrees of freedom m are equal to the number of observations added by the prior. The penalty imposed by the log-F(m,m) priors is equal to $\exp (m\mathbf{\beta }/2)/{\{1+\exp \left(\mathbf{\beta }\right)\}}^m$ multiplied by the likelihood function, corresponding to Equation (2). As a result, the corresponding penalized log-likelihood can be calculated as

$${\ell }^{LF}\left(\mathbf{\beta }\right)=\ell \left(\mathbf{\beta }\right)+m\mathbf{\beta }/2-m\log \{1+\exp \left(\mathbf{\beta }\right)\},$$

(8)

The corresponding score function is expressed as

$$U^{**}\left(\mathbf{\beta }\right)=U\left(\mathbf{\beta }\right)+m/2-\exp \left(\mathbf{\beta }\right)/\{1+\exp \left(\mathbf{\beta }\right\}.$$

(9)

When $m=0$, the function simplifies to the log-likelihood function in Equation (2) from the standpoint of this log-likelihood function. In other words, the penalized estimator with a logF(0,0) prior is the same as the MLE. Similarly, logF(1, 1) contains a Jefrreys prior in the one-parameter model, such as matched-pair case control. The log-F prior should be favored as a default penalty for general sparse data circumstances [12]. Taking simplicity of implementation and interpretation as our chief criteria, we consider the logF(1, 1) and logF(2, 2) priors in this study [11,12,13].

2.5. Shen and Gao’s Double-Penalized Likelihood Estimator (DPLE)

For handling both separation and multicollinearity, Shen and Gao proposed a double-penalized maximum likelihood estimator for logistic regression models that combines Firth’s penalized likelihood function with a ridge parameter [24]. The corresponding double-penalized log-likelihood can then be written as

$${\ell }^{DPLE}\left(\mathbf{\beta }\right)=\ell \left(\mathbf{\beta }\right)+\frac{1}{2}\log \left|\mathit{I}\left(\mathbf{\beta }\right)\right|-{\lambda \parallel \mathbf{\beta }\parallel }^2,$$

(10)

The corresponding score function is expressed as

$$U^{***}\left(\mathbf{\beta }\right)=U\left(\mathbf{\beta }\right)+\frac{1}{2}\mathrm{trace}\left\{{\mathit{I}\left(\mathbf{\beta }\right)}^{-1}\left[\frac{\partial \mathit{I}\left(\mathbf{\beta }\right)}{\partial \mathbf{\beta }}\right]\right\}-2\lambda \beta ,$$

(11)

The ridge parameter $\lambda$ determines the amount of shrinkage of the norm of $\mathbf{\beta }$ in the above log-likelihood function ${\ell }^{DPLE}\left(\mathbf{\beta }\right)$. The value of $\lambda$ is determined by the number of covariates and their degree of multicollinearity.

In general, the method is the development of Firth’s logistic regression with the added ability to select $\lambda$ to decrease multicollinearity. However, according to Section 2.3, there are several serious shortcomings in the Firth-type penalty. The same issues persist in Shen and Gao’s double-penalized likelihood estimator. Above all, Shen and Gao’s estimator also introduces some bias in the average predicted probability, and there’s a chance that the bias in the predicted probability is not insignificant. Nonetheless, by ignoring the intercept in the penalty, log-F(m,m) priors produce an average predicted probability equal to the observed proportion of occurrences in each sample. Greenland and Mansournia found that log-F(m,m) priors outperformed the Firth-type penalty [11]. The Jeffreys prior (Firth’s penalty term) is then included in DPLE, which is data-dependent and creates correlations between covariates. The logF-type prior, which is not data-dependent and overcomes this issue, is included in the lFRE we propose. Thus, we propose making a change to this double-penalized method: replacing Firth’s penalized likelihood approach with a log-F penalized approach while leaving the rest unaltered. Finally, as we previously stated, the Firth-type penalty does not minimize the MSE, whereas log-F priors do so. Consequently, of the two penalties, the logF-type penalty could be used to avoid these drawbacks that Firth’s penalty includes. Consistent with intuition, DPLE may provide a larger MSE than lFRE, as demonstrated in Simulations 1 and 2. We propose that lFRE may be a better strategy for dealing with the problems of separation and multicollinearity than DPLE in terms of contextual transparency, computational simplicity, and reasonableness for logistic regression. For more information on the double-penalized likelihood estimator that combines a logF-type penalty with a ridge penalty, see Section 3 below (lFRE).

3. The logF-Type Penalty with a Ridge-Based Estimator (lFRE)

3.1. The Double-Penalized Likelihood Estimator Combining a logF-Type Penalty with a Ridge Penalty

Based on the analysis in Section 2.5, an alternative approach for Shen and Gao’s double-penalized likelihood estimator that avoids these drawbacks is to replace Firth-type penalization with logF-type penalization. As a result, we propose a new double-penalized likelihood estimator that incorporates a logF-type penalty as well as a ridge penalty (lFRE). The log-likelihood function corresponding to this can be expressed as

$${\ell }^{lFRE}\left(\mathbf{\beta }\right)=\ell \left(\mathbf{\beta }\right)+m\mathbf{\beta }/2-m\log \{1+\exp \left(\mathbf{\beta }\right)\}-\lambda {\parallel \mathbf{\beta }\parallel }^2,$$

(12)

where $\ell \left(\mathbf{\beta }\right)$ is the unconstrained log-likelihood function, m represents the prior degree of freedom m in a log-F prior, $\lambda$ is the ridge parameter that regulates how much the norm of $\mathbf{\beta }$ shrinks, and $\left|\right|.\left|\right|$ denotes a parameter vector’s Euclidean nor, which imposes linear constraints on the parameters of $\mathbf{\beta }$.

A one-parameter issue without an intercept can be used to illustrate the core concept of lFRE. Multiparameter extensions will be covered in the following sections. Consider a single independent variable $x_i$ with just two possible values (zero or one), as well as a binary response Y (see

Table 1. A $2\times 2$ contingency table of a one-parameter issue without an intercept.

	${\mathit{x}}_{\mathit{i}}$
${\mathit{y}}_{\mathit{i}}$	0	1
0	$n_{00}$	$n_{01}$
1	$n_{10}$	$n_{11}$

).

In Table 1, $n_{00}=\Sigma I(y_i=0,x_i=0)$, $n_{01}=\Sigma I(y_i=0,x_i=1)$, $n_{10}=\Sigma I(y_i=1,x_i=0)$, and $n_{11}=\Sigma I(y_i=1,x_i=1)$. Here, $I(.)$ is the indicator function. By writing $P(Y=1|X=x_i)=1/(1+e^{-x_i\beta })$, we obtain $p_1=P(y_i=1|x_i=1)=1/(1+e^{-\beta })$ and $p_0=P(y_i=1|x_i=0)=1/2$. Now, let $n_1=n_{11}+n_{01}$.

Therefore, the likelihood function can be written as

$$L={p_0}^{n_{10}}{(1-p_0)}^{n_{00}}{p_1}^{n_{11}}{(1-p_1)}^{n_1-n_{11}}.$$

(13)

It is obvious that ${p_0}^{n_{10}}{(1-p_0)}^{n_{00}}$ is a constant which does not include the parameter $\beta$. We will use $C={p_0}^{n_{10}}{(1-p_0)}^{n_{00}}$ for the sake of derivation. As a result, the corresponding log-likelihood function can be written as

$$\ell =\log C+n_{11}\beta +n_1\log (1-p_1).$$

(14)

For this logistic regression model, the maximum likelihood estimate of $\beta$ is expressed as

$$\widehat{\beta }=\log \frac{n_{11}}{n_1-n_{11}}.$$

(15)

Clearly, in the situation of $n_1=n_{11}$, $\widehat{\beta }$ is nonexistent (i.e., there is no observation with the combination of $x_i=1$ and $y_i=0$). As a result, complete separation occurs.

Following that, we apply this simple logistic model to the log-F prior penalty. In general, penalization by log-F(m,m) priors is equivalent to multiplying the likelihood function corresponding to Equation (13) by $\exp (m\beta /2)/{\{1+\exp \left(\beta \right)\}}^m$. Therefore the likelihood function for this model is written as

$$L^{*}=C{p_1}^{n_{11}}{(1-p_1)}^{n_1-n_{11}}\exp (m\beta /2)/\left\{1+{\exp \left(\beta \right)}^m\right\}.$$

(16)

The corresponding log-likelihood function is expressed as

$${\ell }^{*}=\log C+n_{11}\beta +n_1\log (1-p_1)+m\beta /2-m\log \{1+\exp \left(\beta \right)\}.$$

(17)

The parameter estimate for the logistic model with a log-F prior penalty is equal to

$${\widehat{\beta }}^{*}=\log \frac{n_{11}+m/2}{m/2+n_1-n_{11}}.$$

(18)

The double-penalized log-likelihood function we propose is written as

$${\ell }^{**}=\log C+n_{11}\beta +n_1\log (1-p_1)+m\beta /2-m\log \{1+\exp \left(\beta \right)\}-\lambda {\beta }^2.$$

(19)

Because the analytical solution of ${\widehat{\beta }}^{**}$ is difficult to derive, we use the iterative algorithm to calculate its numerical solution, and the iterative algorithm is defined as

$${\widehat{\beta }}^{**(t+1)}=\log \frac{n_{11}+m/2-2\lambda {\beta }^{**\left(t\right)}}{m/2+n_1-n_{11}+2\lambda {\beta }^{**\left(t\right)}}.$$

(20)

When $\lambda =0$, it can be demonstrated that lFRE is the same as the logF-type penalized likelihood method. Given this viewpoint, lFRE is a log-F prior penalty with the added capability of selecting $\lambda$ to improve multicollinearity. Section 3.2 then goes over the algorithm implementation of coefficient estimates.

3.2. Algorithm Implementation

The maximum likelihood estimates (MLEs) of $\mathbf{\beta }$ could be obtained by maximizing ${\ell }^{lFRE}\left(\mathbf{\beta }\right)$. To put it another way, the coefficient estimates can be calculated as follows:

$$\widehat{\mathbf{\beta }}=\mathrm{argmax}\left\{\ell \left(\mathbf{\beta }\right)+m\mathbf{\beta }/2-m\log \{1+\exp \left(\mathbf{\beta }\right)\}-{\lambda \parallel \mathbf{\beta }\parallel }^2\right\}.$$

(21)

As a consequence, similar to unconstrained MLEs, the Newton–Raphson maximization algorithm approach may be used to solve $\widehat{\mathbf{\beta }}$ for $\mathbf{\beta }$. The Newton–Raphson iterative algorithm is defined as

$${\widehat{\mathbf{\beta }}}^{(t+1)}={\widehat{\mathbf{\beta }}}^{\left(t\right)}+{\mathbf{A}}^{-1\left(t\right)}\mathbf{U}\left({\widehat{\mathbf{\beta }}}^{\left(t\right)}\right),$$

(22)

where t stands for the number of iterations, ${\left(A\right)}^{-1\left(t\right)}$ represents the information matrix of the double-penalized log-likelihood function described in Section 3.1, and $\mathbf{U}\left({\widehat{\mathbf{\beta }}}^{(t)}\right)$ is the first derivative of the log-likelihood function (Equation (12)). In other words, we have

$$\begin{array}{cc}\hfill \mathbf{U}({\widehat{\beta }}_j^{\left(t\right)})& =\frac{\partial \ell \left(\mathbf{\beta }\right)}{\partial {\beta }_j}+\frac{\partial (m\mathbf{\beta }/2-m\log \{1+\exp \left(\mathbf{\beta }\right)\left\}\right)}{\partial {\beta }_j}-\frac{\partial \left({\lambda \parallel \mathbf{\beta }\parallel }^2\right)}{\partial {\beta }_j}\hfill \\ \hfill & =\sum _{i=1}^n(Y_i-{\pi }_i){\mathbf{x}}_j+m/2-m\exp \left({\beta }_j\right)/\{1+\exp \left({\beta }_j\right)\}-2\lambda {\beta }_j(j=0,\cdots ,p),\hfill \end{array}$$

(23)

$\mathit{H}$ is the Hessian matrix of the log-likelihood function corresponding to Equation (12) such that

$$\mathit{H}=\left(\begin{array}{ccc}{\displaystyle \sum _{i=1}^n}{\pi }_i({\pi }_i-1)-m\frac{\exp \left({\beta }_0\right)}{{\{1+\exp \left({\beta }_0\right)\}}^2}-2\lambda & \cdots & {\displaystyle \sum _{i=1}^n}{\pi }_i({\pi }_i-1){\mathbf{x}}_p\\ {\displaystyle \sum _{i=1}^n}{\pi }_i({\pi }_i-1){\mathbf{x}}_1& \cdots & {\displaystyle \sum _{i=1}^n}{\pi }_i({\pi }_i-1){\mathbf{x}}_1{\mathbf{x}}_p\\ ⋮& ⋮& ⋮\\ {\displaystyle \sum _{i=1}^n}{\pi }_i({\pi }_i-1){\mathbf{x}}_p& \cdots & {\displaystyle \sum _{i=1}^n}{\pi }_i({\pi }_i-1){\mathbf{x}}_p{\mathbf{x}}_p-m\frac{\exp \left({\beta }_p\right)}{{\{1+\exp \left({\beta }_p\right)\}}^2}-2\lambda \end{array}\right).$$

We discovered that solving the second-order partial derivative for the log-likelihood function presented in this research was considerably easier than solving the partial derivative derived by Shen and Gao [24]. Because the information matrix of the double-penalized likelihood function is difficult to derive in Shen and Gao’s double-penalized likelihood function, the approximation information matrix was used to obtain the variance estimates of the parameters at convergence. We favor lFRE over DPLE because of its interpretive and computational simplicity, as well as the aforementioned concerns. The choice of $\lambda$ is discussed further in the following section:

Theorem 1.

${\ell }^{lFRE}\left(\mathbf{\beta }\right)$ in Equation (12) is a convex function.

Proof 

We consider the Hessian matrix $\mathit{H}$ of the log-likelihood function ${\ell }^{lFRE}\left(\mathbf{\beta }\right)$. For simplicity, we let $g\left(\beta \right)=exp\left(\beta \right)/{\left\{1+exp\left(\beta \right)\right\}}^2$ and $z_i={\pi }_i({\pi }_i-1)$. Here, we consider the case of $p=2$ and have

$$\mathit{H}=\left(\begin{array}{ccc}{\displaystyle \sum _{i=1}^n}{z}_i-mg\left({\beta }_0\right)-2\lambda & {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1& {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_2\\ {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1& {\displaystyle \sum _{i=1}^n}{z}_i{{\mathbf{x}}_1}^2-mg\left({\beta }_1\right)-2\lambda & {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1{\mathbf{x}}_2\\ {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_2& {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1{\mathbf{x}}_2& {\displaystyle \sum _{i=1}^n}{z}_i{{\mathbf{x}}_2}^2-mg\left({\beta }_2\right)-2\lambda \end{array}\right).$$

Let ${\mathbf{D}}_k$ denote the kth sequential principal minor of $\mathit{H}$, where $k=1,2,3$. $\mathit{H}$ is a negative definite matrix if ${(-1)}^k{\mathbf{D}}_k>0$, ($k=1,2,3$). The first-order sequential principal minor of $\mathit{H}$ can be expressed as

$${\mathbf{D}}_1=\sum _{i=1}^n{z}_i-mg\left({\beta }_0\right)-2\lambda .$$

(24)

According to $z_i<0$, $g\left({\beta }_0\right)>0$ and $\lambda >0$, we have ${\mathbf{D}}_1<0$. Thus, $(-1){\mathbf{D}}_1>0$:

$$\begin{array}{cc}\hfill {\mathbf{D}}_2& =\left|\begin{array}{cc}{\displaystyle \sum _{i=1}^n}{z}_i-mg\left({\beta }_0\right)-2\lambda & {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1\\ {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1& {\displaystyle \sum _{i=1}^n}{z}_i{{\mathbf{x}}_1}^2-mg\left({\beta }_1\right)-2\lambda \end{array}\right|\hfill \\ & =-\sum _{i=1}^{n}m{z}_i\left\{g\left({\beta }_0\right)+g\left({\beta }_1\right){{\mathbf{x}}_1}^2\right\}-2\lambda \sum _{i=1}^n{z}_i(1+{{\mathbf{x}}_1}^2)\hfill \\ & +2\lambda m\{g\left({\beta }_0\right)+g\left({\beta }_1\right)\}+m^{2}g\left({\beta }_0\right)g\left({\beta }_1\right)+4{\lambda }^2.\hfill \end{array}$$

According to $z_i<0$, $g\left({\beta }_0\right)>0$, $g\left({\beta }_1\right)>0$, $m>0$, and $\lambda >0$, we find that ${\mathbf{D}}_2>0$. Then, ${(-1)}^2{\mathbf{D}}_2>0$:

$$\begin{array}{cc}\hfill {\mathbf{D}}_3& =\left|\begin{array}{ccc}{\displaystyle \sum _{i=1}^n}{z}_i-mg\left({\beta }_0\right)-2\lambda & {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1& {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_2\\ {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1& {\displaystyle \sum _{i=1}^n}{z}_i{{\mathbf{x}}_1}^2-mg\left({\beta }_1\right)-2\lambda & {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1{\mathbf{x}}_2\\ {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_2& {\displaystyle \sum _{i=1}^n}{z}_i{\mathbf{x}}_1{\mathbf{x}}_2& {\displaystyle \sum _{i=1}^n}{z}_i{{\mathbf{x}}_2}^2-mg\left({\beta }_2\right)-2\lambda \end{array}\right|\hfill \\ & =\left\{2\sum _{i=1}^{n}m{z}_i-mg\left({\beta }_0\right)-2\lambda \right\}\left\{m^{2}g\left({\beta }_1\right)g\left({\beta }_2\right)+2\lambda m\{g\left({\beta }_1\right)+g\left({\beta }_2\right)\}+4{\lambda }^2\right\}\hfill \\ & +\{mg\left({\beta }_0\right)+2\lambda \}\left\{\sum _{i=1}^n{z}_{i}m{{\mathbf{x}}_1}^{2}g\left({\beta }_2\right)+\sum _{i=1}^n{z}_{i}m{{\mathbf{x}}_2}^{2}g\left({\beta }_1\right)+2\lambda \sum _{i=1}^n{z}_i({{\mathbf{x}}_1}^2+{{\mathbf{x}}_2}^2)\right\}.\hfill \end{array}$$

Because $\left\{2{\displaystyle \sum _{i=1}^n}m{z}_i-mg\left({\beta }_0\right)-2\lambda \right\}\left\{m^{2}g\left({\beta }_1\right)g\left({\beta }_2\right)+2\lambda m\{g\left({\beta }_1\right)+g\left({\beta }_2\right)\}+4{\lambda }^2\right\}<0$ and $\{mg\left({\beta }_0\right)+2\lambda \}\left\{{\displaystyle \sum _{i=1}^n}{z}_{i}m{{\mathbf{x}}_1}^{2}g\left({\beta }_2\right)+{\displaystyle \sum _{i=1}^n}{z}_{i}m{{\mathbf{x}}_2}^{2}g\left({\beta }_1\right)+2\lambda {\displaystyle \sum _{i=1}^n}{z}_i({{\mathbf{x}}_1}^2+{{\mathbf{x}}_2}^2)\right\}<0$, we can obtain that ${\mathbf{D}}_3<0$. Thus, ${(-1)}^3{\mathbf{D}}_3>0$.

Therefore, the Hessian matrix $\mathit{H}$ is a negative definite matrix, and ${\ell }^{lFRE}\left(\mathbf{\beta }\right)$ is a convex function.

According to Theorem 1, there is a unique maximum for ${\ell }^{lFRE}\left(\mathbf{\beta }\right)$. □

3.3. The Choice of the Ridge Parameter

The most typical technique for finding the appropriate $\lambda$ ridge parameter is to minimize the prediction error of logistic regression as the primary criterion. The maximizer in Equation (12) is written as ${\widehat{\mathbf{\beta }}}^{\lambda }$. Various techniques for defining prediction errors were discussed by Efron as well as Van Hovelingen and Le Cessie [20,26]. Following that, Van Hovelingen et al. and Van Wieringen [20,27] developed three different methods for quantifying prediction error:

(a) Classifition or counting error ($CE$):

$$CE=\left\{\begin{array}{cc}1,\hfill & if{Y}_i=1and{\widehat{\pi }}_i<\frac{1}{2};or{Y}_i=0and{\widehat{\pi }}_i>\frac{1}{2},\hfill \\ \frac{1}{2},\hfill & if{\widehat{\pi }}_i>\frac{1}{2},\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(b) Prediction error ($PE$):

$$PE={(Y_i-{\widehat{\pi }}_i)}^2.$$

(25)

(c) Minus log-likelihood error ($ML$):

$$ML=-\{Y_{i}log{\widehat{\pi }}_i+(1-Y_i)log(1-{\widehat{\pi }}_i)\}.$$

(26)

The merits and disadvantages of these three measures were debated by Van Hovelingen and Le Cessie [20]. $PE$ is very sensitive to the model prediction near $\pi =\frac{1}{2}$, whereas the other two indicators take into account model prediction across the whole p-value range. In this paper, we use the intuitive square error as the measure of prediction error due to its ease of calculation. When comparing the effects of various ridge parameters, the prediction sum of squares ($PRESS$) given by Allen is a credible criterion of good prediction when calculated on the entire dataset [28]. We employed cross-validation (CV) estimation of $PRESS$ in the absence of external validation datasets, which is defined as

$$PRES{S}_{{CV}^{\lambda }}=\frac{1}{n}\sum _{i=1}^n{(Y_i-{\widehat{\pi }}_{-i}\left(X_i\right))}^2,$$

(27)

where ${\widehat{\beta }}_{-i}\left(\lambda \right)$ represents the estimate based on all observations except $(X_i,Y_i)$ and ${\widehat{\pi }}_{-i}\left(x\right)$ is the estimate of $\pi \left(x\right)$ based on ${\widehat{\beta }}_{-i}\left(\lambda \right)$. The optimal $\lambda$ is then chosen by minimizing $PRESS$. The estimate ${\widehat{\mathbf{\beta }}}^{\lambda }$ is predicted to be closer to the real value of $\mathbf{\beta }$ than the standard MLE; that is, $PRESS\left({\widehat{\mathbf{\beta }}}^{\lambda }\right)<PRESS\left(\widehat{\mathbf{\beta }}\right)$ for an ideal $\lambda$. There is always a ridge parameter $\lambda >0$ for which the estimates have a lower $PRESS$ than the maximum likelihood estimates for lFRE. In the following section, we will conduct two extensive simulation studies to compare the performance of LFRE with other methods based on logistic regression (MLE, Firth, Ridge, LF22, and DPLE) in various scenarios.

4. Simulations

The purpose of this section is to assess the properties of the regression coefficients of the LR, Ridge, Firth, LF22, DPLE, lFRE11, and lFRE22 methods by conducting two simulation studies. The following briefly describes how data were generated and cases varied in the simulation study.

4.1. Software and Data Generation

The simulations were programmed in R 4.0.5. The R functions glm and glmnet [29] were used to implement LR and Ridge. Firth was implemented in the brglm2 package [30]. The LF11 and LF22 models were implemented using the R function plogit [12]. To generate the mixed continuous and binary covariates in a dataset, we first generated three continuous covariates (${\mathbf{x}}_1,{\mathbf{x}}_2$, and ${\mathbf{x}}_3$) from the multivariate normal distribution with zero means, unit variances, and a specified correlation matrix. Then, we produced two binary covariates (${\mathbf{x}}_4$ and ${\mathbf{x}}_5$) from binomial distribution, followed by a binary response variable generated from a Bernoulli distribution with a probability ${\pi }_i$$(i=1,\cdots ,n)$ calculated from true logistic model $\mathrm{logit}\left(\pi \right)={\beta }_0+{\beta }_1{\mathbf{x}}_1+{\beta }_2{\mathbf{x}}_2+{\beta }_3{\mathbf{x}}_3+{\beta }_4{\mathbf{x}}_4+{\beta }_5{\mathbf{x}}_5$, where ${\beta }_0=-2$, ${\beta }_1=1$, ${\beta }_2=1$, ${\beta }_3=1$, ${\beta }_4=1$, and ${\beta }_5=1$. To ensure that the results were comparable, we used the same random number seed throughout the procedure.

4.2. Performance Evaluation of the Methods

The average parameter estimation bias and mean squared error (MSE) results were considered to evaluate the performances of the penalized methods in previous studies as mentioned in Section 2. The average MSE for a replication was calculated using

$$MSE=\frac{1}{100}\sum _{s=1}^{100}{({\widehat{\beta }}_{s,p}-{\beta }_{s,p})}^2,$$

(28)

where ${\widehat{\beta }}_{s,p}$ is the estimate of ${\beta }_{s,p}$ and ${\beta }_{s,p}$ denotes the true parameter for the pth parameter of the sth simulated dataset.

In addition, the average parameter estimation bias was calculated by using

$$bias=\frac{1}{100}\sum _{s=1}^{100}({\widehat{\beta }}_{s,p}-{\beta }_{s,p}).$$

(29)

For the Ridge, DPLE, lFRE11, and lFRE22 penalized methods with a ridge parameter, the average MSE was calculated as follows:

$$MSE=\frac{1}{100}\sum _{s=1}^{100}{({\widehat{\beta }}_{s,p}\left(\lambda \right)-{\beta }_{s,p})}^2.$$

(30)

Additionally, the average parameter estimation bias was computed as

$$bias=\frac{1}{100}\sum _{s=1}^{100}({\widehat{\beta }}_{s,p}-{\beta }_{s,p}),$$

(31)

where the choice of ridge parameter ($\lambda$) depends on the cross-validation criterion, which was mentioned in Section 3.3, and ${\widehat{\beta }}_{s,p}\left(\lambda \right)$ was obtained from these estimators with optimal $\lambda$. The appropriate tuning parameters for fitting Ridge, DPLE, lFRE11, and lFRE22 were chosen using 10-fold cross validation. The average over the number of simulations where convergence was achieved was used to calculate the estimations of the regression coefficients for the respective models.

4.3. Simulation 1

In this section, we carried out a simulation study to assess the properties of the regression coefficients of these methods (LR, Ridge, Firth, LF22, DPLE, lFRE11, and lFRE22) with respect to the bias and mean squared error (MSE). For a fixed correlation coefficient $r=0.85$, we considered alternative scenarios in which there were three covariates with potentially strong correlations. To study the effects of the sample size in the situation of a small severe multicollinearity, the sample sizes (n) were set to 50, 80, 130, and 200. We also used the data from the first simulation here. Five coefficients (${\beta }_1$, ${\beta }_2$, ${\beta }_3$, ${\beta }_4$, and ${\beta }_5$) were estimated in this simulation study, with ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ being continuous covariables and ${\beta }_4$ and ${\beta }_5$ being binary covariables, omitting the intercept term.

Each sample size scenario yielded 100 datasets, which we simulated. The results of the simulations are shown in

Table 2. Bias and MSEs of all explanatory variables (omitting the intercept) for sample size $n\in \{50,80,130,200\}$ and a fixed correlation coefficient $r=0.85$.

		Bias								MSE
n	Coeffient	LR	Firth	Ridge	LF22	DPLE	lFRE11	lFRE22		LR	Firth	Ridge	LF22	DPLE	lFRE11	lFRE22
50	${\beta }_1\left(1\right)$	—	0.02	−0.29	−0.04	−0.17	−0.03	−0.10		—	1.68	0.18	0.41	0.46	0.40	0.28
	${\beta }_2\left(1\right)$	—	0.19	−0.24	0.12	−0.02	0.11	0.02		—	1.83	0.13	0.47	0.50	0.43	0.27
	${\beta }_3\left(1\right)$	—	−0.09	−0.29	−0.08	−0.22	−0.08	−0.13		—	1.14	0.17	0.44	0.47	0.43	0.32
	${\beta }_4\left(1\right)$	—	0.19	−0.39	−0.18	−0.15	−0.17	−0.30		—	1.63	0.57	0.50	0.56	0.49	0.40
	${\beta }_5\left(1\right)$	—	0.17	−0.40	−0.18	−0.15	−0.17	−0.30		—	1.10	0.44	0.50	0.50	0.49	0.42
80	${\beta }_1\left(1\right)$	0.27	0.05	−0.24	0.04	−0.04	0.05	−0.01		0.84	0.51	0.12	0.32	0.33	0.32	0.25
	${\beta }_2\left(1\right)$	0.19	−0.01	−0.21	0.03	−0.07	0.03	−0.02		1.16	0.73	0.11	0.36	0.40	0.35	0.25
	${\beta }_3\left(1\right)$	0.20	0.00	−0.28	0.01	−0.07	0.02	−0.03		0.65	0.37	0.15	0.21	0.22	0.21	0.16
	${\beta }_4\left(1\right)$	0.21	−0.01	−0.35	−0.20	−0.17	−0.19	−0.29		1.17	0.68	0.42	0.44	0.44	0.43	0.38
	${\beta }_5\left(1\right)$	0.22	0.02	−0.29	−0.15	−0.13	−0.14	−0.23		0.96	0.59	0.29	0.38	0.39	0.38	0.33
130	${\beta }_1\left(1\right)$	0.03	−0.07	−0.24	−0.05	−0.10	−0.04	−0.07		0.45	0.36	0.09	0.26	0.28	0.26	0.22
	${\beta }_2\left(1\right)$	0.26	0.13	−0.20	0.13	0.07	0.13	0.09		0.91	0.67	0.08	0.42	0.44	0.40	0.31
	${\beta }_3\left(1\right)$	0.15	0.03	0.25	0.04	−0.01	0.04	0.01		0.45	0.34	0.10	0.26	0.26	0.25	0.21
	${\beta }_4\left(1\right)$	0.07	−0.03	−0.32	−0.15	−0.13	−0.14	−0.22		0.53	0.41	0.22	0.30	0.31	0.30	0.27
	${\beta }_5\left(1\right)$	0.17	0.06	0.42	−0.06	−0.05	−0.06	−0.13		0.58	0.41	0.36	0.28	0.28	0.27	0.23
200	${\beta }_1\left(1\right)$	0.01	−0.05	−0.25	−0.03	−0.07	−0.03	−0.05		0.18	0.16	0.08	0.13	0.14	0.13	0.12
	${\beta }_2\left(1\right)$	0.13	0.07	−0.23	0.07	0.04	0.07	0.05		0.40	0.33	0.08	0.25	0.26	0.25	0.21
	${\beta }_3\left(1\right)$	0.06	−0.01	−0.25	0.01	−0.02	0.01	−0.01		0.19	0.17	0.08	0.14	0.14	0.14	0.12
	${\beta }_4\left(1\right)$	0.10	0.04	−0.32	−0.03	−0.02	−0.03	−0.08		0.24	0.20	0.19	0.17	0.17	0.17	0.16
	${\beta }_5\left(1\right)$	0.08	0.02	−0.36	−0.04	−0.03	−0.04	−0.09		0.25	0.21	0.24	0.18	0.18	0.18	0.17

. The maximum likelihood estimates (MLEs) were nonexistent in the small sample of 50 people (due to separation problems caused by the small sample size, high correlation among covariates, or both). When we created a model using conventional maximum likelihood binary logistic regression with data with a limited number of subjects relative to the number of predictors, our results demonstrated that the MLEs were nonexistent. However, as the sample size grew, the evidence for nonexistence improved. According to the findings in Table 2, the Ridge estimator generally offered the largest bias, followed by Firth and LF22, while DPLE, lFRE11, and lFRE22 offered very little bias. To some extent, all penalized approaches offered improvement. Firth and LF22 reduced the bias of the coefficient estimations when compared with LR in terms of the mean bias. Some bias values obtained by DPLE, lFRE11, and lFRE22 were higher than those obtained by LR, which was due to the ridge parameter penalty term. These results are to be expected, given that the ridge parameter in the double-penalized estimators compromises bias in order to lower the MSE. Firth would yield a significantly higher MSE than LF22 in every situation. This is due to the fact that Firth does not minimize the MSE. Clearly, the statistics in Table 2 reveal that DPLE with a Firth-type penalty had a higher MSE than lFRE11 and lFRE22 with a logF-type penalty, as evidenced by our simulation findings, which are consistent with intuition. In almost all settings, lFRE22 provided slightly larger bias on the binary covariables (${\beta }_4$ and ${\beta }_5$), but it outperformed the other approaches on continuous covariables (${\beta }_1$, ${\beta }_2$, and ${\beta }_3$). However, when it comes to the MSE, lFRE22 was the best, while lFRE11 was at least second. When compared with other penalized methods, lFRE11 and lFRE22 had a significantly lower bias and MSE. The differences were larger when the sample size was small or medium (see Table 2). The difference gradually decreased as the sample size grew larger.

There appeared to be a difference in the parameter estimation of binary and continuous covariates between all penalized estimators in terms of bias and MSE in our simulation. The ridge effect appeared to be stronger in the continuous covariates than in the binary covariates, as seen in Table 2. The reduction in MSE in Firth, Ridge, and LF22 compared with DPLE, lFRE11, and lFRE22 for the binary covariates suggests a compromise in terms of increased bias. In the three double-penalized estimators, the MSE for the continuous covariates was dramatically lowered. When it came to the mean bias and MSE for the binary variable, the three doubly penalized estimators (DPLE, lFRE11, and lFRE11) were indistinguishable.

The MSE results of the DPLE, lFRE11, and lFRE22 are visualized with respect to the continuous and binary variables for different sample sizes in Figure 1 for further information. It is clear that lFRE22 had the lowest MSE for both the continuous and binary covariables. Furthermore, DPLE, lFRE11, and lFRE22 provided greater improvement. When the sample size was small, this trend became more apparent. The difference between the three methods for continuous and binary covariates decreased as the sample size increased.

In the second simulation, we conducted two series of simulations to look at the effects of correlation among covariates ($r\in \{0.65,0.75,0.85,0.95\}$), sample size ($n\in \{40,80\}$), and covariate type (binary and continuous). To investigate the effects of the correlation and small sample size on the estimation of the regression coefficients, we used a variety of correlation coefficients and small sample sizes. We also used the data generated in the first simulation in this case. For each scenario, 100 datasets were generated, and each dataset was fitted with all of the regression approaches under consideration. Two tables present the bias and MSEs of the estimates, and two figures present the bias and MSEs for different scenarios obtained by DPLE, lFRE11, and lFRE22.

4.4. Simulation 2

The estimated bias and MSE values for LR, Firth, Ridge, LF22, DPLE, lFRE11, and lFRE22 are reported in

Table 3. Bias and MSE for all explanatory variables (omitting the intercept) for correlation coefficient $r\in \{0.65,0.75,0.85,0.95\}$ and a fixed sample size $n=40$.

		Bias								MSE
r	Coeffient	LR	Firth	Ridge	LF22	DPLE	lFRE11	lFRE22		LR	Firth	Ridge	LF22	DPLE	lFRE11	lFRE22
0.65	${\beta }_1\left(1\right)$	—	−0.04	−0.26	−0.02	−0.18	−0.01	−0.09		—	0.38	0.19	0.23	0.22	0.23	0.18
	${\beta }_2\left(1\right)$	—	0.03	−0.23	0.04	−0.14	0.04	−0.04		—	0.72	0.17	0.35	0.31	0.34	0.24
	${\beta }_3\left(1\right)$	—	0.12	0.31	0.08	−0.08	0.08	−0.01		—	0.58	0.21	0.30	0.24	0.30	0.21
	${\beta }_4\left(1\right)$	—	0.04	−0.34	−0.30	−0.27	−0.29	−0.41		—	1.33	0.59	0.60	0.61	0.60	0.52
	${\beta }_5\left(1\right)$	—	−0.07	−0.32	−0.37	−0.34	−0.36	−0.47		—	1.55	0.53	0.74	0.77	0.74	0.63
0.75	${\beta }_1\left(1\right)$	—	0.13	0.26	−0.30	−0.10	0.07	−0.03		—	1.33	0.18	0.45	0.41	0.43	0.29
	${\beta }_2\left(1\right)$	—	0.15	−0.29	0.11	−0.10	0.10	0.01		—	2.12	0.19	0.60	0.56	0.56	0.27
	${\beta }_3\left(1\right)$	—	0.14	−0.30	0.03	−0.13	0.04	−0.06		—	1.35	0.22	0.31	0.32	0.30	0.20
	${\beta }_4\left(1\right)$	—	0.05	−0.33	−0.32	−0.28	−0.31	−0.43		—	1.09	0.58	0.60	0.68	0.67	0.57
	${\beta }_5\left(1\right)$	—	0.34	0.31	−0.17	−0.15	−0.16	−0.31		—	1.01	0.39	0.53	0.55	0.52	0.42
0.85	${\beta }_1\left(1\right)$	—	−0.05	−0.35	−0.04	−0.20	−0.03	−0.11		—	0.76	0.24	0.31	0.34	0.30	0.22
	${\beta }_2\left(1\right)$	—	0.09	−0.24	0.01	−0.15	0.01	−0.07		—	2.20	0.18	0.46	0.57	0.43	0.27
	${\beta }_3\left(1\right)$	—	−0.10	−0.26	−0.04	−0.22	−0.04	−0.11		—	1.36	0.16	0.39	0.46	0.38	0.26
	${\beta }_4\left(1\right)$	—	−0.02	−0.49	−0.34	−0.32	−0.33	−0.45		—	1.27	0.68	0.61	0.63	0.59	0.53
	${\beta }_5\left(1\right)$	—	0.00	−0.37	−0.30	−0.29	−0.29	−0.41		—	1.43	0.56	0.64	0.64	0.64	0.54
0.95	${\beta }_1\left(1\right)$	—	0.31	−0.29	0.07	−0.09	0.07	−0.03		—	4.56	0.17	0.45	0.61	0.43	0.25
	${\beta }_2\left(1\right)$	—	−0.02	−0.27	−0.01	−0.18	0.00	−0.08		—	6.27	0.13	0.37	0.67	0.36	0.21
	${\beta }_3\left(1\right)$	—	−0.25	−0.27	−0.12	−0.32	−0.12	−0.17		—	3.57	0.16	0.41	0.64	0.40	0.26
	${\beta }_4\left(1\right)$	—	0.19	−0.35	−0.21	−0.18	−0.19	−0.34		—	1.53	0.52	0.57	0.58	0.56	0.47
	${\beta }_5\left(1\right)$	—	0.05	−0.25	−0.30	−0.27	0.29	−0.41		—	1.04	0.48	0.47	0.47	0.47	0.43

and

Table 4. Bias and MSE for all explanatory variables (omitting the intercept) for correlation coefficient $r\in \{0.65,0.75,0.85,0.95\}$ and a fixed sample size $n=80$.

		Bias								MSE
r	Coeffient	LR	Firth	Ridge	LF22	DPLE	lFRE11	lFRE22		LR	Firth	Ridge	LF22	DPLE	lFRE11	lFRE22
r = 0.65	${\beta }_1\left(1\right)$	0.21	0.02	−0.28	0.03	−0.05	0.03	−0.02		0.42	0.24	0.14	0.19	0.18	0.19	0.16
	${\beta }_2\left(1\right)$	0.23	0.04	−0.24	0.06	−0.03	0.06	0.01		0.64	0.40	0.12	0.28	0.27	0.28	0.21
	${\beta }_3\left(1\right)$	0.24	0.05	−0.26	0.05	−0.03	0.05	0.00		0.35	0.20	0.13	0.16	0.15	0.16	0.13
	${\beta }_4\left(1\right)$	0.33	0.13	−0.36	−0.06	−0.03	−0.05	−0.16		0.75	0.46	0.37	0.30	0.31	0.30	0.25
	${\beta }_5\left(1\right)$	0.31	0.11	−0.27	−0.06	−0.04	−0.05	−0.16		0.96	0.61	0.23	0.42	0.42	0.42	0.35
r = 0.75	${\beta }_1\left(1\right)$	0.11	−0.07	−0.25	−0.05	−0.13	−0.05	−0.09		0.43	0.28	0.13	0.22	0.22	0.22	0.18
	${\beta }_2\left(1\right)$	0.32	0.11	−0.18	0.12	−0.03	0.13	0.07		0.85	0.50	0.10	0.34	0.32	0.33	0.25
	${\beta }_3\left(1\right)$	0.10	−0.08	−0.27	−0.06	−0.14	−0.06	−0.10		0.66	0.40	0.14	0.28	0.28	0.27	0.22
	${\beta }_4\left(1\right)$	0.17	−0.01	−0.36	−0.17	−0.14	−0.16	−0.25		0.78	0.52	0.32	0.38	0.39	0.38	0.34
	${\beta }_5\left(1\right)$	0.23	0.04	−0.33	−0.13	−0.11	−0.12	−0.22		0.88	0.53	0.30	0.33	0.34	0.33	0.29
r = 0.85	${\beta }_1\left(1\right)$	0.27	0.05	−0.24	0.04	−0.04	0.05	−0.01		0.84	0.51	0.12	0.32	0.33	0.32	0.25
	${\beta }_2\left(1\right)$	0.19	−0.01	−0.21	0.03	−0.07	0.03	−0.02		1.16	0.73	0.11	0.36	0.40	0.35	0.25
	${\beta }_3\left(1\right)$	0.20	0.00	−0.28	0.01	−0.07	0.02	−0.03		0.65	0.37	0.15	0.21	0.22	0.21	0.16
	${\beta }_4\left(1\right)$	0.21	−0.01	−0.35	−0.20	−0.17	−0.19	−0.29		1.17	0.68	0.42	0.44	0.44	0.43	0.38
	${\beta }_5\left(1\right)$	0.22	0.02	−0.29	−0.15	−0.13	−0.14	−0.23		0.96	0.59	0.29	0.38	0.39	0.38	0.33
r = 0.95	${\beta }_1\left(1\right)$	−0.02	−0.18	−0.24	−0.11	−0.21	−0.11	−0.13		2.11	1.38	0.10	0.43	0.57	0.41	0.28
	${\beta }_2\left(1\right)$	0.24	0.02	−0.23	0.02	−0.07	0.02	−0.03		3.72	2.46	0.08	0.51	0.76	0.48	0.29
	${\beta }_3\left(1\right)$	0.34	0.12	−0.26	0.09	0.02	0.09	0.03		1.87	1.20	0.12	0.40	0.49	0.38	0.25
	${\beta }_4\left(1\right)$	0.18	−0.02	−0.35	−0.21	−0.19	−0.21	−0.30		0.85	0.54	0.35	0.38	0.39	0.38	0.36
	${\beta }_5\left(1\right)$	0.20	0.11	−0.30	−0.15	−0.13	−0.14	−0.23		0.85	0.56	0.27	0.36	0.37	0.36	0.32

, omitting the intercept. Other methods, with the exception of Ridge and LR, were slightly biased. Ridge produced a coefficient deviation that was even greater than that for LR and could not be ignored. In one set of simulations, these estimators were tested with a sample size of $n=40$. A second series tested these estimators with a sample size of $n=80$. LR offered infinite estimates in a sample size of 40, as shown in Table 3, which is regarded as conditional on the presence of uncorrected MLEs due to sample size separation. Nonetheless, all of the approaches evaluated had finite bias and MSEs, allowing us to reasonably conclude that they could address the small sample separation problem. The maximum likelihood estimation converged as the sample size grew from 40 to 80, and LR produced an effective bias and MSE. One can also conclude from Table 4 that the MSE of LR was inflated, especially when the correlation coefficient was between 0.85 and 0.95, and some MSE values exceeded 1. According to Table 3 and Table 4, all penalized methods outperformed LR, as evidenced by the smaller MSE. Furthermore, the biases of the Firth, LF11, and LF22 methods were less severe than that of the LR model. Because of the ridge penalty term in DPLE, lFRE11, and lFRE22, a slight increase in bias was required to ensure a decrease in the MSE. As the correlation coefficient increased, so did the MSEs of LR, Firth, Ridge, and LF22. However, it appears that DPLE, lFRE11, and lFRE22 performed the best in terms of reducing the MSE. It is worth noting that lFRE22 performed best because it achieved the greatest reduction in MSE in all experimental settings. The findings appear to suggest that lFRE in logistic regression warrants further investigation. When the covariables were highly correlated, adding a ridge parameter improved the estimator’s performance.

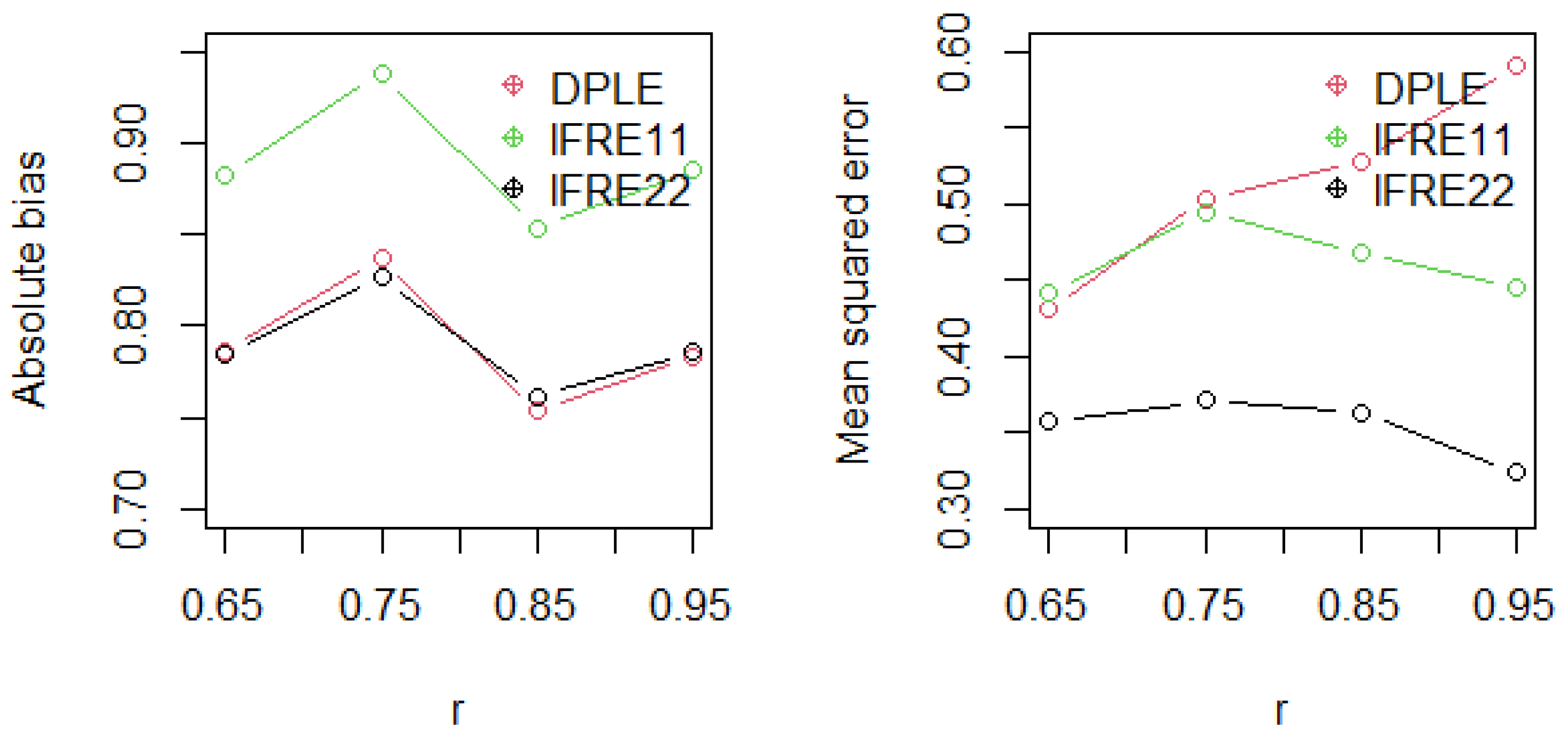
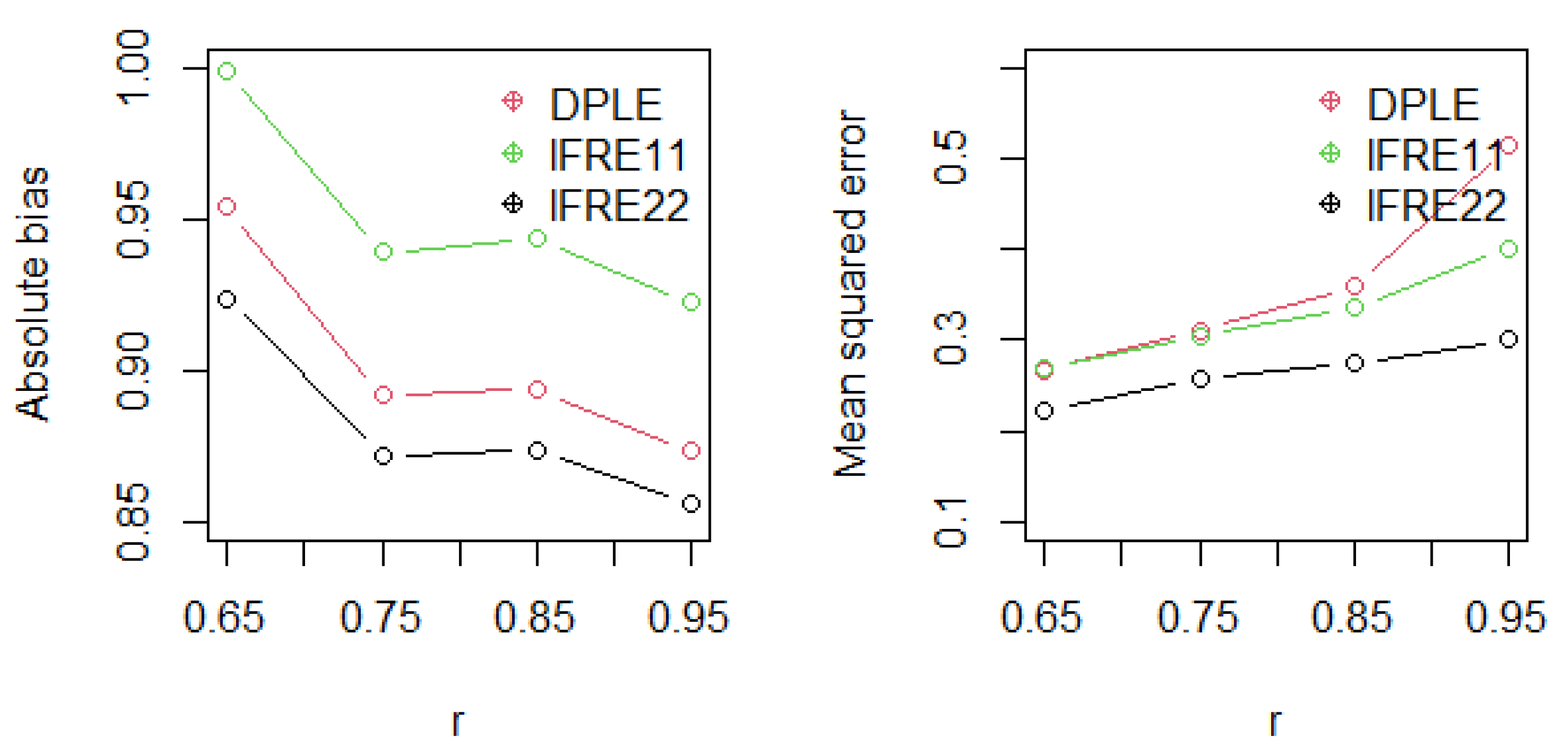
Figure 2 and Figure 3 analyze the biases and MSEs of the DPLE, lFRE11, and lFRE22 methods over all explanatory variables, omitting the intercept for $n=40$ and $n=80$, respectively. The results in Figure 2 reveal that they provided almost the same level of bias, followed by lFRE11, lFRE22 provided the lowest MSE, and DPLE provided the highest MSE, especially when the correlation coefficient value was high in the sample size of 40. In practically all situations, lFRE22 performed best in terms of bias and MSE, as shown in Figure 3. In the situation of increasing collinearity, DPLE also performed poorly. It was revealed that when the sample size was small and the multicollinearity was severe, it was recommended to use lFRE22, which not only yielded modest absolute bias but also provided the lowest MSE when compared with other penalized approaches.

As a result, we believe that the lFRE approach is frequently the best method for small datasets with strongly correlated independent variables, as it efficiently removes bias from predicted probabilities and provides the smallest MSE while also delivering very accurate regression coefficients. When the sample size is small and the independent variables are highly correlated, lFRE is more computationally simple than competing penalized regression approaches.

5. Breast Cancer Study

The dataset used to evaluate the predictive performance of our proposed estimator and compare it to other estimators under study is available from the University of California Irvine machine learning repository, and it was originally extracted from the study conducted by M. Pereira et al. (2018) [31], where the goal was to obtain the selection of effective breast cancer biomarkers in predicting the presence or absence of breast cancer in 116 patients (64 patients with breast cancer and 52 healthy controls). The presence or absence of breast cancer was of particular interest as an outcome (1 = healthy controls; 2 = patients). There were nine quantitative predictors in total. Anthropometric data and parameters could be acquired during standard blood analysis. Age, BMI, blood glucose, insulin, HOMA, leptin, adiponectin, resistin, and MCP-1 were all measured or observed in each of the 166 subjects. These clinical characteristics are detailed as follows:

• Age (years);
• BMI (kg/m${}^2$) was calculated by dividing the weight by the square of the height;
• Glucose (mg/dL), namely the serum glucose levels, were measured using a commercial kit and an automated analyzer;
• Insulin ($\mathsf{\mu }$U/mL), adiponectin ($\mathsf{\mu }$g/mL), resistin (ng/mL), and MCP-1(pg/dL) levels in the serum were determined using commercial enzyme-linked immunosorbent test kits for leptin, adiponectin, and resistin, as well as the chemokine Monocyte Chemoattractant Protein 1 (MCP-1);
• To assess insulin resistance, the Homeostasis Model Assessment (HOMA) index was calculated ($HOMA=\log \left(\right(If)\times (Gf\left)\right)/22.5$, where (If) is the fasting insulin level ($\mathsf{\mu }$U/mL) and Gf is the fasting glucose level (mmol/L)).

There were nine predictors in total, and they were all continuous. The HOMA index and insulin had a strong correlation ($r=0.93$). The results from fitting the logistic regression models using LR, Firth, LF11, LF22, Ridge, DPLE, lFRE11, and lFRE22 are summarized in

Table 5. Real data example: BS and AUROC obtained by fitting LR, Firth, LF11, LF22, Ridge, DPLE, lFRE11, and lFRE22 for a breast cancer study.

ID	Model	BS	AUROC
1	LR	0.2108	0.6973
2	Firth	0.2117	0.7626
3	LF11	0.2079	0.7732
4	LF22	0.2072	0.7749
5	Ridge	0.2024	0.7775
6	DPLE	0.2003	0.7762
7	lFRE11	0.1985	0.7816
8	lFRE22	0.1985	0.7816

. The model’s discriminating ability was quantified using the area under the receiver operating characteristic curve (AUROC), which is a measure that distinguishes subjects with and without events of interest. When the AUROC value was around 0.5, that meant there was no discrimination, and when it was close to 1, that meant there was excellent discrimination. The Brier Score (BS) was used to assess the overall predictive performance, and it is the mean of the squared difference between each patient’s observed and predicted risk as determined by the model. The better the performance, the lower the value. When $BS=0$, the prediction is perfect. Table 5 reveals their predictive performance using the two most common approaches to predictive accuracy (BS and AUROC).

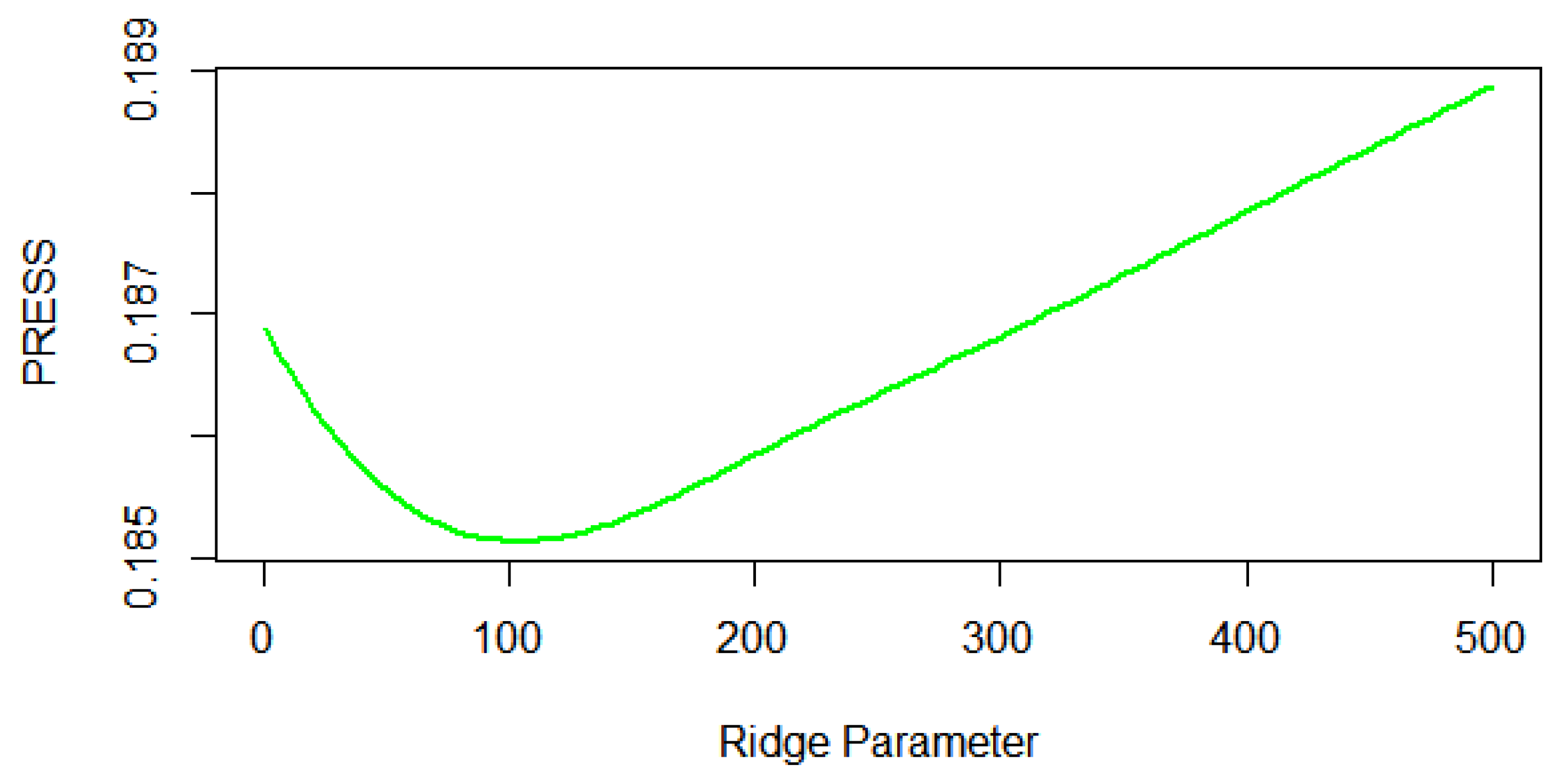
The results of ridge parameter selection using cross-validation are provided in Figure 4. The ideal ridge parameter for this dataset was determined to be 100. The assessment metrics BS and AUROC chose the same model, lFRE22, according to the results. Table 5 indicates that all penalized estimators increased in AUROC over LR for both predictive performance measures (BS and AUROC). It should be noted that Firth’s performance in BS was significantly worse than that of the LR model, which is consistent with earlier findings [13]. Furthermore, the magnitudes of the three double-penalized estimators (DPLE, lFRE11, and lFRE22) were significantly smaller than those of the three single-penalized estimators (Firth, LF11, and LF22) for all items. It was also observed from the results in Table 5 that the three double-penalized estimators with ridge parameters outperformed the three single-penalized estimators. This is because, as previously stated, the two variables of the HOMA index and insulin were highly correlated, and the ridge penalty penalized the multicollinearity effect. Regarding the the BS and AUROC, LF22 surpassed Firth and LF11, whereas Firth and LF11 outperformed each other. Similarly, lFRE11 and lFRE22 provided roughly the same degree of improvement in BS and AUROC, but DPLE gave the greatest BS value and the lowest AUROC value of the three doubly penalized estimators. As a result, in the setting of a small dataset with strongly correlated covariates, such analysis adequately demonstrates the superiority of lFRE22’s predictive ability.

Given the sample size of 116, finite MLEs were available in the conventional logistic regression model for this dataset. As a result, based on the convergent simulation results, the simulation findings for the LR model are relevant and comparable. In general, lFRE22 had the lowest BS and the highest AUROC compared with the other models discussed in this study. Such a result demonstrates that lFRE22 should be emphasized.

6. Discussion and Conclusions

In this study, separation and multicollinearity problems in logistic regression were discussed. Despite the issue being a hot topic for more than 40 years, few studies have attempted to handle both types of problems at the same time. This paper reviewed some shortcomings in Shen and Gao’s method (DPLE) and investigated a new double-penalty likelihood estimation method called lFRE, which combines a logF-type penalty with a ridge penalty to effectively solve separation and multicollinearity problems in logistic regression.

The results revealed that lFRE (lFRE11 and lFRE22) was superior to Firth, LF11, LF22, and DPLE in terms of prediction performance. Separation is commonly solved using Firth, LF11, and LF22. As long as there is no multicollinearity in logistic regression, LF22 has been proven to be the preferred method for obtaining unbiased prediction probability and the minimum MSE of coefficient estimation. However, when the separation and multicollinearity problems emerge at the same time in logistic regression, they are not appropriate. Considering separation and multicollinearity, based on the simulation results, we support that lFRE is superior to DPLE because lFRE is effective not only in solving separation problems but also in solving multicollinearity problems. On the other hand, when multicollinearity is taken seriously, DPLE will provide a non-negligible MSE.

In conclusion, Shen and Gao’s double-penalized likelihood estimator may provide a more appropriate reference point than previous penalized estimators, given that the generated estimates remain finite even when separation occurs. However, based on the research results, we suggest using lFRE instead of Shen and Gao’s method to deal with the separation and multicollinearity problems of small or sparse data with strong correlation of variables. The reasons for this are as follows. First, the proposed lFRE provides the minimum MSE in regression coefficient estimation and has greater improvement in prediction performance than other penalty method, such as DPLE. Secondly, since a logF-type penalty releases the intercept from the penalty and accurately estimates the average prediction probability, lFRE provides an unbiased prediction probability. In contrast, DPLE penalizes the intercept and introduces bias into the prediction probability. Thirdly, the logF-type penalty used by lFRE is not data-dependent, and it does not incorporate the correlation between explanatory variables, which is different from the Firth-type penalty. Finally, lFRE performs reasonably well in the case of high correlation between covariates. However, in this scenario, DPLE will result in a large MSE. As a result, lFRE is superior to DPLE, and lFRE22 is superior to lFRE11 among the two forms of lFRE11. Although both have similar prediction efficiencies, lFRE22 has a smaller MSE in terms of the regression coefficient, especially for continuous variables.

In addition, lFRE can be applied to any generalized linear model (GLIM) for future research.