Abstract
Background: The assessment of the evolution or fall of the temperature distribution of all biological tissues, and particularly human in vivo tissues at adverse temperatures, is crucial because excess cold or heat can impair the human body and its physiological processes. However, this estimation through experimental investigations is challenging due to the ability of the human body to bear a wide range of unfavourable temperatures. Thus, it becomes imperative to frame a mathematical model and its solution for the measurement of the temperature distribution in the selected tissue. Method: The three-dimensional cylindrical bioheat equation, with initial and boundary conditions, was used to formulate a mathematical model. The model was solved using the variables-separable method. Results: The model was solved analytically, and MATLAB software was used for numerical calculations and a graphical representation. The model was applied to display the temperature distributions in human skin and in the head. Conclusions: The paper helps predict the distribution of heat and corresponding burn or cold injuries in human tissue well in advance of applying any thermal treatment such as targeted tumour hyperthermia or cryosurgery.
Keywords:
temperature distribution; cylindrical bioheat equation; variables-separable method; hyperthermia; cryosurgery MSC:
92B05; 92C10; 92C30; 92C35; 92C50; 46N60
1. Introduction
The process of heat transfer in human tissues is uneven due to the heterogeneous structure of the body. Therefore, experimental investigations seem cumbersome to serve this purpose. However, the theoretical and mathematical analyses of the bioheat transfer mechanism have proven to be pivotal tools. In a wide range of biomathematics, bioengineering and biomedical applications, including cancer hyperthermia, brain hypothermia, burn and cold injury assessment, the diagnosis of diseases through tests, thermal comfort analysis, cryopreservation and cryosurgery, it is imperative to gauge the temperature distribution in selected tissues. There are many parameters responsible for the heat transfer processes in the human body, which include generalised initial and boundary conditions, blood perfusion rate, the volumetric heating of fluids, heat exchange, etc. All these factors need to be fully taken into account for a sufficiently comprehensive analysis, and Penne’s [1] bioheat equation fulfils the requirement. Most human organs, such as the arm, leg, neck, head or torso, resemble cylindrical shapes. Therefore, to study the process of heat transfer and its distribution in human skin, the cylindrical form of the bioheat equation seems an appropriate differential equation to formulate a model. Therefore, a mathematical model based on the cylindrical form of Penne’s bioheat equation has been formulated and solved analytically by the variables-separable method. Earlier, systematic work on heat transfer in the human body on different issues has been carried out by researchers. Srivastava et al. [2] derived an analytical solution of the cylindrical heat equation by the separation of variables, and hence a complete solution by the superposition approach was obtained. The authors compiled the results from the Fourier–Bessel series to obtain a direct blending of the results for the heat transfer and temperature distribution. Endalew [3] used the five-point central difference method to solve the three-dimensional transient heat conduction equation in cylindrical coordinates. The author showed that compared to the three-point central difference method, the numerical method could compute a solution to the heat conduction equation more precisely and claimed that the calculations were simple when utilizing the five-point central difference method with cylindrical grids as the grid sites were rounded. Mir Aijaz et al. [4] studied targeted hyperthermia using the spherical bioheat simulation of temperature profiles in tumour tissue and its peripherals. Comprehensive studies on heat transfer in human tissue were accomplished by Shen and Zhang [5], Maurício and Jurandir [6], Liu and Deng [7], Yuko and Masaki [8] and Majchrzak E. and Turchan [9]. In the study by Malekmohamadi [10], the exact solution of the steady and unsteady states of the hyperbolic bioheat equations was examined for multilayer skin with a tumour at different heat fluxes on its surface and the generation of internal heat in the tumour. The issue of thermal stresses on the human head due to inauspicious environmental temperatures were addressed by Aijaz et al. [11]. However, none of these researchers used the three-dimensional cylindrical bioheat equation. Researchers studied these issues using different methodologies and approaches. In this paper, we use the cylindrical form of the bioheat equation for the study of heat transfer in human tissue.
One of the biggest challenges is having a precise understanding of temperature profiles appropriate for the normal functioning of the human body. According to Mackowiak et al. [12], the human body’s typical temperature range is between 37.2 C and 37.7 C. To prevent neurologic injury, the body temperature needs monitoring during hyperthermia or hypothermia. Hyperthermia encompasses heat rash, heat cramps, heat exhaustion, heat stroke, etc., whereas hypothermia results from environmental exposure, metabolic disorders or therapeutic intervention. Shirkavand and Nazif [13] used a numerical study to obtain the conditions for hyperthermia without causing burn injury. Tae et al. [14] carried out a numerical analysis to determine the temperature distribution in human dermal tissues and any potential burns produced by local heating of the skin. Luchakov and Nozdrachev [15] concluded that in terms of heat transfer, the core and surface tissue zones behaved differently and depended upon blood circulation and other factors. Kashcooli et al. [16] investigated the effects of blood vessels on temperature distribution in skin tissue subjected to various thermal therapy conditions. Jinao et al. [17] developed new iterative procedures along with improved iteration schemes to adjust the heat exposure time and instrument power for desired thermal lesion volumes. The proposed methodology was analysed quantitatively using a multilayered tissue model with a scope of applying it to a clinically relevant scenario of personalized HIFU treatment of hepatic cancers. Jinao and Sunita [18] presented a fast numerical algorithm based on the FED-FEM framework for the analysis of Penne’s bioheat transfer in soft tissue, and it was particularly suited for real-time applications. The authors justified their claim of fast computation with solid reasons. Yansheng et al. [19] aimed to deduce and numerically prove an analytical transient-time solution for the temperature profiles due to a point source of electrical current in an infinite medium. Jinao and Sunita [20] presented a new cellular neural network methodology for real-time prediction and analysis of tissue temperatures and thermal dose for thermotherapeutic applications. The authors concluded that the simulation and comparison of results demonstrated that their proposed method could achieve a significant numerical accuracy compared to a commercial finite-element analysis package and achieved significant computation time reductions. Andreozzi et al. [21] formulated a thermoporoelastic model for heat transfer and fluid flow through tumour tissue, and the governing equations were scaled and solved by employing a finite-element scheme for a one-dimensional spherical coordinate system. A sensitivity analysis was also carried out for different scaling parameters. The results showed excellent agreement when compared with analytical solutions available in the literature for displacement, velocity, pressure, and temperature profiles. Sensitivity analyses for various scaling parameters were also presented.
The human brain is one of the most sensitive organs in the human body. Therefore, to prevent brain damage in patients from cerebral ischaemia, a mild or moderate hypothermia has been suggested for use in clinical settings. The situation becomes more intense when dealing with tumour patients during hyperthermia treatment. In their research, Zhu and Diao [22] used a theoretical model to investigate of the temperature gradients in the injured brain during selective cooling of the brain surface. In this paper, the variation of temperature distribution during targeted hyperthermia treatment of the tumour is studied and represented graphically by Figure 1 and Figure 2.
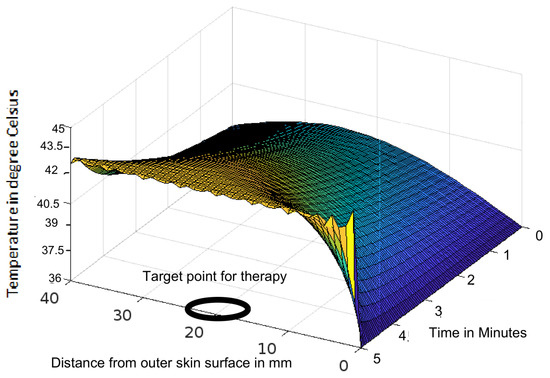
Figure 1.
Variation of temperature profiles during thermotherapy at a temperature of 43 C targeted to a tumour located in a human head.
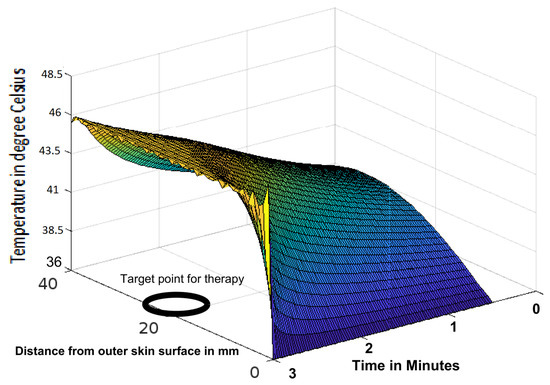
Figure 2.
Variation of temperature profiles during thermotherapy at a temperature of 46 C targeted to a tumour located in a human head.
This paper uses mathematical analysis to examine the issue of heat transfer and temperature distribution in the skin and head. The method can be used on different parts of the human body separately by changing the corresponding numerical values of the parameters. The model can be used to determine the temperature distribution during tumour hyperthermia, burn injury, cold injury and cryosurgery. The model has application for the estimation of heat transfer in the bodies of workers, working in adverse environmental conditions, for example, in factories or in the sun during hot seasons, and similarly in cold environmental conditions, for example, cold stores or polar regions having a below-freezing temperature. One of the advantages of this paper over Srivastava et al. [2] and Endalew [3] is that it uses the bioheat equation instead of the heat equation. Similarly, the novelty is in using the cylindrical type of the bioheat equation instead of the rectangular bioheat equation (Jinao and Sunita [18]). Further, this study is the transient state of the three-dimensional cylindrical bioheat equation, while the earlier studies were either one-dimensional (Khanday and Khalid [23] and Youming et al. [24]) or two-dimensional cases (Makrariya and Adlakha [25]).
2. Mathematical Model
The three-dimensional cylindrical bioheat equation for in vivo tissue is
where the parameters k and are the thermal conductivity and density of tissue, respectively, and denote the heat generated by metabolism and an external source, respectively, c and denote the specific heat of tissue and blood, respectively, is the blood mass flow rate, is the arterial temperature and is the blood density. Further, the following boundary and initial conditions are to be incorporated in the model:
where h is the heat transfer coefficient, and at
At , C and the conditions hold for .
The continuity principle applies to the heat flux at the interfaces between two contiguous regions of the human tissue, and as a result, interface conditions are applicable and hence , where suffixes i and denote two contiguous regions. From Equation (1), we have
Using and , we get
The dimensionless parameters and corresponding to and T are defined as
where is the ambient temperature. Using these parameters in Equation (4) we have
To apply the variables-separable method, assume
Now assume the variables’ separability of as
As a result, from Equation (11), we get
which is Bessel’s equation of order where . The general solutions of Equations (8), (12), (13) and (15) are, respectively,
where
and and are connected by the relation
Using Equations (17)–(19) in Equation (10), and the resultant equation, along with Equation (16) in Equation (7) for a solution of Equation (6), the general solution is the superposition of these elementary solutions as
At using Equation (2) and letting the expression of corresponding to be , from Equation (20), we have
To determine the coefficients, operating Equation (21) by and , and using the following orthogonality conditions
and
where and from Equation (21), we have
where
To determine the coefficients and , operating Equation (22) by and , utilizing the orthogonality conditions and noting that , and
we get for and
Hence, from Equation (22) we have
Using all these values of the parameters in Equation (20), we have
3. Numerical Calculations and Results
The analytical solution to the model was given in Equation (23) but to come up with findings that are applicable and can be graphed, numerical calculations and graphical visuals of the results are required. The integrals of the equation have definite limits and the variables of the function are separable. Therefore, arranging the terms having the same type of variables yields the complete solution by a superposition of all the terms. The superposition and hence the graphical derivations were carried out in MATLAB.
The scope of the model was open for various cases depending upon the domain of the model, heat source and other relevant parameters. Although the model had a good scope of applicability, we studied two cases from two domains. One pertained to heat transfer in the skin and subcutaneous tissue and the other to the human head. Considering the case of heat transfer in human skin through its various regions such as the epidermis, dermis, and subcutaneous tissues, the numerical values of the parameters are given in Table 1 (Aijaz et al. [26,27]), where the suffixes 1, 2, and 3 of the symbols of the parameters correspond to the epidermis, dermis, and subcutaneous tissue, respectively. Similarly, for heat transfer in the human head, the corresponding numerical values of the parameters are given in Table 2 with the domain consisting of the brain mm) and its peripherals, CSF mm), skull mm) and scalp mm). Here, the suffixes 1, 2 and 3 of symbolic parameters correspond to the numerical values of CSF, skull and scalp, respectively. In this simulation, we assumed that the imaginary axis of the organ coincided with the z-axis of the cylindrical frame. When using this model on a human forearm, the z-axis was parallel to the bone (ulna or radius) of the arm. Similarly, when applying this model on a human head, the z-axis was parallel to the spinal cord. Therefore, without loss of generality, we assumed that the numerical results for the temperature with respect to the z-axis were symmetric. Therefore, to avoid the accumulation of variables, we skipped the values of z, so that in the graphical representation, the temperature was treated as a function of r and at minutes, as shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 for skin and subcutaneous tissue, and in a similar way for the human head, graphs were plotted for the temperature as a function of r and time t as shown in Figure 1 and Figure 2.

Table 1.
Numerical values of the parameters of the skin.

Table 2.
Numerical values of the parameters for the head.
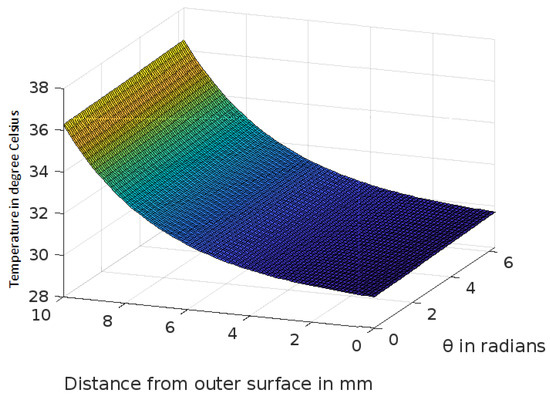
Figure 3.
Variation of temperature profiles in human skin with an external temperature at the skin surface of 25 C.
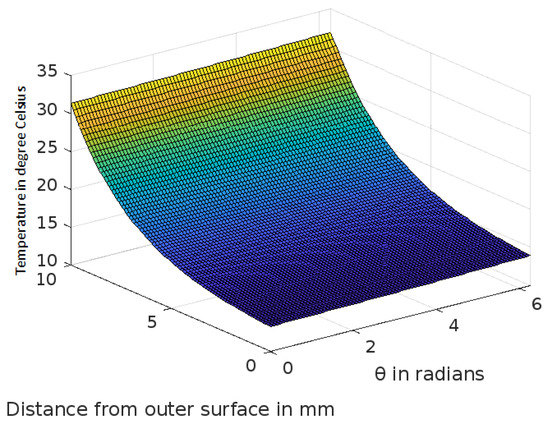
Figure 4.
Variation of temperature profiles in human skin with an external temperature at the skin surface of 10 C.
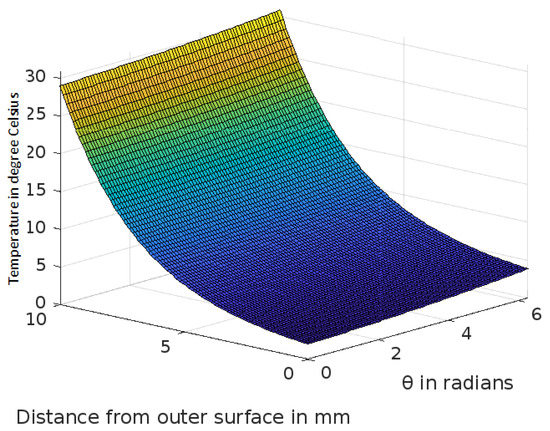
Figure 5.
Variation of temperature profiles in human skin with an external temperature at the skin surface of 0 C.
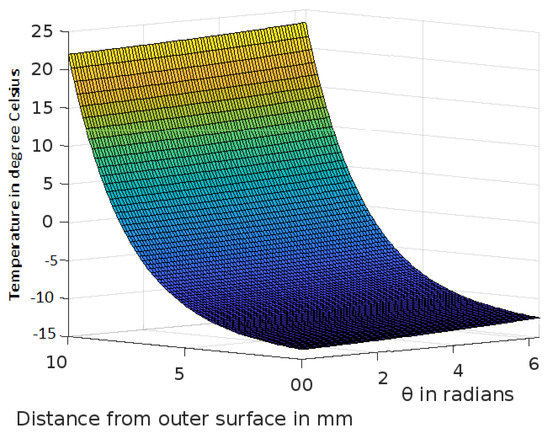
Figure 6.
Variation of temperature profiles in human skin with an external temperature at the skin surface of C.
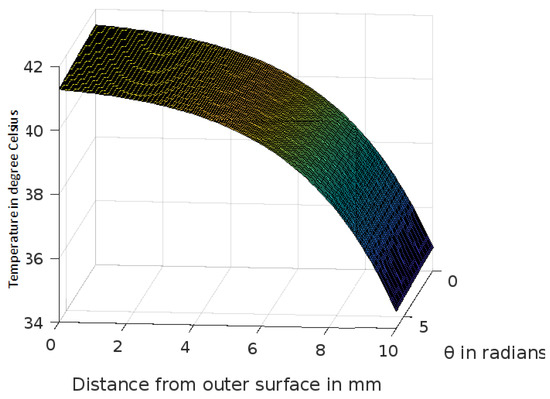
Figure 7.
Variation of temperature profiles in human skin with an external temperature at the skin surface of 42 C.
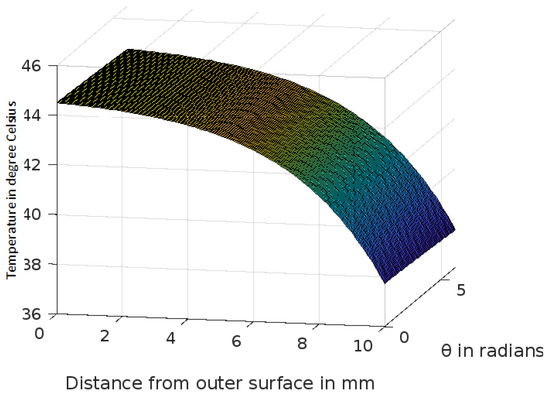
Figure 8.
Variation of temperature profiles in human skin with an external temperature at the skin surface of 45 C.
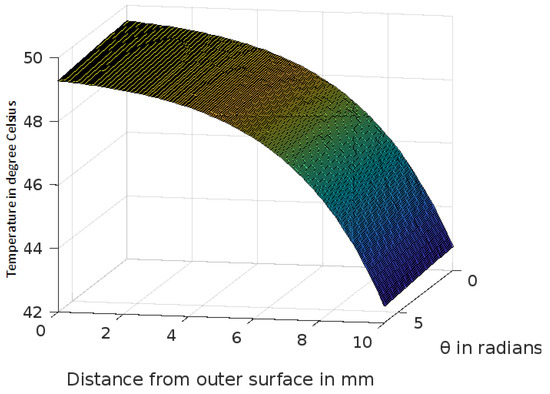
Figure 9.
Variation of temperature profiles in human skin with an external temperature at the skin surface of 50 C.
4. Discussion and Conclusions
The analytic solution of the 3-D cylindrical bioheat equation and its applications to govern heat transfer in human tissues were described in this study. The boundary conditions were taken into account, and the cases about the exposure of skin surfaces to heating and cooling environmental conditions were simulated. The significance of some important thermal properties of biological tissues [28], such as blood perfusion, heat capacity and thermal conductivity were taken into account. The graphs shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 were drawn at external temperatures of 25 C, 10 C, 0 C, C, 42 C, 50 C and 45 C. It is visible in these graphs that the effect of external temperature increases (where the external temperature is greater than the normal temperature) or decreases (where the external temperature is less than the normal temperature) exponentially from the outer skin surface to the inner tissue. Similarly, in therapy cases, the focus of high temperature is on the tumour cells so that the temperature in the centre of the tumour is significantly higher than at its periphery. The effect decreased tending to a normal body temperature in the surroundings of the tumour, as shown in Figure 1 and Figure 2 with a temperature at the targeted point of 43 C and 46 C, respectively. By incorporating the research on burn injuries due to elevated temperatures [26,29,30], fluid regulations in tissue [31], a hybrid system for synergetic effect [32] and other physiological setups, the present study will serve clinical laboratories in reducing the risks of tissue damage during hyperthermic treatments.
The analytic solution can be beneficial in several thermally focused biomedical problems [33]. It can be employed to predict how the temperature distribution would change during tumour hyperthermia, abnormal heat exposure and thermal stress and hence prevent burn injuries [26,30] at the periphery. Similarly, it can be used to anticipate the decline in temperature and hence prevent cold injuries [26,30] during brain hypothermia and cryosurgery. Moreover, for the freezing or heating necrosis temperature of the tissue, this technique can monitor the temperature profiles and hence guide the treatment accordingly to attain the required temperature during cryosurgery or hyperthermic treatment.
A limitation of this study is that the temperature variation was considered only with respect to the radius r and and to avoid the accumulation of variables in three-dimensional space, no variation of the temperature along the z-axis was plotted. Another limitation of this study is that the solution of the model was limited to an analytical one, and the complete solution and graphical display were obtained using MATLAB software. However, no orthogonal validation by any other methods was carried out to validate the results. Thus, there is scope for extending this work to an improved form by addressing either or both of these limitations. There is a direct relation between physiological setup and temperature variation in living tissues. Therefore, test cases with a temperature distribution along the z-direction will significantly improve the results. In future studies, a numerical method can be used as an orthogonal validation to verify the reliability of the model.
Author Contributions
The authors contributed equally to this work. Development of theoretical and mathematical model, J.G.D. and M.A.; formal analysis and validation, M.A.; numerical calculation and graphical representation, M.A. and I.M.A.; writing—review and editing, J.G.D., M.A., I.M.A. and A.W.; formatting and final version of the manuscript, I.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deanship of Scientific Research at King Khalid University through the Research Groups Program under grant number R.G.P. 2/132/43.
Data Availability Statement
The data used in this study are available within the paper.
Acknowledgments
The authors thank and extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting Human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, H.M.; Kung, K.Y.; Lee, S.F.; Lin, S.D. Analytic solutions of the cylindrical heat equation with a heat source. Russ. J. Math. Phys. 2021, 28, 545–552. [Google Scholar] [CrossRef]
- Endalew, G.T. Numerical solution of three-dimensional transient heat conduction equation in cylindrical coordinates. J. Appl. Math. 2022, 2022, 1993151. [Google Scholar] [CrossRef]
- Mir, A.; Ibrahim, M.A.; Javid, G.D. Spherical Simulation of Temperature Profiles in Tumour Tissue and its Peripherals During Targeted Hyperthermia. Chiang Mai J. Sci. 2021, 48, 1149–1160. [Google Scholar]
- Shen, W.; Zhang, J. Modeling and numerical simulation of bioheat transfer and biomechanics in soft tissue. Math. Comput. Model. 2005, 41, 1251–1265. [Google Scholar] [CrossRef]
- Maurício, S.F.; Jurandir, I.Y. A transient three-dimensional heat transfer model of the human body. Int. Commun. Heat Mass Transf. 2009, 36, 718–724. [Google Scholar]
- Liu, J.; Deng, Z.S. Physics of Tumor Hyperthermia; Science Press: Beijing, China, 2008. [Google Scholar]
- Yuko, T.; Masaki, S. Heat transfer, physiological responses, and subjective perceptions during short contact time with wood or other materials. J. Wood Sci. 2021, 67, 27. [Google Scholar]
- Majchrzak, E.; Turchan, L. Numerical analysis of tissue heating using the bioheat transfer porous model. Comput. Assist. Methods Eng. Sci. 2013, 20, 123–131. [Google Scholar]
- Malekmohamadi, M.H.; Ahmadikia, H.; Mosharaf, D.M. The effect of heat flux distribution and internal heat generation on the thermal damage in multilayer tissue in thermotherapy. J. Therm. Biol. 2021, 99, 102920. [Google Scholar] [CrossRef]
- Mir, A.; Khanday, M.A.; Aasma, R. Variational finite element approach to study the thermal stress in multi-layered human head. Int. J. Biomath. 2014, 7, 1450073. [Google Scholar]
- Mackowiak, P.A.; Wasserman, S.; Levine, M. A critical appraisal of 98.6 °F, the upper limit of the normal body temperature, and other legacies of Carl Reinhold August Wunderlich. JAMA 1992, 268, 1578–1580. [Google Scholar] [CrossRef]
- Shirkavand, A.; Nazif, H.R. Numerical study on the effects of blood perfusion and body metabolism on the temperature profiles of human forearm in hyperthermia condition. J. Therm. Biol. 2019, 84, 339–350. [Google Scholar] [CrossRef]
- Tae, I.I.; Youn, S.B.; Kyounghwa, K. Numerical Study on the Temperature Profiles and Degree of Burns in Human Skin Tissue During Combined Thermal Therapy. Numer. Heat Transf. Part A 2015, 67, 921–933. [Google Scholar]
- Luchakov, L.Y.; Nozdrachev, A.D. Mechanism of heat transfer in different regions of human body. Hum. Anim. Physiol. 2009, 36, 53–57. [Google Scholar] [CrossRef]
- Kashcooli, M.; Salimpour, M.R.; Shirani, E. Heat transfer analysis of skin during thermal therapy using thermal wave equation. J. Therm. Biol. 2017, 64, 7–18. [Google Scholar] [CrossRef]
- Jinao, Z.; Bui, N.D.; Cheung, W.; Stuart, K.R.; Sunita, C. Fast computation of desired thermal dose: Application to focused ultrasound-induced lesion planning. Numer. Heat Transf. Part A Appl. 2020, 77, 666–682. [Google Scholar] [CrossRef]
- Jinao, Z.; Sunita, C. Real-time computation of bio-heat transfer in the fast explicit dynamics finite element algorithm (FED-FEM) framework. Numer. Heat Transf. Part B Fundam. 2019, 75, 217–238. [Google Scholar] [CrossRef]
- Yansheng, J.; Peng, L.; Yue, L.; Chong, W. A fundamental solution for radiofrequency heating due to a point electrical current in an infinite spatial domain: Numerical proofs with MATHEMATICA and ANSYS. Eng. Anal. Bound. Elem. 2021, 124, 98–109. [Google Scholar]
- Jinao, Z.; Sunita, C. Neural network methodology for real-time modelling of bio-heat transfer during thermo-therapeutic applications. Artif. Intell. Med. 2019, 101, 101728. [Google Scholar] [CrossRef]
- Andreozzi, A.; Iasiello, M.; Netti, P.A. A thermoporoelastic model for fluid transport in tumour tissues. J. R. Soc. Interface 2019, 16, 20190030. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Diao, C. Theoretical simulation of temperature distribution in the brain during mild hypothermia treatment for brain injury. Med. Biol. Eng. Comput. 2001, 39, 681–687. [Google Scholar] [CrossRef] [PubMed]
- Khanday, M.A.; Khalid, N. Mathematical and numerical analysis of thermal distribution in cancerous tissues under the local heat therapy. Int. J. Biomath. 2017, 10, 1750099. [Google Scholar] [CrossRef]
- Youming, C.; Shengwei, W.; Zheng, Z. An approach to calculate transient heat flow through multilayer spherical structures. Int. J. Therm. Sci. 2003, 42, 805–812. [Google Scholar]
- Makrariya, A.; Adlakha, N. Two dimensional finite element model of temperature distribution in dermal tissues of extended spherical organs of a human body. Int. J. Biomath. 2013, 6, 1250065. [Google Scholar] [CrossRef]
- Mir, A.; Khanday, M.A. Temperature distribution and thermal damage of peripheral tissue in human limbs during heat stress: A mathematical model. J. Mech. Med. Biol. 2016, 16, 1650064. [Google Scholar]
- Mir, A.; Khanday, M.A. Studying the effects of the heat stress on the various layers of human skin using damage function. Int. J. Comput. Mater. Sci. Eng. 2016, 5, 1650003. [Google Scholar]
- El-Brawany, M.A.; Nassiri, D.K.; Terhaar, G.; Shaw, A.; Rivens, I.; Lozhken, K. Measurement of thermal and ultrasonic properties of some biological tissues. J. Med. Eng. Technol. 2009, 3, 249–256. [Google Scholar] [CrossRef]
- Jiang, S.C.; Ma, N.; Li, H.J.; Zhang, X.X. Effects of thermal properties and geometrical dimensions on skin burn injuries. Burns 2002, 28, 713–717. [Google Scholar] [CrossRef]
- Ng, E.Y.K.; Chua, L.T. Comparison of one and two dimensional programmes for predicting the state skin burns. Burns 2002, 28, 27–34. [Google Scholar] [CrossRef]
- Khanday, M.A.; Mir, A.; Aasma, R. Numerical estimation of the fluid distribution pattern in human dermal regions with heterogeneous metabolic fluid generation. Int. J. Mech. Med. Biol. 2015, 15, 1550001. [Google Scholar] [CrossRef]
- Nizam-Uddin, N.; Elshafiey, I. Enhanced energy localization in hyperthermia treatment based on hybrid electromagnetic and ultrasonic system: Proof of concept with numerical simulations. BioMed Res. Int. 2017, 2017, 5787484. [Google Scholar] [CrossRef]
- Yarmolenko, P.S.; Moon, E.J.; Landon, C.; Manzoor, A.; Hochman, D.W.; Viglianti, B.L.; Dewhirst, M.W. Thresholds for thermal damage to normal tissues: An update. Int. J. Hyperth. 2011, 27, 320–343. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).