Deep Spatial-Temporal Neural Network for Dense Non-Rigid Structure from Motion
Abstract
1. Introduction
- We propose a novel deep neural network framework called DST-NRSfM to address the dense NRSfM challenge, which is superior for reconstructing objects with significant deformations because it does not require shape priors.
- We introduce the weighted spatial constraint to minimize the reconstruction error, improve mesh quality, and ensure that the reconstructed item is closer to the original shape. The second set of comparison experiments in Section 4.2 demonstrates the success of the weighted spatial constraint.
- The proposed technique achieves state-of-the-art performance on the most popular dense benchmark datasets. Section 4.3 provides evidence to support this hypothesis.
2. Related Works
3. Methods
3.1. Preliminary
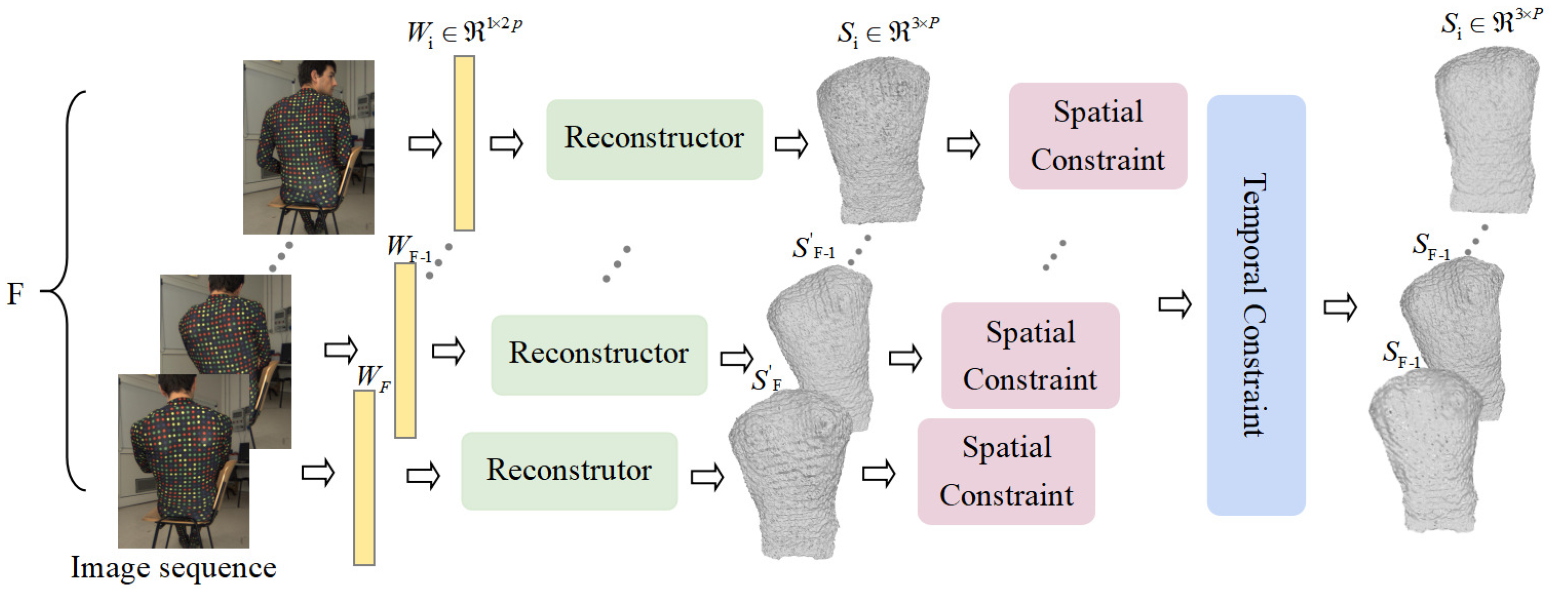
3.2. Deep Spatial-Temporal NRSfM
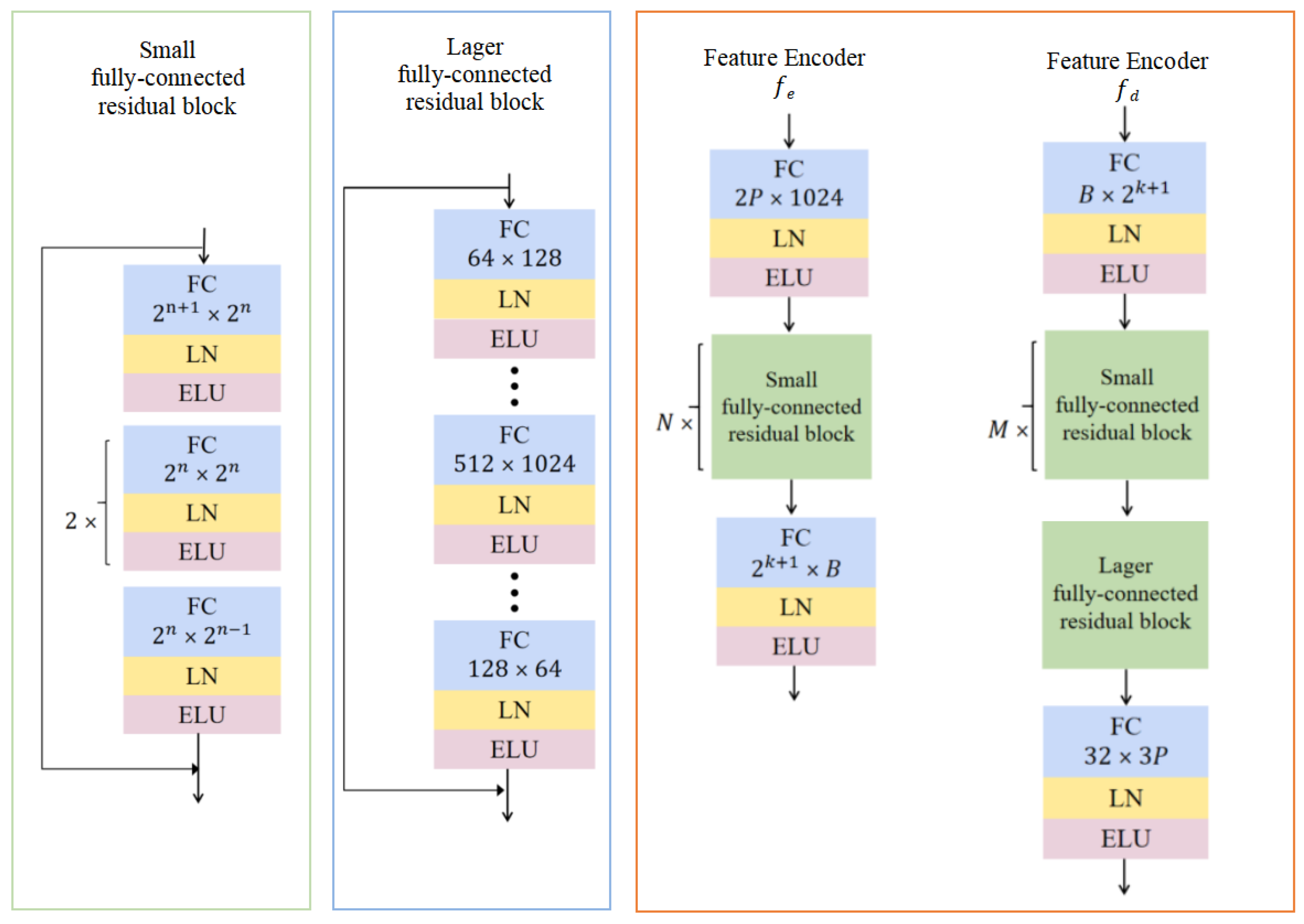
3.2.1. Shape Estimator in Reconstructor
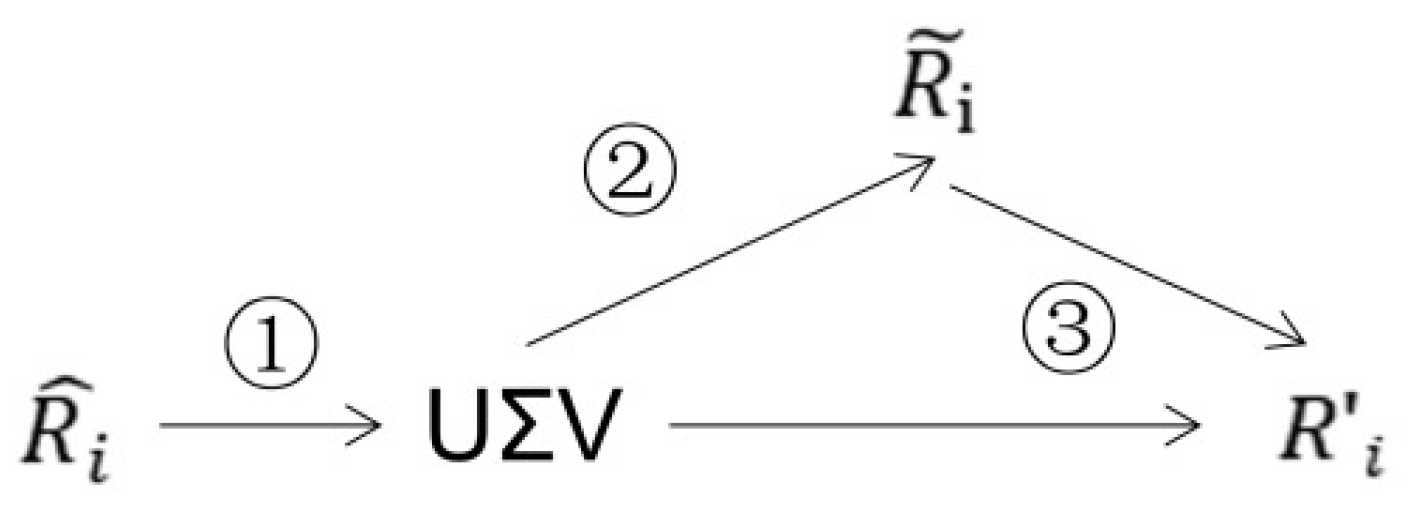
3.2.2. Rotation Estimation Network in Reconstructor
3.3. Temporal Constraint and Spatial Constraint
3.4. Alternative Training
4. Experiments
4.1. Implementation Details
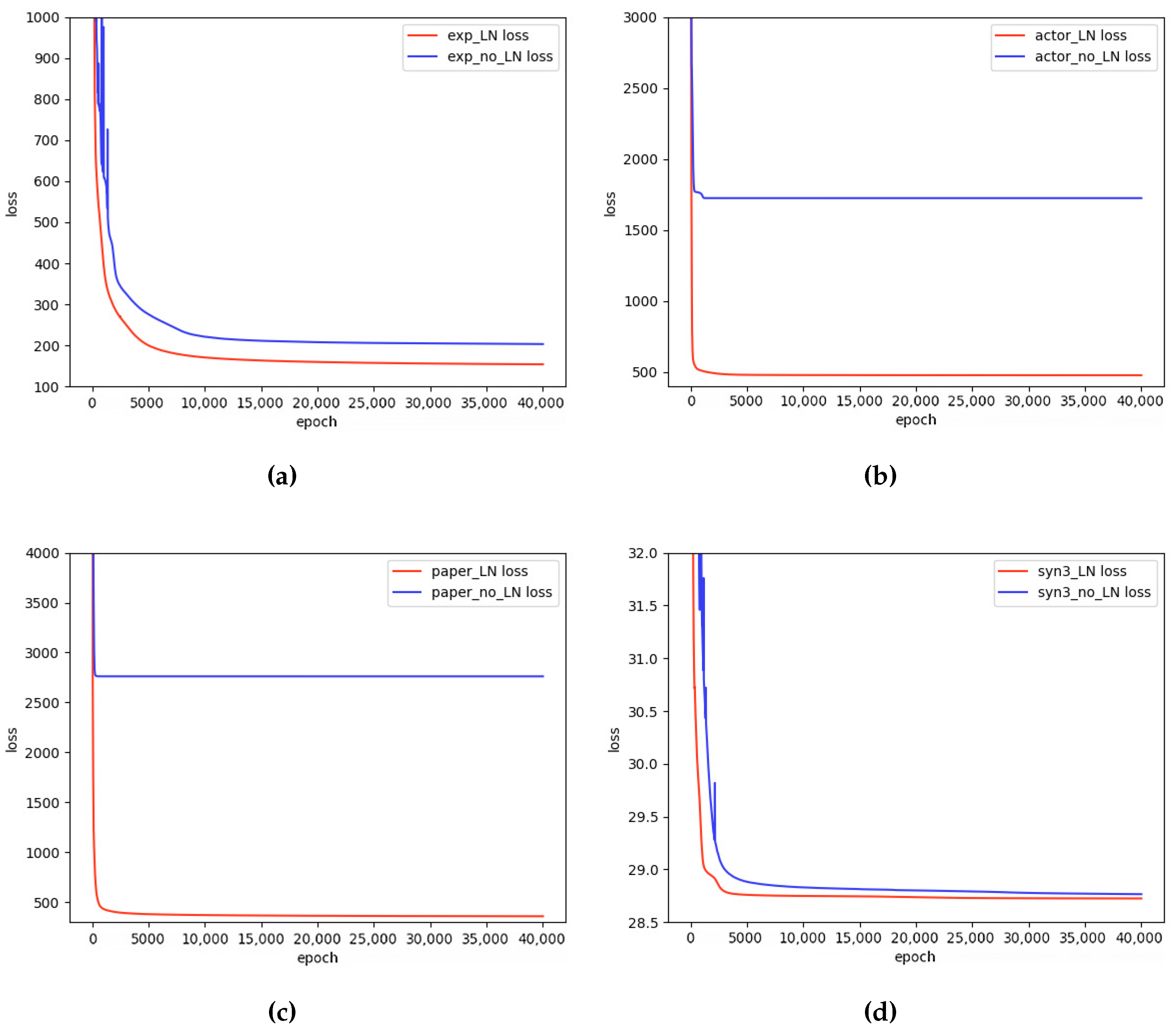
4.2. Network Structure Analysis
4.3. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Russell, C.; Fayad, J.; Agapito, L. Dense non-rigid structure from motion. In Proceedings of the 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 509–516. [Google Scholar]
- Golyanik, V.; Stricker, D. Dense batch non-rigid structure from motion in a second. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 254–263. [Google Scholar]
- Kumar, S.; Van Gool, L. Organic Priors in Non-Rigid Structure from Motion. arXiv 2022, arXiv:2207.06262. [Google Scholar]
- Song, J.; Patel, M.; Jasour, A.; Ghaffari, M. A Closed-Form Uncertainty Propagation in Non-Rigid Structure From Motion. IEEE Robot. Autom. Lett. 2022, 7, 6479–6486. [Google Scholar] [CrossRef]
- Wang, C.; Lucey, S. PAUL: Procrustean Autoencoder for Unsupervised Lifting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 434–443. [Google Scholar]
- Agudo, A.; Montiel, J.; Agapito, L.; Calvo, B. Online Dense Non-Rigid 3D Shape and Camera Motion Recovery. In Proceedings of the BMVC, Nottingham, UK, 1–5 September 2014. [Google Scholar]
- Garg, R.; Roussos, A.; Agapito, L. Dense variational reconstruction of non-rigid surfaces from monocular video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1272–1279. [Google Scholar]
- Kumar, S.; Cherian, A.; Dai, Y.; Li, H. Scalable dense non-rigid structure-from-motion: A grassmannian perspective. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 254–263. [Google Scholar]
- Sidhu, V.; Tretschk, E.; Golyanik, V.; Agudo, A.; Theobalt, C. Neural dense non-rigid structure from motion with latent space constraints. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 204–222. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Shi, F.; Xiao, J.; Wu, W. Non-rigid structure-from-motion on degenerate deformations with low-rank shape deformation model. IEEE Trans. Multimed. 2014, 17, 171–185. [Google Scholar] [CrossRef]
- Wang, Y.M.; Zheng, J.B.; Jiang, M.F.; Xiong, Y.L.; Huang, W.Q. A Trajectory Basis Selection Method for Non-Rigid Structure from Motion. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2014; Volume 644, pp. 1396–1399. [Google Scholar]
- Agudo, A.; Moreno-Noguer, F. A scalable, efficient, and accurate solution to non-rigid structure from motion. Comput. Vis. Image Underst. 2018, 167, 121–133. [Google Scholar] [CrossRef]
- Torresani, L.; Hertzmann, A.; Bregler, C. Nonrigid structure-from-motion: Estimating shape and motion with hierarchical priors. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 878–892. [Google Scholar] [CrossRef]
- Paladini, M.; Del Bue, A.; Stosic, M.; Dodig, M.; Xavier, J.; Agapito, L. Factorization for non-rigid and articulated structure using metric projections. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2898–2905. [Google Scholar]
- Gotardo, P.F.; Martinez, A.M. Non-rigid structure from motion with complementary rank-3 spaces. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3065–3072. [Google Scholar]
- Kong, C.; Lucey, S. Prior-less compressible structure from motion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4123–4131. [Google Scholar]
- Agudo, A.; Moreno-Noguer, F. Force-based representation for non-rigid shape and elastic model estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2137–2150. [Google Scholar] [CrossRef]
- Dai, Y.; Li, H.; He, M. A simple prior-free method for non-rigid structure-from-motion factorization. Int. J. Comput. Vis. 2014, 107, 101–122. [Google Scholar] [CrossRef]
- Parashar, S.; Pizarro, D.; Bartoli, A. Isometric non-rigid shape-from-motion in linear time. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4679–4687. [Google Scholar]
- Agudo, A.; Moreno-Noguer, F.; Calvo, B.; Montiel, J.M.M. Sequential non-rigid structure from motion using physical priors. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 979–994. [Google Scholar] [CrossRef]
- Cha, G.; Lee, M.; Cho, J.; Oh, S. Non-rigid surface recovery with a robust local-rigidity prior. Pattern Recognit. Lett. 2018, 110, 51–57. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Joo, H.; Liu, Y.; Sheikh, Y. Structure from recurrent motion: From rigidity to recurrency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3032–3040. [Google Scholar]
- Dai, Y.; Deng, H.; He, M. Dense non-rigid structure-from-motion made easy—A spatial-temporal smoothness based solution. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4532–4536. [Google Scholar]
- Graßhof, S.; Brandt, S.S. Tensor-Based Non-Rigid Structure From Motion. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 3011–3020. [Google Scholar]
- Collins, T.; Bartoli, A. Locally affine and planar deformable surface reconstruction from video. In Proceedings of the International Workshop on Vision, Modeling and Visualization, Siegen, Germany, 15–17 November 2010; pp. 339–346. [Google Scholar]
- Bartoli, A.; Gérard, Y.; Chadebecq, F.; Collins, T. On template-based reconstruction from a single view: Analytical solutions and proofs of well-posedness for developable, isometric and conformal surfaces. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2026–2033. [Google Scholar]
- Kumar, S. Jumping manifolds: Geometry aware dense non-rigid structure from motion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5346–5355. [Google Scholar]
- Kumar, S.; Van Gool, L.; de Oliveira, C.E.; Cherian, A.; Dai, Y.; Li, H. Dense Non-Rigid Structure from Motion: A Manifold Viewpoint. arXiv 2020, arXiv:2006.09197. [Google Scholar]
- Cha, G.; Lee, M.; Oh, S. Unsupervised 3d reconstruction networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 3849–3858. [Google Scholar]
- Novotny, D.; Ravi, N.; Graham, B.; Neverova, N.; Vedaldi, A. C3dpo: Canonical 3d pose networks for non-rigid structure from motion. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 7688–7697. [Google Scholar]
- Kong, C.; Lucey, S. Deep non-rigid structure from motion. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1558–1567. [Google Scholar]
- Wang, C.; Lin, C.H.; Lucey, S. Deep NRSfM++: Towards Unsupervised 2D-3D Lifting in the Wild. In Proceedings of the 2020 International Conference on 3D Vision (3DV), Fukuoka, Japan, 25–28 November 2020. [Google Scholar]
- Kumar, S. Non-rigid structure from motion: Prior-free factorization method revisited. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2020; pp. 51–60. [Google Scholar]
- Park, S.; Lee, M.; Kwak, N. Procrustean regression: A flexible alignment-based framework for nonrigid structure estimation. IEEE Trans. Image Process. 2017, 27, 249–264. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Lee, M.; Kwak, N. Procrustean regression networks: Learning 3d structure of non-rigid objects from 2d annotations. In Proceedings of the European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–18. [Google Scholar]
- Lee, M.; Cho, J.; Choi, C.H.; Oh, S. Procrustean normal distribution for non-rigid structure from motion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1280–1287. [Google Scholar]
- Zeng, H.; Dai, Y.; Yu, X.; Wang, X.; Yang, Y. PR-RRN: Pairwise-Regularized Residual-Recursive Networks for Non-rigid Structure-from-Motion. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5600–5609. [Google Scholar]
- Deng, H.; Zhang, T.; Dai, Y.; Shi, J.; Zhong, Y.; Li, H. Deep Non-rigid Structure-from-Motion: A Sequence-to-Sequence Translation Perspective. arXiv 2022, arXiv:2204.04730. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Valgaerts, L.; Wu, C.; Bruhn, A.; Seidel, H.P.; Theobalt, C. Lightweight binocular facial performance capture under uncontrolled lighting. ACM Trans. Graph. 2012, 31, 1–11. [Google Scholar] [CrossRef]
- Varol, A.; Salzmann, M.; Fua, P.; Urtasun, R. A constrained latent variable model. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2248–2255. [Google Scholar]
- Agudo, A.; Moreno-Noguer, F. Global model with local interpretation for dynamic shape reconstruction. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 264–272. [Google Scholar]
- White, R.; Crane, K.; Forsyth, D.A. Capturing and animating occluded cloth. ACM Trans. Graph. 2007, 26, 34–es. [Google Scholar] [CrossRef]
- Russell, C.; Fayad, J.; Agapito, L. Energy based multiple model fitting for non-rigid structure from motion. In Proceedings of the CVPR 2011, Providence, RI, USA, 20–25 June 2011; pp. 3009–3016. [Google Scholar]
- Stoyanov, D. Stereoscopic scene flow for robotic assisted minimally invasive surgery. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2012; pp. 479–486. [Google Scholar]
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 Maarch–1 April 1993; pp. 586–591. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 1–13 December 2015; pp. 1026–1034. [Google Scholar]
- Tewari, A.; Bernard, F.; Garrido, P.; Bharaj, G.; Elgharib, M.; Seidel, H.P.; Pérez, P.; Zollhofer, M.; Theobalt, C. Fml: Face model learning from videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10812–10822. [Google Scholar]
- Ansari, M.D.; Golyanik, V.; Stricker, D. Scalable dense monocular surface reconstruction. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 78–87. [Google Scholar]
- Golyanik, V.; Jonas, A.; Stricker, D. Consolidating segmentwise non-rigid structure from motion. In Proceedings of the 2019 16th International Conference on Machine Vision Applications (MVA), Tokyo, Japan, 27–31 May 2019; pp. 1–6. [Google Scholar]
- Golyanik, V.; Jonas, A.; Stricker, D.; Theobalt, C. Intrinsic dynamic shape prior for fast, sequential and dense non-rigid structure from motion with detection of temporally-disjoint rigidity. arXiv 2019, arXiv:1909.02468. [Google Scholar]
- Wang, Y.; Peng, X.; Huang, W.; Wang, M. A Convolutional Neural Network for Nonrigid Structure from Motion. Int. J. Digit. Multimed. Broadcast. 2022, 2022, 3582037. [Google Scholar] [CrossRef]
- Paladini, M.; Del Bue, A.; Xavier, J.; Agapito, L.; Stošić, M.; Dodig, M. Optimal metric projections for deformable and articulated structure-from-motion. Int. J. Comput. Vis. 2012, 96, 252–276. [Google Scholar] [CrossRef]
- Garg, R.; Roussos, A.; Agapito, L. A variational approach to video registration with subspace constraints. Int. J. Comput. Vis. 2013, 104, 286–314. [Google Scholar] [CrossRef] [PubMed]
- Gotardo, P.F.; Martinez, A.M. Kernel non-rigid structure from motion. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 802–809. [Google Scholar]



| syn3 | syn4 | Expressions | Actor Mocap | Paper | |
|---|---|---|---|---|---|
| 0.1196 | 0.1201 | 0.2205 | 0.2624 | 0.0376 | |
| 0.0149 | 0.0255 | 0.0273 | 0.0174 | 0.0342 | |
| 0.0134 | 0.0241 | 0.0226 | 0.0163 | 0.0296 |
| Dataset | Actor Mocap () | syn3 () | Paper () | Expressions () | Heart Surgery () | Back () | Real Face () | |
|---|---|---|---|---|---|---|---|---|
| Shape Estimator | FLOPS | |||||||
| Params | ||||||||
| Rotation Estimator | FLOPS | |||||||
| Params |
| Dataset | FML [50] | SMSR [51] | CMDR [52] | RONN [54] | N-NRSfM [9] | Ours () |
|---|---|---|---|---|---|---|
| actor mocap | 0.092 | 0.054 | 0.0257 | 0.0226 | 0.0181 | 0.0163 |
| Classical Sparse NRSfM Methods | Neural Dense NRSFM Methods | |||||||
|---|---|---|---|---|---|---|---|---|
| Dataset | MP [55] | CSF2 [17] | BMM [20] | OP [3] | N-NRSfM [9] | RONN [54] | Ours () | |
| syn3 | 0.0611 | 0.5474 | 0.0784 | 0.0279 | 0.0320 | 0.0309 | 0.0134 | |
| syn4 | 0.0762 | 0.5292 | 0.0918 | 0.0419 | 0.0389 | 0.0359 | 0.0263 | |
| Conventional Dense NRSfM Methods | ||||||||
| Dataset | VA [7] | DSTA [25] | GM [8] | JM [29] | PPTA [14] | CMDR [52] | SMSR [51] | Ours() |
| syn3 | 0.0346 | 0.0374 | 0.0294 | 0.0280 | 0.0390 | 0.0324 | 0.0304 | 0.0134 |
| syn4 | 0.0379 | 0.0428 | 0.0309 | 0.0327 | 0.052 | 0.0369 | 0.0319 | 0.0263 |
| Dataset | MP [55] | DSTA [25] | GM [8] | JM [29] | N-NRSfM [9] | Ours |
|---|---|---|---|---|---|---|
| paper | 0.0827 | 0.0612 | 0.0394 | 0.0338 | 0.0332 | 0.0296 () |
| t-shirt | 0.0741 | 0.0636 | 0.0362 | 0.0386 | 0.0309 | 0.0396 () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, M.; Huang, W.; Ye, X.; Jiang, M. Deep Spatial-Temporal Neural Network for Dense Non-Rigid Structure from Motion. Mathematics 2022, 10, 3794. https://doi.org/10.3390/math10203794
Wang Y, Wang M, Huang W, Ye X, Jiang M. Deep Spatial-Temporal Neural Network for Dense Non-Rigid Structure from Motion. Mathematics. 2022; 10(20):3794. https://doi.org/10.3390/math10203794
Chicago/Turabian StyleWang, Yaming, Minjie Wang, Wenqing Huang, Xiaoping Ye, and Mingfeng Jiang. 2022. "Deep Spatial-Temporal Neural Network for Dense Non-Rigid Structure from Motion" Mathematics 10, no. 20: 3794. https://doi.org/10.3390/math10203794
APA StyleWang, Y., Wang, M., Huang, W., Ye, X., & Jiang, M. (2022). Deep Spatial-Temporal Neural Network for Dense Non-Rigid Structure from Motion. Mathematics, 10(20), 3794. https://doi.org/10.3390/math10203794







