Multitask Emergency Logistics Planning under Multimodal Transportation
Abstract
1. Introduction
- Limited available infrastructure capacity: emergency logistics rely on transportation routes with limited capacity, and the capacity of loading and unloading nodes is typically limited, which can easily lead to traffic network congestion in mass transportation;
- Insufficient available transport capacity: when performing emergency logistics tasks, we are usually faced with a relatively fragile traffic network and cannot undertake large-scale air transportation missions. For example, the design of the load and size of the bridges, culverts, railway beds and highway beds restrict the passage of some heavy rescue equipment;
- Many tasks involved: emergency logistics typically involve multiple emergency tasks, and these tasks are scattered with different destinations, which incur great difficulties to model and solve the emergency logistics planning problem.
2. Literature Review
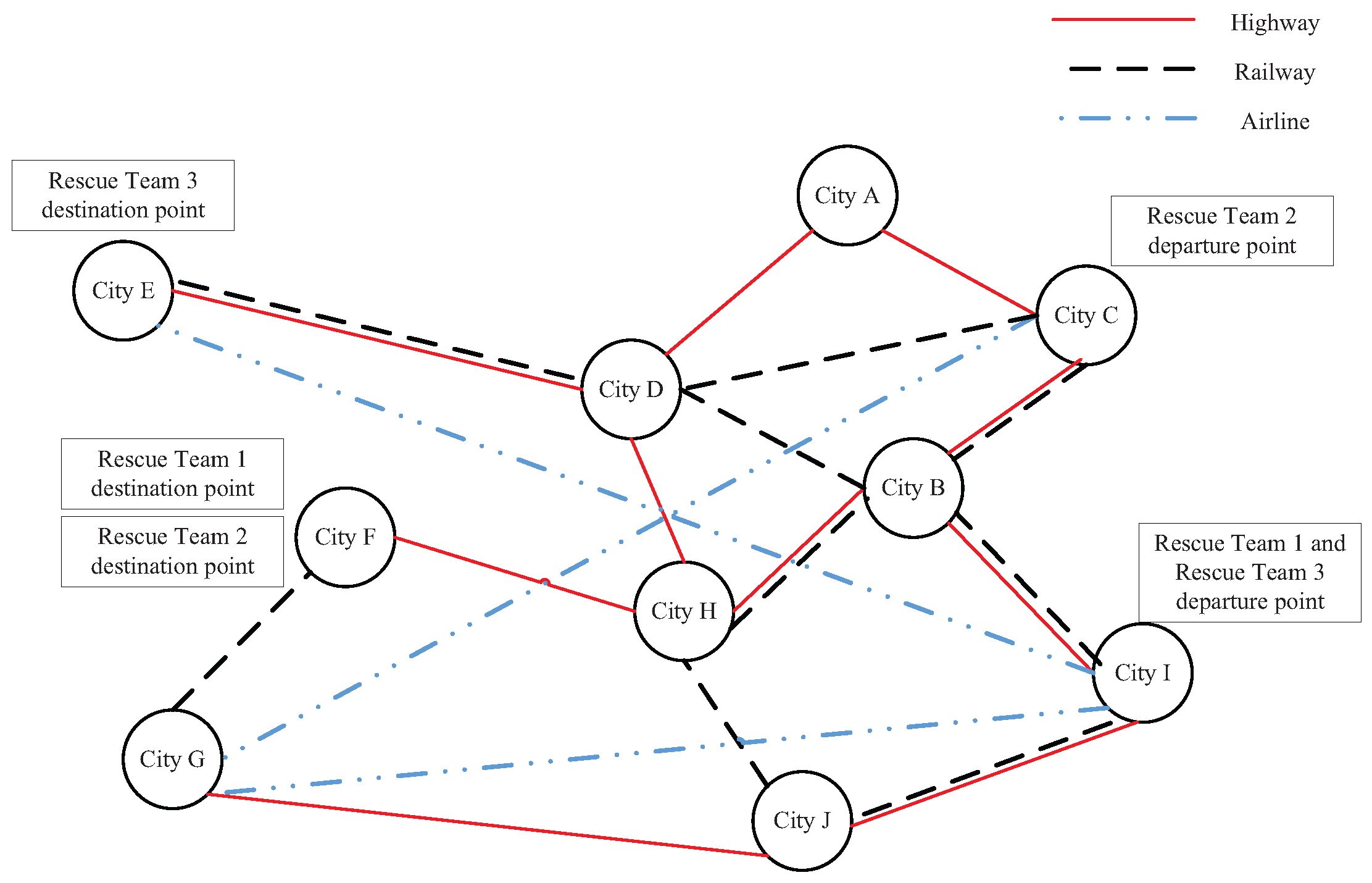
3. Problem Description and Mathematical Formulation
- Traffic network (i.e., the topology of the emergency logistics transportation system): the traffic network is composed of nodes and arcs, where nodes are typically cities, stations and transfer stations; and arcs are typically transportation lines between two nodes;
- Loading and unloading capacity (i.e., the maximum periodic loading and unloading capacity of a node for a specified transportation mode);
- Transport capacity: the transport capacity refers to the periodic maximum number of batches passing arcs between two nodes, which is jointly determined by the type of route, logistics support capacity and other factors;
- Transportation routes (i.e., the collection of routes that connect the departure point and destination point of each task);
- Periodic delivery quantity (i.e., the number of batches delivered periodically for each task): if the number of task batches is greater than the maximum single-day transport capacity of its transportation route, it will likely take several periods to complete the delivery. The maximum single-day transport capacity is determined by the loading and unloading capacity of the departure point, destination point and transfer node as well as the transport capacity of its transportation route.
- Traffic resource constraints: these constraints primarily include the maximum capacity of each route, the maximum loading and unloading capacity of each node, and the requirements of each task on the type of transportation mode;
- Emergency principle constraints: these constraints primarily include the last arrival time of each task, arrival order of the batches in different tasks, batch continuity in time and space during transportation;
- Natural environment Constraints (e.g., logistic requirements of high-altitude areas and the transport time limitations of severe weather);
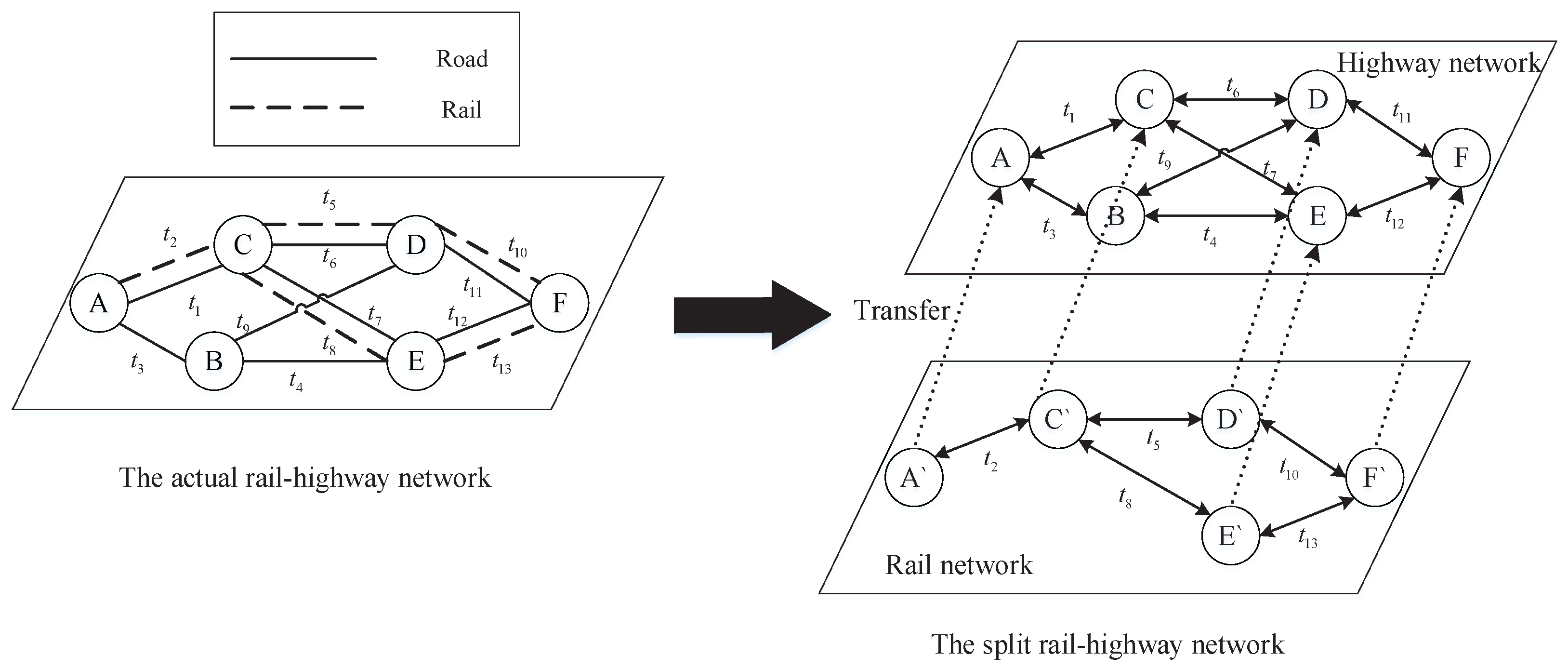
- Transfer condition constraints: these constraints primarily include the maximum capacity of each node and the priority requirements for different modes of transport. In theory, transfer is possible between any two modes of transportation. However, in the real transport process, we consider that emergency logistics should take the time benefit as the first goal. The transport time is faster with the mode of transportation with higher priority, and the transport distance should be as far as possible with a high priority without transfer. Therefore, we assume that priority exists between different traffic networks and stipulate that transfer can only occur from a high-priority to a low-priority traffic network.
- Each task to be delivered can be split into batches. Each batch in each task cannot be split during transportation, and a batch is the smallest unit;
- The transportation of each task must be continuous, in terms of both time and space;
- Transfer can be made instantaneous and can only be carried out from a transportation mode of a higher priority to that of a lower priority.
4. Solution Method for Single-Task Route Planning
4.1. Single-Task Route Planning Model
4.2. Shortest-Path Algorithm under Multimodal Traffic Networks
| Algorithm 1: Shortest-Path Algorithm under Multimodal Traffic Network |
 |
4.3. Extensions of the Algorithm
| Algorithm 2: Real Transport Time Calculation Algorithm |
 |
5. Solution Method for the Optimization Model of Multitask Emergency Logistics Planning
5.1. Particle Swarm Optimization
- for the solution space of the optimization problem, a group of particles are randomly initialized as the feasible solution of the objective function, and the fitness function is defined to describe the advantages and disadvantages of each solution;
- then, each particle moves randomly in the solution space, while the particle’s position is determined by the particle’s velocity. The incumbent solution found by the particle itself and found by the particle swarm will affect the particle velocity, respectively;
- all particles are searched step-by-step in this manner to find a high-quality solution in the solution space.
5.2. Two-Dimensional Array Encoding and Cross Operation
- operator ⊖ retrieves the commutator series required to transform the latter sequence into former sequence. For instance, given that sequence and , then means that an obtained commutator series can transfer sequence to sequence a;
- operator ⊕ merges two commutator series into one commutator series, e.g., ;
- operator ⊗ operates on a sequence according to the commutator series .
5.3. General Optimization Algorithm for Multitask Emergency Logistics Planning
| Algorithm 3: General Optimization Algorithm of Multitask Emergency Logistics Planning |
 |
6. Computational Results
6.1. Test Set
- city node information contains the periodic loading and unloading capacity in different transportation modes of each city node. We consider the different numbers of nodes in the test set, ranging from 20 to 65. The periodic loading and unloading capacity range from , , in air, rail and highway, respectively;
- primary arcs data describe the structure of different traffic networks; the periodic transport capacity; time consumption; and distance of each arc. We primarily consider air, rail and highway three modes of transportation networks and generate these three modes of transportation network topologies based on the number of nodes in each instance. The number of arcs in the air, rail and highway modes of transportation network ranges from , , , respectively. The distance of each arc ranges from , , and by air, rail and highway, respectively. the time consumption of each arc is the ratio of distance to the speed of its mode of transportation. The periodic transport capacity of each arc ranges from , , and by air, rail and highway, respectively;
- task lists include the specific information of each task, including its designated transportation mode, departure point, destination point, higher priority task and alternative paths. The three alternative routes for each task are obtained under different circumstances using the solution method presented in Section 4. Some tasks, such as specifying air transport, are point-to-point transport and have only one path; thus, multiple alternative paths cannot be recommended. ranges from in the first 20 instances, and from in the last 10 instances.
6.2. Results and Comparison
6.2.1. Results of Instances with Small
6.2.2. Results of Instances with Large
6.2.3. Sensitivity Analysis
6.3. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MIP | Mixed-integer programming |
| PSO | Particle swarm optimization |
| ACO | Ant colony optimization |
| DNF | Dynamic network flow |
| SNF | Static network fow |
| RE | Route enumeration |
| LRP | Location-routing problem |
| VRP | Vehicle routing problem |
| MTTS | Multimodal Transportation System |
References
- Alem, D.; Clark, A.; Moreno, A. Stochastic network models for logistics planning in disaster relief. Eur. J. Oper. Res. 2016, 255, 187–206. [Google Scholar] [CrossRef]
- Yáñez-Sandivari, L.; Cortés, C.E.; Rey, P.A. Humanitarian logistics and emergencies management: New perspectives to a sociotechnical problem and its optimization approach management. Int. J. Disaster Risk Reduct. 2021, 52, 101952. [Google Scholar] [CrossRef]
- Sheu, J.B. Special issue on emergency logistics management transportation research part E: Logistics and transportation review. Transp. Res. Part E 2005, 41, 459–460. [Google Scholar]
- Özdamar, L.; Ertem, M.A. Models, solutions and enabling technologies in humanitarian logistics. Eur. J. Oper. Res. 2015, 244, 55–65. [Google Scholar] [CrossRef]
- Udomwannakhet, J.; Vajarodaya, P.; Manicho, S.; Kaewfak, K.; Ruiz, J.B.; Ammarapala, V. A review of multimodal transportation optimization model. In Proceedings of the 2018 5th International Conference on Business and Industrial Research (ICBIR), Bangkok, Thailand, 17–18 May 2018; IEEE: Piscatvey, NJ, USA, 2018; pp. 333–338. [Google Scholar]
- Basallo-Triana, M.J.; Vidal-Holguín, C.J.; Bravo-Bastidas, J.J. Planning and design of intermodal hub networks: A literature review. Comput. Oper. Res. 2021, 136, 105469. [Google Scholar] [CrossRef]
- Archetti, C.; Peirano, L.; Speranza, M.G. Optimization in multimodal freight transportation problems: A Survey. Eur. J. Oper. Res. 2021, 1, 1–20. [Google Scholar] [CrossRef]
- Barbarosoğlu, G.; Özdamar, L.; Cevik, A. An interactive approach for hierarchical analysis of helicopter logistics in disaster relief operations. Eur. J. Oper. Res. 2002, 140, 118–133. [Google Scholar] [CrossRef]
- Kalinina, M.; Olsson, L.; Larsson, A. A multi objective chance constrained programming model for intermodal logistics with uncertain time. Int. J. Comput. Sci. Issues 2013, 10, 35–44. [Google Scholar]
- Barzinpour, F.; Esmaeili, V. A multi-objective relief chain location distribution model for urban disaster management. Int. J. Adv. Manuf. Technol. 2014, 70, 1291–1302. [Google Scholar] [CrossRef]
- Jernigan, N.R. Multi-Modal, Multi-Period, Multi-Commodity Transportation: Models and Algorithms. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Mohammadi, M.; Jula, P.; Tavakkoli-Moghaddam, R. Design of a reliable multi-modal multi-commodity model for hazardous materials transportation under uncertainty. Eur. J. Oper. Res. 2017, 257, 792–809. [Google Scholar] [CrossRef]
- Manopiniwes, W.; Irohara, T. Stochastic optimisation model for integrated decisions on relief supply chains: Preparedness for disaster response. Int. J. Prod. Res. 2017, 55, 979–996. [Google Scholar] [CrossRef]
- Drezner, Z. Heuristic solution methods for two location problems with unreliable facilities. J. Oper. Res. Soc. 1987, 38, 509–514. [Google Scholar] [CrossRef]
- Haghani, A.; Oh, S.C. Formulation and solution of a multi-commodity, multi-modal network flow model for disaster relief operations. Transp. Res. Part A Policy Pract. 1996, 30, 231–250. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Mason, S.J. Multiple-objective analysis of integrated relief supply and network restoration in humanitarian logistics operations. Int. J. Prod. Res. 2016, 54, 49–68. [Google Scholar] [CrossRef]
- Najafi, M.; Eshghi, K.; Dullaert, W. A multi-objective robust optimization model for logistics planning in the earthquake response phase. Transp. Res. Part E Logist. Transp. Rev. 2013, 49, 217–249. [Google Scholar] [CrossRef]
- Yoon, S.; Albert, L.A. Dynamic dispatch policies for emergency response with multiple types of vehicles. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102405. [Google Scholar] [CrossRef]
- Barbarosoǧlu, G.; Arda, Y. A two-stage stochastic programming framework for transportation planning in disaster response. J. Oper. Res. Soc. 2004, 55, 43–53. [Google Scholar] [CrossRef]
- Gao, X.; Jin, X.; Zheng, P.; Cui, C. Multi-modal transportation planning for multi-commodity rebalancing under uncertainty in humanitarian logistics. Adv. Eng. Inf. 2021, 47, 101223. [Google Scholar] [CrossRef]
- Ding, Z.; Xu, X.; Jiang, S.; Yan, J.; Han, Y. Emergency logistics scheduling with multiple supply-demand points based on grey interval. J. Saf. Sci. Resil. 2022, 3, 179–188. [Google Scholar] [CrossRef]
- Song, X.; Wang, J.; Chang, C. Nonlinear continuous consumption emergency material dispatching problem. Syst. Eng. 2017, 32, 163–176. [Google Scholar]
- Barnhart, C.; Sheffi, Y. A network-based primal-dual heuristic for the solution of multicommodity network flow problems. Transp. Sci. 1993, 27, 102–117. [Google Scholar] [CrossRef]
- Barnhart, C. Dual-ascent methods for large-scale multicommodity flow problems. Nav. Res. Logist. (NRL) 1993, 40, 305–324. [Google Scholar] [CrossRef]
- Yi, W.; Kumar, A. Ant colony optimization for disaster relief operations. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 660–672. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Zhang, L. A study on the paths choice of intermodal transport based on reliability. In LISS 2014; Springer: Berlin/Heidelberg, Germany, 2015; pp. 305–315. [Google Scholar]
- Lei, K.; Zhu, X.; Hou, J.; Huang, W. Decision of multimodal transportation scheme based on swarm intelligence. Math. Probl. Eng. 2014, 2014, 932832. [Google Scholar] [CrossRef] [PubMed]
- Kai, K.; Haijiao, N.; Yuejie, Z.; Weicun, Z. Research on improved integrated optimization model for mode and Route in multimodal transportation basing on the PSO-ACO. In Proceedings of the 2010 International Conference on Logistics Systems and Intelligent Management (ICLSIM), Harbin, China, 9–10 January 2010; IEEE: Piscatvey, NJ, USA, 2010; Volume 3, pp. 1445–1449. [Google Scholar]
- Li, H.; Su, L. Multimodal transport path optimization model and algorithm considering carbon emission multitask. J. Supercomput. 2020, 76, 9355–9373. [Google Scholar] [CrossRef]
- Fazayeli, S.; Eydi, A.; Kamalabadi, I.N. Location-routing problem in multimodal transportation network with time windows and fuzzy demands: Presenting a two-part genetic algorithm. Comput. Ind. Eng. 2018, 119, 233–246. [Google Scholar] [CrossRef]
- Das, M.; Roy, A.; Maity, S.; Kar, S.; Sengupta, S. Solving fuzzy dynamic ship routing and scheduling problem through new genetic algorithm. Decis. Making Appl. Manag. Eng. 2021. [Google Scholar] [CrossRef]
- Subramanian, A.; Penna, P.H.V.; Uchoa, E.; Ochi, L.S. A hybrid algorithm for the heterogeneous fleet vehicle routing problem. Eur. J. Oper. Res. 2012, 221, 285–295. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, S.; Xu, M. Emergency logistics network design based on space–time resource configuration. Knowl.-Based Syst. 2021, 223, 107041. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Wojciechowski, P.; Williamson, M.; Subramani, K. On finding shortest paths in arc-dependent networks. In Proceedings of the International Symposium on Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2020; pp. 249–260. [Google Scholar]
- Tan, J.; Leong, H.W. Least-cost path in public transportation systems with fare rebates that are path-and time-dependent. In Proceedings of the 7th International IEEE Conference on Intelligent Transportation Systems (IEEE Cat. No. 04TH8749), Washington, WA, USA, 3–6 October 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 1000–1005. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Ergün, S.; Usta, P.; Alparslan Gök, S.Z.; Weber, G.W. A game theoretical approach to emergency logistics planning in natural disasters. Ann. Oper. Res. 2021, 1–14. [Google Scholar] [CrossRef]
- Wang, L.; Song, J.; Shi, L. Dynamic emergency logistics planning: Models and heuristic algorithm. Optim. Lett. 2015, 9, 1533–1552. [Google Scholar] [CrossRef]
- Sabouhi, F.; Bozorgi-Amiri, A.; Moshref-Javadi, M.; Heydari, M. An integrated routing and scheduling model for evacuation and commodity distribution in large-scale disaster relief operations: A case study. Ann. Oper. Res. 2019, 283, 643–677. [Google Scholar] [CrossRef]
- Salehi, F.; Mahootchi, M.; Husseini, S.M.M. Developing a robust stochastic model for designing a blood supply chain network in a crisis: A possible earthquake in Tehran. Ann. Oper. Res. 2019, 283, 679–703. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Y.; Kundu, T.; Zhang, F. Impact of entry restriction policies on international air transport connectivity during COVID-19 pandemic. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102411. [Google Scholar] [CrossRef]
- Zhou, Y.; Kundu, T.; Qin, W.; Goh, M.; Sheu, J.B. Vulnerability of the worldwide air transportation network to global catastrophes such as COVID-19. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102469. [Google Scholar] [CrossRef] [PubMed]
| Notations | Definition |
|---|---|
| F | The set of transportation modes |
| f | The index of transportation modes and |
| T | The set of planning horizon |
| t | The index of time and |
| Subnetwork of transportation mode f | |
| Periodic loading capacity of node i under transportation mode f | |
| Periodic unloading capacity of node i under transportation mode f | |
| Periodic traffic capacity of arc under transportation mode f | |
| Transportation time of arc under transportation mode f | |
| M | The set of tasks |
| m | The index of tasks and |
| The number of batches in task m | |
| Minimum number of batches in task m transported in a period | |
| Whether task m can transfer from transportation mode to ( has a higher priority than ) | |
| The departure point of task m | |
| The destination point of task m | |
| The earliest departure time of task m | |
| The last arrival time of task m | |
| U | A large constant |
| Notations | Definition |
|---|---|
| Binary variable indicating whether there is any task being executed on period t and | |
| Binary variable indicating whether task m begins delivering from departure point on period t under the transportation mode f and | |
| Binary variable indicating whether task m finishes delivering from departure point on period t under the transportation mode f and | |
| Binary variable indicating whether task m chooses the arc to transport under the transportation mode f and | |
| Binary variable indicating whether task m chooses the arc to transport on period t under the transportation mode f and | |
| The number of batches in task m transport in arc on period t under the transportation mode f | |
| Whether task m transfer from transportation mode to at node i ( has a higher priority than ) | |
| Task m’s auxiliary variable of loading capacity at node i on period t under the transportation mode f | |
| Task m’s auxiliary variable of unloading capacity at node i on period t under the transportation mode f | |
| Binary variable indicating whether there are any batches in task m deliver from departure point on period t and |
| Instance | Z (Period) | CPU Runtime (s) | |||
|---|---|---|---|---|---|
| instance1 | 20 | 110 | 25 | 10 | 36.335 |
| instance2 | 20 | 122 | 24 | 13 | 48.913 |
| instance3 | 25 | 130 | 30 | 8 | 52.650 |
| instance4 | 25 | 138 | 24 | 6 | 51.160 |
| instance5 | 30 | 162 | 32 | 8 | 65.500 |
| instance6 | 30 | 182 | 29 | 7 | 48.742 |
| instance7 | 35 | 210 | 36 | 7 | 78.947 |
| instance8 | 35 | 198 | 41 | 10 | 91.720 |
| instance9 | 40 | 228 | 52 | 11 | 103.285 |
| instance10 | 40 | 292 | 52 | 11 | 157.455 |
| instance11 | 45 | 306 | 61 | 15 | 158.226 |
| instance12 | 45 | 336 | 63 | 17 | 163.906 |
| instance13 | 50 | 328 | 50 | 9 | 163.127 |
| instance14 | 50 | 320 | 59 | 23 | 183.715 |
| instance15 | 55 | 360 | 59 | 8 | 183.043 |
| instance16 | 55 | 366 | 57 | 10 | 155.145 |
| instance17 | 60 | 376 | 73 | 12 | 192.868 |
| instance18 | 60 | 378 | 72 | 13 | 192.188 |
| instance19 | 65 | 478 | 72 | 13 | 227.981 |
| instance20 | 65 | 452 | 84 | 10 | 227.794 |
| Task Name | Departure Point | Arrival Point | Departure Day | Arrival Day | Batch Number | Periodic Batch Arrangement | Transport Route |
|---|---|---|---|---|---|---|---|
| task1 | Node2 | Node1 | 3 | 3 | 2 | [2] | Node2–C0(air)–Node1 |
| task2 | Node20 | Node17 | 0 | 3 | 15 | [4, 4, 4, 3] | Node20–A0(air)–Node17 |
| task3 | Node14 | Node13 | 0 | 10 | 10 | [1, 1, 1, 1, 1, 1, 1, 1, 1, 1] | Node14–A279(air)–Node13 |
| task4 | Node13 | Node14 | 3 | 5 | 2 | [1, 1] | Node13–A279(air)–Node14 |
| task5 | Node16 | Node11 | 3 | 4 | 4 | [3, 1] | Node16–A7(air)–Node11 |
| task6 | Node16 | Node6 | 0 | 4 | 23 | [6, 6, 6, 5] | Node16–K545(rail)–Node19–G664(rail)–Node10–Y06(road)–Node6 |
| task7 | Node17 | Node1 | 3 | 10 | 29 | [5, 5, 3, 3, 3, 5, 5] | Node17–K42(rail)–Node11–G3(rail)–Node3–G53(rail)–Node20–X411(road)–Node9–X8(road)–Node1 |
| task8 | Node11 | Node16 | 3 | 8 | 30 | [1, 4, 8, 8, 8, 1] | Node11–G3(rail)–Node3–G53(rail)–Node20–K344(rail)–Node15–G01(rail)–Node13–K4(rail)–Node19–K545(rail)–Node16 |
| task9 | Node9 | Node6 | 3 | 4 | 12 | [8, 4] | Node9–G6(road)–Node6 |
| task10 | Node13 | Node2 | 0 | 4 | 21 | [5, 5, 5, 5, 1] | Node13–K4(rail)–Node19–G664(rail)–Node10–G749(rail)–Node2 |
| task11 | Node9 | Node8 | 0 | 4 | 18 | [3, 3, 3, 5, 4] | Node9–K1(rail)–Node20–K344(rail)–Node15–G01(rail)–Node13–K4(rail)–Node19–K545(rail)–Node16–K29(rail)–Node8 |
| task12 | Node10 | Node11 | 2 | 6 | 20 | [2, 7, 7, 4] | Node10–G664(rail)–Node19–K4(rail)–Node13–G01(rail)–Node15–Y225(road)–Node20–G6(road)–Node3–Z03(road)–Node11 |
| task13 | Node11 | Node5 | 0 | 3 | 21 | [7, 7, 7] | Node11–G3(rail)–Node3–G53(rail)–Node20–K344(rail)–Node15–G01(rail)–Node13–S1(road)–Node5 |
| task14 | Node8 | Node5 | 3 | 8 | 22 | [4, 4, 4, 4, 4, 2] | Node8–S674(road)–Node12–Y566(road)–Node15–S7(road)–Node13–S1(road)–Node5 |
| task15 | Node11 | Node6 | 0 | 4 | 17 | [5, 5, 5, 2] | Node11–G3(rail)–Node3–G53(rail)–Node20–K344(rail)–Node15–G01(rail)–Node13–K4(rail)–Node19–K545(rail)–Node16–K29(rail)–Node8–G993(rail)–Node18 |
| task16 | Node7 | Node16 | 0 | 0 | 5 | [5] | Node7–D60(rail)–Node19–K545(rail)–Node16 |
| task17 | Node8 | Node9 | 3 | 7 | 24 | [5, 5, 5, 5, 4] | Node8–K29(rail)–Node16–K545(rail)–Node19–K4(rail)–Node13–G01(rail)–Node15–K344(rail)–Node20–K1(rail)–Node9 |
| task18 | Node11 | Node4 | 0 | 2 | 16 | [6, 6, 4] | Node11–S880(road)–Node17–Z786(road)–Node4 |
| task19 | Node2 | Node11 | 3 | 5 | 27 | [11, 11, 5] | Node2–K2(rail)–Node1–D62(rail)–Node9–K1(rail)–Node20–G53(rail)–Node3–G3(rail)–Node11 |
| task20 | Node20 | Node17 | 0 | 3 | 10 | [2, 2, 4, 2] | Node20–G6(road)–Node3–Z03(road)–Node11–S880(road)–Node17 |
| task21 | Node4 | Node1 | 0 | 5 | 30 | [6, 6, 6, 6, 6] | Node4–K15(rail)–Node7–D60(rail)–Node19–G664(rail)–Node10–Z601(road)–Node2–S0(road)–Node1 |
| task22 | Node7 | Node9 | 3 | 5 | 9 | [6, 3] | Node7–G466(rail)–Node13–G01(rail)–Node15–Y225(road)–Node20–X411(road)–Node9 |
| task23 | Node3 | Node1 | 3 | 5 | 14 | [6, 6, 2] | Node3–G6(road)–Node20–X411(road)–Node9–X8(road)–Node1 |
| task24 | Node15 | Node3 | 0 | 3 | 16 | [5, 5, 3, 3] | Node15–Y225(road)–Node20–G6(road)–Node3 |
| task25 | Node11 | Node13 | 0 | 4 | 15 | [2, 2, 4, 4, 3] | Node11–G1(road)–Node18–Z5(road)–Node19–S08(road)–Node13 |
| Instance | Z (Period) | CPU Runtime (s) | |||
|---|---|---|---|---|---|
| instance21 | 20 | 120 | 58 | 18 | 71.536 |
| instance22 | 25 | 140 | 52 | 28 | 84.455 |
| instance23 | 30 | 178 | 73 | 18 | 130.854 |
| instance24 | 35 | 222 | 103 | 26 | 204.818 |
| instance25 | 40 | 312 | 104 | 18 | 237.317 |
| instance26 | 45 | 258 | 121 | 25 | 246.684 |
| instance27 | 50 | 292 | 140 | 28 | 311.662 |
| instance28 | 55 | 348 | 137 | 32 | 298.705 |
| instance29 | 60 | 386 | 158 | 30 | 336.258 |
| instance30 | 65 | 358 | 150 | 56 | 397.488 |
| Instance | CPU Runtime (s) | Z (Period) | CPU Runtime (s) | Z (Period) | CPU Runtime (s) | Z (Period) | CPU Runtime (s) | Z (Period) | CPU Runtime (s) | Z (Period) |
|---|---|---|---|---|---|---|---|---|---|---|
| instance1 | 36.335 | 10 | 21.398 | 10 | 20.265 | 10 | 13.247 | 10 | 7.631 | 10 |
| instance3 | 52.650 | 8 | 27.013 | 8 | 19.951 | 8 | 13.618 | 9 | 11.956 | 9 |
| instance5 | 65.500 | 8 | 53.363 | 8 | 30.317 | 8 | 22.275 | 10 | 17.18 | 10 |
| instance7 | 78.947 | 7 | 48.231 | 7 | 33.194 | 7 | 21.05 | 9 | 15.035 | 9 |
| instance9 | 103.285 | 11 | 74.073 | 11 | 55.746 | 11 | 31.584 | 12 | 22.711 | 13 |
| instance11 | 158.226 | 15 | 95.339 | 15 | 66.237 | 15 | 41.694 | 15 | 29.536 | 18 |
| instance13 | 163.127 | 9 | 98.162 | 9 | 70.314 | 9 | 43.009 | 9 | 29.239 | 12 |
| instance15 | 183.043 | 8 | 116.62 | 8 | 76.799 | 10 | 45.784 | 10 | 30.998 | 9 |
| instance17 | 192.868 | 12 | 115.921 | 12 | 85.789 | 13 | 50.901 | 13 | 35.105 | 14 |
| instance19 | 227.981 | 13 | 145.831 | 13 | 102.033 | 14 | 60.927 | 14 | 45.779 | 14 |
| instance21 | 71.536 | 18 | 58.663 | 18 | 32.347 | 18 | 21.355 | 18 | 14.512 | 20 |
| instance23 | 130.854 | 18 | 83.617 | 18 | 53.516 | 18 | 34.96 | 19 | 23.624 | 20 |
| instance25 | 237.317 | 18 | 164.489 | 21 | 115.582 | 22 | 66.999 | 21 | 45.646 | 22 |
| instance27 | 311.662 | 28 | 196.318 | 34 | 136.812 | 35 | 86.469 | 35 | 59.745 | 38 |
| instance29 | 336.258 | 30 | 228.203 | 31 | 176.163 | 33 | 107.372 | 33 | 76.182 | 37 |
| , | Z (Period) | CPU Runtime (s) |
|---|---|---|
| 11 | 60.203 | |
| 11 | 56.518 | |
| 12 | 57.916 | |
| 15 | 59.642 | |
| 17 | 58.53 | |
| 16 | 59.592 | |
| 18 | 57.509 | |
| 26 | 67.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Song, G.; Liu, T.; Guo, B. Multitask Emergency Logistics Planning under Multimodal Transportation. Mathematics 2022, 10, 3624. https://doi.org/10.3390/math10193624
Liu H, Song G, Liu T, Guo B. Multitask Emergency Logistics Planning under Multimodal Transportation. Mathematics. 2022; 10(19):3624. https://doi.org/10.3390/math10193624
Chicago/Turabian StyleLiu, Hongbin, Guopeng Song, Tianyu Liu, and Bo Guo. 2022. "Multitask Emergency Logistics Planning under Multimodal Transportation" Mathematics 10, no. 19: 3624. https://doi.org/10.3390/math10193624
APA StyleLiu, H., Song, G., Liu, T., & Guo, B. (2022). Multitask Emergency Logistics Planning under Multimodal Transportation. Mathematics, 10(19), 3624. https://doi.org/10.3390/math10193624








