Abstract
The past decade has seen an increase in the number of satellites in orbit and in highly dynamic satellite requests, making the control by ground stations inefficient. The traditional management composed of ground planning with separate onboard execution is seriously lagging in response to dynamically incoming tasks. To meet the demand for the real-time response to emergent events, a multi-autonomous-satellite system with a central-distributed collaborative architecture was formulated by an integer programming model. Based on the structure, evolutionary rules were proposed to solve this problem by the use of sequence solution construction and a constructed heuristic method based on gene expression programming evolution. First, the features of the problem are extracted based on domain knowledge, then, the problem-solving rules are evolved by gene expression programming. The simulation results reflect that the evolutionary rule completely surpasses the three types of heuristic rules with adaptive mechanisms and achieves a solution effect close to meta-heuristic algorithms with a reasonably fast solving speed.
MSC:
90C35
1. Introduction
In recent years, the development of satellite systems has entered a new phase where the demand is becoming increasingly higher in terms of autonomous satellite management, online decision-making, and inter-satellite collaboration, thanks to the growth of satellite capability. It is difficult for solely ground management to give full play to the efficiency of new autonomous satellites, and impossible to achieve a rapid allocation of real-time response tasks. Based on this information, the advantages of onboard autonomous mission planning, including independent online planning ability and quick response capability, make it an inevitable trend for the future. The enhancement of onboard computing capabilities and the development of AI technology provide a prerequisite for onboard autonomous intelligence, bringing opportunities to solve shortcomings. In this situation, novel and effective frameworks and algorithms need to be more fully utilized with onboard resources.
The Multi-Satellite Collaborative Task Assignment Problem (MSCTAP) aims to achieve the efficient coordination of task planning and fast response to the dynamic environment through rapid onboard task assignment and has attracted the attention of many researchers. In addition, the structure of a multi-satellite constellation is also an important issue to consider where three structural types have been used, including a centralized structure, distributed structure, and centralized-distributed structure. The centralized approaches are the most widely used and typically require one central controller to determine the mission assignment for each team member and consider the problem as an integer programming model solved by a precise solution. Kennedy [1] adopted a two-layer scheduling method for the joint planning problem of the Walker constellation, which is composed of 18 Cube satellites, and solved the resource allocation problem with mixed integer programming with a depth-first search. However, it is difficult to achieve large-scale collaboration due to the high computational complexity. He [2] considered the problems of satellite online decision-making and task planning under uncertain and dynamic environments and proposed a linear programming model based on the Multi-agent Markov process. The satellite made autonomous decisions based on its state and improved the total benefits using periodic communication, which improved the response-ability to an uncertain environment. However, the solving process relied on a precise solution, which is difficult to solve in large-scale instances. As for the above centralized satellite task scheduling, the allocation mechanism is heavily dependent on the main controller, which makes it vulnerable to the failure of the main controller and leads to a heavy computation load.
For the distributed structure, the majority of works focus on the multi-agent-based negotiation assignment method. Most researchers use a contract network to resolve the conflict of task assignment so the computation load of the main controller of the centralized structure can be distributed to other agents. Compared with the main controller, the computational power requirement of the information hub is lower. However, the efficiency of the distributed multi-satellite mission cooperation architecture depends on the inter-satellite communication delay, which determines the effectiveness of allocation and the feasibility of task execution. However, it is not often considered in multi-satellite task allocation. Schetter [3] addressed the collaborative planning problem of the TechSat constellation. According to the autonomous capabilities in the formation, satellites were divided into agents of four intelligence levels. This partition is used to organize satellites of different intelligence levels to collaborate on tasks. Van [4,5] adopted a market-based behavior mechanism when considering multi-satellite collaboration, enabling the satellite with the highest bid to perform corresponding tasks. Wu [6] considered the dynamic topology of inter-satellite communication and proposed a method to predict communication links to carry out multi-satellite collaboration. Li [7] studied the problem of multi-satellite autonomous mission planning and proposed a multi-autonomous satellite collaborative mission planning framework. The multi-satellite system based on JADE (Java Agent Development Framework, TILAB, State of California, United States) was designed under this framework and was composed of a single-satellite autonomous layer and a multi-satellite collaborative layer. On the whole, distribution is relatively robust, but distribution relies heavily on communication networks because planning needs to capture global information as completely as possible.
Based on the defects of centralized and distributed architectures, a central-distributed collaborative architecture is proposed to solve the MSCTAP. In other words, a centralized task allocation based on global information is adopted in the multi-satellite coordination layer to improve the effect of allocation, and distributed collaborative architecture is adopted in the single-satellite autonomous scheduling layer. Meanwhile, the global information of centralized task allocation can utilize the distributed computing capability to reduce the computing load of the primary satellite allocation. Yao [8] considered the task allocation problem of multi-autonomous satellite cooperative task planning, approved a central-distributed cooperative architecture, proposed 10 allocation strategies based on this architecture, and adopted the Support Vector Machine (SVM) to realize the selection of allocation strategies in different scenarios. However, only two strategies are included in the study. Yang [9] studied the problem of online collaboration and scheduling of autonomous satellites under uncertain conditions and proposed a dynamic distributed collaboration architecture for this problem. On this basis, an improved contract network method and the blackboard model were adopted to achieve the onboard task allocation.
Among the central-distributed collaborative architecture, multi-satellite collaborative task planning still needs to consider task scheduling, in which high-quality task allocation strategies are needed. However, many offline-based algorithms cannot support this due to their limited onboard computing resources. Therefore, it is necessary for the algorithm to achieve a fast and efficient response to emergency tasks. At the same time, we have noticed that, in recent years, machine learning methods have become popular in many research fields due to the improvement in computing power. Machine learning is widely used and can obtain better solution results compared with the traditional heuristic algorithm; in addition, it has a higher solution efficiency compared with the precise solution algorithm. Compared with the meta-heuristic algorithm, it not only has advantages in solving efficiency but also does not weaken the solution quality. It can better meet the needs of the actual working environment, especially for onboard autonomous mission planning, because the machine learning model can quickly provide the scheduling scheme. Chong [10] took the inter-satellite communication delay into consideration when studying multi-satellite autonomous collaboration, adopting the Markov model for modeling, and designed a method based on multi-agent reinforcement learning. Du [11] proposed a data-driven parallel scheduling framework for large-scale multi-agile satellite scheduling which consists of the scheduling probability prediction model, task allocation strategy, and parallel scheduling algorithm. The model was used to predict the probability of the task being completed on different satellites by means of Cooperative Neuro-Evolution of Augmenting Topologies (C-NEAT) and assigns the task to the satellite with the highest probability. The given model can transform the multi-satellite planning problem into a multi-single satellite planning problem to solve it quickly. However, this method is also based on supervised learning data and has limited applicability as well as problem applicability as it is also a kind of supervised learning. Ren [12] proposed a hierarchical reinforcement learning method to improve the response speed and stability of autonomous satellites to urgent tasks. The base layer is used to learn and train the network, while the top layer uses the network to assign tasks. However, this method greatly simplifies the time-dependent transition time constraints and is difficult to apply in engineering.
The above machine learning methods can achieve the rapid assignment of centralized tasks, but the solving process is regarded as the black box and is difficult to explain. Using neural networks to solve a problem is more similar to predicting than explaining. Meanwhile, another interesting machine learning approach, Genetic Programming (GP), and its variant, Gene Expression Programming (GEP), [13] can evolve explicable dispatching rules by adopting classical evolutionary algorithm architecture. Different from individuals in the evolutionary algorithm population, individuals do not represent a solution but some kind of dispatching rule, which can be used to give the fitness evaluation for training scenes. The rules of GP and GEP evolution can be transformed into expression trees to help find problem features more intuitively. GP and GEP are essentially the evolution of problem-solving rules andcan be classified as unsupervised learning in a sense. In addition, GEP adopts a linear coding method that is more efficient than classical GP. Zhu [14] used GEP to solve the TSP problem and obtained better results. Zhu [15] also adopted GEP to solve the task assignment problem. Deng [16] used GEP to solve the problem of grid resource allocation. Sabar [17] discussed the application of GEP to construct a super-heuristic solving framework, which achieved good results for a variety of combinatorial optimization problems. Zhang [18] studied the dynamic shop scheduling problem and proposed a dynamic scheduling framework based on improved GEP to build scheduling rules, which achieved good solving results. Ozturk [19] highlighted the application in the dynamic multi-objective flexible shop scheduling problem and used GEP to extract the composite priority rules of the scheduling problem. Zhang [20] provided an analysis of the mixed-model multi-manned assembly line balancing problem where GEP evolution rules were adopted to generate line configurations quickly. Experiments show that the scheduling rules based on GEP evolution are better than other heuristic rules for large instances.
In this paper, in order to better solve MSCTAP, a satellite cooperation framework is first presented. Based on the limitations of centralized and distributed cooperation, the central-distributed collaborative architecture is first presented. According to the actual working environment of the satellite, a GEP-based satellite allocation algorithm is proposed which can meet the requirements of calculation speed and calculation effect.
The rest of this paper is organized as follows: In Section 2, the cooperative architecture of multi-autonomous satellites is presented; based on this, a multi-satellite autonomous task allocation model is established. In Section 3, the online single satellite scheduling algorithm is presented. Section 4 illustrates the performance of these methods through experiments, and finally, Section 5 summarizes the work.
2. Problem Formulation
To introduce MSCTAP in detail, we divide it into two sub-problems, i.e., the satellite coordination problem and the task allocation problem. In this section, the central-distributed collaborative architecture is first presented and its collaborative process is explained. Then, the multi-satellite autonomous task assignment problem is modeled based on the given architecture following the complexity analysis.
2.1. Organizational Architecture
In this paper, a central-distributed collaborative architecture is proposed according to the current situation of onboard satellite hardware and inter-satellite communication. Centralized task allocation based on global information is adopted in the multi-satellite coordination layer to improve the effect of allocation, and distributed collaborative architecture is adopted in the single-satellite autonomous scheduling layer. The framework for this combination possesses the advantage of combining the powerful ability of constellation distributed computing with the ability of centralized task allocation on the satellite to achieve global optimization.
The satellite constellation consists of multiple types of autonomous satellites, namely, master satellites and slave satellites. The master satellite is responsible for the planning of cooperative missions and the slave satellites can generate their own observation plan. The corresponding collaborative process is shown in Figure 1. Firstly, satellite TT & C telecommunication can share the target mission information with the satellite, and the satellite with the longest transit time acts as the master satellite. Then, the master satellite distributes the tasks to each slave satellite. Combined with their own state and orbit information, each satellite can quickly calculate the observation information and feed it back to the master satellite. According to the feedback information, the assignment can be conducted on the master satellite. Finally, after obtaining the tasks assigned by the master satellite, each slave satellite conducts independent scheduling, maximizes the sum of observation benefits, and feeds the observation results back to the master satellite.
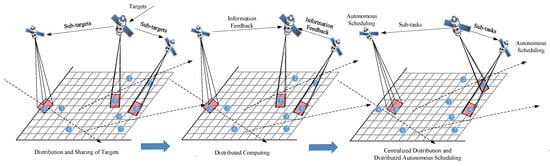
Figure 1.
The Multi-satellite collaborative process in centralization-distributed collaborative architecture.
As the name implies, central-distributed collaborative architecture combines the global information advantage of centralized task allocation with the efficiency of distributed scheduling computing. This paper focuses on the task assignment under centralized and distributed collaborative architecture with limited resources, multi-type constraints, and a short timeframe, aiming to maximize the sum of all single-satellite scheduling benefits.
2.2. Mathematical Model
In this paper, we underline the complexity of the activity planning problem for MSCTAP when trying to consider all the real problem aspects for the agile Earth-observing satellite. In our model, variables are rounded off as integers. Thus, MSCTAP can be modeled as a kind of integer programming problem with a nonlinear optimization objective function. The problem is actually a kind of multi-constraint problem which contains all constraints of single-satellite autonomous task scheduling. The interpretation of the relevant symbols appearing in the MSCTAP is shown in Table 1.

Table 1.
Variables.
Objective (1) is to maximize the total planning revenue, where refer to the single satellite scheduling constraints. Constraint (2) represents each task that can only be assigned to one satellite at most. Constraint (3) indicates that the task must be assigned to a satellite with a visible window to it. Constraint (4) defines the assigned task set of satellite j, which is also the solution of the problem.
To give a further explanation of , the single-satellite scheduling problem follows the following constraints:
Objective (5) is to maximize the sum of priorities of completed tasks. Constraint (6) represents the hard time window constraint of the satellite, that is, the target must be observed within the visible time window of the satellite. Constraint (7) gives the equation relationship between imaging start and end and duration of the task. Constraint (8) indicates the time-dependent transition time constraints between tasks. Constraint (9) shows that the satellite energy consumption cannot exceed the power threshold. Constraints (10)–(12) limit the number of precursor and successor tasks corresponding to each task. Constraint (13) defines the decision variables. Constraints (14) and (15) give the calculation for the shortest transition time and transition angle between two attitude angles.
2.3. Problem Analysis
The MSCTAP can be classified as a classical node matching problem that has exponential spatial complexity. Given the MSCTAP with tasks and satellites, there are also matching selections for each task, regardless of constraints such as visible time windows. So, the spatial complexity of this problem is . The spatial complexity of the problem increases exponentially with the growth of mission and satellite scale. It is difficult to obtain the optimal solution in a short time with accurate algorithms. For the current metaheuristic method, the timeliness of the solution is still not high. Heuristic solutions have high timeliness and poor quality, but those with domain knowledge will bring better benefits.
The MSCTAP is modeled as a sequential decision-making problem by referring to heuristic ideas. The optimal allocation scheme is gradually constructed through the sequential decision of the optimal satellite allocation for each mission. The idea of the serialization decision to solve the MSCTAP problem is shown in Figure 2. Tasks are sorted and the assignment of tasks is considered one by one. In the decision-making of each step, the set of assignable satellites is first screened by constraints (as shown in the dotted line), optimal allocation rules are adopted to allocate tasks considering the current allocation status, and matching relationships are established (as shown in the solid line). The most critical problem is how to make the optimal allocation rules and describe the current allocation state. In the next section, we first introduce an adaptive mechanism to improve the quality of general heuristic methods to serve as a comparison template for the algorithms proposed in the subsequent research. Then, we will design a heuristic algorithm based on GEP evolution and train decision rules through examples of different sizes, finally evolving a nearly perfect rule.
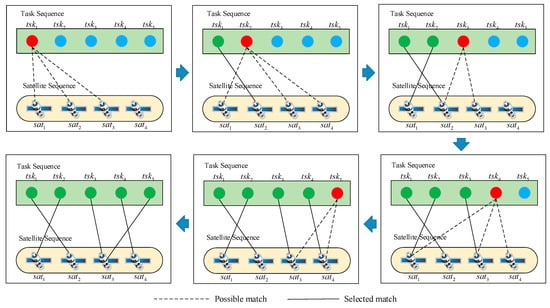
Figure 2.
The sequential decision-making model for MSCTAP.
3. Proposed Algorithms
A Constructed Heuristic Method for multi-satellite collaborative task assignment based on GEP evolution (CHMGEP) is proposed in this paper, inspired by the idea of the hyper-heuristic algorithm. Technically, GP is a special evolutionary algorithm (EA) where different individuals represent different heuristic algorithms composed of various attributes. The fitness of each individual is evaluated by mapping the mathematical function to a dispatching rule. Attribute features represent the essential characteristics of the problem, and the rule training method determines the quality of the results of evolutionary rules, which are the key points of this study.
3.1. Algorithm Framework
The general framework of CHMGEP is shown in Figure 3. First, the feature vectors are extracted based on the transformation of the problem instance to the problem model. Then, the evolution method based on gene expression programming is used to train the multi-satellite task assignment rules. Finally, the optimal multi-satellite task assignment rule obtained by training is selected and used to generate the optimal scheme from instances.
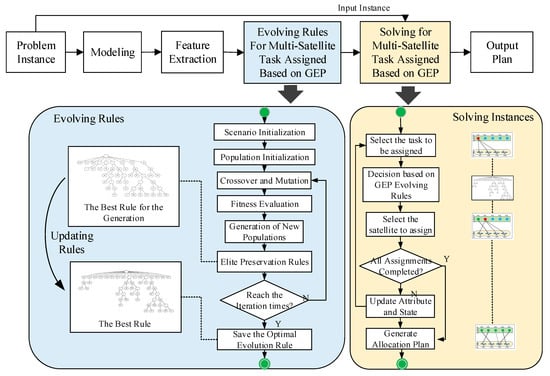
Figure 3.
The CHMGEP Algorithm framework.
The flow chart of the CHMGEP evolutionary method is shown in Figure 4 and is the core of the algorithm. In the chart, the main body and two sub-bodies are introduced to show the details for operators. The procedure starts with population initialization. The evolution operators and fitness evaluation are then used to realize the individual selection mechanism and the diversification of rules individually. In the fitness evaluation module, individuals are converted into dispatching rules for task allocation, following the single satellite scheduling using CPLEX. Each evaluation of a single instance is a task allocation decision-making process based on the dispatching rule of the individual.
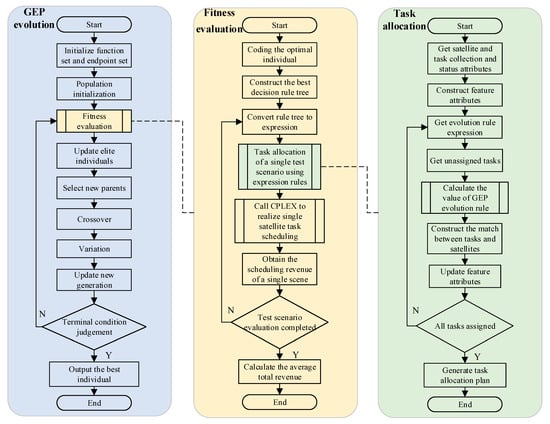
Figure 4.
The CHMGEP evolutionary framework.
3.2. Feature Definition and Normalization
To describe the characteristics of the problem more comprehensively, we consider three sets of features: satellite status-related features (No. 1–8), task-related features (No. 9–10), and satellite-task correlation features (No. 11–16) which indicate the relationship between the unallocated task and allocated tasks on a satellite. All of the features are from time window attributes or scheduling system states. In addition to the normalization of features, (No. 3–16) is considered to improve the applicability and scale generalization of the evolution rules. The features are described as Table 2:

Table 2.
Feature definition.
The above features are selected as the components of the feature vector to characterize MSCTAP. In each generation, the heuristic functions are evolved with GP with the inputs of the feature vector. It should be noted that when the above features violate the operation rules during calculation (for example, when the assigned task of the satellite is 0, it violates the calculation rules of division), zero will be set without special instructions.
3.3. Chromosome Design
In GEP, each chromosome corresponds to a dispatching rule which leads to a solution. The dispatching rules, which are expressed as trees of expressions, assign heuristic values to visible time windows and can be considered constructive heuristics. Chromosomes are decoded by mapping the mathematical functions to a single satellite task scheduling problem solution produced by a timeline-based construction heuristic algorithm. The details of the program encoding and decoding schemes are shown in Figure 5.
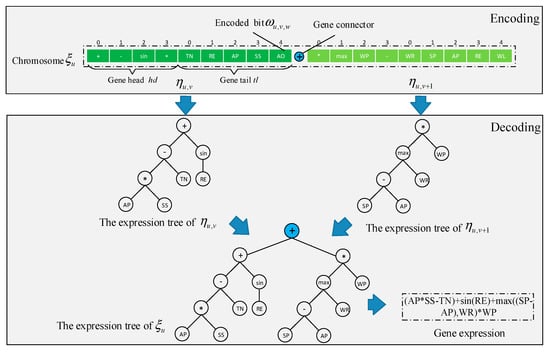
Figure 5.
The encoding and decoding of the chromosome.
During the evolution of GEP, the algorithm maintains a fixed-size population , in which each individual corresponds to a chromosome , . Each chromosome contains coding genes , and each gene contains coding bits . The corresponding encoding in each encoding bit is a function set or a terminal set. The encoding scheme is formed once the terminals and functions are determined.
The function sets include:
- Arithmetic operators, such as +, −, *, and /.
- Mathematical functions, such as sin, cos, and max.
- Relational operators, such as >, <, and =.
- Logical operators, such as And, Or, Nor, and Xor.
- Conditional operators, such as if.
The terminal sets include:
- Variable values that correspond to attribute variables with weights.
- Constant values that correspond to a constant, such as .
- Nonparametric functions, such as random number generation function rand().
Each gene can be divided into two parts: the head and the tail. The head can contain both functions and terminals, while the tail and the first element in the head can only contain terminals. Each gene corresponds to a tree of expressions in which the function set is the non-leaf nodes and the terminal set is the leaf nodes. Given the maximum parameter number in the function, the number of encoding bits in the head , and the number of encoding bits in the tail , Formula (17) must be satisfied in order to meet the validity of the expression tree conversion.
According to the above coding rules, each population contains chromosomes, and each chromosome has genes, which can be expressed as
In the process of chromosome decoding, each gene in the chromosome corresponds to an expression tree and is generated in width first order according to the encoded bit. The expression trees corresponding to multiple genes are connected by gene connectors (+, −, *, /, etc.). Finally, the expression tree corresponding to chromosomes can be transformed into an arithmetic expression through bottom-up order, so as to realize the decoding of chromosomes.
The encoding and decoding parameters, in which the random parameter is introduced to produce scalability compensation for attributes, are shown in Table 3. The length of the gene head is set to 12 because each gene with a length of 25 (, ) can carry 7 function sets and 17 terminal sets. In addition, the number of genes in a chromosome is set to 16, which is expected to support the evolution of 16 independent rules for each chromosome.

Table 3.
The variables in the chromosome.
3.4. Fitness Evaluation
Fitness is an index that evaluates chromosomes from the perspective of problem optimization objectives. In the calculation of specific functions, the object of evaluation is the corresponding dispatching rules of chromosomes. The function is used to describe the arithmetic expression of the dispatching rule corresponding to each chromosome, which outputs the matching score between task and satellite . In each decision step, the match with the highest matching score is selected as follows.
For test scenarios, the assignment is constructed using sequence matching as shown in Figure 6. The scheduling benefits of each satellite obtained based on single-satellite scheduling. For the fitness of the rule , the fitness of the rule defined by the average profit of test scenarios is shown in Formula (21).
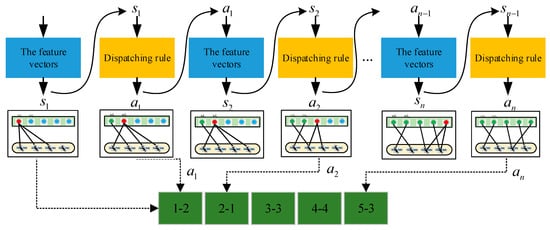
Figure 6.
The construction of sequential solutions for task assignment.
3.5. Population Initialization and Selection
Population initialization is used to generate chromosomes on the basis of satisfying coding rules. In Formula (22), represents the function set, represents the terminal set, is to classify the generated code bits, and the method of generating genes is given in the initialization of the population. Each chromosome is made up of multiple genes, and the population is made up of chromosomes.
As for the population selection, in each generation, both elite individuals and a certain number of inferior individuals should be reserved to avoid falling into the local optimum. In this study, the classic tournament ranking algorithm is adopted. When constructing the new generation, the elite individual is retained according to the proportion of population size . Then, individuals are randomly selected from the population, and the individual with maximum fitness is put into the new generation, as shown in Figure 7.
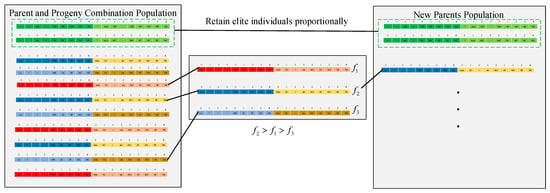
Figure 7.
The selection of individuals in the population.
4. Experiments
This section presents numerical results via experiments to evaluate the effectiveness of CHMGEP and demonstrate its superiority to existing methods. A set of well-designed test scenarios will be introduced first since there are no existing well-recognized benchmarks for the MSCTAP. Then, the analysis of the training process and training results will be given to illustrate the convergence and feasibility, respectively. Finally, comparisons and results will be presented with a detailed discussion.
4.1. Design of Scenarios
The test scenarios are generated by the orbit characteristics of satellite resources. Targets obey specific distribution (mainly uniform distribution, ), which makes the conflict between tasks greater and can better test the efficiency of the algorithm in terms of resource scheduling. The parameter distributions of the scenarios are shown in Table 4, and the satellite capability parameter settings are shown in Table 5. In this experiment, three training scene scales are set, sc100-s4-t160, sc100-s7-t280, and sc100-s10-t400, where sc represents the number of example samples, s represents the number of satellites, and t represents the number of tasks to be assigned. The experimental environment is the Windows 7 Intel(R) core i5-4460 processor (3.20 GHz), 12 G RAM.

Table 4.
The distribution of the test scenarios.

Table 5.
The parameter distribution of the satellite capability.
4.2. Evolution Process Analysis
Evolution process analysis mainly checks the convergence and evolution results of the GEP evolution process. In evolution, this experiment conducts rule evolution for the three task scale scenarios described in the previous section, representing small, medium, and large-scale scenarios, respectively. Table 6 shows the parameter settings of the evolution.

Table 6.
The parameter settings of the evolution.
The maximum, minimum, and average fitness of the individuals of each generation in the evolutionary process of the three scenarios are shown in Figure 8. The fitness values rise very quickly in the first 50 generations, indicating that the algorithm has an obvious effect on improving rule evolution in the early stage. For small-scale scenarios, it gradually slows down after the evolution generation reaches 50, converges around 200 generations, and then remains steady. Although the medium scale and large scale tend to be stable after 100 generations, they increase slightly after 350 and 300 generations, respectively, then stop growing and are stable. In the whole evolution process, the average fitness of the population keeps the same trend as the maximum fitness, while the minimum fitness is basically in the stage of fluctuation, which is also conducive to maintaining the diversity of the population and avoiding falling into the local optimum. In general, the fitness of rules under the three scenarios converges during the evolution process.
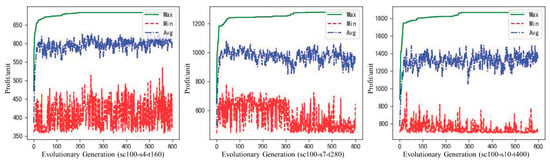
Figure 8.
The GEP evolutionary process.
In addition to the convergence of evolution, the final evolution rules are obtained through rule evolution under the three scenarios, as shown in Table 7, and the corresponding expression tree is shown in Figure 9. From the perspective of the rules, there is no overly complex rule, which indicates that the algorithm tends to be simplified as far as possible in the evolution process. Additionally, rules represent only order relations in which individual constant terms can be removed. From the expression tree, it can be found that WR is an important attribute and has obtained the multiplier of coefficient 4 in the medium and large-scale scenario and positive feedback of coefficient 1 in the small-scale scenario. In addition, during the evolution, attribute AS presents negative feedback. From the perspective of scale, the three rules all have their applicability to the scenario scale, but the rules themselves are universal in the model, and the trend of guiding order relationship is also consistent.

Table 7.
The results of optimal evolution rules.
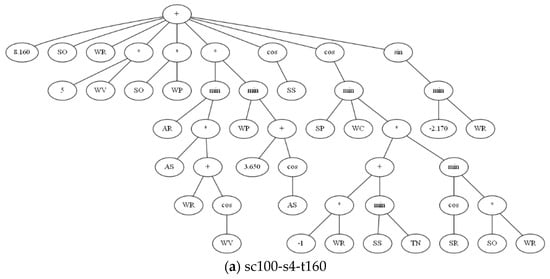
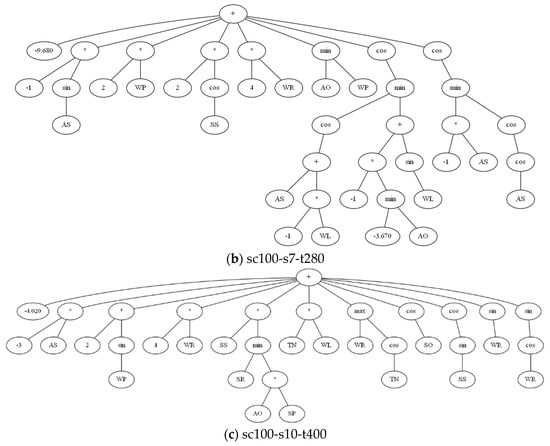
Figure 9.
The expression trees of the best dispatching rules.
In general, both convergence and trend consistency of evolution rules are guaranteed in the GEP algorithm. The GEP has a relatively good effect on the evolution of solving rules for MSCTAP.
4.3. Comparation with Heuristic Algorithms
Assignment results cannot be evaluated by the task assignment algorithm alone. It is also dependent on single satellite scheduling results. Therefore, the total scheduling revenue SP (average scheduling revenue ASP in multiple scenarios), scheduling time ST (average scheduling time AST in multiple scenarios), and the percentage of CHMGEP’s revenue over other algorithms’ PSPs are mainly used in the comparison process.
To validate the effect of the algorithm, comparative results between CHMGEP and heuristic algorithms are presented. The heuristic algorithm allocates based on the value of the heuristic rules. At each assignment, all satellites and the remaining tasks are given a matching index. After selecting the match with the best index, the new allocation is started again.
Heuristic algorithms are selected including heuristic multi-satellite task assignment rules based on NATA (Number of Assigned Task Ascending), LVTD (Length of Visible time-window Descending), and CDTA (Conflict Degree of Assigned Task ascending). They are the three heuristic rules. NATA gives assignment priority to the satellite with the least number of assigned tasks, LVTD gives assignment priority to the satellite with the longest visible time window, and CDTA gives assignment priority to the satellite with the least conflict degree of the assigned task. In the experiment, 50 test examples are generated for the s4-T160, S7-T280, and S10-T400 scenarios, and the scheduling benefit (SP) and scheduling time (ST) of each scenario are counted. The test results of 50 examples of the three scenarios are shown in Figure 10.
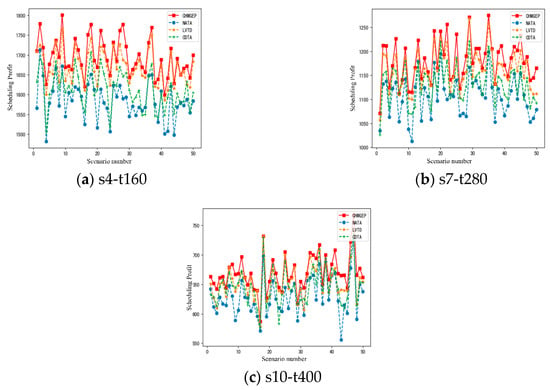
Figure 10.
The comparison of heuristic algorithms in different scenarios. (a) The scenario of s4-t160; (b) The scenario of s7-t280; (c) The scenario of s10-t400.
From Figure 10, it can be seen that in the case of three scenarios of the small, medium, and large scales, the CHMGEP algorithm has comprehensively surpassed the other three heuristic algorithms on SP. The three heuristic algorithms have their own advantages and disadvantages in solving the problem quality, while CHMGEP stands out. In order to further evaluate the advantages, the indexes of ASP (Average Scheduling Profit) and AST (Average Scheduling Time) are calculated according to the test results of 50 examples of each scale. The index of PSP (Profit Surpass Percentage) is also given to show the percentage of CHMGEP’s profit over other algorithms. The results are shown in Table 8.

Table 8.
The comparative results of CHMGEP with heuristic algorithms.
It can be seen from Table 8 that CHMGEP has the best performance in the three scale scenarios and the highest ASP index. The LVTD algorithm is the best among the heuristic algorithms, followed by CDTA and NATA.
In terms of the PSP index, the advantage of CHMGEP over the heuristic algorithm is not obvious. For the best heuristic LVTD, the scheduling profit overruns are only about 2%, and for the worst NATA algorithm, the overruns are about 6%. However, in terms of the solution time AST, the four algorithms remain in the same order of magnitude with little difference. Therefore, it is confirmed that CHMGEP can achieve efficiency beyond the best heuristic algorithm without consuming too much time cost.
4.4. Comparation with Meta-Heuristic Algorithms
Compared with the exact algorithm, the meta-heuristic algorithm can obtain satisfactory solutions and its solving efficiency is much higher. For example, Simulated Annealing (SA) and Variable Neighborhood Search (VNS), which are random search algorithms, can accept poor solutions with a certain probability in the process of searching. This strategy prevents the algorithm from falling into the local optimum. Compared with the population-based evolutionary algorithm, the local search algorithm is characterized by searching on the basis of a single solution, which has lower memory consumption and does not require complex crossover and mutation operations within the population. The algorithm flow charts are given as Figure 11.
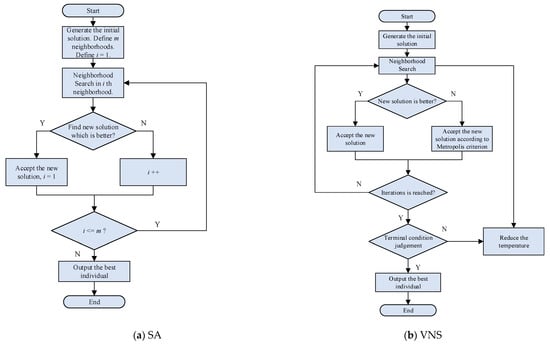
Figure 11.
The algorithm flow charts of SA and VNS. (a) The algorithm flow charts of SA; (b) The algorithm flow charts of VNS.
Based on the classical SA and VNS algorithm, this experiment introduces the best heuristic rule LVTD to generate the initial solution of SA and VNS. Thus, ISA (Improved Simulated Annealing) and IVNS (Improved Variable Neighborhood Search) are obtained and are used as representatives of meta-heuristic algorithms for comparison.
The solutions of the two algorithms are coded by integers, with each encoded bit representing the index of the assigned satellite. Table 9 and Table 10 show the parameters of ISA and IVNS, respectively.

Table 9.
The parameters in ISA.

Table 10.
The parameters in IVNS.
To analyze the effect of CHMGEP, another 7 scenarios varying from S4-T160 to S10-T400, with an increment step of one satellite and 40 tasks, are also proposed. Scenarios of each size contain 10 test cases. In the test, the ASP and AST indicators of each scale scenario were counted, as shown in Table 11. Results illustrate that CHMGEP does not always find the best solution. IVNS had the 4 best out of 7 scenarios, followed by CHMGEP with 2 and ISA with only 1 best. Moreover, CHMGEP also surpassed ISA in scenarios S7-T280. In terms of PSP index, the gap between CHMGEP and ISA and IVNS is as large as −1.47%, and even achieves 2% (S6-T240) in some small and medium scale scenarios, indicating that CHMGEP can approach the performance of meta-heuristic in solving the MSCTAP. From the perspective of the AST index, the CHMGEP algorithm can be controlled within 20 s in small and medium-scale scenarios, while the ISA algorithm is on the order of magnitude of hundreds of seconds. The IVNS algorithm achieves an amazing AST of thousands of seconds, although most of the new solutions are very good. While the iteration number of IVNS is only set for 30 times, its mechanism of breaking out of the loop is determined by the quality of the solution. When a local solution can find a better solution, its iteration counter does not increase, which leads to a large increase in algorithm time. In terms of algorithm efficiency, CHMGEP is obviously much higher than the latter two.

Table 11.
The comparison of metaheuristic algorithms on scheduling profit.
In order to further analyze the influence of scenarios on the timeliness of algorithm calculation, the results of AST were obtained as shown in Figure 12. As can be seen from Figure 12, the slope of the calculation timeliness curve corresponding to ISA and IVNS is larger than that of CHMGEP, and the increase in calculation time is faster than that of the CHMGEP algorithm. Notably, the CHMGEP algorithm is better than the general meta-heuristic algorithm in the large-scale scenario of MSCTAP. To sum up, although the CHMGEP algorithm proposed in this study can only surpass the meta-heuristic algorithm in a small number of examples, the algorithm has good solving efficiency and quality and the solving time does not show explosive growth with the scenario size.
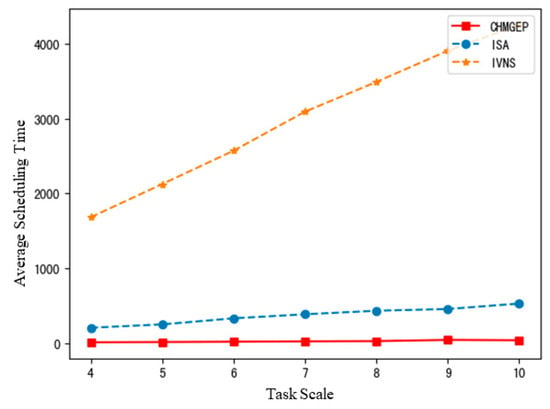
Figure 12.
The comparison with metaheuristic algorithms on scheduling time.
5. Conclusions and Future Work
This paper first discusses the structural design and cooperative process of a satellite constellation consisting of multiple autonomous satellites and provides a model based on this structure. After discussing the computing complexity of the problem, this study proposes a GEP-based construction heuristic method to solve the multi-satellite task assignment problem. On the basis of extracting 16 features of the problem, GEP is used to realize the evolution of the dispatching rules. Experimental results show that the proposed algorithm can completely surpass heuristic algorithms, outperform the meta-heuristic algorithm in a few cases, and has a higher solving efficiency than the meta-heuristic algorithm. In the future, we will enhance the effect of task assignment solving rules by evaluating more task assignment features, and, at the same time, more scenarios will be designed to evaluate the models. The allocation algorithm has both timeliness and technical feasibility, and future research needs to be oriented toward application and deployment. We will then study the cooperation scenario of the fully distributed autonomous satellite constellation which has higher robustness and intellectual abilities.
Author Contributions
Conceptualization, L.X. and F.Y.; Funding acquisition, L.X.; Methodology, W.Q., W.Y. and F.Y.; Software, W.Y.; Validation, W.Q.; Writing—original draft, W.Q.; Writing—review and editing, W.Y., L.X. and F.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Technical Field Foundation in 173 Program of National Defense Technology: 2021-JCJQ-JJ-0049.
Data Availability Statement
The data presented in this study are available upon request from the author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Variables | Descriptions |
| ASP | Average Scheduling Profit |
| AST | Average Scheduling Time |
| CDTA | Conflict Degree of Assigned Task Ascending |
| CHMGEP | Constructed Heuristic Method for Multi-Satellite Collaborative Task Assignment Based on GEP Evolution |
| C-NEAT | Cooperative Neuro-Evolution of Augmenting Topologies |
| EA | Evolutionary Algorithm |
| GP | Genetic Programming |
| GEP | Gene Expression Programming |
| ISA | Improved Simulated Annealing |
| IVNS | Improved Variable Neighborhood Search |
| JADE | Java Agent Development Framework |
| LVTD | Length of Visible Time-Window Descending |
| MSCTAP | Multi-Satellite Collaborative Task Assignment Problem |
| NATA | Number of Assigned Task Ascending |
| PSP | The Percentage of CHMGEP’s Profit over other Algorithms |
| SA | Simulated Annealing |
| SP | Scheduling Profit |
| ST | Scheduling Time |
| SVM | Support Vector Machine |
| VNS | Variable Neighborhood Search |
References
- Kennedy, A.K. Resource Optimization Algorithms for an Automated Coordinated CubeSat Constellation. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2015. [Google Scholar]
- Lei, H.; Liu, X.; Chu, X.; Chen, Y.; Ke, L. Multiple Autonomous Agile Satellites Coordinating and Planning in an Uncertain Environment. In Proceedings of the 15th International Conference on Space Operations, Marseille, France, 28 May–1 June 2018. [Google Scholar]
- Schetter, T.; Campbell, M.; Surka, D. Multiple Agent-Based Autonomy for Satellite Constellations. Artif. Intell. 2003, 145, 147–180. [Google Scholar] [CrossRef]
- Van Der Horst, J. Market-Based Task Allocation in Distributed Satellite Systems. Ph.D. Thesis, University of Southampton, Southampton, UK, 2012. [Google Scholar]
- van der Horst, J.; Noble, J. Task Allocation in Networks of Satellites with Keplerian Dynamics. Acta Futur. 2012, 5, 143–150. [Google Scholar]
- Wu, J.; Liu, L.; Hu, X. Predictive-Reactive Scheduling for Space Missions in Small Satellite Clusters. In Proceedings of the 2016 International Symposium on Computer, Consumer and Control (IS3C), Xi’an, China, 4–6 July 2016; pp. 475–480. [Google Scholar]
- Li, J.; Chen, Y.; Liu, X.; He, R. JADE Implemented Multi-Agent Based Platform for Multiple Autonomous Satellite System. In Proceedings of the 2018 Space Operations Conference, Marseille, France, 28 May–1 June 2018; p. 2349. [Google Scholar]
- Yao, F.; Li, J.; Chen, Y.; Chu, X.; Zhao, B. Task Allocation Strategies for Cooperative Task Planning of Multi-Autonomous Satellite Constellation. Adv. Space Res. 2019, 63, 1073–1084. [Google Scholar] [CrossRef]
- Yang, W.; He, L.; Liu, X.; Chen, Y. Onboard Coordination and Scheduling of Multiple Autonomous Satellites in an Uncertain Environment. Adv. Space Res. 2021, 68, 4505–4524. [Google Scholar] [CrossRef]
- Chong, W.; Jun, L.; Ning, J.; Jun, W.; Hao, C. A Distributed Cooperative Dynamic Task Planning Algorithm for Multiple Satellites Based on Multi-Agent Hybrid Learning. Chin. J. Aeronaut. 2011, 24, 493–505. [Google Scholar]
- Du, Y.; Wang, T.; Xin, B.; Wang, L.; Chen, Y.; Xing, L. A Data-Driven Parallel Scheduling Approach for Multiple Agile Earth Observation Satellites. IEEE Trans. Evol. Comput. 2019, 24, 679–693. [Google Scholar] [CrossRef]
- Ren, L.; Ning, X.; Li, J. Hierarchical Reinforcement-Learning for Real-Time Scheduling of Agile Satellites. IEEE Access 2020, 8, 220523–220532. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Zhu, M.F. Solving TSP Problem Based on Gene Expression Programming. Comput. Eng. Appl. 2008, 44, 4. [Google Scholar]
- Zhu, M.F.; Ye, F.Y.; Ding, X.W. Solving Algorithm of Task Assigned Problem Using Gene Expression Programming. Comput. Eng. Appl. 2014, 50, 50–53. [Google Scholar]
- Deng, S.; Wang, R.; Zhang, Y.; Zhang, J. Grid Resource Allocation Algorithm Based on Parallel Gene Expression Programming. Acta Electonica Sin. 2009, 37, 272. [Google Scholar]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. Automatic Design of a Hyper-Heuristic Framework with Gene Expression Programming for Combinatorial Optimization Problems. IEEE Trans. Evol. Comput. 2014, 19, 309–325. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Peng, K.; Li, X.; Lian, K.; Zhang, S. Dynamic Flexible Job Shop Scheduling Method Based on Improved Gene Expression Programming. Meas. Control. 2021, 54, 1136–1146. [Google Scholar] [CrossRef]
- Ozturk, G.; Bahadir, O.; Teymourifar, A. Extracting Priority Rules for Dynamic Multi-Objective Flexible Job Shop Scheduling Problems Using Gene Expression Programming. Int. J. Prod. Res. 2019, 57, 3121–3137. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, Q.; Chica, M. A Robust MILP and Gene Expression Programming Based on Heuristic Rules for Mixed-Model Multi-Manned Assembly Line Balancing. Appl. Soft Comput. 2021, 109, 107513. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).