A Novel Approach of Fuzzy Control Chart with Fuzzy Process Capability Indices Using Alpha Cut Triangular Fuzzy Number

Abstract

Statistical Quality Control is a valuable strategy that applies to the statistical technique for monitoring a manufacturing system under particular situations. On the other hand, the fuzzy set theory is an ideal instrument to cope with an unclear situation. The existing studies are restricted, and there is still mystery behind the unclear data. This paper deals with technique: namely, the fuzzy control chart based on fuzzy process capability indices (FCPI) using triangular fuzzy numbers (TFNs). Alpha cut theory is applied in statistical quality control for fuzzy process control industrial application. This is a five-phase study that deals with the control chart using capability indices. The numerical example is also performed using the proposed technique. This paper would help to better assess/understand the manufacturing system data and would explore the application of the fuzzy control techniques.

1. Introduction

Quality has long been regarded as an important factor in the performance and competitiveness of industrial and service enterprises in both local and worldwide markets. Shewhart statistical quality controls are the typical control charts used to monitor a process under specified situations (Montgomery [1]). While dealing with numerical variables, one has to take both the process mean and process variability into account. There is a lot of fuzzy knowledge (i.e., hazy, unsure, inexact, etc.) in the real world. Fuzzy set is a method of variable processing that allows for the processing of numerous potential truth values using the identical variable. Fuzzy set tries to solve issues by using an open, inaccurate spectrum of facts and heuristics to arrive at a variety of accurate conclusions. The $\overline{X}$ and R charts are the most commonly utilized by practitioners and scholars in the literature [1]. However, these standard charts do not function when the data are vague. In this case, fuzzy set theory is an effective method for monitoring a manufacturing system. The fully fuzzy linear programming method was developed by Ghoushchi et al. [2] by modified triangular number, and an illustrative example is presented by the proposed method. Yeh [3] adopted the technique of weighted triangular approximation of fuzzy numbers (WTAFN), which was proposed by Zheng and Li, and they show an example of (WTAFN). In many sectors, $\overline{X}$-R charts are the most extensively used control chart for variable data to analyze process stability. The $\overline{X}$ and R control chart with specified process capability was demonstrated by Subramani and Balamurali [4]. The $\overline{X}$ control chart for the Inverse Rayleigh Distribution (IRD) is constructed by Shafqat et al. [5] under repeated group sampling by the lower record values. The mean and standard deviation of the Inverse Rayleigh Distribution based on lower record values are utilized to calculate the breadth and power of the $\overline{X}$ control limits. As far as the $\overline{X}$-R and $\overline{X}$-S chart for the food industry in the UK are concerned, these two were evolved by Lim et al. [6]. The fuzzy control chart was developed with TFNs into three phases for the $\overline{X}$-S chart and process capability indices (CPI) using unbalanced data, converted the data for each sample into the fuzzy form, and then decided the fuzzy limits and illustrated them for uncertain data [7]. The most popular control chart for univariate data, the exponential weighted moving average (EWMA) control chart under fuzzy environment and the control chart for fuzzy nonconformities per unit by using alpha cut technique, are well applied and established in real case applications [8,9]. The fuzzy rank set theories to build fuzzy charts under a generic variable sample size constraint, which is well suited to this fuzzy data domain and fuzzy $\overline{X}$ and S control charts, show data flexibility and human acceptance for fuzzy data [10]. Process capability indices may be used to identify whether a process is capable of generating goods within the customer-defined specification restrictions. The first capability index $C_p$ developed by Kane [11] is defined as the ratio of the process standard deviation to the Upper and Lower specification limits (USL&LSL). Kaya and Kahraman [12] used TFNs to compute the fuzzy $C_p$ and $C_{pk}$ indices. A control chart using a fuzzy multivariate exponentially weighted moving average (F-MEWMA) was created by Alipour and Noorossana [13]. The proposed technique is developed using a combination of multivariate statistical quality control and fuzzy set theory in this study. The fuzzy exponential weighted moving average and cumulative sum control chart (CUSUM) were derived by Erginel and Şentürk [14] with a suitable example. Erginel [15] developed a fuzzy control chart by using the rules that introduces the fuzzy p and np chart based on the constant sample size and variable sample size. In addition, the decision is made regarding whether it is under control or out of control. In the context of fuzzy set theory, Bradshaw [16] showed how to interpret economic control constraints. Wang and Raz [17] developed quality control charts and built control charts employing linguistic variables for regulating the process average using the fuzzy set theory. In the same context, the linguistic control charts for the process average and the process variability were created by Kanagawa et al. [18]. Additionally, Franceschini and Romano [19] presented an on-line process control using control charts for linguistic variables. In a similar way, Taleb and Limam [20] created control charts utilizing linguistic data while taking fuzzy and probability theory into consideration. Gulbay [21] created α-cut control charts for characteristics. By choosing an appropriate α-level, this method enables one to ascertain the tightness of the inspection. By using the α cut to provide the ability to determine the tightness of the inspection: the greater the value of α, the tighter the inspection. Gulbay and Kahraman [22] addressed some additions to fuzzy control charts based on fuzzy transformation methods. This work also develops the Direct Fuzzy Approach (DFA), which is a new alternative methodology. The suggested approach is significantly different from the current fuzzy control charts in that it does not involve defuzzification. Hou et al. [23] developed the fuzzy control chart and talked about the fuzzy numbers created by converting expert scores into the plotted data. The need and possibility measurement rules are two different nonconformity judgement rule types that are offered. Fernandez [24] also looked into the primary objectives of the proposed fuzzy control charts in the pertinent studies. Using fuzzy random variables, Hesamian et al. [25] provided a quality control procedure. Fuzzy information was used by Hryniewicz et al. [26] to create control charts for autocorrelated observations. Fuzzy adaptive control was used by Zohoori et al. [27] to track the performance of production time and cost. By utilizing the knowledge and carrying out a process capability control, Choi et al. [28] provided a decision-making technique with fuzzy inference to facilitate process capability analysis. A fuzzy chart was suggested by Faraz and Moghadam [29] for tracking the process mean. Hryniewicz [30] gave a concise review of statistical quality control for fuzzy data, including difficulties for the future, in relation to the issues with fuzzy control charts. According to Amirzadeh [31] et al., the “degree of nonconformity” based on fuzzy notions is defined, and a fuzzy p-chart based on the mean degree of nonconformity is produced rather than considering an item to be either conforming or nonconforming. For the X-bar control chart, Demirli and Vijayakumar [32] suggested a rule-based fuzzy inference system. A fuzzy exponentially weighted moving average (EWMA) control chart with a α level cut for monitoring a production process was developed by Goztok et al. [33]. Khan et al. [34] developed the model for an average run of the fuzzy EWMA control chart and also provided a comparative study of classical EWMA and fuzzy EWMA. Alakoc [35] created the fuzzy control chart using a confidence interval. Al-Refaie et al. [36] discussed how the lower, average, and highest values of the replicate’s observation are represented by a triangular membership function. A common output measure (COM) value is the output of the fuzzy logic after the fuzzy numbers have been normalized and assigned as input. Finally, the EWMA and CUSUM control charts with various cut values are developed using the original values of the COM variables.

This study examines a new approach to solve the fuzzy $\overline{X}$-R control chart for variables with fuzzy process capability indices problems through the fuzzy decision parameter and variability using TFNs. The technique, which is based on alpha cut theory, is suggested to find the optimal fuzzy control chart solution for real world problems. In this method, the problem is considered as a fuzzy one and is solved by the presented method. First, the control chart model with FCPI was written based on the alpha cut TFNs, and second, we calculate the fuzzy $C_p$ and $C_{pk}$ with the help of USL&LSL and solved the model with FPCI. Based on this model, the flexibility of the control chart is increased.

The remainder of the research is divided into sections. Section 2 represents the methodological progress. The offered approach is used to conduct a numerical example, and the results are given in Section 3. Finally, the conclusion is presented in Section 4.

2. Methodology Development

2.1. Preliminaries

The fuzzy theory defines the notion of membership function and alpha cut theory to represent variables [2]. A membership function can be defined as ${\mu }_A\left(x\right):X\to \left[0,1\right]$ for set A. The membership amount ${\mu }_A\left(x\right)$ indicates the degree of dependence $x\in X$ in set A. The degree of conformity of member $x\in R$ to the intended concept of the set $\tilde{A}$ or the degree of membership of any element $x\in R$ to a fuzzy set $\tilde{A}$ is defined as the degree of acceptance of $x$ as a member of the fuzzy set $\tilde{A}$.

Triangular Fuzzy Number

Definition 1.

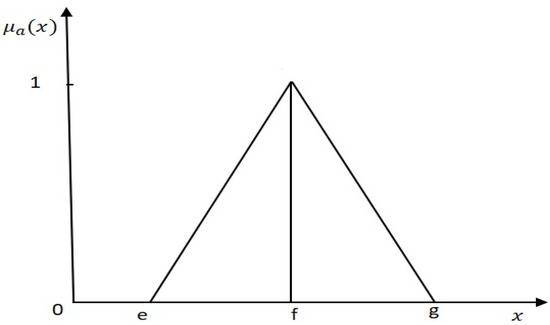
A triangular fuzzy number $\tilde{A}$ (as shown in Figure 1) is defined as a ternary number (e, f, g), and its membership function is as follows [2]:

$${\mu }_A\left(x\right)=\{\begin{array}{cc}\hfill 0& x\le e,\hfill \\ \hfill \frac{x-e}{f-e}& e\le x\le f\hfill \\ \hfill \frac{g-x}{g-f}& f\le x\le g\hfill \\ \hfill 0& x\ge g\hfill \end{array}$$

(1)

Figure 1. Triangular Fuzzy Number.

Definition 2

(Alpha-cut).The alpha cut for the fuzzy set $\tilde{A}$ ($A_{\alpha }$) is a certain set that contains a set of elements whose degree of membership is equal to or greater than the alpha value [2].

$$A_{\alpha }=\left\{x\in X|{\mu }_{\tilde{A}}\left(x\right)\ge \alpha \right\}$$

(2)

where A = (e, f, g) is implied as a TFN, with its alpha cut being as follows:

$$A_{\alpha }=\left[e+\alpha \left(f-e\right),f,g-\alpha \left(g-f\right)\right]$$

(3)

For the traditional control chart for a variable with specified $C_p$ and $C_{pk}$ values, the upper control limit (UCL), the center limit (CL), and the lower control limit (LCL) are found as follows [4].

The various mathematical concepts used to build control charts and calculate the process capacity indices are listed below.

$$\mathrm{Overall}\mathrm{mean}(\stackrel{=}{X})=\frac{{{\displaystyle \sum }}_{i=1}^N{\overline{x}}_i}{N}$$

Tolerance (T) = USL − LSL

$$\mathrm{process}\mathrm{capability}\left(C_p\right)=\frac{USL-LSL}{\raisebox{1ex}{$6\overline{R}$}\!\left/ \!\raisebox{-1ex}{$d_2$}\right.}$$

$\overline{R}$ is the average range for each sample. It is noted that $\sigma$ is unknown.

$$\mathrm{Upper}\mathrm{process}\mathrm{capability}\mathrm{index}\left(C_{pu}\right)=\frac{USL-\stackrel{=}{X}}{\raisebox{1ex}{$3\overline{R}$}\!\left/ \!\raisebox{-1ex}{$d_2$}\right.}$$

$$\mathrm{Lower}\mathrm{process}\mathrm{capability}\mathrm{index}\left(C_{pl}\right)=\frac{\stackrel{=}{X}-LSL}{\raisebox{1ex}{$3\overline{R}$}\!\left/ \!\raisebox{-1ex}{$d_2$}\right.}$$

$$\mathrm{Process}\mathrm{capability}\mathrm{index}\left(C_{pk}\right)=Min\left\{C_{pu},C_{pl}\right\}$$

$$\mathrm{Target}(M)=\frac{USL+LSL}{2}$$

$\overline{X}$ Control chart with specified $C_p$ value:

$$UCL\&LCL=\stackrel{=}{X}\pm A_2^{*}\frac{T}{C_p}$$

(4)

$$CL=\stackrel{=}{X}$$

(5)

R Control chart with specified $C_p$ value:

$$LCL=D_3^{*}\frac{T}{C_p}$$

(6)

$$UCL=D_4^{*}\frac{T}{C_p}$$

(7)

$$CL=D^{*}\frac{T}{C_p}$$

(8)

$\overline{X}$ Control chart with specified $C_{pk}$ value:

$$UCL\&LCL=\stackrel{=}{X}\pm A_{2k}^{*}\frac{[\frac{T}{2}-|\stackrel{=}{X}-M|]}{C_{pk}}$$

(9)

$$CL=\stackrel{=}{X}$$

(10)

R Control chart with specified $C_{pk}$ value:

$$LCL=D_{3k}^{*}\frac{[\frac{T}{2}-|\stackrel{=}{X}-M|]}{C_{pk}}$$

(11)

$$UCL=D_{4k}^{*}\frac{[\frac{T}{2}-|\stackrel{=}{X}-M|]}{C_{pk}}$$

(12)

$$CL=D_k^{*}\frac{[\frac{T}{2}-|\stackrel{=}{X}-M|]}{C_{pk}}$$

(13)

where $A_2^{*},D^{*},D_3^{*},D_4^{*},$ $A_{2k}^{*},D_k^{*},D_{3k}^{*},\mathrm{and}{D}_{4k}^{*}$ are the constant values for different sample size defined in phase 4.

2.2. Proposed Control Chart with $C_p$ and $C_{pk}$ Values

We adopted the Subramani and Balamurali [4] control chart and suggested a new fuzzy control chart. In this study, the aim is to build the control charts model for uncertain situations. We have provided fuzzy control charts for variables to make it easier for users to determine if the fuzzy process is under statistical control or not: that is, to decide whether the fuzzy process can continue without adjustment or, if necessary, to take corrective action to return the process to statistical control. The process can be allowed to proceed without modification or adjustment if the values of the fuzzy process capability indices are at a sufficient level. If not, appropriate adjustments must be made in order for the process to meet the needs of both fuzzy control charts and FPCI. The explanation of how a control chart and flow control chart work follows (Figure 2).

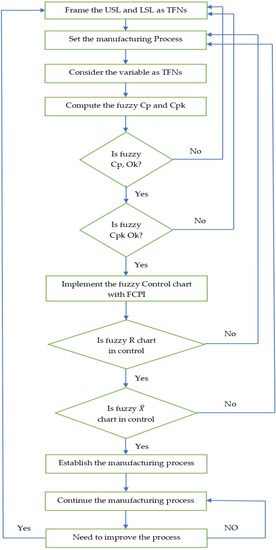
Figure 2. Flow control chart of the proposed technique.

Phase 1: Select the random sample of size n from the production process and convert it into the TFNs. Then, calculate the sample mean and sample range, and calculate the average of sample mean and sample range according to the Definition 2. Each sample or subgroup is designated as a TFN in the fuzzy set theory. The fuzzy overall mean and range are defined below:

$$\left(\stackrel{=}{X_e^{\alpha }},\stackrel{=}{X_f^{\alpha }},\stackrel{=}{X_g^{\alpha }}\right)=\left\{\left({\stackrel{=}{X}}_e+\alpha \left({\stackrel{=}{X}}_f-{\stackrel{=}{X}}_e\right)\right),{\stackrel{=}{X}}_f,\left({\stackrel{=}{X}}_g-\alpha \left({\stackrel{=}{X}}_g-{\stackrel{=}{X}}_f\right)\right)\right\}$$

(14)

$$\left(\overline{R_e^{\alpha }},\overline{R_f^{\alpha }},\overline{R_g^{\alpha }}\right)=\left\{\left({\overline{R}}_e+\alpha \left({\overline{R}}_f-{\overline{R}}_e\right)\right),{\overline{R}}_f,\left({\overline{R}}_g-\alpha \left({\overline{R}}_g-{\overline{R}}_f\right)\right)\right\}$$

(15)

Phase 2: Calculate the fuzzy tolerance values according to Definition 2, and the fuzzy $C_p$ values by using T are as follows:

$$T_{\left(e,f,g\right)}=\left\{\left(US{L}_e^{\alpha }-LS{L}_e^{\alpha }\right),\left(US{L}_f^{\alpha }-LS{L}_f^{\alpha }\right),\left(US{L}_g^{\alpha }-LS{L}_g^{\alpha }\right)\right\}$$

(16)

where $US{L}_{\left(e,f,g\right)}^{\alpha }\mathrm{and}LS{L}_{\left(e,f,g\right)}^{\alpha }$ are given below

$$\left(US{L}_e^{\alpha },US{L}_f^{\alpha },US{L}_g^{\alpha }\right)=\left\{\left(US{L}_e+\alpha \left(US{L}_f-US{L}_e\right)\right), US{L}_f,\left(US{L}_g-\alpha \left(US{L}_g-US{L}_f\right)\right)\right\}$$

(17)

and

$$\left(LS{L}_e^{\alpha },LS{L}_f^{\alpha },LS{L}_g^{\alpha }\right)=\left\{\left(LS{L}_e+\alpha \left(LS{L}_f-LS{L}_e\right)\right),LS{L}_f,\left(LS{L}_g+\alpha \left(LS{L}_g-LS{L}_f\right)\right)\right\}$$

(18)

It is noted that $\sigma$ is unknown. $\sigma =\frac{\overline{R}}{d_2}$ where $d_2$ is a table value, as given in Subramani and Balamurali [4].

$$\left(C_{p_e},C_{p_f},C_{p_g}\right)=\left(\frac{T_e}{6\frac{\overline{R_e^{\alpha }}}{d_2}},\frac{T_f}{6\frac{\overline{R_f^{\alpha }}}{d_2}},\frac{T_g}{6\frac{\overline{R_g^{\alpha }}}{d_2}}\right)$$

(19)

The specification limitations and the process’s standard deviation are used to calculate the C_p value. The majority of the researchers demand a process C_p of at least 1.33. If any fuzzy C_p is less than the defined value, then we need to make an improvement; otherwise, we do not need improvement. If the fuzzy $C_p$ values are more than the defined value, then we proceed to phase 4.

Phase 3: Calculate the fuzzy $C_{pk}$ values. The proposed formula is given as:

$$C_{p{k}_e}=\min \left(\frac{\left(US{L}_e^{\alpha }-\stackrel{=}{X_e^{\alpha }}\right)}{3\frac{\overline{R_e^{\alpha }}}{d_2}},\frac{\left(\stackrel{=}{X_e^{\alpha }}-LS{L}_e^{\alpha }\right)}{3\frac{\overline{R_e^{\alpha }}}{d_2}}\right)$$

(20)

$$C_{p{k}_f}=\min \left(\frac{\left(US{L}_f^{\alpha }-\stackrel{=}{X_f^{\alpha }}\right)}{3\frac{\overline{R_f^{\alpha }}}{d_2}},\frac{\left(\stackrel{=}{X_f^{\alpha }}-LS{L}_f^{\alpha }\right)}{3\frac{\overline{R_f^{\alpha }}}{d_2}}\right)$$

(21)

$$C_{p{k}_g}=\min \left(\frac{\left(US{L}_g^{\alpha }-\stackrel{=}{X_g^{\alpha }}\right)}{3\frac{\overline{R_g^{\alpha }}}{d_2}},\frac{\left(\stackrel{=}{X_g^{\alpha }}-LS{L}_g^{\alpha }\right)}{3\frac{\overline{R_g^{\alpha }}}{d_2}}\right)$$

(22)

The C_pk value ought to range from 1 to 3. The process has to be improved if the value is less than 1; otherwise, it does not need improvement. If the fuzzy $C_{pk}$ values are in the range, then we proceed to phase 4 and calculate the fuzzy control limits.

Phase 4: Find the fuzzy control limit with fuzzy $C_p$ and $C_{pk}$ values. The proposed chart formula is given below:

Fuzzy$\overline{\mathit{X}}$and R Control Chart with fuzzy${\mathit{C}}_{\mathit{p}}$values:

$$UC{L}_{{\overline{X}}_e} \& LC{L}_{{\overline{X}}_e}=\stackrel{=}{X_e^{\alpha }}\pm A_2^{*}\frac{T_e}{C_{p_e}}$$

(23)

$$UC{L}_{{\overline{X}}_f} \& LC{L}_{{\overline{X}}_f}=\stackrel{=}{X_f^{\alpha }}\pm A_2^{*}\frac{T_f}{C_{p_f}}$$

(24)

$$UC{L}_{{\overline{X}}_g} \& LC{L}_{{\overline{X}}_g}=\stackrel{=}{X_g^{\alpha }}\pm A_2^{*}\frac{T_g}{C_{p_g}}$$

(25)

$$C{L}_{{\overline{X}}_{\left(e,f,g\right)}}=(\stackrel{=}{X_e^{\alpha }},\stackrel{=}{X_f^{\alpha }},\stackrel{=}{X_g^{\alpha }})$$

(26)

$$\left(UC{L}_{R_e},UC{L}_{R_f},UC{L}_{R_g}\right)=\left(D_4^{*}\frac{T_e}{C_{p_e}},D_4^{*}\frac{T_f}{C_{p_f}},D_4^{*}\frac{T_g}{C_{p_g}}\right)$$

(27)

$$\left(LC{L}_{R_e},LC{L}_{R_f},LC{L}_{R_g}\right)=\left(D_3^{*}\frac{T_e}{C_{p_e}},D_3^{*}\frac{T_f}{C_{p_f}},D_3^{*}\frac{T_g}{C_{p_g}}\right)$$

(28)

$$\left(C{L}_{R_e},C{L}_{R_f},C{L}_{R_g}\right)=\left(D^{*}\frac{T_e}{C_{p_e}},D^{*}\frac{T_f}{C_{p_f}},D^{*}\frac{T_g}{C_{p_g}}\right)$$

(29)

Fuzzy$\overline{\mathit{X}}$and R Control Chart with fuzzy${\mathit{C}}_{\mathit{p}\mathit{k}}$values:

$$UC{L}_{{\overline{X}}_e}\&LC{L}_{{\overline{X}}_e}=\stackrel{=}{X_e^{\alpha }}\pm A_{2k}^{*}\frac{\left[\frac{T_e}{2}-\left|\stackrel{=}{X_e^{\alpha }}-M_e\right|\right]}{C_{p{k}_e}}$$

(30)

$$UC{L}_{{\overline{X}}_f}\&LC{L}_{{\overline{X}}_f}=\stackrel{=}{X_f^{\alpha }}\pm A_{2k}^{*}\frac{\left[\frac{T_f}{2}-\left|\stackrel{=}{X_f^{\alpha }}-M_f\right|\right]}{C_{p{k}_f}}$$

(31)

$$UC{L}_{{\overline{X}}_g}\&LC{L}_{{\overline{X}}_g}=\stackrel{=}{X_g^{\alpha }}\pm A_{2k}^{*}\frac{\left[\frac{T_g}{2}-\left|\stackrel{=}{X_g^{\alpha }}-M_g\right|\right]}{C_{p{k}_g}}$$

(32)

$$\left(UC{L}_{R_e},UC{L}_{R_f},UC{L}_{R_g}\right)=\left(D_{4k}^{*}\frac{\left[\frac{T_e}{2}-\left|\stackrel{=}{X_e^{\alpha }}-M_e\right|\right]}{C_{p{k}_e}},D_{4k}^{*}\frac{\left[\frac{T_f}{2}-\left|\stackrel{=}{X_f^{\alpha }}-M_f\right|\right]}{C_{p{k}_f}},D_{4k}^{*}\frac{\left[\frac{T_g}{2}-\left|\stackrel{=}{X_g^{\alpha }}-M_g\right|\right]}{C_{p{k}_g}}\right)$$

(33)

$$\left(LC{L}_{R_e},LC{L}_{R_f},LC{L}_{R_g}\right)=\left(D_{3k}^{*}\frac{\left[\frac{T_e}{2}-\left|\stackrel{=}{X_e^{\alpha }}-M_e\right|\right]}{C_{p{k}_e}},D_{3k}^{*}\frac{\left[\frac{T_f}{2}-\left|\stackrel{=}{X_f^{\alpha }}-M_f\right|\right]}{C_{p{k}_f}},D_{3k}^{*}\frac{\left[\frac{T_g}{2}-\left|\stackrel{=}{X_g^{\alpha }}-M_g\right|\right]}{C_{p{k}_g}}\right)$$

(34)

$$\left(C{L}_{R_e},C{L}_{R_f},C{L}_{R_g}\right)=\left(D_k^{*}\frac{\left[\frac{T_e}{2}-\left|\stackrel{=}{X_e^{\alpha }}-M_e\right|\right]}{C_{p{k}_e}},D_k^{*}\frac{\left[\frac{T_f}{2}-\left|\stackrel{=}{X_f^{\alpha }}-M_f\right|\right]}{C_{p{k}_f}},D_k^{*}\frac{\left[\frac{T_g}{2}-\left|\stackrel{=}{X_g^{\alpha }}-M_g\right|\right]}{C_{p{k}_g}}\right)$$

(35)

where $D^{*}=\frac{d_2}{6}$; $A_2^{*}=A_2\times D^{*}$; $D_3^{*}=\frac{\left(D_3\times d_2\right)}{6}$; $D_4^{*}=\frac{\left(D_4\times d_2\right)}{6}$; $D_k^{*}=\frac{d_2}{3}$; $A_{2k}^{*}=A_2\times D_k^{*}$; $D_{3k}^{*}=D_3\times D_k^{*}$; $D_{4k}^{*}=D_4\times D_k^{*}$

The above values are the table values given in Subramani and Balamurali [4].

Phase 5: Interpretation of the result for fuzzy $C_p$ and $C_{pk}$. We declare it out of control if ${\overline{X}}_e\ge UC{L}_{{\overline{X}}_e},{\overline{X}}_f\ge UC{L}_{{\overline{X}}_f}and{\overline{X}}_g\ge UC{L}_{{\overline{X}}_g}or{\overline{X}}_e\le UC{L}_{{\overline{X}}_e},{\overline{X}}_f\le UC{L}_{{\overline{X}}_f}and{\overline{X}}_g\le UC{L}_{{\overline{X}}_g}$, and in control if $LC{L}_{{\overline{X}}_e}\le {\overline{X}}_e\le UC{L}_{{\overline{X}}_e},LC{L}_{{\overline{X}}_f}\le {\overline{X}}_f\le UC{L}_{{\overline{X}}_f}andLC{L}_{{\overline{X}}_g}\le {\overline{X}}_g\le UC{L}_{{\overline{X}}_g}$; Similarly for R control chart, the R chart is in control if $LC{L}_{R_e}\le R_e\le UC{L}_{R_e}, LC{L}_{R_f}\le R_f\le UC{L}_{R_f} , and LC{L}_{R_g}\le R_g\le UC{L}_{R_g}$. Otherwise out of control and there is a need for improvement. Similar rules apply for $C_{pk}$.

3. Numerical Example and Results

In this study, we consider the following fuzzy SQC problem. For fulfilling the purpose, we have used the data of a power loom change gear (Figure 3). The information regarding the gear for each observation was collected from a private firm in India. The exact information about the parameters is not available. We have fuzzy information about the parameters in the form of a triangular fuzzy number, as shown in Table 1. Table 1 represents the fuzzy data; each sample consists of five observations, each within triangular form.

Figure 3. Power loom change gear.

Table 1. The inside diameter (in mm) of power loom change gear in fuzzy environment.

Sample No.	${\mathit{X}}_1 = \left({\mathit{X}}_{\mathit{e}1},{\mathit{X}}_{\mathit{f}1},{\mathit{X}}_{\mathit{g}1}\right)$	${\mathit{X}}_2 = \left({\mathit{X}}_{\mathit{e}2},{\mathit{X}}_{\mathit{f}2},{\mathit{X}}_{\mathit{g}2}\right)$	${\mathit{X}}_3 = \left({\mathit{X}}_{\mathit{e}3},{\mathit{X}}_{\mathit{f}3},{\mathit{X}}_{\mathit{g}3}\right)$	${\mathit{X}}_4 = \left({\mathit{X}}_{\mathit{e}4},{\mathit{X}}_{\mathit{f}4},{\mathit{X}}_{\mathit{g}4}\right)$	${\mathit{X}}_5 = ({\mathit{X}}_{\mathit{e}5},{\mathit{X}}_{\mathit{f}5},{\mathit{X}}_{\mathit{g}5})$
1	(38.077, 38.082, 38.087)	(38.07, 38.075, 38.08)	(38.08, 38.085, 38.09)	(38.051, 38.056, 38.061)	(38.061, 38.066, 38.071)
2	(38.05, 38.055, 38.06)	(38.078, 38.083, 38.088)	(38.058, 38.063, 38.068)	(38.081, 38.086, 38.091)	(38.074, 38.079, 38.084)
3	(38.063, 38.068, 38.073)	(38.038, 38.043, 38.048)	(38.084, 38.089, 38.094)	(38.064, 38.069, 38.074)	(38.062, 38.067, 38.072)
4	(38.061, 38.066, 38.071)	(38.05, 38.055, 38.06)	(38.076, 38.081, 38.086)	(38.059, 38.064, 38.069)	(38.053, 38.058, 38.063)
5	(38.076, 38.081, 38.086)	(38.068, 38.073, 38.078)	(38.081, 38.086, 38.091)	(38.079, 38.084, 38.089)	(38.071, 38.076, 38.081)
6	(38.045, 38.0538.055)	(38.084, 38.089, 38.094)	(38.067, 38.072, 38.077)	(38.053, 38.058, 38.063)	(38.056, 38.061, 38.066)
7	(38.072, 38.077, 38.082)	(38.044, 38.049, 38.054)	(38.052, 38.057, 38.062)	(38.076, 38.081, 38.086)	(38.056, 38.061, 38.066)
8	(38.069, 38.074, 38.079)	(38.081, 38.086, 38.091)	(38.065, 38.07, 38.075)	(38.062, 38.067, 38.072)	(38.065, 38.07, 38.075)
9	(38.062, 38.067, 38.072)	(38.081, 38.086, 38.091)	(38.076, 38.081, 38.086)	(38.049, 38.054, 38.059)	(38.056, 38.061, 38.066)
10	(38.079, 38.084, 38.089)	(38.075, 38.08, 38.085)	(38.074, 38.079, 38.084)	(38.056, 38.061, 38.066)	(38.068, 38.073, 38.078)
11	(38.088, 38.093, 38.098)	(38.073, 38.078, 38.083)	(38.08, 38.085, 38.09)	(38.075, 38.08, 38.085)	(38.06, 38.065, 38.07)
12	(38.047, 38.052, 38.057)	(38.048, 38.053, 38.058)	(38.078, 38.083, 38.088)	(38.063, 38.068, 38.073)	(38.075, 38.08, 38.085)
13	(38.07, 38.075, 38.08)	(38.06, 38.065, 38.07)	(38.049, 38.054, 38.059)	(38.073, 38.078, 38.083)	(38.065, 38.07, 38.075)
14	(38.069, 38.074, 38.079)	(38.047, 38.052, 38.057)	(38.081, 38.086, 38.091)	(38.078, 38.083, 38.088)	(38.073, 38.078, 38.083)
15	(38.063, 38.068, 38.073)	(38.073, 38.078, 38.083)	(38.065, 38.07, 38.075)	(38.055, 38.06, 38.065)	(38.056, 38.061, 38.066)
16	(38.075, 38.08, 38.085)	(38.051, 38.056, 38.061)	(38.079, 38.084, 38.089)	(38.048, 38.053, 38.058)	(38.066, 38.071, 38.076)
17	(38.076, 38.081, 38.086)	(38.066, 38.071, 38.076)	(38.062, 38.067, 38.072)	(38.069, 38.074, 38.079)	(38.058, 38.063, 38.068)
18	(38.058, 38.063, 38.068)	(38.072, 38.077, 38.082	(38.052, 38.057, 38.062)	(38.063, 38.068, 38.073)	(38.059, 38.064, 38.069)
19	(38.06, 38.065, 38.07)	(38.064, 38.069, 38.074)	(38.065, 38.07, 38.075)	(38.057, 38.062, 38.067)	(38.051, 38.056, 38.061)
20	(38.057, 38.062, 38.067)	(38.048, 38.053, 38.058)	(38.064, 38.069, 38.074)	(38.06, 38.065, 38.07)	(38.05, 38.055, 38.06)
21	(38.089, 38.094, 38.099)	(38.048, 38.053, 38.058)	(38.065, 38.07, 38.075)	(38.069, 38.074, 38.079)	(38.069, 38.074, 38.079)
22	(38.068, 38.073, 38.078)	(38.082, 38.087, 38.092)	(38.066, 38.071, 38.076	(38.072, 38.077, 38.082)	(38.064, 38.069, 38.074)
23	(38.056, 38.061, 38.066)	(38.08, 38.085, 38.09)	(38.075, 38.08, 38.085)	(38.069, 38.074, 38.079)	(38.059, 38.064, 38.069)
24	(38.07, 38.075, 38.08)	(38.043, 38.048, 38.053)	(38.074, 38.079, 38.084)	(38.054, 38.059, 38.064)	(38.056, 38.061, 38.066)
25	(38.049, 38.054, 38.059)	(38.049, 38.054, 38.059)	(38.074, 38.079, 38.084)	(38.061, 38.066, 38.071)	(38.055, 38.06, 38.065)

The $\alpha =0.5$ by the researcher because this value can reflect the accurate control limit for the power loom change gear. The fuzzy average of the sample mean and sample range are calculated with $\alpha =0.5$ according to Equations (14) and (15). The next step is to find the upper and lower specification limit defined by the customer, but in this example, the specification limit is defined for further calculation. The USL and LSL were converted into TFN form using Equations (17) and (18). The value of the fuzzy specification limit with $\alpha =0.5$ for the data is $\left(US{L}_e^{\alpha },US{L}_f^{\alpha },US{L}_g^{\alpha }\right)=\left(38.1145,38.117,38.1195\right)$ and $\left(LS{L}_e^{\alpha },LS{L}_f^{\alpha },LS{L}_g^{\alpha }\right)=\left(38.0145,38.017,38.0195\right)$. It is noted that the values of $d_2=2.326,$ $A_2=0.557, D^{*}=0.3877, A_2^{*}=0.2159, D_3^{*}=0, D_4^{*}=0.8199, D_k^{*}=0.775, A_{2k}^{*}=0.432, D_{3k}^{*}=0 and D_{4k}^{*}=1.64$. After this, we calculated fuzzy tolerance values by using Equations (17) and (18) and found the value of $T_{\left(e,f,g\right)}=\left(0.1,0.1,0.1\right)$. Further, we calculate the fuzzy $C_p$ using Equation (19), and we obtain the values of $\left(C_{p_e},C_{p_f},C_{p_g}\right)=\left(1.5,1.5,1.5\right)$. Here, we defined the C_p value in phase 2. It is shown that the fuzzy C_p by using $\alpha$ cut is greater than 1.33, so we do not need any improvement in specification limit. The next phase is to calculate the fuzzy $C_{pk}$ value for the $\overline{X}$ and R control chart using Equations (20)–(22), and we obtained the values of $\left(C_{p{k}_e},C_{p{k}_f},C_{p{k}_g}\right)=\left(1.3799,1.3799,1.3799\right)$. The calculated value is greater than the defined value (in phase 3), so we do not need any improvement in specification limit. In phase 4, we obtained the fuzzy $\overline{X}$ and R control limit with fuzzy $C_p$ and $C_{pk}$ using Equations (23)–(35) and the values are written in Table 2, Table 3, Table 4 and Table 5. For example, the calculation of the ${\overline{X}}_e$ control limit is $38.0673+0.2159\times \left(\raisebox{1ex}{$0.1$}\!\left/ \!\raisebox{-1ex}{$1.5$}\right.\right)=38.0525$ similarly for others. Finally, the last step is to interpret the result of this illustrative example.

Table 2. Fuzzy $\overline{X}$ control limit with fuzzy C_p value.

$\mathit{L}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{e}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{f}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{g}}}$	$\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{e}}}$	$\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{f}}}$	$\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{g}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{e}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{f}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{g}}}$
38.0525	38.0550	38.5753	38.0673	38.0698	38.0723	38.0821	38.0845	38.0871

Table 3. Fuzzy R control limit with fuzzy $C_p$ value.

$\mathit{L}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{e}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{e}}}$	$\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{g}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{e}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{g}}}$
0	0	0	0.0265	0.0265	0.0265	0.0561	0.0561	0.0561

Table 4. Fuzzy $\overline{X}$ control limit with fuzzy $C_{pk}$ value.

$\mathit{L}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{e}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{f}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{g}}}$	$\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{e}}}$	$\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{f}}}$	$\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{g}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{e}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{f}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\overline{\mathit{X}}}_{\mathit{g}}}$
38.0525	38.0550	38.0575	38.0673	38.0698	38.0723	38.0821	38.0845	38.0871

Table 5. Fuzzy R control limit with fuzzy $C_{pk}$ value.

$\mathit{L}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{e}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{L}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{e}}}$	$\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{g}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{e}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{f}}}$	$\mathit{U}\mathit{C}{\mathit{L}}_{{\mathit{R}}_{\mathit{g}}}$
0	0	0	0.0265	0.0265	0.0265	0.0561	0.0561	0.0561

The decisions for the $\overline{X}$ and R control charts with $C_p$ and $C_{pk}$ values are shown in Table 6 and Table 7. We declare it out of control if the ${\overline{X}}_e\ge UC{L}_{{\overline{X}}_e}and{\overline{X}}_g\ge UC{L}_{{\overline{X}}_g}or{\overline{X}}_e\le UC{L}_{{\overline{X}}_e}and{\overline{X}}_g\le UC{L}_{{\overline{X}}_g}$, but as per the decision table, all the values are in control: $LC{L}_{{\overline{X}}_f}\le {\overline{X}}_f\le UC{L}_{{\overline{X}}_f}$ and the R chart is in a control situation where all the points are between the control limits. Table 2, Table 3, Table 4 and Table 5 shows how the cut affects the power loom change gear manufacturing process’s upper, middle, and lower control limits. As a result, selecting the appropriate $\alpha$ cut to obtain the required control limits for the manufacturing process might be tricky. When used for the power loom change gear process, the proposed control chart with an $\alpha$ cut significantly improves the efficiency of identifying and fixing the source of undesirable variation. Table 6 and Table 7 show that gear production is under control; hence, there is no need to take any preventative measures. The proposed method proves that there are no uncontrolled variables in the production process. There is no out-of-the-ordinary circumstance that occurs while making gears using the proposed method that involves an $\alpha$ cut. The formulation and attributes described in the preceding sections are evidently beneficial for comprehending the nature of the issue and its solutions as well as for effectively driving the optimal fuzzy control charts with FCPI. The calculation used in the Subramani and Balamurali [4] technique for numerical findings is in specific conditions; nevertheless, sample data may have uncertainties arising from measurement methods and ambient factors, and fuzzy numbers can be employed to reflect these uncertainties. We obtained LCL and UCL values with $C_p$ and $C_{pk}$ for each model of (38.0550, 38.0845) (38.0550, 38.0845) and for R control limits (0, 0.0561) and (0, 0.0561), while in this study, we consider it as a fuzzy problem; in a fuzzy set theory, each sample or subgroups is denoted as a TFN. The values of the fuzzified control limit of the $\overline{X}$ and R chart with FCPI are shown in Table 2, Table 3, Table 4 and Table 5. The existing control chart with specified $C_p$ and $C_{pk}$ values were developed by Subramani and Balamurali [4], which shows that all the values under certain situations are in control while using the proposed technique developed in a fuzzy environment. There is a lack of $\alpha$ value if we increase the alpha value; then, sometimes, control limits could be meaningless, while in the existing study, there is no need for $\alpha$ and other values. The decision maker can choose the different control limits appropriate to their needs.

Table 6. Decision table for fuzzy $\overline{X}$ and R control limit with fuzzy $C_p$ values.

S.N.	${\overline{\mathit{X}}}_{\mathit{e}}$	In Control (✓) or Out of Control (×)	${\overline{\mathit{X}}}_{\mathit{f}}$	In Control (✓) or Out of Control (×)	${\overline{\mathit{X}}}_{\mathit{g}}$	In Control (✓) or Out of Control (×)	${\mathit{R}}_{\mathit{e}}$	In Control (✓) or Out of Control (×)	${\mathit{R}}_{\mathit{f}}$	In Control (✓) or Out of Control (×)	${\mathit{R}}_{\mathit{g}}$	In Control (✓) or Out of Control (×)
1	38.0678	✓	38.073	✓	38.0778	✓	0.029	✓	0.029	✓	0.029	✓
2	38.0682	✓	38.073	✓	38.0782	✓	0.031	✓	0.031	✓	0.031	✓
3	38.0622	✓	38.067	✓	38.0722	✓	0.046	✓	0.046	✓	0.046	✓
4	38.0598	✓	38.064	✓	38.0698	✓	0.026	✓	0.026	✓	0.026	✓
5	38.075	✓	38.08	✓	38.085	✓	0.013	✓	0.013	✓	0.013	✓
6	38.061	✓	38.066	✓	38.071	✓	0.039	✓	0.039	✓	0.039	✓
7	38.06	✓	38.065	✓	38.07	✓	0.032	✓	0.032	✓	0.032	✓
8	38.0684	✓	38.073	✓	38.0784	✓	0.019	✓	0.019	✓	0.019	✓
9	38.0648	✓	38.069	✓	38.0748	✓	0.032	✓	0.032	✓	0.032	✓
10	38.0704	✓	38.075	✓	38.0804	✓	0.023	✓	0.023	✓	0.023	✓
11	38.0752	✓	38.080	✓	38.0852	✓	0.028	✓	0.028	✓	0.028	✓
12	38.0622	✓	38.067	✓	38.0722	✓	0.031	✓	0.031	✓	0.031	✓
13	38.0634	✓	38.068	✓	38.0734	✓	0.024	✓	0.024	✓	0.024	✓
14	38.0696	✓	38.074	✓	38.0796	✓	0.034	✓	0.034	✓	0.034	✓
15	38.0624	✓	38.067	✓	38.0724	✓	0.018	✓	0.018	✓	0.018	✓
16	38.0638	✓	38.068	✓	38.0738	✓	0.031	✓	0.031	✓	0.031	✓
17	38.0662	✓	38.071	✓	38.0762	✓	0.018	✓	0.018	✓	0.018	✓
18	38.0608	✓	38.065	✓	38.0708	✓	0.02	✓	0.02	✓	0.02	✓
19	38.0594	✓	38.064	✓	38.0694	✓	0.014	✓	0.014	✓	0.014	✓
20	38.0558	✓	38.061	✓	38.0658	✓	0.016	✓	0.016	✓	0.016	✓
21	38.068	✓	38.073	✓	38.078	✓	0.041	✓	0.041	✓	0.041	✓
22	38.0704	✓	38.075	✓	38.0804	✓	0.018	✓	0.018	✓	0.018	✓
23	38.0678	✓	38.073	✓	38.0778	✓	0.024	✓	0.024	✓	0.024	✓
24	38.0594	✓	38.064	✓	38.0694	✓	0.031	✓	0.031	✓	0.031	✓
25	38.0576	✓	38.062	✓	38.0676	✓	0.025	✓	0.025	✓	0.025	✓

Table 7. Decision table for fuzzy $\overline{X}$ and R control limit with fuzzy $C_{pk}$ values.

S.N.	${\overline{\mathit{X}}}_{\mathit{e}}$	In Control (✓) or Out of Control (×)	${\overline{\mathit{X}}}_{\mathit{f}}$	In Control (✓) or Out of Control (×)	${\overline{\mathit{X}}}_{\mathit{g}}$	In Control (✓) or Out of Control (×)	${\mathit{R}}_{\mathit{e}}$	In Control (✓) or Out of Control (×)	${\mathit{R}}_{\mathit{f}}$	In Control (✓) or Out of Control (×)	${\mathit{R}}_{\mathit{g}}$	In Control (✓) or Out of Control (×)
1	38.0678	✓	38.0728	✓	38.0778	✓	0.029	✓	0.029	✓	0.029	✓
2	38.0682	✓	38.0732	✓	38.0782	✓	0.031	✓	0.031	✓	0.031	✓
3	38.0622	✓	38.0672	✓	38.0722	✓	0.046	✓	0.046	✓	0.046	✓
4	38.0598	✓	38.0648	✓	38.0698	✓	0.026	✓	0.026	✓	0.026	✓
5	38.075	✓	38.08	✓	38.085	✓	0.013	✓	0.013	✓	0.013	✓
6	38.061	✓	38.066	✓	38.071	✓	0.039	✓	0.039	✓	0.039	✓
7	38.06	✓	38.065	✓	38.07	✓	0.032	✓	0.032	✓	0.032	✓
8	38.0684	✓	38.0734	✓	38.0784	✓	0.019	✓	0.019	✓	0.019	✓
9	38.0648	✓	38.0698	✓	38.0748	✓	0.032	✓	0.032	✓	0.032	✓
10	38.0704	✓	38.0754	✓	38.0804	✓	0.023	✓	0.023	✓	0.023	✓
11	38.0752	✓	38.0802	✓	38.0852	✓	0.028	✓	0.028	✓	0.028	✓
12	38.0622	✓	38.0672	✓	38.0722	✓	0.031	✓	0.031	✓	0.031	✓
13	38.0634	✓	38.0684	✓	38.0734	✓	0.024	✓	0.024	✓	0.024	✓
14	38.0696	✓	38.0746	✓	38.0796	✓	0.034	✓	0.034	✓	0.034	✓
15	38.0624	✓	38.0674	✓	38.0724	✓	0.018	✓	0.018	✓	0.018	✓
16	38.0638	✓	38.0688	✓	38.0738	✓	0.031	✓	0.031	✓	0.031	✓
17	38.0662	✓	38.0712	✓	38.0762	✓	0.018	✓	0.018	✓	0.018	✓
18	38.0608	✓	38.0658	✓	38.0708	✓	0.02	✓	0.02	✓	0.02	✓
19	38.0594	✓	38.0644	✓	38.0694	✓	0.014	✓	0.014	✓	0.014	✓
20	38.0558	✓	38.0608	✓	38.0658	✓	0.016	✓	0.016	✓	0.016	✓
21	38.068	✓	38.073	✓	38.078	✓	0.041	✓	0.041	✓	0.041	✓
22	38.0704	✓	38.0754	✓	38.0804	✓	0.018	✓	0.018	✓	0.018	✓
23	38.0678	✓	38.0728	✓	38.0778	✓	0.024	✓	0.024	✓	0.024	✓
24	38.0594	✓	38.0644	✓	38.0694	✓	0.031	✓	0.031	✓	0.031	✓
25	38.0576	✓	38.0626	✓	38.0676	✓	0.025	✓	0.025	✓	0.025	✓

4. Conclusions

In this study, it is shown that the process should be controlled with $\alpha$-cut TFNs, and it is suitable when there is uncertainty presented in the data. We developed the methodology for a fuzzy $\overline{X}$ and R control chart with fuzzy $C_p$ and $C_{pk}$ for unknown population parameters (µ and $\sigma$). The fuzzy control chart with FCPI that has been suggested is a statistic to monitor the fuzzy production process in a fuzzy environment. In addition, a stable level at the steady-state values can be achieved through the utilization of the suggested fuzzy control charts. The proposed control chart with the $\alpha$-cut for the fuzzy process enables accurate and efficient observation of the control limits as well. In order to combine the useful aspects of traditional control charts with those of process capability indices, we have presented a fuzzy control chart based on the FCPI for real-time process monitoring. To monitor the fuzzy process online and evaluate the manufacturing process’s appropriateness, the authors suggest using a single-stage regulating mechanism comprised of both fuzzy control charts and the FCPI. The numerical example is presented for the power loom change gear data by the proposed technique; there are no false alarms for the average of TFNs, and the proposed fuzzy control chart with fuzzy $C_p$ and $C_{pk}$ is effective and increases the process’s flexibility regarding the power loom change gear information. The decision maker can choose the control limit according to the $\alpha$ values. This study will help the decision maker find the suitable control limit. The suggested control chart may be constructed on the same line for a trapezoidal fuzzy number, linguistic observation, and $C_{pm}$ and $C_{pkm}$ as future research.