Abstract
This article presents a comparative study of Kiepert’s trefoil and its related curves, combining a variety of tools from differential and algebraic geometry, integrable systems, elastica theory, and special functions. While this curve was classically known and well studied in the literature, some related open problems were recently solved, and the goal of this paper is to present and characterize the general solution of the equation that governs this trefoil’s family of curves by involving elliptic functions and elastica theory in the mechanics.
MSC:
14H55; 53A04; 37K40
1. Introduction
Folium is a term that comes from Latin, where it means leaf. In mathematics, it represents a closed curve with several lobes. Generally, trifolium means a three-lobed closed curve in plane. The authors are interested in the Kiepert trefoil as a particular case of trifolium from the view points of differential geometry, theory of elastica and flows, geometric PDE and elliptic integrals.
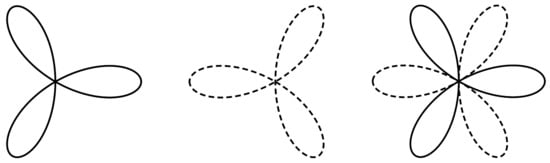
A very interesting paper [1] was published recently by David Singer in this Special Issue, which triggered our interest in the subject and inspired us to provide a classification of the related families of curves and corresponding integrable systems. Surprisingly, it turns out that trifolium is an ambivalent name which refers to several curves. Most commonly, this name denotes the regular trifolium, which represents the quartic algebraic curve:
This is depicted as a rose with three petals (cf. Figure 1).
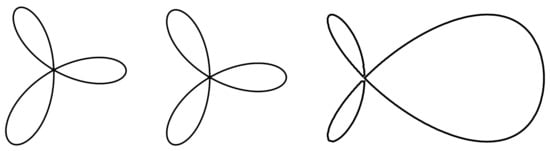
This name also denotes one of the Rhodonea curves presented by the following quartic which is a particular case of Equation (1):
Alternatively, the last curve can be seen in many places presented equivalently by the following equation:
This is accomplished by taking into account that the change , transforms Equation (3) into Equation (2). This is illustrated in Figure 2.
The above figures have been drawn through their explicit parameterizations:
and the intrinsically related to them formulas
What is more, the curve associated with Equation (3) (written without tildes) can be considered a particular case of the Kepler folium (cf. [2] (p. 85))
taken with and translation along the -axis: .
Finally, in many other situations, this notion also refers to Cramer trifolium (see [3] (p. 354) and [4] (p. 463)), specified by a fourth quartic
The parameterization of the Cramer trifolium is provided by the formulas
Additionally, its shape is presented by the last graphic in Figure 1.
All these curves arise in various contexts or following concrete ideas and have been considered from different perspectives. As a concept, trifoliums lie at the intersection between algebraic and differential geometry [5]. We are interested in the latter approach. Despite the fact that these curves have been known for centuries, their explicit parameterizations, except for the polar presentations, implicit equations, and exotic description via Dixon functions [6], are missing.
In the next section, we show that the arclength of the Kiepert trefoil is fully determined by an elliptic integral of the first kind, which was the initial impulse for its consideration [7]. Other goals for this paper are the following: (1) to represent the Kiepert trefoil as a special curve in differential geometry, for which the curvature is a quadratic function of the distance from the origin (see Equation (13)), (2) to show that relative to the curve flow equation (Equation (23)), the Kiepert trefoil is regarded as a time-independent solution in addition to being an elastic curve, and (3) to interpret Kiepert’s trefoil equation (Equation (20)) as the Free Buckled Ring Equation (Equation (28)), thus clarifying why it corresponds to a generalized Euler elastica.
2. Kiepert Trefoil: Methods and Results
(1) The Kiepert trefoil is a well-known curve in algebraic geometry. It represents a sextic curve in the Euclidean plane , which is given in Cartesian coordinates by the algebraic equation
The Kiepert trefoil is special curve in differential geometry. In arclength, this trefoil is expressible by first-kind elliptic integrals, in addition to the widely known lemniscates and Serret’s curves. It is named after the German mathematician Friedrich Wilhelm August Ludwig Kiepert (1846–1934), who had written a thesis on the subject [8].
The polar coordinates are expressed as
Equation (9) can be rewritten as
Using the well-known expression for the curvature of an implicitly defined curve in , we have
One can easily verify that the curvature of the trefoil is given by the following formula:
The components of the position vector of a plane curve whose curvature meets the relation in Equation (13) are determined by the following system of equations (see, e.g., [9,10]):
where the dots denote derivatives with respect to the arclength s. It is easy to verify (see [9,10]) that two conservation laws (first integrals) hold for the solutions to the system in Equation (14), which in terms of the polar coordinates r and can be written as
and
where is an arbitrary real constant.
By differentiating both sides of Equation (13) with respect to the variable s, one obtains the following equation:
(2) The Kiepert trefoil can be regarded as a time-independent solution of a curve flow.
Theorem 1.
The Kiepert trefoil is a time-independent solution of the curve flow.
Proof.
Based on Equation (15) of the previous paragraph 1, the above equality takes the following form:
If in Equation (18) we set , then as Equation (13) implies, we obtain
which has to be recognized as the intrinsic equation of any plane curve whose curvature is specified by Equation (13). In the special case of the Kiepert trefoil, Equation (11) implies . In other words, we have
Additionally we have the fundamental relation
in which denotes the slope angle of the tangent line, and after integration, we end up with the remarkable formula
Let a regular plane curve parameterized by its arclength s evolve smoothly and without extension in time t according to the following curve flow equation:
where is the position vector of the curve, is its curvature, and and are the unit tangent and inward unit normal vectors of the curve, respectively. Then, the curvature of this curve satisfies the focusing mKdV equation:
This represents the well-known result of Goldstein and Petrich [11] and Nakayama et al. [12] (see also [13]), where the plane curve flow of the special form in Equation (23) is an mKdV flow; that is, if a curve evolves according to Equation (23), then the curvature of this curve satisfies the focusing mKdV equation (Equation (24)).
Evidently, the stationary solutions of Equation (24) also satisfy the equation
which can be integrated twice to obtain
where and are the constants of integration. Thus, by setting and here, one obtains the intrinsic equation of the Kiepert trefoil (Equation (20)). This means that the Kiepert trefoil is a time-independent solution of the curve flow specified by Equation (23), which finalizes the proof of the theorem. □
(3) The Kiepert trefoils can also be viewed as generalized Euler’s elasticas, and thus their arclength representations via elliptic integrals. Singer [1] had recognized the Kiepert trefoil as a particular solution of the Buckled Rings Equation, which is nothing more than the Generalized Elastica Equation [14]:
where (tension), (pressure), and (energy) are the physical characteristics of the elastica or the elastic ring (, ). What is more, the Kiepert’s trefoil equation (Equation (20)) actually represents the Free Buckled Ring Equation (, , ):
This is a counterpart of the so-called Free Euler’s Elastica Equation (, , ) [15] (p. 114):
The solutions to Equations (27) and (28) are documented in [14,15], while their periodicity is discussed in [16]. Here, we choose to follow the scheme developed in [17] which is based on Cartan’s repère mobile (moving frame). In technical terms, the curve specified by its curvature is reconstructed through the formulas
in which are the coordinates of the point in the moving frame and is the tangential angle. They are defined by another set of formulas:
Effectively, this scheme is realized via integration of the following intrinsic equation (more details can be found in [15] (pp. 47–49)):
Proposition 1.
The arclength of the Kiepert trefoil is given by an elliptic integral of the first kind.
Proof.
One finds an explicit expression for r as a function of the arclength s, which via the fundamental relation (13) produces the required expression for the curvature:
where denotes the cosine Jacobian elliptic function and k is the so-called elliptic modulus. The formulas above enable us to find in the form
while the computation of and is almost straightforward and produces
By combining the obtained results for Equations (34) and (35) through the formulas in Equation (30), we find the sought explicit parameterization of the Kiepert trefoil. It is clear that the length L of a single leaf coincides with the lowest period T of the curvature , which is given by the formula
where denotes the complete elliptic integral of the first kind, and obviously, the total perimeter of the trefoil is exactly
Equation (36) represents a direct confirmation of the fact that the arclength of the Kiepert trefoil is given by the elliptic integral of the first kind, thus proving the proposition. □
For completeness, we list below the rescaled () Kiepert’s parameterization of the Trefoil in terms of the Weierstrass ℘ function, which is borrowed from his dissertation [8]:
Graphics of the Kiepert trefoil and the Kepler folium (Equation (3)) with the same parameter a are presented and compared below in Figure 3.
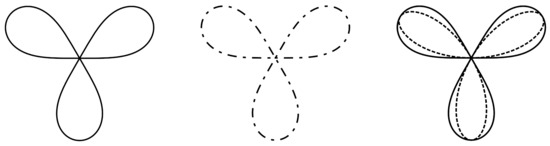
Figure 3.
The first two graphics here represent the Kiepert trefoils drawn via Equations (30) (solid curve) and (38) (dashed line) with the same a, while the third one illustrates the difference between the Kiepert trefoil (solid curve) and the trefoil associated with Equation (3) (after rotation of 30°).
3. Discussion, Open Problems, and Future Directions
By solving the algebraic Equation (9), one finds another interesting parameterization by means of circular functions, namely
The radical which appears in the expression of the z coordinate suggests use of the Jacobian elliptic functions, and this leads to an alternative parameterization in the form of
More details about elliptic functions and integrals can be found in [18,19]. Here, we can mention that it would be very interesting to interpret other n foliums (i.e., ) as generalized elasticas and obtain their explicit parameterizations in terms of, for example, (hyper)elliptic functions. This represents one of our further directions of research. Similarly, it would also be interesting to compare the PDE-based and analytic approaches with the n foliums (cf. [20,21]) that were studied in algebraic geometry. Another interesting area of research lies in studying foliums on non-planar surfaces in particular on spheres, which is a current project for some of the authors.
Author Contributions
Investigation, V.I.P., M.D.T., V.M.V. and I.M.M.; writing—review and editing, V.I.P., M.D.T., V.M.V. and I.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
One of the authors (M. Toda) would like to acknowledge the support received from the Simons Foundation as a Collaboration Grant for Mathematicians in Mathematics and Physical Sciences for the project entitled Applications of Willmore Energy Functionals to Protein Biology at Texas Tech University under award number 632274. V. M. Vassilev would like to acknowledge support from the Bulgarian Science Fund under grant KΠ-06-H22/2. I. M. Mladenov and V. M. Vassilev were supported through a project within the realm of the scientific cooperation between the Bulgarian and Polish Academies of Sciences for the period of 2022–2023.
Institutional Review Board Statement
Not applicable, none allowed.
Informed Consent Statement
We are aware of the editorial terms and conditions.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Abbreviations and Notations
The following abbreviations and notations are used in this manuscript:
| a | size of a single folium of the Kiepert’s Trefoil |
| auxiliary parameters in the trefoil parameterizations | |
| tension | |
| pressure | |
| energy | |
| coordinates in moving frame representations | |
| slope angle of the tangent line | |
| L | arclength of a single folium of the Kiepert’s trefoil |
| k, | moduli of elliptic functions |
| n | the parameter of the elliptic integral of the third kind |
| invariants of the Weierstrass ℘ function | |
| u | parameter along the trefoil curve |
| s | arclength parameter |
| Cartesian coordinates | |
| polar coordinates | |
| unit tangent vector | |
| unit normal vector | |
| mKdV | modified Korteweg–de Vries equation |
| parameter of a family of curves including Kiepert’s trefoil for | |
| curvature | |
| T | lowest period of the curvature |
References
- Singer, D. The trefoil soliton. Mathematics 2022, 10, 1512. [Google Scholar] [CrossRef]
- Gray, A.; Abbena, E.; Salamon, S. Modern Differential Geometry of Curves and Surfaces with Mathematica®, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Shikin, E.V. Handbook and Atlas of Plane Curves; CRC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Khelif, H. Le Jardin des Courbes; Ellipses: Paris, France, 2010. [Google Scholar]
- Brieskorn, E.; Knörrer, H. Plane Algebraic Curves; Springer: Basel, Switzerland, 1986. [Google Scholar]
- Langer, J.C.; Singer, D.A. The trefoil. Milan J. Math. 2014, 82, 161–182. [Google Scholar] [CrossRef]
- Serret, J.-A. Mémoire sur la représentation géométrique des fonctions elliptiques et ultra-elliptiques. J. Math. Pures Appl. 1845, 10, 257–285. [Google Scholar]
- Kiepert, L. De Curvis Quarum Arcus Integralibus Ellipticis Primi Generis Exprimuntur; Friedrich-Wilhelms-Universität: Berlin, Germany, 1870. [Google Scholar]
- Vassilev, V.M.; Djondjorov, P.A.; Mladenov, I.M. Integrable dynamical systems of the Frenet–Seret type. In Proceedings of the 9th International Workshop on Complex Structures, Integrability and Vector Fields, Sofia, Bulgaria, 25–29 August 2008; Sekigawa, K., Gerdjikov, V., Dimiev, S., Eds.; World Scientific Publishing Co.: Singapore, 2009; pp. 261–271. [Google Scholar] [CrossRef]
- Djondjorov, P.A.; Vassilev, V.M.; Mladenov, I.M. Plane curves associated with integrable dynamical systems of the Frenet–Seret type. In Proceedings of the 9th International Workshop on Complex Structures, Integrability and Vector Fields, Sofia, Bulgaria, 25–29 August 2008; Sekigawa, K., Gerdjikov, V., Dimiev, S., Eds.; World Scientific Publishing Co.: Singapore, 2009; pp. 57–63. [Google Scholar] [CrossRef]
- Goldstein, R.E.; Petrich, D.M. The Korteweg–de Vries hierarchy as dynamics of closed curves in the plane. Phys. Rev. Lett. 1991, 67, 3203–3206. [Google Scholar] [CrossRef] [PubMed]
- Nakayama, K.; Segur, H.; Wadati, M. Integrability and the motion of curves. Phys. Rev. Lett. 1992, 69, 2603–2606. [Google Scholar] [CrossRef] [PubMed]
- Vassilev, V.M.; Djondjorov, P.A.; Hadzhilazova, M.T.; Mladenov, I.M. Traveling wave solutions of the Gardner equation and motion of plane curves governed by the mKdV flow. AIP Conf. Proc. 2011, 1404, 86–93. [Google Scholar] [CrossRef]
- Vassilev, V.M.; Djondjorov, P.A.; Mladenov, I.M. Cylindrical equilibrium shapes of fluid membranes. J. Phys. A: Math. Theor. 2008, 10, 435201. [Google Scholar] [CrossRef]
- Mladenov, I.; Hadzhilazova, M. The Many Faces of Elastica; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Djondjorov, P.A.; Vassilev, V.M.; Mladenov, I.M. Analytic description and explicit parametrisation of the equilibrium shapes of elastic rings and tubes under uniform hydrostatic pressure. Int. J. Mech. Sci. 2011, 53, 355–364. [Google Scholar] [CrossRef]
- Mladenov, I.M.; Hadzhilazova, M.T.; Djondjorov, P.A.; Vassilev, V.M. On the plane curves whose curvature depends on the distance from the origin. AIP Conf. Proc. 2010, 1307, 112–118. [Google Scholar]
- Legendre, A. Traité des Fonctions Elliptiques; Imprimerie de Huzard-Courcier: Paris, France, 1925; Volume I. [Google Scholar]
- Greenhill, A.G. The Elastic Curve, under uniform normal pressure. Math. Ann. 1899, 52, 465–500. [Google Scholar] [CrossRef]
- Clark, T.A. The Trefoil: An Analysis in Curve Minimization and Spline Theory. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2020. Available online: http://rave.ohiolink.edu/etdc/view?acc_num=case1596460534956624 (accessed on 3 August 2022).
- Clark, T.A.; Singer, D.A. The Trefoil Spline. Comput. Aided Des. Appl. 2022, 19, 1255–1269. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).