Abstract
In this paper, we present a new reference model that approximates the actual shape of the Earth, based on the concept of the deformed spheres with the deformation parameter . These surfaces, which are called -spheres, were introduced in another setting by Faridi and Schucking as an alternative to the spheroids (i.e., ellipsoids of revolution). Using their explicit parametrizations that we have derived in our previous papers, here we have defined the corresponding isothermal (conformal) coordinates as well as obtained and solved the differential equation describing the loxodromes (or rhumb lines) on such surfaces. Next, the direct and inverse problems for loxodromes have been formulated and the explicit solutions for azimuths and arc lengths have been presented. Using these explicit solutions, we have assessed the value of the deformation parameter for our reference model on the basis of the values for the semi-major axis of the Earth a and the quarter-meridian (i.e., the distance between the Equator and the North or South Pole) for the current best ellipsoidal reference model for the geoid, i.e., WGS 84 (World Geodetic System 1984). The latter is designed for use as the reference system for the GPS (Global Positioning System). Finally, we have compared the results obtained with the use of the newly proposed reference model for the geoid with the corresponding results for the ellipsoidal (WGS 84) and spherical reference models used in the literature.
Keywords:
deformed spheres; incomplete elliptic integrals; geoid’s reference models; loxodromes or rhumb lines; azimuths and arc lengths; geodesy and navigation problems MSC:
33E05; 53A05; 53A35; 53C22; 86A30
1. Introduction
So-called deformed spheres with deformation parameter were introduced in [1] as an alternative to spheroids (ellipsoids of revolution) in a dynamical context for the easy description of geodesics on these surfaces. It turns out that they can also serve as an alternative for the actual shape of the Earth that is defined through the geoid (the equipotential surface that has the same sum of gravitational and centrifugal potential energies which would coincide with the mean sea level over the oceans if only gravity and rotational acceleration were at work [2]).
The main difference between the proposed new reference model for the geoid and the traditional ellipsoidal one is that the geodesics on the -spheres are expressed through well-known analytical functions (see, e.g., [3]), whereas the geodesics on the rotational ellipsoids are described through the complete set of the incomplete elliptic integrals (see, e.g., [4]). In the present article, we show that the same is true for the calculation of azimuths and arc lengths for the loxodromes (or rhumb lines) on the -spheres. From the other side, for the -spheres, the incomplete elliptic integrals (of all three kinds) will only appear when we must embed these surfaces (or the corresponding solutions for geodesics or loxodromes on them) into the three-dimensional Euclidean space (see Section 2 for details).
The above-described features of the newly proposed reference model for the geoid simplify all the calculations that have to be done in local coordinates in geodesy and navigation (see Section 3 and Section 4), even though the geometrical definition of the -spheres is more complicated in comparison to the rotational ellipsoids. Finally, in Section 5, we have compared the results obtained with the use of the newly proposed reference model for the geoid with the corresponding results for the ellipsoidal (WGS 84 [5]) reference model, which is used currently and is the simplest possible spherical one [6].
2. Geometrical Description of -Spheres
Let us consider a deformed sphere with a deformation parameter (the case when corresponds to the usual, non-deformed sphere). The chosen range of the deformation parameter ensures that the Gaussian curvature K for -spheres under consideration is strictly positive, and simultaneously the shape of the corresponding surface of revolution is oblate (i.e., it is slightly flattened in the direction of its axis of symmetry, as it should be for the reference model for the geoid describing the actual shape of the Earth). Then, the parametrization of the -sphere’s surface, which is embedded into the three-dimensional Euclidean space, can be written as [3,7]
where , are the latitude and longitude local variables, and is the scaling factor such that the value corresponds to the equatorial radius of the geoid (which is taken in WGS 84 as the semi-major axis of the Earth: 6,378,137.0 m). In the above expression , , and denote the incomplete elliptic integrals of the first, second, and third kind, respectively, which are defined as follows [8]:
In this notation, is the so-called Jacobian amplitude, k is the elliptic modulus, n is the characteristic and they are given by the expressions
The signs ± in (1) correspond to the Northern and Southern Hemisphere of the -sphere, respectively. The first fundamental form (the line element) for the -spheres can be easily written as [3,7]
where the auxiliary function is defined as . In the above expression, the isometric latitude on the -spheres ranges from at the South Pole () through 0 at the level of the Equator () to ∞ at the North Pole (). Its analytical dependency on the local latitude variable u is given as
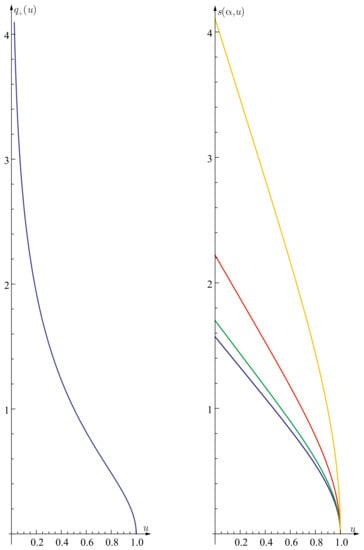
The dependency of calculated for the Northern Hemisphere is shown in Figure 1 (left).
Apart from the isometric latitude defined by (5), we can also introduce the geocentric latitude (i.e., the angle between the radius-vector to the point and the equatorial plane) for the -sphere’s reference model for the geoid. It is expressed through the incomplete elliptic integrals of the first, second, and third kind, i.e.,
since is given by (1). Contrary to this, the geodetic latitude (i.e., the angle between the normal vector to the surface at the point and the equatorial plane) for the -sphere’s reference model for the geoid is expressed through the composition of simple analytical functions, i.e.,
where the derivative of with respect to the local variable u is given by the expression (see Figure 2)
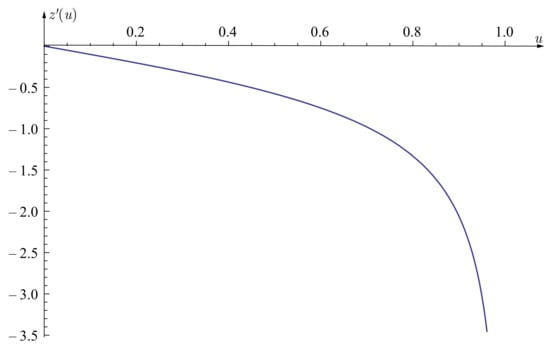
Figure 2.
Dependency of given by (8) with and = .
Therefore, when the geodetic latitude is known, to find the corresponding local latitude on the -sphere’s reference model for the geoid, we need only to solve the algebraic equation
with respect to the variable u. From Figure 2 we can see that the function given by (9) and (8) is a monotonically decreasing analytical function, and therefore, for any given constant term , it has a unique real root that can be quite easily found with high precision using well-known numerical algorithms.
3. Loxodromes (Rhumb Lines) on -Spheres
Although the loxodromes and rhumb lines are basically synonyms (loxodrome is a Latin word for rhumb), in the literature they are mainly used in different contexts, i.e., loxodrome describes a geometrical curve on the corresponding surface of revolution that intersects all the meridians at the same angle, whereas rhumb describes a practically realized course on the Earth of constant bearing (see, e.g., [9]). Although such a course of constant bearing is not generally the shortest route between two points on the Earth (see, e.g., Figure 3 (right), where the loxodrome connecting two points on the -sphere is compared to the corresponding geodesic), it is extremely easy to realize during the navigation, even for the beginner sailors or airplane pilots.
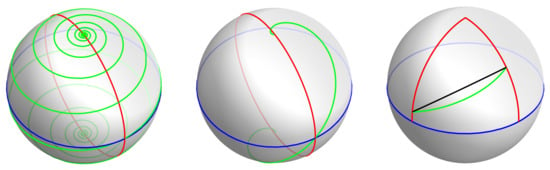
Figure 3.
Loxodromes (green lines) of the azimuths (left), (middle) on the -sphere with the deformation parameter together with the meridians (red lines) and the Equator (blue lines). On the right, the comparison between the loxodrome and geodesic solving the corresponding inverse problems is shown when , , , .
Relying on the metric specified in (4), the differential equation defining the loxodromes can be written in the form (see, e.g., [10,11])
where is the azimuth of the loxodrome. Therefore, the azimuth of the loxodrome that connects two points with the isothermal coordinates and can be expressed as
Similarly, the differential distance along the meridian is equal to
Then from (4) we obtain that the arc length, i.e., the distance along the loxodrome with azimuth between two points when one of them is placed on the Equator () and another has the latitude equal to , is given as
For instance, in Figure 1 (right) the dependencies are shown for the chosen values of the azimuth , i.e., (blue line), (green line), (red line), and (orange line). Let us note that for the North Pole (), in all cases we obtain the highest but finite values in the range, despite the fact that any loxodrome, with the exception of the parallels, is winding infinitely many times around the poles (see, e.g., Figure 3) and resembles closely the Seifert’s spirals on the spheres [12].
Finally, for any two points with the local latitudes and (or equivalently, the isometric latitudes and ) in the same hemisphere (Northern or Southern) and longitudes and , the distance along the loxodrome with the azimuth given by (11) is expressed as
On the other side, for the points which belong to different hemispheres, we have
4. Direct and Inverse Problems for Loxodromes on -Spheres
The direct geodetic problem is defined as follows (cf., e.g., [6,13]). Given the latitude and the longitude of the starting point on the -sphere, the azimuth of the loxodrome passing through , and the arc length along it, we need to find out the latitude and the longitude of the destination point as well as the reverse azimuth .
To solve this problem we need to perform the following computational steps (for illustration purposes, let us suppose that the point is taken from the Northern Hemisphere, i.e., the isometric latitude , the azimuth , and the meridional distance between the points and is such that ):
- (1)
- Using (13) we can obtain the meridional distance from the starting point to the Equator, i.e.,
- (2)
- Relying on (14), we can obtain the meridional distance from the ending point to the Equator, i.e.,
- (3)
- By solving (13) with respect to the local latitude of the ending point , we obtain that
- (4)
- (5)
- Next, using Equation (11), we can obtain the local longitude of the destination point , i.e.,
- (6)
- Finally, the reverse azimuth is given as
Analogously, the inverse problem is defined as follows. Given the latitudes , and the longitudes , of the starting and ending points , on the -sphere, we need to find out the azimuth of the shortest loxodrome that connects these two points, the arc length along it as well as the reverse azimuth (see, e.g., Figure 3 (right) for the exemplary solution of the inverse problem for loxodromes on the -sphere in comparison to the corresponding geodesic).
To solve the inverse problem, we need to perform the following computational steps (the same assumptions):
- (1)
- Using Equation (5), we obtain the difference between the isometric latitudes of the destination and starting points, i.e.,
- (2)
- (3)
- As before, the reverse azimuth is given by the formula
Let us also note that inverse problems are generally considered more difficult because they start with the results (observations) and then calculate the causes that produced those results (observations), in contrast to the direct problems that start with the causes and then calculate the results (observations) using some models. We can distinguish two main reasons for the above-mentioned difficulties: (1) non-uniqueness, i.e., different causes (values of the model parameters) may be consistent with the observations, (2) lack of stability, i.e., small noise or uncertainty in observations may be tremendously amplified in the calculated causes. This means that the second and/or third of three conditions for well-posed problems in mathematical modeling suggested by Jacques Hadamard (i.e., existence, uniqueness, and stability of the solution) are most often violated in the inverse problems (as in calculating images in X-ray computed tomography or reconstructing parameters in heat conduction models with fractional derivatives).
In the case considered in this paper, the solution of the inverse problem for loxodromes on -spheres given by the Formulas (22)–(24) is unique due to the fact that it is described through the one-to-one elementary functions arctan and (see, e.g., Figure 1). However, in the above formulas, we suppose that the input data are perfect (i.e., there is no noise or uncertainty in them), and further analysis of the stability of the obtained solution of the inverse problem can be performed, e.g., making some assumptions about the specific form of the noise (Gaussian, non-Gaussian, etc.).
5. Comparison with the Ellipsoidal and Spherical Reference Models
To compare our reference model for the geoid with the best ellipsoidal reference model for the current moment (i.e., WGS 84), we need to assess the possible value of the deformation parameter for the -sphere’s reference model. Elsewhere [3], we have obtained that the deformation parameter should take values in the interval []. To further assess its value, let us use Formula (13) and calculate the quarter-meridian (the distance between the Equator and the North or South Pole) of the -sphere’s, i.e.,
where a is the equatorial radius of the geoid. In the WGS 84 model, we find that a corresponds to the semi-major axis of the Earth, i.e., 6,378,137.0 m, and the quarter-meridian’s length is 10,001,965.729 m (cf., e.g., [14]).
Therefore, relationship (25) provides us with a quite simple analytic formula for assessing the value of the deformation parameter for the -sphere’s reference model for the geoid based on the data for the ellipsoidal reference model WGS 84, i.e.,
Next, using the above value of the deformation parameter , we have solved the inverse problems for loxodromes (described in Section 4) to obtain the azimuths and arc lengths given by (22) and (23) for several selected cities on important air routes on the Earth’s surface. Their geodetic longitudes v and latitudes (that were taken from [6]) are presented in Table 1. Additionally, we have numerically solved relationship (9) to obtain the corresponding local latitudes u (see the last column in Table 1).

Table 1.
Geodetic and local coordinates of cities on the important air routes on the Earth’s surface.
For the selected routes (presented in Table 2 and Table 3), we have calculated azimuths and arc lengths connecting the chosen cities using the newly proposed -sphere’s reference model for the geoid. Next, we have compared them with the corresponding values obtained using the current best WGS 84 ellipsoidal reference model and the simplest possible spherical one (see [6]).

Table 2.
Comparison of values for azimuths calculated from the inverse problems for loxodromes based on the -sphere’s, WGS 84 ellipsoidal, and spherical reference models for the geoid.

Table 3.
Comparison of values for arc lengths calculated from the inverse problems for loxodromes based on the -sphere’s, WGS 84 ellipsoidal, and spherical reference models for the geoid.
In Table 2 and Table 3, we have also added the columns that describe the differences and between the -sphere’s and WGS 84 ellipsoidal reference models. The largest (by absolute value) difference in azimuths is equal to which corresponds to the route from New York to London, whereas the smallest (by absolute value) difference is equal to which corresponds to the route from Buenos Aires to Sydney. Similarly, the largest (by absolute value) difference in arc lengths is equal to m which corresponds to the route from London to Seattle (of the total length of about km), whereas the smallest (by absolute value) difference is equal to m which corresponds to the route from Hong Kong to Taipei (of the total length of around km).
Let us end with an interesting observation: it appears that the smallest (by absolute values) differences in azimuths and arc lengths between the -spheres and WGS 84 ellipsoidal reference models are realized for the same routes as the smallest (by absolute values) differences in azimuths and arc lengths between the WGS 84 ellipsoidal and spherical reference models, i.e., for the route from Buenos Aires to Sydney and m () for the route from Hong Kong to Taipei (see [6]).
6. Conclusions
It is well known that spheres are among the most perfect forms in nature. The book by Hilbert and Cohn-Vossen [15] highlights the 11 properties that are responsible for the uniqueness of this shape. In geometrical terms, this can be spelled out by saying that spheres can be described by elementary functions and that this applies also to their geodesics. Nevertheless, when a small deviation from this form is taken to obtain spheroids (i.e., rotational ellipsoids), the new surfaces do not share these nice properties, since for the description of their geodesics (orthodromes), one needs to employ elliptic functions and elliptic integrals. On the other hand, the -spheres that are considered here can be viewed as mirror objects to ellipsoids of revolution in the sense that their extrinsic geometry is described by the elliptic functions and elliptic integrals, but their intrinsic geometry (geodesics) relies entirely on the elementary analytical functions. This is extremely important for navigation purposes, where the shape is clear in advance but parametric lines (e.g., geodesics or loxodromes) on the surface must be found and described in the easiest possible way. Hence, we really hope that the new reference model for the geoid presented here will receive due attention from the navigation community.
Apart from the above-described obvious application in geodesy and navigation areas, some applications are also possible in material science and engineering, e.g., for description of the twisting behavior of spindle-shaped polymer liquid crystalline microparticles (see, e.g., [16,17]). Those polymeric particles are considered to be candidates for designing artificial materials capable of emulating the complex twisting-based functionality observed in biological systems. Using geometrical modeling, the bulk-twisting structures in such polymer nematic systems can be approximated on general surfaces of revolution by twisted loxodromes whose twist angle is determined by the corresponding length-constraint condition. We expect that the use of -spheres with deformation parameter (which corresponds to the spindle-like shapes) together with the description of the loxodromes on them presented in the current article will also be quite advantageous for the geometrical description of the above-mentioned chiral polymer nematics.
Author Contributions
Conceptualization, V.K. and I.M.M.; methodology, V.K. and I.M.M.; formal analysis, V.K. and I.M.M.; investigation, V.K. and I.M.M.; writing—original draft preparation, V.K.; writing—review and editing, V.K. and I.M.M.; visualization, V.K. and I.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This paper presents part of the results obtained during the realization of the joint research project #17 under the title “Classical and quantum models of deformable bodies on curved surfaces”. The project was accomplished within the realm of the scientific cooperation between Bulgarian and Polish Academies of Sciences for the period of 2022–2023. The authors are thankful to the above-mentioned Institutions for their support of the exchange visits conducted in both directions. The authors are also thankful to the reviewers for their valuable remarks and suggestions helping to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WGS 84 | World Geodetic System 1984 |
| GPS | Global Positioning System |
References
- Faridi, A.M.; Schucking, E.L. Geodesics and deformed spheres. Proc. Am. Math. Soc. 1987, 100, 522–525. [Google Scholar] [CrossRef]
- Li, X.; Götze, H.-J. Ellipsoid, geoid, gravity, geodesy, and geophysics. Geophysics 2001, 66, 1660–1668. [Google Scholar] [CrossRef]
- Kovalchuk, V.; Mladenov, I.M. λ-spheres as a new refernce model for the geoid. Math. Methods Appl. Sci. 2022. submitted. [Google Scholar]
- Karney, C.F.F. Geodesics on an ellipsoid of revolution. arXiv 2011, arXiv:1102.1215. [Google Scholar]
- National Geospatial-Intelligence Agency (NGA). World Geodetic System 1984. Its Definition and Relationships with Local Geodetic Systems; Standardization Document, NGA.STND.0036-1.0.0-WGS84; Department of Defence—Office of Geomatics: Springfield, VA, USA, 2014.
- Meyer, T.H.; Rollins, C. The direct and indirect problem for loxodromes. J. Inst. Navig. 2011, 58, 1–6. [Google Scholar] [CrossRef]
- Kovalchuk, V.; Mladenov, I.M. Mechanics of incompressible test bodies moving on λ-spheres. Math. Methods Appl. Sci. 2022, 45, 5559–5572. [Google Scholar] [CrossRef]
- Gradstein, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products, 7th ed.; Jeffrey, A., Zwillinger, D., Eds.; Academic Press: Oxford, UK, 2007. [Google Scholar]
- Alexander, J. Loxodromes: A rhumb way to go. Math. Mag. 2004, 77, 349–356. [Google Scholar] [CrossRef]
- Kos, S.; Vranić, D.; Zec, D. Differential equation of a loxodrome on a sphere. J. Navig. 1999, 52, 418–420. [Google Scholar] [CrossRef]
- Petrović, R.E. Differential equation of a loxodrome on the spheroid. Naše More 2007, 54, 87–89. [Google Scholar]
- Erdös, P. Spiraling the Earth with C. G. J. Jacobi. Am. J. Phys. 2000, 68, 888–895. [Google Scholar] [CrossRef]
- Deakin, R.E. The loxodrome on an ellipsoid. In Geometric Geodesy. Part B; Deakin, R.E., Hunter, M.N., Eds.; School of Mathematical and Geospatial Science, RMIT University: Melbourne, Australia, 2010; pp. 193–212. [Google Scholar]
- Weintrit, A. So, what is actually the distance from the equator to the pole?—Overview of the meridian distance approximations. Int. J. Mar. Navig. Saf. Sea Transp. 2013, 7, 259–272. [Google Scholar] [CrossRef]
- Hilbert, D.; Cohn-Vossen, S. Geometry and the Imagination; AMS, Chelsea: New York, NY, USA, 1952. [Google Scholar]
- Ansell, H.S.; Kim, D.S.; Kamien, R.D.; Katifori, E.; Lopez-Leon, T. Threading the spindle: A geometrical study of chiral liquid crystal polymer microparticles. Phys. Rev. Lett. 2019, 123, 157801. [Google Scholar] [CrossRef] [PubMed]
- Ansell, H.S.; Kamien, R.D. Twisted loxodromes in spindle-shaped polymer nematics. Soft Matter 2021, 17, 7076–7085. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).