Portfolio Insurance through Error-Correction Neural Networks
Abstract
:1. Introduction and Motivation
- The TMCPI problem is defined and explored;
- Three novel ENN models for addressing the TMCPI problem are defined;
- We use ENN solvers on real-world datasets;
- The performance of the ENN solvers versus the conventional MATLAB solver is demonstrated and contrasted in trials using four different portfolio configurations.
2. Minimum-Cost Portfolio Insurance
TV Variation of the MCPI Problem
3. The Error-Correction Neural Network Approach
3.1. TMCPI Problem via ZNN
- Step 1:(TMCPI problem reformulation) The TMCPI problem of (3)–(5) can be reformulated as follows:or equivalentlywhere and .
- Step 2:(Minimization conditions) To address the TLP problem of (11)–(12), the following Lagrange function is defined:where and is a non-negative time-varying term that converts the inequality constraint to an equality constraint. Then, using the KKT conditions [35], we have
- Step 3:(ZNN method) Considering the next equation group of error matricesand then substituting defined in (15) in place of into (6), one obtainswhere,
3.2. TMCPI Problem via LVI-PDNN and S-LVI-PDNN
4. Real-World Experiments
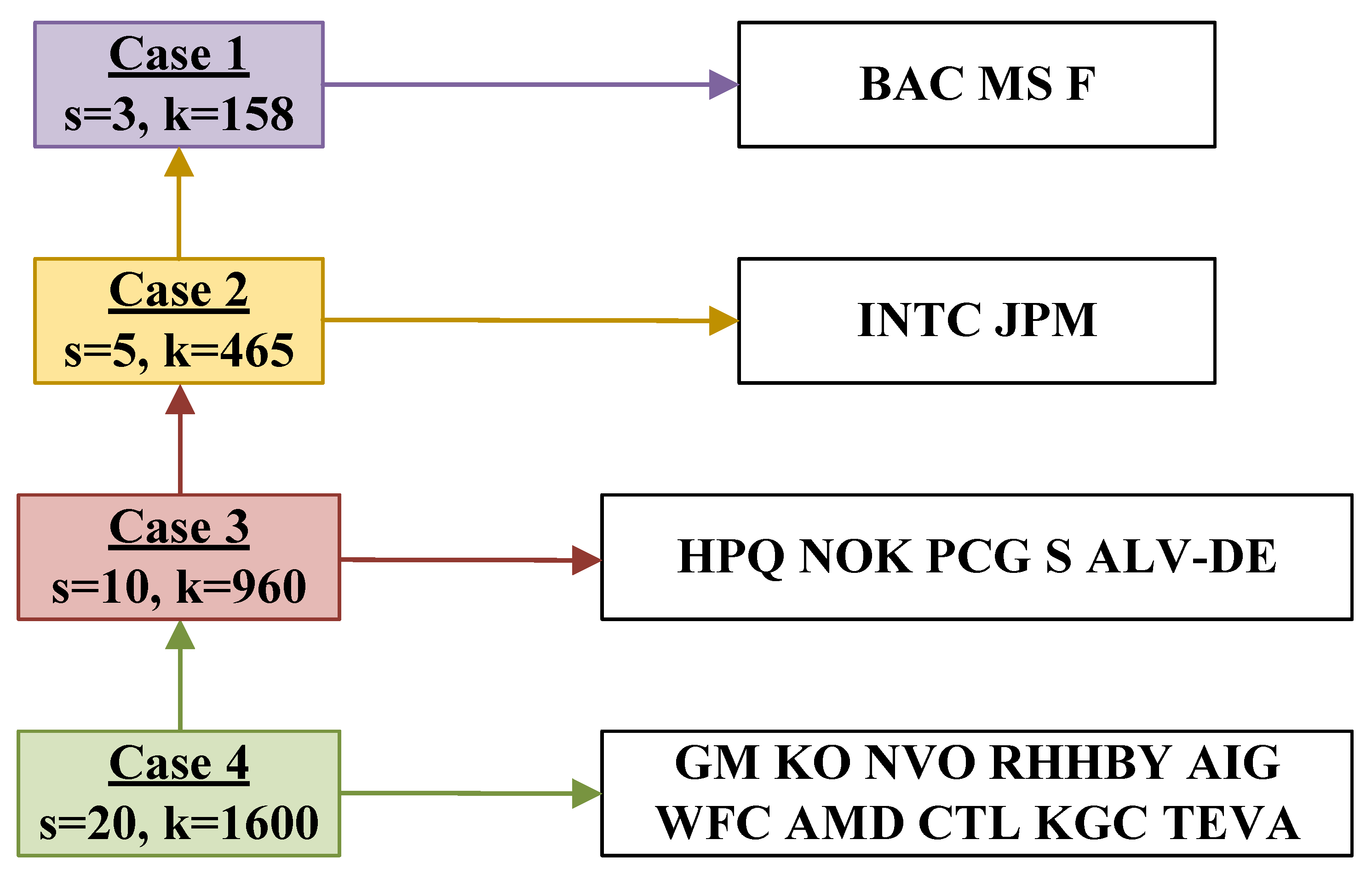
Portfolio Cases
5. Conclusions
- The application of ENNs to higher-dimensional portfolios.
- The application of ENNs to a variety of financial portfolio optimization problems.
- The improvement of ENNs’ performance in real-world problems by making use of various activation functions.
- The application of ENNs to portfolios derived from noisy data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NN | neural network |
| TLP | time-varying linear programming |
| ENN | error-correction neural network |
| RNN | recurrent neural network |
| MCPI | minimum-cost portfolio insurance |
| TMCPI | time-varying minimum-cost portfolio insurance |
| ZNN | zeroing neural network |
| LVI-PDNN | linear-variational-inequality primal-dual neural network |
| S-LVI-PDNN | simplified linear-variational-inequality primal-dual neural network |
| TV | time-varying |
| CT | continuous-time |
| DT | discrete-time |
| KKT | Karush–Kuhn–Tucker |
References
- Katsikis, V.N.; Mourtas, S.D. A heuristic process on the existence of positive bases with applications to minimum-cost portfolio insurance in C[a, b]. Appl. Math. Comput. 2019, 349, 221–244. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D. ORPIT: A matlab toolbox for option replication and portfolio insurance in incomplete markets. Comput. Econ. 2019, 56, 711–721. [Google Scholar] [CrossRef]
- Medvedeva, M.A.; Katsikis, V.N.; Mourtas, S.D.; Simos, T.E. Randomized time-varying knapsack problems via binary beetle antennae search algorithm: Emphasis on applications in portfolio insurance. Math. Methods Appl. Sci. 2020, 44, 2002–2012. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Li, S.; Cao, X. Time-varying minimum-cost portfolio insurance under transaction costs problem via Beetle Antennae Search Algorithm (BAS). Appl. Math. Comput. 2020, 385, 125453. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D. Portfolio Insurance and Intelligent Algorithms. In Modeling and Optimization in Science and Technologies; Springer: Berlin/Heidelberg, Germany, 2021; Volume 18, pp. 305–323. [Google Scholar] [CrossRef]
- Simos, T.E.; Mourtas, S.D.; Katsikis, V.N. Time-varying Black-Litterman portfolio optimization using a bio-inspired approach and neuronets. Appl. Soft Comput. 2021, 112, 107767. [Google Scholar] [CrossRef]
- Simos, T.E.; Katsikis, V.N.; Mourtas, S.D. A multi-input with multi-function activated weights and structure determination neuronet for classification problems and applications in firm fraud and loan approval. Appl. Soft Comput. 2022, 127, 109351. [Google Scholar] [CrossRef]
- Leung, M.F.; Wang, J. Minimax and biobjective portfolio selection based on collaborative neurodynamic optimization. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2825–2836. [Google Scholar] [CrossRef]
- Yaman, I.; Dalkılıç, T.E. A hybrid approach to cardinality constraint portfolio selection problem based on nonlinear neural network and genetic algorithm. Expert Syst. Appl. 2021, 169, 114517. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, X.Y. Continuous-time mean-variance portfolio selection: A reinforcement learning framework. Math. Financ. 2020, 30, 1273–1308. [Google Scholar] [CrossRef]
- Imajo, K.; Minami, K.; Ito, K.; Nakagawa, K. Deep portfolio optimization via distributional prediction of residual factors. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 35, pp. 213–222. [Google Scholar] [CrossRef]
- Zhang, Z.; Zohren, S.; Roberts, S. Deep learning for portfolio optimization. J. Financ. Data Sci. 2020, 2, 8–20. [Google Scholar] [CrossRef]
- Ma, Y.; Han, R.; Wang, W. Portfolio optimization with return prediction using deep learning and machine learning. Expert Syst. Appl. 2021, 165, 113973. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, S.S. Design and analysis of a general recurrent neural network model for time-varying matrix inversion. IEEE Trans. Neural Netw. 2005, 16, 1477–1490. [Google Scholar] [CrossRef]
- Kornilova, M.; Kovalnogov, V.; Fedorov, R.; Zamaleev, M.; Katsikis, V.N.; Mourtas, S.D.; Simos, T.E. Zeroing neural network for pseudoinversion of an arbitrary time-varying matrix based on singular value decomposition. Mathematics 2022, 10, 1208. [Google Scholar] [CrossRef]
- Simos, T.E.; Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Gerontitis, D. A higher-order zeroing neural network for pseudoinversion of an arbitrary time-varying matrix with applications to mobile object localization. Inf. Sci. 2022, 600, 226–238. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Zhang, Y. Solving complex-valued time-varying linear matrix equations via QR decomposition with applications to robotic motion tracking and on angle-of-arrival localization. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Jiang, W.; Lin, C.L.; Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Simos, T.E. Zeroing neural network approaches based on direct and indirect methods for solving the Yang–Baxter-like matrix equation. Mathematics 2022, 10, 1950. [Google Scholar] [CrossRef]
- Mourtas, S.D.; Katsikis, V.N. Exploiting the Black-Litterman framework through error-correction neural networks. Neurocomputing 2022, 498, 43–58. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Li, S.; Cao, X. Time-varying mean-variance portfolio selection problem solving via LVI-PDNN. Comput. Oper. Res. 2022, 138, 105582. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Zhang, Y. Continuous-time varying complex QR decomposition via zeroing neural dynamics. Neural Process. Lett. 2021, 53, 3573–3590. [Google Scholar] [CrossRef]
- Simos, T.E.; Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S. Unique non-negative definite solution of the time-varying algebraic Riccati equations with applications to stabilization of LTV systems. Math. Comput. Simul. 2022, 202, 164–180. [Google Scholar] [CrossRef]
- Ke, F.; Li, Z.; Yang, C. Robust tube-based predictive control for visual servoing of constrained differential-drive mobile robots. IEEE Trans. Ind. Electron. 2018, 65, 3437–3446. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, Y.; Li, S.; Zhang, Y. Modified ZNN for time-varying quadratic programming with inherent tolerance to noises and its application to kinematic redundancy resolution of robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 6978–6988. [Google Scholar] [CrossRef]
- Annaert, J.; Ceuster, M.D.; Vandenbroucke, J. Mind the floor: Enhance portfolio insurance without borrowing. J. Investig. 2019, 28, 39–50. [Google Scholar] [CrossRef]
- Matsumoto, K. Portfolio insurance with liquidity risk. Asia-Pac. Financ. Mark. 2008, 14, 363. [Google Scholar] [CrossRef]
- Aliprantis, C.D.; Brown, D.J.; Werner, J. Minimum-cost portfolio insurance. J. Econ. Dyn. Control. 2000, 24, 1703–1719. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, D. Linear programming versus quadratic programming in robots’ repetitive redundancy resolution: A chattering phenomenon investigation. In Proceedings of the 4th IEEE Conference Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009; pp. 2822–2827. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, W.; Li, X.; Tan, H.; Chen, K. MATLAB Simulink modeling and simulation of LVI-based primal-dual neural network for solving linear and quadratic programs. Neurocomputing 2009, 72, 1679–1687. [Google Scholar] [CrossRef]
- Zhang, Y.; Leithead, W.E. Exploiting Hessian matrix and trust-region algorithm in hyperparameters estimation of Gaussian process. Appl. Math. Comput. 2005, 171, 1264–1281. [Google Scholar] [CrossRef]
- Zhang, Y. On the LVI-based primal-dual neural network for solving online linear and quadratic programming problems. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 2, pp. 1351–1356. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. Recurrent neural networks for nonlinear output regulation. Automatica 2001, 37, 1161–1173. [Google Scholar] [CrossRef]
- Jin, L.; Li, S. Nonconvex function activated zeroing neural network models for dynamic quadratic programming subject to equality and inequality constraints. Neurocomputing 2017, 267, 107–113. [Google Scholar] [CrossRef]
- Li, J.; Shi, Y.; Xuan, H. Unified model solving nine types of time-varying problems in the frame of zeroing neural network. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1896–1905. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization Problems; Cambridge University Press: New York, NY, USA, 2004; pp. 127–214. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, F.; Xiao, Z.; Li, Z.; Cai, B. Performance analysis of LVI-based PDNN applied to real-time solution of time-varying quadratic programming. In Proceedings of the 2014 International Joint Conference on Neural Networks, IJCNN 2014, Beijing, China, 6–11 July 2014; pp. 3155–3160. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Tan, H.Z.; Fan, Z. On the simplified lvi-based primal-dual neural network for solving LP and QP problems. In Proceedings of the 2007 IEEE International Conference on Control and Automation, Guangzhou, China, 30 May–1 June 2007. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Li, S.; Cao, X. Time-varying mean-variance portfolio selection under transaction costs and cardinality constraint problem via beetle antennae search algorithm (BAS). SN Oper. Res. Forum 2021, 2, 18. [Google Scholar] [CrossRef]


| Interpolation Method | Case 1 | Case 3 | |||||
| 3 Stocks Portfolio | 10 Stocks Portfolio | ||||||
| ZNN | LVI-PDNN | S-LVI-PDNN | Linprog | ZNN | LVI-PDNN | Linprog | |
| Linear | 0.6 s | 0.45 s | 2.1 s | 3.6 s | 1.3 s | 1.6 s | 3.6 s |
| P.C. Hermite | 5.3 s | 0.5 s | 2.5 s | 3.8 s | 2.4 s | 5.1 s | 3.6 s |
| C. Spline | 0.55 s | 0.45 s | 0.53 s | 3.5 s | 3.9 s | 5.5 s | 3.7 s |
| Interpolation Method | Case 2 | Case 4 | |||||
| 5 Stocks Portfolio | 20 Stocks Portfolio | ||||||
| ZNN | LVI-PDNN | S-LVI-PDNN | Linprog | ZNN | LVI-PDNN | Linprog | |
| Linear | 5.8 s | 0.6 s | 3.6 s | 3.8 s | 6.3 s | 5.1 s | 3.7 s |
| P.C. Hermite | 11.1 s | 1.3 s | 4.6 s | 3.6 s | 58 s | 12.2 s | 4.3 s |
| C. Spline | 1.1 s | 1.8 s | 5.1 s | 3.8 s | 6.1 s | 10.7 s | 3.5 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalnogov, V.N.; Fedorov, R.V.; Generalov, D.A.; Chukalin, A.V.; Katsikis, V.N.; Mourtas, S.D.; Simos, T.E. Portfolio Insurance through Error-Correction Neural Networks. Mathematics 2022, 10, 3335. https://doi.org/10.3390/math10183335
Kovalnogov VN, Fedorov RV, Generalov DA, Chukalin AV, Katsikis VN, Mourtas SD, Simos TE. Portfolio Insurance through Error-Correction Neural Networks. Mathematics. 2022; 10(18):3335. https://doi.org/10.3390/math10183335
Chicago/Turabian StyleKovalnogov, Vladislav N., Ruslan V. Fedorov, Dmitry A. Generalov, Andrey V. Chukalin, Vasilios N. Katsikis, Spyridon D. Mourtas, and Theodore E. Simos. 2022. "Portfolio Insurance through Error-Correction Neural Networks" Mathematics 10, no. 18: 3335. https://doi.org/10.3390/math10183335
APA StyleKovalnogov, V. N., Fedorov, R. V., Generalov, D. A., Chukalin, A. V., Katsikis, V. N., Mourtas, S. D., & Simos, T. E. (2022). Portfolio Insurance through Error-Correction Neural Networks. Mathematics, 10(18), 3335. https://doi.org/10.3390/math10183335











