Abstract
In this paper, a fluid model is presented which contains the general linear equation of state including the gravitation term. The obtained spherical symmetric Euler equation and the continuity equations were investigated with the Sedov-type time-dependent self-similar ansatz which is capable of describing physically relevant diffusive and disperse solutions. The result of the space and time-dependent fluid density and radial velocity fields are presented and analyzed. Additionally, the role of the initial velocity on the kinetic and total energy densities of the fluid is discussed. This leads to a model, which can be considered as a simple model for a dark-fluid.
PACS:
34.10. + x; 34.50. − s; 34.50.Fa
MSC:
35Q31; 83C56
1. Introduction
Einstein equations can be solved with fluid energy-momentum tensors and some of them are possible candidates for the description of dark (fluid) matter. In our study, one of the simplest polytropic equations of state (EoS) is investigated, the linear one, which can be inserted into the spherical Euler equation. Thus far, there is no general mathematical technique to ascertain all solutions and properties of nonlinear partial differential equations (PDE) or systems; however, there are some methods that give us a glimpse into some kinds of solutions.
One of the main directions of this research is to find scaling solutions of the gravitational fields, which can be good candidates to describe the evolution of the Universe or collapse of compact astrophysical objects even in multi-dimensional space-time [1,2,3,4]. In these self-similar scaling models, the time evolution of the scaling is usually restricted by the metric. Another proposed analytic solution method is the self-similar ansatz by Sedov [5], which usually provides physically reasonable solutions with disperse features and with asymptotic power-law decays. This ansatz has already been applied successfully in some other hydrodynamical solutions [6,7,8].
There are some studies available that investigate the stability (or other properties of) various relativistic or non-relativistic gravitating fluids [9,10,11,12,13,14,15,16]. In their monograph, Deruelle and Uzan [17] analyse gravitating fluids and present some solutions as well. Based on our knowledge, there are no time-dependent self-similar solutions known and discussed for any kind of fluid hydrodynamical model. Our motivation here is to investigate this disperse solution in relation to the evolution of a gravitating system. Moreover, our results are compatible with the ideas of dark matter powered evolution of the early Universe [18,19,20] or they can be also applied to celestial dark matter objects [21].
In this paper, a simplified fluid EoS is applied, and we study the behavior and the physical relevance of the self-similar numeric hydrodynamic solutions for specific cases in the Newtonian approximation [22]. Finally, we provide the velocity, density, and kinetic energy density profiles for the space-time evolution.
2. The Model
Let us assume a one-dimensional, spherical symmetric system that is described by a compressible continuity and Euler coupled PDE, respectively:
Here, the subscripts t and r mean the corresponding time- and spatial partial derivatives. Additionally, , , and mean the density, the radial velocity component and the pressure field distributions, respectively. Note that the speed of the light and the gravitational coupling constant are set to be unity.
The second term in the Euler Equation (1) on the right-hand side is the gravitating term: the radial component of the gradient of the Newtonian potential. Figure 1 represents the corresponding geometry.
Figure 1.
Representation of the corresponding geometry. The sphere represents the expanding dark fluid, and the arrow the radial velocity.
The general linear EoS, which has other names in different scientific communities like barotropic or “stiff matter” EoS, has been applied:
There are numerous EoS available for fluids or in astrophysics; for more, see Emden [23]. He was the first who investigated polytropic EoS inside stars at the beginning of the 20th century. The physics of various polytropic EoS in astrophysics can be found in the monograph [24]. It is automatically fulfilled that the adiabatic speed of sound is constant:
which is a necessary physical condition. Different numerical values of the EoS strength w may lead to different dark matter scenarios for negative values as it was outlined by Perkov [25]. For a better understanding of our calculations, we give some examples according to [26,27,28,29,30,31,32]:
- (i)
- means the EoS for ordinary non-relativistic ‘matter’ (e.g., cold dust);
- (ii)
- means ultra-relativistic ‘radiation’ (including neutrinos) and, in the very early universe, other particles that later become non-relativistic;
- (iii)
- is the simplest case and describes the expanding universe, hypothetical phantom energy would cause Big Rip;
- (iv)
- means quintessence as hypothetical fluid;
- (v)
- is responsible for the flatness of the Big Bang;
- (vi)
- A scalar field can be viewed as a sort of perfect fluid with EoS ofwhere is the time derivative of , and is the potential energy. A free scalar field has and the one with vanishing kinetic energy is equivalent to . Any EoS in between but not crossing the barrier is known as the Phantom Divide Line (PDL) [27] and is achievable,which makes scalar fields useful models for any phenomena in cosmology.
The Universe has gone through three distinct eras characterized by the z red shift parameter values: radiation-dominated at ; matter-dominated if ; and dark-energy-dominated when . The evolution of the scale factor is controlled by the dominant energy form based on the Friedmann–Lemaître–Robertson–Walker equations: (for constant w). During the radiation-dominated era, , while in the matter-dominated era, . Finally, for the dark energy-dominated era, one can assume , which is asymptotically [33]. In our solutions, we will consider most of the above cases, which lead to the same solution family, but our main focus will be on the case with .
3. Analytic Solution with the Sedov–Ansatz
Disperse analytic solutions will be presented and analysed by applying the well-known self-similar ansatz [5,34,35] of
where can be an arbitrary variable of a PDE, where t means time and x means spatial dependence. The function is called the shape function. The similarity exponents and have crucial importance because represents the rate of decay of the magnitude , and is responsible for the rate of spread (or contraction if ) of the spatial distribution for large times. Solutions with integer exponents have the name of self-similar solutions of the first kind (in some cases, these can be derived from dimensional analysis of the investigated problem). This ansatz can be generalized when we consider real and continuous functions and instead of the exponents and .
The most remarkable result of this ansatz is the Gaussian- or fundamental solution of the regular heat conduction equation (or for the regular diffusion equation) when ; this result is clearly presented in Figure 2. This applied Ansatz is based on the statement that a self-similar solution exists, and every physical parameter preserves its form during the expansion. Self-similar solutions in most cases explain the asymptotic behavior of an unbounded or a far-field problem; the space coordinate x and the time t appear only in the function of . This clearly means that the existence of the self-similar variables implies the lack of characteristic time and length scales. These kinds of solutions are in most cases not unique and do not take into consideration the initial stage of the physical process. The solutions of these kinds describe the so-called intermediate asymptotic of the investigated problem: they hold only when the precise initial conditions are no longer relevant, but before the system has achieved its final steady state. For some peculiar systems, it can be clearly shown that the self-similar solution fulfils the source type or (Dirac-delta type) initial condition. This is not the case. Self-similar solutions are much simpler than the full solutions and therefore are easier to understand and investigate in different domains of the parameter space. A final reason for studying these functions is that they are solutions of a system of ODEs and hence do not suffer from the full numerical problems of the initial PDEs. For some systems, self-similar solutions help us to understand the global properties of the process e.g., the existence of compact supports.
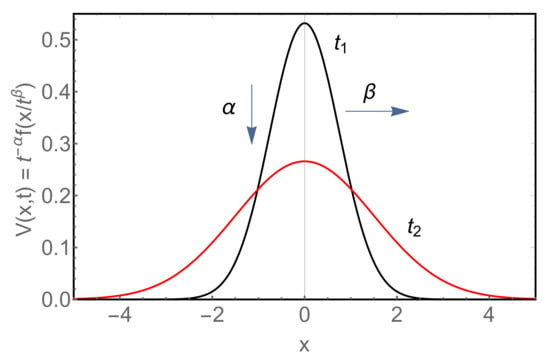
Figure 2.
A self-similar solution of Equation (5) for . The presented curves are Gaussians for regular heat conduction.
In the last decade, this ansatz has been successfully applied for numerous physical systems like heat conduction [36], a nonlinear Maxwell equation [37] and especially multidimensional Euler and Navier–Stokes equations [6,7] or the Madelung–Schrödinger quantum fluid equations [8] ending up with Refs. [38,39].
For our system, we apply the following notations for the two shape functions in natural units
where the new variable is .
Calculate time and spatial derivatives of the Equation (6) and substitute with Equation (1) and, using the relation, , we finally obtain the next nonlinear ordinary differential equation (ODE) system
where prime means derivation with respect to .
For the initially free three self-similar exponents , , and , we obtained the following numerical values: , , and . This means that dynamical variables, velocity and density, have a spreading property as time goes on (). Our physical intuition says that spreadings are somehow similar to expansion, which is a basic property of the Universe. The two “decay’’ exponents ( and ) are, however, not positive, which means that the magnitude of the velocity, u, remains the same even for large times. The role of the density, , is even more relevant; it increases linearly in time. We note the usual decaying and dispersive solutions with zero asymptotic values.
The analysis of the relations among the self-similar exponents can end up with three different scenarios:
- The linear algebraic equation system which contains the exponents is overdetermined, and leads to a contradiction. In this case, the system has inherently no physically self-similar power-law decaying or exploding solutions. Such systems are very rare; however, damped wave equations like the telegraph equations are like this.
- All exponents have given numerical values. In that case, the analysis of the solutions is simple. The derived coupled nonlinear ODE system can be analyzed, sometimes it can be decoupled and in best cases all variables can be written down in analytic formulas.
- The given linear algebraic equation system is under-determined, leaving usually one or two self-similar exponents completely free, this means extra free parameters in the obtained ODE system. Such systems have a very rich mathematical structure. The derived free exponent can have either negative or positive sign. Negative values in most cases result in power-law divergent or exploding solutions on the other side; positive exponents usually mean power-law decaying solutions, which are very desirable for dissipative systems.
In our former works, mostly viscous fluids have been analysed, like incompressible or compressible viscous Newtonian fluids, where all exponents had positive values, which is also true for the regular diffusion process, where and . In our recent case, these values are rather expected to be negative since the observed, approximately-flat Euclidian Universe scenario.
Our present ODE system of Equation (7) cannot be separated and solved with analytic means. Non-autonomous ODE systems can be linearized, and the stationer points can be found which helps to sketch the global qualitative properties of the solutions in the phase space. No such mathematical method exists for non-autonomous nonlinear systems. Therefore, there is no general tool in our hands that could help us to determine the global properties of the fluid. The equations of the stationary points, however, can be given as and , then we obtain
From the first equation for case, we obtain that the function contains the stationary points, with the dimensional definition of velocity, , with a lack of information on the general properties of the solutions. From the second equation, one can obtain that is stationary point, which is a trivial statement meaning that zero density is a stationery point.
According to our best knowledge, it is unclear whether for this ODE system mathematically rigorous existence or unicity theorems have been proven or not. The only physically reasonable way is to perform numerous calculations with a large number of parameter sets to explore the properties of the solutions in a wide range. Our numerical experiences say that both field variables have a continuous solution on a closed interval on the half axis of time and radial distance. We found no compact supports or ruptures in the solutions.
4. Results
To understand the physics of the presented model, a systematic parameter study of Equation (7) is required. First, we investigate the role of the w, which is the strength of the linear equation of state as well.
Figure 3 presents the density and velocity shape functions for four physically relevant different EoS strength parameters, , , 0, and . We integrate the ODE system between and . As initial conditions for velocity and density, and have been taken. The ratio was set to 50 here. This choice of the initial velocity (a positive value) means an initially radially expanding fluid and a physically reasonable positive density. It turned out that all four dashed velocity curves are constant and indistinguishable at this range and line widths. All four solid, density curves have a linear dependence of . From now on, we fix , which could be the simplest choice of a dark fluid.
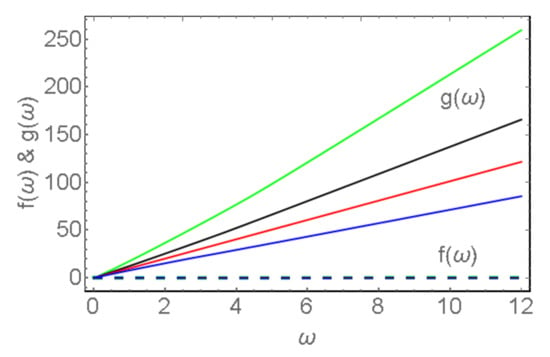
Figure 3.
The shape functions of Equation (7) for different EoS strength parameters: (green), (black), 0 (red), and (blue). The solid and dashed lines represent shape functions of density and velocity , respectively. Note that all velocity curves coincide. The initial conditions are and .
Figure 4 shows the space and time projections of the obtained density and the radial velocity distributions in natural units. Upper panels are the radial (space) evolution of the density (left) and radial velocity (right) functions. Lower panels present the time-projections of the above distributions at fixed radius values, respectively.
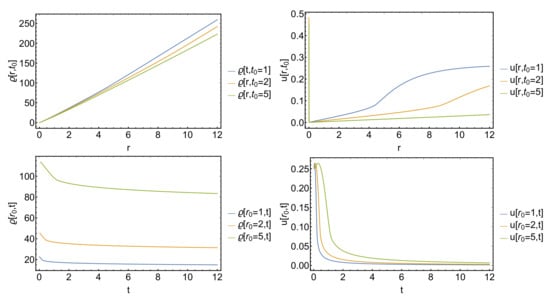
Figure 4.
The space-time evolution of the density (left) and the velocity (right) distributions for the case, . Curves are for the radial (top panels) and time (bottom panels) dependence at different fixed time- and space points. The initial conditions are and .
The density has linear dependence on the radius at any time. The radial dependence of velocity function looks, however, a bit more different: at very small distances close to the origin for all time points, it has a sharp down running edge with a minima and a linear dependence at larger distances.
The time dependences are different. The density has a quick but linear decay at small times and another but more slower (and almost linear) decay at larger times. The velocity shape functions start from non-zero values and have a quick decay in time at all distances. These properties cannot be anticipated directly from the shape functions. Note that these are the direct results of our presented model with initial conditions for the same point, and .
It is more relevant to investigate the dynamics of the complete fluid in time and space to understand some general trends or physical phenomena as the function of the initial conditions. For this reason, one can calculate the total energy density of the system including the kinetic and potential terms,
Figure 5 presents the kinetic, and the potential energy, densities—the two reasonable physical quantities which can be evaluated from the hydrodynamical model for a given parameter set. The kinetic energy is zero in the origin, has a linearly enhancing maxima at larger distances and has a quick decay in time for all radial distances. This means practically a blowing up sphere where the fluid moves. The potential energy has different properties, finite values in the origin at practically all times, and a slow decay for large times and distances.
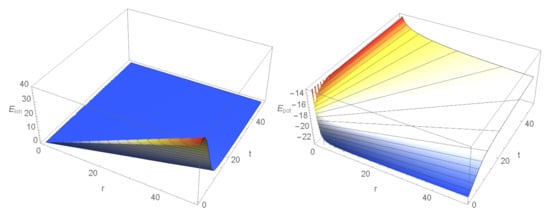
Figure 5.
The kinetic and potential energy densities of the investigated fluid for , with initial conditions and .
Since the solutions of our non-autonomous nonlinear ODE systems are not known, the dependence of the solutions on the initial conditions has been investigated. Drastically changing the ratio of the initial velocity and density results in different physical scenarios. Another point is the effect of changing the sign of the initial velocity. Positive sign means expansion, which may be stopped later, while a negative sign result in an initial collapse of the fluid.
Figure 6 depicts three different kinetic and total energy density distributions of the fluid under each other for different ratios. The initial density is fixed to 0.01 for all five cases. For a better comparison, both the time and the space domains were taken: ] in natural units for all panels. The chosen ranges vary because it is not possible to present all functions in the same range in an informative manner.
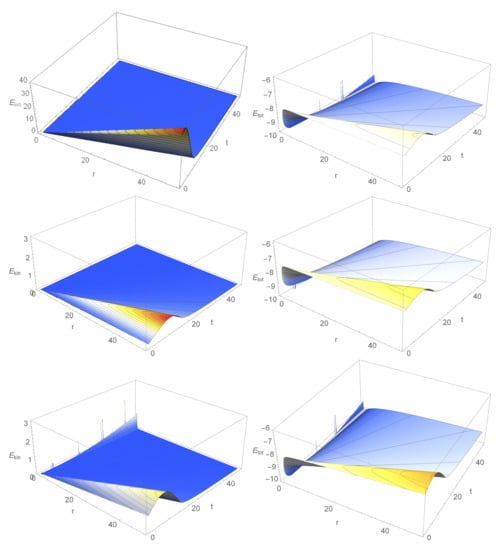
Figure 6.
The first column presents the kinetic energies and the second is for the total energies calculated with different initial velocities for the same initial density of , and for . The five following rows show the corresponding physical quantities for , 0, and initial velocities, respectively.
- case is seen in the first line panels with setting the kinetic-to-potential energy ratio to −50. Both physical quantities changed radically. The feature that the center of the fluid gains more and more kinetic and potential energy density is much more suppressed; on the other side, at small times, the kinetic energy density of the total fluid enhances. The larger the radius, the larger the energy density gain. Note that the values of the maximum linearly enhance with time. One may say that this phenomenon is a kind of “delayed” acceleration and deceleration of the fluid due to the enhanced potential energy density. This effect is not visible for larger initial velocities, where the initial kinetic energy densities dominate the potential energy. In this scenario, the strength of the two energy density terms lies almost in the same range. The figure of the total energy density function is drastically different to the former case, since it becomes negative everywhere. The effect of the kinetic energy density for small time values at any radius is clearly seen as a "bump" which lifts the potential energy density. The same statements are valid also for the panel of the third line panels, where the dynamics for a small positive initial velocity case, is presented.
- case describes the dynamics of a fluid with zero initial velocity (middle panels). Here, the effect of the potential energy density can be studied in a non-perturbed way. The “bump” of the kinetic energy color density for small times at an all fluid radius—a short acceleration and deceleration—of the fluid is originated by the gravitational potential of the fluid itself.
Our results can be summarized as follows: for this ideal hydrodynamical model, which does not include any kind of viscous damping, the self-similar ansatz may give solutions which explode in time, if the initial conditions are so.
5. Discussion
One possible application of our analytical solution is to investigate its relation to cosmological models and observations. The Hubble-law provides a velocity scaling [40] for the expansion of the Universe, and numerous possible scaling mechanisms are coded in our model via the choice of the self-similar ansatz several exponents that can describe various time decay scenarios. Figure 3 presented a linear scale parameter is obtained. Although the scaling curves are linear everywhere, at around certain r values, a quick change in the velocity is provided naturally as an in-coded inflation-like behavior by the ansatz. This critical r value depends on the initial condition. As right panels of Figure 4 show high initial velocity in the dark-fluid limit, (iii), become relaxed for a small, constant ‘non-relativistic’ value at a long timescale. Meanwhile, the dependence on the distance is getting saturated and close to flat at far distances from the initial ‘Big Bang’ point. It has been found that it is effect for nearby objects. This precision, however, is well beyond the uncertainty of the measured Hubble-constant value [41,42,43,44]. All curves in the lower right part of Figure 4 are getting fully flat for r ranging from 2 to 4.
The solution for the local density scaling is increasing in space but flat in time. This results in the space-time density evolution function in the left panels of Figure 4. Around the center, this function starts linearly with the distance, and after a rapid rise, the density of the fluid gets flat. An interesting feature of the model is that, apart from the initial point, the local density is increasing with time—due to the dispersing shock-wave and the dark fluid equation of state.
The structure of the ODE and the choice of the initial conditions leave us with enough freedom for a valid physical picture. As it can be seen, the is well supported by the solution, especially in the infinite space-time limit presented in Figure 6.
6. Summary and Outlook
A model where the spherically symmetric compressible Euler equation was used with a general linear matter equation of state and gravitation has been presented and analysed. This model with could be considered as the simplest candidate for dark fluid. As a method of investigation, the self-similar ansatz has been applied, which let us solve the problem analytically. Our model has enough freedom to be in agreement with the valid physical picture; however, one can improve according to the recent standard cosmology data and models.
Further work is in progress to improve the presented hydrodynamical model, e.g., via including fluctuations [45], rotation, relativistic or two-fluid effects [46,47] in the near future.
Author Contributions
Formal analysis, I.F.B. and G.G.B.; Software, M.A.P.; Visualization, G.G.B.; Writing—original draft, I.F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Hungarian National Research Fund (OTKA) grants K123815, K135515, NKFIH 2019-2.1.11-TÉT-2019-00050, 2019-2.1.11-TÉT-2019-00078, THOR COST action CA15213, and Wigner Scientific Computing Laboratory (WSCLAB), the former Wigner GPU Laboratory.
Data Availability Statement
This work is based on analytic calculation of the given formulae. All data are the plots. The data underlying this article will be shared upon reasonable request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Density | |
| u | Radial velocity |
| p | Pressure field |
| w | Strength of the EoS |
| Adiabatic speed of sound | |
| f | Shape function of the radial velocity |
| g | Shape function of the density |
| The argument of the shape functions | |
| Kinetic energy | |
| Potential energy |
References
- Brandt, C.F.C.; Lin, L.M.; da Rocha, J.F.V.; Wang, A.Z. Gravitational collapse of spherically symmetric perfect fluid with kinematic selfsimilarity. Int. J. Mod. Phys. D 2002, 11, 155–186. [Google Scholar] [CrossRef]
- Brandt, C.F.C.; Chan, R.; da Silva, M.F.A.; da Rocha, J.F.; Villas, J.F. Dressing a Naked Singularity: An Example. Int. J. Mod. Phys. D 2010, 19, 317–328. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Sepangi, H.R. Can local bulk effects explain the galactic dark matter? J. Cosmol. Astropart. Phys. 2008, 2008, 12. [Google Scholar] [CrossRef]
- Worrakitpoonpon, T. Spherical symmetry breaking in cold gravitational collapse of isolated systems. Mon. Not. R. Astron. Soc. 2014, 446, 1335–1346. Available online: https://academic.oup.com/mnras/article-pdf/446/2/1335/9380591/stu2159.pdf (accessed on 13 July 2022). [CrossRef][Green Version]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Barna, I.F. Self-Similar Solutions of Three-Dimensional Navier–Stokes Equation. Commun. Theor. Phys. 2011, 56, 745. [Google Scholar] [CrossRef]
- Barna, I.F.; Mátyás, L. Analytic solutions for the three-dimensional compressible Navier–Stokes equation. Fluid Dyn. Res. 2014, 46, 055508. [Google Scholar] [CrossRef]
- Barna, I.F.; Pocsai, M.A.; Mátyás, L. Analytic Solutions of the Madelung Equation. J. Gen. Lie Theory Appl. 2017, 11, 271. [Google Scholar] [CrossRef]
- Tabensky, R.; Taub, A.H. Plane symmetric self-gravitating fluids with pressure equal to energy density. Commun. Math. Phys. 1973, 29, 61–77. [Google Scholar] [CrossRef]
- Christodoulou, D. Self-gravitating relativistic fluids: A two-phase model. Arch. Ration. Mech. Anal. 1995, 130, 343–400. [Google Scholar] [CrossRef]
- Ducomet, B.; Feireisl, E.; Petzeltová, H.; Straškraba, I. Global in time weak solutions for compressible barotropic self-gravitating fluids. Discret. Contin. Dyn. Syst. 2004, 11, 113–130. [Google Scholar] [CrossRef]
- Ahmad, S.; Jami, A.R.; Mughal, M.Z. Stability of anisotropic self-gravitating fluids. Mod. Phys. Lett. A 2018, 33, 1850095. [Google Scholar] [CrossRef]
- Amodio, P.; Giordano, D.; Iavernaro, F.; Labianca, A.; Lazzo, M.; Mazzia, F.; Pisani, L. Mathematical aspects relative to the fluid statics of a self-gravitating perfect-gas isothermal sphere. Eur. J. Mech. B Fluids 2019, 78, 62. [Google Scholar] [CrossRef]
- Yuen, M. Analytically periodic solutions to the three-dimensional Euler–Poisson equations of gaseous stars with a negative cosmological constant. Class. Quantum Gravity 2009, 26, 235011. [Google Scholar] [CrossRef]
- Gratton, J. Fundamentals of Cosmic Physics; Gordon and Breach: New York, NY, USA, 2012; Volume 15. [Google Scholar]
- Fedi, M. Physical vacuum as a dilatant fluid yields exact solutions to Pioneer anomaly and Mercury’s perihelion precession. Can. J. Phys. 2019, 97, 417–420. [Google Scholar] [CrossRef]
- Deruelle, N.; Uzan, J.P. Relativity in Modern Physics; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Valev, D. Estimations of total mass and energy of the universe. Phys. Int. 2014, 5, 15–20. [Google Scholar] [CrossRef][Green Version]
- Peacock, J.A.; Cole, S.; Norberg, P.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.D.; Colless, M.; Collins, C.; Couch, W.; et al. A measurement of the cosmological mass density from clustering in the 2dF Galaxy Redshift Survey. Nature 2001, 410, 169–173. [Google Scholar] [CrossRef]
- Hinshaw, G.; Weiland, J.L.; Hill, R.S.; Odegard, N.; Larson, D.; Bennett, C.L.; Dunkley, J.; Gold, B.; Greason, M.R.; Jarosik, N.; et al. Five-Year Wilkinson Microwave Anisotropy Probe Observations: Data Processing, Sky Maps, and Basic Results. Astrophys. J. Suppl. Ser. 2009, 180, 225–245. [Google Scholar] [CrossRef]
- Freese, K.; Rindler-Daller, T.; Spolyar, D.; Valluri, M. Dark stars: A review. Rep. Prog. Phys. 2016, 79, 066902. [Google Scholar] [CrossRef]
- Rácz, G.; Szapudi, I.; Csabai, I.; Dobos, L. The anisotropy of the power spectrum in periodic cosmological simulations. Mon. Not. R. Astron. Soc. 2021, 503, 5638–5645. Available online: https://academic.oup.com/mnras/article-pdf/503/4/5638/37057174/stab874.pdf (accessed on 13 July 2022). [CrossRef]
- Emden, R. Gaskugeln: Anwendungen der Mechanischen Wärmetheorie auf Kosmologische und Meteorologische Probleme; B. G. Teubner: Leipzig, Germany; Berlin, Germany, 1907. [Google Scholar]
- Horedt, G.P. Polytropes: Applications in Astrophysics and Related Fields; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 2004. [Google Scholar] [CrossRef]
- Perković, D.; Štefančić, H. Dark sector unifications: Dark matter-phantom energy, dark matter-constant w dark energy, dark matter-dark energy-dark matter. Phys. Lett. B 2019, 797, 134806. [Google Scholar] [CrossRef]
- Hogan, J. Welcome to the dark side. Nature 2007, 448, 240–245. [Google Scholar] [CrossRef] [PubMed]
- Vikman, A. Can dark energy evolve to the phantom? Phys. Rev. D 2005, 71, 023515. [Google Scholar] [CrossRef]
- Yousaf, Z.; Khlopov, M.Y.; Bhatti, M.Z.; Naseer, T. Influence of modification of gravity on the complexity factor of static spherical structures. Mon. Not. R. Astron. Soc. 2020, 495, 4334–4346. Available online: https://academic.oup.com/mnras/article-pdf/495/4/4334/33372154/staa1470.pdf (accessed on 13 July 2022). [CrossRef]
- Arbey, A. Is it possible to consider Dark Energy and Dark Matter as a same and unique Dark Fluid? arXiv 2005. [Google Scholar] [CrossRef]
- Arbey, A. Dark fluid: A complex scalar field to unify dark energy and dark matter. Phys. Rev. D 2006, 74, 043516. [Google Scholar] [CrossRef]
- Farnes, J.S. A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified framework. Astron. Astrophys. 2018, 620, A92. [Google Scholar] [CrossRef]
- Arbey, A.; Mahmoudi, F. One-loop quantum corrections to cosmological scalar field potentials. Phys. Rev. D 2007, 75, 063513. [Google Scholar] [CrossRef]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark Energy and the Accelerating Universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Stein, N.; van Dyke, M. Similarity, Self-Similarity, and Intermediate Asymptotics; Consultants Bureau: New York, NY, USA, 1979. [Google Scholar]
- Zel’dovich, Y.B.; Raizer, Y.P.; Hayes, W.D.; Probstein, R.F.; Landshoff, R. (Eds.) Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Academic Press: New York, NY, USA, 1967. [Google Scholar] [CrossRef]
- Barna, I.F.; Kersner, R. Heat conduction: A telegraph-type model with self-similar behavior of solutions. J. Phys. Math. Theor. 2010, 43, 375210. [Google Scholar] [CrossRef]
- Barna, I.F. Self-similar shock wave solutions of the nonlinear Maxwell equations. Laser Phys. 2014, 24, 086002. [Google Scholar] [CrossRef]
- Barna, I.F. Self-Similar Analysis of Various Navier–Stokes Equations in Two or Three Dimensions. In Handbook on Navier–Stokes Equations: Theory and Applied Analysis; Campos, D., Ed.; Physics Research and Technology, Nova Publishers: Hauppauge, NY, USA, 2017; Chapter 16; pp. 275–304. [Google Scholar]
- Barna, I.F.; László, M. Self-Similar and Traveling-Wave Analysis of the Madelung Equation. In Understanding the Schrödinger Equation: Some Non[Linear] Perspectives; Simpao, V., Little, H.C., Eds.; Mathematics Research Developments, Nova Publishers: Hauppauge, NY, USA, 2020; Chapter 6; pp. 181–224. [Google Scholar]
- Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. Available online: https://www.pnas.org/content/15/3/168.full.pdf (accessed on 13 July 2022). [CrossRef]
- Freedman, W.L.; Madore, B.F.; Gibson, B.K.; Ferrarese, L.; Kelson, D.D.; Sakai, S.; Mould, J.R.; Kennicutt, R.C., Jr.; Ford, H.C.; Graham, J.A.; et al. Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. Astrophys. J. 2001, 553, 47–72. [Google Scholar] [CrossRef]
- Jarosik, N.; Bennett, C.L.; Dunkley, J.; Gold, B.; Greason, M.R.; Halpern, M.; Hill, R.S.; Hinshaw, G.; Kogut, A.; Komatsu, E.; et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results. Astrophys. J. Suppl. Ser. 2011, 192, 14. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Alves, M.I.R.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Aussel, H.; et al. Planck 2013 results. I. Overview of products and scientific results. Astron. Astrophys. 2014, 571, A1. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; The Las Cumbres Observatory Collaboration; The VINROUGE Collaboration and The MASTER Collaboration. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Kovács, A.; Beck, R.; Szapudi, I.; Csabai, I.; Rácz, G.; Dobos, L. A common explanation of the Hubble tension and anomalous cold spots in the CMB. Mon. Not. R. Astron. Soc. 2020, 499, 320–333. Available online: https://academic.oup.com/mnras/article-pdf/499/1/320/33852113/staa2631.pdf (accessed on 13 July 2022). [CrossRef]
- Harko, T.; Lobo, F.S.N. Two-fluid dark matter models. Phys. Rev. D 2011, 83, 124051. [Google Scholar] [CrossRef]
- Barna, I.F.; Mátyás, L. Analytic Solutions of a Two-Fluid Hydrodynamic Model. Math. Model. Anal. 2021, 26, 582–590. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).