Abstract
We investigate a hydrodynamic equation system which—with some approximation—is capable of describing the tsunami propagation in the open ocean with the time-dependent self-similar Ansatz. We found analytic solutions of how the wave height and velocity behave in time and space for constant and linear seabed functions. First, we study waves on open water, where the seabed can be considered relatively constant, sufficiently far from the shore. We found original shape functions for the ocean waves. In the second part of the study, we also consider a seabed which is oblique. Most of the solutions can be expressed with special functions. Finally, we apply the most common traveling wave Ansatz and present relative simple, although instructive solutions as well.
Keywords:
partial differential equations; conservation laws and constitutive relations; tsunamis; physical oceanography; ocean waves and oscillations PACS:
02.30.Jr; 47.10.ab; 91.30.Nw; 92.10.-c; 92.10.Hm
MSC:
76B15; 35Q35
1. Introduction
Wave propagation in nonlinear media is a fascinating field in physics with enormous literature, (without completeness, we just mention some relevant monographs) [1,2,3,4,5,6,7]. Narrowing the scientific question to the dynamics of various waves in sea or fresh water is still an immerse problem with considerable literature [8,9,10,11,12,13,14,15,16,17]. The very first pioneering work was written by Airy in 1841 with the title of “Tides and Waves” [18]. Interaction of water waves with ships [19] is also a crucial question both from theoretical and engineering sides as well.
Regarding water waves, one may find important numerical and analytical studies of Bussinesq approximation [20,21,22,23,24,25,26,27,28,29]. There is also a Boussinesq approximation with dissipative dynamics and possible density variations [30,31,32,33,34,35]. Experiments for certain parameter values are also realized [36,37]. Connections related to radiation and environment can be found in [38]. One may find a detailed review of ocean wave modelling in [39].
Tragedies caused by tsunamis in the last several decades highlighted that investigation of the physics of water waves are indispensable, and the obtained results can save human lives. One may fine studies on destructive weather phenomena one in [40].
To study such effects, diverse nonlinear partial differential equations (PDEs) have to be investigated with various methods. Tsunamis are long life non-dispersive waves which can be well described with solitons and with the corresponding mathematics. One may also find wave equations with fractional derivatives in [41,42].
In the following, we choose a completely different path, and we investigate the long-time dispersion and decay of such kind of fluid equations with the self-similar Ansatz [43,44]. This Ansatz inherently contains two exponents—for each dynamical variable—which describes the asymptotic decay and dispersion of the solutions. This Ansatz is the natural trial function of the regular diffusion (or heat conduction) equation and gives the Gaussian (or fundamental) solution after some easy mathematical steps. If the parameter dependences of these solutions are systematically studied and analyzed, then a well-established physical image emerges in front of us. Of course, additional mathematical methods (like using generalized symmetries) also exist to obtain other solutions like those in [45].
This study is organically linked to our personal long-term strategy in which we systematically investigate the fundamental hydrodynamic systems one after another and analyze with the physically relevant self-similar Ansatz. Up to now, we have published more than ten papers—(some of them are [46,47,48,49])—and a book chapter [50] in this field. In our last two publications, we investigate the question of finding analytic solutions for the rotating and stratified Euler equations [51], and the analysis of a two-fluid model where the Euler and the Navier–Stokes equations were coupled [52].
With the use of self-similar transformation, we arrive for the first time to solutions of the tsunami wave equations, presented in [9]. A further new feature of the present study is that we apply different analytic sea-bed functions and present analytic solutions for each of them. We successfully applied this investigation method for the KPZ surface growth model [53,54] where half a dozen different kinds of noise terms were considered and analyzed with the self-similar and traveling wave Ansätze. To the best of our knowledge, there are no such time-dependent self-similar solutions known, presented and analyzed in the scientific literature for this water-wave equation system.
2. Theory and Results
In the following, we apply the equations of motion for ocean waves, based on the study of [9]. These are considered to be also amenable for tsunami waves, in open ocean, sufficiently far from the shore. The results may be also true for smaller scales, with the condition that the depth is smaller than the horizontal dimensions of the water surface,
where the dynamical variables are the wave height and the two orthogonal horizontal fluid velocity components . The function or is the depth of the sea, or the function of the seabed. We will investigate both cases, time-independent and time-dependent seabed functions, and the differences will be highlighted. The mathematical form of the self-similar Ansatz inherently makes this comparison possible. We consider that water is inviscid, incompressible and irrotational. The variable local wave propagation speed is with the gravity acceleration. Figure 1 shows the geometry of the investigated flow problem. The wave height of a surface wave is the difference between the elevations of a crest and a neighboring trough. The original depth of the water is the distance between the minima of the wave height function and the maxima of the negative seabed function (or ), and can be shifted with any arbitrary constant.
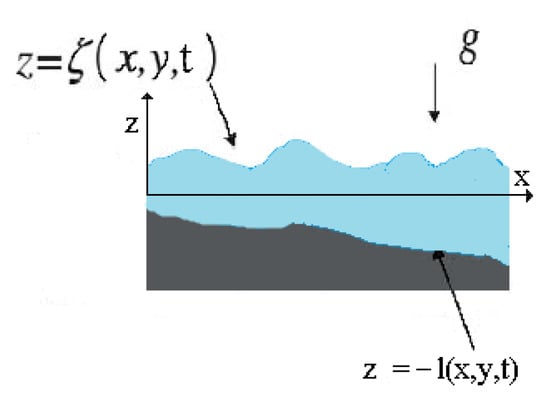
Figure 1.
The geometry of the flow where is the wave height and is the seabed function, respectively.
At this point, we have to mention that a large number of such equations are derived and part of them solved in the work of [16]. Unfortunately, the solution functions are not analyzed, not visualized on figures, and no detailed parameter studies were presented, which would be desirable for physicists or engineers. Water waves on variable depth are also an exhaustively investigated topic in the last few decades [55]. The linear water wave scattering by variable depth (or with other name bottom topography) in the absence of a floating plate has been investigated by many authors. Two approaches have been developed. The first is analytical, and the solution is derived in an almost closed form [56,57]. The second approach is numerical, and developed by Liu and Liggett [58], in which the boundary element method in a finite region is coupled to a separation of variables solution in the semi-infinite outer domains. For both the analytic and numerical approach, the region of variable depth must be bounded. Wave scattering by a floating elastic plate on water of variable bottom topography was treated by Wang and Meylan [59] in 2002. Using a Zakharov integral equation approach, a pair of coupled nonlinear evolution equations are derived for two co-propagating weakly nonlinear gravity wave packets over finite depth fluid [60]. Additional interesting and new results about water waves can be found in the publications of [61,62,63,64,65]. The newest results about disperse shallow water waves can be found in the monograph of Khakimzyanov et al. [66].
We apply the following well-known self-similar Ansatz [43,44] for the dynamical variables:
with the new reduced variable of . All the exponents are real numbers. (Solutions with integer exponents are called self-similar solutions of the first kind, non-integer exponents generate self-similar solutions of the second kind.) This Ansatz is one kind of reduction mechanism where the original PDE system is reduced to an Ordinary Differential Equation (ODE) system. Unfortunately, both initial and the boundary problems become undefined. The obtained results can fulfil some kind of well-defined initial and boundary problems only via fixing their integration constants during the integration of the obtained ODE system. The shape functions should be continuous functions and will be evaluated later on. (For first order Euler-type PDEs, no continuous higher order derivatives of the shape functions are needed; therefore, shock waves solutions, solutions with jumps or with singularity may occur.)
The logic, the physical and geometrical interpretation of the Ansatz were exhaustively analyzed in all our former publications [46,47,48,49,50]; therefore, we neglect it. Except for some extreme cases, positive exponents—now and —mean physically reasonable and well-behaving disperse solutions which decay and spread out in time. The exponent has direct connections to the spreading velocity of the solution. The case occupies a special place in our analysis and could mean physically relevant solutions without any temporal decay, and, in this sense, these are similar to solitons. (We cannot describe real solitons with our Ansatz because that would mean zero dispersion and decay as well.)
The big advantage of the self-similar Ansatz of (2) that it directly gives us the Gaussian (or fundamental) solutions of the regular diffusion (or heat conduction) equation where the above-mentioned physical meaning of the exponents are clear to identify. Applying this kind of Ansatz to any kind of nonlinear PDE system gives us clear information about the dispersive properties of the investigated phenomena. Solutions with negative exponents usually mean divergent solutions which will be mentioned later and might represent tsunamis or rough waves.
Now, we have to make a case study for different well defined bed functions or . Such kind of an analysis was performed with the Kardar–Parisi–Zhang (KPZ) interface growing equation where the effect of the different noise terms was investigated, and numerous analytic solutions were derived [53]. We used the Maple 12 mathematical software to evaluate the analytic solutions of Equation (1a)–(1c) for different seabed functions from now on.
2.1. The Constant Seabed Function
Let us start with the simplest seabed function, namely with the case, where is a real number. The obtained ODE system reads
where the prime means derivation with respect to the variable , and the corresponding self-similar exponents are
Note that the system is symmetric in the two velocity coordinates. It is important to say that all three exponents which are responsible for the temporal decay of the dynamical variables ( and ) are arbitrary, which gives a relatively large freedom for the solutions. Usually, positive exponents mean physically reasonable non-explosive solutions for large times. The common exponent , which is responsible for the spreading, is positive, which is a promising sign for possible solutions. Furthermore, because , a construction , where C is a constant, yields , which in itself is a kind of decaying wave in time.
Unluckily, there are no closed form analytic solutions available for all three dynamical variables of (3a)–(3c) for general and d parameters. However, for the wave height, the general solution can be formulated in the next closed form of:
Note that, for , we automatically have the relation with (which is a real wave speed). After some simple algebraic steps, (5) can be reformulated to
which are left and right running traveling waves, with shape function of , with velocity of and with power-law time-varying amplitude of . Of course, the shape functions are now not the well-known sine or cosine functions but the power-law of the wave argument. This is an interesting and rare feature of the derived results. Such phenomena (when the original self-similar Ansatz leads to traveling-wave solutions with time-varying amplitude) has already occurred in our former studies. More than a decade ago, we investigated a heat conduction model based on the Euler–Poisson–Darboux equation which is a “kind of time-dependent telegraph-type equation” with the usual self-similar Ansatz, and we found a solution which is a product of two (left-running and right-running) traveling waves with additional temporal decay [67]. As further explanation, we may say that the original PDE system (1) is “so hyperbolic” (by that, we mean a first-order system without any kind of additional dispersion) that even the self-similar Ansatz (which is very successful to obtain disperse and decaying solutions of parabolic systems—school example Gaussian solution of the diffusion equation) provides traveling wave solutions. Another interpretation could be the following time-decaying traveling wave solutions of hyperbolic systems can be found with the self-similar Ansatz due to its internal structure. In other words, this effect is a clear fingerprint of the in-depth entanglement of diffusion and wave phenomena.
Figure 2a presents the shape function of the wave height function for different exponents. Note that, for , the derived solutions have either a local minimum or maximum or both and an asymptotic decay to zero at large arguments. For , the solution is divergent at large arguments. Figure 2b shows the final wave height function for , which has a very sharp peak at the origin at small times and distances and a steep decay. All other positive s show similar behaviour as well. The case means no wave at all, just a constant function everywhere.
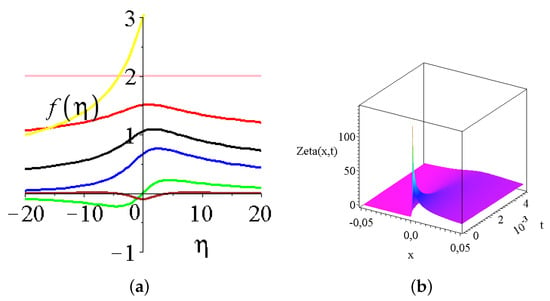
Figure 2.
The shape function and the solution of the wave height. (a) The shape functions of the wave height (5) are presented for various self-similar exponents. The yellow, pink, black, blue, red, green and brown curves are for and 2, respectively. The integration constants were set to unity, and water depth . (b) the solution of the wave height function of for the parameter set of , the water depth is .
For a better understanding, we give the explicit forms of the function f in case , and some values of .
If , and , we have for the function f:
In this case, if one assumes that
then
in the above evaluation. Considering
then we have
Consequently, the formula for :
If we insert value for p, one obtains
If is inserted, one obtains
in case
Note that our PDE or even the obtained ODE system is symmetric in the two velocity coordinates, so it is enough to evaluate and analyze one of them. For the velocity variables, the general solutions can be formulated but contain an integral which can be evaluated in closed forms for given integer values only. For , the solutions are proper rational fractions, having singularity in the origin and zero asymptotic values in infinity; for , the results are polynomials. We give two examples:
In Figure 3a, we present the velocity shape function for four different exponents. The projection of the velocity function for is visualized in Figure 3b. Note the power law decay for large distances. The wave velocity as a relevant dynamical variable of the system shows no extra features.
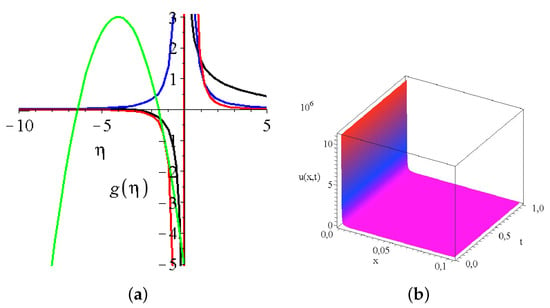
Figure 3.
The shape function and the solution for the x component of the velocity. (a) The shape function of the x velocity component for four different exponents for the constant seabed function. The black, blue, red and green line correspond to and values, respectively. The integral constants and . (b) The velocity projection ; for , other integration constants and the water depth remain the same.
2.2. The Linear Seabed Function
The next choice is the linear case. We have to distinguish two different cases and have to make a clear separation:
where the negative sign was taken from geometrical reasons, and we would like to have the seabed in the negative region, and c are just free positive real numbers which are responsible for the slope of the seabed and the depth in the origin. The first case means a rigid sea-bed which does not change its shape during the wave motion. Probably this model is more relevant for deeper water where the sea bottom is rigid. In our forthcoming analysis, we have to introduce the following identity:
The second case (17b) represents a physical situation where the sea-bed function is continuously modified during the corresponding wave propagation, which is feasible in very shallow water and loose ground soil like slime. Note that the factor should play a relevant role in the time asymptotic.
Let us analyze the time-independent case first. After some simple algebraic manipulations, we can derive the ODE system of:
with exponents of
Note the slight difference compared to the constant seabed function. The exponent, which is responsible for the “spreading”, is favourably high; in regular diffusion processes, it is usually just . There are no general formulas available for all three dynamical variables for arbitrary parameters and for the exponent. The exception is the shape function of the wave height, which is the following:
where are the hypergeometric functions [68]. The hypergeometrical function is defined for by the power series of
where in the (rising) Pochhammer symbol, which is defined by:
It is clear to see from the infinite power series definition of the hypergeometric function using the Pochhammer symbols that the function is undefined (or infinite) if the third parameter equals a non-positive integer. On the other side, the infinite series terminates if the first two parameters of the hypergeometric functions are non-positive integers.
It is a hopeless undertaking to give a general parameter study of the solution for arbitrary and b. It is logically clear that larger parameters cause a steeper slope, which affects the numerical values of the exponent. Thus, let us fix and investigate the role of the self-similar exponent ; now, the former formula (21) is changed to
Figure 4a presents (24) for various s. It is clearly visible that, for , all shape functions diverge at large argument . For positive s, the shape functions go to zero at infinity. Note the lower limit of the domain of all shape functions which lies uniformly at , which is half of the gravitational acceleration parameter of the system. We obtain the usual features that negative exponents mean non-decaying solutions at large arguments.
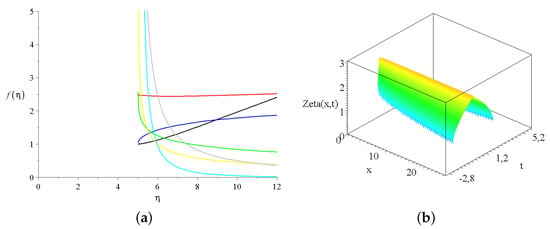
Figure 4.
The shape function and the solution for the spatial and temporal dependence of the wave height. (a) The shape function of the wave height for seven different exponents for the linear seabed function. The black, blue, red, green, yellow, gray and light blue lines correspond to and 2 values, respectively. The integral constants and ; (b) the wave height projection for other integration constants, and the water depth remains the same.
On the right side of Figure 4, the projection of the wave height is presented for , which means that the global maximum is not changing in time. The most important property of the solution is its shape, which describes a continuously widening ridge with a compact support in space. The function together with the first spatial and temporal derivatives remain finite at the border of the domain. The value and the spatial position of the maximum is not changing in time; therefore, it cannot be interpreted as any kind of traveling wave.
There is no general formula available for arbitrary for the velocity shape function; however, for fixed and well-defined s, closed formulas can be evaluated. We present some shape functions for
For other e.g., non-integer s, we obtain expressions which contain an additional integration with some extra constants. These integrals can be evaluated only when all constants are fixed. In Figure 5a, we can see the three analytic velocity shape functions of (25). Note that all three functions are defined for only. To have a complete picture, Figure 5b shows the velocity distribution for the exponent, which means that the global maximum has temporal decay again. The general feature of the wave velocity function is very similar to the former wave height function. It is a continuously widening ridge with a compact support in space again. The function together with the corresponding first spatial and temporal derivatives has finite values the the border of the domain. However, the spatial position moves in time, which means that it is a traveling wave solution. To have a very picturesque presentation of how the water wave behaves, we present a plot which shows the “kinetic-energy like” property of the wave, namely the
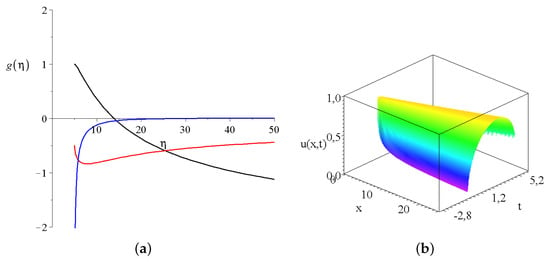
Figure 5.
The shape function and the solution for the spatial and temporal dependence of the x component of the wave velocity. (a) The shape function of the x velocity component for the above given three exponents for the time-independent seabed function. The black, red and blue lines correspond to and 1 values, respectively. The integral constants and the geometrical constants are and ; (b) the spatial and temporal dependence of velocity component for ; all other constants remain the same.
Our argumentation is the following: we do not have the density as a dynamical variable of the model, but we think that the true height of the waver wave is proportional to the mass of the wave; therefore, the presented quantity gives us a physically acceptable hint of the wave. As we can see, the domain of the height and the velocity functions are slightly different, and a physical true wave is only present when the mass (or now the wave height) and the velocity are different from zero. Figure 6 presents the distribution of Equation (26). Note that the shape of the wave describes a true finite traveling wave in space and time with constant amplitude. Due to the self-similar exponent (which is responsible for the dispersion ratio of the dynamical variables), the obtained wave has strong spreading; therefore, despite the constant maximum, our wave is not a solitary wave. The rising edge of the wave has a finite non-zero time derivative at the border of the domain, and a falling edge has a zero derivative at . Finally, we have to note that the role of depth of the seabed c does not explicitly appear in the shape functions; however, it does affect the final solutions and can be visualized on the final space and temporal dependences of the wave height and velocity (Figure 4b and Figure 5b) or in Figure 6. The larger the water depth, the broader is the corresponding physical quantity. Larger water depth does not modify the quality of the solutions; it just makes them more disperse. Thus, with a fixed numerical value (of e.g., ) and a maximal wave height of 3, we have a good approximation of deep water phenomena. In general, it is a remarkable fact that our self-similar Ansatz is capable of describing traveling wave pattern in a first-order hyperbolic PDE system.
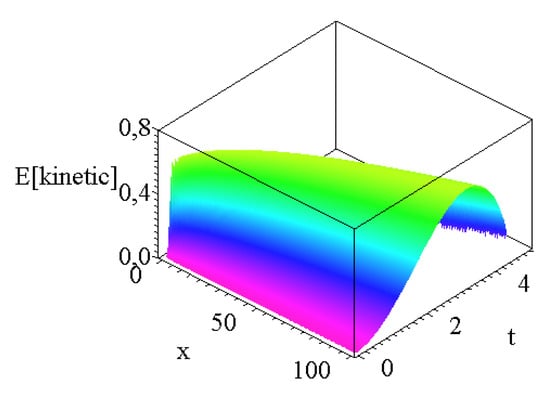
Figure 6.
The “kinetic energy-like property” of the wave according to Equation (26) with all numerical parameters given above.
For our last case for a time-dependent linear seabed function (17b), we have a bit different reduced ODE system of
with the exponents of
Note that all the exponents which are responsible for dissipation can have arbitrary values as before (which allow for exploding or decaying solutions or solutions with constant maximum in time). The only difference is the numerical value of , which is now unity.
As in the previous case, no closed-form analytic solutions exist for all dynamical variables for arbitrary parameters, except for the wave height
where the two s are still the hypergeometric functions [68]. The complete general parameter study looks hopeless. Let us fix first, and now the solution looks a bit more transparent
For some relevant rational values, the shape function becomes more simple like:
where and are the regular and irregular Legendre functions [68]. The left part of Figure 7 presents the shape function of the water height (30) for some exponent values. If is equal to and , the graphs (the black and red curves) are almost vertical lines. Zero alpha means a constant shape function which is quite reasonable. For , the shape functions have finite values in the origin, can be expressed with Legendre functions, and are defined for negative arguments only. For positive integer s, the functions have at asymptote at . On the right side of Figure 7, the water height function is plotted for the exponent. The solution is the constant wave height function for every time and space point.
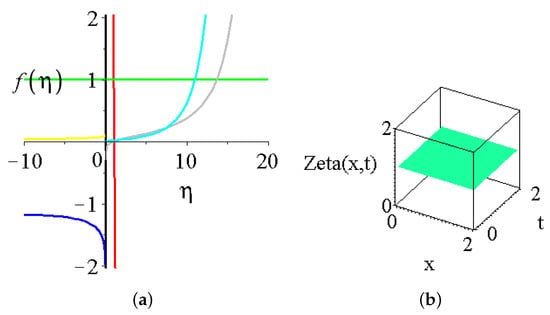
Figure 7.
The shape function and the solution for the spatial and temporal dependence of the wave height. (a) the shape function of wave height for various s for time-dependent linear seabed functions. The black, red, blue, green, yellow, gray and cyan colours are for and for 2, the geometrical constants are and ; (b) the spatial and temporal dependence of the water wave height for .
Now comes the the analysis of the velocity field. As before, there are no analytic solutions available for the entire parameter space. For fixed a and b steepness, there are closed formulas available for integer s only. Unfortunately, for rational s, the solutions contain an additional formal integration which cannot be evaluated with analytic means. The shape functions for the x component of water velocity are the following for the most relevant three integer s:
For the sake of completeness, Figure 8a presents these three shape functions and Figure 8b shows the projected velocity field for . We tried to evaluate and plot Equation (26) for various s; unfortunately, we cannot find a reasonable function which could be interpreted as any kind of finite water wave. Thus, there are analytic solutions available, but these are outside of any physical interest.
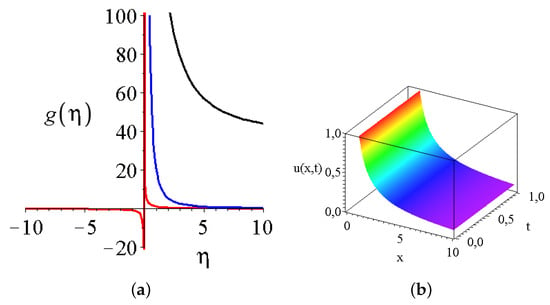
Figure 8.
The shape function and the solution for the spatial and temporal dependence of the x component of the wave velocity. (a) the shape function of the x velocity component for three exponents for the time-dependent seabed function. The black, red and blue lines correspond to and 1 values, respectively. The integral constants are and the geometrical constants remain the same as above. (b) the spatial and temporal dependence of velocity component for .
2.3. Traveling Wave Analysis
Lastly, we try to analyze the original PDE system of Equation (1) with the traveling wave Ansatz. Numerous kinds of traveling wave solutions exist for numerous water wave equations. One of them is the Wilton ripple, which is a type of periodic traveling wave solution of the full water wave problem incorporating the effects of surface tension [69].
For our system, we take the form of the traveling wave as
where c is the velocity of the wave. The obtained ODE system is slightly different from (3a)–(3c)
Note that, for generality, we consider that the sea bed ‘l’ has the dependence of the traveling wave argument . The physical meaning of such a space and time-dependent surface is of course questionable, and can be a scope of a different study. Here, we just present the mathematical obtained results. According to Maple12, the undetermined system of (19) has three different kinds of solutions:
where are the usual integration constants. Note that, for the third kind of solution, the wave velocities are inversely proportional to the sea-bed function. Above deep lying sea-beds, the velocity is low, which can be understood as the direct manifestation of the Bernoulli principle.
3. Conclusions and Outlook
We investigated a hydrodynamic system which is capable of describing water wave propagation over a variable water depth. The question of constant and linear sea-bed functions were addressed and analyzed. We found general analytic formulas for the spatial and time dependent wave heights; unfortunately, for the velocity functions, no general formulas are available. If all the parameters are fixed, then closed formulas can be derived as well which contain various hypergeometric functions with non-trivial arguments. As a second case, the water waves are investigated above a time-independent (we may say) linear seabed function. We found that dispersive traveling wave solutions may exist with constant wave height in time. As a third case, we considered a time dependent linear seabed function and tried to find physical water waves with reasonable velocities and wave height. Unfortunately, no such waves can be found among the mathematically existing solutions. Finally, we investigated the traveling solutions and found not so interesting solutions of the problem.
In a former independent study, we investigated the self-similar solutions of rotating and stratified fluids [51] and presented analytic results. We think that, thanks to Nathan Paldor’s monograph [70], investigating a rotating shallow water fluid system could be a natural generalization of our present study. Investigating waves in ferrofluids could be a delicate problem as well [71]. We hope that our results may have future applications in open ocean engineering.
Author Contributions
The corresponding author (I.F.B.) provided the original idea of the study, performed the analytic calculations, created the figures and wrote some part of the manuscript. The second author (M.A.P.) checked and collected the presented literature. Finally, he helped to improve the language of the manuscript. The last author (L.M.) evaluated certain formulas, checked all the analytic calculations, the spelling, improved the language of the final manuscript and collected some part of the cited references as well. The authors discussed the manuscript on a regular weekly basis. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by project No. 129257 implemented with the support provided from the National Research, Development and Innovation Fund of Hungary, financed under the K_18 funding scheme. Authors I.F. Barna and M.A. Pocsai were supported by the NKFIH, the Hungarian National Research Development and Innovation Office.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are all available within the article. At the request of readers, the appropriate Maple files are available.
Acknowledgments
We would like to acknowledge the support by the Wigner GPU Laboratory of the Wigner RCP for providing the computational capacity required to carry out the numerical simulations. Authors M.A. Pocsai and I.F. Barna were supported by the NKFIH, the Hungarian National Research Development and Innovation Office.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Crawford, F.S., Jr. Waves; Berkeley Physics Course; McGraw-Hill: New York, NY, USA, 1965; Volume 3. [Google Scholar]
- Coulson, C.A.; Jeffrey, A. Waves: A Mathematical Approach to the Common Types of Wave Motion, 2nd ed.; Longman: London, UK, 1977. [Google Scholar]
- King, G.C. Vibration and Waves; The Manchester Physics Series; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons: Hoboken, NJ, USA, 1974. [Google Scholar]
- Brillouine, L. Wave Propagation and Group Velocity, 1st ed.; Academic Press: New York, NY, USA, 1960. [Google Scholar]
- Fritz, J. Nonlinear Wave Equations, Formation of Singularities; University Lecture Series; American Mathematical Society: Providence, RI, USA, 1990; Volume 2. [Google Scholar]
- Ablowitz, M.J. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Debnath, L. Nonlinear Dispersive Waves, 1st ed.; Cambridge University Press: New York, NY, USA, 1994. [Google Scholar]
- Kundu, A. (Ed.) Tsunami and Nonlinear Waves; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Pedlosky, J. (Ed.) Waves in the Ocean and Atmosphere; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Holthuijsen, L.H. (Ed.) Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Johnson, R.S. (Ed.) A Modern Introduction to the Mathematical Theory of Water Waves; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Pelinovsky, E.; Kharif, C. (Eds.) Extreme Ocean Waves; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Komen, G.J.; Cavaleri, L.; Donel, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Young, I.R. Wind Generated Ocean Waves; Elsevier Ocean Engineering Series; Elsevier: Amsterdam, The Netherlands, 1999; Volume 2. [Google Scholar]
- Huang, H. Dynamics of Surface Waves in Coastal Waters, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Barber, N.F.; Ghey, G. Water Waves; The Wykeham Science Series for Schools and Universities, Wykeham Publications and London & Winchester: London, UK, 1969; Volume 5. [Google Scholar]
- Airy, G.B. Tides and Waves. In Encyclopedia Metropolitana; Smedley, E., Rose, H.J., Rose, H.J., Eds.; Part Publication: London, UK, 1841. [Google Scholar]
- Timman, R.; Hermans, A.J.; Hsiao, G.C. Water Waves and Ship Hydrodynamics, 1st ed.; Mechanics of Fluids and Transport Processes; Springer: Dodrecht, The Netherlands, 1985; Volume IX. [Google Scholar]
- Madsen, P.A.; Fuhrman, D.R.; Wang, B. A Boussinesq-type method for fully nonlinear waves interacting with a rapidly varying bathymetry. Coast. Eng. 2006, 53, 487–504. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method for rational solutions for KdV, K(2,2), Burgers, and cubic Boussinesq equations. J. Comput. Appl. Math. 2007, 207, 18–23. [Google Scholar] [CrossRef]
- Wazwaz, A.M. New travelling wave solutions to the Boussinesq and the Klein–Gordon equations. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 889–901. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 2012, 43–44, 36–51. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A Variety of Soliton Solutions for the Boussinesq–Burgers Equation and the Higher-Order Boussinesq–Burgers Equation. Filomat 2017, 31, 831–840. [Google Scholar] [CrossRef]
- Helal, M.; Seadawy, A.; Zekry, M. Stability analysis of solitary wave solutions for the fourth-order nonlinear Boussinesq water wave equation. Appl. Math. Comput. 2014, 232, 1094–1103. [Google Scholar] [CrossRef]
- Kazolea, M.; Delis, A.I. Irregular wave propagation with a 2DH Boussinesq-type model and an unstructured finite volume scheme. Eur. J. Mech. B Fluids 2018, 72, 432–448. [Google Scholar] [CrossRef]
- Vucheva, V.; Kolkovska, N. High order symplectic finite difference scheme for double dispersion equations. AIP Conf. Proc. 2021, 2321, 030037. [Google Scholar] [CrossRef]
- Yan, X.J.; Machado, J.A.T.; Baleanu, D. Exact Traveling-Wave Solution for Local Fractional Boussinesq Equation in Fractal Domain. Fractals 2017, 25, 1740006. [Google Scholar] [CrossRef]
- Danchin, R.; Paicu, M. Global Existence Results for the Anisotropic Boussinesq System in Dimension Two. Math. Model. Methods Appl. Sci. 2011, 21, 421–457. [Google Scholar] [CrossRef]
- Gastine, T.; Wicht, J.; Aurnou, J.M. Turbulent Rayleigh–Bénard convection in spherical shells. J. Fluid Mech. 2015, 778, 721–764. [Google Scholar] [CrossRef]
- Animasaun, I.L. Double diffusive unsteady convective micropolar flow past a vertical porous plate moving through binary mixture using modified Boussinesq approximation. Ain Shams Eng. J. 2016, 7, 755–765. [Google Scholar] [CrossRef]
- Weiss, S.; He, X.; Ahlers, G.; Bodenschatz, E.; Shishkina, O. Bulk temperature and heat transport in turbulent Rayleigh–Bénard convection of fluids with temperature-dependent properties. J. Fluid Mech. 2018, 851, 374–390. [Google Scholar] [CrossRef]
- Xi, H.D.; Zhou, Q.; Xia, K.Q. Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 2006, 73, 056312. [Google Scholar] [CrossRef]
- Lappa, M.; Gradinscak, T. On the oscillatory modes of compressible thermal convection in inclined differentially heated cavities. Int. J. Heat Mass Transf. 2018, 121, 412–436. [Google Scholar] [CrossRef]
- Ahlers, G.; He, X.; Funfschilling, D.; Bodenschatz, E. Heat transport by turbulent Rayleigh–Bénard convection for Pr≃0.8 and 3·1012≲Ra≲1015: Aspect ratio Γ = 0.50. New J. Phys. 2012, 14, 103012. [Google Scholar] [CrossRef]
- Ahlers, G.; Bodenschatz, E.; He, X. Logarithmic temperature profiles of turbulent Rayleigh–Bénard convection in the classical and ultimate state for a Prandtl number of 0.8. J. Fluid Mech. 2014, 758, 436–467. [Google Scholar] [CrossRef][Green Version]
- Parodi, A.; Emanuel, K.A.; Provenzale, A. Plume patterns in radiative–convective flows. New J. Phys. 2003, 5, 106. [Google Scholar] [CrossRef]
- Cavaleri, L.; Alves, J.H.; Ardhuin, F.; Babanin, A.; Banner, M.; Belibassakis, K.; Benoit, M.; Donelan, M.; Groeneweg, J.; Herbers, T.; et al. Wave modelling – The state of the art. Prog. Oceanogr. 2007, 75, 603–674. [Google Scholar] [CrossRef]
- Li, T.H. An analysis to a model of tornado. Z. Angew. Math. Phys. 2021, 73, 17. [Google Scholar] [CrossRef]
- Xiao-Jun, Y.; Baleanu, D.; Khan, Y.; Mohyud-Din, S.T. Local Fractional Variational Iteration Method for Diffusion and Wave Equations on Cantor Sets. Rom. J. Phys. 2014, 59, 36–48. [Google Scholar]
- Abu-Irwaq, I.; Alquran, M.; Jaradat, I.; Noorani, M.; Momani, S.; Baleanu, D. Numerical investigations on the physical dynamics of the coupled fractional boussinesq-burgers system. Rom. J. Phys. 2020, 65, 111. [Google Scholar]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Zel’dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High Temperature Hydrodynamic Phenomena; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Bluman, G.W.; Cole, J.D. The General Similarity Solution of the Heat Equation. J. Math. Mech. 1969, 18, 1025–1042. [Google Scholar]
- Barna, I.F. Self-Similar Solutions of Three-Dimensional Navier–Stokes Equation. Commun. Theor. Phys. 2011, 56, 745. [Google Scholar] [CrossRef]
- Barna, I.F.; Mátyás, L. Analytic solutions for the three-dimensional compressible Navier–Stokes equation. Fluid Dyn. Res. 2014, 46, 055508. [Google Scholar] [CrossRef]
- Barna, I.F.; Mátyás, L. Analytic self-similar solutions of the Oberbeck–Boussinesq equations. Chaos Solitons Fractals 2015, 78, 249–255. [Google Scholar] [CrossRef]
- Barna, I.F.; Mátyás, L.; Pocsai, M.A. Self-similar analysis of a viscous heated Oberbeck–Boussinesq flow system. Fluid Dyn. Res. 2020, 52, 015515. [Google Scholar] [CrossRef]
- Campos, D. (Ed.) Handbook on Navier–Stokes Equations; Nova Publishers: New York, NY, USA, 2017; Chapter 16; pp. 275–304. [Google Scholar]
- Barna, I.F.; Mátyás, L. Analytic Solutions of the Rotating and Stratified Hydrodynamical Equations. Asian J. Res. Rev. Phys. 2021, 4, 1426. [Google Scholar] [CrossRef]
- Barna, I.F.; Mátyás, L. Analytic solutions of a two-fluid hydrodynamic model. Math. Model. Anal. 2021, 26, 582–590. [Google Scholar] [CrossRef]
- Barna, I.F.; Bognár, G.; Guedda, M.; Hriczó, K.; Mátyás, L. Analytic Self-Similar Solutions of the Kardar–Parisi–Zhang Interface Growing Equation with Various Noise Terms. Math. Model. Anal. 2020, 25, 241–256. [Google Scholar] [CrossRef]
- Barna, I.F.; Bognár, G.; Mátyás, L.; Guedda, M.; Hriczó, K. Travelling-wave solutions of the Kardar–Parisi–Zhang interface growing equation with different kind of noise terms. AIP Conf. Proc. 2020, 2293, 280005. [Google Scholar] [CrossRef]
- Provis, D.G.; Radok, R. (Eds.) Waves on Water of Variable Depth; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1977; Volume 64. [Google Scholar]
- Staziker, D.J.; Porter, D.; Stirling, D.S.G. The scattering of surface waves by local bed elevations. Appl. Ocean. Res. 1996, 18, 283–291. [Google Scholar] [CrossRef]
- Porter, R.; Porter, D. Water wave scattering by a step of arbitrary profile. J. Fluid Mech. 2000, 411, 131–164. [Google Scholar] [CrossRef]
- Liggett, J.A.; Liu, P.L.F. Basic Principles and Applications; Topics in Boundary Element Research, Chapter Applications of Boundary Element Methods to Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 1984; Volume 1, pp. 78–96. [Google Scholar]
- Wang, C.D.; Meylan, M.H. The linear wave response of a floating thin plate on water of variable depth. Appl. Ocean. Res. 2002, 24, 163–174. [Google Scholar] [CrossRef]
- Chowdhury, D.; Debsarma, S. Nonlinear Evolution Equations of Co-propagating Waves over Finite Depth Fluid. Water Waves 2019, 1, 259–273. [Google Scholar] [CrossRef]
- Manafian, J.; Mohammed, S.A.; Alizadeh, A.; Baskonus, H.M.; Gao, W. Investigating lump and its interaction for the third-order evolution equation arising propagation of long waves over shallow water. Eur. J. Mech. B/Fluids 2020, 84, 289–301. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Manafian, J.; Baskonus, H.M.; Lakestani, M. Solitary wave solitons to one model in the shallow water waves. Eur. Phys. J. Plus 2021, 136, 337. [Google Scholar] [CrossRef]
- Lakestani, M.; Manafian, J. Application of the ITEM for the modified dispersive water-wave system. Opt. Quantum Electron. 2017, 49, 128. [Google Scholar] [CrossRef]
- Shen, G.; Manafian, J.; Huy, D.T.N.; Nisar, K.S.; Abotaleb, M.; Trung, N.D. Abundant soliton wave solutions and the linear superposition principle for generalized (3+1)-D nonlinear wave equation in liquid with gas bubbles by bilinear analysis. Results Phys. 2022, 32, 105066. [Google Scholar] [CrossRef]
- Qian, Y.; Manafian, J.; Mohyaldeen, S.Y.; Esmail, L.S.; Gorovoy, S.A.; Singh, G. Multiple-order line rogue wave, lump and its interaction, periodic, and cross-kink solutions for the generalized CHKP equation. Propuls. Power Res. 2021, 10, 277–293. [Google Scholar] [CrossRef]
- Khakimzyanov, G.; Dutykh, D.; Fedotova, Z.; Gusev, O. Dispersive Shallow Water Waves; Lecture Notes in Geosystems Mathematics and Computing; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Barna, I.F.; Kersner, R. Heat conduction: A telegraph-type model with self-similar behavior of solutions. J. Phys. A Math. Theor. 2010, 2010. 43, 375210. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Trichtchenko, O.; Deconinck, B.; Wilkening, J. The instability of Wilton ripples. Wave Motion 2016, 66, 147–155. [Google Scholar] [CrossRef]
- Paldor, N. Shallow Water Waves on the Rotating Earth; SpringerBriefs in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Bognár, G.; Hriczó, K. Ferrofluid Flow in Magnetic Field Above Stretching Sheet with Suction and Injection. Math. Model. Anal. 2020, 25, 461–472. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).