Generalized Johnson Distributions and Risk Functionals
Abstract
:1. Introduction: Generalized Johnson Distributions and Their Use
2. Parameter Estimation
3. Thresholds and Endpoints
4. Approximation of Risk Functionals
5. Recommendations and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- 1.
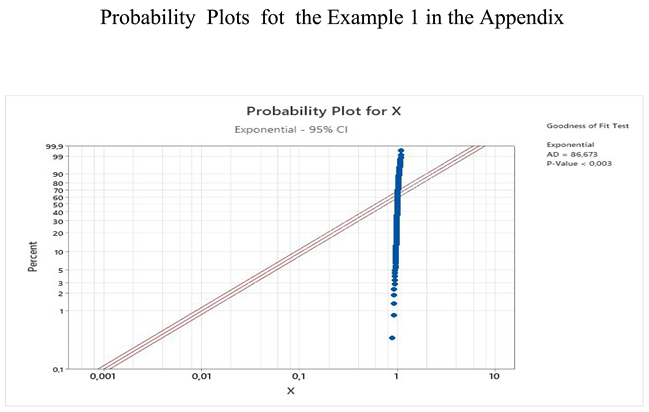
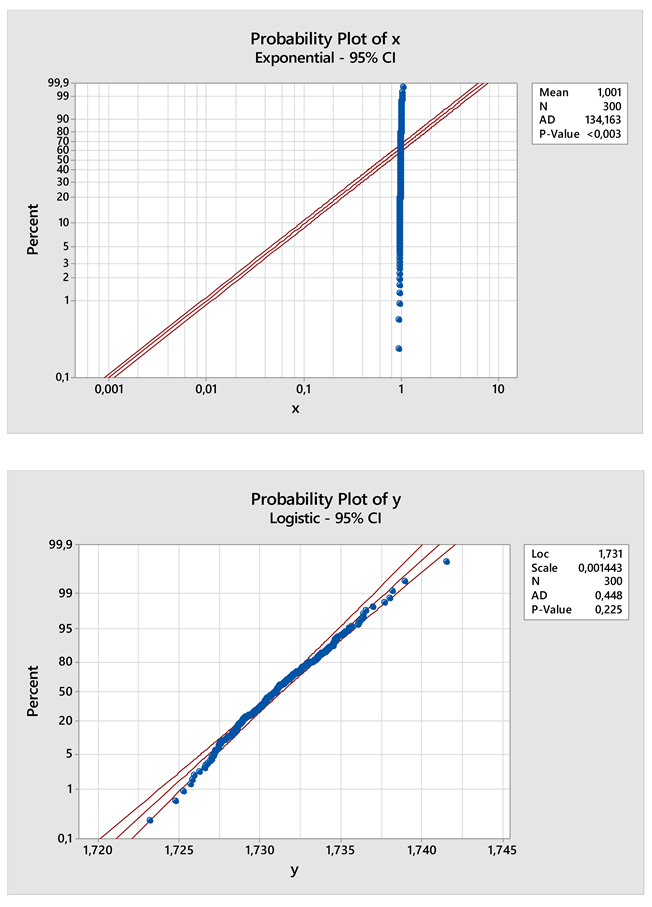
- The sample of the returns’ variable X is ’marginally’ well-fitted on any normal distribution.
- 2.
- The sample of the returns’ variable X is out-of-fit, with respect to the exponential distribution.
- 3.
- The sample of the Johnson transformation , where is well-fitted on the logistic distribution. X is the random variable of the sample above, namely, the sample of the returns’ variable.

References
- Johnson, N.L. Systems of Frequency Curves Generated by Methods of Translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef] [PubMed]
- Johnson, N.L. Bivariate Distributions Based on Simple Translation Systems. Biometrika 1949, 36, 297–304. [Google Scholar] [CrossRef] [PubMed]
- Corlu, C.G.; Corlu, A. Modelling exchange rate returns: Which flexible distribution to use? Quant. Financ. 2015, 15, 1851–1864. [Google Scholar] [CrossRef]
- Simonato, J.G. The Performance of Johnson distributions for Computing value at risk and expected shortfall. J. Deriv. 2011, 19, 7–24. [Google Scholar] [CrossRef]
- Lien, D.; Stroud, C.; Ye, K. Comparing VaR Approximation Methods that Use the First Four Moments as Inputs. Commun. Stat. Simul. Comput. 2016, 45, 491–503. [Google Scholar] [CrossRef]
- Tuenter, H.J.H. An algorithm to determine the parameters of SU-curves in the johnson system of probabillity distributions by moment matching. J. Stat. Comput. Simul. 2001, 70, 325–347. [Google Scholar] [CrossRef]
- Huang, Z.; Kwok, Y.K. Efficient risk measures calculations for generalized CreditRisk+ models. Int. J. Theor. Appl. Financ. 2021, 24, 2150012. [Google Scholar] [CrossRef]
- Artzner, P.; Delbean, F.; Eber, J.M.; Heath, D. Coherent Measures of Risk. Math. Financ. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Nadarajah, S.; Zhang, B.; Chan, S. Estimation methods for expected shortfall. Quant. Financ. 2014, 14, 271–291. [Google Scholar] [CrossRef]
- Inui, M.L.; Kijima, M. On the significance of expected shortfall as a coherent risk measure. J. Bank. Financ. 2005, 29, 853–864. [Google Scholar] [CrossRef]
- Cooray, K.; Ananda, M.M.A. Modeling actuarial data with a composite LognormalPareto model. Scand. Actuar. J. 2005, 5, 321334. [Google Scholar]
- Pigeon, M.; Denuit, M. Composite Lognormal–Pareto model with random threshold. Scand. Actuar. J. 2011, 3, 177–192. [Google Scholar] [CrossRef]
- Scollnik, D.P.M. On composite Lognormal-Pareto models. Scand. Actuar. J. 2007, 1, 20–33. [Google Scholar] [CrossRef]
- Akatov, N.; Mingaleva, Z.; Klaĉková, I.; Galieva, G.; Shaidurova, N. Expert Technology for Risk Management in the Implementation of QRM in a High-Tech Industrial Enterprise. Manag. Syst. Prod. Eng. 2019, 27, 250–254. [Google Scholar] [CrossRef]
- Hanggraeni, D.; Ślusarczyk, B.; Sulung, L.A.K.; Subroto, A. The impact of internal, external and enterprise risk management on the performance of micro, small and medium enterprises. Sustainability 2019, 11, 2172. [Google Scholar] [CrossRef]
- Mingaleva, Z.; Akatov, N.; Butakova, M.; Akatov, N.; Butakova, M. A syndinic approach to enterprise risk management. In Lecture Notes in Networks and Systems; LNNS; Springer: Cham, Switzerland, 2022; Volume 315, pp. 293–305. [Google Scholar]
- Anderson, T.W.; Darling, D.A. Asymptotic theory of certain “goodness-of-fit” criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A Test of Goodness-of-Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Resnick, S.I. Tail Equivalence and Its Applications. J. Appl. Probab. 1971, 8, 136–156. [Google Scholar] [CrossRef]
- Acerbi, C.; Tasche, D. On the coherence of expected shortfall. J. Bank. Financ. 2002, 26, 1487–1503. [Google Scholar] [CrossRef]
- Ahmadi- Javid, A. Entropic Value-at-Risk: A New Coherent Risk Measure. J. Optim. Theory Appl. 2012, 155, 1105–1123. [Google Scholar] [CrossRef]
- Cantelli, F.P. Sulla determinazione empirica delle leggi di probabilitá. Giorn. Ist. Ital. Attuari 1933, 4, 421–424. [Google Scholar]
- Glivenko, V. Sulla determinazione empirica delle leggi di probabilitá. Giorn. Ist. Ital. Attuari 1933, 4, 92–99. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Floros, C.; Gkillas, K.; Kountzakis, C. Generalized Johnson Distributions and Risk Functionals. Mathematics 2022, 10, 3200. https://doi.org/10.3390/math10173200
Floros C, Gkillas K, Kountzakis C. Generalized Johnson Distributions and Risk Functionals. Mathematics. 2022; 10(17):3200. https://doi.org/10.3390/math10173200
Chicago/Turabian StyleFloros, Christos, Konstantinos Gkillas, and Christos Kountzakis. 2022. "Generalized Johnson Distributions and Risk Functionals" Mathematics 10, no. 17: 3200. https://doi.org/10.3390/math10173200
APA StyleFloros, C., Gkillas, K., & Kountzakis, C. (2022). Generalized Johnson Distributions and Risk Functionals. Mathematics, 10(17), 3200. https://doi.org/10.3390/math10173200






